Log-linear Dynamic Inversion Control with Provable Safety Guarantees in Lie Groups

Based on the log-linear property, we can log-linearize the nonlinear system with feedback control, bounded disturbance, and noise to an exact linear bounded input system using the derivative of the exponential map. The invariant set for the linear bounded input system can be found efficiently employing LMIs.

Consider the dynamics of two mixed-invariant vector fields, where $X\in G$ is the state of the vehicle and $\bar{X}\in G$ is the state of the reference trajectory:

where $l,r,\bar{l},\bar{r}\in\mathbb{R}^{n}$ are inputs of the systems and may be functions of time. The relationship between the two inputs is $l=\bar{l}+u_{l},r=\bar{r}+u_{r}$. $u_{l}$ is the deviation of the system from the reference left-invariant vector field, $l$, and $u_{r}$ is the deviation of the system from the reference right-invariant vector field, $r$. The left- and right-invariant errors, $\eta_{l},\eta_{r}\in G$ are defined as follows [13]:

In this paper, we are interested in deriving the exact log-linearization for the error dynamics, $\dot{\eta_{l}},\dot{\eta_{r}}$, of mixed-invariant systems, and designing a robust controller with provable safety guarantees.

Based on 4 and 5, we have an exact solution for log-linearization of the error dynamics of mixed-invariant systems. Since the log-linearization causes nonlinear input distortion, $U_{l}$ and $U_{r}$, the log-linear dynamics in the Lie algebra are nearly linear for a small deviation from the reference trajectory.

For control, 4 and 5 suggest a direct approach for dynamic inversion of the log-linearized mixed-invariant vector field dynamics. We will focus on 4 but this can also be extended to 5.

When using dynamic inversion control, it is important to determine if inputs are saturated in the controller. Since we use a state feedback control law, this can be efficiently checked and verified using the invariant set of the states.

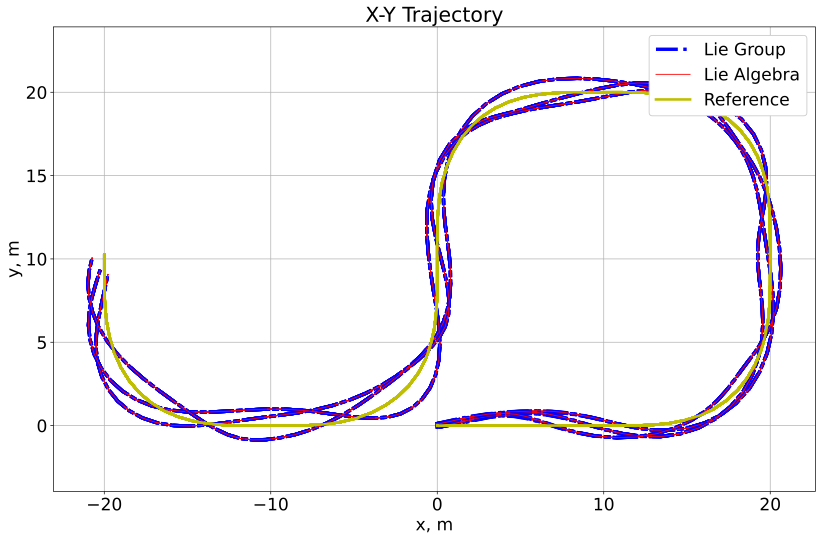
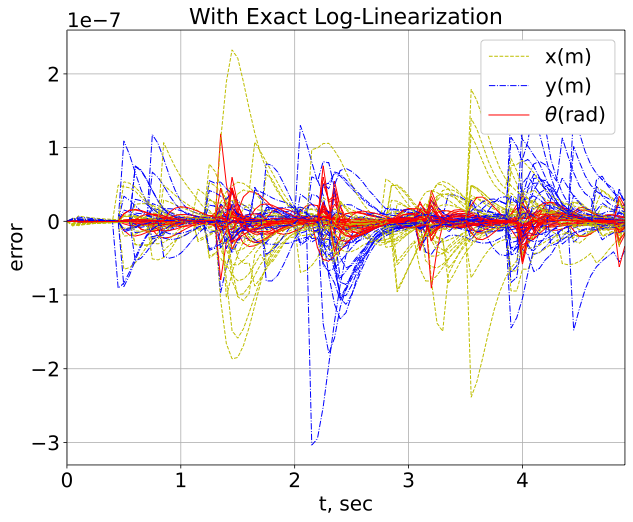
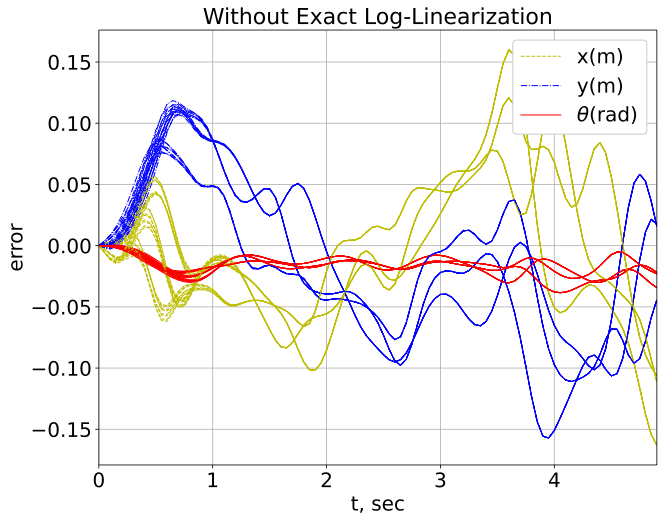
Figure 1 shows a 2D example of the bijection between the vehicle trajectories in the $SE(2)$ Lie group and the $\mathfrak{se}(2)$ Lie algebra, which are simulated with sinusoidal disturbances of fixed magnitude at varying frequencies. In order for a bijection to exist, the exponential map must be injective and surjective, which holds if the domain of the Lie algebra is restricted to $[-\pi,\pi]$ [24]. Effectively meaning that our control law will disregard multiple rotations, which is the intended behaviour. If the invariant set in the Lie algebra extends beyond the domain of $[-\pi,\pi]$, this would indicate a possibly instability through a continuous spinning motion. Thus, the LMI approach is invalidated, as the linear dynamics do not consider the angle wrapping. The figure on the left in Fig. 2 shows that the log-linearized system dynamics in the Lie algebra do not deviate from the closed loop mixed-invariant system dynamics when the exact log-linearization is applied (the shown deviation can be arbitrarily reduced using numerical tolerances); however, there are significant deviations from the closed loop mixed-invariant system if our log-linearization is not applied (figure on the right). Therefore, we numerically demonstrate 4 and 5 by showing that a bijection exists between the trajectories in the Lie group and Lie algebra even in the presence of disturbance and control feedback, given a domain sufficiently close to the reference trajectory (e.g. avoiding angle wrapping). This is a useful result, as the Lie algebra is a vector space that is more convenient for analysis than the Lie group which is a nonlinear manifold [24].

Consider the kinematic aircraft model evolving on a 2D plane, as follows:

where $\theta\in[-\pi,\pi]$ denotes the heading angle, $p_{x}$ and $p_{y}$ denote the position. $\omega$ represents the angular velocity, $v_{x}$ and $v_{y}$ represent the forward and side translational velocity respectively. We assume our kinematic aircraft model as a holonomic model due to the side-slip angle of the aircraft and mentioned in [27].

The kinematic aircraft model in 8 can be embedded in the $SE(2)$ Lie group in 9, a matrix Lie group. Special in the Special Euclidean group indicates that all matrices have determinant $1$. A Lie group is a group that is also a smooth manifold. The associated Lie algebra is a vector space tangent to the Lie group at the identity [30]. A Lie group and its Lie algebra are closely related, which allows calculations in one to be mapped into the other. The exponential map maps the Lie algebra to the Lie group and the logarithm map, the inverse of the exponential map, maps the Lie group to the Lie algebra [24].

The corresponding left-invariant system dynamics [14, 15, 19, 17] of the 2D holonomic aircraft problem, which is a mixed-invariant system with the right-invariant vector field, $r$, equal to zero, is given by:

where $X$ represents the state of the 2D holonomic aircraft in the $SE(2)$ Lie group. Note that $l\in\mathbb{R}^{3}$ may be a function of time and represents the input of the vehicle, including feedback control and disturbances. The $SE(2)$ Lie group may be represented by matrices of the form:

where $R\in SO(2)$, which is an element of the 2D rotation group, and $p=\begin{bmatrix}p_{x}&p_{y}\end{bmatrix}^{T}\in\mathbb{R}^{2}$. The $SE(2)$ Lie group is a semi-direct product of the $SO(2)$ and $\mathbb{R}^{2}$ [24].

The corresponding Lie algebra, $\mathfrak{se}(2)$ may be represented by matrices of the form:

where $x=\begin{bmatrix}v&\omega\end{bmatrix}^{T}$ is the element in the Lie algebra. $\omega_{\times}$ is the corresponding skew-symmetric matrix of $\omega\in\mathbb{R}$, such that $\omega_{\times}=-\omega_{\times}^{T}$, $v=\begin{bmatrix}v_{x}&v_{y}\end{bmatrix}^{T}\in\mathbb{R}^{2}$. In Lie group theory, the adjoint representation [24] transports a Lie algebra element from one tangent space to another. Here, for an element $x$ of the $\mathfrak{se}(2)$ Lie algebra, we use $ad_{x}$ to represent the adjoint in the Lie algebra, which can be written as:

The 2D kinematics aircraft kinematics can be embedded in the $SE(2)$ Lie group as $\dot{X}=X[l]^{\wedge}$. We also consider the reference kinematics embedded in the $SE(2)$ Lie group differential equation, as $\dot{\bar{X}}=\bar{X}{[\bar{l}]}^{\wedge}$, where $\bar{X}$ denotes the state of the reference trajectory, and $\bar{l}$ denotes the input of the reference trajectory, and may be functions of time to account for non-trivial reference trajectories.

As we mention in the previous section, the relationship between $l$ and $\bar{l}$ is $l=\bar{l}+u_{l}$, here, we consider $u_{l}=u+w$, where $u$ is the feedback control input, and $w$ is the disturbance. The left-invariant error between our kinematic aircraft model and the reference kinematics is $\eta_{l}=X^{-1}\bar{X}$. From 4 and 6, the error dynamics in the Lie algebra can be written as:

where $u=U^{-1}BK\zeta$ and $\zeta\equiv\begin{bmatrix}\zeta_{x}&\zeta_{y}&\zeta_{\theta}\end{bmatrix}^{T}$.

For the $SE(2)$ Lie group, the inverse of the nonlinear input distortion matrix, $U^{-1}$, can be written in a series-form function and a closed-form matrix, which is found by reducing the sine and cosine series:

where $a=(-2\zeta_{\theta}\cos(\zeta_{\theta})+2\zeta_{\theta}-2\sin(\zeta_{\theta})+\sin(2\zeta_{\theta}))$ and $b=(-4\cos(\zeta_{\theta})+2\cos(\zeta_{\theta})+3)$. The determinant of $U^{-1}$ is $\det(U^{-1})=\frac{2(\cos(\zeta_{\theta})-1)}{\zeta_{\theta}^{2}}=-1+\frac{\zeta_{\theta}^{2}}{12}-\frac{\zeta_{\theta}^{4}}{360}+O(\zeta_{\theta}^{6})$, since we limit $\zeta_{\theta}\in[-\pi,\pi]$, the determinant will never be zero, $U^{-1}$ is always invertible. Therefore, the closed-form matrix of $U$ for the $SE(2)$ Lie group is:

where $c=\frac{\zeta_{\theta}\sin{\left(\zeta_{\theta}\right)}}{2\left(\cos{\left(\zeta_{\theta}\right)}-1\right)}$ and $d=\frac{\zeta_{\theta}}{2}$.

The invariant set for a system can be calculated by finding an upper bound for the singular value of the nonlinear input distortion matrix, $U$, over the invariant set. The nonlinear input distortion, $U$, depends on the error state, $\zeta=[\zeta_{x},\zeta_{y},\zeta_{\theta}]^{T}$. If there exists an invariant set, since the invariant set is a set of the error states, $U$ will depend on the invariant set itself. And the calculation of the invariant set also depends on the singular value of $U$, we propose a Log-linear LMI-based iterative method to compute the invariant set in Algorithm 1. An invariant set calculated by this algorithm is shown in Figure 3.

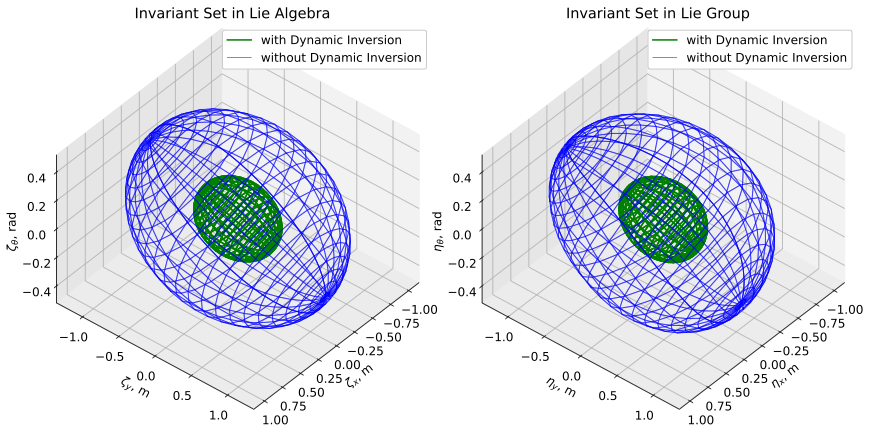
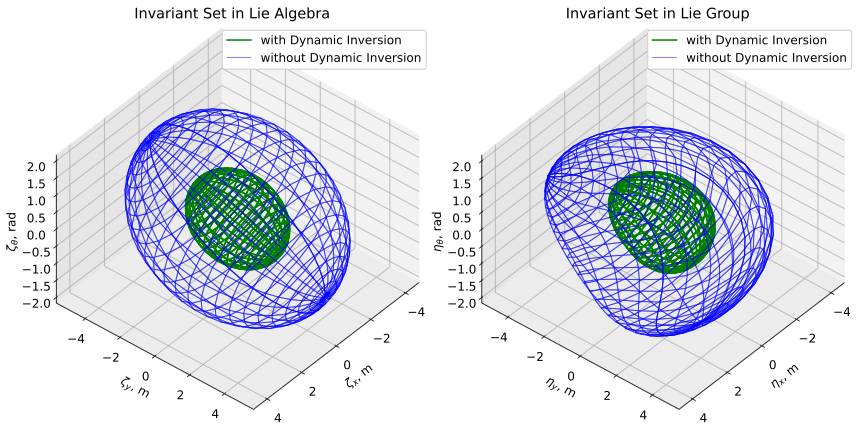
Since the inputs of the reference trajectory may be functions of time, we use the LMI to calculate the invariant set for a linear polytopic system with bounded disturbances [12]. The bounds of the inputs to calculate the invariant set are based on the bounds of the reference inputs, where $\bar{v}_{x}\in[18,20]$ m/s, $\bar{v}_{y}=0$ m/s, and $\bar{\omega}\in[-\pi/2,\pi/2]$ rad/s. We use the Linear-Quadratic-Regular (LQR) method to find the feedback controller for the log-linearized system in the $\mathfrak{se}(2)$ Lie algebra. After employing our iterative method, Algorithm 1, to find the desired maximum singular value of $U$, the final result of the invariant set in the Lie algebra and the Lie group is shown in Fig. 3. The figures show the invariant set with small initial states in the $SE(2)$ Lie group, $[x_{0},y_{0},\theta_{0}]=[0.1,0.1,\pi/100]$. The invariant set in the Lie group is constructed by applying the exponential map from the set in the Lie algebra.

If the control input does not employ dynamic inversion, the control input $u$ in 6 becomes $BK\zeta$, and the error dynamics in the Lie algebra in 13 can be rewritten as:

Here, we use the $SE(2)$ example to compare the difference between the two controllers. For the control input without dynamics inversion, we consider the nonlinear term of the control input as a bounded input in the LMI calculation. Blue lines in Fig. 3 show the result of the invariant set for the controller without dynamic inversion. Since the nonlinear term of the control input is considered a bounded input, the invariant set has a larger tracking error bound than the controller with dynamic inversion. Comparing the invariant sets in Fig. 3, we can see that the invariant set is approximately twice as large in the case of the control input without dynamic inversion compared to the case with dynamic inversion. Therefore, the invariant set has a smaller tracking error bound with our designed controller.

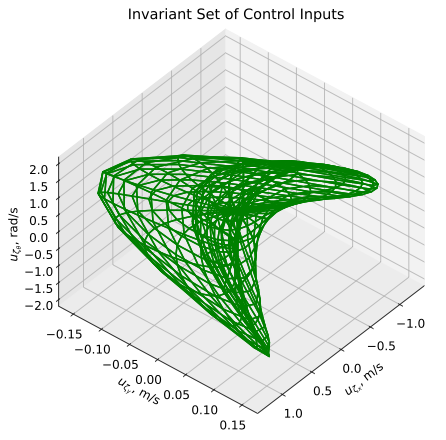
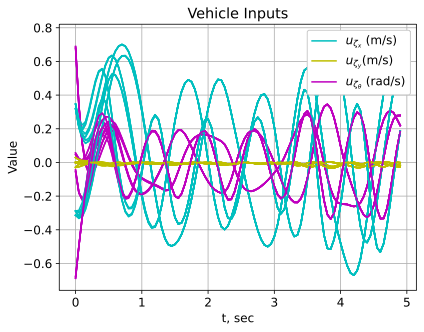
The Lyapunov function in the LMI approach is an ellipsoid, which is the shape of the invariant set for the log-linearized system in the $\mathfrak{se}(2)$ Lie algebra as shown on the left of Fig. 3 with green lines. The invariant sets in the $SE(2)$ Lie group, which are mapped from the invariant sets in the $\mathfrak{se}(2)$ Lie algebra using the exponential map, are shown on the right of Fig. 3 with green lines. Since the invariant set in the $SE(2)$ Lie group is not an ellipsoid after mapping, as shown in Fig. 3, and is in the vehicle body frame; therefore, the invariant set must be rotated along the trajectory to create flow pipes. The left figure in Fig. 4 shows the invariant set of our log-linear dynamic inversion control inputs for the small disturbance case, the saturation bounds for each direction are $u_{\zeta_{x}}\in[-1.25,1.25]$ m/s, $u_{\zeta_{y}}\in[-0.16,0.16]$ m/s, and $u_{\zeta_{\theta}}\in[-1.92,1.92]$ rad/s. The right figure in Fig. 4 shows the time history plot of the control inputs for the simulated trajectories with sinusoidal and square wave disturbances in the small disturbance case, and each control input stays within the saturation bound for all time.

To verify the safety properties for the UAM mission, we construct flow pipes along a reference trajectory. Any Lyapunov function will be sufficient for our method and we follow a general approach of the flow pipes creation in [4]. To construct the flow pipe, we first propagate the reference trajectory using polynomial trajectory planning for a fixed time interval and compute the interval hull of the reference trajectory. The interval hull is the smallest box enclosing the set for the propagation duration. Since our invariant set depends on the direction of the reference trajectory, we sweep the invariant set from the minimum rotational angle to the maximum rotational angle in that time interval. Using the swept invariant set and interval hull, we then compute the convex hull for the flow pipe segment using the Minkowski sum [33]. Therefore, the flow pipe for the trajectory can be constructed by repeating the above processes for the next time interval.

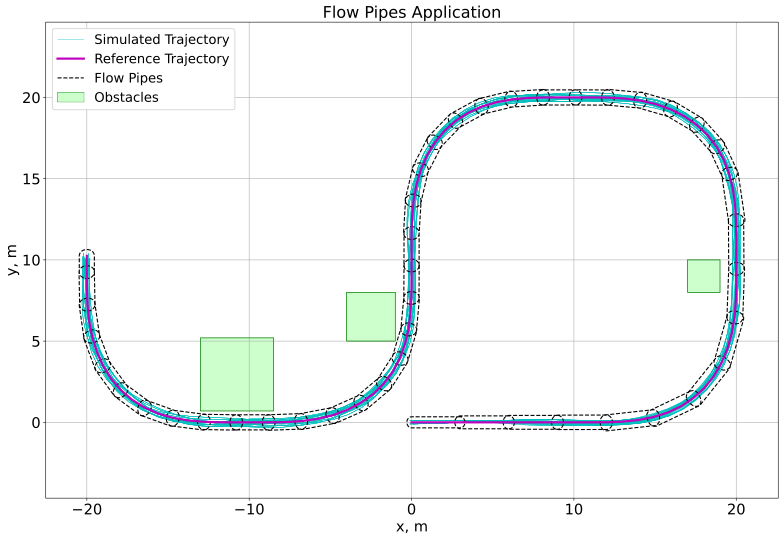
Figure 5 shows the application of flow pipes to the UAM problem. The green squares represent collision zones or obstacles (e.g., buildings) that the vehicle needs to avoid. Here, we simulate both sinusoidal and square wave wind disturbances. We simulate two different scenarios for the vehicle. The first scenario is simulated with small wind disturbances with a magnitude of $1$ m/s, which is shown at the top of Fig. 5. We can see that the green collision zones, obstacles, and the flow pipes do not intersect; therefore, we can confirm the safety of the vehicle, since the simulation shows that the vehicle won’t hit the buildings during the mission. Another scenario is simulated with large wind disturbances with a magnitude of $5$ m/s, which is shown at the bottom of Fig. 5. We can see that the buildings and the flow pipes are now intersecting. Therefore, we are able to confirm that it is not safe for the vehicle to conduct the mission with wind disturbances of this magnitude. We can also see that some simulated trajectories collide with obstacles and the mission is therefore unsafe.