Localized modes and dark solitons sustained by nonlinear defects
Abstract
Dark solitons and localized defect modes against periodic backgrounds are considered in arrays of waveguides with defocusing Kerr nonlinearity constituting a nonlinear lattice. Bright defect modes are supported by local increase of the nonlinearity, while dark defect modes are supported by a local decrease of the nonlinearity. Dark solitons exist for both types of the defect, although in the case of weak nonlinearity they feature side bright humps making the total energy propagating through the system larger than the energy transferred by the constant background. All considered defect modes are found stable. Dark solitons are characterized by relatively narrow windows of stability. Interactions of unstable dark solitons with bright and dark modes are described.
Periodic modulations of parameters and localized defects embedded in a guiding medium are two common tools for manipulating, confining, and directing the light. When guiding media are nonlinear these factors can be introduced as variations of either linear refractive index, or Kerr coefficients, or both. Nowadays the effect of linear and nonlinear lattices on nonlinear wave propagation is very-well understood and particularly well studied in optical applications REVNL and in the physics of Bose-Einstein condensates BECS ; BECS1 (see also Malomed for specific description of the soliton management). Due to versatility of those tools, the combined effect of linear localized defects and linear lattices has been thoroughly studied too. Focusing on continuous models (for a review on discrete systems see e.g. Tsironis ; review ), bright and dark solitons have been described in linear lattices with defects Yang2005 ; BKP1 ; BKP2 ; DS2 , in nonlinear lattices with linear defects DEF5 ; DEF6 , in media with periodically varying saturable nonlinearity in the presence of defects Yang2011 , in periodic media with a dissipative KKV1 and parity-time symmetric PT1 ; PT2 defects, combined linear and nonlinear lattices NZB ; NPNL2 , as well as at the interface between dissimilar nonlinear lattices NPNL1 . Waves in pure nonlinear lattices (without defects) were also studied theoretically Berger ; Stuart ; BECS2 ; Abdullaev2005 ; Fibich ; Abdullaev2008 ; NL2 ; Cuevas ; Marek ; NL2019 and observed experimentally nonlin_latt1 . In spite of the considerable attention to the effect of the nonlinear lattices, modes in pure nonlinear lattices with a (nonlinear) defect remain unexplored. This determines our main goal, that is description of defect modes sustained by nonlinear defects of the periodically varying defocusing Kerr nonlinearity. The linear properties of the medium are considered homogeneous. We are interested in nonlinear modes sustained by localized defects against nonzero backgrounds. More specifically we describe the shapes and stability of dark solitons, defect modes, as well as coupled states of defects modes and dark solitons propagating in such media.
We consider a paraxial beam polarized along -axis and propagating along direction. Denoting the dimensionless field amplitude by , the model equation can be written as
| (1) |
Here describes periodic modulation of the nonlinearity (a nonlinear lattice). The function models the nonliner lattice, while describes a localized defect or several defects. It will be assumed that the nonlinearity is either defocusing or eventually can acquire zero values. Respectively, we require , and with at . Thus, . In the absence of the defect both the amplitude and the period of the nonlinear lattice can be scaled out. The scaling of the amplitude and of the transverse width of the defect can also be done in the absence of the lattice. When both types of the modulation of the nolinearity are present the spatial scale and the amplitude of one of them is fixed. Below we fix the scales by setting . For this choice the medium becomes purely linear in the points where is an integer.
We consider stationary solutions of Eq. (1) , where is the propagation constant, satisfying nonzero boundary conditions
| (2) |
where and is a periodic solution of the equation
| (3) |
with the period 1: . One can show that the background solution can be chosen as pure real (or having an unessential constant phase). Since one readily concludes that solutions exist only for . We also mention that Eq. (3) admits singular periodic solutions. In particular, for the propagation constant , we obtain . The consideration here is restricted only to bounded background solutions with . The stability properties of such background solution are established in Stuart .
A single defect having a strength and width , and centered at , will be modeled by the Heaviside step-function : . Below we address two situations, where (strong nonlinearity defect) and (weak nonlinearity defect). In order to characterize families of nonlinear modes we introduce the quantity
| (4) |
characterizing ”excess” of the transferred by these modes with respect to the power of the background.
We start by considering local decrease of the defocusig nonlinearity. In Fig. 1 we show results for representative intensity distributions of the bright defect modes obtained subject to the boundary condition (2) with (left column) and their families (yellow lines in the middle columns), which are verified to be stable. The stability of the modes has been verified using both the standard linear stability analysis and the direct propagation with initial perturbation in a form of the random noise (whose amplitude is of the solution amplitude). For linear stability analysis we consider the perturbed field , where are small perturbations, is a complex spectral parameter, and asterisk denotes complex conjugation. Respectively we solve the linear eigenvalue problem:
| (5) |
The solution is stable when is pure imaginary and unstable otherwise.
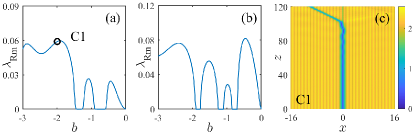
We investigated different defect widths and different locations of the defects as illustrated in Fig. 1. Generally speaking, the shape of the defect does not follow exactly the profile of the nonlinearity modulation: in panel (a1) one observes change from the single hump to double hump shapes of the defect mode when the the absolute value of the propagation constant increases. Thus at sufficiently small the pick intensity is achieved in the local maximum of the defocusing nonlinearity. In Figs. 1 (b1) and (c1) we show bright defect modes at different widths of the defects. Panel (d1) illustrates a stable asymmetric mode supported by asymmetric defect. Interestingly, at the same value of the propagation constant the asymmetric mode has appreciably large amplitude and the intensity almost two times bigger than the symmetric mode sustained by the defect of the same width (cf. the modes and intensities on the upper and lower panels of Fig. 1). All bright modes obtained in the interval were found stable.
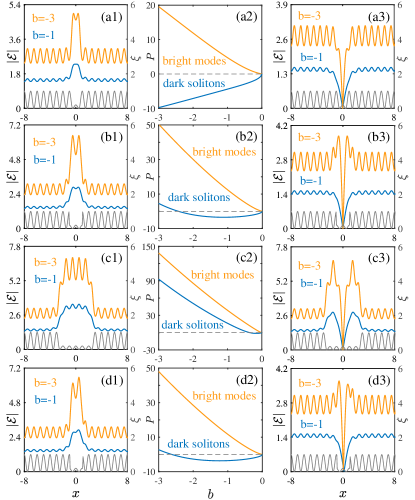
In the right column of Fig. 1 we show dark soliton solutions sustained by the weak-nonlinearity defects and obtained subject to boundary conditions (2) with . As one could expect, dark soliton families start with powers decaying with absolute values of the negative propagation constant (the middle column of Fig. 1). The slope of however changes as increases (see in the non-monotonous families of dark solitons in panels (b2), (c2), and (d2) of Fig. 1) and below some value of the ”excess” power of a dark mode becomes positive. The increase of is explained by the change of the soliton shapes with : we observe that black solitons feature relatively large energy humps (Figs. 1 (b3) and d(3)). The humps are out of phase, and thus the profile of the dark soliton can be viewed as a dipole soliton against a background. The positive power propagating in the area of the bright humps grows with and at some point it overpasses the negative power excess of the central dark domain. Such solitons are beams with side power picks. When the defect is asymmetric, the asymmetry of the soliton shape is more pronounced at large [see Fig. 1 (d3)].
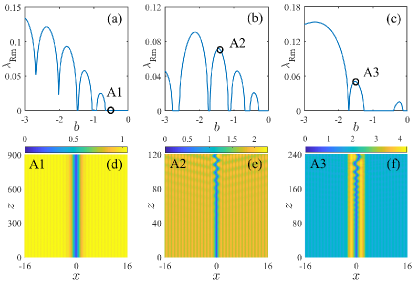
In the upper row of Fig. 2 we show the instability increments of the branches of dark solitons shown in Fig. 1 . The distribution of the stability domains depends on the width of the defect. Dark solitons feature some stability domains. The characteristic scenarios of the development of the oscillatory instability of dark solitons are clearly displayed.
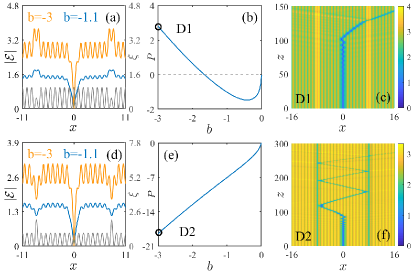
Now we turn to coupled states of dark solitons and bright defect modes, examples of which are shown in Fig. 3. One can show that there is a minimal distance between the zero of a dark soliton and the nearest maximum of the defect mode (we call them and respectively). Mathematically, it is obtained from a simple upper bound on the derivative of the field, that follows from (1). Recalling that the field is real, and considering (the case is treated similarly) we obtain:
| (6) |
where , and we used that as well as the fact that . Thus
| (7) |
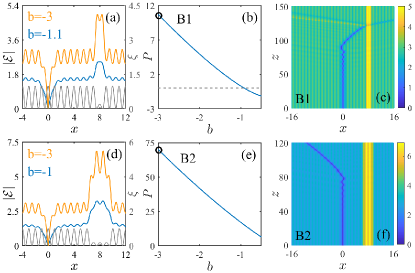
Due to the presence of a dark soliton, the coupled states bifurcate starting from finite negative value of the propagation constant with either negative [Fig 3 (b)] or positive [Fig 3 (e)] power depending on the width of the defect (The larger , the larger the maximal power of these coupled state). In Figs. 3 (c) and (f) we show unstable dynamics of the coupled dark soliton and bright modes. Being initially perturbed by small random perturbation, a dark soliton after an initial interval of developing instability starts motion either towards the bright mode (the latter being trapped by the local decrease of the nonlinearity) as illustrated in Fig. 3 (c) or outwards the bright modes, as shown in Fig. 3 (f). After interaction with the bright defect mode the dark soliton is split in backward propagating small-amplitude bright soliton against a background and a small-amplitude dark pulse moving outwards the defect in the positive direction. This type of evolution is illustrated in Fig. 3 (c).
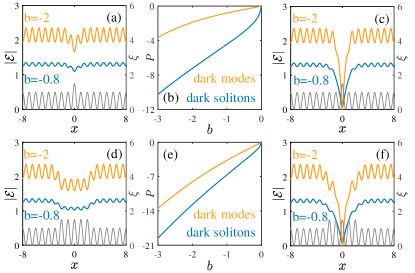
Turning to a strong nonlinearity defect, i.e., to a defect where the nonlinear lattice has local increase of the amplitude, in Fig. 4 we show representative examples of defect modes (left column) and dark solitons (right column). As before, the defect modes and solitons are subject to the boundary conditions (2) with and , respectively. The respective families of the solutions are shown in the middle column. Now the defect modes represent local decrease of the field amplitude, i.e., they are ”dark”, while dark solitons do not feature bright humps at any intensity of the background (cf. the Figs. 4 (c), (f) and Figs. 1 (b3), (c3), and (d3)).
Like in the case of weak nonlinearity defect, the dark defect modes are stable for the whole domain shown in Figs. 4 (b) and (e), while the dark soliton is stable only in small intervals of the propagation constant, featuring instability in the small-amplitude (small ) limit. Typical example of the evolution of the unstable dark soliton is shown in Fig. 5 (c).
Finally, in Fig. 6 we addressed the cases of nonlinear lattices with two identical defects, of weak nonlinearity (upper row) and strong nonlinearty (bottom row) where a dark soliton is created in the central part having no defect. Unlike in all above cases, now the dark soliton is centered at a regular lattice site, i.e., at a the local maximum of the nonlinear lattice, exactly in the middle between the defect modes (similar behaviour, not shown here, we also observed for dark solitons centered at the zero at the points where the potential is exactly zero). The upper row illustrates the complex of a dark soliton with two bright defects. The family of such complexes behave similarly to the family of dark solitons on the defect local minimum (cf. Fig. 6 (b) and Figs. 1 (b2), (d2)) although the change of the sign of now is due to the bright defect modes, while bright side humps observed for a single soliton (see the right column of Fig. 1) are not observed. Initial perturbation due to oscillatory instability results in motion of a dark soliton to towards one of the defect modes. The dynamics of the interaction of the dark soliton with the mode is the same as observed above (in Fig. 3 (c)).
When an unstable dark soliton is created between two dark defect modes, at sufficiently large nonlinearity it can be reflected by defect modes, thus manifesting trapped oscillatory motion as shown in Fig. 6 (f). After loosing energy due to radiation, at some instant (approximately at in Fig. 6 (f)), passes through the defect mode.
To conclude we have reported the localized (defect) modes and dark solitons on the defects of the nonlinear lattices. Such solitons and modes are created against a stable periodic background sustained by the periodically modulated nonlinearity. While dark solitons and defect modes separately can also be obtained in a homogeneous medium, their coupling, stability and dynamics are governed by the characteristics of the periodical background. The defect modes are remarkably stable in the whole studied domains, while dark solitons manifest oscillatory instabilities. An unstable dark soliton splits into a grey soliton and a weak bright soliton against a background propagating in opposite directions.
Funding. National Natural Science Foundation of China (61827815, 62075138), Science and Technology Project of Shenzhen (JCYJ20190808121817100, JCYJ20190808164007485, JSGG20191231144201722), Portuguese Foundation for Science and Technology (FCT) under Contract no. UIDB/00618/2020.
Disclosures. The authors declare no conflicts of interest.
References
- (1) Y. V. Kartashov, B. A. Malomed, and L. Torner, “Solitons in nonlinear lattices,” Rev. Mod. Phys. 83, 247-306 (2011).
- (2) V. A. Brazhnyi and V. V. Konotop, “Theory of Nonlinear Matter Waves in Optical Lattices,” Mod. Phys. Lett. B 18, 627-651 (2004).
- (3) O. Morsch and M. Oberthaler, “Dynamics of Bose-Einstein condensates in optical lattices,” Rev. Mod. Phys. 78, 179-215 (2006).
- (4) B. A. Malomed, “Soliton management in periodic systems,” (Springer 2006).
- (5) D. Hennig and G. P. Tsironis, “Wave transmission in nonlinear lattices,” Phys. Rep. 307, 333-432 (1999).
- (6) F. Lederer, G. I. Stegeman, D. N. Christodoulides, G. Assanto, M. Segev, and Y. Silberberg, “Discrete solitons in optics,” Phys. Rep. 463, 1-126 (2008).
- (7) J. Yang and Z. Chen, “Defect solitons in photonic lattices,” Phys. Rev. E 73, 026609 (2006).
- (8) V. A. Brazhny, V. V. Konotop, and V. M. Perez-García, “Driving Defect Modes of Bose-Einstein Condensates in Optical Lattices,” Phys. Rev. Lett. 96, 060403 (2006).
- (9) V. A. Brazhny, V. V. Konotop, and V. M. Perez-García, “Defect modes of a Bose-Einstein condensate in an optical lattice with a localized impurity,” Phys. Rev. A 74, 023614 (2006).
- (10) L. Zeng and J. Zeng, “Gap-type dark localized modes in a Bose-Einstein condensate with optical lattices,” Adv. Photon. 1, 046004 (2019).
- (11) A. V. Yulin, Yu. V. Bludov, V. V. Konotop, V. Kuzmiak, and M. Salerno, “Superfluidity breakdown of periodic matter waves in quasi-one-dimensional annular traps via resonant scattering with moving defects,” Phys. Rev. A 84, 063638 (2011).
- (12) A. V. Yulin, Yu. V. Bludov, V. V. Konotop, and M. Salerno, “Superfluidity breakdown of periodic matter waves in quasi-one-dimensional annular traps via resonant scattering with moving defects,” Phys. Rev. A 87, 033625 (2013).
- (13) J. Wang, Z. Ye, A. Miller, Y. Hu, C. Lou, P. Zhang, Z. Chen, and J. Yang, “Nonlinear beam deflection in photonic lattices with negative defects,” Phys. Rev. A 83, 033836 (2011).
- (14) Y. V. Kartashov, V. V. Konotop, V. A. Vysloukh, and L. Torner, “Dissipative defect modes in periodic structures,” Opt. Lett. 35, 1638-1640 (2010).
- (15) S. M. Hu and W. Hu, “Defect solitons in optical lattices with parity-time symmetric defect,” Eur. Phys. J. D 66, 266 (2012).
- (16) J. Xie, Z. Su, W. Chen, G. Chen, J. Lv, D. Mihalache, and Y. He, “Defect solitons in two-dimensional photonic lattices with parity-time symmetry,” Opt. Commun. 313, 139-145 (2014).
- (17) Y. Kominis and K. Hizanidis, “Lattice solitons in self-defocusing optical media: analytical solutions of the nonlinear Kronig-Penney model,” Opt. Lett. 31, 2888-2890 (2006).
- (18) Y. Kominis, “Bright, dark, antidark, and kink solitons in media with periodically alternating sign of nonlinearity,” Phys. Rev. A 87, 063849 (2013).
- (19) Y. Kominis, A. Papadopoulos, and K. Hizanidis, “Surface solitons in waveguide arrays: Analytical solutions,” Opt. Express 15, 10041-10051 (2007).
- (20) V. Berger, “Nonlinear Photonic Crystals,” Phys. Rev. Lett. 81, 4136-4139 (1998).
- (21) H. Hajaiej and C. A. Stuart, “On the Variational Approach to the Stability of Standing Waves for the Nonlinear Schrödinger equation,” Adv. Nonlin. Stud. 4, 469-501 (2004).
- (22) H. Sakaguchi and B. A. Malomed, “Matter-wave solitons in nonlinear optical lattices,” Phys. Rev. E 72, 046610 (2005).
- (23) F. Kh. Abdullaev and J. Garnier, “Propagation of matter-wave solitons in periodic and random nonlinear potentials,” Phys. Rev. A 72, 061605(R) (2005).
- (24) G. Fibich, Y. Sivan, and M.I. Weinstein, “Bound states of nonlinear Schrodinger equations with a periodic nonlinear microstructure,” Physica D 217, 31-57 (2006).
- (25) F. Kh. Abdullaev, A. Gamma, M. Salerno, and L. Tomio, “Localized modes of binary mixtures of Bose-Einstein condensates in nonlinear optical lattices,” Phys. Rev. A 77, 023615 (2008).
- (26) Y. V. Kartashov, B. A. Malomed, V. A. Vysloukh, and L. Torner, “Two-dimensional solitons in nonlinear lattices,” Opt. Lett. 34, 770-772 (2009).
- (27) J. Belmonte-Beitia and J. Cuevas, “Existence of dark solitons in a class of stationary nonlinear Schrödinger equations with periodically modulated nonlinearity and periodic asymptotics,” J. Math. Phys. 52, 032702 (2011).
- (28) T. Wasak, V. V. Konotop, and M. Trippenbach, “Atom laser based on four-wave mixing with Bose-Einstein condensates in nonlinear lattices,” Phys. Rev. A 88, 063626 (2013).
- (29) L. Zeng and J. Zeng, “One-dimensional solitons in fractional Schrödinger equation with a spatially periodical modulated nonlinearity: nonlinear lattice,” Opt. Lett. 44, 2661-2664 (2019).
- (30) R. Yamazaki, S. Taie, S. Sugawa, and Y. Takahashi, “Submicron Spatial Modulation of an Interatomic Interaction in a Bose-Einstein Condensate,” Phys. Rev. Lett. 105, 050405 (2010).