Local Routing in a Tree Metric 1-Spanner

In this section we describe the tree metric 1-spanner construction of Solomon and Elkin [14].

We first define some notation used in this section. $T$ will denote a weighted, rooted tree and $wt(T)$ will denote its weight. Given a graph $G$, $V(G)$ and $E(G)$ denote its vertex and edge sets respectively. The root of $T$ is denoted $rt(T)$ and $ch(v)$ denotes the number of children of $v$. As in the notation of [14], the children of a vertex $v$ are denoted $c_{1}(v),...,c_{ch(v)}(v)$ and $p(v)$ denotes the parent of a vertex $v$. The lowest common ancestor of two vertices $u,v\in V(T)$ will be denoted by $lca(u,v)$. Given $u,v\in V(T)$, $P(u,v)$ denotes the unique path from $u$ to $v$ in $T$. Given $v\in V(T)$, $T_{v}$ will denote the subtree of $T$ rooted at $v$.

The shortcutting procedure selects a constant number of cut vertices in the tree whose removal results in a forest of trees which are at most a constant fraction of the size of the input tree. The spanner is obtained by building the complete graph on these cut vertices and recursively applying the procedure to all subtrees obtained by removing the cut vertices. We note that the original construction appearing due to Solomon and Elkin [14] actually builds a low diameter spanner on the cut vertices rather than the complete graph.

We first outline the method by which the cut vertices are selected. We assume that among all subtrees rooted at children of a vertex $v$, the subtree rooted at the leftmost vertex is the largest. That is, $|T_{c_{1}(v)}|\geq|T_{c_{i}(v)}|$, for all $i>1$.

For an integer $d$, we call a vertex $v$ $d$-balanced if $|T_{c_{1}(v)}|\leq|T|-d$. We label an edge $(u,v)$ of $T$ as leftmost if $u=c_{1}(v)$ or $v=c_{1}(u)$. Let $P(v)$ denote the path of maximum length from $v$ to some descendant of $v$ which includes only leftmost edges. We say the last vertex on $P(v)$ is the leftmost vertex in $T_{v}$ and we denote it by $l(v)$. We define $l(T):=l(rt(T))$. The construction we describe involves taking subtrees of an input tree. These subtrees inherit the ‘leftmost’ labelling of the input tree so it may be the case that $l(T)=rt(T)$. If there is a $d$-balanced vertex along $P(v)$, we denote the first such vertex by $b_{d}(v)$. Otherwise, $b_{d}(v)=NULL$.

Given a rooted tree $T$ and a positive integer $d$, we define a set of vertices $CV(T,d)$ as follows. Set $v:=rt(T)$. If $b_{d}(v)=NULL$, $CV(T,d)$ is defined to be $\emptyset$. Otherwise,

Let $k$ be a positive integer. We define a set of vertices

where $d:=n/k$. (See Figure 1 for an example.) The spanner is constructed via the following recursive procedure which takes as input a tree $T$ and an integer parameter $k\geq 4$. Initialize the spanner as $G=T$. Compute the set $C_{T}$, with respect to $k$, and add the edges of the complete graph on $C_{T}$ to $G$. Denote by $T\setminus C_{T}$ the forest obtained by removing the vertices in $C_{T}$, along with all incident edges, from $T$. Recursively run the algorithm on all trees in the forest $T\setminus C_{T}$ and add the resulting edges to $G$. Note that the parameter $k$ is passed down to recursive calls of the algorithm while the parameter $d$ is recomputed based on the size of the subtree on which the algorithm is called. The following lemmas are established by Solomon and Elkin [14]:

In particular, Lemma 3.2 implies that the recursion depth of the spanner construction algorithm is $O(\log n)$ for $k\geq 4$.

Solomon and Elkin [14] show that the graph resulting from a slightly more elaborate version of this shortcutting scheme has weight $O(\log n)\cdot wt(T)$. Their scheme differs from what we have presented in that instead of building the complete graph on the set of cut vertices $C_{T}$, they build a certain 1-spanner with $O(k)$ edges and diameter $O(\alpha(k))$ where $\alpha$ is the inverse Ackermann function. Since we consider the parameter $k$ to be constant, this modification does not affect the weight bound of the construction.

Let $G$ be the spanner resulting from running the algorithm described above on some tree $T$ with respect to the parameter $k$. We define canonical subtrees of $T$ with respect to $k$ to be the subtrees computed during the course of the construction of $G$. Canonical subtrees are defined recursively as follows. As a base for the recursive definition, the input tree $T$ is considered to be a canonical subtree with respect to $T$ and $k$. Suppose $T^{\prime}$ is a canonical subtree with respect to $T$ and $k$. Then each tree in the forest $T^{\prime}\setminus C_{T^{\prime}}$ is a canonical subtree with respect to $T$ and $k$. We speak of canonical subtrees without reference to the parameters $T$ and $k$ when they are clear from the context. Given a vertex $v$ of $T$, we denote by $T^{v}$ the canonical subtree for which $v\in C_{T^{v}}$. When a canonical subtree $T^{\prime}$ is small enough, $C_{T^{\prime}}=V(T^{\prime})$ and so it is clear that $C_{T^{v}}$ is well defined for each $v\in V(T)$. We say that $T^{v}$ is the canonical subtree of $v$ and that $v$ is a cut vertex of $T^{v}$.

We establish some technical properties of canonical subtrees which will be of use in the following section. We reword statement 4 in Corollary 2.17 from the paper of Solomon and Elkin [14] in Lemma 3.3 and prove it using our terminology for completeness.

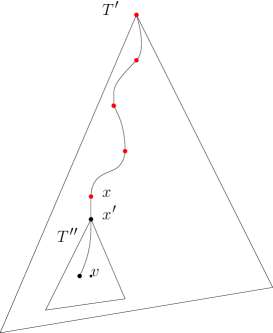
In the spanner, a vertex $u$ is connected to all vertices in $C_{T^{u}}$. The following lemma ensures that in the routing algorithm described in the next section, under certain conditions, it is safe to make a ‘greedy’ choice from a subset of vertices in $C_{T^{u}}$.

In this section, we describe a local routing algorithm for the spanner defined above. Throughout what follows, let $G$ denote the graph obtained when the algorithm of the previous section is applied to a weighted, rooted tree $T$ using a parameter $k\geq 4$. We first define the labels $label(v)$ for vertices $v\in V(G)$. We make use of the interval labelling scheme of Santaro and Khatib [13]. Let $rank(v)$ denote the rank of $v$ in a post-order traversal of $T$. We define

We define the label of $v$ to be $label(v)=[L(v),rank(v)]$. The observation used in the routing algorithm of Santaro and Khatib [13] is that a vertex $w$ is a descendant of $v$ if and only if $rank(w)\in[L(v),rank(v)]$. Note that the label of each vertex can be computed in linear time in a single traversal of the tree.

For our routing algorithm, no auxiliary data structure is required at each vertex and so the total storage requirement per vertex is $O((\Delta+k)\log n)$ bits. Our routing algorithm considers a number of cases depending on the labels of the current vertex $u$ and destination vertex $v$. For convenience of analysis, in each case we specify two routing steps. For ease of exposition, we consider a vertex to be both a descendant and ancestor of itself.

Case 0: If $v$ is a neighbour of $u$, route to $v$.

Case 1: $u$ is an ancestor of $v$ in $T$. Let $X$ be the set of vertices in $C_{T^{u}}$ which are ancestors of $v$. Let $x$ be the deepest element of $X$. Route first to $x$ and then to the child of $x$ which is an ancestor of $u$.

Case 2: $u$ is a descendant of $v$ in $T$. Let $X$ be the set of vertices in $C_{T^{u}}$ which are descendants of $v$ and ancestors of $u$. Let $x$ be the highest vertex in $X$. Route first to $X$ and then to its parent.

Case 3: $u$ is not an ancestor or descendant of $v$. Let $X$ be the set of vertices in $C_{T^{u}}$ which are ancestors of $v$ and not ancestors of $u$. If $X\neq\emptyset$, we define $x$ to be the deepest vertex in $X$ and define $x^{\prime}$ to be the child of $x$ which is an ancestor of $v$. Let $Y$ be the set of vertices in $C_{T^{u}}$ which are ancestors of $u$ but not ancestors of $v$. We define $y$ to be the highest vertex in $Y$.

The routing algorithm uses a greedy strategy. Given the destination vertex and neighbours due to tree edges and shortcut edges, the algorithm simply selects the edge that appears to make the most progress. It is not obvious that this strategy gives the desired $O(\log n)$ diameter of the routing algorithm. Indeed, this bound would not hold if the shortcuts were arbitrary edges and hinges on the particular structure of the 1-spanner.

The arguments we make in our analysis will make use of certain integer sequences we assign to vertices of $G$. Note that these sequences are used only for the analysis of the algorithm and are not part of the labelling scheme. We define a unique integer sequence for each canonical subtree computed during the course of the spanner construction. Each vertex $v$ will be assigned the sequence corresponding to the tree $T^{v}$.

The integer sequence for each canonical subtree is defined recursively as follows. The input tree $T$ is given the empty sequence. Suppose $T^{\prime}$ is a canonical subtree which has already been associated with some sequence $S$. Consider the forest $T^{\prime}\setminus C_{T^{\prime}}=\{T_{1},...,T_{p}\}$. Each tree $T_{j}\in T^{\prime}\setminus C_{T^{\prime}}$ is associated with the sequence obtained by appending $j$ to $S$. It is clear that every vertex of $T$ appears in $C_{T^{\prime}}$ for exactly one canonical subtree $T^{\prime}$. Let $S_{v}$ denote the sequence assigned to the vertex $v$. We refer to $S_{v}$ as the canonical sequence of $v$.

Observe that if for two vertices $u,v\in V(G)$ we have that $S_{u}=S_{v}$, by definition of the spanner construction algorithm, $u$ and $v$ must be cut vertices of the same canonical subtree of $T$ and are therefore connected by an edge in $G$. The routing algorithm works by choosing a successor vertex so as to incrementally transform the canonical sequence of the current vertex into the canonical sequence of the destination vertex.

Lemma 3.8 and Lemma 3.9 are immediate from the definition of the routing steps.

Lemmas 3.8, 3.9, 3.10 and 3.11 imply the following:

Using Lemma 3.12, we can show the routing algorithm has a routing ratio of 1.

We now argue that the routing algorithm is guaranteed to terminate after traversing $O(\log n)$ edges. To this end, we first prove the following lemma.

Note that if $u$ is an ancestor (resp. descendant) of $v$, then by Lemma 3.12 the vertex reached after executing the steps of Case 1 (resp. Case 2) will also be an ancestor (resp. descendant) of $v$.

Consider the case where $u$ is neither an ancestor nor a descendant of $v$. The following lemma shows that in this case, the algorithm either routes to a vertex on the path $P(lca(u,v),v)$ or it follows the routing steps that would be executed if the algorithm were routing from $u$ to $lca(u,v)$.

Using Lemmas 3.14 and 3.15, we establish the main result of this section.

The spanner we describe here is a simplified version of the spanner described by Chan et al. [7]. The starting point of their construction is based on the spanner of Gao et al. [10].

In this section, $(M,d)$ will denote an $n$-point doubling metric. Let $\dim(M)$ denote the doubling dimension of $M$. We assume without loss of generality that the distance between the closest pair of points in $M$ is 1.

The first step of the construction is to compute a certain sequence of nets. Specifically, we compute a nested sequence of sets $M=N_{0}\supseteq N_{1}\supseteq...\supseteq N_{\log D}$ where $N_{i}$ is a $2^{i}$-net of $N_{i-1}$ and $D$ is the largest inter-point distance among pairs of points in $M$. Note that $N_{\log D}$ consists of a single point. An efficient method for computing such a sequence of nets is given by Har-Peled and Mendel [12]. Next, we describe the so-called net tree which we denote $\mathcal{T}$. The net tree has a node at level-$i$ for each point in the set $N_{i}$. If a level-$i$ node corresponds to a point $p\in N_{i}$, we say that $p$ is the representative of $v$ and write $rep(v)=p$. Note that a given point in $p$ can be the representative of multiple nodes in $\mathcal{T}$. The root of the tree corresponds to the singleton set $N_{\log D}$ and the leaves of $\mathcal{T}$ are in one-to-one correspondence with the points of $M$. The parent of each node $v$ at level-$i$ is a node $w$ at level-($i+1$) for which $d(rep(v),rep(w))\leq 2^{i+1}$. The constant doubling dimension of $M$ immediately implies that nodes in $\mathcal{T}$ have a constant number of children. The tree induces a graph $H$ on $M$ in the natural way, i.e., each edge $(u,v)\in E(\mathcal{T})$ corresponds to the edge $(rep(u),rep(v))\in E(H)$. For a point $p\in M$, we also use $p$ to denote the leaf of $\mathcal{T}$ which has $p$ as its representative. Given a leaf $p$, we denote by $p^{(i)}$ the level-$i$ ancestor of $p$ in $\mathcal{T}$. Given two nodes $u,v\in V(\mathcal{T})$, we define $d(u,v):=d(rep(u),rep(v))$. The graph $H$ as currently defined is not a $(1+\epsilon)$-spanner for $M$. To guarantee a $1+\epsilon$ spanning ratio, certain cross edges are added at each level. Fix a constant $\gamma>4$. For each pair of level-$i$ points $u,v\in V(\mathcal{T})$ for which $d(rep(u),rep(v))\leq\gamma\cdot 2^{i}$, we add the cross edge $(u,v)$ to $\mathcal{T}$. If we make a sufficiently large choice of $\gamma=O(1/\epsilon)$, the graph $H$ resulting from the addition of these cross edges to $\mathcal{T}$ can be shown to be a $(1+\epsilon)$-spanner for $M$. The following theorem is established in the proof of Theorem 3.2 in [10].

The maximum degree of the spanner as described above is $O(\epsilon^{-\dim(M)}\log D)$ as some points in $M$ may represent many nodes in $\mathcal{T}$. Gottlieb and Roddity [11] devised a technique to reduce the degree bound to $O(\epsilon^{-dim(M)})$ by carefully reassigning representatives.

The depth of the net tree is $O(\log D)$. In particular, if $D$ is not bounded by a polynomial in $n$, the net tree may have linear depth and so the diameter of the spanner may be linear. We say a subtree of $\mathcal{T}$ is light if it has height $\log(\frac{D}{n})$. Chan et al. [7] show that by applying the tree metric construction of the previous section to all light subtrees of $\mathcal{T}$, it is possible to reduce the diameter of the spanner to $O(\log n)$ without increasing the asymptotic bound on the weight. Chan et al. [7] show that the weight of the spanner, after shortcuts are added, is at most $O(\epsilon^{-dim(M)}\log n)\cdot wt(MST(M))$, where $MST(M)$ is a minimum spanning tree of $M$. Chan et al. [7] make additional modifications to ensure fault tolerance although we will not work with this version of the spanner.

To summarise, the spanner we work with has $(1+\epsilon)$-stretch, $O(\epsilon^{-\dim(M)})$ degree, $O(\epsilon^{-dim(M)}\log n)\cdot wt(MST(M))$ weight and $O(\log n)$ diameter.

For the remainder of this section, $\mathcal{T}^{*}$ will denote the net tree with cross edges and shortcuts. $H$ denotes the constant degree spanner of $(M,d)$ induced by $\mathcal{T}^{*}$. Our routing algorithm will make use of the following property of the spanner $H$.