Local Reweighting for Adversarial Training

The objective function of SAT [18] is

where $\tilde{x}_{i}=\mathop{\operatorname*{arg\,max}}_{\tilde{x}_{i}\in\mathcal{B}_{\epsilon}[x]}\ell(f_{\theta}(\tilde{x}_{i}),y_{i})$. The selected $\tilde{x}$ is the most adversarial variant within the $\epsilon$-ball center at $x$. The loss function $\ell:\mathbb{R}^{K}\times\mathcal{Y}\to\mathbb{R}$ is a composition of a base loss $\ell_{B}:\bigtriangleup^{K-1}\times\mathcal{Y}\to\mathbb{R}$ (e.g., the cross-entropy loss) and an inverse link function $\ell_{L}:\mathbb{R}^{K}\to\bigtriangleup^{K-1}$ (e.g., the soft-max activation), where $\bigtriangleup^{K-1}$ is the corresponding probalility simplex. Namely, $\ell(f_{\theta}(\cdot),y)=\ell_{B}(\ell_{L}(f_{\theta}(\cdot)),y)$. PGD [18] is the most common approximation method for searching the most adversarial variant. Starting from $x^{(0)}\in\mathcal{X}$, PGD (with step size $\alpha>0$) works as follows:

where $\mathbb{N}$ is the number of iterations; $x^{(0)}$ refers to the starting point that natural instance (or a natural instance perturbed by a small Gaussian or uniformly random noise); $y$ is the corresponding label for $x^{(0)}$; $x^{(t)}$ is the adversarial variant at step $t$; $\Pi_{\mathcal{B}_{\epsilon}[x^{(0)}]}(\cdot)$ is the projection function that projects the adversarial variant back into the $\epsilon$-ball centered at $x^{(0)}$ if necessary.

The Reweighting is Beneficial. As suggested by GAIRAT [38], the global reweighting indeed improves the robustness when tested on the given attack simulated in training. Figures 1(b) and 1(c) also show that, as a global reweighting, GAIRAT improves the robustness against PGD (when PGD is simulated in training). Thus, when training and testing on the same attack, the rationale that we do not need to pay much attention to an already-safe instance under the attack is significant.

Local Reweighting can Take Care of Various Attacks Simultaneously. As introduced in Section 3, there is inconsistent vulnerability between instances in different views. Thus, we should perform local reweighting inside each pair, while performing no global reweighting—the rationale is to fit the instance itself if it is immune to the attack, but not to skip the pair, in order to passively defend different attacks in future. In addition, it is inefficient (practically impossible) to simulate all attacks in training, so a gentle lower bound on the instance weights is necessary to defend against potentially adaptive adversarial attacks.

Let $\omega(\tilde{x},y)$ be the weight assignment function on the loss of adversarial variant $\tilde{x}$. The inner optimization for generating $\tilde{x}$ depends on attacks, such as PGD (Eq. (2)). The outer minimization is:

where $n$ is the number of instances in one mini-batch; $m$ is the number of used attacks; $\mathcal{C}$ is a constant representing the minimum weight sum of each instance; the notation $[a]_{+}$ stands for $\max\{a,0\}$. We impose two constraints on our objective Eq. (5): the first constraint ensures that $\omega(\tilde{x},y)>0$ and the second constraint ensures that $\mathcal{C}>0$. The non-negative coefficient $[\mathcal{C}-\sum_{j=1}^{m}\omega(\tilde{x}_{ij},y_{i})]_{+}$ assigns some weight to the natural data term, which serves as a gentle lower bound to avoid discarding instances during training. It can also be seen that different weights are assigned to different adversarial variants, respectively. LRAT pairs each instance with its adversarial variants and performs local reweighting inside each pair. Figure 3 provides an illustrative schematic of the learning objective of LRAT. If $\omega(\tilde{x},y)=1$, $\mathcal{C}<1$, $m=1$ and $\tilde{x}$ is generated by PGD, LRAT recovers the SAT [18], which assigns equal weights to the losses of PGD adversarial variant.

The objective in Eq. (5) implies the optimization process of an adversarially robust network, with one step generating adversarial variants from natural counterparts and then reweighting loss on them, and one step minimizing the reweighted loss w.r.t. the model parameters $\theta$.

It is still an open question how to calculate the optimal $\omega$ for different variants. Zhang et al. [38] heuristically design some non-increasing functions $\omega$, such as:

where $\kappa/K\in[0,1]$, $K\in\mathbb{N}^{+}$, and $\lambda\in\mathbb{R}$. $\kappa(x,y)$ is the GD defined as the least steps that the PGD method needs to successfully attack the natural instance. $K$ is the maximally allowed steps.

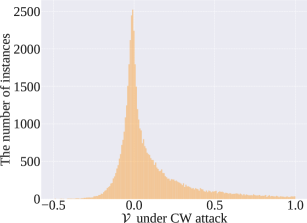
However, the efficacy of this heuristic reweighting function is limited to PGD. When CW is simulated in training, Figure 5 shows the same decrease as in Figure 1 (c) when tested on CW.

Therefore, in this section, we propose a general vulnerability-based and attack-dependent reweighting strategy to calculate the weights of the corresponding variants:

where $\mathcal{V}$ is a predetermined function that measures the vulnerability between the classifier and a certain adversarial variant, and $g$ is a decreasing function of the variable $\mathcal{V}$.

The generations of adversarial variants follow different rules under different attacks. For example, the adversarial variant generated by PGD misleads the classifier with the lowest probability of predicting the correct label [18]. In contrast, the adversarial variant generated by CW misleads the classifier with the highest probability of predicting a wrong label [5]. Motivated by these different generating processes, we define the vulnerability in the view of PGD and CW in the following.

For the CW-based adversarial variant, the relatively higher predicted probability it has on the false class, the larger $\mathcal{V}^{\textnormal{CW}}$ in Eq. (9). In this paper, we consider the decreasing function $g$ with the form

where $\alpha>0$ and $\beta>0$ are hyper-parameters of each attack. In Eq. (10), adversarial variants with higher $\mathcal{V}$ are given lower weights. We present our locally reweighted adversarial training in Algorithm 1. LRAT uses different given attacks (e.g., PGD, Algorithm 2 in Appendix A) to obtain different adversarial variants, and leverages the attack-dependent reweighting strategy for obtaining their corresponding weights. For each mini-batch, LRAT reweights the loss of different adversarial variants according to our vulnerability-based reweighting strategy, and then updates the model parameters by minimizing the sum of the reweighted loss on each instance.

We compare LRAT with the no-reweighting strategy (i.e., SAT [18]) and the global-reweighting strategy (i.e., GAIRAT [38]). Rice et al. [24] show that, unlike in standard training, overfitting in robust adversarial training decays test set performance during training. Thus, as suggested by Rice et al. [24], we compare different methods on the performance of the best checkpoint model (the early stopping results at epoch 60). Besides, we also design LRAT for TRADES [36], denoted as (LRAT-TRADES), and the details of the algorithm are in Appendix B. Accordingly, we also compare LRAT-TRADES with TRADES [36] and GAIR-TRADES [38]. Trades-based methods effectively mitigate the overfitting Rice et al. [24], so we compare different methods on both the best checkpoint model and the last checkpoint model (used by Madry et al. [18]), respectively.

We employ the small-capacity network, ResNet (ResNet-18) [14], and the large-capacity network, Wide ResNet (WRN-32-10) [35]. Our experimental setup follows previous works [18, 31, 38]. All networks are trained for 100 epochs using SGD with $0.9$ momentum. The initial learning rate is $0.01$, divided by $10$ at epoch $60$ and $90$, respectively. The weight decay is 0.0035. For generating the PGD adversarial data for updating the network, $L_{\infty}$-norm bounded perturbation $\epsilon_{train}=8/255$; the maximum PGD step $K=10$; step size $\alpha=\epsilon_{train}/10$. For generating the CW adversarial data [5], we follow the setup in [3, 37], where the confidence $\kappa=50$, and other hyper-parameters are the same as that of PGD above. Robustness to adversarial data is the main evaluation indicator in adversarial training [6, 8, 9, 10, 21, 33, 40]. Thus, we evaluate the robust models based on four evaluation metrics, i.e., standard test accuracy on natural data (Natural), robust test accuracy on adversarial data generated by projected gradient descent attack (PGD) [18], Carlini and Wagner attack (CW) [5] and AutoAttack (AA). In testing, $L_{\infty}$-norm bounded perturbation $\epsilon_{test}=8/255$, the maximum PGD step $K=20$, and step size $\alpha=\epsilon/4$. There is a random start in training and testing, i.e., uniformly random perturbations ($[-\epsilon_{train},+\epsilon_{train}]$ and $[-\epsilon_{test},+\epsilon_{test}]$) added to natural instances. Due to the random start, we test our methods and baselines five times with different random seeds.

Tables 1 and 2 report the medians and standard deviations of the results. In our experiments of LRAT, we simulate the PGD and CW in training ($m=2$ in Eq. (5)). For adversarial variants, we use our vulnerability-based reweighting strategy (Eq. (7)) to obtain their corresponding weights, where $\mathcal{V}^{\textnormal{PGD}}$ follows Eq. (8) and $\mathcal{V}^{\textnormal{CW}}$ follows Eq. (9). We choose the three hyper-parameters ($\mathcal{C}$ in Eq. (5), $\alpha,\beta$ in Eq. (10)) that $\alpha=2$, $\beta=0.5$, and $\mathcal{C}=0.1$, and we analyze it in Appendix C.

This subsection validates that each component in LRAT can improve the adversarial robustness. P (or C) represents that only PGD (or CW) with its corresponding reweighting strategy is simulated during training. [N] (or [P]) represents assigning some weights to the natural (or PGD adversarial) data, which serves as a gentle lower bound to avoid discarding instances during training. The objective functions are in Table 3, where $\tilde{x}^{p}$ is the adversarial data under PGD, and $\tilde{x}^{c}$ is the adversarial data under CW. The results are reported in Table 4. Results show that the robustness of global reweighting (P) and (C) is lower than that of the other three local reweighting when tested on attacks different from the given attack simulated during training. Results also show that the robustness of ([N]+P+C) and ([P]+P+C) is higher than that of the other three with no lower bounds when tested on AA, which confirms that a gentle lower bound on instance weights is useful for defending against potentially adaptive adversarial attacks.