Local interstellar spectra and solar modulation of cosmic ray electrons and positrons
Abstract
Low energy cosmic rays are modulated by the solar activity when they propagation in the heliosphere, leading to ambiguities in understanding their acceleration at sources and propagation in the Milky Way. By means of the precise measurements of the , , , and spectra by AMS-02 near the Earth, as well as the very low energy measurements of the fluxes by Voyager-1 far away from the Sun, we derive the local interstellar spectra (LIS) of and components individually. Our method is based on a non-parametric description of the LIS of and and a force-field solar modulation model. We then obtain the evolution of the solar modulation parameters based on the derived LIS and the monthly fluxes of cosmic ray and measured by AMS-02. To better fit the monthly data, additional renormalization factors for and have been multiplied to the modulated fluxes. We find that the inferred solar modulation parameters of positrons are in good agreement with that of cosmic ray nuclei, and the time evolutions of the solar modulation parameters of electrons and positrons differ after the reversal of the heliosphere magnetic field polarity, which shows clearly the charge-sign dependent modulation effect.
keywords:
acceleration of particles — cosmic rays — solar modulationiint \savesymboliiint \savesymboliiiint \savesymbolidotsint \restoresymbolAMSiint \restoresymbolAMSiiint \restoresymbolAMSiiiint \restoresymbolAMSidotsint
1 Introduction
Large progresses have been achieved in the direct measurements of cosmic rays (CR) in the past decade, by space experiments including the AMS, Fermi-LAT, DAMPE, CALET, and NUCLEON, providing very important information about the origin, acceleration, and propagation of cosmic rays in the Milky Way (e.g., Gabici et al. 2019; Kachelrieß and Semikoz 2019). Nevertheless, there is still strong degeneracy among the acceleration and propagation effects (including those in the heliosphere), which hinders an unambiguous understanding of the CR problems. Very interestingly, the Cosmic Ray Subsystem (CRS) instrument on the Voyager-1 spacecraft launched more than 40 years ago keeps on operation and measuring the low-energy CR fluxes even outside the heliosphere111Note that it is still possible that there is tiny residual modulation effect on the Voyager-1 spectra (Scherer et al. 2011; Kóta and Jokipii 2014). In this work we assume that the Voyager-1 measurement is the LIS without considering such subtlety. (Stone et al. 2013; Cummings et al. 2016). In addition, the PAMELA and AMS-02 experiments further reported time variations of the CR fluxes with very high precisions (Adriani et al. 2013b, 2016; Martucci et al. 2018; Aguilar et al. 2018c, a), which are also direct relevant to the solar modulation. The Voyager-1 data, and/or the time series of CR fluxes, are very important in probing the local interstellar spectra (LIS) and solar modulation effect of CRs (e.g., Bisschoff and Potgieter 2016; Ghelfi et al. 2016; Corti et al. 2016; Boschini et al. 2017; Tomassetti et al. 2017; Zhu et al. 2018; Boschini et al. 2018; Tomassetti et al. 2018; Corti et al. 2019; Wang et al. 2019).
In Zhu et al. (2018) we studied the LIS of CR nuclei from He to O with a non-parametric spline interpolation method and the force-field model of the solar modulation (Gleeson and Axford 1967, 1968), according to AMS-02 (Aguilar et al. 2017, 2018b), Voyager-1 (Cummings et al. 2016), and ACE-CRIS data. The time-evolution of the solar modulation parameters were then derived based on the monthly ACE-CRIS fluxes of CR nuclei, which are consistent with those inferred from the neutron monitors (Usoskin et al. 2011; Ghelfi et al. 2017).
In this work we extend the previous study to electrons and positrons. One of our motivations is to examine the possible differences between the LIS of electrons and that of nuclei, which may have important implication in the propagation of different particle species in the Milky Way (Lin et al. 2015). Furthermore, the differences of solar modulation effects among electrons, positrons, and nuclei may help to understand the charge-sign dependent modulation effects.
The CR electron and positron spectra and flux ratios have been measured precisely by several space experiments, such as PAMELA (Adriani et al. 2009, 2011, 2013a), Fermi-LAT (Abdollahi et al. 2017), AMS-02 (Aguilar et al. 2014b, a; Accardo et al. 2014; Aguilar et al. 2019a, b), DAMPE (DAMPE Collaboration et al. 2017), and CALET (Adriani et al. 2018). The Voyager-1 experiment also measure the total fluxes from to MeV outside the heliosphere (Cummings et al. 2016). Here the data obtained on top-of-atmosphere (TOA) by AMS-02 and in the local interstellar space by Voyager-1 will be used. Following the method of Zhu et al. (2018), we adopt a non-parametric spline interpolation method to describe the LIS of electrons and positrons, which are then modulated under the force-field model and fitted to the long-term average data. Based on the LIS derived above and the monthly fluxes of electrons and positrons, we then derive the time-series of the modulation parameters. We are aware that the force-field model should be over-simplified in modeling the solar modulation effect. However, the more physical modulation model usually has a considerable number of free parameters and is computationally heavy (Kappl 2016; Luo et al. 2017; Potgieter and Vos 2017; Vittino et al. 2019; Kuhlen and Mertsch 2019). Thus we keep the framework of the force-field model, but with some extension with additional remormalization factors. Also the electrons and positrons have different modulation parameters. We expect that the extended force-field approximation can reasonably reflect the main features of the solar modulation.

2 Methodology
Usually the CR spectra are parameterized with power-law or broken power-law function (Moskalenko and Strong 1998; Boschini et al. 2018). However, the actual CR spectrum, either the accelerated one or the detected one, may be more complicated. More and more new features of the CR spectra have been revealed by recent observations (e.g., DAMPE Collaboration et al. 2017; An et al. 2019; Ahn et al. 2010; Atkin et al. 2018). To minimize the impact of the assumed function form of the energy spectra of CRs, following Ghelfi et al. (2016) and (Zhu et al. 2018), we adopt a cubic spline interpolation method to describe the wide-band LIS of both electrons and positrons. Note that in this current work the propagation of electrons and positrons in the Milky Way is not discussed. The cubic spline interpolation is a way to get a smoothly connecting piecewise function passing through a set of energy points. We work in the space, where is the energy of electrons or positrons in unit of GeV and is the flux in unit of GeV m-2 s-1 sr-1. The selected positions of knots are:
| (1) |
In the low energy range the knots are sparse because the data points in such energy ranges are very limited. The corresponding fluxes and are free parameters to be fitted.
Since most of the observations are carried out near the Earth, they just give the modulated TOA spectra. As we have mentioned before, we use the force-field solar modulation model (Gleeson and Axford 1967, 1968) to link the LIS with the TOA spectra as
| (2) |
where is the kinetic energy of the particle, with being the solar modulation potential, MeV is the electron mass, and is the differential flux of electrons or positrons. Note that here the modulation parameters for electrons and positrons, and , are assumed to be independent and fitted simultaneously.
The statistics is defined as
| (3) |
where is the expected TOA/LIS fluxes of , , or the ratios , and are the measured data and error for the th data bin.
We use the Markov Chain Monte Carlo (MCMC) method (Lewis and Bridle 2002) to fit the parameters. The MCMC is based on the Bayesian framework which can minimize the function, and give the posterior distributions of the high-dimensional parameter space with a high efficiency. The likelihood function of the model parameters is
| (4) |
The posterior probability of model parameters is then
| (5) |
where is the prior probability of parameters . Here we assume flat priors of all the parameters.
We adopt the Metropolis-Hastings algorithm which generates Markov chains as follows. For a set of parameters and its successor , we calculate an accept probability . If is accepted, then repeat the precedure from . Otherwise, we go back to . The procedure is continued until a convergence criterion is satisfied.
The data used in the fit include the TOA measurements of the , , fluxes and ratios by AMS-02 in 2014 (Aguilar et al. 2014a, b; Accardo et al. 2014), and 2019 (Aguilar et al. 2019a, b), and the LIS of measured by Voyager-1 (Cummings et al. 2016). The LIS of both and are assumed to monotonically decrease with energies, and the LIS of is further assumed to be smaller than that of . The latter requirement is based on the fact that there are primary accelerated at the sources. The fit determines the LIS of and , and the average solar modulation potentials for the time from May, 2011 to November, 2013, and from May, 2011 to November, 2017 during which the measurements of , , fluxes and ratios by AMS-02 were made. After deriving the LIS through the above fits, the time-dependent measurements of the and fluxes for every Bartels rotation period ( days) are then used to derive the time-variation of the solar modulation parameters .
3 Results
3.1 The LIS of and
In Fig. 1 we show the fitting spectra of (upper left), (upper right), (lower left) and the positron fraction (lower right), compared with the AMS-02 (2014)(Aguilar et al. 2014b, a; Accardo et al. 2014), AMS-02 (2019) (Aguilar et al. 2019a, b), and Voyager-1 (Cummings et al. 2016) data. The gray bands show the 68% uncertainty ranges of the fits. Note that the Voyager-1 data are the fluxes, which are also shown in the top panels for comparison. Since there are lack of measurements of and fluxes at low energies (for GeV), there are relatively large uncertainties of the fitting results in such an energy range. The degeneracy between the solar modulation parameters and the low energy fluxes further enlarge the uncertainties. Therefore we observe relatively wide bands of the and LIS at low energies. The sum of the and is constrained by the Voyager-1 data, and is less uncertain.

In Fig. 2 we compare our best-fitting LIS of (top panel) and (bottom panel) with previous works with somehow different methods and assumptions (Vittino et al. 2019; Bisschoff et al. 2019; Boschini et al. 2018). For the spectrum, our result is very close to that of Vittino et al. (2019) and Boschini et al. (2018) at low and high energies. The main differences appear at medium energies (from GeV to GeV), which show the uncertainties of the solar modulation modelings. The result of Bisschoff et al. (2019) is higher than the others at lower energies (from GeV to GeV), with a harder spectrum, due to the use of a different data sample from Voyager-1 Stone et al. (2013); Cummings et al. (2016). The LIS of obtained in Vittino et al. (2019); Bisschoff et al. (2019) shows relatively large differences from our best-fit result but is still consistent with our relatively wide uncertainty band (see Fig. 1).
| Species | (GV) | |
|---|---|---|
| (2014) | 31.4 | |
| (2014) | 45.7 | |
| (2014) | 23.3 | |
| (2014) | 124.3 | |
| (2019) | 26.8 | |
| (2019) | 40.5 | |
| (2019) | 22.15 | |
| (2019) | 83.1 | |
| (Voyager) | 8.95 |

The fitting results of the solar modulation potentials and , and the values are given in Table 1. We find that the values for positron fluxes and positron fractions are relatively large. As we will do below, if we multiply two renormalization factors on the 2014 data, we find and , and the fits will be improved significantly. This result shows that the simple force-field modulation model may be not enough to describe the solar modulations at different solar conditions.
The normalized probability distributions of are shown in Fig. 3. The results show that the electrons were modulated more severely than positrons during the period from 2013 to 2017. From 2011 to 2014, the electrons and positrons were modulated similarly with each other. Based on the derived modulation potentials, we de-modulate the AMS-02 (2019) electron and positron fluxes from the TOA to the LIS, as shown by the balck points in Fig. 1. Note that the errors of are included in the total errors of the de-modulated fluxes via the error propagation method. The de-modulated AMS-02 data are provided in Tables 2 and 3 in the Appendix.
3.2 Time-dependent TOA fluxes of and

Given the LIS fluxes, we can then investigate the time-evolutions of the TOA fluxes, and compare them with the long-term AMS-02 measurements (Aguilar et al. 2018c). However, we find that the direct fit (with the MCMC method) to the monthly data with the derived LIS plus a force-field modulation model can not always give a good fit. The minimum values diveded by the number of degree-of-freedom (dof) are shown in the left panel of Fig. 4 with the green line. We can see that these fits give typically too large reduced values. This is perhaps due to the complicated perturbations of the interplanetary space by solar activity whose effect can not be easily accounted for by the simple force-field modulation model. To improve the fits of the time-dependent fluxes, more complicated solar modulation model and more free parameters are needed (Wang et al. 2019; Kuhlen and Mertsch 2019; Vittino et al. 2019).
Empirically we extend the force-field approximation through multiplying two renormalization factors, , on the LIS as
| (6) |
The fits can be improved significantly, as shown by the green line in Fig. 4. We also show the reduced for and separately in Fig. 4. Generally we see that the goodness-of-fits for positrons are better than that for electrons.
The values of are given in Fig. 5. The renormalization factors show a general correlation with the solar activity. We expect that this is due to the mismatch between the energy-dependence of the force-field modulation model and the measurements for different time. To see these results in more details, we plot in Fig. 6 and Fig. 7 the time variations of the and fluxes in 6 energy bins, respectively. Taking the results before 2013 as illustration, we can see that without including the renormalization factors, the model (red dashed line) predicts lower fluxes at low energies than the measurements and higher at high energies. In other words, the model spectrum is harder than the data. The renomalization factor , together with a smaller modulation potential compared with the cases of (as can be seen in Fig. 8), can solve this discrepancy satisfactorily. Smaller gives higher low-energy fluxes, while suppresses high-energy fluxes when the solar modulation is weak. Therefore the model spectrum (blue solid lines) becomes softer and better match the data. Things become opposite at solar maximums, when is required. Furthermore, we note that differences of the renormalization factors of and appear after the heliospheric magnetic field reversal. This gives a charge-sign dependence of the solar modulation effect as expected.
The correlation between and may be understood as the drift effect of CRs in the heliosphere. As shown in Jokipii and Kopriva (1979) and Strauss et al. (2011), the presence of drift in the Parker equation tends to give a softer TOA spectrum. In the force-field approximation, a softer TOA spectrum means a smaller . To match with the data with relatively high energies (above a few GeV), a renormalization factor is required. This case applies for the periods from 2011 to 2013, and from 2015 to 2017. For the period from 2015 to 2017, the drift effect is weak, and the modulated spectrum is thus harder. Therefore we need larger and .




3.3 The time variation of
In this sub-section, we derive the time series of the solar modulation potentials, according to the fits to the monthly AMS-02 data discussed above, with the renormalization factors. To properly take into account the uncertainties of the LIS, we adopt a Bayesian approach with the posterior probability of being given by
| (7) |
where is the likelihood of model parameters (), is the prior probability distribution of which is obtained in the fit in Sec. 3.1, and is the prior of which is assumed to be a flat distribution within .
In the left panel of Fig. 8, we compare the fitting results of for the cases without (dashed) and with (solid) renormalization factors. The overall behaviors of are similar for both cases. However, small changes of the parameters appear when including the renormalization factors. Specifically, when (), become smaller (larger) than that without renormalization factors.
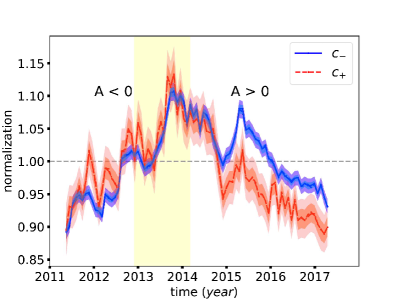
The right panel of Fig. 8 shows the time series of from 2011 to 2017, compared with the results derived from fitting to the B, C, and O nuclei data from ACE (Zhu et al. 2018). It is very interesting to find that the profile of results derived in this work are in good agreement with . The modulation potentials for negative charge particles, , show systematical differences from that of positive charge particles, especially for regime. Specifically, in the regime, positive charged particles are less significantly modulated than negative charged particles. This could be understood as a drift effect of particles with different charge sign. For the heliosphere magnetic field polarity of , positrons mainly drift from high latitudes to low latitudes, while electrons are remain confined to low latitudes and drift along the heliospheric current sheet (HCS; Strauss et al. 2011, 2012). The strength of the heliospheric magnetic field is weaker in the polar region, and thus positrons are less confined by the magnetic field and can reach the Earth more easily. As a result, the modulation potential is smaller than . For the period from 2011 to 2014, the solar activity was at maximum, and the effect of drift was not important. Therefore electrons and positrons were modulated similarly (Vittino et al. 2019), with positrons being modulated a little bit more than electrons.
4 Conclusion and discussion
With the recent precise measurements of electrons and positions from Voyager-1 at outside of the heliosphere and AMS-02 at the TOA, we study the LIS and the solar modulation effects of electrons and positions. We adopt a a non-parametric spline interpolation method to describe the LIS of and , to minimize the effect of improper function form assumed. Since there are no measurements of the separate and fluxes in the Voyager-1 energy window, our resulting LIS show relatively large uncertainties at low energies. Such LIS may be used further in the study of electron and positron propagation in the Milky Way (Lin et al. 2015).
We then study the time variations of the and fluxes and the modulation potentials at different time. We extend the simple force-filed approximation to fit the AMS-02 monthly spectra of and , by multiplying two renormalization factors . Such renormalization factors show correlations with the solar activity, and are larger than 1 around the solar maximum and smaller than 1 otherwise. The renormalization factors might be an empirical approach of a more comprehensive solar modulation model other than the force-field approximation, such as the power-law diffusion model in Wang et al. (2019) with , where is the diffusion coefficient and is particle rigidity, or even a broken power-law diffusion coefficient (Vittino et al. 2019), or the more complicated model including the drift effect (Kuhlen and Mertsch 2019). We leave the detailed investigation in future works.
The time variations of fluxes give a time series of the modulation parameters. Our results show that the modulation potentials for positrons are well consistent with that for nuclei, which are all positive charge particles. Nevertheless, the modulation potentials for electrons are different from those for positrons and nuclei, indicating clearly the charge-sign dependent modulation. Including the drift effect may explain such differences. Although the solar modulation model assumed in this work may be over-simplified, we expect that the more complicated and physical interpretation of the solar modulation is actually contained in the time-variations of the modulation potentials and the renormalization factors.
Acknowledgements
This works is supported by the National Key Research and Development Program of China (No. 2016YFA0400204), the Key Research Program of Frontier Sciences of Chinese Academy of Sciences (No. QYZDJ-SSW-SYS024), the National Natural Science Foundation of China (Nos. 11851305, 11722328, U1738205). QY is also supported by the 100 Talents program of Chinese Academy of Sciences and the Program for Innovative Talents and Entrepreneur in Jiangsu.
References
- Abdollahi et al. (2017) Abdollahi, S., Ackermann, M., Ajello, M., Atwood, W. B., Baldini, L., Barbiellini, G., Bastieri, D., Bellazzini, R., Bloom, E. D., Bonino, R., Brandt, T. J., Bregeon, J., Bruel, P., Buehler, R., Cameron, R. A., Caputo, R., Caragiulo, M., Castro, D., Cavazzuti, E., Cecchi, C., Chekhtman, A., Ciprini, S., Cohen-Tanugi, J., Costanza, F., Cuoco, A., Cutini, S., D’Ammando, F., de Palma, F., Desiante, R., Digel, S. W., Di Lalla, N., Di Mauro, M., Di Venere, L., Drell, P. S., Drlica-Wagner, A., Favuzzi, C., Focke, W. B., Funk, S., Fusco, P., Gargano, F., Gasparrini, D., Giglietto, N., Giordano, F., Giroletti, M., Green, D., Guillemot, L., Guiriec, S., Harding, A. K., Jogler, T., Jóhannesson, G., Kamae, T., Kuss, M., La Mura, G., Latronico, L., Longo, F., Loparco, F., Lubrano, P., Maldera, S., Malyshev, D., Manfreda, A., Mazziotta, M. N., Michelson, P. F., Mirabal, N., Mitthumsiri, W., Mizuno, T., Moiseev, A. A., Monzani, M. E., Morselli, A., Moskalenko, I. V., Negro, M., Nuss, E., Orlando, E., Paneque, D., Perkins, J. S., Pesce-Rollins, M., Piron, F., Pivato, G., Porter, T. A., Principe, G., Rainò, S., Rando, R., Razzano, M., Reimer, A., Reimer, O., Sgrò, C., Simone, D., Siskind, E. J., Spada, F., Spandre, G., Spinelli, P., Tajima, H., Thayer, J. B., Tibaldo, L., Torres, D. F., Troja, E., Wood, M., Worley, A., Zaharijas, G., Zimmer, S., Fermi-LAT Collaboration, Apr. 2017. Cosmic-ray electron-positron spectrum from 7 GeV to 2 TeV with the Fermi Large Area Telescope. Phys. Rev. D95 (8), 082007.
- Accardo et al. (2014) Accardo, L., Aguilar, M., Aisa, D., Alvino, A., Ambrosi, G., Andeen, K., Arruda, L., Attig, N., Azzarello, P., Bachlechner, A., et al., Sep. 2014. High Statistics Measurement of the Positron Fraction in Primary Cosmic Rays of 0.5-500 GeV with the Alpha Magnetic Spectrometer on the International Space Station. Physical Review Letters 113 (12), 121101.
- Adriani et al. (2018) Adriani, O., Akaike, Y., Asano, K., Asaoka, Y., Bagliesi, M. G., Berti, E., Bigongiari, G., Binns, W. R., Bonechi, S., Bongi, M., Brogi, P., Buckley, J. H., Cannady, N., Castellini, G., Checchia, C., Cherry, M. L., Collazuol, G., di Felice, V., Ebisawa, K., Fuke, H., Guzik, T. G., Hams, T., Hareyama, M., Hasebe, N., Hibino, K., Ichimura, M., Ioka, K., Ishizaki, W., Israel, M. H., Kasahara, K., Kataoka, J., Kataoka, R., Katayose, Y., Kato, C., Kawanaka, N., Kawakubo, Y., Kohri, K., Krawczynski, H. S., Krizmanic, J. F., Lomtadze, T., Maestro, P., Marrocchesi, P. S., Messineo, A. M., Mitchell, J. W., Miyake, S., Moiseev, A. A., Mori, K., Mori, M., Mori, N., Motz, H. M., Munakata, K., Murakami, H., Nakahira, S., Nishimura, J., de Nolfo, G. A., Okuno, S., Ormes, J. F., Ozawa, S., Pacini, L., Palma, F., Papini, P., Penacchioni, A. V., Rauch, B. F., Ricciarini, S. B., Sakai, K., Sakamoto, T., Sasaki, M., Shimizu, Y., Shiomi, A., Sparvoli, R., Spillantini, P., Stolzi, F., Suh, J. E., Sulaj, A., Takahashi, I., Takayanagi, M., Takita, M., Tamura, T., Tateyama, N., Terasawa, T., Tomida, H., Torii, S., Tsunesada, Y., Uchihori, Y., Ueno, S., Vannuccini, E., Wefel, J. P., Yamaoka, K., Yanagita, S., Yoshida, A., Yoshida, K., Calet Collaboration, Jun 2018. Extended Measurement of the Cosmic-Ray Electron and Positron Spectrum from 11 GeV to 4.8 TeV with the Calorimetric Electron Telescope on the International Space Station. Phys. Rev. Lett.120 (26), 261102.
- Adriani et al. (2013a) Adriani, O., Barbarino, G. C., Bazilevskaya, G. A., Bellotti, R., Bianco, A., Boezio, M., Bogomolov, E. A., Bongi, M., Bonvicini, V., Bottai, S., Bruno, A., Cafagna, F., Campana, D., Carbone, R., Carlson, P., Casolino, M., Castellini, G., De Donato, C., De Santis, C., De Simone, N., Di Felice, V., Formato, V., Galper, A. M., Karelin, A. V., Koldashov, S. V., Koldobskiy, S. A., Krutkov, S. Y., Kvashnin, A. N., Leonov, A., Malakhov, V., Marcelli, L., Martucci, M., Mayorov, A. G., Menn, W., Mergé, M., Mikhailov, V. V., Mocchiutti, E., Monaco, A., Mori, N., Munini, R., Osteria, G., Palma, F., Papini, P., Pearce, M., Picozza, P., Pizzolotto, C., Ricci, M., Ricciarini, S. B., Rossetto, L., Sarkar, R., Scotti, V., Simon, M., Sparvoli, R., Spillantini, P., Stochaj, S. J., Stockton, J. C., Stozhkov, Y. I., Vacchi, A., Vannuccini, E., Vasilyev, G. I., Voronov, S. A., Yurkin, Y. T., Zampa, G., Zampa, N., Zverev, V. G., Aug. 2013a. Cosmic-Ray Positron Energy Spectrum Measured by PAMELA. Physical Review Letters 111 (8), 081102.
- Adriani et al. (2009) Adriani, O., Barbarino, G. C., Bazilevskaya, G. A., Bellotti, R., Boezio, M., Bogomolov, E. A., Bonechi, L., Bongi, M., Bonvicini, V., Bottai, S., Bruno, A., Cafagna, F., Campana, D., Carlson, P., Casolino, M., Castellini, G., de Pascale, M. P., de Rosa, G., de Simone, N., di Felice, V., Galper, A. M., Grishantseva, L., Hofverberg, P., Koldashov, S. V., Krutkov, S. Y., Kvashnin, A. N., Leonov, A., Malvezzi, V., Marcelli, L., Menn, W., Mikhailov, V. V., Mocchiutti, E., Orsi, S., Osteria, G., Papini, P., Pearce, M., Picozza, P., Ricci, M., Ricciarini, S. B., Simon, M., Sparvoli, R., Spillantini, P., Stozhkov, Y. I., Vacchi, A., Vannuccini, E., Vasilyev, G., Voronov, S. A., Yurkin, Y. T., Zampa, G., Zampa, N., Zverev, V. G., Apr. 2009. An anomalous positron abundance in cosmic rays with energies 1.5-100GeV. Nature458, 607–609.
- Adriani et al. (2011) Adriani, O., Barbarino, G. C., Bazilevskaya, G. A., Bellotti, R., Boezio, M., Bogomolov, E. A., Bongi, M., Bonvicini, V., Borisov, S., Bottai, S., Bruno, A., Cafagna, F., Campana, D., Carbone, R., Carlson, P., Casolino, M., Castellini, G., Consiglio, L., de Pascale, M. P., de Santis, C., de Simone, N., di Felice, V., Galper, A. M., Gillard, W., Grishantseva, L., Jerse, G., Karelin, A. V., Koldashov, S. V., Krutkov, S. Y., Kvashnin, A. N., Leonov, A., Malakhov, V., Malvezzi, V., Marcelli, L., Mayorov, A. G., Menn, W., Mikhailov, V. V., Mocchiutti, E., Monaco, A., Mori, N., Nikonov, N., Osteria, G., Palma, F., Papini, P., Pearce, M., Picozza, P., Pizzolotto, C., Ricci, M., Ricciarini, S. B., Rossetto, L., Sarkar, R., Simon, M., Sparvoli, R., Spillantini, P., Stochaj, S. J., Stockton, J. C., Stozhkov, Y. I., Vacchi, A., Vannuccini, E., Vasilyev, G., Voronov, S. A., Wu, J., Yurkin, Y. T., Zampa, G., Zampa, N., Zverev, V. G., May 2011. Cosmic-Ray Electron Flux Measured by the PAMELA Experiment between 1 and 625 GeV. Physical Review Letters 106 (20), 201101.
- Adriani et al. (2013b) Adriani, O., Barbarino, G. C., Bazilevskaya, G. A., Bellotti, R., Boezio, M., Bogomolov, E. A., Bongi, M., Bonvicini, V., Borisov, S., Bottai, S., Bruno, A., Cafagna, F., Campana, D., Carbone, R., Carlson, P., Casolino, M., Castellini, G., De Pascale, M. P., De Santis, C., De Simone, N., Di Felice, V., Formato, V., Galper, A. M., Grishantseva, L., Karelin, A. V., Koldashov, S. V., Koldobskiy, S., Krutkov, S. Y., Kvashnin, A. N., Leonov, A., Malakhov, V., Marcelli, L., Mayorov, A. G., Menn, W., Mikhailov, V. V., Mocchiutti, E., Monaco, A., Mori, N., Nikonov, N., Osteria, G., Palma, F., Papini, P., Pearce, M., Picozza, P., Pizzolotto, C., Ricci, M., Ricciarini, S. B., Rossetto, L., Sarkar, R., Simon, M., Sparvoli, R., Spillantini, P., Stozhkov, Y. I., Vacchi, A., Vannuccini, E., Vasilyev, G., Voronov, S. A., Yurkin, Y. T., Wu, J., Zampa, G., Zampa, N., Zverev, V. G., Potgieter, M. S., Vos, E. E., Mar. 2013b. Time Dependence of the Proton Flux Measured by PAMELA during the 2006 July-2009 December Solar Minimum. ApJ765, 91.
- Adriani et al. (2016) Adriani, O., Barbarino, G. C., Bazilevskaya, G. A., Bellotti, R., Boezio, M., Bogomolov, E. A., Bongi, M., Bonvicini, V., Bottai, S., Bruno, A., Cafagna, F., Campana, D., Carlson, P., Casolino, M., Castellini, G., De Santis, C., Di Felice, V., Galper, A. M., Karelin, A. V., Koldashov, S. V., Koldobskiy, S. A., Krutkov, S. Y., Kvashnin, A. N., Leonov, A., Malakhov, V., Marcelli, L., Martucci, M., Mayorov, A. G., Menn, W., Mergé, M., Mikhailov, V. V., Mocchiutti, E., Monaco, A., Mori, N., Munini, R., Osteria, G., Panico, B., Papini, P., Pearce, M., Picozza, P., Ricci, M., Ricciarini, S. B., Simon, M., Sparvoli, R., Spillantini, P., Stozhkov, Y. I., Vacchi, A., Vannuccini, E., Vasilyev, G. I., Voronov, S. A., Yurkin, Y. T., Zampa, G., Zampa, N., Potgieter, M. S., Vos, E. E., Jun 2016. Time Dependence of the Electron and Positron Components of the Cosmic Radiation Measured by the PAMELA Experiment between July 2006 and December 2015. Phys. Rev. Lett.116 (24), 241105.
- Aguilar et al. (2014a) Aguilar, M., Aisa, D., Alpat, B., Alvino, A., Ambrosi, G., Andeen, K., Arruda, L., Attig, N., Azzarello, P., Bachlechner, A., et al., Nov. 2014a. Precision Measurement of the (e++e-) Flux in Primary Cosmic Rays from 0.5 GeV to 1 TeV with the Alpha Magnetic Spectrometer on the International Space Station. Physical Review Letters 113 (22), 221102.
- Aguilar et al. (2014b) Aguilar, M., Aisa, D., Alvino, A., Ambrosi, G., Andeen, K., Arruda, L., Attig, N., Azzarello, P., Bachlechner, A., Barao, F., et al., Sep. 2014b. Electron and Positron Fluxes in Primary Cosmic Rays Measured with the Alpha Magnetic Spectrometer on the International Space Station. Physical Review Letters 113 (12), 121102.
- Aguilar et al. (2017) Aguilar, M., Ali Cavasonza, L., Alpat, B., Ambrosi, G., Arruda, L., Attig, N., Aupetit, S., Azzarello, P., Bachlechner, A., Barao, F., et al., Dec. 2017. Observation of the Identical Rigidity Dependence of He, C, and O Cosmic Rays at High Rigidities by the Alpha Magnetic Spectrometer on the International Space Station. Phys. Rev. Lett.119 (25), 251101.
- Aguilar et al. (2018a) Aguilar, M., Ali Cavasonza, L., Alpat, B., Ambrosi, G., Arruda, L., Attig, N., Aupetit, S., Azzarello, P., Bachlechner, A., Barao, F., et al., Aug 2018a. Observation of Fine Time Structures in the Cosmic Proton and Helium Fluxes with the Alpha Magnetic Spectrometer on the International Space Station. Phys. Rev. Lett.121 (5), 051101.
- Aguilar et al. (2018b) Aguilar, M., Ali Cavasonza, L., Alpat, B., Ambrosi, G., Arruda, L., Attig, N., Aupetit, S., Azzarello, P., Bachlechner, A., Barao, F., et al., Jan. 2018b. Observation of New Properties of Secondary Cosmic Rays Lithium, Beryllium, and Boron by the Alpha Magnetic Spectrometer on the International Space Station. Phys. Rev. Lett.120 (02), 021101.
-
Aguilar et al. (2019a)
Aguilar, M., Ali Cavasonza, L., Alpat, B., Ambrosi, G., Arruda, L., Attig, N.,
Azzarello, P., Bachlechner, A., Barao, F., Barrau, A., Barrin, L., Bartoloni,
A., Basara, L., Başeğmez-du Pree, S., Battiston, R., Becker, U.,
Behlmann, M., Beischer, B., Berdugo, J., Bertucci, B., Bindi, V., de Boer,
W., Bollweg, K., Borgia, B., Boschini, M. J., Bourquin, M., Bueno, E. F.,
Burger, J., Burger, W. J., Cai, X. D., Capell, M., Caroff, S., Casaus, J.,
Castellini, G., Cervelli, F., Chang, Y. H., Chen, G. M., Chen, H. S., Chen,
Y., Cheng, L., Chou, H. Y., Choutko, V., Chung, C. H., Clark, C., Coignet,
G., Consolandi, C., Contin, A., Corti, C., Crispoltoni, M., Cui, Z., Dadzie,
K., Dai, Y. M., Datta, A., Delgado, C., Della Torre, S., Demirköz, M. B.,
Derome, L., Di Falco, S., Di Felice, V., Dimiccoli, F., Díaz, C., von
Doetinchem, P., Dong, F., Donnini, F., Duranti, M., Egorov, A., Eline, A.,
Eronen, T., Feng, J., Fiandrini, E., Fisher, P., Formato, V., Galaktionov,
Y., García-López, R. J., Gargiulo, C., Gast, H., Gebauer, I., Gervasi,
M., Giovacchini, F., Gómez-Coral, D. M., Gong, J., Goy, C., Grabski, V.,
Grandi, D., Graziani, M., Guo, K. H., Haino, S., Han, K. C., He, Z. H., Heil,
M., Hsieh, T. H., Huang, H., Huang, Z. C., Incagli, M., Jia, Y., Jinchi, H.,
Kanishev, K., Khiali, B., Kirn, T., Konak, C., Kounina, O., Kounine, A.,
Koutsenko, V., Kulemzin, A., La Vacca, G., Laudi, E., Laurenti, G.,
Lazzizzera, I., Lebedev, A., Lee, H. T., Lee, S. C., Leluc, C., Li, J. Q.,
Li, Q., Li, T. X., Li, Z. H., Light, C., Lin, C. H., Lippert, T., Liu, F. Z.,
Liu, H., Liu, Z., Lu, S. Q., Lu, Y. S., Luebelsmeyer, K., Luo, F., Luo,
J. Z., Luo, X., Lyu, S. S., Machate, F., Mañá, C., Marín, J.,
Martin, T., Martínez, G., Masi, N., Maurin, D., Menchaca-Rocha, A.,
Meng, Q., Mo, D. C., Molero, M., Mott, P., Mussolin, L., Nelson, T., Ni,
J. Q., Nikonov, N., Nozzoli, F., Oliva, A., Orcinha, M., Palermo, M.,
Palmonari, F., Paniccia, M., Pashnin, A., Pauluzzi, M., Pensotti, S.,
Perrina, C., Phan, H. D., Picot-Clemente, N., Plyaskin, V., Pohl, M.,
Poireau, V., Popkow, A., Quadrani, L., Qi, X. M., Qin, X., Qu, Z. Y.,
Rancoita, P. G., Rapin, D., Conde, A. R., Rosier-Lees, S., Rozhkov, A.,
Rozza, D., Sagdeev, R., Solano, C., Schael, S., Schmidt, S. M., von Dratzig,
A. S., Schwering, G., Seo, E. S., Shan, B. S., Shi, J. Y., Siedenburg, T.,
Song, J. W., Sun, Z. T., Tacconi, M., Tang, X. W., Tang, Z. C., Tian, J.,
Ting, S. C. C., Ting, S. M., Tomassetti, N., Torsti, J., Urban, T., Vagelli,
V., Valente, E., Valtonen, E., Acosta, M. V., Vecchi, M., Velasco, M.,
Vialle, J. P., Vizán, J., Wang, L. Q., Wang, N. H., Wang, Q. L., Wang, X.,
Wang, X. Q., Wang, Z. X., Wei, J., Weng, Z. L., Wu, H., Xiong, R. Q., Xu, W.,
Yan, Q., Yang, Y., Yi, H., Yu, Y. J., Yu, Z. Q., Zannoni, M., Zeissler, S.,
Zhang, C., Zhang, F., Zhang, J. H., Zhang, Z., Zhao, F., Zheng, Z. M.,
Zhuang, H. L., Zhukov, V., Zichichi, A., Zimmermann, N., Zuccon, P., Mar
2019a. Towards understanding the origin of cosmic-ray electrons.
Phys. Rev. Lett. 122, 101101.
URL https://link.aps.org/doi/10.1103/PhysRevLett.122.101101 -
Aguilar et al. (2019b)
Aguilar, M., Ali Cavasonza, L., Ambrosi, G., Arruda, L., Attig, N., Azzarello,
P., Bachlechner, A., Barao, F., Barrau, A., Barrin, L., Bartoloni, A.,
Basara, L., Başeğmez-du Pree, S., Battiston, R., Becker, U., Behlmann, M., Beischer,
B., Berdugo, J., Bertucci, B., Bindi, V., de Boer, W., Bollweg, K., Borgia,
B., Boschini, M. J., Bourquin, M., Bueno, E. F., Burger, J., Burger, W. J.,
Cai, X. D., Capell, M., Caroff, S., Casaus, J., Castellini, G., Cervelli, F.,
Chang, Y. H., Chen, G. M., Chen, H. S., Chen, Y., Cheng, L., Chou, H. Y.,
Choutko, V., Chung, C. H., Clark, C., Coignet, G., Consolandi, C., Contin,
A., Corti, C., Crispoltoni, M., Cui, Z., Dadzie, K., Dai, Y. M., Datta, A.,
Delgado, C., Della Torre, S., Demirköz, M. B., Derome, L., Di Falco, S.,
Dimiccoli, F., Díaz, C., von Doetinchem, P., Dong, F., Donnini, F.,
Duranti, M., Egorov, A., Eline, A., Eronen, T., Feng, J., Fiandrini, E.,
Fisher, P., Formato, V., Galaktionov, Y., García-López, R. J.,
Gargiulo, C., Gast, H., Gebauer, I., Gervasi, M., Giovacchini, F.,
Gómez-Coral, D. M., Gong, J., Goy, C., Grabski, V., Grandi, D., Graziani,
M., Guo, K. H., Haino, S., Han, K. C., He, Z. H., Heil, M., Hsieh, T. H.,
Huang, H., Huang, Z. C., Incagli, M., Jia, Y., Jinchi, H., Kanishev, K.,
Khiali, B., Kirn, T., Konak, C., Kounina, O., Kounine, A., Koutsenko, V.,
Kulemzin, A., La Vacca, G., Laudi, E., Laurenti, G., Lazzizzera, I., Lebedev,
A., Lee, H. T., Lee, S. C., Leluc, C., Li, J. Q., Li, Q., Li, T. X., Li,
Z. H., Light, C., Lin, C. H., Lippert, T., Liu, F. Z., Liu, H., Liu, Z., Lu,
S. Q., Lu, Y. S., Luebelsmeyer, K., Luo, F., Luo, J. Z., Luo, X., Lyu, S. S.,
Machate, F., Mañá, C., Marín, J., Martin, T., Martínez, G.,
Masi, N., Maurin, D., Menchaca-Rocha, A., Meng, Q., Mo, D. C., Molero, M.,
Mott, P., Mussolin, L., Nelson, T., Ni, J. Q., Nikonov, N., Nozzoli, F.,
Oliva, A., Orcinha, M., Palermo, M., Palmonari, F., Paniccia, M., Pashnin,
A., Pauluzzi, M., Pensotti, S., Perrina, C., Phan, H. D., Picot-Clemente, N.,
Plyaskin, V., Pohl, M., Poireau, V., Popkow, A., Quadrani, L., Qi, X. M.,
Qin, X., Qu, Z. Y., Rancoita, P. G., Rapin, D., Conde, A. R., Rosier-Lees,
S., Rozhkov, A., Rozza, D., Sagdeev, R., Solano, C., Schael, S., Schmidt,
S. M., Schulz von Dratzig, A., Schwering, G., Seo, E. S., Shan, B. S., Shi,
J. Y., Siedenburg, T., Song, J. W., Sun, Z. T., Tacconi, M., Tang, X. W.,
Tang, Z. C., Tian, J., Ting, S. C. C., Ting, S. M., Tomassetti, N., Torsti,
J., Urban, T., Vagelli, V., Valente, E., Valtonen, E., Vázquez Acosta, M.,
Vecchi, M., Velasco, M., Vialle, J. P., Vizán, J., Wang, L. Q., Wang,
N. H., Wang, Q. L., Wang, X., Wang, X. Q., Wang, Z. X., Wei, J., Weng, Z. L.,
Wu, H., Xiong, R. Q., Xu, W., Yan, Q., Yang, Y., Yi, H., Yu, Y. J., Yu,
Z. Q., Zannoni, M., Zeissler, S., Zhang, C., Zhang, F., Zhang, J. H., Zhang,
Z., Zhao, F., Zheng, Z. M., Zhuang, H. L., Zhukov, V., Zichichi, A.,
Zimmermann, N., Zuccon, P., Jan 2019b. Towards understanding the
origin of cosmic-ray positrons. Phys. Rev. Lett. 122, 041102.
URL https://link.aps.org/doi/10.1103/PhysRevLett.122.041102 - Aguilar et al. (2018c) Aguilar, M., Cavasonza, L. A., Ambrosi, G., Arruda, L., Attig, N., Aupetit, S., Azzarello, P., Bachlechner, A., Barao, F., Barrau, A., et al., Aug 2018c. Observation of Complex Time Structures in the Cosmic-Ray Electron and Positron Fluxes with the Alpha Magnetic Spectrometer on the International Space Station. Phys. Rev. Lett.121 (5), 051102.
- Ahn et al. (2010) Ahn, H. S., Allison, P., Bagliesi, M. G., Beatty, J. J., Bigongiari, G., Childers, J. T., Conklin, N. B., Coutu, S., DuVernois, M. A., Ganel, O., Han, J. H., Jeon, J. A., Kim, K. C., Lee, M. H., Lutz, L., Maestro, P., Malinin, A., Marrocchesi, P. S., Minnick, S., Mognet, S. I., Nam, J., Nam, S., Nutter, S. L., Park, I. H., Park, N. H., Seo, E. S., Sina, R., Wu, J., Yang, J., Yoon, Y. S., Zei, R., Zinn, S. Y., May 2010. Discrepant Hardening Observed in Cosmic-ray Elemental Spectra. ApJ714, L89–L93.
- An et al. (2019) An, Q., Asfandiyarov, R., Azzarello, P., Bernardini, P., Bi, X. J., Cai, M. S., Chang, J., Chen, D. Y., Chen, H. F., Chen, J. L., Chen, W., Cui, M. Y., Cui, T. S., Dai, H. T., D’Amone, A., De Benedittis, A., De Mitri, I., Di Santo, M., Ding, M., Dong, T. K., Dong, Y. F., Dong, Z. X., Donvito, G., Droz, D., Duan, J. L., Duan, K. K., D’Urso, D., Fan, R. R., Fan, Y. Z., Fang, F., Feng, C. Q., Feng, L., Fusco, P., Gallo, V., Gan, F. J., Gao, M., Gargano, F., Gong, K., Gong, Y. Z., Guo, D. Y., Guo, J. H., Guo, X. L., Han, S. X., Hu, Y. M., Huang, G. S., Huang, X. Y., Huang, Y. Y., Ionica, M., Jiang, W., Jin, X., Kong, J., Lei, S. J., Li, S., Li, W. L., Li, X., Li, X. Q., Li, Y., Liang, Y. F., Liang, Y. M., Liao, N. H., Liu, C. M., Liu, H., Liu, J., Liu, S. B., Liu, W. Q., Liu, Y., Loparco, F., Luo, C. N., Ma, M., Ma, P. X., Ma, S. Y., Ma, T., Ma, X. Y., Marsella, G., Mazziotta, M. N., Mo, D., Niu, X. Y., Pan, X., Peng, W. X., Peng, X. Y., Qiao, R., Rao, J. N., Salinas, M. M., Shang, G. Z., Shen, W. H., Shen, Z. Q., Shen, Z. T., Song, J. X., Su, H., Su, M., Sun, Z. Y., Surdo, A., Teng, X. J., Tykhonov, A., Vitillo, S., Wang, C., Wang, H., Wang, H. Y., Wang, J. Z., Wang, L. G., Wang, Q., Wang, S., Wang, X. H., Wang, X. L., Wang, Y. F., Wang, Y. P., Wang, Y. Z., Wang, Z. M., Wei, D. M., Wei, J. J., Wei, Y. F., Wen, S. C., Wu, D., Wu, J., Wu, L. B., Wu, S. S., Wu, X., Xi, K., Xia, Z. Q., Xu, H. T., Xu, Z. H., Xu, Z. L., Xu, Z. Z., Xue, G. F., Yang, H. B., Yang, P., Yang, Y. Q., Yang, Z. L., Yao, H. J., Yu, Y. H., Yuan, Q., Yue, C., Zang, J. J., Zhang, F., Zhang, J. Y., Zhang, J. Z., Zhang, P. F., Zhang, S. X., Zhang, W. Z., Zhang, Y., Zhang, Y. J., Zhang, Y. L., Zhang, Y. P., Zhang, Y. Q., Zhang, Z., Zhang, Z. Y., Zhao, H., Zhao, H. Y., Zhao, X. F., Zhou, C. Y., Zhou, Y., Zhu, X., Zhu, Y., Zimmer, S., Sep 2019. Measurement of the cosmic-ray proton spectrum from 40 GeV to 100 TeV with the DAMPE satellite. Science Advances 5 (9), eaax3793.
- Atkin et al. (2018) Atkin, E., Bulatov, V., Dorokhov, V., Gorbunov, N., Filippov, S., Grebenyuk, V., Karmanov, D., Kovalev, I., Kudryashov, I., Kurganov, A., Merkin, M., Panov, A., Podorozhny, D., Polkov, D., Porokhovoy, S., Shumikhin, V., Tkachenko, A., Tkachev, L., Turundaevskiy, A., Vasiliev, O., Voronin, A., Jul. 2018. New Universal Cosmic-Ray Knee near a Magnetic Rigidity of 10 TV with the NUCLEON Space Observatory. Soviet Journal of Experimental and Theoretical Physics Letters 108, 5–12.
- Bisschoff and Potgieter (2016) Bisschoff, D., Potgieter, M. S., Feb 2016. New local interstellar spectra for protons, helium and carbon derived from PAMELA and Voyager 1 observations. Astrophys. Space Sci361, 48.
-
Bisschoff et al. (2019)
Bisschoff, D., Potgieter, M. S., Aslam, O. P. M., Jun 2019. New very local
interstellar spectra for electrons, positrons, protons, and light cosmic ray
nuclei. The Astrophysical Journal 878 (1), 59.
URL http://dx.doi.org/10.3847/1538-4357/ab1e4a - Boschini et al. (2018) Boschini, M. J., Della Torre, S., Gervasi, M., Grand i, D., Jóhannesson, G., La Vacca, G., Masi, N., Moskalenko, I. V., Pensotti, S., Porter, T. A., Quadrani, L., Rancoita, P. G., Rozza, D., Tacconi, M., Feb 2018. HelMod in the Works: From Direct Observations to the Local Interstellar Spectrum of Cosmic-Ray Electrons. ApJ854 (2), 94.
- Boschini et al. (2017) Boschini, M. J., Della Torre, S., Gervasi, M., Grandi, D., Jóhannesson, G., Kachelriess, M., La Vacca, G., Masi, N., Moskalenko, I. V., Orlando, E., Ostapchenko, S. S., Pensotti, S., Porter, T. A., Quadrani, L., Rancoita, P. G., Rozza, D., Tacconi, M., May 2017. Solution of Heliospheric Propagation: Unveiling the Local Interstellar Spectra of Cosmic-ray Species. ApJ840, 115.
- Corti et al. (2016) Corti, C., Bindi, V., Consolandi, C., Whitman, K., Sep. 2016. Solar Modulation of the Local Interstellar Spectrum with Voyager 1, AMS-02, PAMELA, and BESS. ApJ829, 8.
- Corti et al. (2019) Corti, C., Potgieter, M. S., Bindi, V., Consolandi, C., Light, C., Palermo, M., Popkow, A., Feb 2019. Numerical Modeling of Galactic Cosmic-Ray Proton and Helium Observed by AMS-02 during the Solar Maximum of Solar Cycle 24. ApJ871 (2), 253.
- Cummings et al. (2016) Cummings, A. C., Stone, E. C., Heikkila, B. C., Lal, N., Webber, W. R., Jóhannesson, G., Moskalenko, I. V., Orlando, E., Porter, T. A., Nov. 2016. Galactic Cosmic Rays in the Local Interstellar Medium: Voyager 1 Observations and Model Results. ApJ831, 18.
- DAMPE Collaboration et al. (2017) DAMPE Collaboration, Ambrosi, G., An, Q., Asfandiyarov, R., Azzarello, P., Bernardini, P., Bertucci, B., Cai, M. S., Chang, J., Chen, D. Y., Chen, H. F., Chen, J. L., Chen, W., Cui, M. Y., Cui, T. S., D’Amone, A., de Benedittis, A., De Mitri, I., di Santo, M., Dong, J. N., Dong, T. K., Dong, Y. F., Dong, Z. X., Donvito, G., Droz, D., Duan, K. K., Duan, J. L., Duranti, M., D’Urso, D., Fan, R. R., Fan, Y. Z., Fang, F., Feng, C. Q., Feng, L., Fusco, P., Gallo, V., Gan, F. J., Gao, M., Gao, S. S., Gargano, F., Garrappa, S., Gong, K., Gong, Y. Z., Guo, D. Y., Guo, J. H., Hu, Y. M., Huang, G. S., Huang, Y. Y., Ionica, M., Jiang, D., Jiang, W., Jin, X., Kong, J., Lei, S. J., Li, S., Li, X., Li, W. L., Li, Y., Liang, Y. F., Liang, Y. M., Liao, N. H., Liu, H., Liu, J., Liu, S. B., Liu, W. Q., Liu, Y., Loparco, F., Ma, M., Ma, P. X., Ma, S. Y., Ma, T., Ma, X. Q., Ma, X. Y., Marsella, G., Mazziotta, M. N., Mo, D., Niu, X. Y., Peng, X. Y., Peng, W. X., Qiao, R., Rao, J. N., Salinas, M. M., Shang, G. Z., H. Shen, W., Shen, Z. Q., Shen, Z. T., Song, J. X., Su, H., Su, M., Sun, Z. Y., Surdo, A., Teng, X. J., Tian, X. B., Tykhonov, A., Vagelli, V., Vitillo, S., Wang, C., Wang, H., Wang, H. Y., Wang, J. Z., Wang, L. G., Wang, Q., Wang, S., Wang, X. H., Wang, X. L., Wang, Y. F., Wang, Y. P., Wang, Y. Z., Wen, S. C., Wang, Z. M., Wei, D. M., Wei, J. J., Wei, Y. F., Wu, D., Wu, J., Wu, L. B., Wu, S. S., Wu, X., Xi, K., Xia, Z. Q., Xin, Y. L., Xu, H. T., Xu, Z. L., Xu, Z. Z., Xue, G. F., Yang, H. B., Yang, P., Yang, Y. Q., Yang, Z. L., Yao, H. J., Yu, Y. H., Yuan, Q., Yue, C., Zang, J. J., Zhang, C., Zhang, D. L., Zhang, F., Zhang, J. B., Zhang, J. Y., Zhang, J. Z., Zhang, L., Zhang, P. F., Zhang, S. X., Zhang, W. Z., Zhang, Y., Zhang, Y. J., Zhang, Y. Q., Zhang, Y. L., Zhang, Y. P., Zhang, Z., Zhang, Z. Y., Zhao, H., Zhao, H. Y., Zhao, X. F., Zhou, C. Y., Zhou, Y., Zhu, X., Zhu, Y., Zimmer, S., Dec. 2017. Direct detection of a break in the teraelectronvolt cosmic-ray spectrum of electrons and positrons. Nature552, 63–66.
- Gabici et al. (2019) Gabici, S., Evoli, C., Gaggero, D., Lipari, P., Mertsch, P., Orlando, E., Strong, A., Vittino, A., Jan 2019. The origin of Galactic cosmic rays: Challenges to the standard paradigm. International Journal of Modern Physics D 28 (15), 1930022–339.
- Ghelfi et al. (2016) Ghelfi, A., Barao, F., Derome, L., Maurin, D., Jun. 2016. Non-parametric determination of H and He interstellar fluxes from cosmic-ray data. A&A591, A94.
- Ghelfi et al. (2017) Ghelfi, A., Maurin, D., Cheminet, A., Derome, L., Hubert, G., Melot, F., Aug. 2017. Neutron monitors and muon detectors for solar modulation studies: 2. time series. Advances in Space Research 60, 833–847.
- Gleeson and Axford (1967) Gleeson, L. J., Axford, W. I., Sep. 1967. Cosmic Rays in the Interplanetary Medium. ApJ149, L115.
- Gleeson and Axford (1968) Gleeson, L. J., Axford, W. I., Dec. 1968. Solar Modulation of Galactic Cosmic Rays. ApJ154, 1011.
- Jokipii and Kopriva (1979) Jokipii, J. R., Kopriva, D. A., Nov. 1979. Effects of particle drift on the transport of cosmic rays. III. Numerical models of galactic cosmic-ray modulation. ApJ234, 384–392.
- Kachelrieß and Semikoz (2019) Kachelrieß, M., Semikoz, D. V., Nov 2019. Cosmic ray models. Progress in Particle and Nuclear Physics 109, 103710.
- Kappl (2016) Kappl, R., Oct. 2016. SOLARPROP: Charge-sign dependent solar modulation for everyone. Computer Physics Communications 207, 386–399.
- Kóta and Jokipii (2014) Kóta, J., Jokipii, J. R., Feb. 2014. Are Cosmic Rays Modulated beyond the Heliopause? ApJ782 (1), 24.
-
Kuhlen and Mertsch (2019)
Kuhlen, M., Mertsch, P., Dec 2019. Time-dependent ams-02 electron-positron
fluxes in an extended force-field model. Physical Review Letters 123 (25).
URL http://dx.doi.org/10.1103/PhysRevLett.123.251104 - Lewis and Bridle (2002) Lewis, A., Bridle, S., Nov. 2002. Cosmological parameters from CMB and other data: A Monte Carlo approach. Phys. Rev. D66 (10), 103511.
- Lin et al. (2015) Lin, S.-J., Yuan, Q., Bi, X.-J., Mar. 2015. Quantitative study of the AMS-02 electron/positron spectra: Implications for pulsars and dark matter properties. Phys. Rev. D91 (6), 063508.
- Luo et al. (2017) Luo, X., Potgieter, M. S., Zhang, M., Feng, X., Apr. 2017. A Numerical Study of Forbush Decreases with a 3D Cosmic-Ray Modulation Model Based on an SDE Approach. ApJ839, 53.
- Martucci et al. (2018) Martucci, M., Munini, R., Boezio, M., Di Felice, V., Adriani, O., Barbarino, G. C., Bazilevskaya, G. A., Bellotti, R., Bongi, M., Bonvicini, V., Bottai, S., Bruno, A., Cafagna, F., Campana, D., Carlson, P., Casolino, M., Castellini, G., De Santis, C., Galper, A. M., Karelin, A. V., Koldashov, S. V., Koldobskiy, S., Krutkov, S. Y., Kvashnin, A. N., Leonov, A., Malakhov, V., Marcelli, L., Marcelli, N., Mayorov, A. G., Menn, W., Mergè, M., Mikhailov, V. V., Mocchiutti, E., Monaco, A., Mori, N., Osteria, G., Panico, B., Papini, P., Pearce, M., Picozza, P., Ricci, M., Ricciarini, S. B., Simon, M., Sparvoli, R., Spillantini, P., Stozhkov, Y. I., Vacchi, A., Vannuccini, E., Vasilyev, G., Voronov, S. A., Yurkin, Y. T., Zampa, G., Zampa, N., Potgieter, M. S., Raath, J. L., Feb 2018. Proton Fluxes Measured by the PAMELA Experiment from the Minimum to the Maximum Solar Activity for Solar Cycle 24. ApJ854 (1), L2.
- Moskalenko and Strong (1998) Moskalenko, I. V., Strong, A. W., Jan. 1998. Production and Propagation of Cosmic-Ray Positrons and Electrons. ApJ493, 694–707.
- Potgieter and Vos (2017) Potgieter, M. S., Vos, E. E., May 2017. Difference in the heliospheric modulation of cosmic-ray protons and electrons during the solar minimum period of 2006 to 2009. A&A601, A23.
- Scherer et al. (2011) Scherer, K., Fichtner, H., Strauss, R. D., Ferreira, S. E. S., Potgieter, M. S., Fahr, H. J., Jul. 2011. On Cosmic Ray Modulation beyond the Heliopause: Where is the Modulation Boundary? ApJ735 (2), 128.
- Stone et al. (2013) Stone, E. C., Cummings, A. C., McDonald, F. B., Heikkila, B. C., Lal, N., Webber, W. R., Jul. 2013. Voyager 1 Observes Low-Energy Galactic Cosmic Rays in a Region Depleted of Heliospheric Ions. Science 341, 150–153.
- Strauss et al. (2011) Strauss, R. D., Potgieter, M. S., Büsching, I., Kopp, A., Jul. 2011. Modeling the Modulation of Galactic and Jovian Electrons by Stochastic Processes. ApJ735 (2), 83.
- Strauss et al. (2012) Strauss, R. D., Potgieter, M. S., Büsching, I., Kopp, A., Jun. 2012. Modelling heliospheric current sheet drift in stochastic cosmic ray transport models. Astrophys. Space Sci339 (2), 223–236.
- Sun et al. (2015) Sun, X., Hoeksema, J. T., Liu, Y., Zhao, J., Jan. 2015. On Polar Magnetic Field Reversal and Surface Flux Transport During Solar Cycle 24. ApJ798, 114.
- Tomassetti et al. (2018) Tomassetti, N., Barão, F., Bertucci, B., Fiand rini, E., Figueiredo, J. L., Lousada, J. B., Orcinha, M., Dec 2018. Testing Diffusion of Cosmic Rays in the Heliosphere with Proton and Helium Data from AMS. Phys. Rev. Lett.121 (25), 251104.
- Tomassetti et al. (2017) Tomassetti, N., Orcinha, M., Barão, F., Bertucci, B., Nov. 2017. Evidence for a Time Lag in Solar Modulation of Galactic Cosmic Rays. ApJ849, L32.
- Usoskin et al. (2011) Usoskin, I. G., Bazilevskaya, G. A., Kovaltsov, G. A., Feb. 2011. Solar modulation parameter for cosmic rays since 1936 reconstructed from ground-based neutron monitors and ionization chambers. Journal of Geophysical Research (Space Physics) 116, A02104.
- Vittino et al. (2019) Vittino, A., Mertsch, P., Gast, H., Schael, S., Aug 2019. Breaks in interstellar spectra of positrons and electrons derived from time-dependent AMS data. Phys. Rev. D100 (4), 043007.
- Wang et al. (2019) Wang, B.-B., Bi, X.-J., Fang, K., Lin, S.-J., Yin, P.-F., Sep 2019. Time-dependent solar modulation of cosmic rays from solar minimum to solar maximum. Phys. Rev. D100 (6), 063006.
- Zhu et al. (2018) Zhu, C.-R., Yuan, Q., Wei, D.-M., Aug 2018. Studies on Cosmic-Ray Nuclei with Voyager, ACE, and AMS-02. I. Local Interstellar Spectra and Solar Modulation. ApJ863 (2), 119.
| Flux | ||
|---|---|---|
| (GeV) | (m-2s-1sr-1GeV-1) | (m-2s-1sr-1GeV-1) |
| 1.362e+00 | 9.884e+01 | 6.048e+00 |
| 1.522e+00 | 7.434e+01 | 3.808e+00 |
| 1.702e+00 | 5.801e+01 | 2.516e+00 |
| 1.902e+00 | 4.587e+01 | 1.715e+00 |
| 2.122e+00 | 3.541e+01 | 1.149e+00 |
| 2.372e+00 | 2.705e+01 | 7.625e-01 |
| 2.642e+00 | 2.095e+01 | 5.260e-01 |
| 2.942e+00 | 1.574e+01 | 3.546e-01 |
| 3.262e+00 | 1.203e+01 | 2.462e-01 |
| 3.612e+00 | 9.030e+00 | 1.710e-01 |
| 3.962e+00 | 6.882e+00 | 1.221e-01 |
| 4.332e+00 | 5.324e+00 | 8.943e-02 |
| 4.712e+00 | 4.131e+00 | 6.618e-02 |
| 5.112e+00 | 3.191e+00 | 4.864e-02 |
| 5.552e+00 | 2.449e+00 | 3.624e-02 |
| 6.032e+00 | 1.867e+00 | 2.701e-02 |
| 6.532e+00 | 1.430e+00 | 2.060e-02 |
| 7.052e+00 | 1.106e+00 | 1.528e-02 |
| 7.602e+00 | 8.580e-01 | 1.161e-02 |
| 8.182e+00 | 6.668e-01 | 8.916e-03 |
| 8.782e+00 | 5.206e-01 | 6.966e-03 |
| 9.412e+00 | 4.071e-01 | 5.330e-03 |
| 1.007e+01 | 3.236e-01 | 4.271e-03 |
| 1.075e+01 | 2.569e-01 | 3.311e-03 |
| 1.146e+01 | 2.053e-01 | 2.738e-03 |
| 1.220e+01 | 1.645e-01 | 2.195e-03 |
| 1.298e+01 | 1.327e-01 | 1.696e-03 |
| 1.378e+01 | 1.076e-01 | 1.405e-03 |
| 1.461e+01 | 8.775e-02 | 1.153e-03 |
| 1.548e+01 | 7.152e-02 | 9.430e-04 |
| 1.638e+01 | 5.870e-02 | 7.742e-04 |
| 1.731e+01 | 4.812e-02 | 6.407e-04 |
| 1.827e+01 | 3.998e-02 | 5.342e-04 |
| 1.927e+01 | 3.325e-02 | 4.408e-04 |
| 2.030e+01 | 2.786e-02 | 3.706e-04 |
| 2.137e+01 | 2.314e-02 | 3.143e-04 |
| 2.247e+01 | 1.938e-02 | 2.675e-04 |
| 2.362e+01 | 1.632e-02 | 2.216e-04 |
| 2.480e+01 | 1.378e-02 | 1.887e-04 |
| 2.604e+01 | 1.169e-02 | 1.669e-04 |
| 2.735e+01 | 9.795e-03 | 1.359e-04 |
| 2.874e+01 | 8.292e-03 | 1.160e-04 |
| 3.022e+01 | 6.983e-03 | 9.828e-05 |
| 3.179e+01 | 5.816e-03 | 8.179e-05 |
| 3.345e+01 | 4.915e-03 | 6.980e-05 |
| 3.522e+01 | 4.131e-03 | 5.859e-05 |
| 3.711e+01 | 3.457e-03 | 4.978e-05 |
| 3.912e+01 | 2.923e-03 | 4.238e-05 |
| 4.127e+01 | 2.436e-03 | 3.567e-05 |
| 4.357e+01 | 2.024e-03 | 3.034e-05 |
| 4.605e+01 | 1.693e-03 | 2.510e-05 |
| 4.871e+01 | 1.413e-03 | 2.136e-05 |
| 5.159e+01 | 1.154e-03 | 1.711e-05 |
| 5.471e+01 | 9.572e-04 | 1.476e-05 |
| 5.811e+01 | 7.876e-04 | 1.235e-05 |
| 6.182e+01 | 6.353e-04 | 1.012e-05 |
| 6.590e+01 | 5.196e-04 | 8.374e-06 |
| 7.041e+01 | 4.168e-04 | 6.763e-06 |
| 7.544e+01 | 3.366e-04 | 5.614e-06 |
| 8.108e+01 | 2.665e-04 | 4.473e-06 |
| 8.748e+01 | 2.086e-04 | 3.567e-06 |
| 9.481e+01 | 1.606e-04 | 2.829e-06 |
| 1.034e+02 | 1.233e-04 | 2.237e-06 |
| 1.135e+02 | 9.016e-05 | 1.688e-06 |
| 1.258e+02 | 6.542e-05 | 1.261e-06 |
| 1.409e+02 | 4.582e-05 | 9.370e-07 |
| 1.597e+02 | 3.040e-05 | 6.509e-07 |
| 1.839e+02 | 1.869e-05 | 4.380e-07 |
| 2.170e+02 | 1.083e-05 | 2.881e-07 |
| 2.626e+02 | 6.014e-06 | 1.805e-07 |
| 3.276e+02 | 3.144e-06 | 1.111e-07 |
| 4.293e+02 | 1.283e-06 | 5.657e-08 |
| 5.896e+02 | 4.572e-07 | 2.940e-08 |
| 8.331e+02 | 1.774e-07 | 1.704e-08 |
| 1.179e+03 | 4.129e-08 | 7.348e-09 |
| Flux | ||
|---|---|---|
| (GeV) | (m-2s-1sr-1GeV-1) | (m-2s-1sr-1GeV-1) |
| 1.263e+00 | 1.311e+01 | 1.045e+00 |
| 1.423e+00 | 9.791e+00 | 5.609e-01 |
| 1.603e+00 | 7.052e+00 | 3.311e-01 |
| 1.803e+00 | 5.091e+00 | 2.042e-01 |
| 2.023e+00 | 3.536e+00 | 1.225e-01 |
| 2.273e+00 | 2.476e+00 | 7.476e-02 |
| 2.543e+00 | 1.746e+00 | 4.641e-02 |
| 2.843e+00 | 1.225e+00 | 2.920e-02 |
| 3.163e+00 | 8.760e-01 | 1.907e-02 |
| 3.513e+00 | 6.182e-01 | 1.248e-02 |
| 3.863e+00 | 4.491e-01 | 8.469e-03 |
| 4.233e+00 | 3.343e-01 | 6.019e-03 |
| 4.613e+00 | 2.505e-01 | 4.252e-03 |
| 5.013e+00 | 1.871e-01 | 3.051e-03 |
| 5.453e+00 | 1.403e-01 | 2.278e-03 |
| 5.933e+00 | 1.052e-01 | 1.649e-03 |
| 6.433e+00 | 7.886e-02 | 1.210e-03 |
| 6.953e+00 | 6.074e-02 | 9.165e-04 |
| 7.503e+00 | 4.722e-02 | 7.086e-04 |
| 8.083e+00 | 3.611e-02 | 5.333e-04 |
| 8.683e+00 | 2.842e-02 | 4.220e-04 |
| 9.313e+00 | 2.218e-02 | 3.306e-04 |
| 9.973e+00 | 1.767e-02 | 2.573e-04 |
| 1.065e+01 | 1.421e-02 | 2.128e-04 |
| 1.136e+01 | 1.142e-02 | 1.716e-04 |
| 1.210e+01 | 9.341e-03 | 1.428e-04 |
| 1.288e+01 | 7.727e-03 | 1.186e-04 |
| 1.368e+01 | 6.289e-03 | 9.868e-05 |
| 1.451e+01 | 5.120e-03 | 8.104e-05 |
| 1.538e+01 | 4.237e-03 | 6.774e-05 |
| 1.628e+01 | 3.559e-03 | 5.815e-05 |
| 1.721e+01 | 2.951e-03 | 4.939e-05 |
| 1.817e+01 | 2.478e-03 | 4.176e-05 |
| 1.917e+01 | 2.081e-03 | 3.517e-05 |
| 2.020e+01 | 1.786e-03 | 3.105e-05 |
| 2.127e+01 | 1.554e-03 | 2.701e-05 |
| 2.237e+01 | 1.293e-03 | 2.367e-05 |
| 2.352e+01 | 1.081e-03 | 1.974e-05 |
| 2.470e+01 | 9.560e-04 | 1.798e-05 |
| 2.594e+01 | 8.073e-04 | 1.549e-05 |
| 2.725e+01 | 7.114e-04 | 1.386e-05 |
| 2.864e+01 | 6.036e-04 | 1.209e-05 |
| 3.012e+01 | 5.304e-04 | 1.071e-05 |
| 3.169e+01 | 4.466e-04 | 9.349e-06 |
| 3.335e+01 | 3.839e-04 | 8.295e-06 |
| 3.512e+01 | 3.253e-04 | 7.175e-06 |
| 3.701e+01 | 2.860e-04 | 6.503e-06 |
| 3.902e+01 | 2.413e-04 | 5.452e-06 |
| 4.117e+01 | 2.073e-04 | 5.016e-06 |
| 4.347e+01 | 1.779e-04 | 4.426e-06 |
| 4.595e+01 | 1.491e-04 | 3.839e-06 |
| 4.861e+01 | 1.362e-04 | 3.545e-06 |
| 5.149e+01 | 1.057e-04 | 2.965e-06 |
| 5.461e+01 | 9.089e-05 | 2.608e-06 |
| 5.801e+01 | 7.742e-05 | 2.283e-06 |
| 6.172e+01 | 6.255e-05 | 1.949e-06 |
| 6.580e+01 | 5.620e-05 | 1.768e-06 |
| 7.031e+01 | 4.454e-05 | 1.475e-06 |
| 7.534e+01 | 3.897e-05 | 1.295e-06 |
| 8.098e+01 | 3.065e-05 | 1.084e-06 |
| 8.738e+01 | 2.551e-05 | 9.272e-07 |
| 9.471e+01 | 2.067e-05 | 7.762e-07 |
| 1.033e+02 | 1.481e-05 | 6.495e-07 |
| 1.134e+02 | 1.187e-05 | 5.264e-07 |
| 1.257e+02 | 8.774e-06 | 4.097e-07 |
| 1.408e+02 | 7.067e-06 | 3.311e-07 |
| 1.596e+02 | 4.635e-06 | 2.385e-07 |
| 1.838e+02 | 3.225e-06 | 1.750e-07 |
| 2.169e+02 | 1.883e-06 | 1.185e-07 |
| 2.625e+02 | 1.164e-06 | 8.170e-08 |
| 3.275e+02 | 5.798e-07 | 5.204e-08 |
| 4.292e+02 | 2.499e-07 | 3.011e-08 |
| 5.895e+02 | 8.332e-08 | 1.848e-08 |
| 8.330e+02 | 1.930e-08 | 1.176e-08 |