Liouvillian-gap analysis of open quantum many-body systems in the weak dissipation limit

We begin our discussion with the unitary time evolution of an Hermitian operator $\hat{A}(t)$ in the Heisenberg picture, which obeys Eq. 4 with $\gamma=0$, i.e., $d\hat{A}(t)/dt=i[\hat{H}(t),\hat{A}(t)]$. The effect of dissipation is taken into account in Sec. III.2.

Due to spin-spin interactions, even if $\hat{A}(0)$ is a local operator, $\hat{A}(t)$ at $t>0$ will spread over the system. In order to describe such operator growth, we introduce the notion of the average operator size $S[\hat{A}]$ of $\hat{A}$ [38, 39, 40, 41]. It is given by

where

According to this definition, a Pauli string $\hat{\sigma}_{i_{1}}^{\alpha_{1}}\hat{\sigma}_{i_{2}}^{\alpha_{2}}\dots\hat{\sigma}_{i_{\ell}}^{\alpha_{\ell}}$ with $1\leq i_{1}<i_{2}<\dots<i_{\ell}<L$ and $\alpha_{i}\in\{x,y,z\}$ has the operator size $\ell$. The average operator size of $\sigma_{i}^{x}\sigma_{j}^{x}+\sigma_{k}^{z}$ with $i\neq j$, for example, is $1.5$. The relation between the average operator size of Eq. 7 and out-of-time-ordered correlations (OTOCs) [42, 43, 44] is discussed in Refs. [38, 39, 41].

In a short-range interacting spin chain, $S[\hat{A}(t)]$ usually increases in a linear way: $S[\hat{A}(t)]\sim vt$ with $v>0$ being a constant that is independent of the system size (its upper bound is given by the Lieb-Robinson velocity [45]). Eventually, the operator will spread over the entire system for $t\gtrsim L/v$, and the operator size will be saturated at a value that is proportional to $L$, which is called the operator scrambling.

In the absence of dissipation, the time evolution is unitary and Liouvillian eigenvalues $\{\lambda_{\alpha}\}$ are pure imaginary. Therefore, $g=0$ at $\gamma=0$ for any finite system. It would be a bit surprise if we have $g>0$ in the limit of $\gamma\to+0$, which is indeed the case as we argue below.

In the previous subsection, we discuss the operator spreading under the unitary time evolution. Now we consider the effect of very weak bulk dissipation $\gamma>0$ to this operator dynamics. In this section, we assume that the system is intrinsically chaotic and has no local conserved quantity when it is completely isolated from the environment (i.e. $\gamma=0$). When $\gamma t\ll 1$, it is expected that dissipation has essentially no effect. Therefore, if $\gamma\ll v/L$, the system undergoes dissipative relaxation after the saturation of the operator size $S[\hat{A}(t)]\sim L$. A crucial observation is that the influence of the bulk dissipation on $\hat{A}(t)$ is proportional to its operator size $S[\hat{A}(t)]$ [34]. It is understood from the fact that the dissipator $\mathcal{D}=\sum_{i=1}^{L}\mathcal{D}_{i}$ of Eq. 4 with

has the property $\mathcal{D}_{i}\hat{A}=0$ if $[\hat{A},\hat{L}_{i}]=[\hat{A},\hat{L}_{i}^{\dagger}]=0$. If the support of $\hat{A}$ does not contain the site $i$, $\mathcal{D}_{i}\hat{A}$ vanishes. As a result, we have

Since $S[\hat{A}(t)]\sim L$ after the operator scrambling, the effective dissipation strength for $\hat{A}(t)$ is proportional to $\gamma L$. This conclusion is valid for an arbitrary local operator $\hat{A}$ under the assumption that the many-body Hamiltonian $\hat{H}(t)$ is chaotic and has no local conserved quantity. It implies that the asymptotic decay rate, which is nothing but the Liouvillian gap $g$, is also proportional to $\gamma L$:

When $v/L\ll\gamma\ll v$, dissipation takes place before the operator spreads over the entire system. The operator size approximately grows without dissipation up to $t_{\gamma}\sim\gamma^{-1}$ and reaches $S[\hat{A}(t_{\gamma})]\sim vt_{\gamma}\sim\gamma^{-1}$. Afterwards, the operator-size growth stops due to dissipation: $S[\hat{A}(t)]\approx S[\hat{A}(t_{\gamma})]$ for $t>t_{\gamma}$. As a result, the asymptotic decay rate is given by

which is independent of $L$ and $\gamma$.

The above argument implies discontinuity of the Liouvillian gap at $\gamma=0$ in the thermodynamic limit. We have argued that there are two different regimes: $g\sim\gamma L$ for $\gamma\lesssim v/L$ and $g\sim 1$ for $v/L\ll\gamma\ll v$. In the thermodynamic limit, the former regime disappears. We therefore expect that

The Liouvillian gap remains finite in the weak dissipation limit if the thermodynamic limit is taken first. As we have already mentioned, we have $g=0$ if we put $\gamma=0$ before the thermodynamic limit. Equation 13 thus manifests a singularity (discontinuity) of the Liouvillian gap in the thermodynamic limit, which is a generic feature of chaotic open many-body Floquet systems.

It should be noted that a similar observation was reported in the dissipative Sachdev-Ye-Kitaev model [46, 47].

This theoretical prediction is validated by numerical calculations for the kicked Ising chain under bulk dephasing. Numerical results on the Liouvillian gap are presented in Fig. 2 for $\tau=0.65$, $0.7$, and $0.75$. We see that the Liouvillian gap increases with $L$ at a sufficiently small $\gamma$, but is almost independent of $L$ for larger $\gamma$, which is consistent with the above theoretical prediction. The dashed lines in Fig. 2 are quadratic functions fitted to the data of (a) $\gamma\geq 0.015$, (b) $\gamma\geq 0.03$, and (c) $\gamma\geq 0.05$ for $L=14$. Extrapolated values to $\gamma=0$ are our numerical estimates of $\bar{g}$. We obtain $\bar{g}=0.0682$, $0.157$, and $0.268$ for $\tau=0.65$, $0.7$, and $0.75$, respectively.

The reason why a quadratic fitting is used is that an accurate extrapolation requires numerical data for relatively large values of $\gamma$ ($\lesssim 0.2$) in the largest system size $(L=14)$ accessible in our numerical calculations. If we could perform numerical calculations for larger system sizes, an accurate extrapolation using numerical data for smaller values of $\gamma$ would be possible, and then a linear fitting would be enough.

In Sec. III.2, we have seen that the Liouvillian gap shows singularity at $\gamma=0$: the Liouvillian gap converges to a nonzero value $\bar{g}$ in the weak dissipation limit. A natural question is what its physical meaning is. In Sec. III.4, we will argue that $\bar{g}$ is interpreted as a quantum RP resonance. Before that, we begin with a brief exposition of RP resonances of the Hamiltonian dynamics.

Suppose a classical system with the Hamiltonian $H_{t}(\Gamma)$, where

denotes a point in the classical phase space. Here, $\{q_{i}\}$ and $\{p_{i}\}$ are canonical variables, and the Hamiltonian may explicitly depend on $t$ with period $\tau$, i.e., $H_{t}(\Gamma)=H_{t+\tau}(\Gamma)$. A dynamical trajectory is given by a one-parameter family $\Gamma_{t}$ of phase-space points, where the canonical variables obey the Hamilton equations of motion: $\dot{q}_{i}=\partial H(\Gamma_{t})/\partial p_{i}$ and $\dot{p}_{i}=-\partial H(\Gamma_{t})/\partial q_{i}$. Let us denote by $P(\Gamma)$ the phase-space probability density. Its time evolution $P_{t}(\Gamma)$ is formally expressed as

where $\Gamma=\Gamma_{0}$ and $\mathcal{U}_{t}$ is the time evolution operator of the phase-space density, which is referred to as the Frobenius-Perron operator [23, 24]. We can generally write $\mathcal{U}_{t}=\mathcal{T}e^{\int_{0}^{t}\mathcal{L}_{\mathrm{cl}}(t^{\prime})dt^{\prime}}$, where the generator $\mathcal{L}_{\mathrm{cl}}(t)$ is the classical Liouvillian in the absence of dissipation:

where $\{\cdot,\cdot\}_{\mathrm{PB}}$ denotes the Poisson bracket. It corresponds to $-i[\hat{H}(t),\cdot]$ in quantum mechanics.

The classical Liouvillian is anti-Hermitian, i.e., $\braket{f,\mathcal{L}_{\mathrm{cl}}(t)g}=-\braket{\mathcal{L}_{\mathrm{cl}}(t)f,g}$, under the inner product

where $d\Gamma=dq_{1}dq_{2}\dots dq_{N}dp_{1}dp_{2}\dots dp_{N}$. It means that the Frobenius-Perron operator $\mathcal{U}_{t}$ is unitary within the Hilbert space of square-integrable functions, which expresses the reversibility of the Hamiltonian dynamics.

Because of the unitarity, the Floquet operator $\mathcal{U}_{\tau}$ has a spectrum on the unit circle in the complex plane. Moreover, $\mathcal{U}_{t}$ has a continuous spectrum when the dynamics is chaotic. With this in mind, let us consider the resolvent of the Floquet operator

The resolvent is regularly behaved for any $z$ with $|z|\neq 1$. The continuous spectrum of $\mathcal{U}_{t}$ gives a branch cut of $R(z)$, and hence we can perform an analytic continuation from $|z|>1$ to $|z|<1$ through the continuous spectrum [23, 48]. It turns out that $R(z)$ may have poles inside the unit circle in the second Riemann sheet. Those poles are written as $e^{\nu_{i}\tau}$ with $\operatorname{\mathrm{Re}}\nu_{i}<0$, and $\{\nu_{i}\}$ are known as RP resonances [21, 22, 48, 23]. RP resonances are not true eigenvalues in the Hilbert space of square-integrable functions, but are understood as generalized eigenvalues in a wider Hilbert space [23].

By using RP resonances, we can decompose the time evolution of the expectation value $\braket{A}_{t}=\int d\Gamma\,A(\Gamma)P_{t}(\Gamma)$ of a physical quantity $A(\Gamma)$ into the sum of exponential decays as follows:

where $t=n\tau$ with $n$ being an integer and we assume $\lim_{t\to\infty}\braket{A}_{t}=0$. The long-time limit is governed by the leading RP resonance $\nu_{*}$ (the RP resonance with the largest real part):

RP resonances thus extract exponential decays hidden in the unitary time evolution.

Numerically, RP resonances can be obtained by diagonalizing a coarse-grained Frobenius-Perron operator [49, 50]. In numerical calculations, we discretize the phase space and express the Frobenius-Perron operator as a finite-dimensional matrix. This discretization procedure corresponds to a coarse graining, which makes the Frobenius-Perron operator non-unitary. Therefore, if we write eigenvalues of the Frobenius-Perron operator as $e^{\lambda_{i}\tau}$, where we call $\{\lambda_{i}\}$ (classical) Liouvillian eigenvalues, $\lambda_{i}$ have negative real part. Interestingly, some of them still have negative real part even in the limit of the continuous phase space [49]. It means that even infinitesimal coarse graining drastically changes the Liouvillian eigenvalues. Those Liouvillian eigenvalues with negative real part in the continuous limit are nothing but RP resonances.

A natural question is whether quantum analogs of RP resonances exist. As we have discussed above, a continuous spectrum of the Liouvillian for the pure Hamiltonian dynamics is crucial to get RP resonances (recall that the continuous spectrum plays the role of a branch cut of the resolvent, and an analytic continuation of the resolvent through the continuous spectrum brings about RP resonances as poles in the second Riemann sheet). In classical systems, chaos ensures the existence of a continuous spectrum, whereas any finite quantum system has only discrete energy eigenvalues. In quantum mechanics, a continuous spectrum appears in the semiclassical limit, and hence quantum analogs of RP resonances may exist in this limit. Indeed, some previous works found RP resonances by considering the semiclassical limit of quantum systems [51, 52, 53].

There is another limit that leads to a continuous spectrum in quantum mechanics: that is the thermodynamic limit. It is much less trivial whether there exist quantum RP resonances in a quantum many-body system that is far from any classical limit. This problem has rarely been investigated in the literature, except for Refs. [54, 55], where Prosen found quantum RP resonances of the kicked Ising chain by introducing an appropriate coarse graining procedure in the operator space.

It should be noted that RP resonances differ from Lyapunov exponents: the former is concerned with long-time behavior, whereas the latter with short-time behavior. Indeed, García-Mata et al. [56] showed that the long-time decay of OTOCs in a semiclassical model gives a quantum RP resonance, whereas Lyapunov exponents are related with short-time behavior of OTOCs.

As we have seen in Sec. III.3, RP resonances are related to instabilities against infinitesimal coarse graining. Instead of performing a coarse graining, we can mimic it by introducing stochastic noise to the deterministic Hamiltonian dynamics. As we explain below, RP resonances are also regarded as a manifestation of instabilities against infinitesimally weak stochastic noise [57, 58, 59] (also see Ref. [60] for a pedagogical exposition on this and related topic).

When white Gaussian noise is added to the Hamiltonian dynamics, the dynamics is described by the Langevin equation. The corresponding time evolution equation of the probability density $P_{t}(\Gamma)$ is given by the Kramers equation (or the Fokker-Planck equation in the overdamped limit): $\partial P_{t}(\Gamma)/\partial t=\mathcal{L}_{K}(t)P_{t}(\Gamma)$ with $\mathcal{L}_{K}(t)=\mathcal{L}_{K}(t+\tau)$. The eigenvalues of the corresponding Floquet operator $\mathcal{U}_{K}=\mathcal{T}e^{\int_{0}^{\tau}\mathcal{L}_{K}(t)dt}$ are expressed as $e^{\lambda_{i}\tau}$. Here, $\{\lambda_{i}\}$ are Liouvillian eigenvalues in the classical dynamics under stochastic noise. In the presence of noise, Liouvillian eigenvalues have negative real part. Surprisingly, some Liouvillian eigenvalues still have negative real part even in the weak noise limit. Those nontrivial Liouvillian eigenvalues in the weak noise limit are nothing but RP resonances of the deterministic Hamiltonian dynamics.

Now an analogy between this situation and our Liouvillian gap analysis in open quantum systems would be obvious. What we have found in Sec. III.2 is that if we add weak dissipation to the Schrödinger dynamics of a quantum many-body system, Liouvillian eigenvalues have negative real part even in the weak dissipation limit. Considering the analogy with classical chaotic systems, it is natural to conjecture that $\bar{g}$ in Eq. 13 corresponds to (the real part of) the leading RP resonance of the isolated quantum many-body system.

A numerical evidence of this interpretation for the kicked Ising model is presented in Fig. 3. Solid lines show $-E(t)=-\braket{\psi(t)}{\hat{H}_{0}}{\psi(t)}$ that is obtained by numerically solving the Schrödinger equation starting with the ground state of $\hat{H}_{0}$ (i.e., the all-down state). Dashed lines show exponential decays $e^{-\bar{g}t}$ predicted by the Liouvillian gap analysis in the weak dissipation limit. We find that $\bar{g}$ excellently reproduces the long-time exponential decay in the unitary time evolution. In this way, thermalization dynamics of an isolated quantum many-body system is better characterized as the weak dissipation limit of the Lindblad dynamics.

Up to here, numerical results for the bulk dephasing $\hat{L}_{i}=\hat{\sigma}_{i}^{z}$ have been presented. Now we numerically show that $\bar{g}$ does not depend on the choice of dissipator.

Let us consider jump operators $\hat{\sigma}_{i}^{+}$ and $\hat{\sigma}_{i}^{-}$ at every site $i$ with strength $\gamma_{+}$ and $\gamma_{-}$, respectively. The Lindblad equation is given as

where $\hat{H}(t)$ is the Hamiltonian of the kicked Ising chain that is given by Eq. 5. In this paper, we fix the ratio of $\gamma_{\pm}$ as $\gamma_{-}/\gamma_{+}=0.5$ and vary the value of $\gamma\equiv\gamma_{+}$.

Next, we also consider the “XX dissipator” corresponding to the jump operator $\hat{L}_{i}=\hat{\sigma}_{i}^{x}\hat{\sigma}_{i+1}^{x}$ at each site $i$. The Lindblad equation reads

In Fig. 4, we compare the $\gamma$-dependence of the Liouvillian gap for the above two dissipators as well as for the bulk dephasing. At finite $\gamma$, we see that the Liouvillian gap depends on the dissipator, but the extrapolated value $\bar{g}$ towards $\gamma\to+0$ does not. This is consistent with the conjecture that $\bar{g}$ describes an intrinsic property of the system, not a property of the dissipator.

In Sec. III, it is pointed out that the operator spreading under the unitary time evolution of a Floquet system results in a large asymptotic decay rate under weak bulk dissipation. More precisely, we have $g\sim L\gamma$ when $\gamma\lesssim v/L$, which implies a singularity of the Liouvillian gap at $\gamma=0$.

However, we now argue that a static system does not exhibit such a singularity. In Sec. III.2, we have seen that the operator spreading under the unitary time evolution is a key ingredient to have a large asymptotic decay rate $g\sim L\gamma$ for $\gamma\to+0$ with a fixed system size $L$. In static systems, the Hamiltonian is invariant under the unitary time evolution at $\gamma=0$, and hence the Hamiltonian does not undergo the operator spreading. As a consequence, If we consider the effect of weak bulk dissipation, the decay rate of the Hamiltonian under weak bulk dissipation does not increase with time, and the asymptotic decay rate will behave regularly at $\gamma=0$ in the thermodynamic limit.

This argument is consistent with previous studies on the Liouvillian gap in static systems under bulk dissipation [31, 32]. For example, Shibata and Katsura [31] analytically calculated the thermodynamic limit of the Liouvillian gap in the quantum compass model, and obtained $g=2\gamma$ when $\gamma$ is smaller than a certain critical value. Obviously, $\lim_{\gamma\to+0}\lim_{L\to\infty}g=0$, and thus no singularity appears at $\gamma=0$. The discontinuity of the Liouvillian gap in the weak dissipation limit is a generic feature of open Floquet systems, but not of open static systems.

In general, when there is a local conserved quantity $\hat{Q}$ in the absence of dissipation (in static systems, we generically have $\hat{Q}=\hat{H}$), the Liouvillian gap does not show singularity in the limit of $\gamma\to+0$ because the conserved quantity does not undergo the operator spreading. The Liouvillian gap in the weak dissipation regime describes the relaxation of $\hat{Q}$ under dissipation, which is not related to the intrinsic relaxation process of the isolated system. The Liouvillian gap therefore does not give the leading RP resonance in static systems.

One may ask whether some Liouvillian eigenvalues with smaller real part (i.e. higher decay rates) can be interpreted as RP resonances. Because the suppression of the singularity is due to the presence of local conserved quantities, it would be expected that one can extract the information of intrinsic decay rates (i.e. RP resonances) by discarding the effect of conserved quantities. In the energy basis, it is encoded in diagonal matrix elements. Therefore, we can discard it by applying the following projection superoperator $\mathcal{P}$:

where $\hat{H}\ket{n}=E_{n}\ket{n}$. Let us define the projected Liouvillian as

and its spectral gap as

where $\lambda_{\alpha}^{\mathrm{P}}$ are eigenvalues of $\mathcal{L}_{\mathrm{P}}$ corresponding to right eigenvectors within the projected subspace, i.e., $\mathcal{L}_{\mathrm{P}}\rho_{\alpha}^{\mathrm{P}}=\lambda_{\alpha}^{\mathrm{P}}\rho_{\alpha}^{\mathrm{P}}$ and $\mathcal{P}\rho_{\alpha}^{\mathrm{P}}=\rho_{\alpha}^{\mathrm{P}}$.

In Fig. 5, we compare the Liouvillian eigenvalues $\{\lambda_{\alpha}\}$ and the projected Liouvillian eigenvalues $\{\lambda_{\alpha}^{\mathrm{P}}$ in the quantum Ising model under bulk dissipation for $L=4$. Interestingly, we find that each $\lambda_{\alpha}^{\mathrm{P}}$ is almost identical to one of the Liouvillian eigenvalues, and hence we find approximately $\{\lambda_{\alpha}^{\mathrm{P}}\}\subset\{\lambda_{\alpha}\}$. The projection thus picks up selective eigenvalues of the Liouvillian, and it is plausible to expect that they are related to intrinsic decay rates of the isolated system. In particular, we expect that the projected Liouvillian gap $g_{\mathrm{P}}$ corresponds to (real part of) the leading RP resonance.

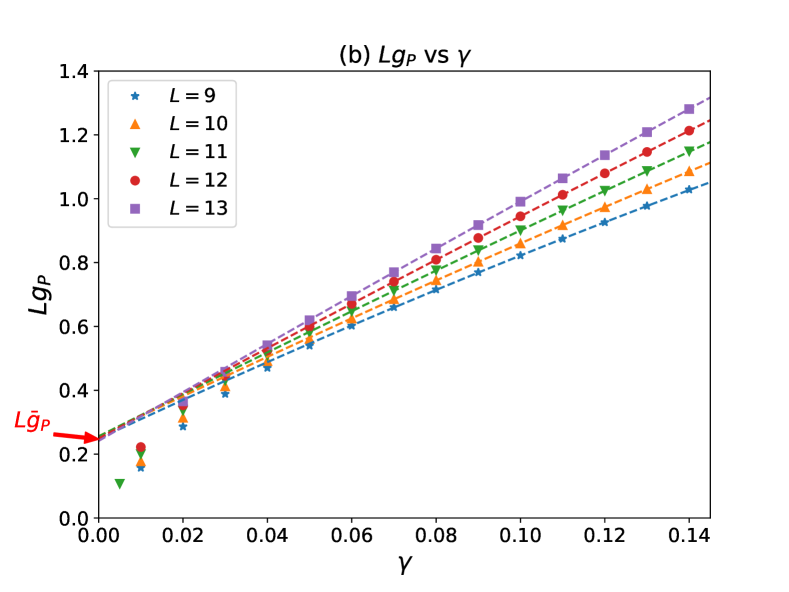
We now numerically test our conjecture on the correspondence between the projected Liouvillian gap and the leading RP resonance. In a static isolated system, the long-time relaxation is governed by hydrodynamic modes which are related to the transport of the energy. It is expected that the decay rate of the hydrodynamic model of the wave length $L$ vanishes as $L^{-z}$ in the thermodynamic limit, where $z>0$ is the dynamical exponent. We therefore expect that the leading RP resonance also vanishes in the thermodynamic limit.

We numerically compute the projected Liouvillian gap $g_{\mathrm{P}}$ as a function of $\gamma$ for various system sizes. Our numerical results are given in Fig. 6. As in Floquet systems, we have a nonzero value by extrapolating the data of $g_{\mathrm{P}}$ only for $\gamma\geq\gamma_{*}$ into $\gamma=0$. This finite value is identified as the leading RP resonance. In numerical calculations, we set $\gamma_{*}=0.05$.

As expected, the extrapolated value $\bar{g}_{\mathrm{P}}$ decreases as the system size increases. Our numerical results suggest the scaling $\bar{g}_{\mathrm{P}}\sim L^{-1}$. Figure 6 (b) demonstrates that the extrapolated curves for different system sizes cross at $\gamma=0$ if we plot $Lg_{\mathrm{P}}$ as a function of $\gamma$. This scaling is rather counterintuitive because the diffusive transport of the energy, which occurs in quantum chaotic systems, implies that the decay rate of the slowest hydrodynamic mode is proportional to $L^{-2}$ (i.e. $z=2$). Indeed, in classical Hamiltonian dynamics, Gaspard [61] found that in strongly chaotic systems, the leading RP resonance is proportional to $L^{-2}$, which is called the deterministic diffusion. The scaling $\bar{g}_{\mathrm{P}}\sim L^{-1}$ indicates the difference between classical and quantum Hamiltonian dynamics. This apparent discrepancy between transport properties and the dynamical exponent of the projected Liouvillian gap might be related to the gap discrepancy problem in open quantum systems [28, 36].

The $L^{-1}$ scaling of $\bar{g}_{\mathrm{P}}$ is more strongly evidenced by comparing the intrinsic decay rate of the isolated system with $\bar{g}_{\mathrm{P}}$. In Fig. 7, we plot

with the solid line, where $\ket{\psi(t)}$ is a numerical solution of the Schrödinger equation $id\ket{\psi(t)}/dt=\hat{H}\ket{\psi(t)}$ starting with the all-down initial state for $L=26$, and $\hat{M}^{z}=\sum_{i=1}^{L}\hat{\sigma}_{i}^{z}$ is the total magnetization. The overline in Eq. 27 denotes the long-time average. The dashed line of Fig. 7 is $e^{-\bar{g}_{\mathrm{P}}t}$, where $\bar{g}_{\mathrm{P}}$ for $L=24$ is estimated as follows: By using numerical data for $L=9$, $10$, $11$, $12$, and $13$, and assuming $\bar{g}_{\mathrm{P}}\propto L^{-1}$, we obtain $\bar{g}_{\mathrm{P}}\approx 0.247/L$, which gives an estimate at $L=26$ as $\bar{g}_{\mathrm{P}}\approx 0.0095$. We find that the projected Liouvillian gap extrapolated to $\gamma\to+0$ excellently reproduces the intrinsic decay rate. Thus, in static systems, the projected Liouvillian gap gives the leading RP resonance, and our numerical results strongly support an unexpected scaling $\bar{g}_{\mathrm{P}}\sim L^{-1}$.