Linear Video Transformer with
Feature Fixation
Abstract
Vision Transformers have achieved impressive performance in video classification, while suffering from the quadratic complexity caused by the Softmax attention mechanism. Some studies alleviate the computational costs by reducing the number of tokens in attention calculation, but the complexity is still quadratic. Another promising way is to replace Softmax attention with linear attention, which owns linear complexity but presents a clear performance drop. We find that such a drop in linear attention results from the lack of attention concentration on critical features. Therefore, we propose a feature fixation module to reweight feature importance of the query and key before computing linear attention. Specifically, we regard the query, key, and value as various latent representations of the input token, and learn the feature fixation ratio by aggregating Query-Key-Value information. This is beneficial for measuring the feature importance comprehensively. Furthermore, we enhance the feature fixation by neighborhood association, which leverages additional guidance from spatial and temporal neighbouring tokens. The proposed method significantly improves the linear attention baseline and achieves state-of-the-art performance among linear video Transformers on three popular video classification benchmarks. With fewer parameters and higher efficiency, our performance is even comparable to some Softmax-based quadratic Transformers.
1 Introduction
Vision Transformers [21; 92; 52; 88; 16] have been successfully applied in video processing. Recent video Transformers [61; 4; 7; 6; 22] have achieved remarkable performance on challenging video classification benchmarks, e.g., Something-Something V2 [27] and Kinectics-400 [10]. However, they always suffer from quadratic computational complexity, which is caused by the Softmax operation in the attention module [83; 99]. The quadratic complexity severely constrains the application of video Transformers, since the task of video processing always requires to handle a huge amount of input tokens, considering both the spatial and temporal dimensions.
Most of the existing efficient designs in video Transformers attempt to reduce the number of tokens attended in attention calculation. For example, [4; 6] factorize spatial and temporal tokens with different encoders or multi-head self-attention modules, to only deal with a subset of input tokens. [7] calculates the attention only from the target frame, i.e., space-only. [61] restricts tokens to a spatial neighbourhood that can reflect dynamic motions implicitly. Despite reducing the computational costs, they still have the inherent quadratic complexity, which prohibits them from scaling up to longer input, e.g., more video frames or larger resolution [6; 61].
Another practical way, widely used in the Natural Language Processing (NLP) community, is to decompose Softmax with certain kernel functions and linearize the attention via the associate property of matrix multiplication [64; 37; 15]. Recent linear video Transformers [61; 99] achieve higher efficiency, but present a clear performance drop compared to Softmax attention. We find that the degraded performance is mainly attributed to the lack of attention concentration to critical features in linear attention. Such an observation is consistent with the concurrent works in NLP [64; 91].
Accordingly, we propose to concentrate linear attention on critical features through feature fixation. To this end, we reweight the feature importance of the query and key prior to computing linear attention. Inspired by the idea of classic Gaussian pyramids [56; 45] and modern contrastive learning [68; 78], we regard the query, key, and value as latent representations of the input token. Latent space projection will not destroy the image structure, i.e., salient features are expected to be discriminative across all spaces [77]. Therefore, we aggregate Query-Key-Value features when generating the fixation ratio, which is beneficial for measuring the feature importance comprehensively.
Meanwhile, the salient feature activations are usually locally accumulative [11; 73]. In the continuous video, critical information contained in the target token could be shared by its spatial and/or temporal neighbour tokens. We hence propose to use neighbourhood association as extra guidance for feature fixation. Specifically, we reconstruct each key and value vectors (they are responsible for information exchange between tokens [31; 7]) by sequentially mixing key/value features of nearby tokens in the spatial and temporal domain. This is efficiently realized by employing the feature shift technique [90; 97]. Experimental results demonstrate the effectiveness of feature fixation and neighbourhood association in improving the classification accuracy.
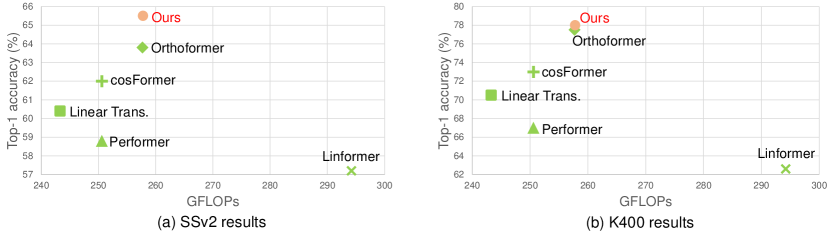
Our primary contributions are summarized as follows: 1) We discover that the performance drop of linear attention results from not concentrating attention distribution on discriminative features in linear video Transformers. 2) We develop a novel linear video Transformer with feature fixation to concentrate salient attention. It is further enhanced by neighbourhood association, which leverages the information from nearby tokens to measure the feature importance better. Our method is simple and effective, and can also be seamlessly applied to other linear attention variants and improve their performance. 3) Our model achieves state-of-the-art results among linear video Transformers on popular video classification benchmarks (see Fig. 1), and its performance is even comparable to some Softmax-based quadratic Transformers with fewer parameters and higher efficiency.
2 Related Work
Video classification by CNNs. CNN-based video networks are normally built upon 2D image classification models. To aggregate temporal information, current works either fuse the features of each video frame [86; 47], or build spatial-temporal relations through 3D convolutions [30; 66; 79] or RNNs [20; 42; 44]. Although the latter ones have achieved state-of-the-art performance, they suffer from being significantly more computationally and memory-intensive. Several techniques have been proposed to enhance efficiency, e.g., temporal shift [47; 54], adaptive frame sampling [39; 3; 94; 93], and spatial/temporal factorization [80; 34; 81; 23].
Video Transformers. Vision Transformers [21; 92; 52; 88; 16] have achieved a great success in computer vision tasks. It is straightforward to extend the idea of vision Transformers to video processing, considering both the spatial and temporal dependencies. However, the full spatial-temporal attention is computationally expensive, and hence several video Transformers try to reduce the costs via factorization. TimeSformer [6] exploits five types of factorization, and empirically finds that the divided attention, where spatial and temporal features are separately processed, leads to the best accuracy. A similar conclusion is drawn in ViViT [4], which separates spatial and temporal features with different encoders or multi-head self attention (MHSA) modules. [7] introduces a local temporal window where features at the same spatial position are mixed. Some other methods have also explored dimension reduction [26; 36], token selection [84; 2], local-global attention stratification [46], deformable attention [83], temporal down-sampling [69; 98], locality strengthening [53; 25], hierarchical learning [96; 95], multi-scale fusion [22; 28; 89], and so on.
Efficient Transformers. The concept of efficient Transformers was originally introduced in NLP, aiming to reduce the quadratic time and space complexity caused by the Transformer attention [41; 75; 37; 38; 87; 51]. The mainstream methods use either patterns or kernels [76]. Pattern-based approaches [65; 48; 5; 13] sparsify the Softmax attention matrix with predefined patterns, e.g., computing attention at fixed intervals [5] or along every axis of the input [32]. Though benefiting from the sparsity, they still suffer from the quadratic complexity to the input length. By contrast, kernel methods [37; 63; 15; 14; 64] reduce the complexity to linear by reformulating the attention with proper functions. As suggested by [64], these functions should be decomposable and non-negative.
3 Problem Formulation
In this section, we first formulate the video Transformer and analyze their quadratic complexity in Section 3.1. Linear attention is introduced in Section 3.2 and its fundamental shortcoming in the performance drop is discussed in Section 3.3.
3.1 Video Transformer
A video clip can be denoted as , containing frames with a resolution of and a channel number of . The video Transformer maps each frame to a sequence of tokens, and hence has tokens in total. The embedding dimension of a token is . These tokens are further projected into the query , key , and value . The self-attention is defined as111For simplicity, we focus on the single head and ignore the scaling term that normalizes .
| (1) |
where is a similarity function, e.g., Softmax in standard Transformers [82; 21]. As shown, has a shape of . Therefore, the use of Softmax will lead to quadratic complexity with respect to the input length, i.e., . This is computationally expensive especially for a long sequence of high-resolution videos. Existing efficient designs in video Transformers [4; 7; 6; 61] mostly focus on reducing the number of attended tokens when calculating the attention, which, however, still suffer from the quadratic complexity. Another promising way is to approximate Softmax in a linear form [61; 99], but it is less comparable in accuracy than quadratic Transformers and always time-consuming in practical use due to the sampling operation.
3.2 Linear Attention
To reduce the complexity close to linear , linear Transformers [37; 63; 15; 14; 64; 87; 72; 71] decompose the similarity function to a kernel function , where . The associative property of matrix multiplication allows to multiply and first without affecting the mathematical result, i.e.,
| (2) |
where the shape of is . By changing the order of matrix multiplication, the complexity is reduced from to . Since we always have in practice, is approximately equal to , i.e., growing linearly with the sequence length. As discussed in [64; 8], a simple ReLU [1] is a good candidate for the kernel function, which satisfies the requirement of being non-negative and easily decomposable. The attended output is formulated with row-wise normalization, i.e.,
| (3) |
3.3 Achilles heel of linear attention
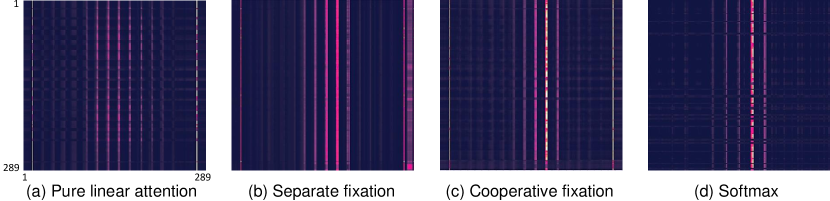
Despite the lower computational complexity, linear attention always presents a clear performance drop compared to Softmax [8; 74; 64]. We also observe this drop when applying the linear attention to video Transformers, as shown in Table 1 and 2. The lack of non-linear attention concentration in the process of dot-product normalization is considered to be the primary cause [64; 8]. From Fig. 2(a), we observe that the distribution of linear attention is smoother, i.e., it cannot concentrate on high attention scores as that in Softmax (Fig. 2(d)). The non-concentration would incur the existence of noisy/irrelevant information, e.g., a number of attention scores have been unexpectedly highlighted in Fig. 2(a) compared with Softmax. This, in turn, would aggravate the diffusion of linear attention. In this work, we propose to improve the concentration in linear attention. Specifically, we aim to inhibit the non-essential parts of and 222This is because the attention matrix is calculated from and . Even though the matrix does not exist in linear attention, and still take effect in normalization in Eq. 3. and highlight the role of discriminative features to sharpen the results of linear attention, as discussed in Section 4.
4 Method
In this section, we will introduce the idea of feature fixation (Section 4.1 and Section 4.2) and neighborhood association (Section 4.3). Feature fixation reweights the feature importance of the query and key, and the cooperative fixation encourages different latent representations of a token to collectively determine the feature importance. Neighborhood association makes use of the features of nearby tokens as extra guidance for feature fixation.
4.1 Separate feature fixation
To highlight the essential parts of and , their features should be reweighted in a non-linear manner, i.e., keeping important features almost unchanged (assigning weights closer to 1) while down-weighting (closer to 0) the non-essential activation. Inspired by the excitation strategy [33] and context gating mechanism [58] in CNNs, we recalibrate the query and key in the feature dimension (see Fig. 3(a) and Appendix A.2). For simplicity, we denote and 333We empirically find that directly reweighting the original and without ReLU activation leads to OOM in network training. as and respectively. The recalibrated results are
| (4) |
where , : learn a nonlinear interaction between feature channels with weights, for measuring feature importance [33]. is the element-wise Sigmoid function individually performed on each feature dimension, so that are fixation ratios (0-1) of and respectively. represents the element-wise multiplication. Fig. 2(b) shows that after reweighting and separately, the attention becomes more concentrated. However, it still has an obvious gap with Softmax, i.e., the concentration on the most essential tokens is not sufficiently sharpened. Though separately learning the fixation ratio is beneficial, it ignores the internal connection of and that is critical to the comprehensive measurement of feature importance.

4.2 Cooperative feature fixation
The feature fixation ratios in Eq. 4 separately come from and , which has the risk of deficiently measuring the feature importance. In fact, the attention mechanism in Transformers naturally projects each input token to three representations, i.e., , , and . Inspired by modern contrastive learning [68; 78] and classic Gaussian Pyramid [56; 45], projecting an image to different latent spaces would not destroy the image structure. For instance, in contrastive learning, an image is projected to various spaces by random augmentation operations, while the latent features of these augmented images are expected to share similar properties, both locally and globally [77]. Besides, take SIFT [56] as an example of Gaussian Pyramid methods. Though an image is processed by different Gaussian kernels, its salient pixels (i.e., keypoints in SIFT) have a high response across all the Gaussian spaces.
Therefore, we propose to obtain the feature fixation ratio by facilitating the cooperation among , , and . This is motivated by the above insight that the essential features of a token should be discriminative among all its three latent spaces, and vice versa for unimportant information. To this end, we adjust Eq. 4 as follows:
| (5) |
where supplies a cooperation space of , , for the purpose of comprehensively estimating the importance degree of each feature channel. Their cooperation, illustrated in Fig. 3(b), can be achieved by aggregating their features, e.g., concatenation (used in our implementation) and addition. Moreover, we keep the fixation ratio identical when reweighting the query and key, which is in line with our design philosophy that feature importance should be consistent across various spaces. Fig. 2(d) shows that using our cooperative feature fixation leads to sharper attention concentration than separate learning of each fixation ratio. In Section 5 we prove that the enhanced concentration can yield better accuracy.
4.3 Neighborhood Association
The vision features are usually continuous in temporal [11; 43; 101; 59] and spatial [73; 62; 70; 18] neighbourhood. Analogously, the prediction confidence increases if all the tokens within a local region can reach a consensus for feature importance. Therefore, it is straightforward to introduce the features of temporal and spatial neighbour tokens as additional guidance. To enhance the communication within the neighbourhood, we take advantage of the feature shift technique [90; 31; 7] that is parameter-free and efficient in use. Considering that each query is attended by key-value pairs from other tokens [31; 7] for information exchange, each and is reconstructed by sequentially mixing its temporally and spatially adjacent tokens including itself (namely, temporal shift and spatial shift). The neighbourhood association is proven to be effective in improving the classification accuracy. Technical details can be found in Appendix A.3.
5 Experiments
In this section, we conduct extensive experiments to verify the effectiveness of our linear video Transformer. We start with experimental settings in Section 5.1, e.g., the backbone, datasets, and training/inference details. Subsequently, we show the competitive performance of our model to SOTA methods in Section 5.2. The importance of each module and more comprehensive model analysis are discussed in Section 5.3.
5.1 Experimental setup
Backbone. We use the standard ViT architecture [21] as the backbone. Our default model, built on top of XViT [7] and pretrained on ImageNet-21k [19], has the embedding dimension of 512, patch size of 16, 12 Transformer layers each with 8 attention heads. We employ the factorized spatial-temporal approach for calculating attention, which is shown to be effective in [6; 4; 52] owing to the distinct learning in spatial and temporal dimensions.
Datasets. We evaluate our method on three popular video action classification datasets. Something-Something V2 (SSv2) [27], focusing more on temporal modelling, consists of 169k training and 24.7k validation videos in 174 classes. Kinectics-400 (K400) [10] contains 240k videos for training and 20k for validation with 400 human action classes. Kinectics-600 (K600) [9] is extended from K400 with 370k training and 28k validation videos containing 600 categories.
Evaluation metrics. When comparing accuracy, we report Top-1 and Top-5 accuracy () on SSv2, K400 and K600. We use GFLOPs for measuring computational costs as in most video classification works, and also provide the throughput (vps: videos per second) when available to reveal the actual processing speed.
| Method | Top-1 | Top-5 | T | # Par. (M) | Views | GFLOPs | |
| CNN | SlowFast [24] | 63.1 | 87.6 | 8 | 53.3 | 106.0 | |
| TSM [47] | 63.3 | 88.2 | 16 | 42.9 | 62.0 | ||
| MSNet [40] | 64.7 | 89.4 | 16 | 24.6 | 67.0 | ||
| Softmax | TSformer-HR [6] | 62.5 | - | 16 | 121.4 | 1703.0 | |
| MViT-B [22] | 64.7 | 89.2 | 16 | 33.6 | 70.5 | ||
| ViViT-L [4] | 65.4 | 89.8 | 32 | 352.1 | 3992.0 | ||
| XViT [7] | 66.2 | 90.6 | 16 | 92.0 | 850.0 | ||
| Mformer [61] | 66.5 | 90.1 | 8 | 109.0 | 369.5 | ||
| Linear | Linformer [87] | 57.2 | 84.4 | 16 | 53.5 | 294.2 | |
| Performer [15] | 58.8 | 85.4 | 16 | 51.7 | 250.6 | ||
| Linear Trans. [37] | 60.4 | 86.7 | 16 | 51.7 | 243.3 | ||
| cosFormer [64] | 62.0 | 87.3 | 16 | 51.7 | 250.6 | ||
| RALA [99] | 63.7 | - | 16 | 102.0 | 257.6 | ||
| Oformer [61] | 63.8 | - | 16 | 102.0 | 257.7 | ||
| Ours | 65.5 | 90.1 | 16 | 52.2 | 257.8 |
Training phase. By default, we follow a similar training and augmentation strategy to XViT [7], e.g., a video input, SGD with the momentum as 0.9, and autoaugment [17] for data augmentation. The base learning rate is 0.035 and scheduled with the cosine policy [55]. We train the models with 35 epochs (5 for warm-up) and a batch size of 32 on 8 V100 GPUs using PyTorch [60]. Detailed training configuration is listed in Appendix A.1.
Inference phase. Following previous works [7; 6; 4; 61], we divide test videos into views, i.e., is the number of uniformly-sampled clips in the temporal dimension and represents the number of spatial crops, and obtain the final prediction by averaging the scores over all views. The views of competing methods are listed in Table 1. See Appendix A.4 for the impact of views.
5.2 Main results
Methods to compare. We compare our model with six state-of-the-art linear attention variants, i.e., Oformer [61], LARA [99], Linformer [87], Performer [15], Linear Trans. [37], and cosFormer [64]. For Oformer and LARA, we report the results from their papers. The remaining four are proposed in the NLP literature, so we re-implement them in our backbone and train with the same settings as the proposed linear Transformer. We also compare representative Softmax-based quadratic Transformers and CNN methods for reference only.
| Method | K400 | K600 | |||||
| Top-1 | Top-5 | Views | Top-1 | Top-5 | Views | ||
| CNN | I3D [9] | 71.1 | 90.3 | - | 71.9 | 90.1 | - |
| X3D-M [23] | 76.0 | 92.3 | 78.8 | 94.5 | |||
| SlowFast [24] | 77.0 | 92.6 | 79.9 | 94.5 | |||
| Softmax | TSformer [6] | 78.0 | 93.7 | 79.1 | 94.4 | ||
| Mformer [61] | 79.9 | 94.2 | 81.6 | 95.6 | |||
| MViT-B [22] | 80.2 | 94.4 | 83.8 | 96.3 | |||
| XViT [7] | 80.2 | 94.7 | 84.5 | 96.3 | |||
| ViViT-L [4] | 80.6 | 94.7 | 83.0 | 95.7 | |||
| Linear | Linformer [87] | 62.6 | 86.0 | 67.5 | 88.5 | ||
| Performer [15] | 67.0 | 88.8 | 72.0 | 91.1 | |||
| Linear Trans. [37] | 70.5 | 90.2 | 74.5 | 92.3 | |||
| cosFormer [64] | 73.0 | 91.1 | 78.4 | 92.5 | |||
| RALA [99] | 77.5 | - | - | - | - | ||
| Oformer [61] | 77.5 | - | - | - | - | ||
| Ours | 78.0 | 94.2 | 84.1 | 96.2 | |||
SSv2. Quantitative results on SSv2 are reported in Table 1. We achieve the best Top-1 accuracy among linear models, and surpass the second best, i.e., Oformer [61], by 1.7% with nearly halved parameters. Remarkably, we outperform several SOTA Softmax-based video Transformers, e.g., TSformer [6], ViViT [4], with significantly smaller FLOPs (6 times). Our performance is also comparable to XViT [7] and Mformer [61], e.g., our Top-5 (90.1%) is identical to that of Mformer. CNN methods are generally less competitive although they tend to be faster with lighter networks.
K400 & K600. Our performance on K400 and K600 is consistent with that on SSv2, i.e., outperforming linear models and CNN methods to a clear margin, and being comparable to Softmax-based Transformers. We achieve notably more competitive results on K600, e.g., only having a 0.4% Top-1 gap compared with the best quadratic Transformer XViT [7].
5.3 Ablation study and model analysis
We ablate primary design choices and analyze our model on SSv2 as it is a more challenging dataset containing fine-grained motion cues [7; 61].
Order of feature fixation and neighbourhood association. From a broad view, we start with the order of the two primary modules in our model. We find that neighbourhood association first produces better accuracy than feature fixation first, i.e., 0.82% and 0.42% gain in Top-1 and Top-5 accuracy respectively. This is reasonable because the shifted features from other tokens can be further refined by the feature fixation mechanism. In the following, our default setting is always neighbourhood association prior to feature fixation unless otherwise specified.
Effect of neighbourhood association. Table 5.3 reports the results of applying spatial and temporal feature shifts to the baseline model with pure linear attention in Eq. 3. The spatial shift brings a 0.32% gain in Top-1 accuracy while the temporal shift improves the performance by 2.51%. This is because the SSv2 dataset is generally more dependent on temporal information (we also find that the spatial shift is more helpful to K400 in Appendix A.5). The results indicate the effectiveness of neighbourhood association to aggregate more features from spatially and temporally nearby tokens.
Effect of feature fixation. In Table 5.3, we observe that feature fixation improves the baseline by 0.90%. Although the gain is smaller than the temporal shift444This may be because that feature fixation is performed on the token itself where the acquired information is obviously less than that from temporally nearby tokens., it has its distinctive usefulness, i.e., reweighting feature importance of the token itself and the features from other tokens. The combination of feature fixation and neighbourhood association yields the best accuracy (surpassing the baseline by 3.87%).
| SS | TS | FF | Top-1 |
|---|---|---|---|
| 61.67 | |||
| 61.99 | |||
| 64.18 | |||
| 64.28 | |||
| 62.57 | |||
| 65.46 |
| Targets | Sep. | Coo. | FS | Top-1 |
|---|---|---|---|---|
| No fixation | 64.28 | |||
| Q, K | 64.46 | |||
| Q, K | 64.61 | |||
| Q, K | 64.78 | |||
| Q, K, V | 65.33 | |||
| Q, K, V | 65.46 |
| Kernel | Top-1 |
|---|---|
| ELU+1 [37] | 60.42 |
| Sigmoid | 63.26 |
| ReLU (ours) | 65.46 |
| Attention | Top-1 |
|---|---|
| Joint [6; 4] | 58.17 |
| Windowed [7] | 61.08 |
| Factorized (ours) | 65.46 |
| Variants | Top-1 | Top-5 | GFLOPs |
|---|---|---|---|
| S | 63.48 | 88.68 | 129.1 |
| H | 65.67 | 90.27 | 530.2 |
| HR | 65.85 | 89.97 | 573.3 |
| Default | 65.46 | 90.11 | 257.8 |
Fixation options. We ablate the design options inherent in feature fixation in more details below, and the baseline switches to the model that only uses the neighbourhood association. Since the attention is calculated from Q and K, we start with the setting that Q and K learn to reweight features by themselves without any cooperation, i.e., Eq. 4. From Table 5.3, we find that the operation only contributes a minor performance gain, i.e., 0.18%. After enabling the cooperation between Q and K, the accuracy is further improved by 0.15% (0.33% better than the baseline). Next, we add V to the cooperation space, i.e., Eq. 5, and the performance is significantly enhanced by 1.05% compared to the baseline. It indicates that simultaneously considering Query-Key-Value is beneficial for discriminating feature importance more comprehensively and appropriately. Sharing the fixation ratio can trigger common feature representations like the weight sharing technique [57; 85; 100; 12], and is also proven to be useful in improving the Top-1 accuracy in both Query-Key and Query-Key-Value cooperation cases. Moreover, it saves 0.1M parameters owing to the shared weights in learning the fixation ratio.
In addition to the channel-wise concatenation in our implementation, we also compare other typical cooperation manners for Query-Key-Value feature aggregation, i.e., element-wise addition and multiplication. Both of them lead to 0.5% drop in Top-1 accuracy, so feature concatenation is our best option in this case with only a minor increase in the parameter scale (0.05M).
Kernel function. We study the options of kernel functions in Table 5.3. Without a kernel function, the network cannot converge properly. As indicated by [64; 37], the functions should be non-negative to facilitate the aggregation of more positively-correlated features. We try two other typical non-negative functions, i.e., ELU+1 [37] and Sigmoid, but their performance is clearly inferior to ReLU.
Attention pattern. By default, we employ the factorized spatial-temporal attention introduced in [6; 4]. Specifically, the attention is first computed spatially (tokens from the same frame) and then temporally (tokens from different frames at the same spatial location). For comparison, we also test another two popular attention patterns, i.e., joint attention [6; 4] and windowed attention [7]. As shown in Table 5.3, our choice of using factorized attention yields the best performance. Joint attention is less comparable as it takes all tokens into account, inevitably containing more redundant and noisy features. Windowed attention only aggregates local temporal information, which is less sufficient than ours that collects tokens from the entire temporal domain.
Model variants. In addition to our default model, we provide three extra variants: 1) S: a shorter video clip as ; 2) H: a longer video clip as ; and 3) HR: a larger spatial resolution as . The results are displayed in Table 5.3. With longer video input or a larger spatial resolution, the classification accuracy can be further improved because more temporal or spatial information is included. However, this always comes with a clear increase in computational costs, e.g., GFLOPs (also see Table 8 for throughput comparison). Our default model can better balance the accuracy and efficiency. In real-world applications, end-users can use any variant as per their practical needs.
| # Frames | 16 | 32 | 64 | 96 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Resolution | 224 | 336 | 448 | 224 | 336 | 448 | 224 | 336 | 448 | 224 | 336 | 448 |
| Orthoformer [61] | 1.79 | 1.59 | 1.41 | 1.71 | 1.56 | 1.15 | 1.53 | 0.97 | OOM | 1.25 | 0.83 | OOM |
| Ours | 10.25 | 8.57 | 5.40 | 8.38 | 4.68 | 3.22 | 6.58 | 3.75 | 2.81 | 4.48 | 2.30 | OOM |
| Softmax | 8.23 | 6.49 | 4.57 | 6.15 | 4.57 | 2.57 | 5.27 | 2.55 | OOM | 4.27 | OOM | OOM |
Efficiency analysis. To measure the actual computational efficiency, we report the throughput (videos/second) in Table 8. For a fair comparison, the Orthoformer attention [61] (linear) and Softmax are incorporated into our backbone as a replacement of the proposed attention. All models are tested on a 80G A100 GPU card with a batch size of 1, and their throughput is the average of ten runs. Our model achieves the best efficiency in various settings of input video frames and their spatial resolution. Remarkably, our good efficiency is maintained even with a larger video input, e.g., and , where the Orthoformer and Softmax tend to be out of memory (OOM). Note that the Orthoformer attention presents significantly lower efficiency, which is also observed in [99] and may be caused by the serial computation in landmark selection. It is natural that all models are OOM when the input scale is extremely large, e.g., . This can be partially solved by token sparsification [67; 29], and we leave it to the future work.
| Method | Baseline | +NA | +FF | +NA+FF |
|---|---|---|---|---|
| Performer [15] | 58.82 | 61.57 | 59.97 | 63.50 |
| Linear Trans. [37] | 60.42 | 62.84 | 61.87 | 64.76 |
| cosFormer [64] | 61.18 | 63.23 | 61.94 | 64.97 |
| XViT (Softmax) [64] | 66.20 | - | 65.94 | 65.94 |
Application to existing models. Lastly, we study the effect of applying neighbourhood association and feature fixation to other linear attention and Softmax in Table 9. The two modules can clearly improve the performance of linear attention, e.g., Performer [15], Linear Trans. [37] and cosFormer [64], and their combination makes the three linear Transformers even closer to the SOTA results. It validates the effectiveness of our method in the linear setting. Nevertheless, there is no performance gain in the Softmax-based Transformer, e.g., XViT [7] (neighbourhood association is not added here because XViT already has the temporal feature shift operation). This is not surprising because it further reveals that our method is specially useful to linear attention.
6 Conclusion
In this paper, we study the linear video Transformer for video classification to reduce the quadratic computational costs of standard Softmax attention. We analyze the performance drop in linear attention, and find that the lack of attention concentration to salient features is the underlying cause. To deal with this issue, we propose to use feature fixation to the query and key prior to calculating the linear attention. To measure feature importance more comprehensively, we facilitate the cooperation among Query-Key-Value by aggregating their features when generating the fixation ratio. Moreover, motivated by the fact that salient vision features are usually locally accumulative, we apply the feature shift technique to get additional feature guidance from spatially and temporally nearby tokens. This, combined with feature fixation, produces state-of-the-art results among linear video Transformers on three popular video classification benchmarks. Our performance is also comparable to some quadratic Transformers with Softmax attention with fewer parameters and higher efficiency. Our future work will focus on further accelerating the linear attention model without degrading the general performance, e.g., token sparsification, network pruning, and so on.
References
- [1] Abien Fred Agarap. Deep learning using rectified linear units (relu). arXiv preprint arXiv:1803.08375, 2018.
- [2] Hassan Akbari, Liangzhe Yuan, Rui Qian, Wei-Hong Chuang, Shih-Fu Chang, Yin Cui, and Boqing Gong. Vatt: Transformers for multimodal self-supervised learning from raw video, audio and text. Advances in Neural Information Processing Systems, 34, 2021.
- [3] Humam Alwassel, Fabian Caba Heilbron, and Bernard Ghanem. Action search: Spotting actions in videos and its application to temporal action localization. In Proceedings of the European Conference on Computer Vision (ECCV), pages 251–266, 2018.
- [4] Anurag Arnab, Mostafa Dehghani, Georg Heigold, Chen Sun, Mario Lučić, and Cordelia Schmid. Vivit: A video vision transformer. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 6836–6846, 2021.
- [5] Iz Beltagy, Matthew E Peters, and Arman Cohan. Longformer: The long-document transformer. arXiv preprint arXiv:2004.05150, 2020.
- [6] Gedas Bertasius, Heng Wang, and Lorenzo Torresani. Is space-time attention all you need for video understanding? In Proceedings of the International Conference on Machine Learning (ICML), July 2021.
- [7] Adrian Bulat, Juan Manuel Perez Rua, Swathikiran Sudhakaran, Brais Martinez, and Georgios Tzimiropoulos. Space-time mixing attention for video transformer. Advances in Neural Information Processing Systems, 34, 2021.
- [8] Han Cai, Chuang Gan, and Song Han. Efficientvit: Enhanced linear attention for high-resolution low-computation visual recognition. arXiv preprint arXiv:2205.14756, 2022.
- [9] Joao Carreira, Eric Noland, Andras Banki-Horvath, Chloe Hillier, and Andrew Zisserman. A short note about kinetics-600. arXiv preprint arXiv:1808.01340, 2018.
- [10] Joao Carreira and Andrew Zisserman. Quo vadis, action recognition? a new model and the kinetics dataset. In proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 6299–6308, 2017.
- [11] Xuelian Cheng, Huan Xiong, Deng-Ping Fan, Yiran Zhong, Mehrtash Harandi, Tom Drummond, and Zongyuan Ge. Implicit motion handling for video camouflaged object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 13864–13873, 2022.
- [12] Xuelian Cheng, Yiran Zhong, Mehrtash Harandi, Tom Drummond, Zhiyong Wang, and Zongyuan Ge. Deep laparoscopic stereo matching with transformers. In International Conference on Medical Image Computing and Computer-Assisted Intervention, pages 464–474. Springer, 2022.
- [13] Rewon Child, Scott Gray, Alec Radford, and Ilya Sutskever. Generating long sequences with sparse transformers. arXiv preprint arXiv:1904.10509, 2019.
- [14] Krzysztof Choromanski, Valerii Likhosherstov, David Dohan, Xingyou Song, Andreea Gane, Tamas Sarlos, Peter Hawkins, Jared Davis, David Belanger, Lucy Colwell, et al. Masked language modeling for proteins via linearly scalable long-context transformers. arXiv preprint arXiv:2006.03555, 2020.
- [15] Krzysztof Marcin Choromanski, Valerii Likhosherstov, David Dohan, Xingyou Song, Andreea Gane, Tamas Sarlos, Peter Hawkins, Jared Quincy Davis, Afroz Mohiuddin, Lukasz Kaiser, David Benjamin Belanger, Lucy J Colwell, and Adrian Weller. Rethinking attention with performers. In International Conference on Learning Representations, 2021.
- [16] Xiangxiang Chu, Zhi Tian, Yuqing Wang, Bo Zhang, Haibing Ren, Xiaolin Wei, Huaxia Xia, and Chunhua Shen. Twins: Revisiting the design of spatial attention in vision transformers. Advances in Neural Information Processing Systems, 34, 2021.
- [17] Ekin D Cubuk, Barret Zoph, Dandelion Mane, Vijay Vasudevan, and Quoc V Le. Autoaugment: Learning augmentation policies from data. arXiv preprint arXiv:1805.09501, 2018.
- [18] Hui Deng, Tong Zhang, Yuchao Dai, Jiawei Shi, Yiran Zhong, and Hongdong Li. Deep non-rigid structure-from-motion: A sequence-to-sequence translation perspective. arXiv preprint arXiv:2204.04730, 2022.
- [19] Jia Deng, Wei Dong, Richard Socher, Li-Jia Li, Kai Li, and Li Fei-Fei. Imagenet: A large-scale hierarchical image database. In 2009 IEEE conference on computer vision and pattern recognition, pages 248–255. Ieee, 2009.
- [20] Jeffrey Donahue, Lisa Anne Hendricks, Sergio Guadarrama, Marcus Rohrbach, Subhashini Venugopalan, Kate Saenko, and Trevor Darrell. Long-term recurrent convolutional networks for visual recognition and description. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 2625–2634, 2015.
- [21] Alexey Dosovitskiy, Lucas Beyer, Alexander Kolesnikov, Dirk Weissenborn, Xiaohua Zhai, Thomas Unterthiner, Mostafa Dehghani, Matthias Minderer, Georg Heigold, Sylvain Gelly, et al. An image is worth 16x16 words: Transformers for image recognition at scale. International Conference on Learning Representations, 2021.
- [22] Haoqi Fan, Bo Xiong, Karttikeya Mangalam, Yanghao Li, Zhicheng Yan, Jitendra Malik, and Christoph Feichtenhofer. Multiscale vision transformers. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 6824–6835, 2021.
- [23] Christoph Feichtenhofer. X3d: Expanding architectures for efficient video recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 203–213, 2020.
- [24] Christoph Feichtenhofer, Haoqi Fan, Jitendra Malik, and Kaiming He. Slowfast networks for video recognition. In Proceedings of the IEEE/CVF international conference on computer vision, pages 6202–6211, 2019.
- [25] Simon Ging, Mohammadreza Zolfaghari, Hamed Pirsiavash, and Thomas Brox. Coot: Cooperative hierarchical transformer for video-text representation learning. Advances in neural information processing systems, 33:22605–22618, 2020.
- [26] Rohit Girdhar, Joao Carreira, Carl Doersch, and Andrew Zisserman. Video action transformer network. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 244–253, 2019.
- [27] Raghav Goyal, Samira Ebrahimi Kahou, Vincent Michalski, Joanna Materzynska, Susanne Westphal, Heuna Kim, Valentin Haenel, Ingo Fruend, Peter Yianilos, Moritz Mueller-Freitag, et al. The” something something” video database for learning and evaluating visual common sense. In Proceedings of the IEEE international conference on computer vision, pages 5842–5850, 2017.
- [28] Yuchao Gu, Lijuan Wang, Ziqin Wang, Yun Liu, Ming-Ming Cheng, and Shao-Ping Lu. Pyramid constrained self-attention network for fast video salient object detection. In Proceedings of the AAAI conference on artificial intelligence, volume 34, pages 10869–10876, 2020.
- [29] John Guibas, Morteza Mardani, Zongyi Li, Andrew Tao, Anima Anandkumar, and Bryan Catanzaro. Efficient token mixing for transformers via adaptive fourier neural operators. In International Conference on Learning Representations, 2021.
- [30] Kensho Hara, Hirokatsu Kataoka, and Yutaka Satoh. Can spatiotemporal 3d cnns retrace the history of 2d cnns and imagenet? In Proceedings of the IEEE conference on Computer Vision and Pattern Recognition, pages 6546–6555, 2018.
- [31] Ryota Hashiguchi and Toru Tamaki. Vision transformer with cross-attention by temporal shift for efficient action recognition. arXiv preprint arXiv:2204.00452, 2022.
- [32] Jonathan Ho, Nal Kalchbrenner, Dirk Weissenborn, and Tim Salimans. Axial attention in multidimensional transformers. arXiv preprint arXiv:1912.12180, 2019.
- [33] Jie Hu, Li Shen, and Gang Sun. Squeeze-and-excitation networks. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 7132–7141, 2018.
- [34] Kan Huang, Ge Li, and Shan Liu. Learning channel-wise spatio-temporal representations for video salient object detection. Neurocomputing, 403:325–336, 2020.
- [35] Zilong Huang, Xinggang Wang, Lichao Huang, Chang Huang, Yunchao Wei, and Wenyu Liu. Ccnet: Criss-cross attention for semantic segmentation. In Proceedings of the IEEE/CVF international conference on computer vision, pages 603–612, 2019.
- [36] Andrew Jaegle, Felix Gimeno, Andy Brock, Oriol Vinyals, Andrew Zisserman, and Joao Carreira. Perceiver: General perception with iterative attention. In International Conference on Machine Learning, pages 4651–4664. PMLR, 2021.
- [37] Angelos Katharopoulos, Apoorv Vyas, Nikolaos Pappas, and François Fleuret. Transformers are rnns: Fast autoregressive transformers with linear attention. In International Conference on Machine Learning, pages 5156–5165. PMLR, 2020.
- [38] Nikita Kitaev, Lukasz Kaiser, and Anselm Levskaya. Reformer: The efficient transformer. In International Conference on Learning Representations, 2020.
- [39] Bruno Korbar, Du Tran, and Lorenzo Torresani. Scsampler: Sampling salient clips from video for efficient action recognition. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 6232–6242, 2019.
- [40] Heeseung Kwon, Manjin Kim, Suha Kwak, and Minsu Cho. Motionsqueeze: Neural motion feature learning for video understanding. In European conference on computer vision, pages 345–362. Springer, 2020.
- [41] Juho Lee, Yoonho Lee, Jungtaek Kim, Adam Kosiorek, Seungjin Choi, and Yee Whye Teh. Set transformer: A framework for attention-based permutation-invariant neural networks. In International Conference on Machine Learning, pages 3744–3753. PMLR, 2019.
- [42] Dong Li, Zhaofan Qiu, Qi Dai, Ting Yao, and Tao Mei. Recurrent tubelet proposal and recognition networks for action detection. In Proceedings of the European conference on computer vision (ECCV), pages 303–318, 2018.
- [43] Dongxu Li, Chenchen Xu, Kaihao Zhang, Xin Yu, Yiran Zhong, Wenqi Ren, Hanna Suominen, and Hongdong Li. Arvo: Learning all-range volumetric correspondence for video deblurring. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 7721–7731, 2021.
- [44] Zhenyang Li, Kirill Gavrilyuk, Efstratios Gavves, Mihir Jain, and Cees GM Snoek. Videolstm convolves, attends and flows for action recognition. Computer Vision and Image Understanding, 166:41–50, 2018.
- [45] Zhengguo Li, Haiyan Shu, and Chaobing Zheng. Multi-scale single image dehazing using laplacian and gaussian pyramids. IEEE Transactions on Image Processing, 30:9270–9279, 2021.
- [46] Yuxuan Liang, Pan Zhou, Roger Zimmermann, and Shuicheng Yan. Dualformer: Local-global stratified transformer for efficient video recognition. arXiv preprint arXiv:2112.04674, 2021.
- [47] Ji Lin, Chuang Gan, and Song Han. Tsm: Temporal shift module for efficient video understanding. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 7083–7093, 2019.
- [48] Peter J Liu, Mohammad Saleh, Etienne Pot, Ben Goodrich, Ryan Sepassi, Lukasz Kaiser, and Noam Shazeer. Generating wikipedia by summarizing long sequences. arXiv preprint arXiv:1801.10198, 2018.
- [49] Sifei Liu, Shalini De Mello, Jinwei Gu, Guangyu Zhong, Ming-Hsuan Yang, and Jan Kautz. Learning affinity via spatial propagation networks. Advances in Neural Information Processing Systems, 30, 2017.
- [50] Sifei Liu, Jinshan Pan, and Ming-Hsuan Yang. Learning recursive filters for low-level vision via a hybrid neural network. In European conference on computer vision, pages 560–576. Springer, 2016.
- [51] Zexiang Liu, Dong Li, Kaiyue Lu, Zhen Qin, Weixuan Sun, Jiacheng Xu, and Yiran Zhong. Neural architecture search on efficient transformers and beyond. arXiv preprint arXiv:2207.13955, 2022.
- [52] Ze Liu, Yutong Lin, Yue Cao, Han Hu, Yixuan Wei, Zheng Zhang, Stephen Lin, and Baining Guo. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 10012–10022, 2021.
- [53] Ze Liu, Jia Ning, Yue Cao, Yixuan Wei, Zheng Zhang, Stephen Lin, and Han Hu. Video swin transformer. arXiv preprint arXiv:2106.13230, 2021.
- [54] Zhaoyang Liu, Limin Wang, Wayne Wu, Chen Qian, and Tong Lu. Tam: Temporal adaptive module for video recognition. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 13708–13718, 2021.
- [55] Ilya Loshchilov and Frank Hutter. Sgdr: Stochastic gradient descent with warm restarts. arXiv preprint arXiv:1608.03983, 2016.
- [56] David G Lowe. Object recognition from local scale-invariant features. In Proceedings of the seventh IEEE international conference on computer vision, volume 2, pages 1150–1157. Ieee, 1999.
- [57] Kaiyue Lu, Nick Barnes, Saeed Anwar, and Liang Zheng. From depth what can you see? depth completion via auxiliary image reconstruction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 11306–11315, 2020.
- [58] Antoine Miech, Ivan Laptev, and Josef Sivic. Learnable pooling with context gating for video classification. arXiv preprint arXiv:1706.06905, 2017.
- [59] Wenjia Niu, Kaihao Zhang, Wenhan Luo, and Yiran Zhong. Blind motion deblurring super-resolution: When dynamic spatio-temporal learning meets static image understanding. IEEE Transactions on Image Processing, 30:7101–7111, 2021.
- [60] Adam Paszke, Sam Gross, Francisco Massa, Adam Lerer, James Bradbury, Gregory Chanan, Trevor Killeen, Zeming Lin, Natalia Gimelshein, Luca Antiga, et al. Pytorch: An imperative style, high-performance deep learning library. Advances in neural information processing systems, 32, 2019.
- [61] Mandela Patrick, Dylan Campbell, Yuki Asano, Ishan Misra, Florian Metze, Christoph Feichtenhofer, Andrea Vedaldi, and João F Henriques. Keeping your eye on the ball: Trajectory attention in video transformers. Advances in neural information processing systems, 34:12493–12506, 2021.
- [62] Badri Narayana Patro, Mayank Lunayach, and Vinay P Namboodiri. Uncertainty class activation map (u-cam) using gradient certainty method. IEEE Transactions on Image Processing, 30:1910–1924, 2021.
- [63] Hao Peng, Nikolaos Pappas, Dani Yogatama, Roy Schwartz, Noah Smith, and Lingpeng Kong. Random feature attention. In International Conference on Learning Representations, 2021.
- [64] Zhen Qin, Weixuan Sun, Hui Deng, Dongxu Li, Yunshen Wei, Baohong Lv, Junjie Yan, Lingpeng Kong, and Yiran Zhong. cosformer: Rethinking softmax in attention. In International Conference on Learning Representations, 2022.
- [65] Jiezhong Qiu, Hao Ma, Omer Levy, Scott Wen-tau Yih, Sinong Wang, and Jie Tang. Blockwise self-attention for long document understanding. arXiv preprint arXiv:1911.02972, 2019.
- [66] Zhaofan Qiu, Ting Yao, and Tao Mei. Learning spatio-temporal representation with pseudo-3d residual networks. In proceedings of the IEEE International Conference on Computer Vision, pages 5533–5541, 2017.
- [67] Yongming Rao, Wenliang Zhao, Benlin Liu, Jiwen Lu, Jie Zhou, and Cho-Jui Hsieh. Dynamicvit: Efficient vision transformers with dynamic token sparsification. Advances in neural information processing systems, 34:13937–13949, 2021.
- [68] Nikunj Saunshi, Orestis Plevrakis, Sanjeev Arora, Mikhail Khodak, and Hrishikesh Khandeparkar. A theoretical analysis of contrastive unsupervised representation learning. In International Conference on Machine Learning, pages 5628–5637. PMLR, 2019.
- [69] Gilad Sharir, Asaf Noy, and Lihi Zelnik-Manor. An image is worth 16x16 words, what is a video worth? arXiv preprint arXiv:2103.13915, 2021.
- [70] Jiadai Sun, Yuxin Mao, Yuchao Dai, Yiran Zhong, and Jianyuan Wang. Munet: Motion uncertainty-aware semi-supervised video object segmentation. arXiv preprint arXiv:2111.14646, 2021.
- [71] Jingyu Sun, Guiping Zhong, Dinghao Zhou, Baoxiang Li, and Yiran Zhong. Locality matters: A locality-biased linear attention for automatic speech recognition. arXiv preprint arXiv:2203.15609, 2022.
- [72] Weixuan Sun, Zhen Qin, Hui Deng, Jianyuan Wang, Yi Zhang, Kaihao Zhang, Nick Barnes, Stan Birchfield, Lingpeng Kong, and Yiran Zhong. Vicinity vision transformer. arXiv preprint arXiv:2206.10552, 2022.
- [73] Weixuan Sun, Jing Zhang, and Nick Barnes. Inferring the class conditional response map for weakly supervised semantic segmentation. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), pages 2878–2887, January 2022.
- [74] Shitao Tang, Jiahui Zhang, Siyu Zhu, and Ping Tan. Quadtree attention for vision transformers. In International Conference on Learning Representations, 2022.
- [75] Yi Tay, Dara Bahri, Liu Yang, Donald Metzler, and Da-Cheng Juan. Sparse sinkhorn attention. In International Conference on Machine Learning, pages 9438–9447. PMLR, 2020.
- [76] Yi Tay, Mostafa Dehghani, Dara Bahri, and Donald Metzler. Efficient transformers: A survey. arXiv preprint arXiv:2009.06732, 2020.
- [77] Yonglong Tian, Chen Sun, Ben Poole, Dilip Krishnan, Cordelia Schmid, and Phillip Isola. What makes for good views for contrastive learning? Advances in Neural Information Processing Systems, 33:6827–6839, 2020.
- [78] Christopher Tosh, Akshay Krishnamurthy, and Daniel Hsu. Contrastive learning, multi-view redundancy, and linear models. In Algorithmic Learning Theory, pages 1179–1206. PMLR, 2021.
- [79] Du Tran, Lubomir Bourdev, Rob Fergus, Lorenzo Torresani, and Manohar Paluri. Learning spatiotemporal features with 3d convolutional networks. In Proceedings of the IEEE international conference on computer vision, pages 4489–4497, 2015.
- [80] Du Tran, Heng Wang, Lorenzo Torresani, and Matt Feiszli. Video classification with channel-separated convolutional networks. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 5552–5561, 2019.
- [81] Du Tran, Heng Wang, Lorenzo Torresani, Jamie Ray, Yann LeCun, and Manohar Paluri. A closer look at spatiotemporal convolutions for action recognition. In Proceedings of the IEEE conference on Computer Vision and Pattern Recognition, pages 6450–6459, 2018.
- [82] Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N Gomez, Łukasz Kaiser, and Illia Polosukhin. Attention is all you need. Advances in neural information processing systems, 30, 2017.
- [83] Jue Wang and Lorenzo Torresani. Deformable video transformer. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 14053–14062, 2022.
- [84] Junke Wang, Xitong Yang, Hengduo Li, Zuxuan Wu, and Yu-Gang Jiang. Efficient video transformers with spatial-temporal token selection. arXiv preprint arXiv:2111.11591, 2021.
- [85] Jianyuan Wang, Yiran Zhong, Yuchao Dai, Kaihao Zhang, Pan Ji, and Hongdong Li. Displacement-invariant matching cost learning for accurate optical flow estimation. Advances in Neural Information Processing Systems, 33:15220–15231, 2020.
- [86] Limin Wang, Yuanjun Xiong, Zhe Wang, Yu Qiao, Dahua Lin, Xiaoou Tang, and Luc Van Gool. Temporal segment networks for action recognition in videos. IEEE transactions on pattern analysis and machine intelligence, 41(11):2740–2755, 2018.
- [87] Sinong Wang, Belinda Z Li, Madian Khabsa, Han Fang, and Hao Ma. Linformer: Self-attention with linear complexity. arXiv preprint arXiv:2006.04768, 2020.
- [88] Wenhai Wang, Enze Xie, Xiang Li, Deng-Ping Fan, Kaitao Song, Ding Liang, Tong Lu, Ping Luo, and Ling Shao. Pyramid vision transformer: A versatile backbone for dense prediction without convolutions. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 568–578, 2021.
- [89] Yuetian Weng, Zizheng Pan, Mingfei Han, Xiaojun Chang, and Bohan Zhuang. An efficient spatio-temporal pyramid transformer for action detection. arXiv preprint arXiv:2207.10448, 2022.
- [90] Bichen Wu, Alvin Wan, Xiangyu Yue, Peter Jin, Sicheng Zhao, Noah Golmant, Amir Gholaminejad, Joseph Gonzalez, and Kurt Keutzer. Shift: A zero flop, zero parameter alternative to spatial convolutions. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 9127–9135, 2018.
- [91] Haixu Wu, Jialong Wu, Jiehui Xu, Jianmin Wang, and Mingsheng Long. Flowformer: Linearizing transformers with conservation flows. In Proceedings of the 39th International Conference on Machine Learning, volume 162 of Proceedings of Machine Learning Research, pages 24226–24242. PMLR, 17–23 Jul 2022.
- [92] Haiping Wu, Bin Xiao, Noel Codella, Mengchen Liu, Xiyang Dai, Lu Yuan, and Lei Zhang. Cvt: Introducing convolutions to vision transformers. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 22–31, 2021.
- [93] Wenhao Wu, Dongliang He, Xiao Tan, Shifeng Chen, and Shilei Wen. Multi-agent reinforcement learning based frame sampling for effective untrimmed video recognition. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 6222–6231, 2019.
- [94] Zuxuan Wu, Caiming Xiong, Chih-Yao Ma, Richard Socher, and Larry S Davis. Adaframe: Adaptive frame selection for fast video recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 1278–1287, 2019.
- [95] Junbo Yin, Jianbing Shen, Chenye Guan, Dingfu Zhou, and Ruigang Yang. Lidar-based online 3d video object detection with graph-based message passing and spatiotemporal transformer attention. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 11495–11504, 2020.
- [96] Xuefan Zha, Wentao Zhu, Lv Xun, Sen Yang, and Ji Liu. Shifted chunk transformer for spatio-temporal representational learning. Advances in Neural Information Processing Systems, 34, 2021.
- [97] Hao Zhang, Yanbin Hao, and Chong-Wah Ngo. Token shift transformer for video classification. In Proceedings of the 29th ACM International Conference on Multimedia, pages 917–925, 2021.
- [98] Yanyi Zhang, Xinyu Li, Chunhui Liu, Bing Shuai, Yi Zhu, Biagio Brattoli, Hao Chen, Ivan Marsic, and Joseph Tighe. Vidtr: Video transformer without convolutions. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 13577–13587, 2021.
- [99] Lin Zheng, Chong Wang, and Lingpeng Kong. Linear complexity randomized self-attention mechanism. In Kamalika Chaudhuri, Stefanie Jegelka, Le Song, Csaba Szepesvari, Gang Niu, and Sivan Sabato, editors, Proceedings of the 39th International Conference on Machine Learning, volume 162 of Proceedings of Machine Learning Research, pages 27011–27041. PMLR, 17–23 Jul 2022.
- [100] Yiran Zhong, Charles Loop, Wonmin Byeon, Stan Birchfield, Yuchao Dai, Kaihao Zhang, Alexey Kamenev, Thomas Breuel, Hongdong Li, and Jan Kautz. Displacement-invariant cost computation for stereo matching. International Journal of Computer Vision, 130(5):1196–1209, 2022.
- [101] Jinxing Zhou, Jianyuan Wang, Jiayi Zhang, Weixuan Sun, Jing Zhang, Stan Birchfield, Dan Guo, Lingpeng Kong, Meng Wang, and Yiran Zhong. Audio-visual segmentation. In European Conference on Computer Vision, 2022.
Appendix A Appendix
A.1 Training details
We provide detailed training configuration on SSv2 and K400/K600 in Table 10.
| SSv2 | K400/K600 | |
| Batch size | 32 | 32 |
| Video sampling rate | 16 | 16 |
| Training jitter scales | ||
| Hidden dimension | 512 | 512 |
| Base learning rate | 0.035 | 0.035 |
| LR policy | cosine | cosine |
| Max epochs | 35 | 35 |
| Weight decay | 0.0004 | 0.0004 |
| Warm-up epochs | 5 | 5 |
| Warm-up start LR | 0.003 | 0.01 |
| Optimizer | sgd | sgd |
| Dropout rate | 0.5 | 0.5 |
| Spatial shift | 1 | 4 |
| Temporal shift | 4 | 8 |
A.2 Further illustration of feature fixation
To illustrate the proposed feature fixation, we give a toy example here. Suppose we have two values, and , from the multiplication of a specific query to two keys, i.e., , and is assumed to be more important. In linear attention, the original score of is , i.e., dot-product normalization. Now we reweight and into and , where and . Consequently, the updated score of is . In that case, , i.e., , indicating that the impact of is enhanced.
In our feature fixation, each feature channel is assigned with different weighting factors (ranging from 0-1), where non-essential features are down-weighted and critical features are almost unchanged. Hence, some multiplication values of the reweighted query and key become smaller if they contain non-essential features. In that case, their final scores are also reduced so that the impact of other important scores is further enhanced in turn (the principle of the toy example above is also applicable here).
A.3 Feature shift
Temporal feature shift. We define a temporal window centred at the target token, similar to [7]. When reconstructing the key/value vector of a patch located at a specific position in that frame, we first retain its first feature channels where is a scaling factor and empirically set as 0.5. The remaining part is filled by the feature concatenation of its nearby key/value vectors, each sequentially contributing channels.
Spatial feature shift. Since the video frame is a 2D image, an intuitive way is to define a squared kernel centered at the target token and set the spatial shift size (i.e., the radius of the kernel) as . In that case, tokens are involved to construct the new key/value vector. However, when the shift size is large, i.e., enlarging the receptive field, the quadratic increase of the token number would weaken the impact of each nearby token as only very limited features are transmitted. Inspired by the criss-cross attention [35] and one-way spatial affinity [50; 49] in CNNs, we only consider tokens in the same column and row of the target, i.e., tokens from each direction (left, right, above, below). Similar to the temporal shift, each nearby token supplies feature channels.
To verify this, we compare the squared kernel shift and spatial shift with different sizes in Table 11. As shown, when the size is 1, the numbers of tokens are similar and their performance is identical. However, with the increased size, the token number grows quadratically in the squared kernel but the performance is degraded. Therefore, the spatial shift we used can fulfill our needs, i.e., allowing the target token to communicate with sufficient nearby tokens without significant performance degradation caused by involving excessive nearby tokens.
| Size | #Tokens | Top-1 | Top-5 | |
| Spatial shift (ours) | 1 | 5 | 65.5 | 90.1 |
| Squared kernel shift | 1 | 9 | 65.5 | 90.1 |
| Spatial shift (ours) | 2 | 9 | 65.4 | 90.0 |
| Squared kernel shift | 2 | 25 | 65.2 | 89.8 |
A.4 Impact of Test views
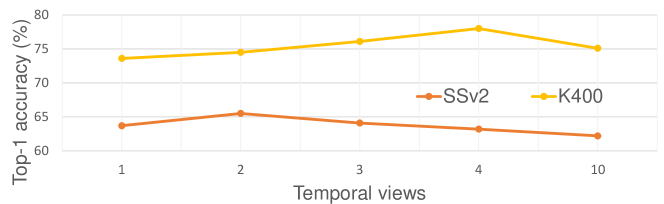
At the inference stage, the number of spatial views are normally set as 3, i.e., left-crop, middle-crop, and right-crop. As shown in Table 1 and 2, almost all the models employ this setting of spatial views, so we do not ablate it here. We study the effect of temporal views in Fig. 4. The performance varies with the number of temporal views on both SSv2 and K400. We can empirically choose the best setting from various choices according to the performance on each dataset.
A.5 Ablation on K400
Lastly, we supplement the ablation study on the effect of neighbourhood association and feature fixation on K400 in Table 12. Compared with the results of SSv2 (Table 5.3), the Top-1 accuracy does not vary too much on K400, but the effectiveness of each module is well validated. A distinction here is that the spatial shift brings more performance gain than the temporal shift. This is because different from SSv2 that reasons more about motion cues, K400 focuses more on spatial content as it has more complicated background information [4; 6; 53].
| SS | TS | FF | Top-1 |
|---|---|---|---|
| 77.27 | |||
| 77.53 | |||
| 77.43 | |||
| 77.70 | |||
| 77.47 | |||
| 77.96 |