vol. 26:220241210.46298/dmtcs.109712023-02-17; 2023-02-17; 2024-02-152024-05-24
Line game-perfect graphs
Abstract
The -edge colouring game is played with a set
of colours on a graph with initially
uncoloured edges by two players, Alice (A) and Bob (B).
The players move alternately. Player has the first move.
. If , then only player may skip any move,
otherwise skipping is not allowed for any player.
A move consists of colouring an uncoloured edge with one of the colours
such that adjacent edges have distinct colours. When no more moves are possible,
the game ends. If every edge is coloured in the end, Alice wins; otherwise,
Bob wins.
The -game chromatic index is the smallest nonnegative integer such that Alice has a winning strategy for the -edge colouring game played on with colours. The graph is called line -perfect if, for any edge-induced subgraph of ,
where denotes the clique number of the line graph of .
For each of the six possibilities , we characterise line -perfect graphs by forbidden edge-induced subgraphs and by explicit structural descriptions, respectively.
keywords:
line graph, line perfect graph, edge colouring game, game-perfect graph, graph colouring game, perfect graph, forbidden subgraph characterisation1 Introduction
A subgraph of a graph is an induced subgraph of if every edge of whose two end-vertices are in the vertex set of is also an edge of . A subgraph of a graph is an edge-induced subgraph of if the vertex set of consists of all end-vertices of edges of . Equivalently, an edge-induced subgraph of is a subgraph of that contains no isolated vertices.
The line graph of a graph is the graph with and where the edge set of is the set of all unordered pairs of elements in such that and are adjacent as edges in .
Edge colouring of a graph is equivalent to vertex colouring of its line graph . Moreover, the colouring parameter for edge colouring, the chromatic index of , equals the chromatic number of the line graph .
In this sense, the well-established concept of perfectness for vertex colouring has an interesting analog for edge colouring, namely line perfectness, which was first defined by Trotter (1977). A graph is line perfect if, for any edge-induced subgraph of ,
where , the clique number of the line graph of , is the maximum number of mutually adjacent edges in . Equivalently, as remarked by Trotter (1977), a graph is line perfect if its line graph is a perfect graph. The reason for this equivalence is the fact that, for any graph , the set of the line graphs of the edge-induced subgraphs of is the same as the set of the induced subgraphs of .
It is known that line perfect graphs are perfect:
Theorem 1 (Trotter (1977)).
Line perfect graphs are perfect.
Trotter (1977) gave a characterisation of line perfect graphs by a set of forbidden edge-induced subgraphs:
Theorem 2 (Trotter (1977)).
A graph is line perfect if and only if it contains no odd cycles of length at least 5 as edge-induced subgraphs.
Maffray (1992) gave a complete characterisation of the structure of line perfect graphs:
Theorem 3 (Maffray (1992)).
A graph is line perfect if and only if each of its blocks is either bipartite or a complete graph on 4 vertices or a triangular book for some positive integer .
Since bipartite graphs, , and triangular books are perfect, the powerful Theorem 3 implies the result of Theorem 1.
In this paper we combine the idea of line perfect graphs with graph colouring games. For each such game, we define a notion of line game-perfectness and give a characterisation of the structure of such line game-perfect graphs. These characterisations include two equivalent descriptions: a characterisation by forbidden edge-induced subgraphs analog to the Theorem of Trotter (Theorem 2) and a characterisation by an explicit structural description analog to the Theorem of Maffray (Theorem 3).
1.1 Vertex colouring games
A vertex colouring game is played with a set of colours () on a graph whose vertices are initially uncoloured by two players, Alice (A) and Bob (B). The players move alternately. A move consists in colouring an uncoloured vertex with one of the colours such that adjacent vertices receive distinct colours. The game ends when such a move is not possible. If every vertex is coloured in the end, Alice wins. Otherwise, i.e., in the case that an uncoloured vertex is adjacent to vertices of all colours, Bob wins.
Such a graph colouring game, defined by Brams, appeared in a mathematical games column by Gardner (1981). Later it was reinvented by Bodlaender (1991) who defined the game chromatic number as the smallest nonnegative integer such that Alice has a winning strategy for the vertex colouring game played on . Since Alice always wins if , the parameter is well-defined.
To be precise, two more rules have to be fixed to make the game well-defined. Firstly, we have to fix the player who moves first. Secondly, we have to fix whether skipping (any) moves is allowed for some player or not allowed (which we denote by ). Thus we have six different games, one game for any of the pairs
and we call such a game the -colouring game and denote its game chromatic number by .
The distinction of the six games is important when we discuss game-theoretic analogs of perfect graphs, the game-perfect graphs.
1.2 Game-perfect graphs
A graph is -perfect (or game-perfect for the -colouring game) if, for any induced subgraph of ,
where , the clique number of , is the maximum number of mutually adjacent vertices in .
The concept of game-perfect graphs was introduced by Andres (2007, 2009). For four of the six games, structural characterisations of game-perfect graphs by forbidden induced subgraphs and by an explicit structural description are known. The characterisation by forbidden induced subgraphs of two of these characterisations will be extremely useful as basis for two of our main theorems in the following sections:



triangle star

-graph


two split 3-stars


mixed graph


two double fans

chair


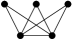
split 3-star



double fan

4-fan

4-wheel






Theorem 4 (Andres (2012)).
A graph is -perfect if and only if it contains none of the seven graphs depicted in Figure 1 as an induced subgraph.
Theorem 5 (Lock (2016); Andres and Lock (2019)).
A graph is -perfect if and only if it contains none of the fifteen graphs depicted in Figure 2 as an induced subgraph.
Furthermore, Andres (2012) characterised the class of -perfect graphs by an explicit structural description. An ear animal is a graph of the form
with and . Here, (resp., ) denotes the disjoint union (resp., the join) of two graphs and .
Theorem 6 (Andres (2012)).
A graph is -perfect if and only if each of its components is an ear animal.
We will use this result in order to simplify the proof of one of our main theorems (Theorem 12).
Lock (2016) and Andres and Lock (2019) characterised the class of -perfect graphs by a (very large) explicit structural description. From this description we will need only two partial results, given in Proposition 7 and Proposition 8, in order to simplify the proof of another one of our main theorems (Theorem 11).


An expanded cocobi is a graph of the type depicted in Figure 3 with , , and , . An expanded cocobi consists of nonempty cliques and two (possibly empty) cliques and with cardinalities , , , and , for , respectively, such that between all pairs of cliques in there is a complete join, between all pairs of cliques in there is a complete join, and, for any , there is a complete join between the cliques and (and no further edges are allowed). The dashed lines in Figure 3 indicate that may be arbitrarily large. An expanded bull is a graph of the type depicted in Figure 4 with and . In both figures, pairs of lines indicate complete joins of the cliques.
1.3 The edge colouring game
An edge colouring game has the same rules as a vertex colouring game, except that the players have to colour uncoloured edges (instead of uncoloured vertices) such that adjacent edges receive distinct colours. And Alice wins if every edge (instead of vertex) is coloured in the end.
The game chromatic index of is the smallest nonnegative integer such that Alice has a winning strategy for the edge colouring game played on with colours.
Thus, the edge colouring game on is equivalent to the vertex colouring game on the line graph of ; and the game chromatic index and the game chromatic number are related by
| (1) |
The edge colouring game was introduced by Lam et al. (1999) and Cai and Zhu (2001). Determining the maximum game chromatic index of some classes of graphs has been the subject of several papers (cf. Andres (2006); Andres et al. (2011); Bartnicki and Grytczuk (2008); Cai and Zhu (2001); Chan and Nong (2014); Charpentier et al. (2018); Fong and Chan (2019a, b); Fong et al. (2018); Lam et al. (1999)) as well as the game chromatic index of random graphs (cf. Beveridge et al. (2008); Keusch (2018)) as well as different types of edge-colouring based games (cf. Boudon et al. (2017); Dunn (2007); Dunn et al. (2015)).
Originally, in the edge colouring game Alice moves first and skipping is not allowed. However, we will distinguish here six variants as in the vertex colouring game. Namely, in the -edge colouring game player has the first move and player may skip moves (in case ) or none of the players is allowed to skip (in case . Its corresponding game chromatic index is denoted by .
1.4 Combining the setting: line game-perfect graphs
A graph is line -perfect (or line game-perfect for the -edge colouring game) if, for any edge-induced subgraph of ,
1.5 Main results
Theorem 9.
The following are equivalent for a graph .
-
(1)
is line -perfect.
-
(2)
None of the following configurations (depicted in Figure 5) is an edge-induced subgraph of : , , mini lobster , trigraph , or two 3-caterpillars .
- (3)
Theorem 10.
The following are equivalent for a graph .
-
(1)
is line -perfect.
-
(2)
None of the following configurations (depicted in Figure 6) is an edge-induced subgraph of : , , or 3-caterpillar .
- (3)
Theorem 11.
The following are equivalent for a graph .
-
(1)
is line -perfect.
-
(2)
None of the following configurations (depicted in Figure 7) is an edge-induced subgraph of : , , , , bull, diamond, or 3-caterpillar .
- (3)
Theorem 12.
The following are equivalent for a graph .

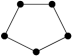

mini lobster

trigraph





3-caterpillar





bull

diamond

3-caterpillar


1.6 Idea of the proof
In order to prove Theorem 9, first, in Section 4, we show that Bob has a winning strategy for the -edge colouring game played on each of the forbidden configurations, which proves the implication (1)(2); then, in Section 5, we show that Alice has a winning strategy for the -edge colouring game played on each of the permitted types from (3) and, in Section 6, we show that the permitted types are hereditary (i.e., every edge-induced subgraph of such a permitted type is in one of the permitted types), which together proves the implication (3)(1); finally, in Section 6, using Theorem 3 we prove the structural description (i.e., the permitted types are exactly those graphs that do not contain any of the forbidden configurations as an edge-induced subgraph), which settles the implication (2)(3).
The proofs of Theorems 10, 11 and 12 have the same structure, however the structural implication (i.e., (2)(3) in Theorem 10 and Theorem 11, respectively, (4)(5) in Theorem 12) can be simplified by using the structural result from Theorem 9.
Furthermore, the other implications in Theorem 11 (respectively, Theorem 12) can be obtained in an easy way by using the structural results known for -perfect (respectively, -, - and -perfect) graphs, namely Theorem 5 and Propositions 7 and 8 (respectively, Theorem 4 and Theorem 6). The method for this last simplification will be described in Section 3.
1.7 Structure of this paper
In Section 2 we give some basic definitions and fix notation. A general idea to simplify the proofs concerning those games where a structural characterisation for game-perfectness is known is given in Section 3. In Section 4 we show that the forbidden configurations are not line game-perfect. In Section 5 we describe winning strategies for Alice on the permitted types for the different games. After these preparations, Section 6 is devoted to the proofs of the four main theorems. We conclude with an open question and a related problem in Section 7.
2 Preliminaries
We start by giving some definitions, easy observations and some results from the literature that we will use.
2.1 Notation
All graphs considered in this paper are simple, i.e., they contain neither loops nor multiple edges. Let be a graph. We denote by
-
•
the set of nonnegative integers;
-
•
the maximum degree of ;
-
•
the clique number of ;
-
•
the line graph of ;
-
•
the chromatic index of ;
-
•
the chromatic number of ;
-
•
the game chromatic index w.r.t. edge game ;
-
•
the game chromatic number w.r.t. vertex game .
Let . By (), (), , and , we denote the path, cycle and complete graph on vertices, and the complete bipartite graph with partite sets of and vertices, respectively.
Definition 13.
Let be a graph. An edge of is called unsafe if it is adjacent to at least edges.
2.2 Basic observations
The different vertex colouring games are related as follows:
Observation 14 (Andres (2009)).
For any graph ,
The same holds for the edge colouring games:
Observation 15 (Andres (2006)).
For any graph ,
2.3 Basic definitions and observations
Recall that the line graph of a graph is the graph where, for any , is an edge in (i.e., ) if and only if the edges and are adjacent in .
Observation 16.
For any graph and any game with and , we have
Observation 16 implies the two following observations, which can be taken as alternative definitions of line perfect graphs and line game-perfect graphs, respectively.
Observation 17 (Trotter (1977)).
A graph is line perfect if is perfect, i.e., for any vertex-induced subgraph of ,
Observation 18.
A graph is line -perfect if is -perfect, i.e., for any vertex-induced subgraph of ,
Let be the class of line -perfect graphs and be the class of line perfect graphs. Then, by the definition of line perfect graphs and line game-perfect graphs, Observation 15 directly implies (or, alternatively, by Observation 17 and Observation 18, Observation 14 directly implies) the following.
Observation 19.
In particular, Observation 19 says that every line -perfect graph is line perfect.
Corollary 20.
The classes of line -perfect graphs are subclasses of the class of perfect graphs.
Definition 21.
A graph is line -nice if
i.e., if Alice has a winning strategy with colours for the -edge colouring game played on .
The definition of line game-perfect graphs and Definition 21 have an obvious relation, given in Observation 22.
Observation 22.
A graph is line -perfect if and only if each of its edge-induced subgraphs is line -nice.
2.4 Characterisations of line graphs
The following well-known theorem will be used in our proofs.
Theorem 23 (Whitney (1932)).
Two connected nonempty graphs and are isomorphic if and only if their line graphs and are isomorphic, with the single exception of the two graphs and , which have the same line graph
Corollary 24.
For any graph ,
of Corollary 24.
Let be nonempty. By Theorem 23, cliques with in originate only from edge-induced stars or the in . Thus, either a star of maximum degree leads to the value of or the three mutually adjacent edges in a . ∎
Using Observation 16 and Corollary 24, we may reformulate Definition 21 for a graph with maximum degree as follows.
Observation 25.
A graph with is line -nice if
The precondition “nonempty” in Theorem 23 is essential as the line graphs of an isolated vertex and an empty graph are both the empty graph. Therefore, considering line graphs, it is convenient to exclude isolated vertices, which motivates the following definition.
Definition 26.
A graph is iso-free if it has no isolated vertices.
Beineke (1970) gave a characterisation of line graphs by forbidden induced subgraphs, which will be used in our proofs.
Theorem 27 (Beineke (1970)).
A graph is a line graph if and only if it contains none of the nine graphs from Figure 9 as an induced subgraph.

: claw

:

:

:

:

:

:

: triangular 3-ladder

: 5-wheel
3 A plan for characterising line game-perfect graphs
Let with .
-
•
For some games , we have a characterisation of game-perfect graphs by a list of forbidden induced subgraphs.
-
•
Let red be the maximal subset of such that no graph in red contains an induced .
-
•
Let the set of all iso-free graphs such that .
-
•
Let (which we call the reduced list) be the set of all iso-free graphs such that .
Then we have following fundamental theorem (which gives us the basic idea how to characterise game-perfect line graphs).
Theorem 28.
The following are equivalent for a graph and a game with and .
-
(1)
is line -perfect.
-
(2)
No graph in is an edge-induced subgraph of .
-
(3)
No graph in is an edge-induced subgraph of .
Proof.
(1)(2): Let be a line -perfect graph. Then is -game-perfect. By the characterisation of (vertex) -perfectness (e.g., by Theorem 4 or Theorem 5) does not contain a graph from the list as an induced subgraph. That means that does not contain a graph from the list as an edge-induced subgraph.
(2)(1): Let not contain any graph from the list as an edge-induced subgraph. Then does not contain any graph from the list as an induced subgraph. By the characterisation of -perfect graphs (e.g., by Theorem 4 or Theorem 5), this means that is -game-perfect. By definition this means that is line -perfect.
(2)(3): holds trivially.
(3)(2): Let . Then there is a graph with . Since is a line graph, by Theorem 27 does not contain any of the forbidden configurations as an induced subgraph. Thus . Thus
∎
General strategy to characterise -game line perfect graphs.
We do the following steps
-
1.
Determine (known from literature for 4 games):
-
2.
Determine red.
-
3.
Determine .
-
4.
Characterise the class of graph which do not contain any member of as an edge-induced subgraph.
4 The forbidden subgraphs
4.1 Forbidden subgraphs for game
The following basic lemma is implied by Theorem 23.
Lemma 29.
We have:
-
•
is the only iso-free graph whose line graph is .
-
•
is the only iso-free graph whose line graph is .
From the lemma above we conclude the following.
Proposition 30.
A graph is line -perfect if and only if it contains no or as an edge-induced subgraph.
Proof.
Let be a graph. By Theorem 28, the graph is line -perfect if and only if no graph in the reduced list is an edge-induced subgraph of . Thus, it is sufficient to prove that
Since is an induced subgraph of the split 3-star and of the double fan, it is an induced subgraph of the triangle star, the -graph, the two split 3-stars, the two double fans, and the mixed graph. Thus we have
Since, by Lemma 29, the only iso-free graph whose line graph is is the , and the only iso-free graph whose line graph is is the , we have
∎
4.2 Forbidden subgraphs for game
We obtain the following characterisation of line -perfect graphs.
Proposition 31.
A graph is line -perfect if and only if it contains no , , , , bull, diamond, or 3-caterpillar as an edge-induced subgraph.
Proof.
Let be a graph . By Theorem 28, is line -perfect if and only if no graph in the reduced list is an edge-induced subgraph of . Thus, to finish the proof it is sufficient to show that the reduced list consists of the forbidden graphs mentioned in the proposition.
Since is an induced subgraph of the chair, the split 3-star, the double fan, the , the , the , the , and the , we have
Furthermore, the following observations are implied by Theorem 23.
-
•
is the only iso-free graph whose line graph is .
-
•
is the only iso-free graph whose line graph is .
-
•
is the only iso-free graph whose line graph is .
-
•
is the only iso-free graph whose line graph is .
-
•
The bull is the only iso-free graph whose line graph is the 4-fan.
-
•
The diamond is the only iso-free graph whose line graph is the 4-wheel.
-
•
The 3-caterpillar is the only iso-free graph whose line graph is the graph depicted in Figure 2.
By these observations we conclude that
∎
4.3 Forbidden subgraphs for game
The next lemma is an auxiliary result that will be used to simplify some strategies in the forthcoming Lemma 33, Lemma 36, and Lemma 39.

Lemma 32.
Bob has a winning strategy with 3 colours in the -edge colouring game on the precoloured graph where the middle edge is precoloured by colour 1 (depicted in Figure 10) if it is Alice’s turn.
Proof.
Assume the colour set is . By symmetry, Alice has four possible types of moves: she can colour with colour 2, she can colour with colour 2 or with colour 1, or she can miss her turn.
-
•
If Alice colours with colour 2, Bob colours with colour 3. Then there is no feasible colour for any more.
-
•
If Alice colours with colour 2, Bob colours with colour 3. Then there is no feasible colour for any more.
-
•
If Alice colours with colour 1 or skips, then Bob colours with colour 2. If Bob will be able to colour or with colour 3 in his next move, he will win, since there would be no feasible colour for in both cases. In order to avoid both threats simultaneously, Alice has only one possibility: she must colour with colour 3. But then Bob colours with colour 2, so that there is no feasible colour for any more.
Thus, in any case, Bob will win. ∎
Lemma 33.
The 3-caterpillar is not line -nice.
4.4 Forbidden subgraphs for game
The first two of the following lemmata are trivial. We list them for the sake of completeness.
Lemma 34.
The graph is not line -nice.
Proof.
We describe a winning strategy with 2 colours for Bob in the -edge colouring game on the path .
If Alice colours an edge in her first move, then Bob colours an edge at distance 1 with the other colour, and the mutual adjacent edge of these two edges cannot be coloured with any of the two colours.
Otherwise, if Alice misses her first turn, then Bob’s winning strategy with 2 colours on the is to colour the central edge in colour 1 in his first move and one of the leaf edges with colour 2 in his second move. Bob can colour at least one such leaf edge , since Alice has coloured at most one edge. Then the mutual adjacent edge of the two edges and cannot be coloured, and Bob wins.
Thus the is not line -nice. ∎
Lemma 35.
The graph is not line -nice.
Proof.
The (is the smallest graph that) is not line perfect, thus it is not line -nice. ∎

Lemma 36.
The mini lobster is not line -nice.
Proof.
By exhausting all possible first moves of Alice we show that Bob has a winning strategy with 3 colours for the -edge colouring game played on . We use the edge labels from Figure 11. By symmetry, it is sufficient to consider the cases that Alice colours , , , or in her first move, or skips her first turn.
-
•
If Alice skips or colours , then Bob colours and thus creates a configuration . In the same way, if Alice colours , then Bob colours and creates a configuration . In both cases, by Lemma 32, Bob will win. (Note that in case Alice colours in a forthcoming move, this may be considered as skipping her turn in the situation of Lemma 32.)
-
•
If Alice colours (w.l.o.g. with colour 1), then Bob colours with colour 2. On the other hand, if Alice colours (w.l.o.g. with colour 2), then Bob colours with colour 1. In both cases, if Bob will be able to colour or with colour 3 in his next move, then he would win as there would be no feasible colour for any more. The only possibility for Alice to avoid both threats simultaneously is to colour with colour 3. But then Bob colours with colour 1, so that there is no feasible colour for any more.
In any case, Bob wins. ∎

The next lemma is an auxiliary result that will be used to simplify some strategies in the forthcoming Lemma 38.
Lemma 37.
Bob has a winning strategy with 4 colours in the -edge colouring game on the precoloured graph (depicted in Figure 12) if it is Alice’s turn.
Proof.
Assume the colour set is . By symmetry, Alice has six possible types of moves: she can miss her turn, colour with colour 1 or with colour 3, she can colour with colour 3, or she can colour with colour 2 or with colour 3.
-
•
If Alice misses her turn or colours (with colour 1 or colour 3), then Bob colours with colour 3. After that only colour 4 is feasible for and , which can be used only for one the these edges.
-
•
If Alice colours or with colour 3, Bob colours with colour 4. Then there is no feasible colour for .
-
•
If Alice colours with colour 2, Bob colours with colour 3. If Bob will be able to colour or with colour 4 in his next move, he will win, since there would be no feasible colour for in both cases. In order to avoid both threats simultaneously, Alice has only one possibility: she must colour with colour 4. But then Bob colours with colour 3, so that there is no feasible colour for any more.
Thus, in any case, Bob will win. ∎

Lemma 38.
The trigraph is not line -nice.
Proof.
We describe a winning strategy for Bob on with colour set . We use the edge labels from Figure 13. Due to symmetry, Alice has three possibilities for her first move: She can colour or with colour 1 or miss her turn.
If Alice colours with colour 1, then Bob colours with colour 2. And, vice-versa, if Alice colours with colour 1, then Bob colours with colour 2. In both cases (by considering the coloured edge broken in two parts) we get the precoloured configuration from Figure 12. By Lemma 37, Bob wins.
If Alice misses her turn, then Bob colours with colour 1. Now, by symmetry, Alice has seven possibilities for her second move: she may miss her turn, colour with colour 1 or with colour 2, colour with colour 2, colour with colour 2, or colour with colour 2 or with colour 1. We make a case distinction according to Alice’s second move.
-
•
If Alice misses her turn, then Bob colours with colour 2. Again, we have a situation as in configuration , and, by Lemma 37, Bob wins.
-
•
If Alice colours with colour 1, then this colour is forbidden for every uncoloured edge. The uncoloured edges form a 3-caterpillar and the game is reduced to the -edge colouring game with three colours (2,3,4) on . Therefore, Bob wins by Lemma 33.
-
•
If Alice colours with colour 2, Bob colours with colour 3. And, vice-versa, if Alice colours with colour 2, Bob colours with colour 3. In both cases the only feasible colour remaining for and is colour 4, which cannot be assigned to both edges.
-
•
If Alice colours with colour 2, then Bob colours with colour 3. If Bob will be able to colour or with colour 4 in his next move, he will win as has no feasible colour. The only possible move of Alice to avoid both threats is to colour with colour 4. But then Bob colours with colour 1 and there is no feasible colour for any more.
-
•
If Alice colours with colour 2, then Bob colours with colour 3. If Bob will be able to colour or with colour 4 in his next move, he will win as has no feasible colour. The only possible move of Alice to avoid both threats is to colour with colour 4. But then Bob colours with colour 1 and there is no feasible colour for any more.
-
•
If Alice colours with colour 1, then Bob colours with colour 2. If Bob will be able to colour or with colour 3 in his next move, he will win as the only feasible colour for the edges and will be colour 4, which can not be used for both edges. The only possible moves of Alice to avoid both threats are to colour or with colour 3. By symmetry, we may assume that Alice colours with colour 3. But then Bob colours with colour 4 and there is no feasible colour for any more.
Thus, in any case, Bob wins. ∎

Lemma 39.
The graph is not line -nice.
Proof.
We describe a winning strategy for Bob with 3 colours in the -edge colouring game played on a graph consisting of two components that are 3-caterpillars. No matter what Alice does in her first move, Bob is able to choose a component where every edge is uncoloured. Bob colours the edge (see Figure 14) in this component and then, by playing always in this component, he has a winning strategy by Lemma 32. ∎
5 The permitted types
5.1 Permitted for game
We start with some definitions.
Definition 40 (vase of flowers).
Let . A vase of flowers is a graph consisting of a and vertices of degree 1 that are adjacent with the same vertex of the , i.e., the graph has the vertex set
and the edge set
A vase of flowers is a vase of flowers for some . A vase of 1 flower is often called a paw, and a vase of 2 flowers is sometimes called a cricket.
Definition 41 (double star).
Let . An -double star is a graph formed by an -star and an -star by connecting the centres of the stars by an additional edge, i.e., the graph has the vertex set
an the edge set
A double star is an -double star for some . The -double star is the complete graph .
vase of 5 flowers

-double star
In order to prove the theorem, we start with some lemmata.
Lemma 42.
Graphs whose components are vases of flowers, double stars, or isolated vertices are line -perfect.
Proof.
Let be a graph whose components are vases of flowers, double stars, or isolated vertices. The line graph of a vase of flowers is an ear animal with , , and . The line graph of an -double star is an ear animal with , , , and . The line graph of an isolated vertex is the empty graph and can thus be ignored. Thus, the line graph of is a graph each of whose components is an ear animal. Therefore, by Theorem 6, is -perfect. By the definition of line game-perfectness this means that is line -perfect. ∎
5.2 Permitted for game
We start with some definitions.
Definition 43 (candy).
Let and . An -candy is a graph consisting of a and vertices of degree 1 that are adjacent to a vertex of degree of the and vertices of degree 1 that are adjacent to the vertex at distance 2 from , i.e., the graph has the vertex set
and the edge set
A candy is an -candy and an empty candy is a -candy for some .
Definition 44 (shooting star).
Let . An -shooting star is a graph formed by a central vertex with adjacent vertices of degree 1 and a pending and another adjacent vertex that is adjacent to vertices of degree 1, i.e., the graph has the vertex set
and the edge set
A shooting star is an -shooting star for some .
Definition 45 (double vase).
Let . A double vase of flowers is a graph formed by a central vertex with adjacent vertices of degree 1 and two pending triangles, i.e., the graph has the vertex set
and the edge set
A double vase is a double vase of flowers for some ; if , it is a 2-windmill.
Definition 46 (amaryllis).
Let . An -amaryllis is a graph formed by a central vertex with adjacent vertices of degree 1 and a pending triangle and another adjacent vertex that is adjacent to vertices of degree 1, i.e., the graph has the vertex set
and the edge set
An amaryllis is an -amaryllis for some ; if , it is a vase of flowers.

-candy

double vase of 5 flowers

-shooting star

-amaryllis
We prove first that Alice wins the -colouring game with colours on the configurations needed for Theorem 11. In the proofs we refer to the notation given above.
A component of a graph is nontrivial if it contains an edge.
Lemma 47.
Graphs whose single nontrivial component is a candy are line -nice.
Proof.
Let be a graph that consists of a -candy () and possibly some isolated vertices. Then the line graph of is an expanded cocobi with , , , , and . Therefore, by Proposition 7, the line graph is -perfect. Thus is line -perfect. ∎
We will use Lemma 47 not only for the proof of Theorem 11, but also for the proofs of Theorem 10 and Theorem 9. Note that the proof given above relies on the results by Lock (2016) and Andres and Lock (2019).
Lemma 48.
Graphs whose single nontrivial component is a shooting star are line -nice.
Proof.
Let be a graph that consists of a -shooting star and possibly some isolated vertices. Then the line graph of is an expanded bull with , , and . Therefore, by Proposition 8, the line graph is -perfect. Thus is line -perfect. ∎
Lemma 49.
Graphs whose single nontrivial component is a double vase are line -nice.
Proof.
Let be a graph that consists of a double vase of flowers and possibly some isolated vertices. Then the line graph of is an expanded bull with , , and . Therefore, by Proposition 8, the line graph is -perfect. Thus is line -perfect. ∎
Lemma 50.
Graphs whose single nontrivial component is an amaryllis are -nice.
Proof.
Let be a graph that consists of an -amaryllis and possibly some isolated vertices. Then the line graph of is an expanded bull with , , , and . Therefore, by Proposition 8, the line graph is -perfect. Thus is line -perfect. ∎
5.3 Permitted for game
Definition 51 (star book).
Let and . An -star book is a graph consisting of a and vertices of degree 1 that are adjacent to a vertex of degree of the and vertices of degree 1 that are adjacent to the vertex at distance 2 from , furthermore there is an additional edge , i.e., the graph has the vertex set
and the edge set
A star book is an -star book for some . Furthermore, a star book with book sheets is an -star book for some .
Thus, a star book is like a candy, but with an additional edge .
Definition 52 (diamond of flowers).
Let . A diamond of flowers is constructed from a diamond by attaching leaves to a vertex of degree 2, i.e., the graph has the vertex set
and the edge set
A diamond of flowers is a diamond of flowers for some .
Definition 53 (tetrahedron of flowers).
Let . A tetrahedron of flowers is constructed from a by attaching leaves to one of its vertices, i.e., the graph has the vertex set
and the edge set
A tetrahedron of flowers is a tetrahedron of flowers for some .
Definition 54 (single galaxy).
Let . A -single galaxy consists of a central vertex and pending triangles and pending , i.e., the graph has the vertex set
and the edge set
A single galaxy is a -single galaxy for some .
Note that a -single galaxy is an isolated vertex.
Definition 55 (double galaxy).
Let . A -double galaxy consists of a central vertex and pending triangles, pending , a pending -star, and pending , i.e., the graph has the vertex set
and the edge set
A double galaxy is a -double galaxy for some .
Note that a -double galaxy is a double star.

-candy

-star book

diamond of 5 flowers

tetrahedron of 5 flowers

-single galaxy

-double galaxy
Lemma 56.
A star book is line -nice.
Proof.
A triangle is line -nice, trivially. We describe a winning strategy for Alice in the -edge colouring game played on a star book that is not a triangle with
colours. We use the vertex labels from Definition 51.
Whenever Bob does not colour the universal edge , then Alice follows her winning strategy for the candy with colours, which exists by Lemma 47. If Bob colours , then Alice misses her turn. After that she uses again her strategy for the candy . This strategy is feasible since the colour of cannot be used on any other edge, since is adjacent to every other edge. ∎
We remark that the same strategy shows that a star book is line -nice. Namely, Alice should colour in her first move in the edge colouring game . However, it is not line -perfect (except in the trivial case when it is a vase of flowers) since it contains a or a , which are forbidden configurations for the edge colouring game .
Lemma 57.
A diamond of flowers is line -nice.
Proof.
Let be a diamond of flowers with the vertex labels from Definition 52. We describe a winning strategy for Alice with colours for the -edge colouring game played on . Consider Bob’s first move.
-
•
If Bob colours , then, if , Alice colours with the same colour, and if , she misses her turn. And vice-versa, if Bob colours a star edge , then Alice colours with the same colour. In all cases this colour may not be used for any other edge. Therefore, after that, Alice may follow her winning strategy with colours for the -edge colouring game played on the candy , which exists by Lemma 47.
-
•
If Bob colours for some , then Alice colours with the same colour, and vice-versa. In any case, this colour may not be used for any other edge. Thus, after that, Alice may follow her winning strategy for the -edge colouring game with colours played on the shooting star , which exists by Lemma 48.
Thus, in any case, Alice wins. ∎
The next lemma is very similar to the preceeding one.
Lemma 58.
A tetrahedron of flowers is line -nice.
Proof.
Let be a tetrahedron of flowers with the vertex labels from Definition 53. We describe a winning strategy for Alice with colours for the -edge colouring game played on . Consider again Bob’s first move.
-
•
If Bob colours , then Alice colours with the same colour and vice-versa. In all cases this colour may not be used for any other edge. Therefore, after that, Alice may follow her winning strategy with colours for the -edge colouring game played on the candy , which exists by Lemma 47.
-
•
If Bob colours for some , then Alice colours with the same colour, and vice-versa. In any case, this colour may not be used for any other edge. Thus, after that, Alice may follow her winning strategy for the -edge colouring game with colours played on the candy , which exists by Lemma 47.
-
•
If Bob colours a star edge for some with , then Alice colours with the same colour. This colour may not be used for any other edge. Thus, after that, Alice may follow her winning strategy for the -edge colouring game with colours played on the star book , which exists by Lemma 56.
Thus, in any case, Alice wins. ∎
A is pending at a vertex of a graph if the is an induced subgraph of , and is a vertex of degree 1 in the , and, if is deleted, the two other vertices of the are disconnected with the vertices of that are not in the . Analoguously, a triangle is pending at a vertex of a graph if the triangle is an induced subgraph of , and is one of the three vertices of the triangle, and, if is deleted, the two other vertices of the triangle are disconnected with the vertices of that are not in the triangle.
For a (single or double) galaxy with the notation of Definition 54 resp. Definition 55, we call a pending at resp. a triangle (pending at ) a pending object. The (one or two) edges of the pending object incident with are called star edges, the other edge of the pending object is called matching edge.
Lemma 59.
A single galaxy is line -nice.
Proof.
Let be a single galaxy with the notation from Definition 54.
If the number of pending objects of is at most 2, then is an isolated vertex, a , a triangle, a , an amaryllis, or a double vase, thus, in any case, line -nice, which implies by Observation 15 that is line -nice.
Otherwise, the maximum degree of is at least 3, and Alice has the following winning strategy with colours in the -edge colouring game played on . She may arbitrarily number the pending objects and perform the following pairing strategy.
-
•
If Bob colours the matching edge of the pending object , then Alice colours a star edge of the pending object with the same colour, if possible. If it is not possible, she uses a new colour for such a star edge.
-
•
If Bob colours the first star edge of the pending object (a triangle or a ), then Alice colours the matching edge of the pending object with the same colour.
-
•
If Bob colours the second star edge of the pending object (a triangle) , then Alice misses her turn.
Note that by this strategy, colouring a star edge with the same colour in the first case is only not possible if the colour has been already used for a star edge and a matching edge. Note further that after Alice’s moves, a star edge is either adjacent to an uncoloured matching edge or to a matching edge coloured in a colour of another star edge. Furthermore, by the pairing strategy, whenever Bob colours a matching edge with a new colour, then there is a nonadjacent uncoloured star edge left that can be coloured with the same colour. Thus every unsafe edge (the star edges) can be coloured feasibly.
∎
Lemma 60.
A double galaxy is line -nice.
Proof.
Let be a double galaxy with the notation from Definition 55.
If the number of pending objects of is at most 1, then is a double star, a shooting star or an amaryllis, thus, in any case, line -nice, which implies by Observation 15 that is line -nice.
Otherwise, the degree of is at least 3, and Alice uses an extension of the strategy for a single galaxy. Note that the maximum degree of is
We describe a winning strategy for Alice with colours in the -edge colouring game played on .
The only unsafe edges are the star edges of pending objects and the edge . Alice may arbitrarily number the pending objects and performs basically the same pairing strategy as in the proof of Lemma 59 with only small extensions, as described in the following.
-
•
If Bob colours the matching edge of the pending object , then, if this was the first such move and the edge is still uncoloured, Alice colours with the same colour (if possible, or a new colour otherwise); otherwise, Alice colours a star edge of the pending object with the same colour, if possible. If it is not possible, she uses a new colour for such a star edge.
-
•
If Bob colours the first star edge of the pending object and there is still a pending object with only uncoloured star edges, then Alice colours the matching edge of the pending object with the same colour. If the matching edge is already coloured, then Alice misses her turn.
-
•
If Bob colours the first star edge of the pending object and there is no pending object with only uncoloured star edges left, then Alice colours with a new colour (if is still uncoloured) or misses her turn (if is already coloured).
-
•
If Bob colours the edge , an edge or the second star edge of the pending object (a triangle) , then Alice misses her turn.
-
•
If Bob colours an edge , then Alice colours (if is still uncoloured) or misses her turn (otherwise).
This strategy has the same properties as the strategy for the single galaxy in the proof of Lemma 59, and, in addition, it guarantees that the edge is coloured before it is in danger to be infeasible for any colour. ∎
5.4 Permitted for game
Definition 61 (full tree).
Let . An -full tree is based on a path , where there are (respectively, , ) leaves attached its three vertices, i.e., the graph has the vertex set
and the edge set
A full tree is an -full tree for some .
Note that an -full tree is a shooting star; a -full tree is an empty candy; an -full tree is a double star; and an -full tree is a star. These trivial configurations are excluded in the next definition.
Definition 62 (full tree of type ).
A full tree of type is a full tree that is neither a shooting star nor a candy nor a double star.
By Definition 62, a full tree of type does not belong to the permitted configurations for game .
Definition 63 (satellite).
Let . An -satellite is based on a triangle , where there are (respectively, ) leaves attached to two of its three vertices and exactly one leaf is attached to its third vertex, i.e., the graph has the vertex set
and the edge set
A satellite is an -satellite for some .
Note that an -satellite is a special star book (with one book sheet). Such a trivial configuration is excluded in the next definition.
Definition 64 (satellite of type ).
A satellite of type is a satellite that is not a star book.
By Definition 64, a satellite of type does not belong to the permitted configurations for game .

-full tree

-satellite
Lemma 65.
A full tree is line -nice.
Proof.
Let be a full tree with the vertex labels from Definition 61. Note that the only possibly unsafe edges are and . We describe a winning strategy for Alice with colours in the -edge colouring game played on .
If there is at most one unsafe edge, then Alice colours this edge (if any) in her first move and wins trivially. In the following, we assume that there are two unsafe edges.
If is the path , which is a trivial shooting star, then Alice misses her first turn and has a trivial winning strategy for the -edge colouring game by Lemma 48.
Otherwise, , and so the number of colours in the game is at least 3. Therefore, Alice may ensure that the two unsafe edges and are coloured after her first two moves, which is possible with three colours since Bob has only one move in between.
Thus, in any case, Alice wins. ∎
Lemma 66.
A satellite is line -nice.
Proof.
Let be a satellite with the vertex labels from Definition 63. Note that the only possibly unsafe edges are the triangle edges , and . We describe a winning strategy for Alice with colours in the -edge colouring game played on .
Alice misses her first turn and then reacts as follows on Bob’s first move.
-
•
If Bob colours , then Alice colours with the same colour, and vice-versa. Now this colour may not be used any more. Note that the graph is an empty candy and we have
Therefore, if Alice follows her winning strategy for the -edge colouring game with colours played on the empty candy , which exists by Lemma 47, then Alice will win.
-
•
Let . If Bob colours , then, if , Alice colours the star edge with the same colour, and if , Alice misses her turn. And vice-versa, if Bob colours a star edge for some with , then Alice colours with the same colour. Now this colour may not be used any more. Note that the graph
is a shooting star and we have
Therefore, if Alice follows her winning strategy for the -edge colouring game with colours played on the shooting star , which exists by Lemma 48, then Alice will win.
Thus, in any case, Alice has a winning strategy. ∎
We remark that, since, in her strategy, Alice misses her first turn, the proof of Lemma 66, indeed, shows that a satellite is line -nice. However, in general, a satellite is not line -perfect, since it may contain a 3-caterpillar as an edge-induced subgraph (which can be seen by deleting the edge ).
6 Proof of the structural characterisations
6.1 Proof of Theorem 9
A basic concept in the proof of Theorem 9 is the concept of a block of a graph. Recall that a graph is 2-connected if it has at least 3 vertices and, for any vertex , if is deleted, the remaining graph is still connected. A vertex of a graph is an articulation point of if deleting increases the number of components, i.e., has strictly more components than . A block of a graph is a maximal subgraph of that is connected and contains no articulation points. Thus, a block is either a maximal 2-connected subgraph of or a . The edges of different blocks do not overlap, but several blocks may share the same articulation point.
of Theorem 9.
We prove the equivalence by a ring closure.
- (1)(2)
-
We have to prove that and are not line -perfect. It is sufficient to prove that they are not line -nice. This was proved in Lemma 34 for path , in Lemma 36 for the mini lobster , and in Lemma 38 for the trigraph . The is not line perfect, thus it is not line -perfect (see Lemma 35). is not line -nice by Lemma 33, so is not line -nice (see Lemma 39).
- (2)(3)
-
Let be a graph that contains no , as edge-induced subgraphs and let be a component of .
Since does not contain or , the component is line perfect by Theorem 2. Thus, by Theorem 3, every block of is either bipartite or a or a triangular book for some . Since contains no and no , the only possible cycles are triangles and 4-cycles.
We first observe that, among the blocks that contains, there is at most one block which is one of the following configurations: with (a nontrivial triangular book), a bipartite block containing at least one 4-cycle, or . Assume to the contrary that contains two such (not necessarily different) configurations. Then there are 3 edges from each of the two configurations which, together with the edges on a shortest path connecting the two configurations, form an edge-induced with , which contains a , contradicting (2).
We observe further that if contains a block that is a triangle (i.e., a trivial triangular book ), then cannot contain any of the configurations with , , or a bipartite block containing at least one 4-cycle. Assume to the contrary that contains one of them. Then there are 3 edges from such a configuration and 2 edges from the triangle which, together with the edges on a shortest path connecting the configuration with the triangle, form an edge-induced with , which contains a , contradicting (2).
-
Case 1:
contains a .
Then there is a vertex of the , so that every edge of that is not part of the is adjacent to , since, otherwise, if outside of the there is an edge that is not adjacent to and an edge that is adjacent to , by using these two edges and 3 edges of the there is a path or a cycle of lenght at least 5, thus contains an edge-induced or , which contradicts (2). Thus is a tetrahedron of flowers.
-
Case 2:
contains a nontrivial triangular book with .
Let be the two vertices of degree and the vertices of degree 2 of the . Let be an edge that does not belong to the .

(a)

(b)

(c)

(d)

(e)
Figure 19: Creating forbidden configurations in Case 2. If connects two vertices and with , then, in case , we have a and are thus in Case 1, which was already discussed above, or, in case , the graph contains an edge-induced (see Figure 19 (a)), which is forbidden by (2).
Now consider the case that is incident with some vertex and another vertex that is not part of the . If , then together with 4 edges of the form a (see Figure 19 (b)), which is forbidden by (2). If , then there is neither an additional edge incident with or other than the edges of the nor an edge different from incident with since, otherwise, contains an edge-induced (see Figures 19 (c) and (d)), which is forbidden by (2). Thus, in this case, is a diamond of flowers.
If is incident with or , then there is no edge adjacent to that is not part of the since, otherwise, contains a (see Figure 19 (e)), which is forbidden by (2). Thus, in this case, is a star book.
-
Case 3:
is bipartite and contains a block with a .
First note that the union of the 4-cycles in the block must form a with . This is because it is the only possibility to combine several 4-cycles in a block without creating cycles with , which are forbidden since its subgraph, the , is forbidden by (2).
Note that in the contradictions of Case 2 in Figure 19 the edge between and was not used, which means they are still valid even if is absent, which is the case here. Only for where there appeared a , there would appear here a diamond (which is not bipartite). Thus, by the same proof as in Case 2, is a candy.
-
Case 4:
contains a block that is a triangle.
Consider one fixed triangle with vertices . Note that no may be pending at since, otherwise, the three edges of the and two of the edges of the triangle would form an edge-induced , which is forbidden by (2). Similarly, no resp. no other triangle may be pending at when is pending at with .
In the following, we disinguish between the cases that the number of vertices that have at least one pending is 2, 3 or at most 1.
-
Subcase 4.1:
.
The case that the block containing is a or a diamond was already discussed in Case 1 or Case 2, respectively. Thus we are left with the case that the block containing is a triangle. Then the component is a star book with exactly one triangle (and two of have at least one pending ).
-
Subcase 4.2:
.
Suppose now at least one is pending at every . Since the trigraph , in which every has two pending s, is forbidden, at least one of has at most one pending , which means that is a satellite.
-
Subcase 4.3:
.
Suppose exactly one of has at least one pending . Note that may contain more than one block which is a triangle. As discussed above, all these triangle blocks share exactly one vertex and we denote this by . At most one pending star with at least 2 star edges may be pending at since, otherwise, if there are two of them, two of the star edges of each pending star and the edges of the pending stars that are incident with together with two of the edges of a triangle would form an edge-induced mini lobster , which is forbidden by (2). Thus, is a double galaxy or a single galaxy.
-
Subcase 4.1:
-
Case 5:
is a tree.
As the is forbidden, has diameter at most 4. If has diameter at most 3, then is an isolated vertex (which is a single galaxy) or a double star (which is a double galaxy). If has diameter 4, can be depicted by configuration in Figure 20.

Figure 20: A generic tree of diameter 4 Since the mini lobster is -forbidden we conclude that, if in configuration , at most two of the stars pending at the central vertex have more than one leaf. If there are exactly two such stars, then the other stars are simply pending s, again since the mini lobster is forbidden, thus is a full tree; otherwise, i.e., when there is at most one such star, is a double galaxy (or a single galaxy) with no triangles.
Thus, in all cases we get a permitted configuration. Furthermore, since is forbidden, at most one of the components may be a full tree of type or a satellite of type (as both of the latter configurations contain a 3-caterpillar by definiton). Therefore, (3) holds.
-
Case 1:
- (3)(1)
-
The permitted configurations for each component are line -nice: we have proved this for the candy in Lemma 47, for the star book in Lemma 56, for the single galaxy in Lemma 59, for the double galaxy in Lemma 60, for the diamond of flowers in Lemma 57, for the tetrahedron of flowers in Lemma 58, for the full tree in Lemma 65, and for the satellite in Lemma 66. With the exception of a full tree of type and a satellite of type , the permitted configurations are even line -nice.
Let be a graph whose components are of the permitted types and where at most one component is a special component, namely a full tree of type or a satellite of type . Then, in her first move, Alice plays according to her strategy for the special component (if there is a special component) or misses her turn (if there is no special component). After that she reacts always in the component where Bob has played in his previous move according to her strategy for the -edge colouring game (respectively, -edge colouring game for the special component) or she misses her turn (if the component where Bob has played in his previous move is completely coloured). By the lemmas mentioned above, Alice will win. Thus is -nice.
In Lemma 67 we will show that the permitted types are hereditary. Thus the permitted types are line -perfect. From this we conclude that is line -perfect, which proves (1).
∎
Lemma 67.
The permitted types for game are hereditary.
Proof.
See Table 1 and its caption. ∎
| Structure | Structure after deleting an edge |
|---|---|
| candy | candy |
| two stars (which are galaxies) | |
| star book | star book |
| candy | |
| double star (which is a double galaxy) | |
| diamond of flowers | diamond of flowers |
| double galaxy | |
| star book | |
| candy | |
| tetrahedron of flowers | tetrahedron of flowers |
| diamond of flowers | |
| star book | |
| single galaxy | double galaxy |
| single galaxy & (which is a double galaxy) | |
| single galaxy | |
| double galaxy | double galaxy |
| double galaxy & star (which is a galaxy) | |
| single galaxy & star (which is a galaxy) | |
| satellite | star book |
| double galaxy | |
| full tree | |
| satellite | |
| full tree | full tree |
| double star & star (which are galaxies) |
In order to illustrate the proof we depict four characteristic situations for the candy when one edge is deleted in Figure 21.
| candy | candy (+isolated vertex) | |
| candy | candy | |
| candy | (empty) candy | |
| (empty) candy | two stars |
6.2 Proof of Theorem 10
of Theorem 10.
We prove the equivalence by a ring closure.
- (1)(2)
- (2)(3)
-
Let be a graph that contains no , , or 3-caterpillar as an edge-induced subgraph. Thus, in particular, the graph contains no , , mini lobster , trigraph , and no .
By Theorem 9, every component of is a candy, a star book, a diamond of flowers, a tetrahedron of flowers, a single galaxy, a double galaxy, a full tree, or a satellite. Since a full tree of type and a satellite of type contain a 3-caterpillar no component of is a full tree of type or a satellite of type . Thus (3) holds.
- (3)(1)
-
The permitted configurations are line -nice: we proved this for the candy in Lemma 47, for the star book in Lemma 56, for the single galaxy in Lemma 59, for the double galaxy in Lemma 60, for the diamond of flowers in Lemma 57, and for the tetrahedron of flowers in Lemma 58.
Let be a graph whose components are of one of the permitted types for game . Then Alice always reacts in the component where Bob has played according to her strategy for the -edge colouring game (or she misses her turn if this component is completely coloured). By the mentioned lemmata, Alice will win. Thus is line -nice.
Furthermore, the permitted configurations are hereditary, which can be seen from the first six entries in Table 1. From this we conclude that is line -perfect, which proves (1).
∎
6.3 Proof of Theorem 11
of Theorem 11.
We prove the equivalence by a ring closure.
- (1)(2)
-
This implication is part of Proposition 31.
- (2)(3)
-
Let be a graph that fulfils (2), i.e., it contains no , , , , bull, diamond, or 3-caterpillar as an edge-induced subgraph.
By (2), the graph , in particular, contains no , , 3-caterpillar. Thus, by Theorem 10, each component of is a diamond of flowers, a tetrahedron of flowers, a candy, a star book, a single galaxy, or a double galaxy. Let be a component of .
The component may neither be a diamond of flowers nor a tetrahedron of flowers, since those two configurations contain a diamond as a subgraph, which is forbidden by (2).
Consider the case that is a star book. It may not contain more than one book sheet, since otherwise it would contain a diamond, which is forbidden by (2). If has exactly one book sheet, it may not have star edges on both sides, since otherwise it would contain a bull, which is forbidden by (2). Thus, in this case, the component is a vase of flowers. If has no book sheet, then is a double star.
Now consider the case that is a single galaxy or a double galaxy. In both cases, the component has a vertex with pending s, pending s, pending triangles, and pending stars, where and . First note that
(2) since otherwise, if , two of the pending objects would contain a and the third would contain a that is not adjacent with the , thus would contain an edge-induced , which is forbidden by (2). So we may assume that (2) holds. We distinguish some cases.
-
•
If and , then is a shooting star.
-
•
If and , then is a double star.
-
•
If and , then is an amaryllis.
-
•
If and , then is a shooting star.
-
•
If and , then is a double vase, a vase of flowers, or a star (which is either a double star or an isolated vertex).
-
•
If and , then is an amaryllis.
-
•
If and , then is a double star.
Finally, we have to prove that if one of the components of is a candy, a shooting star, a double vase, or an amaryllis, but neither a double star nor a vase of flowers, then has only one nontrivial component. We observe that
-
•
a candy that is not a double star contains a or a ,
-
•
a shooting star that is not a double star contains a ,
-
•
a double vase contains a , and
-
•
an amaryllis that is not a vase of flowers contains a .
Thus, if there is such a component in the graph, then there may not be another component that contains an edge, since otherwise would contain a or a , which are forbidden by (2). Therefore, (3) holds.
-
•
- (3)(1)
∎
6.4 Proof of Theorem 12
of Theorem 12.
We prove the equivalence by a ring closure.
- (1)(2)
-
This follows from (Observation 19).
- (2)(3)
-
This follows from (Observation 19).
- (3)(4)
-
This implication is part of Proposition 30.
- (4)(5)
-
Let be a graph that contains neither nor as an edge-induced subgraph. Thus, in particular contains no , , , , bull, diamond, 3-caterpillar (since these configurations either contain a or, in the case of , a ). Thus is line -perfect. Therefore, by Theorem 11 every component of is a double star, a vase of flowers, an isolated vertex, a candy, a shooting star, a double vase, or an amaryllis. Let be a component of .
If is a candy, then it must be an empty candy, since otherwise it would contain a , which is forbidden by (4). Furthermore, it may not have star edges at both sides, since otherwise it would contain a , which is forbidden by (4). Thus is a double star.
If is a shooting star, then it must have diameter 3, since otherwise it would contain a , which is forbidden by (4). Thus is a double star.
Note that may not be a double vase as the two triangles contain an edge-induced , which is forbidden by (4).
Furthermore, if is an amaryllis, then the pending star must be empty, since otherwise two edges of the pending star and two edges of the triangle would form a , which is forbidden by (4). Thus is a vase of flowers.
We conclude that (5) holds.
- (5)(1)
-
We have to prove that graphs each component of which is a double star, vase of flowers or isolated vertex is line -perfect. This was shown in Lemma 42, which proves the last implication of the theorem.
∎
7 Final remarks
In this paper, we completely characterize line game-perfect graphs for all six possible games.
7.1 Similar characterisations for vertex colouring games
Similar characterisations for game-perfect graphs (where vertex games are considered instead of edge games) are only known for the games , , and . Thus the following question might be interesting for further research.
Problem 68.
Characterise game-perfect graphs for the games and (by forbidden induced subgraphs and/or explicit structural descriptions).
Note that we have no idea how to extend our methods to the more general case of Problem 68. This might be very difficult as there are infinitely many minimal forbidden configurations, namely (among others) all odd antiholes (Andres, 2009, Thm 23).
There is a historic analog for this discrepancy: the characterisation of line-perfect graphs by forbidden subgraphs was found by Trotter (1977) in 1977, but the more general result, the characterisation of perfect graphs by forbidden induced subgraphs (the famous Strong Perfect Graph Theorem) was proved by Chudnovsky et al. (2006) nearly 30 years later and published in 2006.
We remark that an analog for the explicit characterisation of line perfect graphs by Maffray (1992) has not yet been found (more than 30 years later) for perfect graphs.
7.2 A variant of line game-perfectness
One might also consider a variant of line game-perfectness: A graph is edge -perfect if, for any edge-induced subgraph of ,
By Corollary 24, the only difference between line -perfect graphs and edge -perfect graphs is that in edge -perfect graphs we have an additional forbidden configuration, namely the triangle . Thus, edge -perfect graphs can be obtained from our explicit structural descriptions of line -perfect graphs by deleting all graphs that contain a triangle, which leaves fairly trivial classes of graphs. Therefore our notion of line -perfect graphs might be the better concept to describe game-perfectness for edge colouring games.
7.3 Games with a bounded number of skipping turns
In our games, skipping a turn was either forbidden or allowed for an unlimited number of turns. Now, we consider the question what happens if we allow only a bounded number of skipping turns.
Let , and , and be a graph. In the edge colouring game played with colours on the graph the players alternately move with player beginning. Player may skip a turn (including the first one) up to times. A move that is not skipped consists in colouring an uncoloured edge of with a colour from the set that is different from the colours of the edges adjacent to . This game defines a game chromatic index of the graph . The graph is line -perfect if, for any edge-induced subgraph of ,
The class of all line -perfect graphs is denoted by . By definition,
We observe the following.
Observation 69.
Let . Then we have:
-
(i)
-
(ii)
Proof.
This holds since the possibility to skip one time more is no disadvantage for the player who is allowed to skip. ∎
Observation 70.
Let . Then we have:
-
(i)
-
(i)
Proof.
Ad (i): If Bob has a winning strategy for the game on a graph , then, by skipping his first turn, he can use the same strategy in order to win the game played on .
Ad (ii): If Alice has a winning strategy for the game on a graph , then, by skipping her first turn, she can use the same strategy in order to win the game played on . ∎
Using the two observations above, we obtain the following corollary of Theorem 12.
Corollary 71.
Let with . Then
Proof.
According to Corollary 71, our new games give no new classes in case the skipping is allowed to Bob. The situation changes if the skipping is allowed to Alice. Here the characterisation of the respective classes of line game-perfect graphs seems to be very intricate. One reason is that in our strategies for Alice sometimes Alice has to miss a turn in order to avoid beginning to colour in a new, uncoloured component, which makes the discussion of disconnected graphs very difficult. But even for connected graphs our strategies require that Alice skips several times. This is the case for single or double galaxies, where our strategies require that Alice skips if Bob plays on the second star edge of a pending triangle. Note that a (single or double) galaxy may have arbitrarily many pending triangles; therefore it might seem to be straightforward that some of the classes are different from the classes and . However, it is not clear whether the strategies given in this paper cannot be improved in some way using fewer skipping moves.
Problem 72.
For any and , characterise the class , i.e., characterise line game-perfect graphs for the game (by forbidden edge-induced subgraphs and/or explicit structural descriptions).
The edge-colouring games defined in this section might be considered more generally, thus, we might define vertex colouring games in the same way. Then we might ask the following question.
Problem 73.
For any and , characterise game-perfect graphs for the game (by forbidden induced subgraphs and/or explicit structural descriptions).
We expect that the answer to this question will be even more intricate than the answer to Problem 72.
Acknowledgements.
The authors thank the two anonymous reviewers for many useful suggestions that helped to improve the presentation of the paper. Furthermore, in particular, we acknowledge that the idea of the games discussed in Section 7.3 originates from one of the reviewers.References
- Andres (2006) S. D. Andres. The game chromatic index of forests of maximum degree . Discrete Applied Mathematics, 154:1317–1323, 2006.
- Andres (2007) S. D. Andres. Digraph coloring games and game-perfectness. Verlag Dr. Hut, München, 2007. Ph.D. thesis, Universität zu Köln.
- Andres (2009) S. D. Andres. Game-perfect graphs. Mathematical Methods of Operations Research, 69:235–250, 2009.
- Andres (2012) S. D. Andres. On characterizing game-perfect graphs by forbidden induced subgraphs. Contributions to Discrete Mathematics, 7:21–34, 2012.
- Andres and Lock (2019) S. D. Andres and E. Lock. Characterising and recognising game-perfect graphs. Discrete Mathematics & Theoretical Computer Science, 21(Paper No. 6):39pp., 2019.
- Andres et al. (2011) S. D. Andres, W. Hochstättler, and C. Schallück. The game chromatic index of wheels. Discrete Applied Mathematics, 159:1660–1665, 2011.
- Bartnicki and Grytczuk (2008) T. Bartnicki and J. Grytczuk. A note on the game chromatic index of graphs. Graphs and Combinatorics, 24:67–70, 2008.
- Beineke (1970) L. W. Beineke. Characterizations of derived graphs. Journal of Combinatorial Theory, 9:129–135, 1970.
- Beveridge et al. (2008) A. Beveridge, T. Bohman, A. Frieze, and O. Pikhurko. Game chromatic index of graphs with given restrictions on degrees. Theoretical Computer Science, 407:242–249, 2008.
- Bodlaender (1991) H. L. Bodlaender. On the complexity of some coloring games. International Journal of Foundations of Computer Science, 2:133–147, 1991.
- Boudon et al. (2017) O. Boudon, J. Przybyło, M. Senhaji, E. Sidorowicz, E. Sopena, and M. Woźniak. The neighbour-sum-distinguishing edge-colouring game. Discrete Mathematics, 340:1564–1572, 2017.
- Cai and Zhu (2001) L. Cai and X. Zhu. Game chromatic index of -degenerate graphs. Journal of Graph Theory, 36:144–155, 2001.
- Chan and Nong (2014) W. H. Chan and G. Nong. The game chromatic index of some trees of maximum degree 4. Discrete Applied Mathematics, 170:1–6, 2014.
- Charpentier et al. (2018) C. Charpentier, B. Effantin, and G. Paris. On the game coloring index of -decomposable graphs. Discrete Applied Mathematics, 236:73–83, 2018.
- Chudnovsky et al. (2006) M. Chudnovsky, N. Robertson, P. Seymour, and R. Thomas. The strong perfect graph theorem. Annals of Mathematics (2), 164:51–229, 2006.
- Dunn (2007) C. Dunn. The relaxed game chromatic index of -degenerate graphs. Discrete Mathematics, 307:1767–1775, 2007.
- Dunn et al. (2015) C. Dunn, D. Morawski, and J. F. Nordstrom. The relaxed edge-coloring game and k-degenerate graphs. Order, 32:347–361, 2015.
- Fong and Chan (2019a) W. L. Fong and W. H. Chan. The edge coloring game on trees with the number of colors greater than the game chromatic index. Journal of Combinatorial Optimization, 38:456–480, 2019a.
- Fong and Chan (2019b) W. L. Fong and W. H. Chan. The game chromatic index of some trees with maximum degree 4 with at most three degree-four vertices in a row. arXiv, 2019b. arXiv:1904.01496.
- Fong et al. (2018) W. L. Fong, W. H. Chan, and G. Nong. The game chromatic index of some trees with maximum degree four and adjacent degree-four vertices. Journal of Combinatorial Optimization, 36:1–12, 2018.
- Gardner (1981) M. Gardner. Mathematical games. Scientific American, 244:23–26, April 1981.
- Keusch (2018) R. Keusch. A new upper bound on the game chromatic index of graphs. Electronic Journal of Combinatorics, 25(Paper No. 2.33):18pp., 2018.
- Lam et al. (1999) P. C. B. Lam, W. C. Shiu, and B. Xu. Edge game-coloring of graphs. Graph Theory Notes New York, 37:17–19, 1999.
- Lock (2016) E. Lock. The structure of -perfect graphs. FernUniversität in Hagen, 2016. Bachelor thesis.
- Maffray (1992) F. Maffray. Kernels in perfect line-graphs. Journal of Combinatorial Theory B, 55:1–8, 1992.
- Trotter (1977) L. E. Trotter. Line perfect graphs. Mathematical Programming, 12:255–259, 1977.
- Whitney (1932) H. Whitney. Congruent graphs and the connectivity of graphs. American Journal of Mathematics, 54:150–168, 1932.