Light Meson Decays at BESIII ^∗

After being discovered more than 50 years, the $\eta/\eta^{\prime}$ meson still attract considerable both of the theoretical and experimental attention, because of it plays a central role in our understanding of quantum chromodynamics (QCD) at low energies. As a mixture of the lowest pseudoscalar singlet and octet, $\eta/\eta^{\prime}$ have inspired a wide variety of physics issues, e.g., $\eta-\eta^{\prime}$ mixing, the light quark masses, the fundamental discrete symmetries, as well as physics beyond the standard model (SM). Precision measurements of its decays provide important tests of effective field theories, such as chiral perturbation theory (ChPT) or the vector meson dominance (VMD) model. Moreover, it is also possible to search for new phenomena in rare or forbidden $\eta/\eta^{\prime}$ decays.

BEPCII is a double-ring multibunch $e^{+}e^{-}$ collider running in the tau-charm energy region. The BESIII detector, described in detail in Ref.bepc , has a geometrical acceptance of 93% of 4$\pi$. It consists of a drift chamber (MDC), a time-of-flight (TOF) system, and an electromagnetic calorimeter (EMC), all enclosed in a superconducting solenoid with 1.0 T (0.9 T in 2012) magnetic field. The small-cell helium based MDC provides the tracking of the charged particle and ionization energy loss ($dE/dx$) measurement. The single cell position resolution is 130 $\mu m$ and the transverse momentum resolution is 0.5% at 1 GeV/c. The TOF system for particle identification (PID) is made of plastic scintillators. It has 80 ps time resolution in the barrel, and 110 ps in the end caps. The EMC is made of 6240 CsI (Tl) crystals. The energy resolution is 2.5% in the barrel and 5% in the end caps for 1.0 GeV photons. Outside the solenoid, a muon chamber system made of 1272 $m^{2}$ resistive plate chambers detects muon tracks with momenta greater than 0.5 GeV.̧

The BESIII experiment has collected a total of $10^{10}$ $J/\psi$ events. Via the $J/\psi$ radiative decay, a sample of $1.1\times 10^{7}$ $\eta$ and $5.2\times 10^{7}$ $\eta^{\prime}$ can obtained. For $\eta^{\prime}$, which is comparatively unexplored, BESIII can measure many decays for the first time and others with unrivaled precision.

The strong decays $\eta^{\prime}\to\pi^{+}\pi^{-}\pi^{+(0)}\pi^{-(0)}$ are not suppressed by approximate symmetries, they are expected to be mediated by chiral anomalies, since an odd number (five) of pseudoscalar particles is involved.

The projections of the fit to $M_{\pi^{+}\pi^{-}\pi^{+(0)}\pi^{-(0)}}$ in the $\eta^{\prime}$ mass region are shown in Figs. 1(a) and  1(b), where the shape of the sum of signal and background shapes are in good agreement with data. We obtain $199\pm 16$ of $\pi^{+}\pi^{-}\pi^{+}\pi^{-}$ events with a statistical significance of $18\sigma$ and $84\pm 16$ of $\pi^{+}\pi^{-}\pi^{0}\pi^{0}$ events with a statistical significance of $5\sigma$ 4pi:c . Using the world average value of $Br(J/\psi\to\gamma\eta{\prime})$ PDG , the branching fraction of $\eta^{\prime}\to\pi^{+}\pi^{-}\pi^{+(0)}\pi^{-(0)}$ are determined to be $Br(\eta^{\prime}\to\pi^{+}\pi^{-}\pi^{+}\pi^{-}=[8.53\pm 0.69(stat.)\pm 0.64(syst.)]\times 10^{-5})$ and $Br(\eta^{\prime}\to\pi^{+}\pi^{-}\pi^{0}\pi^{0}=[1.82\pm 0.35(stat.)\pm 0.18(syst.)]\times 10^{-4})$, which are consistent with the theoretical predictions based on a combination of ChPT and VMD models, but not with the broken-SU${}_{6}\times O_{3}$ quark model 4pi:chpt .

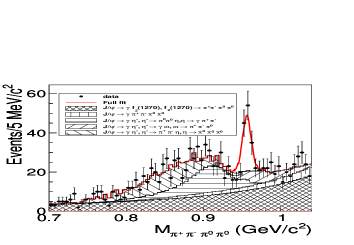
In theory, $\eta^{\prime}\to 4\pi^{0}$ is a highly suppressed decay because of the S-wave CP-violation. In the light of an effective chiral Lagrangian approach, the S-wave CP-violation in $\eta^{\prime}\to 4\pi^{0}$ is induced by the so-called $\theta$-term, which is an additional term in the QCD Lagrangian to account for the solution of the strong-CP problem. It was found that the S-wave CP-violation effect that contributed to this decay is at a level of $10^{-23}$ 4pi0 . While higher-order contributions, involving a D-wave pion loop or the production of two $f_{2}$ tensor mesons, provide a CP-conserving route through which the decay can occur. By ignoring the tiny contribution from the latter process, calculations based on ChPT and VMD model predict the branching fraction caused by D-wave CP-conserving to be at the level of $10^{-8}$ 4pi0:1 . However, the theoretical prediction is not strictly based on the effective field theory due to the lack of knowledge at such a high order in the chiral expansion and the use of a model to make an estimation. One does not know the reliability of that model a priori. Therefore, a search for the decay $\eta^{\prime}\to 4\pi^{0}$ is useful to check the reliability of it.

Figure 1(c) shows the $4\pi^{0}$ invariant mass spectrum in data, together with the total fit result and the contributions from non-peaking background and the peaking background $J/\psi\to\gamma\eta^{\prime},\eta^{\prime}\to\pi^{0}\pi^{0}\eta,\eta\to 3\pi^{0}$. Also shown is the expected shape of the signal contribution, with arbitrary normalization. After our selection, there are no significant $\eta^{\prime}$ signal is evident. With a Bayesian approach, the upper limit on the branching fraction is determined to be $Br(\eta^{\prime}\to 4\pi^{0}<4.94\times 10^{-5})$ at $90\%$ C.L. 4pi:n . This corresponds to an improvement of a factor 6 compared to the previous best value from the GAMS-4$\pi$ experiment 4pi0:2 . However, the current limit is still far to reach the theoretical predication with a level of $10^{-8}$.

The decays $\eta^{\prime}\to\pi\pi\pi$ are isospin-violating processes. Because the electromagnetic contribution is strongly suppressed rhopi:1 , they are induced dominantly by the strong interaction via the explicit breaking of chiral symmetry by the $d-u$ quark mass difference.

A Dalitz plot analysis based on the formalism of the isobar model rhopi:2 is performed. The resonant $\pi-\pi$ S-wave ($L=0$ for $\sigma$) and P-wave ($L=1$ for $\rho^{\pm}$) amplitudes are described as in Ref. rhopi:3 .

Projections of the data and fit results are displayed in Fig. 2. The data are well described by three components: $P$ wave ($\rho^{\pm}\pi^{\mp}$), resonant $S$ wave ($\sigma\pi^{0}$), and phase-space $S$ wave ($\pi\pi\pi$). The interference between $\sigma$ and the non-resonant term is large and strongly depends on the parametrization of $\sigma$. Therefore we are unable to determine the individual contributions and consider only the sum of the $S$-wave amplitudes in this analysis.

Using a combined amplitude analysis of $\eta^{\prime}\to\pi^{+}\pi^{-}\pi^{0}$ and $\eta^{\prime}\to\pi^{0}\pi^{0}\pi^{0}$ decays, the $P$-wave contribution from $\rho^{\pm}$ is observed for the first time with high statistical significance. The pole position of $\rho^{\pm}$, $775.49$ (fixed)$-i(68.5\pm 0.2)$ MeV, is consistent with previous measurements, and the branching fraction ${\mathcal{B}r}(\eta^{\prime}\to\rho^{\pm}\pi^{\mp})$ is determined to be $(7.44\pm 0.60\pm 1.26\pm 1.84)\times 10^{-4}$ rhopi .

Electromagnetic (EM) Dalitz decays of light pseudoscalar mesons, $P\to\gamma l^{+}l^{-}$ ($P=\pi^{0}$, $\eta$, $\eta^{\prime}$; $l=e,\mu$), play an important role in revealing the structure of hadrons and the interaction mechanism between photons and hadrons gee:1 . If one assumes point-like particles, the decay rates can be exactly calculated by Quantum Electrodynamics (QED) gee:2 . Modifications to the QED decay rate due to the inner structure of the mesons are encoded in the transition form factor (TFF) $F(q^{2})$, where $q$ is the momentum transferred to the lepton pair, and $q^{2}$ is the square of the invariant mass of the lepton pair. A recent summary and discussion of this subject can be found in Ref. gee:3 .

We report the first observation of the $\eta^{\prime}\to\gamma e^{+}e^{-}$ decay and the extraction of the TFF. The source of the $\eta^{\prime}$ mesons are from radiative $J/\psi\to\gamma\eta^{\prime}$ decays collected by the BESIII at the BEPCII $e^{+}e^{-}$ collider. The $\eta^{\prime}\to\gamma\gamma$ decay events in the same data sample are used for normalization.

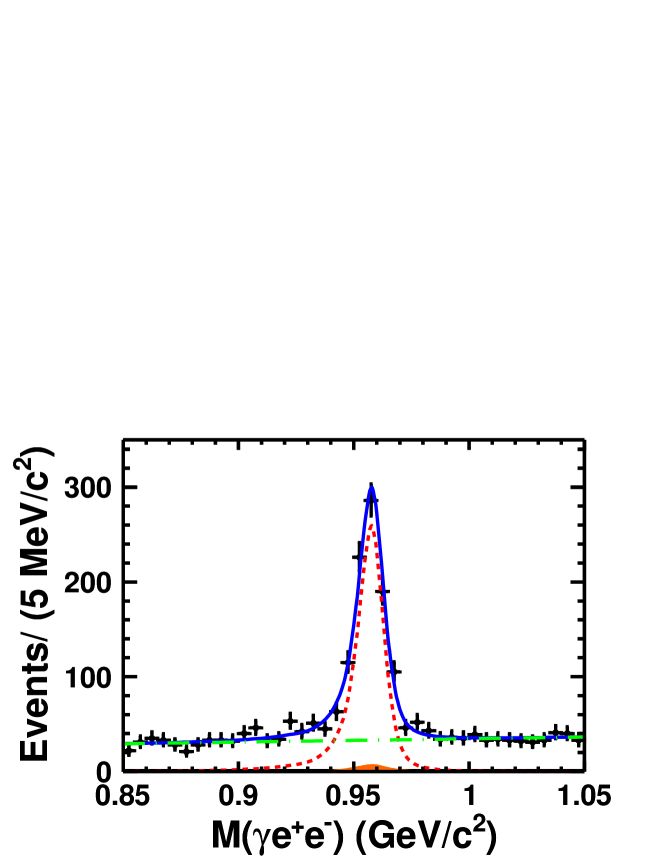
The combination of $\gamma e^{+}e^{-}$ with invariant mass closest to $m_{\eta^{\prime}}$ is taken to reconstruct the $\eta^{\prime}$. The resulting $M(\gamma e^{+}e^{-})$ distribution after the selection criteria is shown in Fig. 3 and exhibits a clear peak at the $\eta^{\prime}$ mass. An unbinned extended maximum likelihood fit is performed to determine the signal yield. Using the $\eta^{\prime}\to\gamma\gamma$ branching fraction value listed in PDG PDG , we obtain the first measurement of the $\eta^{\prime}\to\gamma e^{+}e^{-}$ branching fraction of ${Br}(\eta^{\prime}\to\gamma e^{+}e^{-})=(4.69\pm 0.20(stat.)\pm 0.23(sys.))\times 10^{-4}.$ gee:0

The results of a least-squares fit with the single pole model is shown in Fig. 4, the parameters of the form factors are determined to be $\Lambda_{\eta^{\prime}}=(0.79\pm 0.05)$ GeV, $\gamma_{\eta^{\prime}}=(0.13\pm 0.06)$ GeV. From the fitted value of the parameter $\Lambda_{\eta^{\prime}}$, the slope of the form factor is obtained to be $(1.60\pm 0.19)$ GeV^-2 gee:0 , in agreement with the result $b_{\eta^{\prime}}=(1.7\pm 0.4)$ GeV^-2 obtained in the process of $\eta^{\prime}\to\gamma\mu^{+}\mu^{-}$ gee:1 .

The double Dalitz decays $P\to\ell^{+}\ell^{-}\ell^{\prime+}\ell^{\prime-}$, where $P$ is a pseudoscalar meson ($P=\pi^{0},\eta$, or $\eta^{\prime}$) while $\ell$ and $\ell^{\prime}$ are leptons ($\ell,\ell^{\prime}=e,\mu$), are expected to proceed through an intermediate state of two virtual photons. These processes are of great interest for understanding the pseudoscalar TFF and the interactions between pseudoscalars and virtual photons 4e:1 . These TFFs are necessary inputs to calculate the pseduoscalar-meson-pole contributions to the hadronic light-by-light scattering, which causes the second largest uncertainty in the Standard Model determination of the muon anomalous magnetic moment 4e:2 . Particularly, the double Dalitz decays of pseudoscalar mesons help to determine the TFFs in the small timelike momentum region, i.e. $m_{ll}^{2}\leq q^{2}\leq m_{P}^{2}$, with $m_{ll}$ the invariant mass of the dilepton and $m_{P}$ the mass of the pseudoscalar meson, and thus are suitable to determine the slope of the TFFs at $q^{2}=0$ 4e:2 .

The resulting $M(e^{+}e^{-}e^{+}e^{-})$ distribution is shown in Fig. 5, where a clear $\eta^{\prime}$ signal is visible. An unbinned extended maximum likelihood fit is performed to determine the $\eta^{\prime}$ signal yield. The fit results shows the $\eta^{\prime}$ signal with a significance of 5.7$\sigma$, and the calculated branching fraction is $Br(\eta^{\prime}\to e^{+}e^{-}e^{+}e^{-})=(4.5\pm 1.0(stat.)\pm 0.5(sys.))\times 10^{-6}$ 4e:0 , it is consistent with the theoretical predictions within the uncertainties and provides new information for the studies about $\eta^{\prime}$ TFF and the interactions between $\eta^{\prime}$ and virtual photons 4e:1 .

The radiative decay $\eta^{\prime}\to\gamma\pi^{+}\pi^{-}$ is the second most probable decay mode of the $\eta^{\prime}$ meson with a branching fraction of $(28.9\pm 0.5)$% PDG and is frequently used for tagging $\eta^{\prime}$ candidates. In the VMD model, this process is dominated by the decay $\eta^{\prime}\to\gamma\rho^{0}$. In the past, the dipion mass distribution was studied by several experiments, and a peak shift of about $+20~{}{\rm MeV}$/$c^{2}$ for the $\rho^{0}$ meson with respect to the expected position was observed. Dedicated studies, concluded that a lone $\rho^{0}$ contribution in the dipion mass spectrum did not describe the experimental data gpipi:1 . This discrepancy could be attributed to a higher term of the Wess-Zumino-Witten anomaly, known as the box anomaly, in the ChPT Lagrangian gpipi:2 . Both the model-dependent and model-independent approaches are carried out to investigate the decay dynamics.

In the model-dependent study, binned maximum likelihood fits are performed to the $M({\pi^{+}\pi^{-}})$ distribution between 0.34 and 0.90 GeV$/c^{2}$ with different scenarios. Finally, we find the “$\rho^{0}$-$\omega$-box anomaly” model gives the best goodness of fit $\chi^{2}/ndf$ = 207/107 (Fig. 6(a)) gpipi:0 , An alternative fit by replacing the box anomaly with the $\rho^{\prime}$ component gives considerably worse agreement with $\chi^{2}/ndf$ = 303/106 (Fig. 6(b)).

A model independent approach is also implemented to investigate the decay dynamics. The model independent approach provides a satisfactory parametrization of the dipion invariant mass spectrum, and yields the parameters of the process-specific part $P(s)$ to be $\kappa=0.992\pm 0.039\pm 0.067\pm 0.163$ GeV^-2, $\lambda=-0.523\pm 0.039\pm 0.066\pm 0.181$ GeV^-4, and $\xi=0.199\pm 0.006\pm 0.011\pm 0.007$, where the first uncertainties are statistical, the second are systematic, and the third are theoretical. In contrast to the conclusion in Ref. gpipi:3 based on the limited statistics from the Crystal Barrel experiment gpipi:4 , our result indicates that the quadratic term and the $\omega$ contribution in $P(s)$, corresponding to statistical significances of $13\sigma$ and $34\sigma$, respectively, are necessary.

Experimental studies of light meson decays are important guides to our understanding of how QCD works in the non-perturbative regime. In $\pi\pi$ interaction, one of the prominent features is the loop contribution to the $\pi\pi$ scattering: the $S$-wave charge-exchange rescattering $\pi^{+}\pi^{-}\to\pi^{0}\pi^{0}$ causes a prominent cusp at the center of mass energy corresponding to the summed mass of two charged pions. The cusp effect can shed light on the fundamental properties of QCD at low energies, by determining the strength of the $S$-wave $\pi\pi$ interaction.

Using an unbinned maximum likelihood method, we fit the Dalitz plot of $M^{2}(\pi^{0}\pi^{0})$ versus $M^{2}(\eta\pi^{0})$ within the framework of NREFT. The resolution effect and detection efficiency are studied by MC simulation and taken into account in the fit. We perform alternative fits within the framework of NREFT to evaluate this effect (Fig. 8). The fit with tree level amplitude (Fit I) shows a discrepancy below the charged pion mass threshold, which implies the existence of the cusp effect. To describe the data in this region, the contributions at one- and two-loop level (Fit II $\sim$ Fit IV) are introduced in the decay amplitude. We perform alternative analyses by taking into account the cusp effect. For each case, the amplitude provides a good description of the structure around the charged pion mass threshold and the statistical significance is found to be around $3.5\sigma$ eta2pi0:0 . The scattering length combination $a_{0}-a_{2}$ is measured to be $0.226\pm 0.060\pm 0.013$, which is in good agreement with the theoretical value of $0.2644\pm 0.0051$ eta2pi0:1 within the uncertainties. The observation of the evidence of the cusp effect in $\eta^{\prime}\to\eta\pi^{0}\pi^{0}$ decay demonstrates the excellent potential to investigate the underlying dynamics of light mesons at the BESIII experiment.

As two members of the ground-state nonet of pseudo-scalar mesons, the $\eta$ and $\eta^{\prime}$ mesons play an important part in understanding low energy QCD eta:1 . Precise measurements of their branching fractions (BFs) are important for a wide variety of physics topics. For example, the decay widths of $\eta/\eta^{\prime}\to\gamma\gamma$ are related to the quark content of the two mesons eta:2 , the BFs of $\eta/\eta^{\prime}\to 3\pi$ decays can provide valuable information on light quark masses eta:3 , the BFs of $\eta/\eta^{\prime}\to\pi^{+}\pi^{-}\gamma$ decays are related to details of chiral dynamics eta:4 , and the BFs of some rare decays of the $\eta$ and $\eta^{\prime}$ can test fundamental QCD symmetries eta:5 and probe for physics beyond the standard model eta:6 . As the BFs of the rare decays are obtained via normalization to the dominant decay modes, a precise determination of the BFs of the dominant decay modes of the $\eta$ and $\eta^{\prime}$ is essential.

In Ref. eta:0 ; etap:0 , we developed an approach to measure the absolute BFs of the exclusive decays of the $\eta/\eta^{\prime}$ meson using the data sample collected with the BESIII detector. Taking advantage of the excellent momentum resolution of charged tracks in the MDC, photon conversions to $e^{+}e^{-}$ pairs provide a unique tool to reconstruct the inclusive photon spectrum from radiative $J/\psi$ decays. Take $J/\psi\rightarrow\gamma\eta(\eta^{\prime})$ for example, Monte Carlo (MC) study indicates that the energy resolution of the radiative photon could be improved by a factor of three using the photon conversion events. This enables us to tag the $\eta/\eta^{\prime}$ inclusive decays and then to measure the absolute BF of $J/\psi\rightarrow\gamma\eta(\eta^{\prime})$, using

where $N^{\rm obs}_{J/\psi\rightarrow\gamma\eta/\eta^{\prime}}$ is the observed $\eta/\eta^{\prime}$ yield, $\varepsilon$ is the detection efficiency obtained from MC simulation, and $N_{J/\psi}$ is the number of $J/\psi$ events. The photon conversion process is simulated with GEANT4, and $f$ is a correction factor to account for the difference in the photon conversion efficiencies between data and MC simulation.

After the $\eta/\eta^{\prime}$ inclusive measurement, we present precision measurements of $\eta$ decays to $\pi^{0}\pi^{0}\pi^{0}$, $\pi^{+}\pi^{-}\pi^{0}$, $\pi^{+}\pi^{-}\gamma$, $\gamma\gamma$, and $\eta^{\prime}$ decays to $\gamma\pi^{+}\pi^{-}$, $\eta\pi^{+}\pi^{-}$, $\eta\pi^{0}\pi^{0}$, $\gamma\omega$, $\gamma\gamma$, again using $J/\psi$ decays to $\gamma\eta/\eta^{\prime}$, but with the radiative photon directly detected by the EMC to improve the statistics. With the help of Eq. (1), the BF for each $\eta^{\prime}$ exclusive decay is then calculated using

where $N_{\eta/\eta^{\prime}\to X}^{\rm obs}$ is the number of signal events obtained from a fit to data and $\varepsilon_{\eta/\eta^{\prime}\to X}$ is the MC-determined reconstruction efficiency.

The measured BF of $J/\psi\to\gamma\eta(\eta^{\prime})$ is $(1.067\pm 0.005\pm 0.023)\times 10^{-3}$ ($(5.27\pm 0.03\pm 0.05)\times 10^{-3}$), which is in agreement with the world average value, $(1.085\pm 0.018)\times 10^{-3}$ $((5.25\pm 0.07)\times 10^{-3}$) PDG , but with a significantly improved precision. In addition, we also give the relative BFs for $\eta$ and $\eta^{\prime}$ decays as presented in Tab. 1 and Tab. 2 respectively.

The BESIII collaboration has produced fruitful results related with light meson decays, including the studies of the decay dynamics, tests of discrete symmetries, searches for rare decays, and many other interesting results not covered in this proceeding. The BESIII experiment has accumulated 10 billion $J/\psi$ events in total, which is a unique world wide sample, allows to study the light mesons with unprecedented statistics. Ongoing analyses will produce more precise results in the next years.