Lepton flavor of four-fermion operator and fermion portal dark matter
Abstract
We study the ultraviolet completion of semileptonic four-fermion operator that incorporates Majorana dark matter (DM) in both lepton-flavor-conserving (LFC) and lepton-flavor-violating (LFV) scenarios at the one-loop level via box diagram, which effectively alleviates the lower bounds on the new physics scale. The interplay between the model-independent constraints on the Wilson coefficients and DM direct detection, relic density, and collider searches in the context of fermion portal DM model with two mediators is investigated. We find that both the projected future constraint on the LFC Wilson coefficient from the measurements of neutrino non-standard interaction in the next-generation neutrino oscillation experiments, and LFV constraint from ongoing charged-lepton-flavor-violation searches, provide a complementary exploration of the parameter space encompassing the DM mass and scalar mass. With the colored mediator mass typically around , the sensitivity of the indirect constraints on the four-fermion operator could surpass those of collider searches and DM direct detection, in scenarios where the masses of the DM and scalar are close. By ensuring the correct DM relic density, however, we obtain that the collider searches and DM direct detection are more sensitive to the electroweak scale DM and scalar compared to the indirect constraints.
1 Introduction
While the Standard Model (SM) of particle physics has achieved striking success, its lack of explanation of fundamental phenomena, such as the origins of neutrino masses and fermion flavor structure, and providing particle candidates for dark matter (DM) underscores the need for physics beyond the SM (BSM). In light of null results in searches for new resonances at the Large Hadron Collider (LHC), the effective field theory (EFT) framework offers a powerful way to explore new physics Isidori:2023pyp .
In the EFT approach, BSM interactions are systematically parameterized as a series of higher-dimensional operators with the corresponding Wilson coefficients suppressed with inverse powers of the new physics scale . At the lowest order with mass dimension 5, only one operator is present that gives masses to neutrinos Weinberg:1979sa , while exploding numbers of effective operators emerge at higher orders Buchmuller:1985jz ; Grzadkowski:2010es ; Henning:2015alf .
There has been growing interest in dimension-6 four-fermion operators, as being utilized to fit precision data and address anomalies observed at the LHC and in low-energy experiments Falkowski:2017pss ; Cirigliano:2023nol ; Fernandez-Martinez:2024bxg ; Karmakar:2024gla , and intriguing connections with DM models Cepedello:2023yao . Focusing on the semileptonic operators with two leptons and two quarks, the one-by-one constraints on the lepton-flavor-conserving (LFC) are rather stringent, and global fits are essential to mitigate or even eliminate the tensions in different observables Cirigliano:2023nol . On the other hand, for the lepton-flavor-changing (LFV) operators, possible tensions are milder since less experimental data is available Fernandez-Martinez:2024bxg .
Consider the dimension-6 four-fermion operator Grzadkowski:2010es
| (1) |
where and denote the left-handed doublets of leptons and quarks, respectively. is the isospin index, and , , , are flavor indices. This operator is forbidden under the flavor symmetry, and highly suppressed within minimal flavor violation hypothesis DAmbrosio:2002vsn ; Isidori:2023pyp , rendering it extraordinarily sensitive probe of BSM physics. We will consider the first-generation quarks, , and the lepton flavor indices .
In general, the stringent constraints on the Wilson coefficients of four-fermion operators challenge direct searches for ultraviolet (UV) physics. However, one-loop UV completions of the four-fermion operators with the participation of DM particles in the box diagram can notably alleviate the restrictions on the mass scale . In the class of DM models Cepedello:2023yao , the symmetry that stabilizes the DM prohibits tree-level contributions to the Wilson coefficients of four-fermion operators. Consequently, upon integrating out heavy new particles, the Wilson coefficients are suppressed by a factor of . Moreover, the Wilson coefficients are proportional to , where denotes new physics couplings. This dependency has the potential to further lower the new physics scale for small values of . Previous studies of connections between cLFV observables and DM were conducted in Refs. Herrero-Garcia:2018koq ; Toma:2013zsa ; Vicente:2014wga .
In this work, we will investigate the complementarities of indirect constraints on the Wilson coefficients of the four-fermion operator in both LFC and LFV scenarios from the measurements of neutrino NSI and cLFV searches for conversion, and DM relic density, direct detection, and collider searches in the context of fermion portal DM model Bai:2013iqa12 ; DiFranzo:2013vra ; An:2013xka ; Bai:2014osa with two mediators and Majorana fermionic DM. We highlight that
-
•
In the LFC scenario, the anticipated future sensitivity to the neutrino NSI in next-generation neutrino oscillation experiments could play a nontrivial role in investigating new physics, while ensuring that tensions among various observables are eliminated.
-
•
In the LFV scenario, the scattering of Majorana DM with nuclei can appear at tree level, and conversion arises solely from the contribution of the box diagram at the one-loop level, with no other cLFV processes occurring at this order.
-
•
In both scenarios, the model-independent constraints on the Wilson coefficients of the four-fermion operator offer a distinctive probe of the fermion portal DM model, particularly in the parameter space where the masses of the DM and scalar are either close or large, depending on the requirement of DM relic density.
The remainder of the paper is organized as follows. In Sec. 2, the fermion portal DM model is studied in detail. In Sec. 3, the Wilson coefficients of the four-fermion operator are calculated. In subsequent sections, the sensitivities in DM relic density, direct detection, and collider searches are investigated. In Sec. 7, the combined results are discussed in benchmark scenarios of masses and coupling with the relic density of satisfying or . We conclude in Sec. 8. More details are provided in Appendix A and Appendix B about the anomalous magnetic moment for leptons and DM direct detection with one-loop exchange of photon, respectively.
2 Fermion portal dark matter model
We consider a UV completion model that induces the four-fermion operator , incorporating Majorana fermionic DM , which remains a more viable DM candidate compared to Dirac fermionic DM. In addition to the DM particle , we introduce a fermion doublet , scalar , and colored mediator , all of which are odd. The quantum numbers of these fields under are presented in Table 1, and are documented in the systematic classification of DM models for four-fermion operators Cepedello:2023yao .
| new fields | ||||
| 0 | ||||
The Lagrangian for the UV model of the four-fermion operator is given by
| (2) |
where , , , and are coupling constants. The flavor indices are omitted, and the couplings are assumed to be real and positive for simplicity.
In the presence of the dark mediators and in this fermion portal DM model Bai:2013iqa12 ; An:2013xka ; DiFranzo:2013vra ; Bai:2014osa , the DM candidate interacts with SM particles, leading to distinct observables in direct detection, indirect detection, and collider experiments. In the subsequent sections, we will analyze each type of signature separately.
3 Wilson coefficients
Given the interactions in Eq. (2), the one-loop diagram in Fig. 1 can be generated. We refer to this type of box diagram as “dark loop”, which was proposed to explain the flavor anomalies in physics Huang:2020ris ; Capucha:2022kwo ; Cepedello:2022xgb .
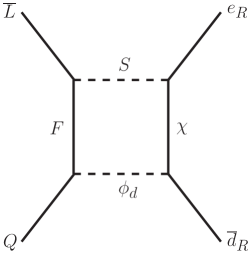
The Wilson coefficient of the effective operator is calculated using Package-X Patel:2015tea ; Patel:2016fam , which is expressed as follows
| (3) |
where the effective coupling and the loop function are defined as
| (4) | ||||
| (5) |
This result agrees with Ref. Bischer:2018zbd by taking .
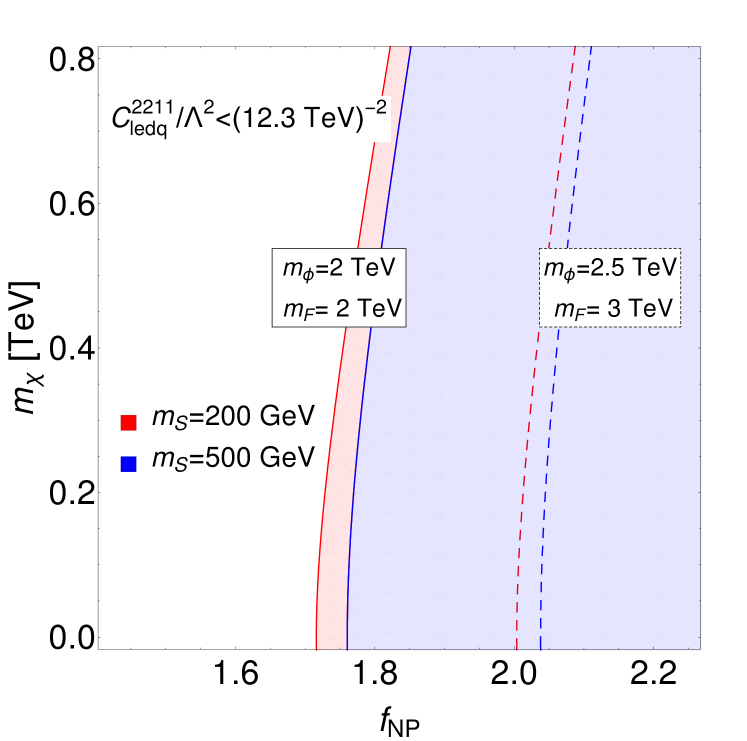
The Wilson coefficient is constrained by searches in low-energy experiments and at colliers depending on the lepton flavor of the four-fermion operator. According to the global analysis in Ref Cirigliano:2023nol , the allowed value of the Wilson coefficient for the LFC operator is , which is consistent with zero within . Refs. Du:2020dwr ; Du:2021rdg have investigated the prospects of next-generation neutrino oscillation experiments in the search for neutrino non-standard interactions (NSIs) Proceedings:2019qno , which are described by certain SMEFT operators at the electroweak scale. These studies indicate the highest sensitivity for the operator , Du:2021rdg . This enhanced sensitivity is attributed to the significant increase in neutrino production from pion decay, particularly in the presence of charged-current (CC) neutrino NSIs induced by at lower energies. Note that this operator does not interfere with the CC neutrino interactions in the SM, so the experimental measurements are blind to the sign of the Wilson coefficient. Henceforth, we will consider the magnitude of the Wilson coefficient with the absolute value symbol being omitted.
We illustrate the constraints on and from future LFC searches in the left panel of Fig. 2 with two benchmark values of the scalar mass (red region) and (blue region) for (solid curve), or , (dashed curves). We find that this constraint does not strongly depend on , but it is highly sensitive to , which is expected to be in the range of approximately 1.7 to 2.1. It is important to note that there are currently no constraints from existing LFC searches, as the results are consistent with the SM predictions.
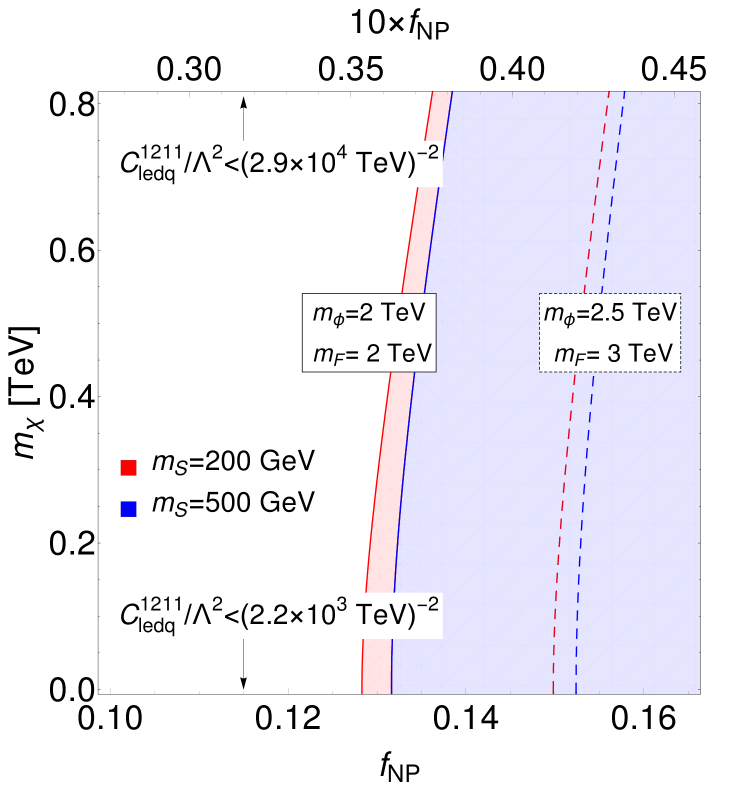
In the case of the LFV operator, the current constraint on the Wilson coefficient Fernandez-Martinez:2024bxg is derived from charged-lepton-flavor-violation (cLFV) searches for conversion in nuclei Badertscher:1981ay ; SINDRUMII:1993gxf ; SINDRUMII:1996fti ; SINDRUMII:2006dvw . The projected limit Haxton:2024lyc in the upcoming Mu2e Mu2e:2014fns ; Bernstein:2019fyh and COMET COMET:2018auw ; COMET:2018wbw experiments, representing an improvement by approximately two orders of magnitude. The cLFV searches are also insensitive to the sign of the Wilson coefficient of the operator , and we omit the absolute value symbol for convenience.
In the right panel of Fig. 2, we present the contours of LFV limits as functions of and , by choosing the benchmark values of , , and as the left panel of Fig. 2. Unlike the LFC scenario, constraints from both the current and future experimental efforts are depicted. The current limit is shown on the lower axis, while the anticipated future limit is displayed on the upper axis. The current limit for will be around 0.13 to 0.15, with expectations that the future limit could improve by an order of magnitude, potentially reaching as low as 0.04. It is important to note that despite the stringent constraint on the LFV interaction, the BSM particles could potentially exist at the TeV scale or even lower, owing to the suppression of loop factor and the coupling dependence .
Besides the effective interaction expressed as the four-fermion operator , the dark particles can also contribute to the anomalous magnetic momentum of leptons. To address the discrepancies between the experimental measurements and the SM predictions, improved SM calculations or other new physics contributions are needed; see Appendix A for details.
4 DM relic density
Given the Lagrangian in Eq. (2), the Majorana DM pair can annihilate to muon pair and quark pair, mediated by and , respectively. In our setup, where and the ratio , the contribution from the process mediated by , is negligible. Tree-level Feynman diagram for the annihilation is depicted in Fig. 3. The corresponding thermal-averaged cross section is Liu:2021mhn
| (6) |
where , and is the relative velocity of two DM particles, which is typically around at the freeze-out temperature. Since , the -wave contribution to the thermal-averaged annihilation cross section is dominant Bai:2013iqa12 ; Bai:2014osa ; Liu:2021mhn .
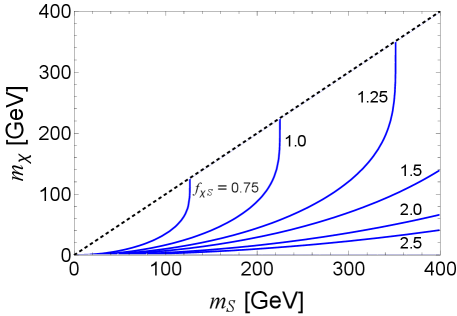
In Fig. 4, we present the DM relic density contours for and with different choices of , considering the relic density Planck:2018vyg . Regions below the contour curves indicate overabundance.
5 DM direct detection
The Majorana DM can interact with the SM quark through the term in Eq. (2), giving rise to the tree-level scattering process depicted in Fig. 5.
By using the Fierz identity Bai:2013iqa
| (7) |
and the relation for Majorana fermion
| (8) |
we can obtain the following effective Lagrangian Jungman:1995df ; Hisano:2010ct ; Mohan:2019zrk ; Arcadi:2023imv :
| (9) |
where the effective operators are
| (10) |
Here, the notation of the operator follows Refs. Hisano:2010ct ; Hill:2014yka ,
| (11) |
The Wilson coefficients are given by
| (12) |
Based on whether the DM-nucleus interactions depend on the spin of nucleus or not, the DM-nucleus scattering is classified as spin-dependent (SD) and spin-independent (SI) scatterings, respectively. The latter is typically proportional to , where is the mass number of nucleus. Table 2 summarizes the suppression factors of DM-nucleon cross sections for the above operators. Here, is the DM-nucleon relative velocity, denotes the momentum transfer, and the transverse relative velocity is defined as , where denotes the DM-nucleon reduced mass.
| & | |||
| 1 |
The DM-nucleon SI and SD cross sections for the operators and depend on the kinematic suppression factors, which agree with the earlier studies Bai:2013iqa12 ; DiFranzo:2013vra ; An:2013xka ; Mohan:2019zrk . On the contrary, the SI cross sections for the operators and are not kinematically suppressed, but suppressed by Jungman:1995df ; Hisano:2010ct ; Mohan:2019zrk ; Arcadi:2023imv . This is because and are obtained by expanding the propagator of at next-to-leading order. Their contributions to the SD cross section are not displayed as they are further suppressed by the DM velocity and momentum transfer Kumar:2013iva .
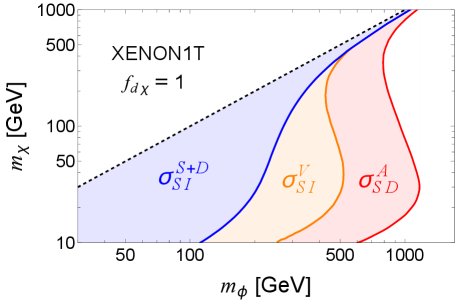
We first consider the SI contributions from these operators. From Eq. (5), the Wilson coefficients of the operators and are the same, so we readily obtain that the contribution of , which is suppressed by , is larger that that of . To derive the exclusion limit for the operator , we evaluate the non-relativistic events generated in the XENON1T experiment XENON:2018voc with an exposure of using DirectDM Bishara:2017nnn and DMFormFactor Anand:2013yka . The 90% confidence level (C.L.) constraint is determined under the assumption of 7 signal events after accounting for SM backgrounds Kang:2018rad ; Liang:2024tef . Our result agrees with the EFT analysis by the XENON Collaboration XENON:2022avm . The exclusion region for and is depicted in orange color in Fig. 6.
The suppression factor for the contributions to the SI cross section from the operators and is . Following Refs. Jungman:1995df ; Hisano:2010ct ; Mohan:2019zrk ; Arcadi:2023imv ; Hill:2014yka , we express the contributions to the SI cross section as a combination of the Wilson coefficients of and . In Fig. 6, we present the exclusion of and using the upper limit on the DM-nucleon SI cross sections by the XENON1T experiment XENON:2018voc with a 1 ton-year exposure. We find that the contribution from dominates over that from the combination of and within our parameter space.
On the other hand, the leading contribution to the SD cross section comes from the operaotr , as clearly shown in Table 2, where the contributions from and are highly suppressed and not presented. The SD DM-nucleon cross section for is expressed as Bai:2013iqa12 ; DiFranzo:2013vra ; An:2013xka ; Mohan:2019zrk
| (13) |
where Belanger:2008sj and denotes the DM-neutron reduced mass. Here, we only consider the limit on the DM-neutron cross section, which is much stronger than that on the DM-proton cross section for the XENON1T XENON:2019rxp , PandaX-4T PandaX:2022xas , and LZ LZ:2022lsv experiments. Using Eq. (13) and the upper limit on the DM-nucleon SD cross section given by the XENON1T experiment XENON:2019rxp with a 1 ton-year exposure, we derive the exclusion of and for the operator , which is shown as the red region in Fig. 6. It is evident that in our case, the exclusion limit from DM direct detection is dominated by the SD interactions associated with the operator .
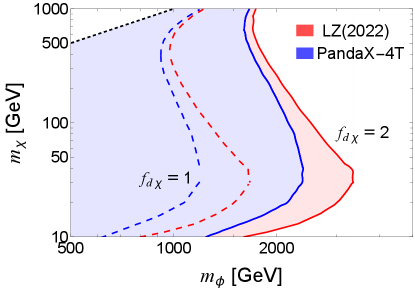
In Fig. 7, we show the exclusion limits on the DM mass and colored mediator mass from the constraints on the SD cross sections measured in the LUX-ZEPLIN (LZ) experiment LZ:2022lsv and the PandaX-4T experiment PandaX:2022xas assuming coupling values or 2. Our result for using the limit by the LZ experiment agrees with Ref. Arcadi:2023imv . It is important to mention that we assume the relic density of as the observed total DM relic density. If the DM relic density depends on a given , the limits could be notably weaker, as we will see in Sec. 7.
It is noted that direct detection can also occur by exchanging photons at the one-loop level, which leads to much weaker direct detection signals compared to the contribution from exchanging at the tree level; see Appendix B for details.
6 Collider searches
The DM can interact with SM particles via , and , resulting in detectable DM signatures at collider experiments. We focus on DM searches at the LHC, where the presence of missing energy is a typical signature indicating the possible existence of DM particles. Assuming the mass hierarchy , and the decay branching ratios of and are determined as
| (14) |
The particle can decay to leptons or jet via the processes or , where represents any first-generation quark. The most relevant collider search for DM involves these channels: (1) leptons and (2) jet(s).
6.1 Leptons
The possible processes for leptons are as follows:
-
•
SL1: , ;
-
•
SL2: , , , ;
-
•
SL3: , , , , or .
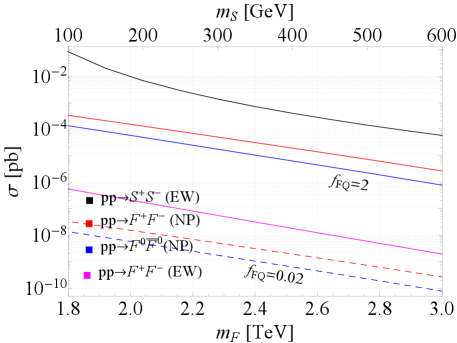
The corresponding Feynman diagrams for the production of , and are illustrated in Fig. 8, which depend on the electroweak or new physics couplings. The cross sections at the 13 TeV LHC are shown in Fig. 9 for the assumption of the coupling or 0.02. The cross sections for production of and are proportional to , and insensitive to the mass . In our study, we focus on the mass range TeV and GeV. Consequently, the cross section for pair production via electroweak processes, as shown in the left panel of Fig. 8, is larger than that for pair production via electroweak interactions. Although increasing the coupling to 2 enhances the production cross section for the pair, it remains smaller than that for pair within our specified mass range. Therefore, we focus exclusively on the signal (denoted as SL1) in the recast of dilepton searches.
Since the scalar interacts with the right-handed charged leptons, which ensembles the right-handed slepton Fuks:2013lya , and decays totally into , one can read off the exclusion limits on the masses of right-handed slepton (smuon) and neutralino, and reinterpret them as the constraints on the masses of and . In Fig. 10, we show the excluded regions by the most stringent searches at the LHC Run 2 ATLAS:2019lff ; ATLAS:2019lng and earlier 8 TeV LHC ATLAS:2014zve .

Besides the dilepton processes, the cascade decays of and can give rise to the multi-lepton process SL3. For , the cross section for the production of is , for which less than 3 signal events are expected even with the integrated luminosity of . Thus there is no constraint from the multi-lepton searches.
6.2 Jet(s)
Depending on the number of jets at the parton level, the possible process for jet(s) are following:
-
•
SJ1: (3-body), , or ;
-
•
SJ2: , ;
-
•
SJ3: , ;
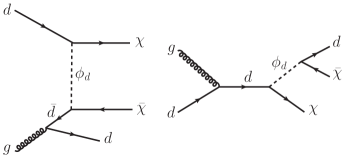
The signal processes SJ1 and SJ2 for DM production at the LHC are categorized as monojet channel, while the signal process SJ3 is categorized as dijet channel. The representative diagrams for monojet are illustrated in Fig. 11. The cross sections of and scale with and , respectively. In Fig. 12, we illustrate these cross sections with the new physics coupling (thick lines) or 1(dashed lines) at the 13 TeV LHC. It is evident that, without any selection cuts applied, the cross section of SJ1 is much larger than SJ2, especially for a larger .
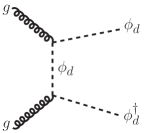
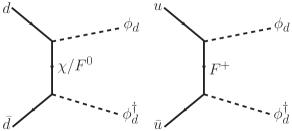
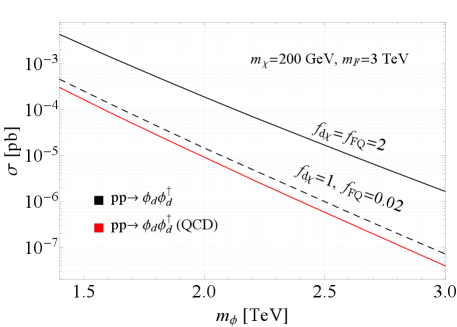
In the dijet channel with two jets at the parton level, the DM is produced from the decay of colored mediator . In Fig. 13, we show the representative diagrams for the production via QCD or new physics interactions, respectively. The cross section for the QCD production of (red line), and benchmark cross sections for the new physics production at the 13 TeV LHC under the assumptions of , , and (black thick line), or , (black dashed line) are illustrated in Fig. 14. We find that the total production cross section is significantly enhanced for substantial new physics couplings, which agrees with the findings in Ref. Bai:2013iqa . In our parameter space of interest, the cross section of new physics production always dominates over that of QCD production.
At the detector level, more jets would emerge from the signal processes discussed, even if only one or two jets are present at the parton level. Therefore, a detailed analysis must include detector-level simulations. Next, we separate the analysis into monojet and dijet searches.
6.2.1 Monojet search
In the jet(s) searches, it is generally essential to consider the processes SJ1, SJ2, and SJ3 simultaneously, including additional jets from the initial state radiation (ISR). However, for monojet searches, which require one hard jet, we only need to consider SJ1 and SJ2, since the parton-level cross section of SJ3 is much smaller. We generate signal events using MadGraph5_aMC@NLO Alwall:2014hca , which are then passed to Pythia8 Sjostrand:2014zea for parton shower, and Delphes3 deFavereau:2013fsa for detector simulation, respectively. Following the most stringent monojet search ATLAS:2021kxv at the LHC Run 2, we apply the selection cuts as follows:
-
•
, leading jet GeV and ;
-
•
up to four jets with GeV and ;
-
•
() for ();
-
•
veto of electron, muon, -lepton or photon.
We further refine our event selection according to 13 inclusive signal regions. By combining model-independent constraints on the observed signal cross section for each of these regions, as outlined in Ref. ATLAS:2021kxv , we derive a C.L. limit on our parameter space of and . The excluded region of and is depicted by the red shaded area in Fig. 15 assuming the new physics coupling , for which the monojet search at the LHC Run 2 sets the lower limit . The exclusion for , falls below and is not depicted. This result agrees with the reinterpretation in Ref. Mohan:2019zrk of the monojet search at the LHC using the data of ATLAS:2017bfj assuming that the signal significance approximately scales as the square root of the integrated luminosity.
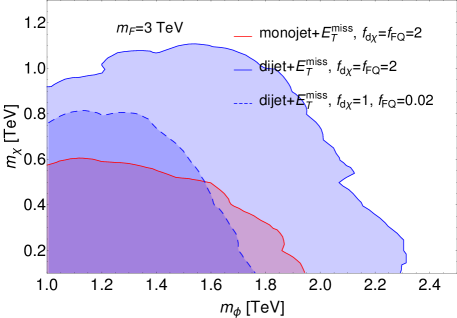
6.2.2 Dijet search
To recast the dijet search, we consider all of the processes SJ1, SJ2, and SJ3, including their ISR, to generate detector-level events. We implement the selection criteria outlined in Ref. ATLAS:2020syg . The signal events are first selected with the following criteria:
-
•
, leading jet with GeV and sub-leading jet with GeV, and ;
-
•
GeV;
-
•
veto of electron (muon) with GeV,
where is defined by the scalar sum of and transverse momentum of jets with GeV. We further apply the selection criteria of model-independent search SR2j-1600, SR2j-2200, and SR2j-2800 that are listed in Ref. ATLAS:2020syg . We then derive our constraints from the model-independent limits of the three signal regions given in Ref. ATLAS:2020syg accordingly.
In Fig. 15, we show the constraints from the monojet and dijet searches for 111For , , the cross section from the -channel exchange of is negligible compared to that from the exchange of , thus the total cross section is insensitive to the mass of in this case. with different choices of the new physics couplings. The blue shaded areas with solid and dashed curves correspond to dijet search with and , , respectively. The constraints from the dijet search are stricter than those from the monojet search with the same choice of and . We find that the most stringent limits on the colored mediator mass from the jet(s) searches in our parameter space are and , respectively.
7 Results and discussion
We have explored the phenomenological implications of the four-fermion operator in our UV model, including DM relic density, direct detection, and collider searches, as well as the model-independent LFC and LFV constraints on the Wilson coefficients. To analyze their complementarities, we examine four benchmark (BM) scenarios detailed in Table 3.
| BM | [TeV] | [TeV] | ||||
| (a) | 2.5 | 3.0 | 2.1 | 2.0 | 2.0 | / |
| (b) | 2.5 | 3.0 | 2.1 | 2.0 | / | 0.1199 |
| (c) | 2.0 | 2.0 | 1.0 | 1.5 | / | |
| (d) | 2.0 | 2.0 | 1.0 | / | 0.1199 |
Based on the collider searches and DM direct detection discussed, we choose the values:
-
•
BM (a) or (b): , ;
-
•
BM (c) or (d): , .
As discussed in Sec. 4, the DM relic density can be determined by the coupling and the mass , . In BM (a) and BM (b), the coupling is taken as an input parameter. Given the constraints on the LFC and LFV Wilson coefficients , as illustrated in Fig. 2, the other couplings are set to be equal, such that their products yield and (cf. Eq. (4)), respectively. In BM (b) and BM (d), is fixed by the observed DM relic density for comparison.
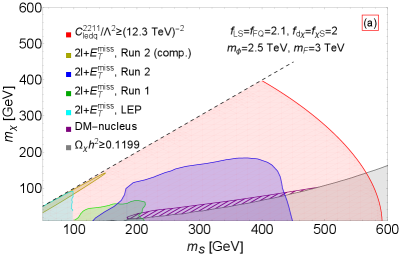
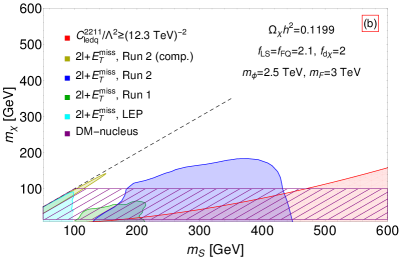
In Figs. 16 and 17, we combine the sensitivities to the DM mass and scalar mass from DM relic density, direct detection, collider searches, and model-independent indirect constraints on the Wilson coefficients of the four-fermion operator . For all benchmark scenarios in Table 3, a large portion of parameter space with and is excluded by the existing searches at the LEP and LHC.
For the LFC operator, we consider the projected future sensitivity to Wilson coefficient, Du:2020dwr ; Du:2021rdg from the neutrino NSI measurements, given that the currently allowed value is consistent with zero as mentioned in Sec. 3. For the LFV operator, we utilize the current constraint, Fernandez-Martinez:2024bxg derived from the cLFV searches for conversion in nuclei, since our aim is to show that the new physics scale can be notably alleviated within the dark loop paradigm.
In the left panel of Fig. 16, we consider , and require the DM relic density to avoid an overabundance of DM, shown as the gray shaded region. Given the values of and , DM direct detection in the LZ experiment LZ:2022lsv rules out a narrow range of and , as depicted in purple slash shading area. The sensitivity of DM direct detection in this case is rather weak, which is suppressed by the relic density of for a relatively large . The exclusion by the LFC constraint on from the neutrino NSI measurements is shown in red color. It is evident that this model-independent constraint exhibits better sensitivity, probing parameter regions beyond the reach of collider searches, and DM direct detection, especially in scenarios where and are close.
In the right panel of Fig. 16, the coupling is not independent but determined by the DM relic density . The coupling decreases as becomes smaller. The purple slash shading band for is ruled out by DM direct detection in the LZ experiment. The region excluded by the model-independent LFC constraint is depicted in red, with the boundary corresponding to . One can see that the Yukawa coupling can yield the correct relic density for the electroweak scale and Liu:2021mhn . In this scenario, the most effective constraints are provided by LHC searches and DM direct detection. For larger values of and , however, the neutrino NSI measurements are more significant.
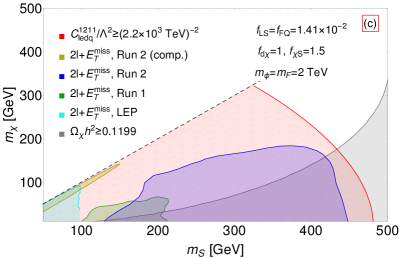
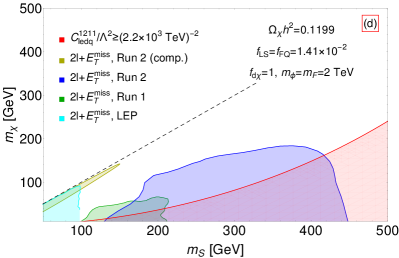
In Fig. 17, the exclusions are derived with the same experimental results as Fig. 16, except for the current model-independent constraint on the Wilson coefficient of the LFV four-fermion operator . As highlighted in Sec. 2, the model-independent constraint on the Wilson coefficient of LFV operator is more stringent and can probe smaller new physics couplings, compared to that on the Wilson coefficient of the LFC operator. For illustration, we consider , for which the colored mediator mass is allowed by the current LHC jet(s) searches. Taking , the DM direct detection in the LZ experiment LZ:2022lsv puts no constraints as shown in Fig. 7. In the case of BM (c) with , the prevailing cLFV constraint rules out most of the parameter space where and , exceeding the sensitivity of the LHC searches, especially for the region where and are close. On the other hand, for BM (d) with the relic density being fixed, the Yukawa coupling can also yield the correct relic density for the electroweak scale and . The LHC searches remain the most sensitive probes of the fermion portal DM model for the scalar mass . As increases or DM mass , the cLFV searches exhibit better sensitivity than the LHC searches.
8 Conclusion
In this work, we have studied the UV completion of the four-fermion operator in both lepton-flavor-conserving (LFC) and lepton-flavor-violating (LFV) scenarios incorporating the Majorana dark matter (DM). Due to the symmetry that stabilizes the DM, the four-fermion operator is firstly generated at one-loop level via box diagram, which could effectively mitigate the lower bounds on the new physics scale.
We investigated the interplay between the model-independent constraints on the Wilson coefficients of the four-fermion operator from the measurements of neutrino NSI in the next-generation neutrino oscillation experiments, charged-lepton-flavor-violation (cLFV) searches in conversion, as well as DM relic density, direct detection, and collider searches in the context of fermion portal DM model with two mediators. In order to illustrate the complementarities, we consider four benchmark scenarios as outlined in Table 3.
In the cases of BM (a) and BM (c), where the Yukawa coupling is considered as an independent parameter, the model-independent constraints on the Wilson coefficients of and provide a complementary investigation of the parameter space of the DM mass and scalar mass , which extends the reach of collider searches and DM direct detection, especially for the region where and are close.
In the cases of BM (b) and BM (d), the coupling is determined by the requirement of DM relic density, . For electroweak scale DM and scalar, the LHC searches demonstrate greater sensitivity than the indirect constraints on the four-fermion operator, while the latter are more significant for larger values of and .
Appendix A Lepton
The lepton magnetic dipole moment can be induced by the couplings and at one-loop level. In Fig. 18, we depict the Feynman diagram with or running in the loop.
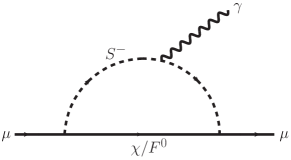
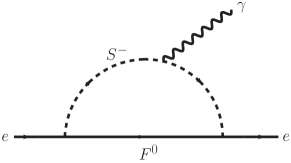
The corresponding contributions to muon is expressed as
| (15) |
where and denotes the contributions from the diagrams involving and , respectively. For the electron , we have
| (16) |
which only includes the contribution from the diagram with given the lepton flavors .
The piece is given by Moroi:1995yh ; Carena:1996qa
| (17) |
where , and can be obtained by taking and replacing and . In the limits of and , the loop function approaches and , respectively. Thus the contributions to the lepton are always negative Liu:2021mhn .
The experimental measurements of the muon yield Muong-2:2021ojo ; Muong-2:2023cdq ; Muong-2:2006rrc
| (18) |
which indicates deviation from the SM prediction. In order to explain this discrepancy, positive contribution to the muon is necessary. This implies that the fermion portal DM model does not account for this anomaly.
There are still large uncertainties in the measurements of the electron . The measurements using Cesium Parker:2018vye and Rubidium Morel:2020dww give
| (19) |
Following Ref. Liu:2021mhn , we take the 95% C.L. bounds on and , so that both of them allow for negative values.
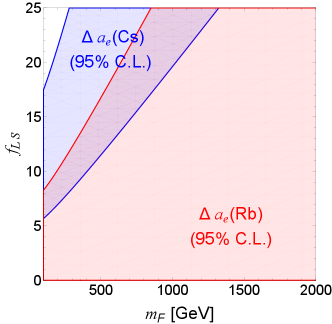
In our model, the electron can be generated by the coupling in the LFV scenario. In Fig. 19, we illustrate the allowed region of and using the 95% C.L. bounds on and in blue and red colors, respectively, for . The mutual region of two measurements requires that and TeV, which has been excluded by the LHC searches. If future measurements are in favor of , our model could potentially offer an explanation for it.
Appendix B DM direct detection via photon exchange
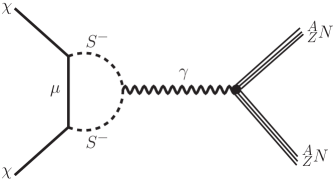
Besides the tree-level contribution to the DM direct detection discussed in Section.5, the DM-nucleus scattering can occur with the exchange of photon at the one-loop level Bai:2014osa ; Herrero-Garcia:2018koq , as illustrated in Fig. 20. The interaction between the Majorana DM and photon can be described by the electromagnetic anapole momentum of the DM. Thus, the contribution to the SI DM-nucleon cross section is suppressed by the DM velocity square, which can be expressed by Bai:2014osa
| (20) |
where denotes the reference value of the recoil energy , and the loop factor is given by
| (21) |
Here, , and are the masses of the nucleus, proton and muon, respectively. denotes the atomic number of the nucleus. As an estimate, following Ref. Bai:2014osa , we take , and calculate using liquid xenon as the target for , and . Given the sensitivities of the DM direct detection experiments LZ:2022lsv ; PandaX:2022xas ; XENON:2023cxc , we obtain that it gives negligible contribution to the DM-nucleus cross section Liu:2021mhn .
Acknowledgements.
GL expresses gratitude to Shao-Long Chen for the enlightening discussion. XZ would like to thank Hao-Lin Li, Jian Tang, Jiang-Hao Yu, and Zhao-Huan Yu for helpful discussions. GL and XZ are supported by the National Natural Science Foundation of China under Grant No. 12347105, the Guangdong Basic and Applied Basic Research Foundation (2024A1515012668), and the Fundamental Research Funds for the Central Universities, Sun Yat-sen University (23qnpy62), and SYSU startup funding. The work of JL is supported by Natural Science Foundation of China under grant No. 12235001 and 12075005. The work of XPW is supported by National Science Foundation of China under Grant No. 12375095, 12005009, and the Fundamental Research Funds for the Central Universities.References
- (1) G. Isidori, F. Wilsch and D. Wyler, The standard model effective field theory at work, Rev. Mod. Phys. 96 (2024) 015006, [2303.16922].
- (2) S. Weinberg, Baryon and Lepton Nonconserving Processes, Phys. Rev. Lett. 43 (1979) 1566–1570.
- (3) W. Buchmuller and D. Wyler, Effective Lagrangian Analysis of New Interactions and Flavor Conservation, Nucl. Phys. B 268 (1986) 621–653.
- (4) B. Grzadkowski, M. Iskrzynski, M. Misiak and J. Rosiek, Dimension-Six Terms in the Standard Model Lagrangian, JHEP 10 (2010) 085, [1008.4884].
- (5) B. Henning, X. Lu, T. Melia and H. Murayama, 2, 84, 30, 993, 560, 15456, 11962, 261485, …: Higher dimension operators in the SM EFT, JHEP 08 (2017) 016, [1512.03433].
- (6) A. Falkowski, M. González-Alonso and K. Mimouni, Compilation of low-energy constraints on 4-fermion operators in the SMEFT, JHEP 08 (2017) 123, [1706.03783].
- (7) V. Cirigliano, W. Dekens, J. de Vries, E. Mereghetti and T. Tong, Anomalies in global SMEFT analyses. A case study of first-row CKM unitarity, JHEP 03 (2024) 033, [2311.00021].
- (8) E. Fernández-Martínez, X. Marcano and D. Naredo-Tuero, Global Lepton Flavour Violating Constraints on New Physics, 2403.09772.
- (9) S. Karmakar, A. Dighe and R. S. Gupta, SMEFT predictions for semileptonic processes, 2404.10061.
- (10) R. Cepedello, F. Esser, M. Hirsch and V. Sanz, SMEFT goes dark: Dark Matter models for four-fermion operators, JHEP 09 (2023) 081, [2302.03485].
- (11) G. D’Ambrosio, G. F. Giudice, G. Isidori and A. Strumia, Minimal flavor violation: An Effective field theory approach, Nucl. Phys. B 645 (2002) 155–187, [hep-ph/0207036].
- (12) J. Herrero-Garcia, E. Molinaro and M. A. Schmidt, Dark matter direct detection of a fermionic singlet at one loop, Eur. Phys. J. C 78 (2018) 471, [1803.05660].
- (13) T. Toma and A. Vicente, Lepton Flavor Violation in the Scotogenic Model, JHEP 01 (2014) 160, [1312.2840].
- (14) A. Vicente and C. E. Yaguna, Probing the scotogenic model with lepton flavor violating processes, JHEP 02 (2015) 144, [1412.2545].
- (15) Y. Bai and J. Berger, Fermion Portal Dark Matter, JHEP 11 (2013) 171, [1308.0612].
- (16) A. DiFranzo, K. I. Nagao, A. Rajaraman and T. M. P. Tait, Simplified Models for Dark Matter Interacting with Quarks, JHEP 11 (2013) 014, [1308.2679].
- (17) H. An, L.-T. Wang and H. Zhang, Dark matter with -channel mediator: a simple step beyond contact interaction, Phys. Rev. D 89 (2014) 115014, [1308.0592].
- (18) Y. Bai and J. Berger, Lepton Portal Dark Matter, JHEP 08 (2014) 153, [1402.6696].
- (19) D. Huang, A. P. Morais and R. Santos, Anomalies in -meson decays and the muon from dark loops, Phys. Rev. D 102 (2020) 075009, [2007.05082].
- (20) R. Capucha, D. Huang, T. Lopes and R. Santos, Impact of electroweak group representation in models for B and g-2 anomalies from dark loops, Phys. Rev. D 106 (2022) 095032, [2207.11556].
- (21) R. Cepedello, P. Escribano and A. Vicente, Neutrino masses, flavor anomalies, and muon g-2 from dark loops, Phys. Rev. D 107 (2023) 035034, [2209.02730].
- (22) H. H. Patel, Package-X: A Mathematica package for the analytic calculation of one-loop integrals, Comput. Phys. Commun. 197 (2015) 276–290, [1503.01469].
- (23) H. H. Patel, Package-X 2.0: A Mathematica package for the analytic calculation of one-loop integrals, Comput. Phys. Commun. 218 (2017) 66–70, [1612.00009].
- (24) I. Bischer, W. Rodejohann and X.-J. Xu, Loop-induced Neutrino Non-Standard Interactions, JHEP 10 (2018) 096, [1807.08102].
- (25) Y. Du, H.-L. Li, J. Tang, S. Vihonen and J.-H. Yu, Non-standard interactions in SMEFT confronted with terrestrial neutrino experiments, JHEP 03 (2021) 019, [2011.14292].
- (26) Y. Du, H.-L. Li, J. Tang, S. Vihonen and J.-H. Yu, Exploring SMEFT induced nonstandard interactions: From COHERENT to neutrino oscillations, Phys. Rev. D 105 (2022) 075022, [2106.15800].
- (27) Neutrino Non-Standard Interactions: A Status Report, vol. 2, 2019. 10.21468/SciPostPhysProc.2.001.
- (28) A. Badertscher et al., A Search for Muon - Electron and Muon - Positron Conversion in Sulfur, Nucl. Phys. A 377 (1982) 406–440.
- (29) SINDRUM II collaboration, C. Dohmen et al., Test of lepton flavor conservation in mu — e conversion on titanium, Phys. Lett. B 317 (1993) 631–636.
- (30) SINDRUM II collaboration, W. Honecker et al., Improved limit on the branching ratio of mu — e conversion on lead, Phys. Rev. Lett. 76 (1996) 200–203.
- (31) SINDRUM II collaboration, W. H. Bertl et al., A Search for muon to electron conversion in muonic gold, Eur. Phys. J. C 47 (2006) 337–346.
- (32) W. Haxton, K. McElvain, T. Menzo, E. Rule and J. Zupan, Effective theory tower for conversion, 2406.13818.
- (33) Mu2e collaboration, L. Bartoszek et al., Mu2e Technical Design Report, 1501.05241.
- (34) Mu2e collaboration, R. H. Bernstein, The Mu2e Experiment, Front. in Phys. 7 (2019) 1, [1901.11099].
- (35) COMET collaboration, R. Abramishvili et al., COMET Phase-I Technical Design Report, PTEP 2020 (2020) 033C01, [1812.09018].
- (36) COMET collaboration, J. C. Angélique et al., COMET - A submission to the 2020 update of the European Strategy for Particle Physics on behalf of the COMET collaboration, 1812.07824.
- (37) J. Liu, X.-P. Wang and K.-P. Xie, Searching for lepton portal dark matter with colliders and gravitational waves, JHEP 06 (2021) 149, [2104.06421].
- (38) Planck collaboration, N. Aghanim et al., Planck 2018 results. VI. Cosmological parameters, Astron. Astrophys. 641 (2020) A6, [1807.06209].
- (39) Y. Bai and J. Berger, Fermion Portal Dark Matter, JHEP 11 (2013) 171, [1308.0612].
- (40) G. Jungman, M. Kamionkowski and K. Griest, Supersymmetric dark matter, Phys. Rept. 267 (1996) 195–373, [hep-ph/9506380].
- (41) J. Hisano, K. Ishiwata and N. Nagata, Gluon contribution to the dark matter direct detection, Phys. Rev. D 82 (2010) 115007, [1007.2601].
- (42) K. A. Mohan, D. Sengupta, T. M. P. Tait, B. Yan and C. P. Yuan, Direct detection and LHC constraints on a -channel simplified model of Majorana dark matter at one loop, JHEP 05 (2019) 115, [1903.05650].
- (43) G. Arcadi, D. Cabo-Almeida, F. Mescia and J. Virto, Dark Matter Direct Detection in -channel mediator models, JCAP 02 (2024) 005, [2309.07896].
- (44) R. J. Hill and M. P. Solon, Standard Model anatomy of WIMP dark matter direct detection I: weak-scale matching, Phys. Rev. D 91 (2015) 043504, [1401.3339].
- (45) J. Kumar and D. Marfatia, Matrix element analyses of dark matter scattering and annihilation, Phys. Rev. D 88 (2013) 014035, [1305.1611].
- (46) XENON collaboration, E. Aprile et al., Dark Matter Search Results from a One Ton-Year Exposure of XENON1T, Phys. Rev. Lett. 121 (2018) 111302, [1805.12562].
- (47) F. Bishara, J. Brod, B. Grinstein and J. Zupan, DirectDM: a tool for dark matter direct detection, 1708.02678.
- (48) N. Anand, A. L. Fitzpatrick and W. C. Haxton, Weakly interacting massive particle-nucleus elastic scattering response, Phys. Rev. C 89 (2014) 065501, [1308.6288].
- (49) S. Kang, S. Scopel, G. Tomar and J.-H. Yoon, On the sensitivity of present direct detection experiments to WIMP–quark and WIMP–gluon effective interactions: A systematic assessment and new model–independent approaches, Astropart. Phys. 114 (2020) 80–91, [1810.00607].
- (50) J.-H. Liang, Y. Liao, X.-D. Ma and H.-L. Wang, Comprehensive constraints on fermionic dark matter-quark tensor interactions in direct detection experiments, 2401.05005.
- (51) XENON collaboration, E. Aprile et al., Effective field theory and inelastic dark matter results from XENON1T, Phys. Rev. D 109 (2024) 112017, [2210.07591].
- (52) XENON collaboration, E. Aprile et al., Constraining the spin-dependent WIMP-nucleon cross sections with XENON1T, Phys. Rev. Lett. 122 (2019) 141301, [1902.03234].
- (53) G. Belanger, F. Boudjema, A. Pukhov and A. Semenov, Dark matter direct detection rate in a generic model with micrOMEGAs 2.2, Comput. Phys. Commun. 180 (2009) 747–767, [0803.2360].
- (54) PandaX collaboration, Z. Huang et al., Constraints on the axial-vector and pseudo-scalar mediated WIMP-nucleus interactions from PandaX-4T experiment, Phys. Lett. B 834 (2022) 137487, [2208.03626].
- (55) LZ collaboration, J. Aalbers et al., First Dark Matter Search Results from the LUX-ZEPLIN (LZ) Experiment, Phys. Rev. Lett. 131 (2023) 041002, [2207.03764].
- (56) B. Fuks, M. Klasen, D. R. Lamprea and M. Rothering, Revisiting slepton pair production at the Large Hadron Collider, JHEP 01 (2014) 168, [1310.2621].
- (57) ATLAS collaboration, G. Aad et al., Search for electroweak production of charginos and sleptons decaying into final states with two leptons and missing transverse momentum in TeV collisions using the ATLAS detector, Eur. Phys. J. C 80 (2020) 123, [1908.08215].
- (58) ATLAS collaboration, G. Aad et al., Searches for electroweak production of supersymmetric particles with compressed mass spectra in 13 TeV collisions with the ATLAS detector, Phys. Rev. D 101 (2020) 052005, [1911.12606].
- (59) ATLAS collaboration, G. Aad et al., Search for direct production of charginos, neutralinos and sleptons in final states with two leptons and missing transverse momentum in collisions at 8 TeV with the ATLAS detector, JHEP 05 (2014) 071, [1403.5294].
- (60) J. Alwall, R. Frederix, S. Frixione, V. Hirschi, F. Maltoni, O. Mattelaer et al., The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations, JHEP 07 (2014) 079, [1405.0301].
- (61) T. Sjöstrand, S. Ask, J. R. Christiansen, R. Corke, N. Desai, P. Ilten et al., An introduction to PYTHIA 8.2, Comput. Phys. Commun. 191 (2015) 159–177, [1410.3012].
- (62) DELPHES 3 collaboration, J. de Favereau, C. Delaere, P. Demin, A. Giammanco, V. Lemaître, A. Mertens et al., DELPHES 3, A modular framework for fast simulation of a generic collider experiment, JHEP 02 (2014) 057, [1307.6346].
- (63) ATLAS collaboration, G. Aad et al., Search for new phenomena in events with an energetic jet and missing transverse momentum in collisions at =13 TeV with the ATLAS detector, Phys. Rev. D 103 (2021) 112006, [2102.10874].
- (64) ATLAS collaboration, M. Aaboud et al., Search for dark matter and other new phenomena in events with an energetic jet and large missing transverse momentum using the ATLAS detector, JHEP 01 (2018) 126, [1711.03301].
- (65) ATLAS collaboration, G. Aad et al., Search for squarks and gluinos in final states with jets and missing transverse momentum using 139 fb-1 of =13 TeV collision data with the ATLAS detector, JHEP 02 (2021) 143, [2010.14293].
- (66) T. Moroi, The Muon anomalous magnetic dipole moment in the minimal supersymmetric standard model, Phys. Rev. D 53 (1996) 6565–6575, [hep-ph/9512396].
- (67) M. Carena, G. F. Giudice and C. E. M. Wagner, Constraints on supersymmetric models from the muon anomalous magnetic moment, Phys. Lett. B 390 (1997) 234–242, [hep-ph/9610233].
- (68) Muon g-2 collaboration, B. Abi et al., Measurement of the Positive Muon Anomalous Magnetic Moment to 0.46 ppm, Phys. Rev. Lett. 126 (2021) 141801, [2104.03281].
- (69) Muon g-2 collaboration, D. P. Aguillard et al., Measurement of the Positive Muon Anomalous Magnetic Moment to 0.20 ppm, Phys. Rev. Lett. 131 (2023) 161802, [2308.06230].
- (70) Muon g-2 collaboration, G. W. Bennett et al., Final Report of the Muon E821 Anomalous Magnetic Moment Measurement at BNL, Phys. Rev. D 73 (2006) 072003, [hep-ex/0602035].
- (71) R. H. Parker, C. Yu, W. Zhong, B. Estey and H. Müller, Measurement of the fine-structure constant as a test of the Standard Model, Science 360 (2018) 191, [1812.04130].
- (72) L. Morel, Z. Yao, P. Cladé and S. Guellati-Khélifa, Determination of the fine-structure constant with an accuracy of 81 parts per trillion, Nature 588 (2020) 61–65.
- (73) XENON collaboration, E. Aprile et al., First Dark Matter Search with Nuclear Recoils from the XENONnT Experiment, Phys. Rev. Lett. 131 (2023) 041003, [2303.14729].