Leptogenesis in the minimal gauged U(1)${}_{L_{\mu}-L_{\tau}}$ model
and the sign of the cosmological baryon asymmetry

The origin of the baryon asymmetry of the Universe is one of the fundamental puzzles in particle physics and cosmology. Leptogenesis [1] provides a simple and elegant explanation to this puzzle. In this scenario, heavy right-handed neutrinos are introduced and play a double role; they explain the small neutrino masses via the seesaw mechanism [2, 3, 4, 5], while their CP-violating decay in the early Universe leads to a lepton asymmetry, which is then partially converted to a baryon asymmetry through the Standard Model sphaleron processes [6]. The resultant amount of baryon asymmetry depends on the structure of the neutrino sector, and a specific model for the neutrino sector could give a distinct prediction for baryon asymmetry.

In this letter, we study leptogenesis in the minimal gauged U(1)${}_{L_{\mu}-L_{\tau}}$ model [7, 8, 9, 10], where a new U(1) gauge symmetry, called the U(1)${}_{L_{\mu}-L_{\tau}}$ gauge symmetry, is introduced to the Standard Model in addition to a scalar field that spontaneously breaks this gauge symmetry. Although this model is a simple extension of the Standard Model, it has rich phenomenological implications because of its strong predictive power for the neutrino sector [11, 12, 13, 14, 15, 16, 17, 18, 19]. In this model, the light neutrino mass matrix has the so-called two-zero minor structure [13, 14, 15, 17, 18, 19], which allows us to determine the masses of light neutrinos, $m_{i}$ ($i=1,2,3$), as well as the three CP phases in the Pontecorvo-Maki-Nakagawa-Sakata (PMNS) mixing matrix [20, 21, 22, 23]—the Dirac phase $\delta$ and the two Majorana phases $\alpha_{2,3}$—as functions of the neutrino mixing angles $\theta_{ij}$ and the squared mass differences $\Delta m_{ij}^{2}$ [17, 18, 19]. Moreover, the mass spectrum and couplings of heavy right-handed neutrinos are also determined as functions of three neutrino Dirac Yukawa couplings.

Because of this restrictive structure of the neutrino sector and the small number of free parameters, we can thoroughly study leptogenesis in this model. This is the aim of the present work. We find that there is a close relationship between the Dirac CP phase and the sign of baryon asymmetry predicted in this model, as pointed out in Ref. [17]. In particular, the sign of baryon asymmetry obtained for $\delta>\pi$ is found to be opposite to that for $\delta<\pi$. As we will show, the Dirac CP phase favored by the current neutrino oscillation experiments, $\delta\sim 220^{\circ}$, naturally leads to the correct sign of baryon asymmetry in most cases.¹¹1The sign of the baryon asymmetry of the Universe in leptogenesis has been discussed in Refs. [24, 25, 26, 27].

To see this feature with a concrete example, we investigate a non-thermal leptogenesis scenario where the U(1)${}_{L_{\mu}-L_{\tau}}$ breaking field is regarded as inflaton and it decays into right-handed neutrinos after inflation ends. These right-handed neutrinos are supposed to be out of thermal equilibrium, and their decay generates a lepton asymmetry non-thermally. It is found that this simple framework offers a successful inflation that is consistent with the CMB observation. We then show that the observed amount of baryon asymmetry can be reproduced and, in particular, its sign is predicted to be positive in a wide range of parameter space.

Let us first briefly review the minimal gauged U(1)${}_{L_{\mu}-L_{\tau}}$ model [28, 29, 17, 18, 30, 19]. To successfully reproduce the neutrino mixing and be consistent with the constraints on the neutrino oscillation parameters, we introduce three heavy right-handed neutrinos and an SU(2)_L singlet field to the Standard Model, denoted by $N_{\alpha}$ ($\alpha=e,\mu,\tau$) and $\sigma$, respectively. The U(1)${}_{L_{\mu}-L_{\tau}}$ charges of the field content in this model are given by

where $e_{R},\mu_{R},\tau_{R}$ are the right-handed charged leptons, and $L_{\alpha}$ ($\alpha=e,\mu,\tau$) are the left-handed lepton doublets. The scalar field $\sigma$ spontaneously breaks the U(1)${}_{L_{\mu}-L_{\tau}}$ gauge symmetry when it develops a vacuum expectation value (VEV). With these fields, the most general renormalizable interaction terms in the neutrino sector are given by

where the dots between $L$ and $H$ indicate the contraction of the SU(2)_L indices, and $h_{\alpha\beta}$ ($\alpha,\beta=e,\mu,\tau$) is a symmetric matrix with $h_{e\mu}=h_{\mu e}$, $h_{e\tau}=h_{\tau e}$, and all other elements being zero. After the Higgs field $H$ and the scalar field $\sigma$ acquire VEVs, $\left\langle H\right\rangle\simeq 174\,\mathrm{GeV}$ and $\left\langle\sigma\right\rangle$, respectively, these Lagrangian terms lead to a diagonal Dirac neutrino mass matrix and a Majorana mass matrix with a special structure of two zero components:

We can take $\lambda_{\alpha}$ ($\alpha=e,\mu,\tau$) and $\left\langle\sigma\right\rangle$ to be real and positive via field redefinitions without loss of generality. The light neutrino mass matrix is then given by the seesaw formula [2, 3, 4, 5], ${\cal M}_{\nu}=-{\cal M}_{D}{\cal M}_{R}^{-1}{\cal M}^{T}_{D}$, and since it is a complex symmetric matrix, it can be diagonalized with a unitary matrix as $U^{T}{\cal M}_{\nu}U=\text{diag}(m_{1},m_{2},m_{3})$, where the unitary matrix $U$ is the PMNS mixing matrix and is parametrized as

where $c_{ij}\equiv\cos\theta_{ij}$ and $s_{ij}\equiv\sin\theta_{ij}$ with the mixing angles $\theta_{ij}\in[0,\pi/2]$, and the Dirac CP phase $\delta\in[0,2\pi]$, and the order $m_{1}<m_{2}$ is chosen without loss of generality. We follow the convention of the Particle Data Group [31], where $0<\Delta m_{21}^{2}\ll|\Delta m_{31}^{2}|$ with $\Delta m_{ij}^{2}=m_{i}^{2}-m_{j}^{2}$.

In the minimal gauged U(1)${}_{L_{\mu}-L_{\tau}}$ model, because of the two-zero matrix structure in Eq. (3), the light neutrino mass matrix is subject to the two-zero minor conditions [32, 33]: $[{\cal M}_{\nu}^{-1}]_{\mu\mu}=[{\cal M}_{\nu}^{-1}]_{\tau\tau}=0$.²²2This two-zero minor structure of ${\cal M}_{\nu}$ is stable against the renormalization group effect, as shown in Ref. [17]. These two complex equations impose four constraints on the parameters. As a result, among the nine degrees of freedom in the light neutrino sector, the lightest neutrino mass $m_{0}$ and the three CP phases $\delta$, $\alpha_{2}$ and $\alpha_{3}$ are uniquely determined as functions of the other five parameters, $\theta_{ij}$ and $\Delta m_{ij}^{2}$, which are observables in neutrino oscillation experiments [17]:

As shown in Ref. [17], the case for inverted hierarchy does not work, and hence we concentrate on the case of the normal hierarchy in the following analysis.

In Fig. 1, we show the Dirac CP phase $\delta$ and the sum of the light neutrino masses $\sum_{i}m_{i}$ as a function of $\theta_{23}$. Fig. 1(a) shows the Dirac CP phase, where the dark (light) red bands show the uncertainty coming from the other parameters, $1\sigma$ ($3\sigma$) errors in the parameters $\theta_{12}$, $\theta_{13}$, $\Delta m_{21}^{2}$, and $\Delta m_{31}^{2}$, adopted from the NuFIT 4.1 global analysis of neutrino oscillation measurements [35, 36]. Note that there are two solutions for Dirac CP phase, $\delta$ and $2\pi-\delta$. Currently, $\delta>\pi$ is favored experimentally; in particular, the latest result given by the T2K Collaboration sets the 3$\sigma$ confidence interval for $\delta$ as [$0.915\pi$–$1.99\pi$] for the normal-ordering case [37]. The prediction of the sum of the light neutrino masses is shown in Fig. 1(b), together with the cosmological constraint for the normal ordering case, $\sum_{i}m_{i}<0.146\,\mathrm{eV}$ (95% C.L.) [34].³³3The analysis in Ref. [34] takes account of the neutrino mass-squared splittings, which results in a more conservative bound than that set by the Planck experiment, $\sum_{i}m_{i}<0.12\,\mathrm{eV}~{}(95\%~{}\text{C.L.})$ [38], obtained on the assumption of degenerate neutrino masses. See also Ref. [39], where a similar conclusion is drawn with a more relaxed bound: $\sum_{i}m_{i}<0.16\,\mathrm{eV}~{}(95\%~{}\text{C.L.})$. As can be seen in this figure, the model is driven into a corner [18], but the region around $\theta_{23}\sim 50^{\circ}$ is still marginally viable.

In the numerical analysis performed in the subsequent sections, as a benchmark point, we adopt the following values of the neutrino oscillation parameters for the normal ordering case:

where we use the central values of $\theta_{12}$, $\theta_{13}$, and $\Delta m_{ij}^{2}$ obtained in the NuFIT 4.1 global analysis of neutrino oscillation measurements [35, 36], while for $\theta_{23}$ we set $\theta_{23}=51^{\circ}$ in order to evade the cosmological constraint on the sum of light neutrino masses. At this benchmark point, the other neutrino parameters are predicted to be $m_{1}=m_{0}\simeq 3.45\times 10^{-2}$ eV, $\delta\simeq 236^{\circ}$, and $(\alpha_{1},\alpha_{2})\simeq(-123^{\circ},84.3^{\circ})$, where between the two-fold degenerate solutions of $\delta$ we have chosen the one with $\delta>\pi$. Another interesting observable is the effective Majorana mass $\langle m_{\beta\beta}\rangle$, which is defined by

The neutrinoless double-beta decay rate is proportional to $\left\langle m_{\beta\beta}\right\rangle^{2}$. For the above benchmark point, we obtain $\langle m_{\beta\beta}\rangle=0.021$ eV. This is well below the current constraint given by the KamLAND-Zen experiment, $\langle m_{\beta\beta}\rangle<0.061$–0.165 eV [40], where the uncertainty of this upper bound is due to the error in the nuclear matrix element of ¹³⁶Xe. Future experiments are expected to be sensitive to $\langle m_{\beta\beta}\rangle=\mathcal{O}(0.01)$ eV [41, 42] and thus potentially able to test this prediction.

Next, we discuss the CP-violating decay of heavy right-handed neutrinos in our model. As seen above, the effective light neutrino mass matrix is subject to the two-zero minor conditions, i.e., the inverse of the matrix, ${\cal M}^{-1}_{\nu}$, contains two zeros among its nine components. These two conditional equations force four free parameters to be dependent on the others, whose values are fixed in the following analysis as in Eq. (6). Still, there are several coupling constants undetermined in the Lagrangian in Eq. (2). It is then convenient to take $\lambda_{\alpha}$ as input parameters; with this choice, all the entries in ${\cal M}_{D}$ and ${\cal M}_{R}$ are uniquely determined in terms of $\lambda_{\alpha}$ and the neutrino oscillation parameters. By diagonalizing the mass matrix of the right-handed neutrinos, the Lagrangian (2) can be rewritten as

where

where $\Omega$ is a unitary matrix and $M_{i}$ ($i=1,2,3$) are the mass eigenvalues of ${\cal M}_{R}$. These quantities are, again, uniquely determined in terms of $\lambda_{\alpha}$, for a given set of the neutrino oscillation parameters.

In leptogenesis, the final baryon asymmetry depends on the asymmetry parameters of the decay of right-handed neutrinos:⁴⁴4 In the following analysis, we assume that the mass of the U(1)${}_{L_{\mu}-L_{\tau}}$ gauge boson, $Z^{\prime}$, is sufficiently large so that the decay modes that contain $Z^{\prime}$ in the final state, such as $\hat{N}_{i}\to\hat{N}_{j}Z^{\prime}$ and $\hat{N}_{i}\to\nu_{j}Z^{\prime}$, are kinematically forbidden.

At the leading order, it is computed as [43, 44, 45]

The significance of the effect of each asymmetry parameter on the resultant lepton asymmetry highly depends on the leptogenesis scenarios. In the thermal leptogenesis, for instance, the decay of the lightest right-handed neutrino tends to give the dominant contribution to the lepton asymmetry, since the asymmetry generated by the heavier right-handed neutrinos are washed out—in this case, the final baryon asymmetry, $n_{B}$, is essentially proportional to $\epsilon_{1}$. In the case discussed in the next section, we will consider the decay of all three right-handed neutrinos.

In the present scenario, the sign of $\epsilon_{i}$, and thus that of the resultant baryon asymmetry as well, for the case of $\delta>\pi$ turns out to be opposite to that for $\delta<\pi$ [17]. As can easily be seen from the analytical expressions for the Majorana CP phases $\alpha_{2,3}$ given in Ref. [17], the transformation $\delta\to 2\pi-\delta$ leads to $U\to U^{*}$, which then results in ${\cal M}_{\nu}\to{\cal M}_{\nu}^{*}$, ${\cal M}_{R}\to{\cal M}_{R}^{*}$, $\Omega\to\Omega^{*}$, $\hat{\lambda}\to\hat{\lambda}^{*}$, and thus $\epsilon_{i}\to-\epsilon_{i}$. In order to obtain the correct sign (positive) for baryon asymmetry in leptogenesis, the generated lepton asymmetry $n_{L}$ must be negative, because the sphaleron processes predict $n_{B}/n_{L}<0$ [46]. This, in particular, indicates that $\epsilon_{1}$ should be negative when the decay of the lightest right-handed neutrino predominantly generates lepton asymmetry.

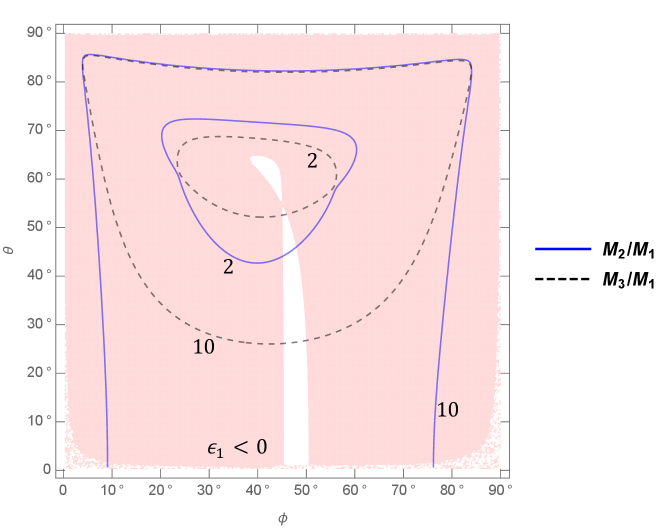
To see the predicted sign of $\epsilon_{1}$ in our scenario, in Fig. 2, we show the sign of the asymmetry parameter for the lightest right-handed neutrino, $\epsilon_{1}$. In visualizing this, we parametrize the coupling constants $\lambda_{\alpha}$ as

with $0\leq\theta,\phi\leq\pi/2$, and show $\text{sgn}(\epsilon_{1})$ in the $\phi$-$\theta$ plane. Here, we take $\delta>\pi$, as favored by the neutrino oscillation data [35, 36]. We see that the desirable sign, $\epsilon_{1}<0$, is obtained in almost all the parameter region, except in the the small crack around $\phi=45^{\circ}$. Notice that, as discussed above, the sign of $\epsilon_{1}$ is flipped under the transformation $\delta\to-\delta+2\pi$. This has interesting implications for our model; the experimentally favored Dirac CP phase, $\delta>\pi$, generically leads to the correct sign of baryon asymmetry, whilst the experimentally disfavored one, $\delta<\pi$, yields the wrong sign.⁵⁵5Note that the sign of $\epsilon_{1}$ obtained here is opposite to that found in Ref. [17]. This difference is attributed to the different choices of the input parameters, especially $\theta_{23}$; in Ref. [17], the value of $\theta_{23}$ was taken from the global fit performed in Ref. [47], which was in the first octant—the preferred value of $\theta_{23}$ has moved to the second octant since then, as found in Refs. [35, 36], and this change results in a sign flip in $\epsilon_{1}$.

We also show in Fig. 2 the ratios of the right-handed neutrino masses, $M_{2}/M_{1}$ and $M_{3}/M_{1}$, in the blue solid and gray dashed contour lines, respectively. It is found that this model predicts a moderately degenerate mass spectrum for right-handed neutrinos, except near the edge of the plane.

As can be seen from Eq. (14), the asymmetry parameters $\epsilon_{i}$ are proportional to $\lambda^{2}$. We have also checked that the magnitude of the asymmetry parameter $\epsilon_{1}$ is predicted to be $|\epsilon_{1}|/\lambda^{2}\lesssim{\cal O}(10^{-4})$ in the typical parameter region in Fig. 2, and thus the observed baryon asymmetry can be reproduced for a sufficiently large $\lambda$. A more detailed analysis for the thermal leptogenesis in the present scenario is beyond the scope of this letter and will be given elsewhere. In the next section, instead, we study the non-thermal leptogenesis for a minimal inflation scenario in our model.

We have examined the non-thermal leptogenesis in the framework of the minimal gauged U(1)${}_{L_{\mu}-L_{\tau}}$ model, where we regard the U(1)${}_{L_{\mu}-L_{\tau}}$-breaking Higgs field as inflaton. We consider the Lagrangian in Eq. (16) for this field and found that this potential can offer a successful inflation that is consistent with the CMB observation. By requiring that the measured value of the power spectrum be reproduced, we determine the value of the inflaton self coupling $\kappa$ as a function of other input parameters, for which we take $\Lambda$ and $\langle\sigma\rangle$ in Eq. (16).

As found in the previous studies [13, 14, 15, 17, 18, 19], the light neutrino mass matrix in this model has the two-zero minor structure, which allows us to determine all of the parameters in the light neutrino sector from the neutrino oscillation data. The resultant neutrino mass spectrum and the Dirac CP phase are found to be compatible with the existing experimental bounds [17, 18, 19]. The sum of the light neutrino masses and the effective Majorana mass $\langle m_{\beta\beta}\rangle$ predicted in ths model will be tested in future experiments. In addition, the structure of the right-handed neutrino mass matrix is determined by fixing three parameters for the Dirac Yukawa couplings, $\lambda_{\alpha}$ ($\alpha=e,\mu,\tau$) [17]. Our model, therefore, has five free parameters, $\Lambda$, $\langle\sigma\rangle$, and $\lambda_{\alpha}$ ($\alpha=e,\mu,\tau$).

We then study the non-thermal leptogenesis in our model, focusing on the case where the inflaton decays only into right-handed neutrinos and these right-handed neutrinos are never thermalized after the Universe is reheated. The successive decay of right-handed neutrinos then generates a lepton asymmetry, which is converted to a baryon asymmetry through sphaleron processes. We find that the observed value of baryon asymmetry can be explained in this scenario. In particular, the correct sign of baryon asymmetry can be obtained in a wide range of the parameter space. We recall that our choice of $\delta>\pi$, which is favored by the present neutrino oscillation data [35, 36, 37], was crucial in obtaining this result; if we instead chose $\delta<\pi$, we would obtain a wrong sign for the baryon asymmetry in most parameter regions.

Our analysis shows that baryon asymmetry tends to be overproduced in the non-thermal leptogenesis scenario. This observation gives a strong motivation for a more detailed study on leptogenesis in this model with the effect of the thermal plasma taken into account—we shall return to this issue in future work [76].

This work is supported in part by JSPS KAKENHI (No. JP19J13812 [KA]) and the Grant-in-Aid for Innovative Areas (No.19H05810 [KH], No.19H05802 [KH], No.18H05542 [NN]), Scientific Research B (No.20H01897 [KH and NN]), and Young Scientists B (No.17K14270 [NN]).