Learning from Temporal Spatial Cubism for Cross-Dataset Skeleton-based Action Recognition
Abstract.
Rapid progress and superior performance have been achieved for skeleton-based action recognition recently. In this paper, we investigate this problem under a cross-dataset setting, which is a new, pragmatic and challenging task in real-world scenario. Following the unsupervised domain adaptation (UDA) paradigm, the action labels are only available on a source dataset, but unavailable on a target dataset in the training stage. Different from the conventional adversarial learning based approaches for UDA, we utilize a self-supervision scheme to reduce the domain shift between two skeleton-based action datasets. Our inspiration is drawn from Cubism, an art genre from the early 20th century, which breaks and reassembles the objects to convey a greater context. By segmenting and permuting temporal segments or human body parts, we design two self-supervised learning classification tasks to explore the temporal and spatial dependency of a skeleton-based action and improve the generalization ability of the model. We conduct experiments on six datasets for skeleton-based action recognition, including three large-scale datasets (NTU RGB+D, PKU-MMD and Kinetics) where new cross-dataset settings and benchmarks are established. Extensive results demonstrate that our method outperforms state-of-the-art approaches. The source codes of our model and all the compared methods are available at https://github.com/shanice-l/st-cubism.
1. Introduction

Skeleton-based action recognition has achieved impressive progress in recent years. As an evidence, under the cross-view setting of NTU RGB+D dataset (Shahroudy et al., 2016), the recognition accuracy has been improved from 70.27% to 96.10% (Shi et al., 2019a) significantly. However, most of the methods apply a fully-supervised learning paradigm where the training and testing data are from the same domain. Meanwhile, there is a lack of exploration under the UDA setting in this field, where the action labels are only available on a source dataset, but unavailable on a target dataset for performance evaluation. This is a more pragmatic and challenging setting because: (1) It is expensive and unfeasible to obtain the annotation of all videos in target dataset from a new environment. (2) Due to the domain shift, there will be a significant performance drop on the target dataset when directly utilizing the model trained on the source dataset, which could not be easily handled by simply pre-processing the skeleton-based data (e.g., rotation). See section 4.4 for more details.
To this end, we propose a self-supervised learning framework for cross-dataset skeleton-based action recognition under the UDA setting in this paper. Different from the mainstream UDA methods which apply an adversarial learning based scheme at the feature level (Ganin et al., 2016; Long et al., 2017, 2018), our proposed self-supervision scheme concentrates on the raw data level, which better preserves their original structure to reduce the domain shift and is easier to implement. In order to design proper self-supervised learning tasks for skeleton-based action, we draw lessons from Cubism111https://en.wikipedia.org/wiki/Cubism, a famous art genre from the early 20th century, which proposes to deconstruct the object and reassemble the pieces into a screwy yet impressive shape to illustrate the object from different views. Specially, we devise a temporal spatial Cubism strategy, which guides the network to be aware of the permutation of the segments in the temporal domain and the body parts in the spatial domain separately. During training phase, we design the objective function based on two criteria: (1) minimizing the original action recognition loss on the source domain to improve the discriminative power and (2) optimizing the self-supervision loss to enhance the generalization ability.
Moreover, there is a scarcity of available datasets for evaluating UDA approaches for skeleton-based action recognition. Although some efforts have been made by a recent work (Tang et al., 2020c) on this direction, it still suffers from an obstruction due to the limited data (See Section IV.A for details). To address this problem, we propose a new experiment setting based on the overlapping action classes of the PKU-MMD (Liu et al., 2020b), NTU RGB+D (Shahroudy et al., 2016) and Kinetics (Carreira and Zisserman, 2017), which are three large-scale and widely used datasets for skeleton-based action analysis. We conduct experiments on a series of UDA methods and the extensive results on these three datasets as well as other three datasets evaluated in (Tang et al., 2020c). Extensive experiments have shown that our method sets new state-of-the-art results in this field.
Our main contributions are summarized as follows:
-
1)
Different from conventional works on skeleton-based action recognition under the fully-supervised paradigm, we explore a new UDA setting in this realm with greater challenge and more pragmatic value.
-
2)
Unlike the popular adversarial learning based approaches for UDA, we propose a self-supervised learning framework, which mines the temporal and spatial dependency for skeleton-based sequence and enhance the generalization ability of the model.
-
3)
In order to facilitate the performance evaluation on this problem, we present a new experiment setting on three large-scale datasets. To our best knowledge, they are currently the largest datasets for cross-dataset skeleton-based action recognition.
-
4)
We conduct experiments on six datasets under the setting proposed in this paper and (Tang et al., 2020c). Both quantitative and qualitative results demonstrate the superiority of our approach compared with the state of the art.
The remainder of this paper is organized as follows: Section II briefly reviews some related works. Section III introduces the proposed approach for cross-dataset skeleton-based action recognition in detail. Section IV reports experimental presents and analysis, and Section V concludes the paper.
2. Related Work
In this section, we briefly review four related topics: 1) skeleton-based action recognition, 2) unsupervised domain adaptation, 3) video-based domain adaptation, and 4) self-supervised learning.
2.1. Skeleton-based Action Recognition
Skeleton-based action recognition has attracted growing attention in the realm of computer vision and a variety of methods have been proposed over the past decades. For a detailed survey we refer the reader to (Han et al., 2017; Liu et al., 2020a; Wang et al., 2018), while here we provide a brief literature review. The early works on skeleton-based action recognition are based on hand-crafted features (Vemulapalli et al., 2014; Weng et al., 2017; Koniusz et al., 2016; Wang et al., 2016b), while recent approaches are devised by designing deep neural networks (DNNs) like convolutional neural networks (CNNs) (Liu et al., 2017; Tang et al., 2018; Li et al., 2018) and recurrent neural networks (RNNs) (Song et al., 2017; Zhang et al., 2017, 2018). In order to better capture the relationship of different joints in the spatial domain or dependency of different frames in the temporal domain, a number of works utilized the attention mechanisms (Song et al., 2017; Zhang et al., 2018; Si et al., 2019) and graph neural networks (GNNs) (Yan et al., 2018; Shi et al., 2019a, b; Li et al., 2019; Si et al., 2019) more recently. Besides, there are various works using both skeleton joints and RGB videos as inputs for action recognition (Choutas et al., 2018; Zolfaghari et al., 2017; Verma et al., 2020). For example, Verma et al. (Verma et al., 2020) design two deep neural networks (DNNs) models for the multi-modal inputs respectively, and use a weight product model (WPM) to fuse the softmax scores obtained from the two DNNs. Different from these works which deal with the input videos from the same dataset during training and testing phases, we study a more practical and challenging UDA setting to deal with the samples across different datasets.
2.2. Unsupervised Domain Adaptation
Reducing the domain shift between the source and target datasets is the core of UDA. In the past few years, a series of models have been built upon deep neural networks for learning domain-independent representations, which show more promising results than early methods based on hand-crafted features (Huang et al., 2006; Pan et al., 2011; Gong et al., 2013). Among these, one representative strategy is to design adaptation layers for aligning different distributions (Long et al., 2017), and another popular scheme is to include a domain discriminator sub-network for adversarial learning (Ganin et al., 2016; Long et al., 2017; Saito et al., 2018; Long et al., 2018). More recently, there are several attempts on leveraging self-supervised learning for UDA (Carlucci et al., 2019; Sun et al., 2019). Under a multi-task learning paradigm, they optimized the model with the supervision from the source domain, and the auxiliary self-supervision from both source and target domains. Motivated by the success of these methods in the image domain, we move a further step in the field of skeleton-based action recognition. Note that our exploration is non-trivial since the intrinsic structure of the skeleton-based video is quite different from image, and further generalization and adaptation are required.
2.3. Video-based Domain Adaptation
Compared with image-based domain adaptation, video-based domain adaptation is a seldom-explored field. In the literature, a few works have been proposed for RGB videos, by foreground-weighted histogram decomposition (Sultani and Saleemi, 2014), or performing adversarial learning on the video features (Jamal et al., 2018). More recently, Chen et al. (Chen et al., 2019a) devised TA3N by introducing a temporal relation module and domain attention mechanism. For skeleton-based video, Tas et al. (Tas and Koniusz, 2018) and Lin et al. (Lin et al., 2020) study the supervised domain adaptation and transfer learning settings, where the action labels of the target dataset are required at the training or fine-tuning stages respectively. The most relevant work to ours is GINs (Tang et al., 2020c), which also studied the problem of cross-dataset skeleton-based action recognition under the UDA setting. In comparison, we proposed a setting with three datasets with larger-scale, and devised a self-supervised learning framework rather the adversarial-based method used in (Tang et al., 2020c). Experimental results also show the advantage of our method.
2.4. Self-supervised Learning
The paradigm of self-supervised learning is to design auxiliary task(s) with the supervision of the data itself, for example, predicting spatial context (Doersch et al., 2015) or image rotation (Gidaris et al., 2018), solving jigsaw puzzles (Noroozi and Favaro, 2016) and many others (Zhang et al., 2016; Larsson et al., 2017; Pathak et al., 2016; Doersch and Zisserman, 2017; He et al., 2020; Chen et al., 2020). There have been a number of self-supervised learning methods for RGB videos, according to the information of ordering (Misra et al., 2016; Fernando et al., 2017; Lee et al., 2017), geometry (Gan et al., 2018), correspondence (Wang et al., 2019a; Dwibedi et al., 2019; Lai et al., 2020), motion and appearance statistics (Wang et al., 2019b) or spatio-temporal cubic puzzles (Kim et al., 2019). Compared with these works, besides temporal ordering, we further explore the relationship of different human body parts for skeleton-based videos by learning from spatial Cubism, and leverage the advantage of self-supervised learning to seek a better alignment between the source and target domains.

3. Approach
3.1. Problem Formulation
We use to denote a source domain, which contains skeleton-based action videos and their action labels . Here denotes the index of the -th video, means the number of videos, and the subscript of denotes the source domain. Similarly, the target domain is defined as , where the action labels are unavailable during the network optimization but can used for the performance evaluation. Since the videos in the source and target domains are from different datasets, they correspond to two different joint distributions as and . The training should be performed on the source domain with the action labels, and a split of target domain data where the action labels are unavailable. The testing process is based on the other split of the target domain data which is invisible during the training phase. See section 4 for more details. There is a more challenging cross-dataset setting which assumes that data from target domain are totally unavailable. The experimental results under this setting are introduced in the section 4.6.
3.2. Pipeline Overview
The motivation of this work is to leverage self-supervised learning and Cubism transformation to reduce the domain shift between the skeleton-based action videos from the source and target datasets. The concept “Cubism” here is originally an art genre from the early 20th century, which breaks and reassembles the objects to convey a greater context. Inspired by this idea and the progress in self-supervised learning (Fernando et al., 2017; Lee et al., 2017; Misra et al., 2016), we design two auxiliary pretext tasks, named as temporal Cubism (section 3.3) and spatial Cubism (section 3.4), for skeleton-based action recognition under a new cross-dataset scenario. Accordingly, we devise two networks as the Tem-Cub Network and Spa-Cub Network, where “Tem-Cub” and “Spa-Cub” are abbreviations of “temporal Cubism” and “spatial Cubism”. During the training phase, each network is optimized based on one of the self-supervised tasks and the main prediction task jointly. At the inference period, the final result is obtained by fusing the prediction scores of two networks. We elaborate on each stage of our pipeline in detail as follows.
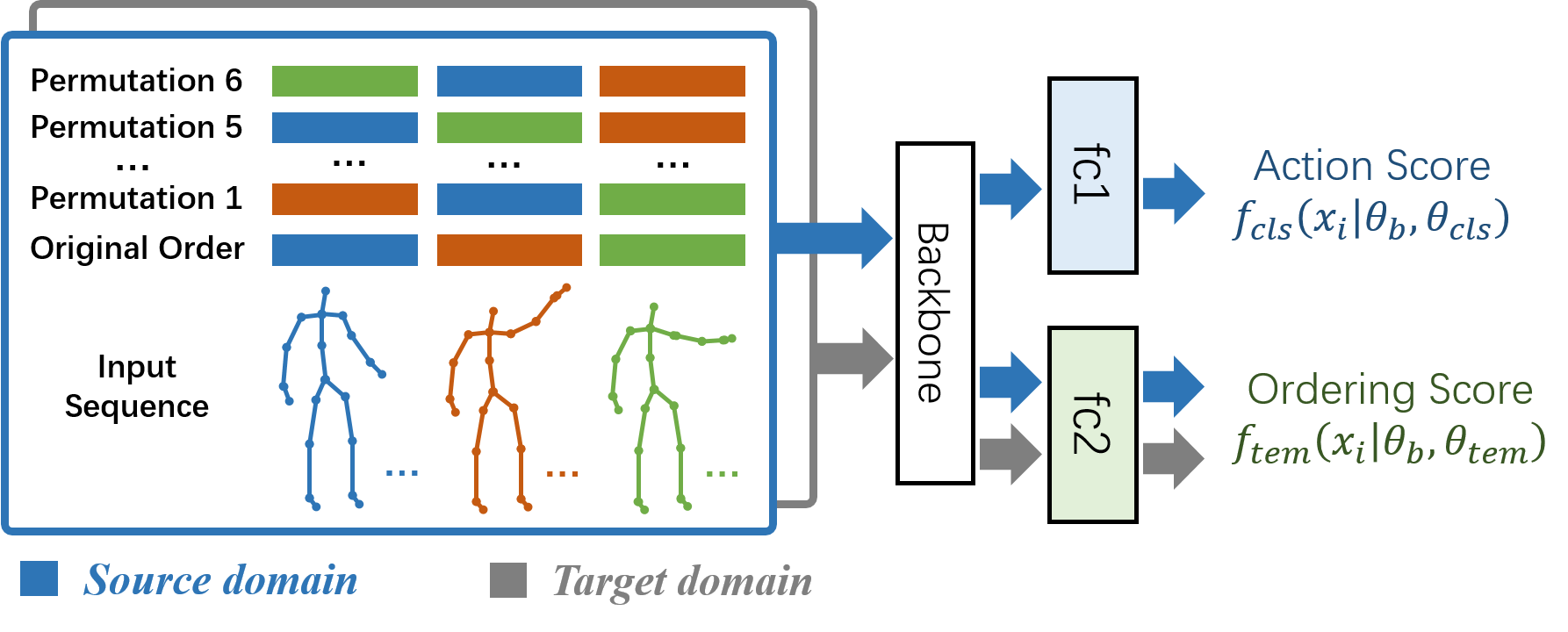
3.3. Learning from Temporal Cubism
Fig. 3 illustrates our proposed strategy of learning from temporal Cubism. The term temporal Cubism here means we shuffle a video in temporal dimension and reorganize them in a new frame order. Mathematically, we organize each skeleton-based action video as a representation with the size of , where denotes the number of the frames, is the number of the joints, and D represents the dimension of joint coordinates. Given a video sample , we first divide it into segments uniformly in the temporal domain as , where we choose in this paper empirically. Then a new video with corresponding permutation label in temporal domain is acquired by permuting the segments. This transformation could be presented by a partitioned permutation matrix as:
| (1) |
There is only one identity matrix on each row and on each column, and the remaining elements are zero matrices. For example, if the permutation is to exchange the order of the first and the third segments, the transformation can be written as below:
| (2) |
In this way, we build the permuted videos and form the augmented source and target datasets which are presented as follows:
| (3) | |||
Here and denote the overall number of videos in the augmented source datasets and the augmented target datasets. For the -th video, and represent the action label and permutation label of temporal Cubism respectively. Based on the augmented datasets, we design an auxiliary classification task in the temporal domain, which guides the network to learn to recognize the temporal permutation. During training, the ordered and permuted video samples are packed into batches with a certain ratio which is dependent on a hyper-parameter indicating the percentage of the ordered samples in a batch. This hyper-parameter will be studied in section 4.4. Moreover, the permutation way is chosen with equal probability so that transformed videos with different ordering labels are of an identical proportion. The mixed batches are fed into a CNN-based backbone (we detail it in section 4.3) followed by two parallel full-connected classifiers. takes the features of the ordered and disordered samples from the source domain and predicts the action classes while targets to recognize the ordering label for the samples from both source and target domains. Two kinds of losses are computed and combined after the classifiers to optimize the network. Comprising two parts of losses, the total loss could be formalized as:
| (4) | ||||
Here we adopt the cross-entropy loss for and . and are the softmax scores of action classes and temporal permutation classes. and denote the trainable parameters of the backbone, action recognition fc layer and temporal permutation recognition fc layer respectively. Here is the hyper-parameters to balance the effects of the losses of the main task and self-supervision learning, which will be studied in section 4.4 as well.

3.4. Learning from Spatial Cubism
As shown in Fig. 4, we design a new self-supervised classification task based on the spatial Cubism among the different body parts. Specifically, for a skeleton-based action video defined in the last subsection, we organize the body parts according to the following ordered list: . The five blocks are corresponding to the data of trunk, left arm, right arm, left leg and right leg respectively. Similar to the temporal Cubism, we can obtain a new sample by performing spatial transformation with another permutation matrix as:
| (5) |
Here we design two concrete instances for as and to swap the coordinates of the joints of the arms and legs respectively:
| (6) |
Through these transformations, the skeleton-based video would convey the screwy actions which refer to the spatial Cubism. By learning to discover these, the network would have a better generalization ability on the spatial domain. Similar to that of the temporal Cubism, we construct the augmented source dataset and target dataset as follows:
| (7) | |||
We introduce a hyper-parameter to indicate the percentage of the ordered samples in a batch during the training phase. The total loss , in this case, could be formalized as:
| (8) | ||||
The variables in Equation (7) and (8) have the similar definitions with those in Equation (3) and (3.3). We present a mathematical algorithm of our method in Algorithm 1.
3.5. Two-Stream Fusion
In order to further boost performance, we explore several approaches to couple the temporal and spatial Cubism transforms. One is to apply the two kinds of transforms simultaneously and therefore divide the videos into finer-grained atoms (see section 4.4 for details). However, this results in a more complex task, which might bring more difficulty for optimizing the network and more cost in data pre-processing.
Though feature-level fusion is a common two-stream fusion strategy, we do not apply it in this paper. This is because spatial and temporal streams implement different auxiliary tasks, and feature-level fusion will make it much more difficult to recognize the ordering label. Actually, as explored by several previous works (Simonyan and Zisserman, 2014; Wang et al., 2016a), it is more effective and efficient to separately deal with the temporal and spatial information and combine them after the network. Hence, we explore several approaches to fuse softmax scores from the temporal and spatial streams during the inference stage, e.g., Weighted Arithmetic Mean (WAM), Weighted Root Squared Mean (WRSM), Weighted Geometric Mean (WGM) and Max Pooling (MP). The experimental results and more details are shown in Table 11 in later section.
4. Experiments
4.1. Datasets and Experiment Settings
To our best knowledge, there are very few benchmarks for cross-dataset skeleton-based action recognition. Although the recent work (Tang et al., 2020c) has proposed two benchmarks for this problem, they mainly have two drawbacks. The first is the scales of these datasets are relatively small, and the second is that it adopts a “test-time training” strategy (Sun et al., 2020), which utilizes the test data (without using their action labels) during training. This might be not practical in some real-world scenarios.
| Training | Testing | |||||
|---|---|---|---|---|---|---|
| Source | # Clips | Target | # Clips | Target | # Clips | |
| NTUSBU (Tang et al., 2020c) | N8 | 7513 | SBU | 282 | SBU | 282 |
| ORGBDMSRA3D (Tang et al., 2020c) | ORGBD | 240 | MSRA3D | 100 | MSRA3D | 100 |
| PN-CV (Ours) | P | 21544 | N51-CV-train | 31989 | N51-CV-test | 16092 |
| PN-CS (Ours) | P | 21544 | N51-CS-train | 34068 | N51-CS-test | 14013 |
| NP-CV (Ours) | N51 | 48081 | P-CV-train | 14356 | P-CV-test | 7188 |
| NP-CS (Ours) | N51 | 48081 | P-CS-train | 18840 | P-CS-test | 2704 |
| NK (Ours) | N12 | 11256 | K-train | 8912 | K-test | 787 |
| KN (Ours) | K | 9699 | N12-CV-train | 7476 | N12-CV-test | 3780 |
To address these issues, we define two groups of experiment settings crossing three large-scale datasets in this paper: NTU RGB+D (Shahroudy et al., 2016), PKU-MMD (Liu et al., 2020b), and Kinetics (Carreira and Zisserman, 2017). We present a comparison of the proposed settings with the previous work (Tang et al., 2020c) in Table 1. We detail the corresponding datasets and the experimental settings as follows.
NTU RGB+D: The NTU RGB+D dataset is a large-scale dataset for evaluating skeleton-based action recognition. The dataset contains 56,880 skeleton-based videos of 60 action categories. There are two evaluation protocols as cross-subject (CS) and cross-view (CV). Under CS setting, there are videos of 40 subjects used for training while the videos of the rest 20 subjects are used for the test. Under CV setting, The videos from view 2 and 3 are used for training, while the videos from view 1 are used for the test.
PKU-MMD: There are 1,076 long videos in the PKU-MMD dataset, which is originally presented for skeleton-based action detection. In order to construct a dataset for unsupervised domain adaptation on action recognition, we trim each long video according to their temporal annotations and obtain 21,544 video clips of 51 actions. Similar to the NTU RGB+D dataset, the cross-subject and cross-view settings are recommended for PKU-MMD dataset. Under CS setting, there are 18,840 training videos and 2,704 test videos. Under CV setting, there are 14,356 training videos and 7,188 test videos.
Kinetics: Kinetics is a large-scale dataset for action recognition containing about 300,000 video clips collected from Youtube. Each clip in Kinetics contains around 300 frames. These video clips cover 400 action categories and under each category, there are more than 400 samples for training and about 100 for the test. The original Kinetics dataset releases only raw RGB sequences. Hence we adopt the estimated poses provided by (Yan et al., 2018) extracted by OpenPose (Cao et al., 2021) to study the skeleton-based UDA task.
PN. We perform unsupervised domain adaptation between PKU-MMD and NTU RGB+D. 51 action categories are extracted from NTU RGB+D to pair with the actions in PKU-MMD. Both CV and CS settings are adopted for evaluation. For clarification, we use N51 to denote the 51-action subset of NTU RGB+D and P to denote PKU-MMD. The infixes CV, CS and suffixes train, test are used to indicate the subset, e.g., N51-CS-train implies the training set of NTU RGB+D under cross-subject setting. Due to the limited space, we show the paired action classes of PN in our project page.
NK. Experiments are carried out between NTU RGB+D and Kinetics as well. We select 12 paired actions from NTU RGB+D and Kinetics for domain adaptation. As the estimated pose data on Kinetics are 2-dimensional, we extract the coordinates of x and y axes from NTU RGB+D to get a similar 2D skeleton. The Kinetics subset is partitioned into the training and test subsets in accordance with the raw division while NTU RGB+D is used under only CV setting. Similarly, the subset of NTU RGB+D is marked as N12 and Kinetics is marked as K. The suffixes train and test are used to indicate the subset as well. Same as before, the paired action classes of N (Shahroudy et al., 2016)K (Carreira and Zisserman, 2017) are presented in the project page.
In order to make a better evaluation of our method, we also conduct experiments on the SBU Kinect Interaction dataset (SBU) (Yun et al., 2012), Online RGBD Action dataset (ORGBD) (Yu et al., 2014) and MSRDaily Activity3D dataset (MSRDA3D) (Wang et al., 2012), following the same settings proposed in the previous work (Tang et al., 2020c). The experimental results and analysis are described in detail as below.
4.2. Compared Methods
In the following section, we first conduct experiments and acquire the results on Source Only and Target Only. Source Only indicates a baseline method which trains a model in the source domain, and directly evaluates the testing data on the target domain without supervision. Target Only denotes to utilize the ground-truth action labels in the target domain for training, which provides an upper bound for this problem. Besides, because there are very few models designed for skeleton-based action recognition under the UDA setting, we compare our model with some image-based UDA models (i.e., MMD, DANN, JAN, CDAN, BSP, MCC) and a RGB video-based model (i.e., TA3N). We replace those models’ backbone with HCN and apply the same experimental setting with our model for fair comparison. Specifically, for TA3N, besides replacing the feature extractor with HCN, we add a fully-connected layer between HCN and the spatial-temporal adversarial module in TA3N to make them compatible. Moreover, we also compare our method with GINs, which is the most related work on cross-dataset skeleton-based action recognition.
In our paper, there are mainly three kinds of information to be utilized for cross-dataset transfer. They are temporal information (T), spatial information (S) and their combination (TS), which are used for our Tem-Cub Network, Spa-Cub Network and TS-Cub Network respectively. For the compared methods, most of them perform transfer based on the temporal-spatial feature extracted by HCN backbone (TS), except the GINs (Tang et al., 2020c) focused on the relation of different joints at the spatial domain (S).
| Method | PN-CV | PN-CS |
|---|---|---|
| Source Only (Li et al., 2018) | 51.9 | 47.9 |
| HCN (Li et al., 2018) | 50.9 | 45.8 |
| HCN + PReLU | 51.9 | 47.9 |
| HCN + Rot. | 53.4 | 50.3 |
| HCN + Rot. + PReLU | 54.9 | 50.5 |
4.3. Implementation Details
We conduct experiments on a system with the Intel(R) Xeon(R) CPU E5-2698 v4 @ 2.00Ghz. We implement our method with the PyTorch toolbox and train the model on Nvidia GTX 1080 Ti GPU. The training epoch is set to 400 for both Tem-Cub and Spa-Cub. We adopt the HCN (Li et al., 2018) as the backbone because of its effectiveness and efficiency. In order to ameliorate the performance, we made two modifications. The PReLU (He et al., 2015) is used as the non-linear activation function instead of the commonly used ReLU and a rotation pre-processing is applied before the networks to eliminate the difficulty for bridging the domain gap induced by the videos captured from different views. specifically, we rotate the skeleton around the z axis to make the connection of the joints right shoulder and left shoulder parallel with the x axis and the connection of spine base and spine parallel with y axis.
4.4. Experimental results
| Method | PN-CV | PN-CS | NP-CV | NP-CS | year |
|---|---|---|---|---|---|
| Target Only | 91.3 | 84.6 | 95.7 | 93.1 | - |
| Source Only | 54.9 | 50.5 | 59.6 | 57.6 | - |
| MMD (Long et al., 2015) | 55.4 | 51.7 | 61.3 | 59.4 | 2015 |
| DANN (Ganin et al., 2016) | 58.1 | 52.4 | 61.9 | 58.8 | 2017 |
| JAN (Long et al., 2017) | 51.9 | 47.1 | 65.3 | 63.1 | 2017 |
| CDAN (Long et al., 2018) | 54.9 | 51.1 | 63.8 | 61.3 | 2018 |
| BSP (Chen et al., 2019b) | 55.7 | 49.3 | 64.0 | 63.0 | 2019 |
| TA3N (Chen et al., 2019a) | 55.9 | 51.2 | 66.2 | 65.9 | 2019 |
| GINs (Tang et al., 2020c) | 44.9 | 40.0 | 54.7 | 52.4 | 2020 |
| MCC (Jin et al., 2020) | 56.1 | 52.2 | 64.2 | 61.7 | 2020 |
| Tem-Cub (Ours) | 58.3 | 52.5 | 65.2 | 62.8 | |
| Spa-Cub (Ours) | 56.5 | 51.0 | 61.2 | 59.3 | |
| TS-Cub (Ours) | 59.2 | 53.6 | 65.5 | 63.3 |
Analysis of the Baseline Model: We adopt the HCN(Li et al., 2018) as the backbone and make two modifications that are introduced in the last subsection. As shown in Table 2, both these two modifications manage to ameliorate the performance of HCN. Combining PReLU and rotation pre-processing could further improve the performance. Hence we will refer baseline to the improved HCN in the sequel. Though pre-processing can reduce the domain gap to some extent, there are still some phenomena that could not be easily handled. For example, bridging the gap between 2D and 3D skeleton-based videos. Moreover, conventional pre-processing methods, e.g., rotation, scale normalization, etc, are executed based on several specific joints. But in skeleton-based videos, these joints might be inaccurate or missing (padding 0). Actually, these are common phenomena in skeleton-based datasets. In this case, performing pre-processing on these data might even cause negative effects. Therefore, our proposed method owns greater generalization ability than pre-processing.

Evaluation on PKU NTU: We show our results compared to the state-of-the-arts under the PN and NP settings in Table 3. We first observe the large difference between Target Only and Source only caused by the domain shift (around 35% accuracy drops), which indicates the greater challenge of the UDA setting compared with conventional fully supervised-learning setting. Moreover, according to the results, our proposed method acquires consistent improvement of the performance of skeleton-based unsupervised domain adaptation. To be specific, it is shown that our TS-Cub method exceeds the baseline by 4.3% and 3.1% under CV and CS settings respectively and achieves remarkable improvement based on the state-of-the-arts. The performance is 3.8%, 1.1%, 7.3%, 4.3%, 3.5%, 3.1% higher than that of MMD, DANN, JAN, CDAN, BSP and MCC in order under PN-CV setting. Meanwhile, our method constantly outperforms the state-of-the-art video domain adaptation model TA3N by 4.4%, 2.7%, 1.5%, 0.7% under four PN settings. Figure 5 shows two failure cases on compared methods but succeeded on TS-Cub. For the two skeleton-based videos under the NP-CV setting, the ground-truth labels are eat meal/snake and take a selfie, while the compared methods give wrong predictions, our TS-Cub approach obtains the right action labels, which demonstrate its effectiveness for cross-dataset action recognition. Besides, it is observed that our Tem-Cub method performs consistently better than Spa-Cub. We explain this fact by that it is a little difficult to discriminate between the ordered and permuted instances keeping strong spatial symmetry, which affects the performance of the Spa-Cub method. As conclusion, our proposed Cubism methods have the capability to improve the domain adaptation performance. Tem-Cub appears to be more effective than Spa-Cub and combining the information from both two streams will further enhance recognition accuracy.
| Method | NK | KN | Year |
| Target Only | 40.8 | 89.1 | - |
| Source Only | 14.4 | 22.5 | - |
| MMD (Long et al., 2015) | 14.9 | 22.8 | 2015 |
| DANN (Ganin et al., 2016) | 16.5 | 22.9 | 2017 |
| JAN (Long et al., 2017) | 15.0 | 24.4 | 2017 |
| CDAN (Long et al., 2018) | 14.9 | 24.0 | 2018 |
| BSP(Chen et al., 2019b) | 14.6 | 16.6 | 2019 |
| TA3N (Chen et al., 2019a) | 15.6 | 25.6 | 2019 |
| GINs (Tang et al., 2020c) | 16.4 | 23.4 | 2020 |
| MCC (Jin et al., 2020) | 15.2 | 26.2 | 2020 |
| Tem-Cub (Ours) | 16.4 | 29.3 | 2021 |
| Spa-Cub (Ours) | 14.6 | 22.9 | 2021 |
| TS-Cub (Ours) | 16.8 | 29.6 | 2021 |

| Method | NTU SBU | ORGBD MSRDA3D | Year |
| Target Only* | - | - | - |
| Source Only | 35.8 | 48.3 | - |
| MMD (Long et al., 2015) | 31.4 | 25.5 | 2015 |
| DANN (Ganin et al., 2016) | 46.3 | 39.3 | 2017 |
| JAN (Long et al., 2017) | 47.6 | 49.2 | 2017 |
| CDAN (Long et al., 2018) | 39.9 | 48.7 | 2018 |
| GAKT (Ding et al., 2018) | 31.8 | 48.4 | 2018 |
| BSP (Chen et al., 2019b) | 32.4 | 41.3 | 2019 |
| GINs (Tang et al., 2020c) | 50.7 | 51.5 | 2020 |
| Tem-Cub (Ours) | 50.7 | 52.5 | 2021 |
| Spa-Cub (Ours) | 46.8 | 53.1 | 2021 |
| TS-Cub (Ours) | 51.1 | 53.0 | 2021 |
Evaluation on NTU Kinetics: We conducted further experiments on NTU RGB+D and Kinetics datasets to verify the effectiveness of our methods and present the results in Table 3. Compared to PN, there is an even larger performance gap between Target Only and Source only in NK. As for our proposed methods, TS-Cub exceeds the baseline by 2.4% and 7.1% under NK and KN settings respectively and exceeds the best one from the state-of-the-arts. Besides, it is noticed that the adaptation performance from Kinetics to NTU RGB+D is significantly higher than that from NTU RGB+D back to Kinetics. This should be attributed to the features of the two underlying datasets. Kinetics is captured from a wider domain, the Youtube videos in the wild, while NTU RGB+D is collected under the artificially predefined settings. Accordingly, Kinetics conveys more information that might facilitate the adaptation and NTU RGB+D carries less noise which brings less difficulty for recognition. For the aforementioned reasons, an adaptation from a more complex domain could result in relatively higher performance. This phenomenon holds for the adaption between PKU-MMD and NTU RGB+D as well.
Evaluation on NTU SBU: We then conducted experiments between NTU and SBU datasets, following the setting in (Tang et al., 2020c). We present the results in Table 5, where the performances of other methods are reported in (Tang et al., 2020c). As a result, we can find that most of the methods can boost the accuracy compared with Source Only, and our TS-Cub method achieves the highest accuracy of 51.1%. We further show the confusion matrices of different methods in the top row of Fig. 6. Our ST-Cubism shows strong performance on the actions of kicking and hugging.
Evaluation on ORGBD MSRDA3D: Table 5 shows the experimental results on the ORGBD MSRDA3D setting (Tang et al., 2020c). Compared with other aforementioned datasets, ORGBD MSRDA3D dataset is rather small and only contains 5 categories. Referring to Table 5, we can find that Source Only exceeds almost all the compared methods. This may attribute to the fact that adversarial learning methods require numerous training data. Meanwhile, the proposed methods achieve the results of 52.5% (Tem-Cub), 53.1% (Spa-Cub) and 53.0% (TS-Cub) respectively, surpassing all the other compared methods. This shows the robustness of our methods to the fewer training data in comparison with the mainstream adversarial methods.
We display the compared confusion matrices in the bottom row of Fig. 6. Our method could recognize the action of reading book well, but would be sometimes confused by the action of eating and using laptop.
| Method | MMD (Long et al., 2015) | DANN (Ganin et al., 2016) | JAN (Long et al., 2017) | CDAN (Long et al., 2018) | BSP (Chen et al., 2019b) | GINs (Tang et al., 2020c) | Tem-Cub | Spa-Cub | TS-Cub |
| Time | 0.106 | 0.153 | 0.083 | 0.093 | 0.305 | 0.241 | 0.112 | 0.109 | 0.211 |
Evaluation of the Computational Cost: We run experiments under the PN-CV setting and report the averaged computational cost based on a single video in Table 6. As it shows, our Tem-Cub network and Spa-Cub network cost 0.112 ms and 0.109 ms to predict the action label of each single video, achieving comparable speed with the fastest method JAN (Long et al., 2017). Though our final model TS-Cub requires more time than some of the compared methods, it can still satisfy the real-time application requirement.

4.5. Analysis of the TS-Cub
Analysis of the Hyper-parameters: We studied the impact of the hyper-parameters in our method, the weight parameter in the multi-task loss and the ratio of the ordered videos in a batch. These experiments are conducted under the PN-CV setting. Fig. 7 (a) and (b) studies the impact of and , the hyper-parameters in the temporal Cubism approach. In Fig. 7 (a) is shown the change of the recognition accuracy when is fixed to 0.8 while varies from 0 to 10. It is noticed that the best performance is acquired when . The value of that is less than 0.1 degrades the effect of the loss of the self-supervised task and furthermore the effect of the self-supervision based method. But the performance is still ameliorated based on the baseline thanks to the data augmentation. On the other hand, a greater value of will possibly make the auxiliary task overwhelm the main task, which will also result in the decrement of the performance. As evidence, the performance plummets sharply when . Moreover, we studied the impact of and show in Fig. 7 (b) the variation of the obtained accuracy in the case that is fixed to 0.1 while varies from 0.2 to 1. It is found that various scales of result in consistent boosting of the adaptation performance base on the baseline while the best performance is achieved with . Meanwhile, we notice that the performance is slightly poorer for the relatively greater value of . This may be explained by that greater degrades the role of the auxiliary task and the method will fall back to the baseline when . Likewise, we verified the impact of the hyper-parameters in the spatial Cubism approach, and , and received the similar curves shown in Fig. 7 (c) and (d). The most effective parameters for spatial Cubism approach appear to be and .

Analysis of the segment number: In section 3.3, a video is divided into () segments uniformly in the temporal domain to perform temporal Cubism. Here we evaluate other numbers for ( and ) under PN-CV setting and present the results in Table 7. We can observe that outperforms other segment numbers. This can be attributed to dividing a video into three segments making the amount of permutation categories properly, which is vital to make the auxiliary task neither too simple nor too complicated.
| Segment number | 2 | 3 | 4 |
|---|---|---|---|
| Accuracy | 56.9 | 58.3 | 56.5 |
t-SNE Visualization: We visualize the distribution of both domains extracted from some experiments under the PN-CV setting using t-SNE(Maaten and Hinton, 2008) in Fig. 8. It is shown that the samples from different domains are not that well-aligned through the baseline model though the source samples could be finely grouped into clusters, while the distributions of two domains get much closer when applied temporal or spatial Cubism methods. These plots intuitively demonstrate the effectiveness of our methods.
Analysis of Different Actions: Fig. 9 illustrates the performance of TS-Cub on the individual action categories compared to the baseline. Our method achieves consistent improvement on most of the action categories and outperforms the best on the actions cross hand in front, give something to other person, shake hand, jump up and touch chest. On these actions, the baseline achieves relatively poorer performance at first and our method manages to enhance the adaptation performance. On the other side, our TS-Cub fails to reach the baseline on the actions eat meal/snack, push other person, take off hat/cap and type on a keyboard. Actually, the videos from eat meal/snack have an unduly longer duration and the videos from push other person have a shorter duration than the videos from other categories, which may bring extra difficulty for the temporal stream. Action take off hat/cap and type on a keyboard hold a little more tiny spatial features that may confuse the spatial stream. For the baseline and our proposed TS-Cub approach, we find that they both fail to recognize the action put something inside pocket. This is because in the NTU dataset, this action involves two people (one person puts something inside the pocket of another person). However, in the PKU dataset this is a single person action (one person puts something inside the pocket of himself/herself). This failure case suggests the limitation of using skeleton-based data as input for recognizing action involving semantic object (e.g., interaction with the pocket). This issue would be tackled by further leveraging the RGB modality. We will explore this interesting direction in the future.

| Method | single action | interacted action | overall |
|---|---|---|---|
| Baseline (source only) | 59.1 | 66.1 | 59.6 |
| Tem-Cub (Ours) | 64.7 | 72.0 | 65.2 |
| Spa-Cub (Ours) | 61.2 | 71.8 | 61.2 |
| TS-Cub (Ours) | 64.8 | 73.0 | 65.5 |
Analysis of the Number of People: In NTU and PKU datasets, there are numbers of interacted actions that involves multiple people in each video (e.g., shaking hands, hugging, etc). For these actions, we follow (Li et al., 2018) to apply element-wise maximum operation to fuse the features of multiple people. Furthermore, we compare the experimental results under the NP-CV setting of the single action and the interacted action in Table 8. We observe that our method obtains larger improvements over the interacted action (66.1% 73.0%) than those over the single action (59.1% 64.8%). These experimental results demonstrate the generalized capability of our TS-Cub model, which can effectively deal with the multiple people cases with the element-wise maximum operation.
| Method | = 25 | = 22 | = 18 | = 12 |
|---|---|---|---|---|
| Tem-Cub (Ours) | 65.2 | 65.8 | 64.5 | 63.5 |
| Spa-Cub (Ours) | 61.2 | 61.9 | 61.8 | 60.2 |
| TS-Cub (Ours) | 65.5 | 65.4 | 64.7 | 63.3 |
Analysis of the Number of Joints: We further conduct experiments to ablate the number of joints in skeleton-based video222Based on the 25 joints used in (Shahroudy et al., 2016), we remove the joints “middle of the spine”, “left thumb” and “right thumb” for = 22, remove the joints “middle of the spine”, “left hand”, “right hand”, “left ankle”, “right ankle”, “left thumb” and “right thumb” for = 18, remove the joints “middle of the spine”, “left hand”, “right hand”, “left ankle”, “right ankle”, “left wrist”, “right wrist”, “left elbow”, “right elbow”, “left knee”, “right knee”, “left thumb” and “right thumb” for = 12.. As shown in Table 9, our final TS-Cub model achieves better results with more joints as input. When only using 12 major joints, it can also obtain a comparable performance with the result of = 25, indicating its robustness to the number of joints. We also find that using less joints could achieve better results in some cases (e.g., versus ), this is because the absent joints (e.g., left thumb and right thumb) sometimes would be redundant or even bring noise to the final action results.
| Method | ||||
|---|---|---|---|---|
| Tem-Cub (Ours) | 65.2 | 63.3 | 62.0 | 43.3 |
| Spa-Cub (Ours) | 61.2 | 60.8 | 60.0 | 39.9 |
| TS-Cub (Ours) | 65.5 | 63.1 | 62.5 | 42.5 |
Analysis of the Gaussian Noise: To evaluate the robustness of our method, we add Gaussian noise to the input video. Specifically, we first normalize the input data into the scale of [-1, 1], add Gaussian noise with zero mean and different standard deviations to them, and re-scale data to the original interval. As shown in Table 10, with perturbation of and , our algorithm achieves comparable performance with that of . But with more noise, TS-Cub has a noticeable decrease from 65.5% () to 42.5% ().
| Task | Spa-Cub | Spa-Jigsaw | Freezing Game | Tem-Cub | Tem-Flip |
|---|---|---|---|---|---|
| Accuracy | 56.5 | 54.2 | 55.3 | 58.3 | 57.1 |
| Fusion way | WRSM | WGM | MP | TS-Cub (WAM) | Coupled-Cub |
| Accuracy | 51.9 | 58.9 | 58.5 | 59.2 | 55.6 |
Exploration of Other Self-supervised Learning Tasks: Besides our proposed Cubism tasks, we also explore other self-supervised learning tasks but receive not that satisfactory results. The comparison of results adopting different supervised tasks is shown in Table 11. For instance, we consider the task Tem-Flip to distinguish the ordered videos from the temporally inverse videos. However, it is hard to discriminate between such actions like ordered put something inside pocket and inverse take out something from pocket. Hence this task cannot be applied to all action categories and fails to lead to higher performance. We explore a task named as Spa-Jigsaw in the temporal domain. There are a number of joints comprising a body, which are stored in a linear list in practice. Hence we simply uniformly divide that list into 3 segments and permute them. This way of permutation thoroughly breaks the spatial relation of the joints and thereby achieves a slightly poor result. Meanwhile, we try another way called Freezing Game to build augmented data by freezing the pose of the arms and the legs from the first frame during the whole video. However, as several actions do not comprise large-amplitude motions at first, this task seems to be so difficult that the importance of the expected classification task gets degraded. Though spatial rotation is a conventional transformation, we do not exploit it further as we have taken it as a part of the data pre-processing. Additionally, several approaches are investigated to combine Tem-Cub and Spa-Cub. Firstly, we explore some softmax scores fusion approaches like , , , and max-pool, named as Weighted Arithmetic Mean (WAM), Weighted Root Squared Mean (WRSM), Weighted Geometric Mean (WGM) and Max Pooling (MP) orderly in Table 11. Here and denote temporal and spatial softmax scores, and are two hyper-parameters. We find that simply add temporal and spatial softmax scores achieves the best result and name it TS-Cub. Besides, there is another method that applies the temporal and spatial transformations simultaneously to the training samples. This combination way couples the temporal Cubism and spatial Cubism and is named as Coupled-Cub. Coupled-Cub will considerably increase the number of the permutation labels and produce more disordered samples, which raises the difficulty of the auxiliary task as well. As a conclusion of our exploration, the auxiliary task is not supposed to be too simple or too difficult. A too simple task has not got enough ability to draw the two domains close while a too difficult task could overwhelm the original classification task. In other words, an inadequate self-supervised task could result in an even worse adaptation performance thus choosing an appropriate additional task is crucial for such a self-supervision based approach.
| Training | Testing | |||
| Source | Clips | Target | Clips | |
| PN-CV | P | 21544 | N51-CV-test | 16092 |
| PN-CS | P | 21544 | N51-CS-test | 14013 |
| NP-CV | N51 | 48081 | P-CV-test | 7188 |
| NP-CS | N51 | 48081 | P-CS-test | 2704 |
| NK | N12 | 11256 | K-test | 787 |
| KN | K | 9699 | N12-CV-test | 3780 |
| Method | PN-CV | PN-CS | NP-CV | NP-CS | NK | KN |
| Target Only | 91.3 | 84.6 | 95.7 | 93.1 | 40.8 | 89.1 |
| Source Only | 54.9 | 50.5 | 59.6 | 57.6 | 14.4 | 22.5 |
| Tem-Cub | 57.1 | 52.7 | 62.7 | 60.0 | 15.6 | 25.5 |
| Spa-Cub | 54.7 | 50.8 | 61.9 | 59.6 | 15.0 | 25.1 |
| TS-Cub | 57.7 | 53.8 | 63.4 | 61.3 | 15.5 | 25.6 |
4.6. Training the TS-Cub without Target Domain Data
We make further exploration about testing our proposed TS-Cub under a more challenging cross-dataset setting, which assumes that data from target domain are totally unavailable during the training period. We detail this unsupervised domain adaptation setting in Table 12. During the training phase, the permuted video samples from source domain are delivered into the network along with the ordering data. The final losses are composed of the main classification task and the auxiliary Cubism task.
We present the experimental results in Table 13, other compared methods in the previous section are absent because they all required the target data during training, which is not available in this setting. As shown in Table 13, our TS-Cub consistently outperforms the baseline Source Only on the six tasks, which indicates its robustness for cross-dataset skeleton-based action recognition.
| Method | PN-CV | PN-CS | NP-CV | NP-CS | NK | KN |
|---|---|---|---|---|---|---|
| Tem-Cub (Ours) | 58.3 | 52.5 | 65.2 | 62.8 | 16.4 | 29.3 |
| Spa-Cub (Ours) | 56.5 | 51.0 | 61.2 | 59.3 | 14.6 | 22.9 |
| TS-Cub (Ours) | 59.2 | 53.6 | 65.5 | 63.3 | 16.8 | 29.6 |
| Tem-Cub (Ours) + CDAN (Long et al., 2018; Choi et al., 2020) | 60.2 | 56.5 | 67.6 | 64.6 | 16.2 | 21.5 |
| Spa-Cub (Ours) + CDAN (Long et al., 2018) | 59.3 | 56.4 | 68.3 | 65.4 | 15.6 | 26.8 |
| TS-Cub (Ours) + CDAN (Long et al., 2018) | 59.5 | 57.8 | 68.9 | 66.1 | 16.6 | 27.1 |
4.7. Combining the Cubism with Adversarial Learning Method
Recently, Choi et al. (Choi et al., 2020) study the cross-dataset action recognition problem by combining the domain adversarial task with the clip order prediction task. Motivated by this work, we further conduct experiments to see whether our self-supervised pretext tasks are complementary with the conventional domain adversarial task. Since (Choi et al., 2020) is designed for RGB video while our work focus on skeleton-based video, we use HCN (Li et al., 2018) as the backbone similar with TA3N (Chen et al., 2019a). Then we perform temporal Cubism at raw data level as well as apply adversarial learning in feature level based on CDAN (Long et al., 2018) (denoted as “Tem-Cub (Ours) + CDAN” in Table 14). We also conduct experiment on combining our Spa-Cub with CDAN (i.e., “Tem-Cub (Ours) + CDAN”), and ensembling the results of “Tem-Cub (Ours) + CDAN” and “Spa-Cub (Ours) + CDAN” (i.e., “TS-Cub (Ours) + CDAN”).
We present the compared results in Table 14. On PN setting, we find the performance could be further improved by combining our approach with CDAN (Long et al., 2018), which shows the complementary characteristics of our method and adversarial approach. However, on the NK setting, we found that the performance drops slightly when combining with CDAN. This might attribute to the videos from the Kinetics are collected in the wild, and the skeleton-based inputs are obtained from 2D pose estimation algorithm rather than 3D sensor for NTU and PKU datasets. In this case, the adversarial approach (e.g., CDAN) might have more difficulty in dealing with this kind of data with more noise. In comparison, our method is more robust to generalize to this more challenging scenario.
5. Conclusions
In this paper, we have investigated the unsupervised domain adaptation setting for skeleton-based action recognition. In order to reduce the domain shift between different datasets, we have devised a self-supervised learning approach based on temporal spatial Cubism. Both quantitative and qualitative experimental results have demonstrated the effectiveness of our method. We expect this work to provide a new direction for skeleton-based action recognition, and inspire applications to other related tasks, such as group activity recognition (Tang et al., 2019), action quality assessment (Tang et al., 2020b) and instructional video analysis (Tang et al., 2020a).
References
- (1)
- Cao et al. (2021) Zhe Cao, Gines Hidalgo, Tomas Simon, Shih-En Wei, and Yaser Sheikh. 2021. OpenPose: Realtime Multi-Person 2D Pose Estimation Using Part Affinity Fields. IEEE Trans. Pattern Anal. Mach. Intell. 43, 1 (2021), 172–186.
- Carlucci et al. (2019) Fabio Maria Carlucci, Antonio D’Innocente, Silvia Bucci, Barbara Caputo, and Tatiana Tommasi. 2019. Domain Generalization by Solving Jigsaw Puzzles. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2229–2238.
- Carreira and Zisserman (2017) João Carreira and Andrew Zisserman. 2017. Quo Vadis, Action Recognition? A New Model and the Kinetics Dataset. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 4724–4733.
- Chen et al. (2019a) Min-Hung Chen, Zsolt Kira, Ghassan Alregib, Jaekwon Yoo, Ruxin Chen, and Jian Zheng. 2019a. Temporal Attentive Alignment for Large-Scale Video Domain Adaptation. In Proceedings of the IEEE International Conference on Computer Vision. 6320–6329.
- Chen et al. (2020) Ting Chen, Simon Kornblith, Mohammad Norouzi, and Geoffrey E. Hinton. 2020. A Simple Framework for Contrastive Learning of Visual Representations. In Proceedings of the International Conference on Machine Learning. 1597–1607.
- Chen et al. (2019b) Xinyang Chen, Sinan Wang, Mingsheng Long, and Jianmin Wang. 2019b. Transferability vs. Discriminability: Batch Spectral Penalization for Adversarial Domain Adaptation. In Proceedings of the International Conference on Machine Learning. 1081–1090.
- Choi et al. (2020) Jinwoo Choi, Gaurav Sharma, Samuel Schulter, and Jia-Bin Huang. 2020. Shuffle and Attend: Video Domain Adaptation. In Proceedings of the European Conference on Computer Vision, Vol. 12357. 678–695.
- Choutas et al. (2018) Vasileios Choutas, Philippe Weinzaepfel, Jérôme Revaud, and Cordelia Schmid. 2018. PoTion: Pose MoTion Representation for Action Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 7024–7033.
- Ding et al. (2018) Zhengming Ding, Sheng Li, Ming Shao, and Yun Fu. 2018. Graph Adaptive Knowledge Transfer for Unsupervised Domain Adaptation. In Proceedings of the European Conference on Computer Vision. 36–52.
- Doersch et al. (2015) Carl Doersch, Abhinav Gupta, and Alexei A. Efros. 2015. Unsupervised Visual Representation Learning by Context Prediction. In Proceedings of the IEEE International Conference on Computer Vision. 1422–1430.
- Doersch and Zisserman (2017) Carl Doersch and Andrew Zisserman. 2017. Multi-task Self-Supervised Visual Learning. In Proceedings of the IEEE International Conference on Computer Vision. 2070–2079.
- Dwibedi et al. (2019) Debidatta Dwibedi, Yusuf Aytar, Jonathan Tompson, Pierre Sermanet, and Andrew Zisserman. 2019. Temporal Cycle-Consistency Learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 1801–1810.
- Fernando et al. (2017) Basura Fernando, Hakan Bilen, Efstratios Gavves, and Stephen Gould. 2017. Self-Supervised Video Representation Learning with Odd-One-Out Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 5729–5738.
- Gan et al. (2018) Chuang Gan, Boqing Gong, Kun Liu, Hao Su, and Leonidas J. Guibas. 2018. Geometry Guided Convolutional Neural Networks for Self-Supervised Video Representation Learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 5589–5597.
- Ganin et al. (2016) Yaroslav Ganin, Evgeniya Ustinova, Hana Ajakan, Pascal Germain, Hugo Larochelle, François Laviolette, Mario Marchand, and Victor S. Lempitsky. 2016. Domain-Adversarial Training of Neural Networks. Journal of Machine Learning Research 17 (2016), 59:1–59:35.
- Gidaris et al. (2018) Spyros Gidaris, Praveer Singh, and Nikos Komodakis. 2018. Unsupervised Representation Learning by Predicting Image Rotations. In Proceedings of the International Conference on Learning Representations.
- Gong et al. (2013) Boqing Gong, Kristen Grauman, and Fei Sha. 2013. Connecting the dots with landmarks: Discriminatively learning domain-invariant features for unsupervised domain adaptation. In Proceedings of the International Conference on Machine Learning. 222–230.
- Han et al. (2017) Fei Han, Brian Reily, William Hoff, and Hao Zhang. 2017. Space-time representation of people based on 3D skeletal data: A review. Computer Vision and Image Understanding 158 (2017), 85–105.
- He et al. (2020) Kaiming He, Haoqi Fan, Yuxin Wu, Saining Xie, and Ross B. Girshick. 2020. Momentum Contrast for Unsupervised Visual Representation Learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 9726–9735.
- He et al. (2015) Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. 2015. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. In Proceedings of the IEEE International Conference on Computer Vision. 1026–1034.
- Huang et al. (2006) Jiayuan Huang, Alexander J. Smola, Arthur Gretton, Karsten M. Borgwardt, and Bernhard Schölkopf. 2006. Correcting Sample Selection Bias by Unlabeled Data. In Proceedings of the International Conference on Neural Information Processing Systems. 601–608.
- Jamal et al. (2018) Arshad Jamal, Vinay P. Namboodiri, Dipti Deodhare, and K. S. Venkatesh. 2018. Deep Domain Adaptation in Action Space. In Proceedings of the British Machine Vision Conference. 264.
- Jin et al. (2020) Ying Jin, Ximei Wang, Mingsheng Long, and Jianmin Wang. 2020. Minimum Class Confusion for Versatile Domain Adaptation. In Proceedings of the European Conference on Computer Vision, Andrea Vedaldi, Horst Bischof, Thomas Brox, and Jan-Michael Frahm (Eds.). 464–480.
- Kim et al. (2019) Dahun Kim, Donghyeon Cho, and In So Kweon. 2019. Self-Supervised Video Representation Learning with Space-Time Cubic Puzzles. In Proceedings of the AAAI Conference on Artificial Intelligence. 8545–8552.
- Koniusz et al. (2016) Piotr Koniusz, Anoop Cherian, and Fatih Porikli. 2016. Tensor Representations via Kernel Linearization for Action Recognition from 3D Skeletons. In Proceedings of the European Conference on Computer Vision. 37–53.
- Lai et al. (2020) Zihang Lai, Erika Lu, and Weidi Xie. 2020. MAST: A Memory-Augmented Self-Supervised Tracker. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 6478–6487.
- Larsson et al. (2017) Gustav Larsson, Michael Maire, and Gregory Shakhnarovich. 2017. Colorization as a Proxy Task for Visual Understanding. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 840–849.
- Lee et al. (2017) Hsin-Ying Lee, Jia-Bin Huang, Maneesh Singh, and Ming-Hsuan Yang. 2017. Unsupervised Representation Learning by Sorting Sequences. In Proceedings of the IEEE International Conference on Computer Vision. 667–676.
- Li et al. (2018) Chao Li, Qiaoyong Zhong, Di Xie, and Shiliang Pu. 2018. Co-occurrence Feature Learning from Skeleton Data for Action Recognition and Detection with Hierarchical Aggregation. In Proceedings of the International Joint Conference on Artificial Intelligence. 786–792.
- Li et al. (2019) Maosen Li, Siheng Chen, Xu Chen, Ya Zhang, Yanfeng Wang, and Qi Tian. 2019. Actional-Structural Graph Convolutional Networks for Skeleton-Based Action Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition.
- Lin et al. (2020) Lilang Lin, Sijie Song, Wenhan Yang, and Jiaying Liu. 2020. MS2L: Multi-Task Self-Supervised Learning for Skeleton Based Action Recognition. In In Proceedings of the ACM International Conference on Multimedia. 2490–2498.
- Liu et al. (2020a) Jun Liu, Amir Shahroudy, Mauricio Perez, Gang Wang, Ling-Yu Duan, and Alex C. Kot. 2020a. NTU RGB+D 120: A Large-Scale Benchmark for 3D Human Activity Understanding. IEEE Trans. Pattern Anal. Mach. Intell. 42, 10 (2020), 2684–2701.
- Liu et al. (2020b) Jiaying Liu, Sijie Song, Chunhui Liu, Yanghao Li, and Yueyu Hu. 2020b. A Benchmark Dataset and Comparison Study for Multi-modal Human Action Analytics. ACM Trans. Multim. Comput. Commun. Appl. 16, 2 (2020), 41:1–41:24.
- Liu et al. (2017) Mengyuan Liu, Hong Liu, and Chen Chen. 2017. Enhanced skeleton visualization for view invariant human action recognition. Pattern Recognit. 68 (2017), 346–362.
- Long et al. (2015) Mingsheng Long, Yue Cao, Jianmin Wang, and Michael I. Jordan. 2015. Learning Transferable Features with Deep Adaptation Networks. In Proceedings of the International Conference on Machine Learning. 97–105.
- Long et al. (2018) Mingsheng Long, Zhangjie Cao, Jianmin Wang, and Michael I. Jordan. 2018. Conditional Adversarial Domain Adaptation. In Proceedings of the International Conference on Neural Information Processing Systems. 1647–1657.
- Long et al. (2017) Mingsheng Long, Han Zhu, Jianmin Wang, and Michael I. Jordan. 2017. Deep Transfer Learning with Joint Adaptation Networks. In Proceedings of the International Conference on Machine Learning. 2208–2217.
- Maaten and Hinton (2008) Laurens van der Maaten and Geoffrey Hinton. 2008. Visualizing data using t-SNE. Journal of machine learning research 9, 11 (2008), 2579–2605.
- Misra et al. (2016) Ishan Misra, C. Lawrence Zitnick, and Martial Hebert. 2016. Shuffle and Learn: Unsupervised Learning Using Temporal Order Verification. In Proceedings of the European Conference on Computer Vision. 527–544.
- Noroozi and Favaro (2016) Mehdi Noroozi and Paolo Favaro. 2016. Unsupervised Learning of Visual Representations by Solving Jigsaw Puzzles. In Proceedings of the European Conference on Computer Vision. 69–84.
- Pan et al. (2011) Sinno Jialin Pan, Ivor W. Tsang, James T. Kwok, and Qiang Yang. 2011. Domain Adaptation via Transfer Component Analysis. IEEE Trans. Neural Networks 22, 2 (2011), 199–210.
- Pathak et al. (2016) Deepak Pathak, Philipp Krähenbühl, Jeff Donahue, Trevor Darrell, and Alexei A. Efros. 2016. Context Encoders: Feature Learning by Inpainting. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2536–2544.
- Saito et al. (2018) Kuniaki Saito, Kohei Watanabe, Yoshitaka Ushiku, and Tatsuya Harada. 2018. Maximum Classifier Discrepancy for Unsupervised Domain Adaptation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 3723–3732.
- Shahroudy et al. (2016) Amir Shahroudy, Jun Liu, Tian-Tsong Ng, and Gang Wang. 2016. NTU RGB+D: A Large Scale Dataset for 3D Human Activity Analysis. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 1010–1019.
- Shi et al. (2019a) Lei Shi, Yifan Zhang, Jian Cheng, and Hanqing Lu. 2019a. Skeleton-Based Action Recognition With Directed Graph Neural Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 7912–7921.
- Shi et al. (2019b) Lei Shi, Yifan Zhang, Jian Cheng, and Hanqing Lu. 2019b. Two-Stream Adaptive Graph Convolutional Networks for Skeleton-Based Action Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 12026–12035.
- Si et al. (2019) Chenyang Si, Wentao Chen, Wei Wang, Liang Wang, and Tieniu Tan. 2019. An Attention Enhanced Graph Convolutional LSTM Network for Skeleton-Based Action Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 1227–1236.
- Simonyan and Zisserman (2014) Karen Simonyan and Andrew Zisserman. 2014. Two-Stream Convolutional Networks for Action Recognition in Videos. In Proceedings of the International Conference on Neural Information Processing Systems. 568–576.
- Song et al. (2017) Sijie Song, Cuiling Lan, Junliang Xing, Wenjun Zeng, and Jiaying Liu. 2017. An End-to-End Spatio-Temporal Attention Model for Human Action Recognition from Skeleton Data. In Proceedings of the AAAI Conference on Artificial Intelligence. 4263–4270.
- Sultani and Saleemi (2014) Waqas Sultani and Imran Saleemi. 2014. Human Action Recognition across Datasets by Foreground-Weighted Histogram Decomposition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 764–771.
- Sun et al. (2019) Yu Sun, Eric Tzeng, Trevor Darrell, and Alexei A. Efros. 2019. Unsupervised Domain Adaptation through Self-Supervision. CoRR abs/1909.11825 (2019).
- Sun et al. (2020) Yu Sun, Xiaolong Wang, Zhuang Liu, John Miller, Alexei A. Efros, and Moritz Hardt. 2020. Test-Time Training with Self-Supervision for Generalization under Distribution Shifts. In Proceedings of the International Conference on Machine Learning. 9229–9248.
- Tang et al. (2019) Yansong Tang, Jiwen Lu, Zian Wang, Ming Yang, and Jie Zhou. 2019. Learning Semantics-Preserving Attention and Contextual Interaction for Group Activity Recognition. IEEE Trans. Image Process. 28, 10 (2019), 4997–5012.
- Tang et al. (2020a) Yansong Tang, Jiwen Lu, and Jie Zhou. 2020a. Comprehensive Instructional Video Analysis: The COIN Dataset and Performance Evaluation. IEEE Trans. Pattern Anal. Mach. Intell. (2020), 1–1. https://doi.org/10.1109/TPAMI.2020.2980824
- Tang et al. (2020b) Yansong Tang, Zanlin Ni, Jiahuan Zhou, Danyang Zhang, Jiwen Lu, Ying Wu, and Jie Zhou. 2020b. Uncertainty-Aware Score Distribution Learning for Action Quality Assessment. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. IEEE, 9836–9845.
- Tang et al. (2018) Yansong Tang, Yi Tian, Jiwen Lu, Peiyang Li, and Jie Zhou. 2018. Deep Progressive Reinforcement Learning for Skeleton-based Action Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 5323–5332.
- Tang et al. (2020c) Yansong Tang, Yi Wei, Xumin Yu, Jiwen Lu, and Jie Zhou. 2020c. Graph Interaction Networks for Relation Transfer in Human Activity Videos. IEEE Trans. Circuits Syst. Video Technol. 30, 9 (2020), 2872–2886.
- Tas and Koniusz (2018) Yusuf Tas and Piotr Koniusz. 2018. CNN-based Action Recognition and Supervised Domain Adaptation on 3D Body Skeletons via Kernel Feature Maps. In Proceedings of the British Machine Vision Conference. 158.
- Vemulapalli et al. (2014) Raviteja Vemulapalli, Felipe Arrate, and Rama Chellappa. 2014. Human Action Recognition by Representing 3D Skeletons as Points in a Lie Group. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 588–595.
- Verma et al. (2020) Pratishtha Verma, Animesh Sah, and Rajeev Srivastava. 2020. Deep learning-based multi-modal approach using RGB and skeleton sequences for human activity recognition. Multimedia Systems 26 (2020), 671–685.
- Wang et al. (2019b) Jiangliu Wang, Jianbo Jiao, Linchao Bao, Shengfeng He, Yunhui Liu, and Wei Liu. 2019b. Self-Supervised Spatio-Temporal Representation Learning for Videos by Predicting Motion and Appearance Statistics. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 4006–4015.
- Wang et al. (2012) Jiang Wang, Zicheng Liu, Ying Wu, and Junsong Yuan. 2012. Mining actionlet ensemble for action recognition with depth cameras. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 1290–1297.
- Wang et al. (2016a) Limin Wang, Yuanjun Xiong, Zhe Wang, Yu Qiao, Dahua Lin, Xiaoou Tang, and Luc Van Gool. 2016a. Temporal Segment Networks: Towards Good Practices for Deep Action Recognition. In Proceedings of the European Conference on Computer Vision. 20–36.
- Wang et al. (2018) Pichao Wang, Wanqing Li, Philip Ogunbona, Jun Wan, and Sergio Escalera. 2018. RGB-D-based human motion recognition with deep learning: A survey. Computer Vision and Image Understanding 171 (2018), 118–139.
- Wang et al. (2016b) Pei Wang, Chunfeng Yuan, Weiming Hu, Bing Li, and Yanning Zhang. 2016b. Graph Based Skeleton Motion Representation and Similarity Measurement for Action Recognition. In Proceedings of the European Conference on Computer Vision. 370–385.
- Wang et al. (2019a) Xiaolong Wang, Allan Jabri, and Alexei A Efros. 2019a. Learning correspondence from the cycle-consistency of time. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2566–2576.
- Weng et al. (2017) Junwu Weng, Chaoqun Weng, and Junsong Yuan. 2017. Spatio-Temporal Naive-Bayes Nearest-Neighbor for Skeleton-Based Action Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 4171–4180.
- Yan et al. (2018) Sijie Yan, Yuanjun Xiong, and Dahua Lin. 2018. Spatial Temporal Graph Convolutional Networks for Skeleton-Based Action Recognition. In Proceedings of the AAAI Conference on Artificial Intelligence. 7444–7452.
- Yu et al. (2014) Gang Yu, Zicheng Liu, and Junsong Yuan. 2014. Discriminative Orderlet Mining for Real-Time Recognition of Human-Object Interaction. In Proceedings of the Asian Conference on Computer Vision. 50–65.
- Yun et al. (2012) Kiwon Yun, Jean Honorio, Debaleena Chattopadhyay, Tamara L. Berg, and Dimitris Samaras. 2012. Two-person interaction detection using body-pose features and multiple instance learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops. 28–35.
- Zhang et al. (2017) Pengfei Zhang, Cuiling Lan, Junliang Xing, Wenjun Zeng, Jianru Xue, and Nanning Zheng. 2017. View Adaptive Recurrent Neural Networks for High Performance Human Action Recognition from Skeleton Data. In Proceedings of the IEEE International Conference on Computer Vision. 2136–2145.
- Zhang et al. (2018) Pengfei Zhang, Jianru Xue, Cuiling Lan, Wenjun Zeng, Zhanning Gao, and Nanning Zheng. 2018. Adding Attentiveness to the Neurons in Recurrent Neural Networks. In Proceedings of the European Conference on Computer Vision. 136–152.
- Zhang et al. (2016) Richard Zhang, Phillip Isola, and Alexei A. Efros. 2016. Colorful Image Colorization. In Proceedings of the European Conference on Computer Vision. 649–666.
- Zolfaghari et al. (2017) Mohammadreza Zolfaghari, Gabriel L. Oliveira, Nima Sedaghat, and Thomas Brox. 2017. Chained Multi-stream Networks Exploiting Pose, Motion, and Appearance for Action Classification and Detection. In Proceedings of the IEEE International Conference on Computer Vision. 2923–2932.