Learning Contrastive Feature Representations for Facial Action Unit Detection
Abstract
Existing methods for facial action unit (AU) detection often rely on encoding pixel-level information of the entire face associated with AU, which not only encodes additional redundant information but also leads to increased model complexity and limited generalizability. Additionally, the accuracy of AU detection is negatively impacted by the class imbalance issue of each AU type, and the presence of noisy and false AU labels. In this paper, we introduce a novel contrastive learning framework aimed for AU detection that incorporates both self-supervised and supervised signals, thereby enhancing the learning of discriminative features for accurate AU detection. To tackle the class imbalance issue, we employ a negative sample re-weighting strategy that adjusts the step size of updating parameters for minority and majority class samples. Moreover, to address the challenges posed by noisy and false AU labels, we employ a sampling technique that encompasses three distinct types of positive sample pairs. This enables us to inject self-supervised signals into the supervised signal, effectively mitigating the adverse effects of noisy labels. Our experimental assessments, conducted on four widely-utilized benchmark datasets (BP4D, DISFA, GFT and Aff-Wild2), underscore the superior performance of our approach compared to state-of-the-art methods of AU detection. Our code is available at https://github.com/Ziqiao-Shang/AUNCE.
keywords:
Facial action unit detection , Contrastive learning , Positive sample sampling , Importance re-weighting strategy1 Introduction
Facial Action Coding System (FACS) [1] is a widely employed approach for facial expression coding, which introduced a set of 44 facial action units (AUs) that establish a link between facial muscle movements and facial expressions [2]. AU detection is a multi-label binary classification problem. Each AU represents a kind of label, and activated and inactivated AUs are respectively labeled 1 and 0. Nowadays, AU detection [3, 4] has emerged as a computer vision technique to automatically identify AUs in videos or images. This advancement holds promise for diverse applications, including human-computer interaction, emotion analysis, car driving monitoring, and stuff like that.
In recent years, there has been a prevailing trend in supervised frameworks for AU detection [5, 6, 7, 8, 9]. These studies have predominantly utilized the binary cross-entropy loss to strictly align predicted and ground truth labels, which is often unnecessary for classification tasks. This overemphasis on label alignment imposes excessive demands on the fitting capacity of models, consequently increasing the risk of overfitting. Moreover, as shown in Fig. 1(a), these methods commonly focus on encoding pixel-level information of the entire face associated with AU, disregarding the fact that capturing subtle feature differences when AUs activate is sufficient. As a result, these learning methods place significant demands on the model complexity to encode excessive redundant information, ultimately limiting the generalization ability of the model.

(a) Pixel-level feature learning methods

(b) Discriminative contrastive learning methods
Representation learning approaches rooted in contrastive learning have demonstrated substantial promise [10] for classification. This approach aims to maximize the consistency of positive samples that are semantically similar while minimizing the consistency of negative samples that are semantically dissimilar [11]. By optimizing the contrastive loss, the mutual information between variables is either explicitly or implicitly optimized [12]. However, the direct integration of contrastive learning into AU detection encounters two principal challenges. The first challenge is the class imbalance issue of each AU type [7]. Most AU classes manifest a substantial imbalance between majority and minority class samples, with inactivated AUs vastly outnumbering their activated counterparts. This imbalance issue influences the classification decision threshold, potentially resulting in the direct classification of the majority of AUs as the negative class. The second challenge pertains to the noisy and false label problem [13]. Due to the subtle feature differences when AUs activate leading to the inherent difficulty in expertly labeling AUs, existing AU datasets may exhibit a few noisy and false labels, significantly undermining the overall fitting ability of models.
To address these challenges, as shown in Fig. 1(b), we propose a discriminative contrastive learning framework designed to encode differential information between AUs from each sample pair, replacing the traditional pixel-level feature learning methods within the field of AU detection. The resultant loss is termed AUNCE, resembling the commonly utilized InfoNCE. Moreover, to mitigate the class imbalance issue of each AU type, we apply a negative sample re-weighting strategy, making modifications to the gradient magnitude of minority and majority class samples during back-propagation by adding importance weight to the denominator of the resultant loss AUNCE. Additionally, in response to the issue of noisy and false labeling in AUs, we introduce a positive sample samplying strategy to augment the supervision signal through self-supervised signals. This is achieved by establishing sampling ratios for various types of positive sample pairs, ensuring that more robust positive samples are derived from data augmentation with the self-supervised signal. The primary contributions of our work are succinctly summarized as follows:
-
1.
We propose a discriminative contrastive learning framework to learn differential feature representations for AU detection, and the resultant loss is named AUNCE.
-
2.
We employ a negative sample re-weighting strategy to tackle the class imbalance issue of each AU type.
-
3.
We introduce a positive sample samplying strategy to address the issue of noisy and false AU labels.
-
4.
We validate the effectiveness of AUNCE by comparing it to state-of-the-art approaches for AU detection on four widely-used datasets, namely BP4D, DISFA, GFT and Aff-Wild2.
2 Related Work
We provide a comprehensive overview of two areas closely connected to our research: discriminative contrastive learning and contrastive learning for AU detection.
2.1 Discriminative contrastive learning
Contrastive learning [14] initially emerged from the realm of self-supervised learning, where the self-supervised learning objectives were defined by assigning tasks to agents. Specifically, this approach encompasses the application of diverse image augmentations to identical images, followed by an assessment of the resultant images and their associated features to determine similarity. The primary objective is to augment the similarity among features extracted from the same image while concurrently attenuating the similarity between features derived from distinct images. Subsequently, the evolution of this technology has led to the extension of contrastive learning to supervised and semi-supervised learning paradigms, wherein the utilization of labeled data is leveraged to enhance the representations of model features.
In recent years, discriminative contrastive learning, a subset of deep self-supervised learning methods [15], has witnessed substantial progress. This approach adheres to the learn-to-compare paradigm [16], wherein a distinction is made between observed data and noisy or erroneous data, preventing the model from engaging in the reconstruction of pixel-level information. For example, Oord et al. [12] optimized feature extraction networks by maximizing consistency between predicted and actual outcomes of sequence data, introducing the widely-utilized InfoNCE loss, which implicitly or explicitly serves as a lower bound for mutual information. Chen et al. [11] proposes a prominent framework named SimCLR, which introduces a base encoder network and a projection head trained to maximize agreement utilizing the contrastive loss InfoNCE. Additionally, MoCo, proposed by He et al. [17], employs a momentum network to maintain a queue of negative samples for efficient contrastive learning. Chen and He [18] mitigate undesired collapsing solutions, eschewing the use of negative sample pairs through a stop-gradient operation. Despite variations and errors in representation encoders (denoted as ) and similarity measures across different tasks [19], the underlying concept remains consistent: training the representation encoder by optimizing the contrastive loss, achieved through contrasting similar pairs () and dissimilar pairs ().
Apart from that, deep contrastive learning not only facilitates the automated extraction of refined feature representations through the comparison of positive and negative sample pairs but also incorporates diverse contrastive losses for optimization. Theoretical analyses concerning the generalization bounds of contrastive learning for classification tasks have been provided by Arora et al. [20]. Khosla et al. [21] extended the contrastive learning concept to supervised settings with a supervised contrastive learning loss, aiming to enhance feature expression using labeled data. Additionally, Chen et al. [22] proposed a semi-supervised contrastive learning algorithm, initially pretraining all data through contrastive learning and subsequently transferring knowledge to new models via distillation learning with the aid of labeled data.
There is a discernible shift in the construction of sample pairs for contrastive learning. In cases where data is labeled or partially labeled, positive samples can be constructed using images belonging to the same category, rather than being confined to identical images. This approach augments the diversity of positive sample pairs, consequently enhancing feature expression. Furthermore, contrastive learning serves as a precursor to supervised learning, enabling model pretraining to significantly enhance the performance of subsequent supervised learning models. However, there has been no prior work that directly applies the InfoNCE-based discriminative contrastive learning framework to AU detection task based on static images, primarily due to inherent challenges in this field: class imbalance problem of each type of AUs, noisy and erroneous annotations, and difficulty in distinguishing hard negative samples.
2.2 Contrastive learning for AU detection
Contrastive learning was firstly designed as a pretext task for unsupervised or self-supervised learning and was introduced to the domain of AU detection with limited annotations [23, 24, 25]. For example, Niu et al. [23] introduced a semi-supervised co-training approach that utilized contrastive loss to enforce conditional independence between facial representations generated by two Deep Neural Networks (DNNs). Chang et al. [24] present a knowledge-driven representation learning framework aimed for AU detection, incorporating a contrastive learning module that leverages dissimilarities among facial regions to effectively train the feature encoder. Additionally, Liu et al. [25] introduced a semi-supervised contrastive learning strategy that concurrently combined region learning, contrastive learning, and pseudo-labeling.
Subsequent research endeavors extended contrastive learning to supervised settings, aiming at enhancing feature representation for AU detection through the utilization of labeled data [26, 27, 28]. Wu et al. [26] introduced a contrastive feature learning method, enabling a Convolutional Neural Network (CNN) to acquire distinctive features that represent differences between neutral and AU-activated facial images. Chen et al. [28] introduced a supervised hierarchical contrastive learning method (SupHCL) aimed at enhancing AU detection by fostering knowledge consistency across distinct facial images and various AUs. In a similar vein, Suresh et al. [27] proposed a feature-based positive matching contrastive loss, which facilitates learning distances between positives based on the similarity of corresponding AU embeddings.
However, the aforementioned methods mostly employed a combination of weighted cross-entropy loss and triplet loss to constrain the training process, which involves encoding pixel-level information of the entire face associated with AU, leading to a substantial amount of redundant information. To address this issue, Li et al. [13] formulated a self-supervised contrastive learning method, which introduced the discriminative contrastive learning framework MoCo [17] into dynamic AU detection task based on extensive amounts of unlabeled facial videos, which is aim to extract differential features between video frames, inspired by some discriminative contrastive learning techniques in video representation learning [29].
In summary, contrastive learning has demonstrated promising results in the field of AU detection. However, how to capture differential information between AUs from each sample pair instead of pixel-level information of the entire face associated with AU in AU detection task based on static images is still a problem that needs to be solved.

3 Method
In Section 3, we present a discriminative contrastive learning framework specifically designed for the task of AU detection, aiming to incentivize the encoder to learn differential information between AUs from each sample pair, rather than focusing on pixel-level information of the entire face associated with AU. Subsequently, we confront two additional challenges: 1. Tackling the issue of class imbalance pertaining to each AU type in order to enhance the accuracy of our framework. 2. Addressing the problem of noisy and false labels, aiming to bolster the robustness of our models against erroneously annotated data.
3.1 Discriminative contrastive learning framework
For the task of AU detection, which falls under the category of multi-label binary classification, the prevalent approach for training models has been the utilization of cross-entropy loss. This loss measures the disparity between predicted labels and ground truth labels. However, there exists variability in the occurrence rates of different AUs, with some AUs exhibiting low occurrence rates while others display high occurrence rates. Consequently, in contrast to the conventional cross-entropy loss, we employ a weighted cross-entropy loss [7] denoted as
| (1) |
where denotes the ground truth value of occurrence (i.e., 0 or 1) of the -th AU, and is the corresponding predicted occurrence probability. This loss effectively guides the training process, encouraging the model to allocate higher probabilities to the correct class labels and lower probabilities to incorrect ones. = is the weight of the -th AU determined by its occurrence frequency for balanced training. It permits reducing the impact of loss values associated with those AUs that are more commonly activated in the training set. represents the occurrence frequency of the -th AU, and is the total number of AUs.
However, the classification methods based on cross-entropy loss suffer from a common issue of being overly constrained, which can lead to overfitting and limited generalization. This constraint becomes particularly problematic in the context of AU detection, where different AUs share a common encoder. For each AU of every sample, the predicted output must satisfy the aforementioned condition, placing a significant burden on the fitting capability of the encoder. To address this challenge, we introduce a discriminative contrastive learning framework for AU detection. As shown in Fig. 2. It comprises a positive sample mining module that integrates self-supervised signals with supervised signals, aiming to address the issue of noisy labels resulting from subtle differences in AUs. Additionally, a negative sample weighting module is included to tackle class imbalance and hard negative sample mining challenges. These modules will be discussed in detail in Sections 3.2 and 3.3, respectively. The resultant loss is formulated as:
| (2) | ||||
where serves as an encoder, mapping the features to a dimensional vector, represents the feature representation of a specific AU. The positive sample of , denoted as , corresponds to samples belonging to the same class as . Specifically, they are derived from three sources: samples from the same class, data augmentation of the anchor point, and feature augmentation of samples from the same class. represents negative samples of , which are samples from different classes compared to . measures the similarity between and its positive example , while measures the similarity between the sample and its negative example. The term represents the data distribution, and respectively denote the class conditional distribution of positive and negative samples of . Inspired by Eq (1), we introduce in Eq (2) to mitigate the influence of loss values related to commonly activated AUs in the training set. Additionally, we incorporate to re-weight the significance of each negative sample.
The contrastive loss distinguishes itself from weighted cross-entropy loss in the following aspects: 1. The weighted cross-entropy loss is computed based on the sample and its corresponding label , requiring the encoding of pixel-level information in order to align with the label. In contrast, the contrastive loss does not involve explicit labels but is computed based on the feature difference values between each pair of samples. This incentivizes the encoder to capture the differential information between AUs from each sample pair, without the need to focus on pixel-level information extraction of individual samples, reducing the borden of encoder. 2. The weighted cross-entropy loss imposes constraints on the absolute values of the predicted probabilities. However, for classification tasks, this is often unnecessary and can lead to overfitting as well as demanding higher fitting capability from the encoder. The contrastive loss focuses on constraining the similarity difference between positive and negative sample pairs without explicitly specifying their exact values. This is because the minimal value of is 0, which is achieved when for all negative sample index .
3.2 Negative sample re-weighting strategy
To address the second challenge of the class imbalance issue, we employ a negative sample re-weighting strategy to minority AUs. This also contributes to hard negative sample mining. Inspired by HCL [30], we apply the following weighting scheme to each negative sample :
| (3) |
where can be viewed as the importance weight if we assume that the negative samples follow a von Mises-Fisher (vMF) distribution. The resulting AUNCE loss is:
| (4) | ||||
Next, we analyze how this weighting scheme addresses the class imbalance issue and facilitates the mining of hard negative samples. Without loss of generality, we consider the similarity calculation as , where is the temperature coefficient. The inclusion of importance weights transforms the gradient of w.r.t similarity scores of positive pairs into the following form:
| (5) |
where , and the gradient of similarity scores of negative pairs w.r.t is
| (6) |
Therefore, the ratio between the gradient magnitude of negative examples and positive examples is given by:
| (7) |
Above equation follows the Boltzmann distribution. As the value of increases, the entropy of the distribution decreases significantly [31], leading to a sharper distribution in the region of high similarity. This has two consequences: 1. It imposes larger penalties on hard negative samples that are in close proximity to the anchor data point, enabling the model to learn more precise decision boundaries from subtle feature differences when AUs activate. 2. It controls the relative contribution of negative samples to the parameter updates, providing a means to address class imbalance issues.
The primary distinction between our weighting method and HCL [30] lies in the fact that Eq. (3) does not divide by the mean as a normalization factor, enabling a more effective solution to the class imbalance issue in the field of AU detection. Specifically, when anchor data point belongs to the majority class, its positive sample belongs to the majority class, while its negative sample belongs to the minority class. In this case, we aim to have smaller gradient magnitudes for the positive samples (majority class) to update fewer parameters, while the negative samples (minority class) should have larger gradient magnitudes to update more parameters. To achieve this, we begin to set , which increases the impact of parameter updates caused by negative samples (minority class). On the other hand, when belongs to minority class, we begin to set to reduce the influence of parameter updates caused by majority class samples. By adjusting the value of , we can control the relative importance of positive and negative samples during the parameter updating, ensuring that the model pays more attention to minority class samples when necessary and balances the gradient magnitudes accordingly. This helps to balance the representation of different AUs in training set and improves the model ability to precisely classify all AU samples. If the mean were used as a normalization factor, the precise control over the parameter updates for majority and minority classes through the setting of would become unfeasible. This is because changes in would concurrently alter the mean, rendering the subsequent increase or decrease in weights after division by the mean uncertain. Therefore, the omission of division by the mean in Eq. (3), motivated by considerations of class imbalance, distinguishes our work from HCL.

3.3 Positive sample samplying strategy
For a given anchor point, samples sharing the same label with the anchor are referred to as positive examples. Among them, positive examples whose ground truth labels do not match the anchor’s label are termed as false positives, primarily stemming from label noise in the samples. Regarding the third challenge of AU labels tainted by noise and errors, we employ a combined approach that integrates label noisy learning and self-supervised learning techniques to obtain enhanced supervised signals for positive samples. As shown in Fig. 3, this approach mitigates the adverse effects of noisy labels by simultaneously introducing a controlled level of self-supervised signal and supervised signal, thereby enhancing the robustness of model to variations and errors present in the labeled dataset.
3.3.1 Supervised Signal
One common technique to address the issue of false data is label smoothing, where a small amount of uncertainty is incorporated into the training process by replacing one-hot labels with smoothed probability distributions. However, it is challenging to directly apply label smoothing to contrastive learning as the computation of contrastive loss does not involve explicit labels. To overcome this challenge, we turn to the memory effect of neural networks. Previous research has shown that neural networks tend to first fit clean samples and then memorize the noise in incorrectly labeled samples [32]. This memory effect is independent of the choice of neural network architecture. The positive samples that are easier fit are those that are closer to the anchor point and have higher similarity. Inspired by this observation, for a given sample and M positive samples with noisy labels belonging to the same class, we calculate the similarity scores between the representation of sample and the representations of all M positive samples. We then select the positive feature representation with the highest similarity to sample :
| (8) |
By selecting the positive samples with the highest similarity, we prioritize clean and reliable positive samples while minimizing the influence of noisy positive samples during the training process.
3.3.2 Self-supervised Signal
In addition to label noisy learning, we incorporate self-supervised learning techniques into the training process. By designing these auxiliary tasks carefully, we can encourage the model to learn more robust and invariant representations, which can help mitigate the effects of label noise and improve generalization performance. Specifically, our second method to obtain positive feature involves performing semantically invariant image augmentation on the anchor point :
| (9) |
where is a stochastic data augmentation module that applies random transformations to a given data example , generating two correlated views referred to as and , which we consider as a positive pair. Follow SimCLR [10], we employ a sequential application of three simple augmentations: random cropping and flipping followed by resizing back to original size, random color distortions, and random Gaussian blur.
Our third method to obtain positive examples involving a mixture of positive feature representations, which can be seen as a mixup of positive samples to obtain the most representative positive instances:
| (10) |
The primary distinction from data augmentation approaches exemplified by SimCLR lies in the nature of positive examples. In SimCLR, positive examples are augmented versions of the anchor point, implying that two views of the same sample are defined as positives, with each sample representing a unique class, leading to instance-level contrast. Under such circumstances, positive examples do not fully encapsulate the general class information. In contrast, the proposed method defines positive examples as the mean of the same-class samples that are identical to the anchor point, essentially representing the most representative features fo positive samples, which can be interpreted as class prototypes. Compared to instance-level contrast, the feature representations of class prototypes offer more robust information for comparison, thereby better capturing class information. The positive feature representation obtained from Eq. (10) represents the class centroid of M positive examples . In other words, it synthesizes a virtual representative positive sample.
The aforementioned three methods of obtaining positive examples combine the use of label noisy learning for supervised signals and data augmentation for self-supervised signals. These three types of positive examples are randomly mixed with probabilities , , and respectively, where . Our approach aims to improve the quality of supervised signals utilized in the training process. By integrating these techniques, we effectively mitigate the impact of noisy and false labels, increase the resilience of models to errors and variations in labeled datasets, and ultimately enhance the generalization ability of models to unseen data.
By addressing the above three challenges, our approach improves the encoding capability of the shared encode, ultimately leading to improved generalization performance in AU detection. The pseudocode for the algorithm is provided in Algorithm. 1.
3.4 Encoder for AU detection
To preserve the fairness of the comparison with conventional pixel-level feature learning methods, our encoder is consistent with the network structure of the first training stage in MEGraph [33], consisting of Swin-transformer backbone and AU Relationship-aware Node Feature Learning module. The input to the encoder consists of an contrastive larning image pair consisting of an anchor and a random sample, and the encoder is optimized by AUNCE only.
4 Evaluation
4.1 Experiment Setting
| Dataset | AU Index | ||||||||||||||
| 1 | 2 | 4 | 6 | 7 | 9 | 10 | 12 | 14 | 15 | 17 | 23 | 24 | 25 | 26 | |
| BP4D [34] | 21.1 | 17.1 | 20.3 | 46.2 | 54.9 | - | 59.4 | 56.2 | 46.6 | 16.9 | 34.4 | 16.5 | 15.2 | - | - |
| DISFA [35] | 5.0 | 4.0 | 15.0 | 8.1 | - | 4.3 | - | 13.2 | - | - | - | - | - | 27.8 | 8.9 |
| GFT [36] | 3.7 | 13.5 | 3.7 | 28.3 | - | - | 24.6 | 29.3 | 3.1 | 10.7 | - | 25.0 | 14.1 | - | - |
| Aff-Wild2 [37] | 11.9 | 5.1 | 16.0 | 26.5 | 39.9 | - | 34.5 | 24.3 | - | 2.8 | - | 3.1 | 2.8 | 62.8 | 7.6 |
4.1.1 Datasets
In our experiments, we extensively utilize three well-established datasets in constrained scenarios for AU detection, namely BP4D [34], DISFA [35], GFT [36], and one well-established dataset in unconstrained scenarios, namely Aff-Wild2 [37]. Our primary focus is on assessing frame-level AU detection, as opposed to datasets that solely provide video-level annotations.
BP4D [34]: This dataset comprises 41 participants, including 23 females and 18 males. Each individual is featured in 8 sessions, recorded using both 2D and 3D videos. The dataset encompasses approximately 140,000 frames, each annotated with AU labels indicating occurrence or non-occurrence. Additionally, each frame is meticulously annotated with 68 facial landmarks. For BP4D dataset, we employ a three-fold cross-validation methodology for rigorous evaluation.
DISFA [35]: This dataset is composed of 27 videos, recorded from 15 men and 12 women. Each video comprises 4,845 frames, resulting in a total of 130,788 images. Frames in this dataset are annotated with 68 facial landmarks and AU intensities ranging from 0 to 5. Frames with intensities equal to or greater than 2 are considered positive, while others are classified as negative. We also employ the same three-fold cross-validation methodology as BP4D dataset for rigorous evaluation of DISFA dataset.
GFT [36]: This dataset comprises 96 participants, organized into 32 groups of three individuals, engaged in unscripted conversations. Each participant is recorded via video, with the majority of frames capturing moderate out-of-plane poses. Annotations for each frame include 10 AUs, alongside 68 facial landmarks. In accordance with the standard training and testing partitions, our training set consists of 78 participants, amounting to approximately 108,000 frames, while the testing set includes 18 participants, totaling around 24,600 frames.
Aff-Wild2 [37]: This dataset is an extensive in-the-wild facial expression dataset, with videos sourced from YouTube, encompassing a broad range of ages, ethnicities, professions, emotions, poses, lighting conditions, and occlusions. This dataset comprises 305 videos, totaling approximately 1,390,000 frames for the training set, and 105 videos, with around 440,000 frames for the validation set. Each frame is annotated with 12 AUs and 68 facial landmark annotations. Following the methodology of Zhang et al. [38], we train our AUNCE on the training set and evaluate it on the validation set.
The occurrence rates of AUs in the training sets of these datasets are presented in Table 1. It is evident from the table that the class imbalance issue of each type of AU is prevalent across all datasets, especially on the DISFA, GFT and Aff-Wild2 datasets.
4.1.2 Implementation Details
Initially, the 68 facial landmarks undergo a conversion into 49 facial internal landmarks, excluding those associated with the facial contour. Subsequently, the images undergo augmentation through similarity transformation, encompassing in-plane rotation, uniform scaling, and translation, utilizing the 49 facial landmarks. The resulting images are standardized to a resolution of 2562563 pixels and then randomly cropped into 2242243 pixels, with the addition of a random horizontal flip.
For the training process, the encoder is conducted on one NVIDIA GeForce RTX 3090 GPU with 24GB for one day and implemented by PyTorch using an AdamW optimizer with = 0.9, = 0.999 and weight decay of . We set a learning rate of and 60 epochs. Due to our discriminative contrastive learning framework that sample pairs are selected in a same batch, so the batch size has a strong influence on the experimental results. In terms of the hyperparameters in AUNCE, is set as 12 for BP4D and 8 for DISFA respectively, and the temperature coefficient is 0.5. The analysis for and , , will introduce in Section. 4.4.2.
In assessing the acquired representations, we adhere to the established linear evaluation protocol, as commonly employed in previous studies [12, 10]. This involves training a linear classifier atop the fixed base network, and the highest test accuracy across our models serves as a surrogate measure for the quality of the learned representations.
4.1.3 Evaluation Metrics
Aligned with current state-of-the-art methodologies, we utilized two prevalent frame-based metrics for AU detection: F1-score() and Accuracy(). F1-score represents the harmonic mean of precision and recall, widely employed in the context of AU detection. For each approach, we calculate average metrics across all AUs.
| Method | Source | AU Index | Avg. | |||||||||||
| 1 | 2 | 4 | 6 | 7 | 10 | 12 | 14 | 15 | 17 | 23 | 24 | |||
| Regional feature learning-based methods | ||||||||||||||
| EAC-Net [4] | 2018 TPAMI | 39.0 | 35.2 | 48.6 | 76.1 | 72.9 | 81.9 | 86.2 | 58.8 | 37.5 | 59.1 | 35.9 | 35.8 | 55.9 |
| ROI [3] | 2017 CVPR | 36.2 | 31.6 | 43.4 | 77.1 | 73.7 | 85.0 | 87.0 | 62.6 | 45.7 | 58.0 | 38.3 | 37.4 | 56.4 |
| ARL [5] | 2019 TAC | 45.8 | 39.8 | 55.1 | 75.7 | 77.2 | 82.3 | 86.6 | 58.8 | 47.6 | 62.1 | 47.4 | 55.4 | 61.1 |
| Multi-task learning-based methods | ||||||||||||||
| MAL [39] | 2023 TAC | 47.9 | 49.5 | 52.1 | 77.6 | 77.8 | 82.8 | 88.3 | 66.4 | 49.7 | 59.7 | 45.2 | 48.5 | 62.2 |
| JA-Net [7] | 2021 IJCV | 53.8 | 47.8 | 58.2 | 78.5 | 75.8 | 82.7 | 88.2 | 63.7 | 43.3 | 61.8 | 45.6 | 49.9 | 62.4 |
| GeoConv [40] | 2022 PR | 48.4 | 44.2 | 59.9 | 78.4 | 75.6 | 83.6 | 86.7 | 65.0 | 53.0 | 64.7 | 49.5 | 54.1 | 63.6 |
| GLEE-Net [8] | 2024 TCSVT | 60.6 | 44.4 | 61.0 | 80.6 | 78.7 | 85.4 | 88.1 | 64.9 | 53.7 | 65.1 | 47.7 | 58.5 | 65.7 |
| Semantic prior knowledge-based methods | ||||||||||||||
| MMA-Net [41] | 2023 PRL | 52.5 | 50.9 | 58.3 | 76.3 | 75.7 | 83.8 | 87.9 | 63.8 | 48.7 | 61.7 | 46.5 | 54.4 | 63.4 |
| SEV-Net [42] | 2021 CVPR | 58.2 | 50.4 | 58.3 | 81.9 | 73.9 | 87.7 | 87.5 | 61.6 | 52.6 | 62.2 | 44.6 | 47.6 | 63.9 |
| Correlational information-based methods | ||||||||||||||
| MCM [43] | 2024 WACV | 44.3 | 40.8 | 51.3 | 77.8 | 70.9 | 82.9 | 87.3 | 65.5 | 50.8 | 63.1 | 48.1 | 54.5 | 61.4 |
| HMP-PS [44] | 2021 CVPR | 53.1 | 46.1 | 56.0 | 76.5 | 76.9 | 82.1 | 86.4 | 64.8 | 51.5 | 63.0 | 49.9 | 54.5 | 63.4 |
| AAR [45] | 2023 TIP | 53.2 | 47.7 | 56.7 | 75.9 | 79.1 | 82.9 | 88.6 | 60.5 | 51.5 | 61.9 | 51.0 | 56.8 | 63.8 |
| ISTR [46] | 2021 ACM MM | 54.0 | 46.0 | 55.7 | 79.4 | 78.8 | 84.5 | 87.0 | 67.0 | 55.6 | 63.1 | 50.7 | 55.3 | 64.8 |
| MEGraph [33] | 2022 IJCAI | 52.7 | 44.3 | 60.9 | 79.9 | 80.1 | 85.3 | 89.2 | 69.4 | 55.4 | 64.4 | 49.8 | 55.1 | 65.5 |
| Contrastive learning-based methods | ||||||||||||||
| SimCLR [10] | 2020 ICML | 38.0 | 36.4 | 37.2 | 66.6 | 64.7 | 76.2 | 76.2 | 51.1 | 29.8 | 56.1 | 27.5 | 37.7 | 49.8 |
| MoCo [17] | 2020 CVPR | 30.8 | 41.3 | 42.1 | 70.2 | 70.4 | 78.7 | 82.5 | 53.3 | 25.2 | 59.1 | 31.5 | 34.3 | 51.6 |
| CLP [13] | 2023 TIP | 47.7 | 50.9 | 49.5 | 75.8 | 78.7 | 80.2 | 84.1 | 67.1 | 52.0 | 62.7 | 45.7 | 54.8 | 62.4 |
| BTFM [47] | 2023 CVPR | 57.4 | 52.6 | 64.6 | 79.3 | 81.5 | 82.7 | 85.6 | 67.9 | 47.3 | 58.0 | 47.0 | 44.9 | 64.1 |
| SupHCL [28] | 2022 ACM MM | 52.8 | 45.7 | 61.6 | 79.5 | 79.3 | 84.7 | 86.9 | 67.6 | 51.4 | 62.5 | 48.6 | 52.3 | 64.4 |
| KSRL [24] | 2022 CVPR | 53.3 | 47.4 | 56.2 | 79.4 | 80.7 | 85.1 | 89.0 | 67.4 | 55.9 | 61.9 | 48.5 | 49.0 | 64.5 |
| CLEF [48] | 2023 ICCV | 55.8 | 46.8 | 63.3 | 79.5 | 77.6 | 83.6 | 87.8 | 67.3 | 55.2 | 63.5 | 53.0 | 57.8 | 65.9 |
| AUNCE(Ours) | - | 53.6 | 49.8 | 61.6 | 78.4 | 78.8 | 84.7 | 89.6 | 67.4 | 55.1 | 65.4 | 50.9 | 58.0 | 66.1 |
| ( | ( | ( | ( | ( | ( | ( | ( | ( | ( | ( | ( | ( | ||
| 0.15) | 0.12) | 0.17) | 0.21) | 0.19) | 0.22) | 0.22) | 0.17) | 0.14) | 0.15) | 0.14) | 0.15) | 0.17) | ||
| Method | Source | AU Index | Avg. | |||||||
| 1 | 2 | 4 | 6 | 9 | 12 | 25 | 26 | |||
| Regional feature learning-based methods | ||||||||||
| EAC-Net [4] | 2018 TPAMI | 41.5 | 26.4 | 66.4 | 50.7 | 80.5 | 89.3 | 88.9 | 15.6 | 48.5 |
| ROI [3] | 2017 CVPR | 41.5 | 26.4 | 66.4 | 50.7 | 80.5 | 89.3 | 88.9 | 15.6 | 48.5 |
| ARL [5] | 2019 TAC | 43.9 | 42.1 | 63.6 | 41.8 | 40.0 | 76.2 | 95.2 | 66.8 | 58.7 |
| Multi-task learning-based methods | ||||||||||
| MAL [39] | 2023 TAC | 43.8 | 39.3 | 68.9 | 47.4 | 48.6 | 72.7 | 90.6 | 52.6 | 58.0 |
| JA-Net [7] | 2021 IJCV | 62.4 | 60.7 | 67.1 | 41.1 | 45.1 | 73.5 | 90.9 | 67.4 | 63.5 |
| GeoConv [40] | 2022 PR | 65.5 | 65.8 | 67.2 | 48.6 | 51.4 | 72.6 | 80.9 | 44.9 | 62.1 |
| GLEE-Net [8] | 2024 TCSVT | 61.9 | 54.0 | 75.8 | 45.9 | 55.7 | 77.6 | 92.9 | 60.0 | 65.5 |
| Semantic prior knowledge-based methods | ||||||||||
| SEV-Net [42] | 2021 CVPR | 55.3 | 53.1 | 61.5 | 53.6 | 38.2 | 71.6 | 95.7 | 41.5 | 58.8 |
| MMA-Net [41] | 2023 PRL | 63.8 | 54.8 | 73.6 | 39.2 | 61.5 | 73.1 | 92.3 | 70.5 | 66.0 |
| Correlational information-based methods | ||||||||||
| HMP-PS [44] | 2021 CVPR | 38.0 | 45.9 | 65.2 | 50.9 | 50.8 | 76.0 | 93.3 | 67.6 | 61.0 |
| ISTR [46] | 2021 ACM MM | 47.5 | 53.3 | 64.4 | 51.8 | 44.4 | 74.7 | 92.1 | 60.7 | 61.1 |
| MEGraph [33] | 2022 IJCAI | 52.5 | 45.7 | 76.1 | 51.8 | 46.5 | 76.1 | 92.9 | 57.6 | 62.4 |
| AAR [45] | 2023 TIP | 62.4 | 53.6 | 71.5 | 39.0 | 48.8 | 76.1 | 91.3 | 70.6 | 64.2 |
| MCM [43] | 2024 WACV | 49.6 | 44.1 | 67.2 | 65.5 | 49.0 | 81.5 | 85.9 | 71.8 | 64.3 |
| Contrastive learning-based methods | ||||||||||
| SIMCLR [10] | 2020 ICML | 21.2 | 23.3 | 47.5 | 42.4 | 35.5 | 66.8 | 81.5 | 52.7 | 46.4 |
| MoCo [17] | 2020 CVPR | 22.7 | 18.2 | 45.9 | 45.4 | 34.1 | 72.9 | 83.4 | 54.5 | 47.1 |
| CLP [13] | 2023 TIP | 42.4 | 38.7 | 63.5 | 59.7 | 38.9 | 73.0 | 85.0 | 58.1 | 57.4 |
| BTFM [47] | 2023 CVPR | 41.5 | 44.9 | 60.3 | 51.5 | 50.3 | 70.4 | 91.3 | 55.3 | 58.2 |
| SupHCL [28] | 2022 ACM MM | 52.5 | 58.8 | 70.0 | 53.5 | 51.4 | 73.1 | 95.6 | 58.0 | 64.1 |
| KSRL [24] | 2022 CVPR | 60.4 | 59.2 | 67.5 | 52.7 | 51.5 | 76.1 | 91.3 | 57.7 | 64.5 |
| CLEF [48] | 2023 ICCV | 64.3 | 61.8 | 68.4 | 49.0 | 55.2 | 72.9 | 89.9 | 57.0 | 64.8 |
| AUNCE(Ours) | - | 61.8 | 58.9 | 74.9 | 49.7 | 56.2 | 73.5 | 92.1 | 64.2 | 66.4 |
| ( | ( | ( | ( | ( | ( | ( | ( | ( | ||
| 0.37) | 0.22) | 0.42) | 0.31) | 0.36) | 0.49) | 0.42) | 0.28) | 0.36) | ||
| Method | Source | AU Index | Avg. | |||||||||
| 1 | 2 | 4 | 6 | 10 | 12 | 14 | 15 | 23 | 24 | |||
| AlexNet [49] | 2012 NIPS | 44 | 46 | 2 | 73 | 72 | 82 | 5 | 19 | 43 | 42 | 42.8 |
| LSVM [50] | 2008 JMLR | 38 | 32 | 13 | 67 | 64 | 78 | 15 | 29 | 49 | 44 | 42.9 |
| TCAE [51] | 2019 CVPR | 43.9 | 49.5 | 6.3 | 71.0 | 76.2 | 79.5 | 10.7 | 28.5 | 34.5 | 41.7 | 44.2 |
| CPAM [52] | 2020 TBIOM | 43.7 | 44.9 | 19.8 | 74.6 | 76.5 | 79.8 | 50.0 | 33.9 | 16.8 | 12.9 | 45.3 |
| EAC-Net [4] | 2018 TPAMI | 15.5 | 56.6 | 0.1 | 81.0 | 76.1 | 84.0 | 0.1 | 38.5 | 57.8 | 51.2 | 46.1 |
| MoCo [17] | 2020 CVPR | 35.9 | 45.4 | 13.5 | 83.4 | 71.3 | 78.1 | 23.3 | 37.3 | 26.6 | 50.7 | 46.5 |
| SimCLR [10] | 2020 ICML | 39.6 | 48.3 | 5.6 | 80.7 | 76.2 | 80.6 | 18.1 | 41.6 | 46.1 | 43.8 | 48.1 |
| ARL [5] | 2019 TAC | 51.9 | 45.9 | 13.7 | 79.2 | 75.5 | 82.8 | 0.1 | 44.9 | 59.2 | 47.5 | 50.1 |
| TAE [53] | 2022 TPAMI | 46.3 | 48.8 | 13.4 | 76.7 | 74.8 | 81.8 | 19.9 | 42.3 | 50.6 | 50.0 | 50.5 |
| JA-Net [7] | 2021 IJCV | 46.5 | 49.3 | 19.2 | 79.0 | 75.0 | 84.8 | 44.1 | 33.5 | 54.9 | 50.7 | 53.7 |
| CLP [13] | 2023 TIP | 44.6 | 58.7 | 34.7 | 75.9 | 78.6 | 86.6 | 20.3 | 44.8 | 56.4 | 42.2 | 54.3 |
| AAR [45] | 2023 TIP | 66.3 | 53.9 | 23.7 | 81.5 | 73.6 | 84.2 | 43.8 | 53.8 | 58.2 | 46.5 | 58.5 |
| MAL [39] | 2023 TAC | 52.4 | 57.0 | 54.1 | 74.5 | 78.0 | 84.9 | 43.1 | 47.7 | 54.4 | 51.9 | 59.8 |
| AUNCE(Ours) | - | 53.6 | 62.8 | 51.3 | 80.6 | 82.1 | 88.2 | 48.2 | 49.8 | 54.6 | 58.9 | 63.0 |
| ( | ( | ( | ( | ( | ( | ( | ( | ( | ( | ( | ||
| 0.33) | 0.18) | 0.28) | 0.24) | 0.41) | 0.11) | 0.35) | 0.23) | 0.42) | 0.35) | 0.29) | ||
| Method | Source | AU Index | Avg. | |||||||||||
| 1 | 2 | 4 | 6 | 7 | 10 | 12 | 15 | 23 | 24 | 25 | 26 | |||
| EAC-Net [4] | 2018 TPAMI | 49.6 | 33.7 | 55.6 | 66.4 | 82.3 | 81.4 | 76.9 | 11.8 | 12.5 | 12.2 | 93.7 | 26.8 | 50.2 |
| ARL [5] | 2019 TAC | 59.2 | 48.2 | 54.9 | 70.0 | 83.4 | 80.3 | 72.0 | 0.1 | 0.1 | 17.3 | 93.0 | 37.5 | 51.3 |
| JA-Net [7] | 2021 IJCV | 61.7 | 50.1 | 56.0 | 71.7 | 81.7 | 82.3 | 78.0 | 31.1 | 1.4 | 8.6 | 94.8 | 37.5 | 54.6 |
| PASN [38] | 2021 ICCV | 65.7 | 64.2 | 66.5 | 76.6 | 74.7 | 72.7 | 78.6 | 18.5 | 10.6 | 55.1 | 80.7 | 41.7 | 58.8 |
| AAR [45] | 2023 TIP | 65.4 | 57.9 | 59.9 | 73.2 | 84.6 | 83.2 | 79.9 | 21.8 | 27.4 | 19.9 | 94.5 | 41.7 | 59.1 |
| AUNCE(Ours) | - | 68.8 | 67.6 | 64.7 | 74.8 | 88.6 | 78.4 | 81.3 | 26.9 | 36.7 | 18.6 | 96.1 | 43.8 | 62.2 |
| ( | ( | ( | ( | ( | ( | ( | ( | ( | ( | ( | ( | ( | ||
| 0.25) | 0.37) | 0.28) | 0.33) | 0.12) | 0.47) | 0.31) | 0.17) | 0.08) | 0.42) | 0.39) | 0.32) | 0.29) | ||
4.2 Comparison with State-of-the-Art Methods
4.2.1 Evaluation on BP4D
Since we use AU labels to assist the process of selecting positive sample pairs, we introduce five groups of supervised AU detection frameworks to compare with our method. The quantitative results of state-of-the-art methods from the past seven years for BP4D dataset are shown in Table 2. Compared to the latest state-of-the-art results, our method AUNCE demonstrates significantly superior performance.
Methods in the first group are based on feature extraction of regional area around AUs, including EAC-Net [4], ROI [3] and ARL [5]. Our approach achieves a notable improvement, with an increase in F1-score ranging from 5.0% to 10.2% over these methods. This advancement is primarily due to early feature extraction methods neglecting critical correlation information among AUs and failing to specifically address the class imbalance issue for each AU. Furthermore, the precision of the encoders utilized by these methods is generally lower.
Methods in the second group are based on a multi-task learning strategy, including JA-Net [7], GeoConv [40], MAL [39] and GLEE-Net [8]. Our method surpasses MAL by 3.9%, primarily due to the ability of AUNCE to help the encoder address the class imbalance issue among different AUs, and the facial expression recognition component in MAL introduces some negative transfer effects on AU detection. The 3.7% improvement over JA-Net can be attributed to the influence of the facial landmark detection task within the multi-task learning framework on AU detection, which is also affected by the weighting of different losses. Additionally, the modest 2.5% and 0.4% improvement over GeoConv and GLEE-Net is due to the relatively limited impact of integrating 3D information on enhancing the performance of 2D AU detection.
Methods in the third group mainly utilize the semantic prior knowledge, including MMA-Net [41] and SEV-Net [42]. Our approach demonstrates an average improvement of 2.7% and 2.2%, respectively. This phenomenon can be attributed to the inherent limitations of these methods in effectively capturing and representing the distinct information encoded within AUs using simple semantic descriptions.
Methods in the fourth group focus on capturing correlational information among AUs, including MCM [43], AAR [45], ISTR [46], HMP-PS [44] and MEGraph [33]. Our approach exhibits a performance advantage of approximately 0.6%-4.7% in F1-score. This underscores the efficacy of our supervised discriminative contrastive learning paradigm in effectively capturing differential information between AUs from each sample pair instead of pixel-level information of the entire face associated with AU. It is noteworthy that the encoder used in our method is only the same as the network MEGraph used for the first stage of training, with reduced parameters by nearly 7M. This highlights learning only the difference information among features is more efficient than learning the whole pixel-level information.
Methods in the last group are based on contrastive learning, including SIMCLR [10], MoCo [17], CLP [13], BTFM [47], SupHCL [28], KSRL [24] and CLEF [48]. When compared to these methods, our approach demonstrates a performance advantage of approximately 0.2% to 16.3% in F1-score. This improvement is attributed to the efficacy of our proposed negative sample re-weighting strategy and positive sample sampling strategy, specifically tailored for the AU detection task using static images. In addition, compared to contrastive learning methods based on weighted cross-entropy loss, our approach significantly reduces the extraction of pixel-level redundant information.
4.2.2 Evaluation on DISFA
Comparable outcomes are evident in the DISFA dataset, as outlined in Table 3, where AUNCE attains the highest overall performance in AU detection. Furthermore, a comparison between Table 2 and Table 3 reveals that recent methods such as SEV-Net, MEGraph, and BTFM demonstrate strong performance on the BP4D dataset but achieve only mediocre results on the DISFA dataset. This disparity suggests their limited generalizability. The more pronounced class imbalance issue in DISFA, as shown in Table 1, likely contributes to this performance gap. In contrast, AUNCE consistently delivers robust performance on both BP4D and DISFA datasets and achieves more stable results across various AUs due to our proposed negative sample re-weighting strategy.
4.2.3 Evaluation on GFT
Table 4 presents the F1-score results on the GFT dataset, where our AUNCE method demonstrates significantly superior performance compared to previous approaches. Unlike BP4D and DISFA, which primarily consist of near-frontal facial images, GFT includes many images captured under out-of-plane poses. In this challenging scenario, other methods such as EAC-Net, ARL and CLP so on struggle to perform well. In contrast, AUNCE achieves a commendable average F1-score of 63.0%.
4.2.4 Evaluation on Aff-Wild2
We have validated the performance of our AUNCE method in constrained scenarios. To further assess its effectiveness in unconstrained scenarios, we compared it with other approaches on the challenging Aff-Wild2 dataset, as shown in Table 5. Our AUNCE method demonstrates a higher average F1-score than previous methods. Notably, while EAC-Net and PASN leverage external training data, our method achieves superior overall performance using only the Aff-Wild2 dataset. By comparing the results of ARL, JA-Net, AAR to our AUNCE method across Table 2 to Table 5, it is evident that the performance margins between our AUNCE method and other methods on GFT and Aff-Wild2 are larger than those on BP4D and DISFA. This indicates that AUNCE is more effective at handling challenging cases in AU detection.
| Backbone | Source | Loss | F1-Score(%) | Accuracy(%) |
| ResNet18 [54] | 2016CVPR | WCE | 52.3 | 73.8 |
| AUNCE | ||||
| ResNet50 [54] | 2016CVPR | WCE | 56.2 | 75.5 |
| AUNCE | ||||
| ROI [3] | 2017CVPR | WCE | 56.4 | 75.9 |
| AUNCE | ||||
| ARL [5] | 2019TAC | WCE | 61.1 | 78.2 |
| AUNCE | ||||
| JA-Net [7] | 2021IJCV | WCE | 62.4 | 78.6 |
| AUNCE | ||||
| MEGraph [33] | 2022IJCAI | WCE | 63.6 | 80.0 |
| (Onestage) | AUNCE |
4.3 Ablation Study
4.3.1 Compared with weighted cross-entropy loss
Due to the primary innovation of this paper being the introduction of a novel contrastive loss, AUNCE, which is compatible with various AU detection encoders, we conducted a comparative analysis between the proposed AUNCE loss and the traditional weighted cross-entropy loss (WCE) across multiple AU detection encoders, as detailed in Table 6. The findings reveal that AUNCE demonstrates superior performance in AU detection. Notably, the MEGraph encoder achieved the best results, with the F1-score on the BP4D dataset improving from 63.6% to 66.1%. This underscores the validity of capturing unique features of different samples over focusing solely on pixel-level information of the entire face associated with AU.
| Dataset | Loss | Frame Rate(FPS) | 1 Epoch Time(s) |
| BP4D | WCE | 0.0271 | 2734 |
| AUNCE | 0.0138 | 1388 | |
| DISFA | WCE | 0.0265 | 2308 |
| AUNCE | 0.0136 | 1189 |
Furthermore, as shown in Table 7, when the number of encoder parameters is the same, our proposed AUNCE loss increases the frame rate and reduces the training time of one epoch by nearly half compared to WCE loss. This indicates that our approach of capturing only differential information between AUs from each sample pair has higher efficiency for training encoder than methods that capture the entire facial information.
| Model | BL | wi | PS | NS | AU Index | F1-Score(%) | Accuracy(%) | |||||||||||
| 1 | 2 | 4 | 6 | 7 | 10 | 12 | 14 | 15 | 17 | 23 | 24 | |||||||
| A | 39.8 | 44.3 | 58.8 | 76.0 | 77.7 | 76.9 | 88.0 | 64.5 | 49.0 | 59.0 | 43.5 | 43.4 | 60.1 | 79.1 | ||||
| B | 40.1 | 43.0 | 58.9 | 75.4 | 79.3 | 78.8 | 87.8 | 64.1 | 48.7 | 61.0 | 46.9 | 47.5 | 61.00.9↑ | 79.30.2↑ | ||||
| C | 51.1 | 45.6 | 58.3 | 77.5 | 77.0 | 84.5 | 89.0 | 63.7 | 54.6 | 65.5 | 46.8 | 53.3 | 63.83.7↑ | 79.80.7↑ | ||||
| D | 50.2 | 43.0 | 58.7 | 77.9 | 77.3 | 83.7 | 88.7 | 64.2 | 53.9 | 64.9 | 50.0 | 56.4 | 64.14.0↑ | 79.90.8↑ | ||||
| E | 53.6 | 49.8 | 61.6 | 78.4 | 78.8 | 84.7 | 89.6 | 67.4 | 55.1 | 65.4 | 50.9 | 58.0 | ||||||
4.3.2 Evaluating other components
We further evaluate the effectiveness of weight coeffcient , negative sample re-weighting strategy and positive sample samplying strategy. Quantitative results of our method with the above component combinations are summarized in Table 8. The baseline (BL) is rooted in SIMCLR [10], but positive sample pairs are changed to images with the highest similarity to original images. Other components are the weight coefficient () for both WCE and AUNCE, the positive sample sampling strategy (PS), and the negative sample re-weighting strategy (NS).
Weight coefficient : The weights have been pointed out as a fixed value in Section. 3.1, which achieve an increase of 0.9% in F1-score and 0.2% in Accuracy. For an AU, its activation indicator is a binary variable, and the corresponding information content can be measured using entropy: . Therefore, AUs with lower activation probabilities carry more information and should be assigned higher weights. This forms the theoretical basis for our weighting strategy.
Positive sample sampling strategy: As outlined in Table 8, the positive sample sampling strategy contributes to a 2.8% increase in F1-score and a 0.5% improvement in Accuracy compared to model B. This validates that selecting different types of positive sample pairs with appropriate probabilities can mitigate issues arising from AU labels tainted by noise and errors. The strategy achieves this by incorporating three types of positive sample pairs: the self-supervised signal pair, the highest similarity pair, and the mixed positive features pair. These pairs provide the models with diverse information from various views, thereby enhancing the generalization ability of the discriminative contrastive learning framework.
Negative sample re-weighting strategy: The negative sample re-weighting strategy to minority AUs results in a 3.1% increase in F1-score and a 0.6% increase in Accuracy compared to model B. This illustrates that the strategy can change the backpropagation gradient of minority and majority class samples, facilitating faster label category gradient updates with a smaller number of samples. Additionally, model E achieves an average increase of 2.3% in F1-score compared to model C, further supporting the efficacy of the re-weighting strategy.

(a)

(b)

(c)

(d)

(e)

(f)

(g)
(h)

(i)

(j)

(k)

(l)
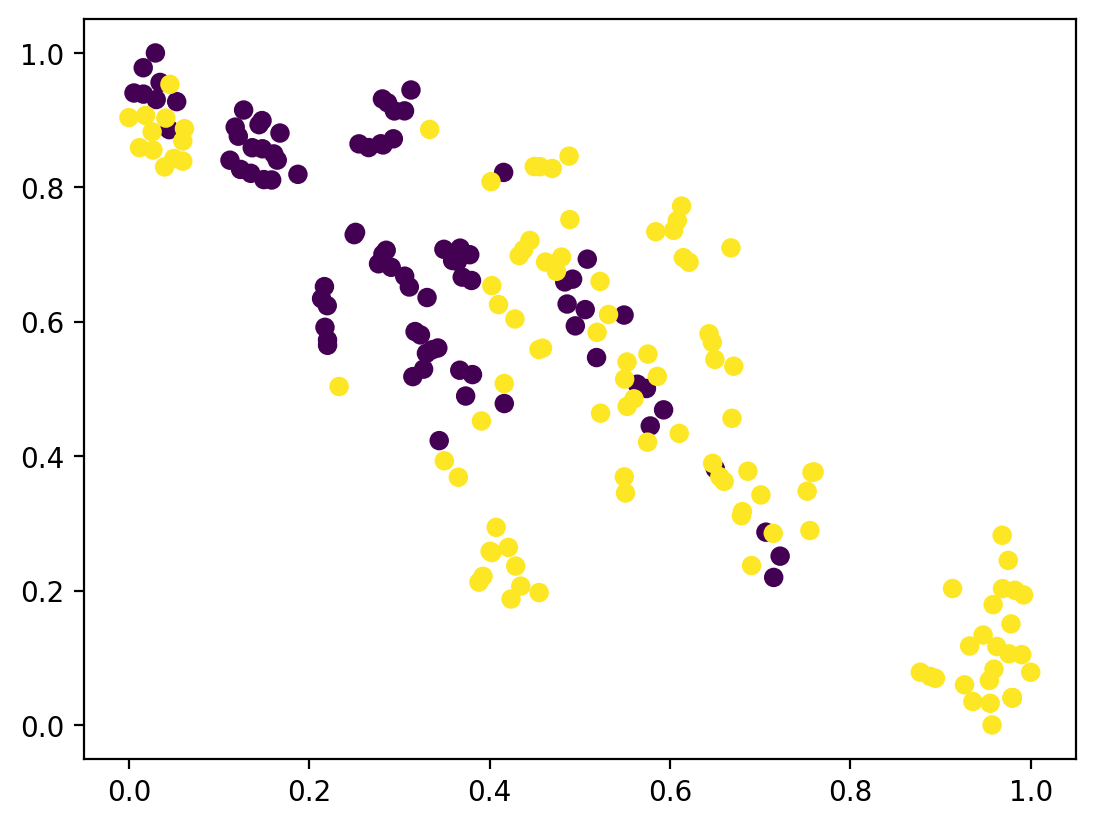
We further show the visualization using T-SNE dimensionality reduction of the learned feature representations optimized by AUNCE and WCE to qualitatively assess the efficacy of our proposed discriminative contrastive learning paradigm, as illustrated in Fig. 4. For each dataset, a random sample of 200 images is utilized for illustration purposes. A comparison between Fig. 4(a), Fig. 4(f) against Fig. 4(g), Fig. 4(l) reveals that the learned representations optimized by AUNCE exhibit greater separability than those optimized by WCE. Additionally, Fig. 4(b)-(f) and Fig. 4(g)-(l) qualitatively showcase the effectiveness of each component in our ablation study.
Based on all ablation studies, it demonstrates that our proposed discriminative contrastive learning paradigm enhances the encoding capability of the shared encoder, improves classification accuracy by addressing the class imbalance issue of each AU type, and bolsters model robustness against AU labels affected by noise and errors. This, in turn, leads to enhanced generalization performance in AU detection. The introduction of each component proves beneficial for performance improvement, with NS emerging as the most effective component. Moreover, the results on each AU are also shown in Table 8. It can be seen that the results on basically every AU have improved or approached after we add , PS and NS.
4.4 Hyperparameters Analysis
| F1-Score(%) | |||||
| Probabilities | 1 | 0 | 0 | 0 | 60.1 |
| 0 | 1 | 0 | 0 | 48.4 | |
| 0 | 0 | 1 | 0 | 63.2 | |
| 0 | 0 | 0 | 1 | 17.6 | |
| 0.1 | 0.1 | 0.8 | 0 | 63.8 | |
| 0.15 | 0.15 | 0.7 | 0 | 66.1 | |
| 0.2 | 0.2 | 0.6 | 0 | 65.7 | |
| 0.25 | 0.25 | 0.5 | 0 | 65.2 | |
| 0.3 | 0.3 | 0.4 | 0 | 64.3 | |
| 0.4 | 0.4 | 0.2 | 0 | 58.8 |
4.4.1 , the probabilities of various positive sample pairs
In our paper, represents the probabilities of images with the highest similarity to original images, represents the probabilities of self-supervised images enhanced by simple augmentations, represents the probabilities of a mixture of all positive samples, and represents the probabilities of images with the lowest similarity to original images. Given that , , , and address the problem of AU labels tainted by noise and errors, we systematically vary these probabilities from 0 to 1 to investigate their impact on our framework. As and are deemed reliable positive samples, we set their values to be the same during the variation.
The experimental results are presented in Table 9. When =0.15, =0.15, =0.7, and =0, the experimental result is optimal. It is observed that images with the lowest similarity to original images contribute minimally to the training process, as these images essentially represent noise and errors. The conclusion is consistent with [55]. The mixture of all positive samples plays a pivotal role, as it encourages the feature representation of each instance to be closer to the class centroid, facilitating the capture of essential characteristics of the positive class. The indispensability of the remaining two positive samples lies in their ability to mitigate the impact of noisy and false samples, thereby reinforcing the robustness of the training process.

(a)

(b)
4.4.2 Backpropagation rate controller
As is well understood, the hyperparameter plays a crucial role in governing the relative importance of minority and majority class samples during the parameter update process. It ensures that the model allocates more attention to minority class samples when necessary and balances the gradient magnitudes accordingly. To explore its effects, we systematically vary the hyperparameter for the minority class from 0.8 to 1.8, with for the majority class fixed at 0.4. Additionally, we vary for the majority class from 0.2 to 1.2, keeping for the minority class fixed at 1.2.
The experimental results are depicted in Fig. 5. The optimal experimental outcome is observed when for the minority class is set to 1.2, and for the majority class is fixed at 0.4. Hence, when , the impact of the class imbalance issue can be effectively mitigated.
5 Conclusion
In this paper, we proposes a discriminative contrastive learning framework tailored for AU detection, introducing a novel contrastive loss named AUNCE. AUNCE builds upon the InfoNCE loss, reformulating the task from learning pixel-level information of the entire face to focusing on the subtle feature variations that occur during AU activation, thereby enhancing detection efficiency. We further introduce a positive sample sampling strategy that constructs three types of positive sample pairs, effectively addressing the challenge of AU labels tainted by noise and errors in four AU datasets. To combat the class imbalance problem often seen in AU detection, we implement a negative sample re-weighting strategy specifically targeting minority AUs, facilitating the identification of hard negative samples. Experimental results reveal that AUNCE consistently outperforms existing methods, particularly those employing weighted cross-entropy loss. However, our negative sample reweighting strategy may inadvertently hinder the model’s ability to learn features of common AUs. An excessive emphasis on minority classes could result in underfitting of the majority classes. To overcome this limitation, our future research will focus on developing dynamic reweighting techniques with adaptive mechanisms that balance minority and majority classes, enhancing the robustness and adaptability of our framework across diverse conditions.
Acknowledgement
This research was supported by the National Natural Science Foundation of China (Nos. 62176221, 61572407), and Sichuan Province Science and Technology Support Program (Nos. 2024NSFTD0036, 2024ZHCG0166). The computation is completed in the HPC Platform of Huazhong University of Science and Technology.
Declaration of generative AI and AI-assisted technologies in the writing process
During the preparation of this work the author(s) used in order to polish our paper. After using this tool/service, the author(s) reviewed and edited the content as needed and take(s) full responsibility for the content of the publication.
References
- [1] E. L. Rosenberg, P. Ekman, What the face reveals: Basic and applied studies of spontaneous expression using the Facial Action Coding System (FACS), Oxford University Press, 2020.
- [2] M. Dahmane, J. Meunier, Prototype-based modeling for facial expression analysis, IEEE Transactions on Multimedia 16 (6) (2014) 1574–1584.
- [3] W. Li, F. Abtahi, Z. Zhu, Action unit detection with region adaptation, multi-labeling learning and optimal temporal fusing, in: Proc. CVPR, 2017, pp. 1841–1850.
- [4] W. Li, F. Abtahi, Z. Zhu, L. Yin, Eac-net: Deep nets with enhancing and cropping for facial action unit detection, IEEE transactions on pattern analysis and machine intelligence 40 (11) (2018) 2583–2596.
- [5] Z. Shao, Z. Liu, J. Cai, Y. Wu, L. Ma, Facial action unit detection using attention and relation learning, IEEE transactions on affective computing (2019).
- [6] N. Sankaran, D. D. Mohan, N. N. Lakshminarayana, S. Setlur, V. Govindaraju, Domain adaptive representation learning for facial action unit recognition, Pattern Recognition 102 (2020) 107127.
- [7] Z. Shao, Z. Liu, J. Cai, L. Ma, Jaa-net: Joint facial action unit detection and face alignment via adaptive attention, International Journal of Computer Vision 129 (2) (2021) 321–340.
- [8] W. Zhang, L. Li, Y. Ding, W. Chen, Z. Deng, X. Yu, Detecting facial action units from global-local fine-grained expressions, IEEE Transactions on Circuits and Systems for Video Technology (2024).
- [9] Z. Shang, B. Liu, Facial action unit detection based on multi-task learning strategy for unlabeled facial images in the wild, Expert Systems with Applications 253 (2024) 124285.
- [10] T. Chen, S. Kornblith, M. Norouzi, G. Hinton, A simple framework for contrastive learning of visual representations, in: Proc. ICML, PMLR, 2020, pp. 1597–1607.
- [11] T. Wang, P. Isola, Understanding contrastive representation learning through alignment and uniformity on the hypersphere, in: Proc. ICML, PMLR, 2020, pp. 9929–9939.
- [12] A. v. d. Oord, Y. Li, O. Vinyals, Representation learning with contrastive predictive coding, arXiv preprint arXiv:1807.03748 (2018).
- [13] Y. Li, S. Shan, Contrastive learning of person-independent representations for facial action unit detection, IEEE Transactions on Image Processing (2023).
- [14] P. H. Le-Khac, G. Healy, A. F. Smeaton, Contrastive representation learning: A framework and review, Ieee Access 8 (2020) 193907–193934.
- [15] A. Jaiswal, A. R. Babu, M. Z. Zadeh, D. Banerjee, F. Makedon, A survey on contrastive self-supervised learning, Technologies 9 (1) (2020) 2.
- [16] M. Gutmann, A. Hyvärinen, Noise-contrastive estimation: A new estimation principle for unnormalized statistical models, in: Proc. ICAIS, JMLR Workshop and Conference Proceedings, 2010, pp. 297–304.
- [17] K. He, H. Fan, Y. Wu, S. Xie, R. Girshick, Momentum contrast for unsupervised visual representation learning, in: Proc. CVPR, 2020, pp. 9729–9738.
- [18] X. Chen, K. He, Exploring simple siamese representation learning, in: Proc. CVPR, 2021, pp. 15750–15758.
- [19] J. D. M.-W. C. Kenton, L. K. Toutanova, Bert: Pre-training of deep bidirectional transformers for language understanding, in: Proc. NAACL, Vol. 1, 2019, p. 2.
- [20] S. Arora, H. Khandeparkar, M. Khodak, O. Plevrakis, N. Saunshi, A theoretical analysis of contrastive unsupervised representation learning, arXiv preprint arXiv:1902.09229 (2019).
- [21] P. Khosla, P. Teterwak, C. Wang, A. Sarna, Y. Tian, P. Isola, A. Maschinot, C. Liu, D. Krishnan, Supervised contrastive learning, Advances in neural information processing systems 33 (2020) 18661–18673.
- [22] T. Chen, S. Kornblith, K. Swersky, M. Norouzi, G. E. Hinton, Big self-supervised models are strong semi-supervised learners, Advances in neural information processing systems 33 (2020) 22243–22255.
- [23] X. Niu, H. Han, S. Shan, X. Chen, Multi-label co-regularization for semi-supervised facial action unit recognition, Advances in neural information processing systems 32 (2019).
- [24] Y. Chang, S. Wang, Knowledge-driven self-supervised representation learning for facial action unit recognition, in: Proc. CVPR, 2022, pp. 20417–20426.
- [25] Z. Liu, R. Liu, Z. Shi, L. Liu, X. Mi, K. Murase, Semi-supervised contrastive learning with soft mask attention for facial action unit detection, in: Proc. ICASSP, IEEE, 2023, pp. 1–5.
- [26] B.-F. Wu, Y.-T. Wei, B.-J. Wu, C.-H. Lin, Contrastive feature learning and class-weighted loss for facial action unit detection, in: Proc. SMC, IEEE, 2019, pp. 2478–2483.
- [27] V. Suresh, D. C. Ong, Using positive matching contrastive loss with facial action units to mitigate bias in facial expression recognition, in: Proc. ACII, IEEE, 2022, pp. 1–8.
- [28] Y. Chen, C. Chen, X. Luo, J. Huang, X.-S. Hua, T. Wang, Y. Liang, Pursuing knowledge consistency: Supervised hierarchical contrastive learning for facial action unit recognition, in: Proc. ACM MM, 2022, pp. 111–119.
- [29] R. Qian, T. Meng, B. Gong, M.-H. Yang, H. Wang, S. Belongie, Y. Cui, Spatiotemporal contrastive video representation learning, in: Proc. CVPR, 2021, pp. 6964–6974.
- [30] J. Robinson, C.-Y. Chuang, S. Sra, S. Jegelka, Contrastive learning with hard negative samples, Proc. ICLR (2020).
- [31] F. Wang, H. Liu, Understanding the behaviour of contrastive loss, in: Proc. CVPR, 2021, pp. 2495–2504.
- [32] D. Arpit, S. Jastrzkebski, N. Ballas, D. Krueger, E. Bengio, M. S. Kanwal, T. Maharaj, A. Fischer, A. Courville, Y. Bengio, et al., A closer look at memorization in deep networks, in: Proc. ICML, 2017, pp. 233–242.
- [33] C. Luo, S. Song, W. Xie, L. Shen, H. Gunes, Learning multi-dimensional edge feature-based au relation graph for facial action unit recognition, arXiv preprint arXiv:2205.01782 (2022).
- [34] X. Zhang, L. Yin, J. F. Cohn, S. Canavan, M. Reale, A. Horowitz, P. Liu, J. M. Girard, Bp4d-spontaneous: a high-resolution spontaneous 3d dynamic facial expression database, Image and Vision Computing 32 (10) (2014) 692–706.
- [35] S. M. Mavadati, M. H. Mahoor, K. Bartlett, P. Trinh, J. F. Cohn, Disfa: A spontaneous facial action intensity database, IEEE Transactions on Affective Computing 4 (2) (2013) 151–160.
- [36] J. M. Girard, W.-S. Chu, L. A. Jeni, J. F. Cohn, Sayette group formation task (gft) spontaneous facial expression database, in: Proc. FG, IEEE, 2017, pp. 581–588.
- [37] D. Kollias, S. Zafeiriou, Expression, affect, action unit recognition: Aff-wild2, multi-task learning and arcface, arXiv preprint arXiv:1910.04855 (2019).
- [38] W. Zhang, Z. Guo, K. Chen, L. Li, Z. Zhang, Y. Ding, R. Wu, T. Lv, C. Fan, Prior aided streaming network for multi-task affective analysis, in: Proc. ICCV, 2021, pp. 3539–3549.
- [39] Y. Li, S. Shan, Meta auxiliary learning for facial action unit detection, IEEE Transactions on Affective Computing (2023).
- [40] Y. Chen, G. Song, Z. Shao, J. Cai, T.-J. Cham, J. Zheng, Geoconv: Geodesic guided convolution for facial action unit recognition, Pattern Recognition 122 (2022) 108355.
- [41] Z. Shang, C. Du, B. Li, Z. Yan, L. Yu, Mma-net: Multi-view mixed attention mechanism for facial action unit detection, Pattern Recognition Letters (2023).
- [42] H. Yang, L. Yin, Y. Zhou, J. Gu, Exploiting semantic embedding and visual feature for facial action unit detection, in: Proc. CVPR, 2021, pp. 10482–10491.
- [43] X. Zhang, H. Yang, T. Wang, X. Li, L. Yin, Multimodal channel-mixing: Channel and spatial masked autoencoder on facial action unit detection, in: Proc. WACV, 2024, pp. 6077–6086.
- [44] T. Song, Z. Cui, W. Zheng, Q. Ji, Hybrid message passing with performance-driven structures for facial action unit detection, in: Proc. CVPR, 2021, pp. 6267–6276.
- [45] Z. Shao, Y. Zhou, J. Cai, H. Zhu, R. Yao, Facial action unit detection via adaptive attention and relation, IEEE Transactions on Image Processing (2023).
- [46] Z. Li, X. Deng, X. Li, L. Yin, Integrating semantic and temporal relationships in facial action unit detection, in: Proc. ACM MM, 2021, pp. 5519–5527.
- [47] Z. Cui, C. Kuang, T. Gao, K. Talamadupula, Q. Ji, Biomechanics-guided facial action unit detection through force modeling, in: Proc. CVPR, 2023, pp. 8694–8703.
- [48] X. Zhang, T. Wang, X. Li, H. Yang, L. Yin, Weakly-supervised text-driven contrastive learning for facial behavior understanding, in: Proc. ICCV, 2023, pp. 20751–20762.
- [49] A. Krizhevsky, I. Sutskever, G. E. Hinton, Imagenet classification with deep convolutional neural networks, Proc. NIPS 25 (2012).
- [50] R.-E. Fan, K.-W. Chang, C.-J. Hsieh, X.-R. Wang, C.-J. Lin, Liblinear: A library for large linear classification, the Journal of machine Learning research 9 (2008) 1871–1874.
- [51] Y. Li, J. Zeng, S. Shan, X. Chen, Self-supervised representation learning from videos for facial action unit detection, in: Proc. CVPR, 2019, pp. 10924–10933.
- [52] I. O. Ertugrul, J. F. Cohn, L. A. Jeni, Z. Zhang, L. Yin, Q. Ji, Crossing domains for au coding: Perspectives, approaches, and measures, IEEE transactions on biometrics, behavior, and identity science 2 (2) (2020) 158–171.
- [53] Y. Li, J. Zeng, S. Shan, Learning representations for facial actions from unlabeled videos, IEEE Transactions on Pattern Analysis and Machine Intelligence 44 (1) (2022) 302–317.
- [54] K. He, X. Zhang, S. Ren, J. Sun, Deep residual learning for image recognition, in: Proc. CVPR, 2016, pp. 770–778.
- [55] S. Joshi, B. Mirzasoleiman, Data-efficient contrastive self-supervised learning: Most beneficial examples for supervised learning contribute the least, in: Proc. ICML, PMLR, 2023, pp. 15356–15370.