Lattice stability of ordered Au-Cu alloys in the warm dense matter regime
Abstract
In the warm dense regime, where the electron temperature is increased to the same order of the Fermi temperature, the dynamical stability of elemental metals depends on its electronic band structure as well as its crystal structure. It has been known that phonon hardening occurs due to an enhanced internal pressure caused by electron excitations as in close-packed simple metals, whereas phonon softening occurs at a specific point in the Brillouin zone as in body-centered cubic metals. Here, we investigate the dynamical stability of binary ordered alloys (Au and Cu) in the L10 and L12 structures. By performing first principles calculations on phonon dispersions, we demonstrate that warm dense Au-Cu systems show phonon hardening behavior except the lowest frequency phonon mode at point R of AuCu in the L10 structure. We show that when a phonon mode is stabilized by long-range interatomic interactions at ambient condition, such a phonon will be destabilized by the short-range nature of the warm dense matters.
I Introduction
Lattice dynamics in metals is determined by the interplay between the direct ion-ion and the indirect ion-electron-ion interactions. In the warm dense matter (WDM) regime realized by an incident of ultrashort laser pulse to metals, the indirect intereaction is strongly modulated due to electron excitations characterized by the electron temperature that is the same order of the Fermi temperature. By using the finite-temperature density-functional theory (DFT) mermin , the phonon hardening has been predicted for elemental metals in the close-packed (i.e., face-centered cubic (fcc) and hexagonal close-packed) structures recoules ; bottin ; kabeer ; giret ; minakov ; yan ; harbour ; ono2019 . For noble metals, this is because the excitation of electrons weakens the electron screening, in turn, yielding an increase in the internal pressure recoules ; bottin . For free electron metals with no bands near the Fermi level, the internal pressure increases with the electron kinetic energy, leading to the phonon hardening again bottin . Within the free-electron approximation using the central potential model, this is understood by an increase in the force constants of the first nearest neighbor (NN) sites ono2019 . In contrast, the phonon softening has been predicted for the body-centered cubic (bcc) structure giret ; yan ; harbour ; ono2019 ; ono2020 . This is intrinsic to the crystal structure symmetry: in the expression for the phonon frequency at point N in the Brillouin zone, a relatively small contribution from the force constants of the first NN sites is present ono2019 ; ono2020 . These studies imply that the phonon hardening or softening properties in WDM are determined by a combined effect of the increase in the internal pressure (weakened screening) and the crystal structure symmetry. In order to study this interplay systematically, it is useful to focus on ordered alloys that can have many crystal structures in thermal equilibrium and phase diagram as a function of ambient temperature and composition.
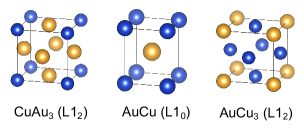
The ordered phases of Au-Cu alloys have been well known as described in the standard textbooks kittel : AuCu in the L10 structure (the distorted fcc structure along the axis) and AuCu3 and CuAu3 in the L12 structure okamoto , as shown in Fig. 1. In this paper, we study the lattice dynamics of ordered Au-Cu alloys in the WDM regime. We demonstrate that the warm dense Au-Cu alloy in the L12 structure shows the phonon hardening, whereas that in the L10 structure is unstable against the lowest frequency phonons at point R. The former can be explained by the weakening of the electron screening effect. To explain the latter, we show that the corresponding phonon mode at point R is stabilized by long-range interatomic interactions at ambient temperature due to the crystal structure symmetry and that the short-range nature of the warm dense matters destabilizes such a phonon mode.
The origin of the phonon softening in L10 AuCu alloy is different from that in warm dense diamond and silicon. For the latter, the phonon softening and lattice instabilities have been understood by the strengthening of the anti-bonding character between atoms created by the electron transition from the valence to the conduction bands, reducing the size of force constants significantly stampfli . Recently, Yan et al. have studied the dynamical stability of warm dense tantalum nitrides (TaN) in various structures yan2020 using finite-temperature DFT. They have shown that under electronic excitations the unstable cubic -phase becomes stable, whereas the hexagonal phases show the phonon softening. They have explained it with respect to the covalent bonding between atoms in more complicated way.
This paper is organized as follows. Section II.1 describes computational details for the total energy and phonon dispersion calculations based on DFT and density-functional perturbation theory (DFPT). Section II.2 briefly explains the theory of lattice dynamics to provide analytical expressions for phonon frequencies at point R of AuCu in the L10 structure. Section III first investigates the equilibrium and phonon properties of Au-Cu alloys by using different exchange-correlation functionals. The phonon dispersions of Au-Cu alloys in the WDM regime is next presented, followed by a consideration of the electron screening that explains the phonon hardening behaviors. The analytical expressions of phonon frequencies derived in Sec. II.2 will be systematically used to explain the phonon softening at point R of L10 AuCu in the WDM regime. Also, nonthermal solid-to-solid transformation of L10 AuCu is discussed. We conclude the paper in Sec. IV.
II Theory
II.1 Computational details
We calculate the total energy and the phonon dispersions of Au-Cu alloys based on DFT and DFPT dfpt implemented in Quantum ESPRESSO (QE) code qe . In order to treat the exchange-correlation energy, we use the Perdew-Zunger (PZ) pz functional of the local density approximation and the Perdew-Burke-Ernzerhof (PBE) pbe functionals of the generalized gradient approximation. We use the ultrasoft pseudopotentials of Au.-n-rrkjus_psl.1.0.0.UPF and Cu.-dn-rrkjus_psl.1.0.0.UPF that are provided in pslibrary.1.0.0 dalcorso . The cutoff energies for the wavefunction and the charge density are 80 Ry and 800 Ry, respectively. The self-consistent field and phonon dispersion calculations are performed by using 161616 grid and 444 grid (333 grid for L12) MK , respectively, which are enough to study the dynamical stability of warm dense alloys. The total energy and forces are converged within Ry and a.u., respectively in geometry optimization. For phonon calculations, the threshold parameter for self-consistency (tr2_ph) is set to . The Marzari-Vanderbilt smearing smearing with a broadening of Ry (0.27 eV) is used for the geometry optimization, while the Fermi-Dirac type smearing is used for the WDM regime (the electron temperature in units of eV and the Boltzmann constant ). The tetrahedron method is used to calculate the electron density-of-states (DOS) tetra . For the WDM regime, the number of electronic bands to be calculated is increased to more than three times larger the sizes in the ground state calculations in order to take into account the occupation of electronic states far above the Fermi level. Imaginary phonon energies ( the Planck constant and the phonon frequency) are represented by negative energies below.
II.2 Analytical expressions for phonon frequencies
Below is a brief description of the basic concepts for the lattice dynamics. We derive analytical expressions for the phonon frequencies at point R in order to study the instability of L10 AuCu in detail. The atomic motion in a crystal is regulated by maradudin
| (1) |
where is the displacement components for the atom ( and 2 for Au and Cu, respectively) along the direction of in the unit cell characterized by the lattice vector expanded by the primitive vectors , and . is the mass of the atom and is the force constant matrix defined as
| (2) |
where and is the -component of the basis vector for : and . Assuming the plane wave solution with the wavevector , one obtains the eigenvalue equation
| (3) |
where is the -component of the polarization vector of the atom and, using the translational symmetry of the crystal, the dynamical matrix is given by
| (4) |
where we used the notation of . Also, due to the translational symmetry, the acoustic sum rule holds: .
We consider the force constants up to the fifth-order NN sites of L10 AuCu: for the Au atom at the origin, the position of the first, second, third, fourth, and fifth NNs are Cu, Au, Au, Au, and Cu, respectively, and these equivalent sites. The dynamical matrix is then expressed as
| (7) |
where the diagonal matrix is given by
| (11) |
and the off-diagonal matrix for is given by
| (15) |
By solving Eq. (3), one obtains the phonon energies at point R in ascending order
| (16) |
with
Based on these expressions for , we interpret the lattice vibrations as follows: the vibration of the Au (Cu) atoms polarized to the direction propagates along the direction with the frequency (); the vibration of the Au atoms polarized to the direction is coupled with the vibration of the Cu atoms polarized to the direction, yielding and ; and the vibration of the Au atoms polarized to the direction is coupled with the vibration of the Cu atoms polarized to the direction, yielding and . Due to the mode mixing, a frequency gap must be present between and ( and ). Negative value in the expression of (i.e., ) will be responsible for the instability of L10 AuCu in the WDM regime. The expressions of as a function of are provided in the Appendix A. The values of are extracted from DFPT calculations described in Sec. II.1.
| PZ | PBE | Experiment | |
|---|---|---|---|
| Au | 4.06 | 4.16 | 4.08 |
| CuAu3 | 3.95 | 4.05 | 3.95 |
| AuCu | 2.80 | 2.88 | 2.85 |
| AuCu | 3.54 | 3.64 | 3.67 |
| AuCu3 | 3.68 | 3.79 | 3.74 |
| Cu | 3.53 | 3.63 | 3.62 |
| MAE | 0.060 | 0.051 |
III Results and discussion
III.1 Functional dependence
It has been known that the cohesive energies and bulk moduli of alloys may be sensitive to the exchange-correlation functionals used zhang ; isaacs ; ruzsinszky2019 ; ruzsinszky2020 . In general, the PBE functional underestimates those values for weakly bonded systems such as Au-Cu alloys. Such a discrepancy can be improved by using the hybrid exchange-correlation functional zhang or the random phase approximation ruzsinszky2019 . For more accuracy, it may be better to use the latter approaches zhang ; ruzsinszky2019 . However, we use the standard functionals described above to reduce the computational costs in phonon dispersion calculations.
For studying numerical accuracy in the present calculations, we list the optimized lattice parameters and (only for L10) predicted by using PZ and PBE functionals in Table 1. These values obtained at agree with the experimental values okamoto : The mean absolute error (MAE) is estimated to be less than 0.1 Å for both cases. For Au-rich phases the PZ results are in good agreement with the experimental lattice constants, while for Cu-rich phases the PBE results are better.
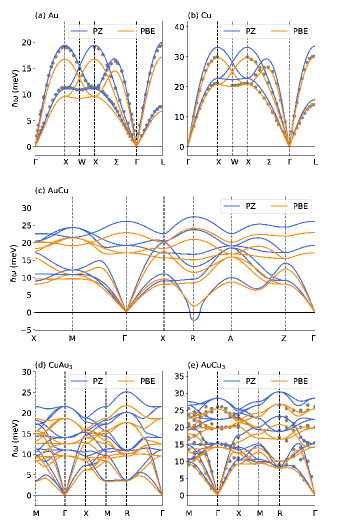
Figure 2 shows the phonon dispersions along the symmetry lines for Au-Cu systems: (a) fcc Au, (b) fcc Cu, (c) L10 AuCu, (d) L12 CuAu3, and (e) L12 AuCu3. Overall, the values of s calculated by using the PBE functional seem to be smaller than those calculated by using the PZ. For simple metals, the PZ and PBE results agree with the experiments of Au lynn and Cu nicklow , respectively. This tendency is similar to the previous calculations tang . For AuCu the lowest at point R is sensitive to the functional used: and meV for PZ and PBE, respectively. For CuAu3 the phonon softening at the point M is observed. For AuCu3, the agreement between the calculated and experimental curves katano is good when the PBE functional is used. Below we will use the PBE functional to study the dynamical stability of AuCu in detail.
III.2 Phonons in the WDM regime
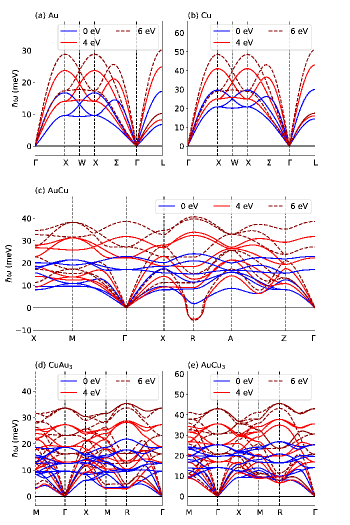
Figure 3 shows the phonon dispersion curves of (a) Au, (b) Cu, (c) AuCu, (d) CuAu3, and (e) AuCu3 in the WDM regime, where is set to 0, 4, and 6 eV. For both simple metals (Au and Cu), the phonon energy increases monotonically (i.e., phonon hardening) with , which is consistent with the previous calculations recoules ; yan . For CuAu3 and AuCu3 in the L12 structure, the phonon hardening behaviors are also observed when is increased, while nonmonotonic increases are observed along the line of M-R for the transverse acoustic phonon branch. As shown in Fig. 3(c), L10 AuCu becomes unstable against . While the optical phonons are hardened significantly, the transverse acoustic mode is unstable because around point R the phonon energy is imaginary.
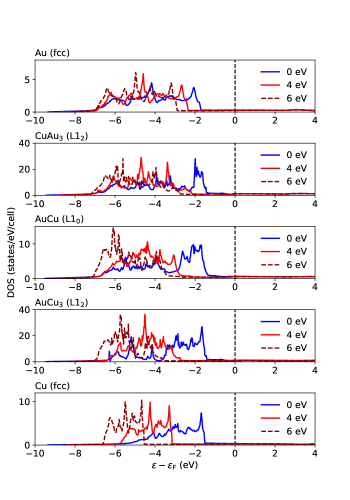
In general, the phonon hardening is attributed to an increase in the internal pressure caused by weakened electron screening. When the screening effect is weakened, bared ions are created, leading to a peak shift and a shrinkage of the width in the electron energy spectrum. This has been illustrated by the electron DOS as a function of recoules . Figure 4 shows the DOS of Au-Cu alloys for several s. At , due to the presence of bands, the high DOS is observed below the Fermi level from to eV, while the band width is narrow in Cu (from to eV). When is increased, the peak position and the width become deep and small, respectively, as described above. Although the variation of DOS with may be correlated with the phonon hardening of Au, Cu, CuAu3, and AuCu3, it never explains the phonon softening observed in L10 AuCu.
| 1NN | 2NN | 3NN | 4NN | 5NN | DFPT | |
|---|---|---|---|---|---|---|
| -6.1 | -5.6 | -4.4 | -3.2 | 0.5 | 1.8 | |
| 8.0 | 6.4 | 6.2 | 6.6 | 7.2 | 8.5 | |
| -6.9 | 9.8 | 10.2 | 10.4 | 10.9 | 11.5 | |
| 14.0 | 13.2 | 13.0 | 13.4 | 14.3 | 15.1 | |
| 19.0 | 19.8 | 19.9 | 20.1 | 20.5 | 21.0 | |
| 22.3 | 23.2 | 23.6 | 23.7 | 24.0 | 24.2 |
| 1NN | 2NN | 3NN | 4NN | 5NN | DFPT | |
|---|---|---|---|---|---|---|
| -12.9 | -8.5 | -5.8 | -5.7 | -5.6 | -5.1 | |
| 11.0 | 8.3 | 8.1 | 8.2 | 8.3 | 9.1 | |
| -11.4 | 11.1 | 12.1 | 12.2 | 12.4 | 12.8 | |
| 19.3 | 17.6 | 17.5 | 17.6 | 17.8 | 18.5 | |
| 28.0 | 31.8 | 32.0 | 32.0 | 32.1 | 32.3 | |
| 31.9 | 33.0 | 33.6 | 33.7 | 33.7 | 33.8 |
To understand the anomalous softening of AuCu in the WDM regime, let us remind that the ion-ion interactions are decomposed into the direct and indirect parts: the former is the repulsive Coulomb interaction that is independent of the magnitude of , while the latter is the electron-mediated attractive interaction that is significantly modified in the WDM regime. At ambient condition, the former and the latter may be partly canceled with each other, producing the repulsive and attractive interactions for the short- and long-range parts, respectively. Given small indirect contribution, the repulsive Coulomb forces are dominant for the short-range part. On the other hand, for the long-range part, the attractive forces compete with the repulsive forces, creating relatively small interaction forces. This situation is exactly realized in WDMs. We thus hypothesize that the lowest energy mode at point R of L10 AuCu is stabilized by the long-range interaction between atoms at eV. With this assumption, it is reasonable to observe the softening of the phonon mode when L10 AuCu is in the WDM regime having weakened long-range interatomic interactions. Similarly, we can expect that when a phonon mode is stabilized by only the short-range interactions, such a mode will show hardening behavior in the WDM regime.
To demonstrate this concept, we list the values of in Eq. (16) for several models accounting for up to the -th NN interactions (NN models) in Table 2. As increases, the phonons at point R are stabilized and their energies approach the DFPT results. It is noteworthy that the sizes of and within the 1NN model are almost comparable to those within DFPT. This means that the optical phonon energies are well determined by only the short-range interaction between atoms. When the interatomic interactions are considered up to the second order NN, becomes positive. However, is positive only within 5NN and DFPT. This implies that the long-range forces between Au and Cu atoms are important to yield positive , i.e., the dynamical stability of L10 AuCu. Table 3 also lists the values of but for eV. As in Table 2, approaches the DFPT results with the inclusion of higher order NN interactions. Again, the sizes of and within the 1NN model almost agree with those within DFPT, indicating that the optical phonon hardening is due to an enhanced short-range forces. The most important fact is that the convergence of is fast compared to the case of eV: meV within 3NN is already similar to meV within DFPT. This reflects the short-range nature of WDM, leading to the instability of the mode.
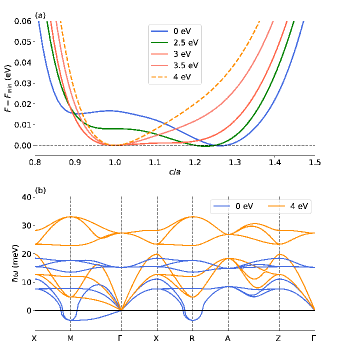
III.3 Solid-to-solid transformation
The stability of AuCu in the L10 structure can also be understood by calculating the free-energy as a function of the ratio with the equilibrium volume fixed (i.e., along the Bain path grimvall ): and correspond to the bcc (or B2) and fcc structures, respectively. Figure 5(a) shows the -dependence of the free-energy of AuCu for several s, where is the equilibrium volume of L10 at eV. At eV, the free energy takes minimum values at (L10) and , whereas that takes a maximum value at (B2). As expected, AuCu in the B2 structure is dynamically unstable (see Fig. 5(b) (blue)). When is increased, the profile of such a double-well-like curve is modified, indicating a non-thermal solid-to-solid transformation, as discussed in warm dense tungsten giret . At eV, the free-energy minimum at smaller vanishes, while that at larger shifts to ; at eV, the free-energy curve becomes relatively flat in the region of and takes a minimum only at ; and at higher s, the curvature around becomes larger, stabilizing the B2 phase. Such a B2 structure is found to be dynamically stable, as shown in Fig. 5(b) (orange), where eV is assumed. We hope that our prediction for the phase transformation in AuCu, before melting occurs, can be confirmed by future experiments.
IV Conclusions
In conclusion, we have studied the dynamical stability of Au-Cu alloys in the WDM regime by calculating the phonon dispersion curves. The phonon hardening is observed in the L12 and L10 structures except the lowest frequency phonon at point R of L10 AuCu. The hardening behavior can be explained by the increase in the internal pressure caused by the electron excitations, as observed in noble metals. The phonon softening observed is attributed to the short-range nature of WDMs because the lowest frequency phonon at point R is stabilized by long-range interactions between Au and Cu.
Although we have used analytical expressions of Eq. (16) to understand the phonon softening of L10 AuCu, those can be applicable to other ordered alloys in the L10 and B2 (the case of ) structures. It is valuable to note that 51 L10 and 325 B2 alloys are found in experimental phase diagrams sluiter . More investigations will lead to a deep understanding of the dynamical stability of ordered alloys.
Finally, it should be noted that the WDM is a transient phase because the excited electron energy created by a laser pulse is transferred to phonons, leading to lattice disordering or melting within a few picoseconds cho ; jourdain2018 ; mo ; dara ; smirnov ; jourdain2021 . Although the phonon hardening of warm dense Au has been reported experimentally ernstorfer , its validity has been controversial dara ; smirnov ; jourdain2021 . It is thus desirable to simulate the time-evolution of lattice displacements in warm dense alloys accurately, which enables us to interpret time-resolved experiments.
Acknowledgements.
A part of numerical calculations has been done using the facilities of the Supercomputer Center, the Institute for Solid State Physics, the University of Tokyo.Appendix A Dynamical matrix
The expressions of used in the NN model calculations are given below. The symmetry properties for the force constants maradudin are used to simplify the expression of Eq. (4). For the L10 structure, there are 16 symmetry operations including the identity, 180 degree rotation around , and axis, 90 degree rotation around axis, and the inversions. The list of the force constants obtained from DFPT calculations is used to check the restrictions imposed. We introduce the step function that takes and for and , respectively. We obtain for and ,
and for ,
| (19) | |||||
The nonzero elements in the off-diagonal matrix for and are
| (20) | |||||
The dynamical matrix is symmetric because of the relation . The acoustic sum rule determines in Eqs. (LABEL:eq:Dxxyy) and (19), depending on the model used.
References
- (1) N. D. Mermin, Thermal properties of the inhomogeneous electron gas, Phys. Rev. 137, A1441 (1965).
- (2) V. Recoules, J. Clérouin, G. Zérah, P. M. Anglade, and S. Mazevet, Effect of Intense Laser Irradiation on the Lattice Stability of Semiconductors and Metals, Phys. Rev. Lett. 96, 055503 (2006).
- (3) F. Bottin and G. Zérah, Formation enthalpies of monovacancies in aluminum and gold under the condition of intense laser irradiation, Phys. Rev. B 75, 174114 (2007).
- (4) F. C. Kabeer, E. S. Zijlstra, and M. E. Garcia, Road of warm dense noble metals to the plasma state: Ab initio theory of the ultrafast structural dynamics in warm dense matter, Phys. Rev. B 89, 100301(R) (2014).
- (5) Y. Giret, S. L. Daraszewicz, D. M. Duffy, A. L. Shluger, and K. Tanimura, Nonthermal solid-to-solid phase transitions in tungsten, Phys. Rev. B 90, 094103 (2014).
- (6) D. V. Minakov and P. R. Levashov, Melting curves of metals with excited electrons in the quasiharmonic approximation, Phys. Rev. B 92, 224102 (2015).
- (7) G. Q. Yan, X. L. Cheng, H. Zhang, Z. Y. Zhu, and D. H. Ren, Different effects of electronic excitation on metals and semiconductors, Phys. Rev. B 93, 214302 (2016).
- (8) L. Harbour, M. W. C. Dharma-wardana, D. D. Klug, and L. J. Lewis, Equation of state, phonons, and lattice stability of ultrafast warm dense matter, Phys. Rev. E 95, 043201 (2017).
- (9) S. Ono, Lattice dynamics for isochorically heated metals: A model study, J. Appl. Phys. 126, 075113 (2019).
- (10) S. Ono and D. Kobayashi, Phonon softening in sodium with a stepwise electron distribution, J. Appl. Phys. 127, 165105 (2020).
- (11) C. Kittel, Introduction to Solid State Physics, 8th edition (Wiley, Hoboken, NJ, 2005).
- (12) H. Okamoto, D. J. Chakrabarti, D. E. Laughlin, and T. B. Massalski, The Au-Cu (Gold-Copper) System, J. Phase Equilib. 8, 454 (1987).
- (13) P. Stampfli and K. H. Bennemann, Theory for the instability of the diamond structure of Si, Ge, and C induced by a dense electron-hole plasma, Phys. Rev. B 42, 7163 (1990).
- (14) G. Q. Yan, X. L. Cheng, and H. Zhang, Phase stability and mechanical response of tantalum nitrides to electronic excitation effect, Mater. Res. Express 7, 066508 (2020).
- (15) S. Baroni, S. Gironcoli, A. D. Corso, and P. Giannozzi, Phonons and related crystal properties from density-functional perturbation theory, Rev. Mod. Phys. 73, 515 (2001).
- (16) P. Giannozzi et al., Advanced capabilities for materials modeling with Quantum ESPRESSO, J. Phys.: Condens. Matter 29, 465901 (2017).
- (17) J. P. Perdew and A. Zunger, Self-interaction correction to density-functional approximations for many-electron systems, Phys. Rev. B 23, 5048 (1981).
- (18) J. P. Perdew, K. Burke, and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett. 77, 3865 (1996).
- (19) A. Dal Corso, Pseudopotentials periodic table: From H to Pu, Computational Material Science 95, 337 (2014).
- (20) H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B 13, 5188 (1976).
- (21) N. Marzari, D. Vanderbilt, A. De Vita, and M. C. Payne, Thermal Contraction and Disordering of the Al(110) Surface, Phys. Rev. Lett. 82, 3296 (1999).
- (22) P. E. Blöchl, O. Jepsen, and O. K. Andersen, Improved tetrahedron method for Brillouin-zone integrations, Phys. Rev. B 49, 16223 (1994).
- (23) A. Maradudin, Theory of Lattice Dynamics in the Harmonic Approximation (Academic Press, New York, 1971).
- (24) Y. Zhang, G. Kresse, and C. Wolverton, Nonlocal First-Principles Calculations in Cu-Au and Other Intermetallic Alloys, Phys. Rev. Lett. 112, 075502 (2014).
- (25) E. B. Isaacs and C. Wolverton, Performance of the strongly constrained and appropriately normed density functional for solid-state materials, Phys. Rev. Materials 2, 063801 (2018).
- (26) N. K. Nepal, S. Adhikari, J. E. Bates, and A. Ruzsinszky, Treating different bonding situations: Revisiting Au-Cu alloys using the random phase approximation, Phys. Rev. B 100, 045135 (2019).
- (27) N. K. Nepal, S. Adhikari, B. Neupane, and A. Ruzsinszky, Formation energy puzzle in intermetallic alloys: Random phase approximation fails to predict accurate formation energies, Phys. Rev. B 102, 205121 (2020).
- (28) J. W. Lynn, H. G. Smith, and R. M. Nicklow, Lattice Dynamics of Gold, Phys. Rev. B 8, 3493 (1973).
- (29) R. M. Nicklow, G. Gilat, H. G. Smith, L. J. Raubenheimer, and M. K. Wilkinson, Phonon Frequencies in Copper at 49 and 298°K, Phys. Rev. 164, 922 (1967).
- (30) X. Tang and B. Fultz, First-principles study of phonon linewidths in noble metals, Phys. Rev. B 84, 054303 (2011).
- (31) S. Katano, M. Iizumi, and Y. Noda, Lattice dynamics of Cu3Au in the ordered and disordered states, J. Phys. F: Met. Phys. 18, 2195 (1988).
- (32) G. Grimvall, B. Magyari-Köpe, V. Ozoliņš, and K. A. Persson, Lattice instabilities in metallic elements, Rev. Mod. Phys. 84, 945 (2012).
- (33) M. Sluiter, Some observed bcc, fcc, and hcp superstructures, Phase Transitions 80, 299 (2007).
- (34) S. L. Daraszewicz, Y. Giret, N. Naruse, Y. Murooka, J. Yang, D. M. Duffy, A. L. Shluger, and K. Tanimura, Structural dynamics of laser-irradiated gold nanofilms, Phys. Rev. B 88, 184101 (2013).
- (35) B. I. Cho, T. Ogitsu, K. Engelhorn, A. A. Correa, Y. Ping, J. W. Lee, L. J. Bae, D. Prendergast, R. W. Falcone, and P. A. Heimann, Measurement of electron-ion relaxation in warm dense copper, Sci. Rep. 6, 18843 (2016).
- (36) N. Jourdain, L. Lecherbourg, V. Recoules, P. Renaudin, and F. Dorchies, Electron-ion thermal equilibration dynamics in femtosecond heated warm dense copper, Phys. Rev. B 97, 075148 (2018).
- (37) M. Z. Mo, Z. Chen, R. K. Li, M. Dunning, B. B. L. Witte, J. K. Baldwin, L. B. Fletcher, J. B. Kim, A. Ng, R. Redmer, A. H. Reid, P. Shekhar, X. Z. Shen, M. Shen, K. Sokolowski-Tinten, Y. Y. Tsui, Y. Q. Wang, Q. Zheng, X. J. Wang, and S. H. Glenzer, Heterogeneous to homogeneous melting transition visualized with ultrafast electron diffraction, Science 360, 1451 (2018).
- (38) N. A. Smirnov, Copper, gold, and platinum under femtosecond irradiation: Results of first-principles calculations, Phys. Rev. B 101, 094103 (2020).
- (39) N. Jourdain, L. Lecherbourg, V. Recoules, P. Renaudin, and F. Dorchies, Ultrafast Thermal Melting in Nonequilibrium Warm Dense Copper, Phys. Rev. Lett. 126, 065001 (2021).
- (40) R. Ernstorfer, M. Harb, C. T. Hebeisen, G. Sciaini, T. Dartigalongue, and R. J. D. Miller, The Formation of Warm Dense Matter: Experimental Evidence for Electronic Bond Hardening in Gold, Science 323, 1033 (2009).