Lattice QCD study of color correlations between static quarks with gluonic excitations

We investigate the color correlation between static quark and antiquark ($q\bar{q}$) by the two-body density matrix $\rho$ evaluated in terms of $q\bar{q}$’s color configuration. A density matrix $\rho$ defined in such a way is nothing but the reduced density matrix that is obtained integrating out the other DOF (e.g. gluonic DOF) in the full density matrix. A reduced two-body density operator $\hat{\rho}(R)$ for a $q\bar{q}$ system with the interquark distance $R$ is defined as

Here $|\bar{q}(0)q(R)\rangle$ represents a quantum state in which the antiquark is located at the origin and the other quark lies at $x=R$. The matrix elements $\rho(R)_{ij,kl}$ of the reduced density operator, where $i$ and $k$ ($j$ and $l$) are quark’s (antiquark’s) color indices, are expressed as

Then, $\rho(R)$ is an $m\times m$ square matrix with the dimension $m=N_{c}^{2}$. The density matrix $\rho(R)$ is evaluated using only quark’s color DOF, but does not explicitly contain gluon’s color DOF in this construction: the gluonic DOF are “integrated out” in the lattice calculation, and $\rho(R)$ can be regarded as a reduced density matrix.

For the time being, we consider a quark and antiquark system without gluonic excitations. In previous studies [6, 7], we found that the reduced color density matrix $\rho(R)$ evaluated by lattice QCD can be precisely reproduced with an ansatz, where $\rho(R)$ is expressed as a sum of an “initial” color singlet configuration at $R\rightarrow 0$ and mixing of the random color configuration due to the color screening effect between quark and antiquark at finite $R$.

Let $\hat{\rho}_{{\bm{s}}}$ the density operator for quark and antiquark forming a color singlet state $|{\bm{s}}\rangle=\sum_{i}^{N_{c}}|\bar{q}_{i}q_{i}\rangle$ in the Coulomb gauge as

In color SU($N_{c}$) QCD, the density operator $\hat{\rho}_{{\bm{a}}_{i}}$ for a $q\bar{q}$ pair in an adjoint state $|{\bm{a}}_{i}\rangle$ is expressed as

In the limit of $R\rightarrow 0$, quark and antiquark are considered to form a color-singlet state ($|{\bm{s}}\rangle$) corresponding to the strong correlation limit, since there exists no gluonic excitation in the system and gluons form a totally colorless state. Its density operator will be written as

Here, the subscript “$\alpha$” means that the matrix is expressed in terms of $q\bar{q}$’s color representation with the vector set of $\{|{\bm{s}}\rangle,|{\bm{a}_{1}}\rangle,...|{\bm{a}_{{N_{c}^{2}-1}}}\rangle\}$.

As $R$ increases, an uncorrelated state represented by random color configurations, where all the $N_{c}^{2}$ components mix with equal weights, enters in $\rho(R)$ due to the color screening effect by in-between gluons. The density operator for such a random-color state is given as

Letting the fraction of the initial color singlet state being ${F_{s}(R)}$ and that of the random contribution being $(1-{F_{s}(R)})$, the density operator for an interquark distance of $R$ in this ansatz is written as

Here, the subscript $(0,{\bm{s}})$ means that the density operator $\hat{\rho}_{0,{\bm{s}}}^{\rm ansatz}(R)$ is dominated by the color singlet contribution $\hat{\rho}_{{\bm{s}}}$ at $R\rightarrow 0$. $\hat{\rho}_{0,{\bm{s}}}^{\rm ansatz}(R)$ can be explicitly expressed as

In this ansatz,

are satisfied at any $R$. The normalization condition ${\rm Tr}\rho=1$ is trivially satisfied in this ansatz as

where $\rho(R)_{{\bm{a}},{\bm{a}}}\equiv\sum_{i=1}^{{N_{c}^{2}-1}}\rho(R)_{{\bm{a}_{i}},{\bm{a}_{i}}}$. It was found that this ansatz reproduces the density matrix element for the ground-state $q\bar{q}$ system (${\Sigma_{g}^{+}}$ channel) evaluated by lattice QCD calculation with a very good accuracy.

This ansatz can be extended to the system with gluonic excitations. In what follows, we limit ourselves to $N_{c}=3$ case, hence we refer to “adjoint” states as “octet” ones. In a $q\bar{q}$ system accompanied by gluonic excitations, a $q\bar{q}$ pair can also form a color octet configuration at $R\rightarrow 0$ region, where excited gluons carry octet color and the total system is kept color singlet. With the density operator averaged for octet states

the ansatz for a $q\bar{q}$ system with gluonic excitations takes the form

Here, ${F_{a}(R)}$ represents the fraction of the initial color octet state, and the subscript $(0,{\bm{a}})$ means that the density operator $\hat{\rho}_{0,{\bm{a}}}^{\rm ansatz}(R)$ is dominated by the color octet contribution $\hat{\rho}_{{\bm{a}}}$ at $R\rightarrow 0$.

In the later sections, we see that this ansatz actually reproduces the color density matrix for a static $q\bar{q}$ system with gluonic excitations.

In a static $q\bar{q}$ system, there exist three quantum numbers. One is the eigenvalue of the projected total angular momentum $\Lambda\equiv{\bm{J}}\cdot\hat{\bm{r}}$, where ${\bm{J}}$ is the total angular momentum gluon fields possess and ${\bm{r}}$ is the unit vector parallel to the $q\bar{q}$ axis. We assign capital Greek letters $\Sigma,\Pi,\Delta$,.. for $\Lambda=0,1,2,..$ states. Second is the eigenvalue $\eta_{CP}$ of the simultaneous operations of charge conjugation and spatial inversion about the midpoint between $q\bar{q}$. States with $\eta_{CP}=1(-1)$ are denoted by the subscripts $g(u)$. Third is a label adopted only for the $\Sigma$ channel. Even (odd) $\Sigma$ states under the reflection in a plane that contains the $q\bar{q}$ axis are represented by the superscripts $+(-)$. The first excited state in each channel is discriminated by a prime mark. Then, the quantum numbers for each state investigated in this paper are denoted as $\Gamma=\Lambda_{\eta_{CP}}^{\pm(^{\prime})}$

The position on the lattice site is denoted as ${\bm{r}}=(x,y,z,t)=x{\bm{e}_{x}}+y{\bm{e}_{y}}+z{\bm{e}_{z}}+t{\bm{e}_{t}}$, and the $\mu$-direction ($\mu=x,y,z,t$) link variable at ${\bm{r}}$ is expressed as $U_{\mu}({\bm{r}})$. With a lower staple $S^{L}(R,T;\Gamma)$ representing $q\bar{q}$ pair creation and propagation and an upper staple $S^{U}(R,T;\Gamma)$ for $q\bar{q}$ pair annihilation that are defined as

we compute $L_{ij,kl}^{(m,n)}(R,T;\Gamma)$ as

Here, $q\bar{q}$-state creation/annihilation operator ${\cal O}^{(n)}_{\Gamma}(R,T)$ that connects $x=0$ and $x=R$ sites at $t=T$ is constructed so that it creates a $q\bar{q}$ state with a quantum number $\Gamma$ [9, 10]. For example, when $\Gamma={\Sigma_{g}^{+}}$, we simply adopt

The superscripts $(n)$ denote the smearing levels for spatial link variables. We finally construct the operator $L_{ij,kl}^{[n]}(R,T;\Gamma)$ which encodes the elements of the density matrix $\rho$ for $n$-th excited state in the $\Gamma$ channel as

where the coefficients $C^{[n]}_{m}$ are determined so as to maximize the overlap of the creation/annihilation operator $\sum_{m}C^{[n]}_{m}{\cal O}^{(m)}_{\Gamma}(R,T)$ to $n$-th excited state signals. The operator optimization is done by solving a generalized eigenvalue problem [19, 20, 11] for $q\bar{q}$ potentials in the target channel $\Gamma$. When $L_{ij,kl}^{[n]}(R,T;\Gamma)$ couples only to the $n$-th excited state in the $\Gamma$ channel, $\langle L^{[n]}_{ij,kl}(R,T;\Gamma)\rangle$ is then expressed as

where $E_{n}$ is the $n$-th excited-state energy. Normalizing $\langle L^{[n]}(R,T;\Gamma)\rangle$ so that ${\rm Tr}\ \langle L^{[n]}(R,T;\Gamma)\rangle=\sum_{ij}\langle L^{[n]}_{ij,ij}(R,T;\Gamma)\rangle=1$, we finally obtain the two-body color density matrix $\rho(R)$ for the $n$-th excited state in the $\Gamma$ channel whose trace is unity (${\rm Tr}\ \rho(R)=1$).

We performed quenched calculations for reduced density matrices of static quark and antiquark ($q\bar{q}$) systems adopting the standard Wilson gauge action. The gauge configurations are generated on the spatial volume of $V=32^{3}$ with the gauge couplings $\beta=5.8$, which corresponds to $V=4.5^{3}$ [fm³]. The temporal extent is $N_{t}=32$. All the gauge configurations are gauge-fixed with the Coulomb gauge condition. While finite volume effects would still remains for $V=4.5^{3}$ [fm³] [6], detailed study taking care of such systematic errors is beyond the scope of the present paper, in which the color structure of a $q\bar{q}$ pair with gluonic excitations is clarified for the first time.

In Fig. 1, the energy spectra for $\Gamma={\Sigma_{g}^{+}}$, ${{\Sigma_{g}^{+}}^{\prime}}$, ${\Pi_{u}}$, ${\Pi_{u}^{\prime}}$, ${\Delta_{g}}$ and ${\Delta_{g}^{\prime}}$ are plotted as a function of interquark distance $R$. The state with the lowest excitation is the ${\Pi_{u}}$ state, and ${\Delta_{g}}$ and ${{\Sigma_{g}^{+}}^{\prime}}$ states are the second-lowest excited states that almost degenerate in energy. The ${\Pi_{u}^{\prime}}$ state’s energy is higher than theirs. These spectra can be compared with the data of the preceding lattice QCD calculation [9] and the data obtained in this study are found to be consistent with them within errors. The energy for ${\Delta_{g}^{\prime}}$ channel, which was not computed in Ref. [9], lies above that for ${\Pi_{u}^{\prime}}$ channel.

Figure 2 shows the $R$ dependence of the singlet and octet components $\rho_{\bm{s},\bm{s}}$ and $\rho_{\bm{a},\bm{a}}$ for the ${\Sigma_{g}^{+}}$ channel, and Figs. 3-7 demonstrate those for the excited channels, ${{\Sigma_{g}^{+}}^{\prime}}$, ${\Pi_{u}}$, ${\Pi_{u}^{\prime}}$, ${\Delta_{g}}$ and ${\Delta_{g}^{\prime}}$, respectively. One can find that a $q\bar{q}$ pair in the ${\Sigma_{g}^{+}}$ channel forms a purely color singlet configuration at $R\rightarrow 0$, and the ratio $\rho_{\bm{s},\bm{s}}:\rho_{\bm{a},\bm{a}}$ approaches $1:8$ of the random color configuration as $R$ increases. The $R$ dependence is consistent with the previous work [6], and we confirm that the diagonalization process of the Hamiltonian is successful. This result indicates that in-between flux-tube formation is expressed by the color leak from color sources to a flux tube, which can be quantified as the color screening effect among color sources, quarks. It is of great interest that $q\bar{q}$ pairs in all the gluonically excited channels form a purely color octet configuration at $R\rightarrow 0$. It is consistent with a simple gluonic excitation picture, where a $q\bar{q}$ pair and one constituent gluon are bound. The random color configuration is mixed as $R$ increases, and in the limit of $R\rightarrow\infty$, the ratio of $\rho_{\bm{s},\bm{s}}$ and $\rho_{\bm{a}_{i},\bm{a}_{i}}$ again approaches that for the random color configuration, $\rho_{\bm{s},\bm{s}}:\rho_{\bm{a},\bm{a}}=1:8$. This observation supports the scenario that the color screening effect by the in-between flux tube occurs also in the excited $q\bar{q}$ systems.

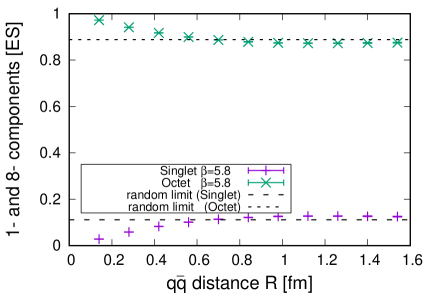
As shown in the results of $\rho_{\bm{s},\bm{s}}$ and $\rho_{\bm{a},\bm{a}}$ for ${\Sigma_{g}^{+}}$ channel, the speed at which the color configuration approaches the random limit in this channel is the slowest in all the channels, meaning that the singlet $q\bar{q}$ correlation remains to some extent. More quantitative discussion of the quenching speed is given in the next subsection.

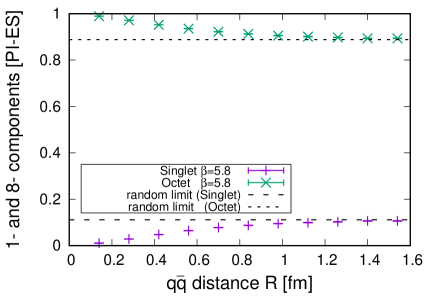
For the lowest excitation channel, ${\Pi_{u}}$, the color components at small $R$ regions are dominated by the octet components, which means that a $q\bar{q}$ pair forms a color octet configuration at $R\rightarrow 0$ (See Fig. 4). It is consistent with the constituent gluon picture for gluonic excitation states, where a color octet $q\bar{q}$ pair and a color octet constituent gluon are bound to form a totally color singlet physical state. At the large $R$ regions, a random color configuration is mixed like ${\Sigma_{g}^{+}}$ channel and the ratio of singlet and octet components again approaches $1:8$. It means that even in the channels with gluonic excitations, the flux-tube formation emerges as the mixture of random color configurations.

The color components for ${{\Sigma_{g}^{+}}^{\prime}}$, ${\Pi_{u}^{\prime}}$, ${\Delta_{g}}$, ${\Delta_{g}^{\prime}}$ channels shown in Figs. 3,5,6,7 indicate that these states are also considered to be gluonic excitation states, since the color configurations of them are dominated by a color octet configuration at small $R$. Similarly to the case of the ${\Pi_{u}}$ channel, a random color configuration is gradually mixed as $R$ increases, and the ratio of singlet and octet components finally approaches $1:8$. The quenching speed of the color correlation in the ${{\Sigma_{g}^{+}}^{\prime}}$, ${\Pi_{u}^{\prime}}$, ${\Delta_{g}}$, ${\Delta_{g}^{\prime}}$ channels is faster compared with that in the ${\Sigma_{g}^{+}}$ and ${\Pi_{u}}$ channels. A closer look reveals a tiny $R$-independent contribution in the ${{\Sigma_{g}^{+}}^{\prime}}$ channel: the ratio of singlet and octet components slightly deviates from $1:8$ at the large $R$ regions, which is clarified in detail in the later sections.

It is naively expected that a $q\bar{q}$ pair in ${\Sigma_{g}^{+}}$ (ground state) channel forms a color singlet configuration at $R\rightarrow 0$ [6, 7], whereas those for other channels (${{\Sigma_{g}^{+}}^{\prime}}$, ${\Pi_{u}}$, ${\Pi_{u}^{\prime}}$, ${\Delta_{g}}$, ${\Delta_{g}^{\prime}}$) are expected to form an octet color configuration at $R\rightarrow 0$, since excited gluon fields carry adjoint colors. These behaviors can be confirmed in Figs. 2-7. Then we expect that the ansatz $\rho_{0,{\bm{s}}}^{\rm ansatz}(R)$ works for ${\Sigma_{g}^{+}}$ channel, and $\rho_{0,{\bm{a}}}^{\rm ansatz}(R)$ is reasonable for ${{\Sigma_{g}^{+}}^{\prime}}$, ${\Pi_{u}}$, ${\Pi_{u}^{\prime}}$, ${\Delta_{g}}$, and ${\Delta_{g}^{\prime}}$ channels (See Eqs. (8)$-$(17)) .

We extract ${F_{s}(R)}$ and ${F_{a}(R)}$ for each channel from the components, $\rho_{\bm{s},\bm{s}}(R)$ and $\rho_{\bm{a},\bm{a}}(R)$, evaluated with lattice QCD calculations. For example, for $\Gamma={{\Sigma_{g}^{+}}^{\prime}}$, ${\Pi_{u}}$, ${\Pi_{u}^{\prime}}$, ${\Delta_{g}}$, and ${\Delta_{g}^{\prime}}$, we can compute ${F_{a}(R)}$ as

Due to the normalization condition

the independent quantity at a given $R$ is only $\rho_{{\bm{s}},{\bm{s}}}$ or $\rho_{{\bm{a}},{\bm{a}}}$.

We define the fraction of the initial state remaining at $R$ for $\Gamma$ channel as

for $\Gamma={\Sigma_{g}^{+}}$, and as

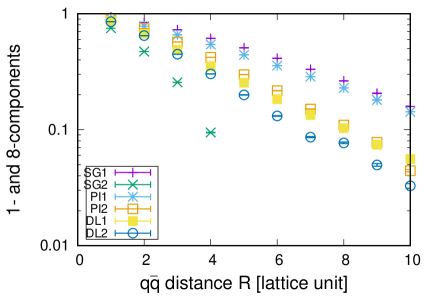
for other channels, $\Gamma={{\Sigma_{g}^{+}}^{\prime}}$, ${\Pi_{u}}$, ${\Pi_{u}^{\prime}}$, ${\Delta_{g}}$, and ${\Delta_{g}^{\prime}}$. In the case of $\Gamma={\Sigma_{g}^{+}}$, the initial ($R\rightarrow 0$) color configuration is dominated by a color singlet one, as $\lim_{R\rightarrow 0}F_{s}(R)=1$, hence we adopt ${F_{s}(R)}$ instead of ${F_{a}(R)}$. Thus defined $F(R;\Gamma)$ indicates the component of the color correlation; it starts from 1 at $R\rightarrow 0$ and decreases as $R$ enlarges. $F(R;\Gamma)$ calculated for all the channels are logarithmically plotted as a function of the interquark distance $R$ in Fig. 8. Most of them show a linear dependence on $R$, which means that initial color correlations are exponentially quenched as $R$ increases, and their color configurations approach the random state: $F(R;\Gamma)$ can be expressed as $F(R;\Gamma)\sim A(\Gamma)\exp(-B(\Gamma)R)$. However, the log plot of $F(R;{{\Sigma_{g}^{+}}^{\prime}})$ does not show a clear linear dependence at all $R$ regions, and it takes a smaller value than others at small $R$ regions. This tendency peculiar to ${{\Sigma_{g}^{+}}^{\prime}}$ channel implies a negative constant contribution mixed to $\rho_{\bm{a},\bm{a}}$. Octet components $\rho_{\bm{a},\bm{a}}$ for $\Gamma={{\Sigma_{g}^{+}}^{\prime}}$ and ${\Pi_{u}}$ ($\rho_{\bm{a},\bm{a}}(R;{{\Sigma_{g}^{+}}^{\prime}})$ and $\rho_{\bm{a},\bm{a}}(R;{\Pi_{u}})$) are compared in Fig. 9.

$\rho_{\bm{a},\bm{a}}(R;{{\Sigma_{g}^{+}}^{\prime}})$ clearly starts from a smaller value than $\rho_{\bm{a},\bm{a}}(R;{\Pi_{u}})$ at small $R$ regions, and $\rho_{\bm{a},\bm{a}}(R;{{\Sigma_{g}^{+}}^{\prime}})$ seems to approach some constant value slightly smaller than $8/9$, which implies that a negative $R$-independent contribution exists in $\rho_{\bm{a},\bm{a}}(R;{{\Sigma_{g}^{+}}^{\prime}})$: $F(R;{{\Sigma_{g}^{+}}^{\prime}})$ is expressed as $F(R;{{\Sigma_{g}^{+}}^{\prime}})\sim A({{\Sigma_{g}^{+}}^{\prime}})\exp(-B({{\Sigma_{g}^{+}}^{\prime}})R)-\delta$. A numerical fit gives a offset value $\delta=0.2043$, and $\tilde{F}(R;{{\Sigma_{g}^{+}}^{\prime}})\equiv F(R;{{\Sigma_{g}^{+}}^{\prime}})+\delta$ plotted along with other $F(R;\Gamma)$’s is shown in Fig. 10.

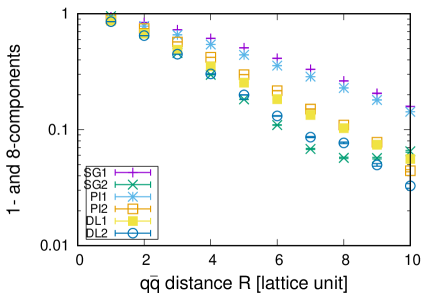
After this correction, the log plot of $\tilde{F}(R;{{\Sigma_{g}^{+}}^{\prime}})$ shows a clear linear $R$ dependence at $R<1.2$ fm. On the other hand, $\tilde{F}(R;{{\Sigma_{g}^{+}}^{\prime}})$ again goes up at $R>1.2$ fm . Taking into account that color configurations evaluated presently are strongly affected by a finite volume effect, it might be a finite-volume artifact. In fact, in Fig.11 in Ref. [6], one can find considerable finite-volume effect for $R>1.0$ fm. Such artifacts can be also found in the fitted parameters (Fig.7 in Ref. [6]). The detailed clarification of color correlation at $R\rightarrow\infty$ region with a huge lattice volume is left for future studies.

The exponential decay of the $q\bar{q}$ correlation $F(R;\Gamma)$ indicates the exponential color screening effects due to in-between gluons. One can find roughly three different magnitudes of slope in Fig. 10. The correlation quenching speed for ${\Sigma_{g}^{+}}$ and ${\Pi_{u}}$ channels is the slowest and the color correlation remains at larger $R$. The quenching speed for ${\Pi_{u}^{\prime}}$ and ${\Delta_{g}}$ channels is faster than that for ${\Sigma_{g}^{+}}$ and ${\Pi_{u}}$ channels. Further fast quenching of the color correlation is found in ${{\Sigma_{g}^{+}}^{\prime}}$ and ${\Delta_{g}^{\prime}}$ channels. In the ground state channel ${\Sigma_{g}^{+}}$, the color leak from quarks to a flux tube is most suppressed. The fact that the color screening speed for the lowest excited channel ${\Pi_{u}}$ is comparable with ${\Sigma_{g}^{+}}$ channel in magnitude may indicate that the ${\Pi_{u}}$ state has the simplest gluonic excitation mode that does not accelerate the color screening effect. Other excited states are considered to have more complicated gluonic excitation and the color correlation between quarks are easily randomized.

We fit $F(R;\Gamma)$ with an exponential function as

and extract the “screening mass” $B(\Gamma)$. For the ${{\Sigma_{g}^{+}}^{\prime}}$ channel, the values of $\tilde{F}(R;{{\Sigma_{g}^{+}}^{\prime}})$ after the correction are used for fitting. The fit range is set to $4\leq R\leq 7$ in lattice unit, in which the data show an exponential damping, as seen in Fig. 10.

In Fig. 11, the fitted parameters $B(\Gamma)$ are plotted, and they are also listed in Table. 1.

One can categorize the screening masses as,

The screening mass for ${\Pi_{u}}$ channel is as small as that for ${\Sigma_{g}^{+}}$, whereas those for other channels are significantly larger. It might imply that in the viewpoint of color screening effects, the gluonic excitations except for ${\Pi_{u}}$ consist of a sum of “fundamental excitations” of the ${\Pi_{u}}$ channel.

In Ref. [7], the color structures of a $q\bar{q}$ pair at finite temperature were investigated in detail by analyzing the color density matrix $\rho$ as well as the corresponding entanglement entropy, and the $q\bar{q}$ color correlations were found to be quickly quenched across the deconfinement phase transition temperature $T_{c}$. It means the $q\bar{q}$ color configuration is strongly randomized above $T_{c}$ as the in-between flux tube disappears. Even below $T_{c}$, it was found that the color correlation gradually weaken as the temperature rises due to the temperature effect. We here clarify if the temperature effect at $T<T_{c}$ can be explained as a thermal ensemble based on the present results for excited $q\bar{q}$ states at $T=0$. We reconstruct the $F(R)$ at $T>0$ from the $F(R;\Gamma)$’s for low-lying 6 channels (${\Sigma_{g}^{+}}$, ${{\Sigma_{g}^{+}}^{\prime}}$, ${\Pi_{u}}$, ${\Pi_{u}^{\prime}}$, ${\Delta_{g}}$, ${\Delta_{g}^{\prime}}$), and compare it with the lattice QCD results shown in Ref. [7]. We define the density operator $\hat{\rho}_{T}$ at finite temperature as

where $T$ is the temperature of the system and $E_{0}(R)$ is a energy of a ground-state $q\bar{q}$ pair ($E_{0}(R)=E(R;{\Sigma_{g}^{+}})$). In Fig. 12, we show the $F(R)$ reconstructed using Eq.(30) as well as the $F(R)$’s shown in Ref. [7]. Here, the temperature $T$ in Eq.(30) is chosen to be 250 MeV.

$F(R)$ reconstructed using Eq.(30) is shown by open squares, and filled squares denote $F(R)$ at $T=0$. Other symbols represent $F(R)$’s at each temperature demonstrated in Ref. [7]. As is seen in Fig. 12, the lattice QCD data at $T>0$ are reproduced by Eq.(30) more or less in the range of $0<R<0.8$ fm. Though the coincidence is lost at larger $R$, this deviation is considered to arise from the finite volume effects. The lattice adopted in Ref. [7] is smaller ($V=24^{3}$) and the finite volume artifact would remain for large $R$.