Lattice QCD calculation of the Collins-Soper kernel from quasi TMDPDFs

Quasi beam functions in a pion external state are computed from ratios of three-point and two-point correlation functions:

		$\displaystyle\mathcal{R}_{\Gamma}(t,\tau,b^{\mu},a,\eta,P^{z})$
		$\displaystyle\qquad=\frac{C_{\text{3pt}}^{\Gamma,u}(t,\tau,b^{\mu},a,\eta,P^{z}\vec{e}_{z})-C_{\text{3pt}}^{\Gamma,d}(t,\tau,b^{\mu},a,\eta,P^{z}\vec{e}_{z})}{C_{\text{2pt}}(t,P^{z}\vec{e}_{z})}$
		$\displaystyle\qquad\xrightarrow{t\gg\tau\gg 0}B^{\text{bare}}_{\Gamma}(b^{z},\vec{b}_{T},a,\eta,P^{z})+\ldots,$		(11)

where

	$\displaystyle C_{\text{3pt}}^{\Gamma,i}(t,\tau,b^{\mu},a,\eta,\vec{P}=P^{z}\vec{e}_{z})$
	$\displaystyle\ =\sum_{\vec{x},\vec{z}}e^{i\vec{P}\cdot\vec{x}}\langle 0|\pi_{\vec{P},S}(\vec{x},t)\mathcal{O}^{i}_{\Gamma}(b^{\mu},(\vec{z},\tau),\eta)\pi_{\vec{P},S}^{\dagger}(0)|0\rangle$
	$\displaystyle\xrightarrow{t\gg\tau\gg 0}\frac{Z_{\vec{P}}}{4aE^{2}_{\vec{P}}}e^{-E_{\vec{P}}t}\tilde{B}^{\Gamma}_{i}(b^{z},\vec{b}_{T},a,\eta,P^{z})+\ldots$		(12)

and

	$\displaystyle C_{\text{2pt}}(t,\vec{P})$	$\displaystyle=\sum_{\vec{x}}e^{i\vec{P}\cdot\vec{x}}\langle 0|\pi_{\vec{P},S}(\vec{x},t)\pi_{\vec{P},S}^{\dagger}(0)|0\rangle$
		$\displaystyle\overset{t\gg 0}{\longrightarrow}\frac{Z_{\vec{P}}}{2aE_{\vec{P}}}e^{-E_{\vec{P}}t}+\ldots.$		(13)

In the construction of the correlation functions, momentum-smeared interpolating operators $\pi_{\vec{P},S}(\vec{x},t)=\overline{u}_{S(\vec{P}/2)}(\vec{x},t)\gamma_{5}d_{S(\vec{P}/2)}(\vec{x},t)$ are built from quasi local smeared quark fields $q_{S(\vec{P})}(\vec{x},t)$ constructed with 50 steps of iterative Gaussian momentum-smearing Bali et al. (2016) with smearing radius $\varepsilon=0.2$. $Z_{\vec{P}}$ denotes the combination of overlap factors for the source and sink interpolating operators.

Two and three-point functions are constructed for three choices of pion boost $\vec{P}=P^{z}\vec{e}_{z}$, with $P^{z}=n^{z}2\pi/L$ for $n_{z}\in\{3,5,7\}$. An effective energy function that asymptotes to $E_{\vec{P}}$ can be defined as

	$\displaystyle E^{\text{eff}}_{\vec{P}}(t)$	$\displaystyle=\frac{1}{a}\text{arccosh}{\left({\frac{C_{\text{2pt}}(t+a,\vec{P})+C_{\text{2pt}}(t-a,\vec{P})}{2C_{\text{2pt}}(t,\vec{P})}}\right)}$
		$\displaystyle\overset{t\gg 0}{\longrightarrow}E_{\vec{P}}+\ldots,$		(14)

where the ellipses denote exponentially-suppressed corrections from excited states. This function is shown for the ensemble investigated here in Fig. 2, including the results of fits to the two-point correlation functions. The fits are performed as described in Appendix A of Ref. Shanahan et al. (2020), with the number of states in each fit chosen by maximizing an information criterion, and different choices of fit range sampled and combined in a weighted average. The relative deviations in the extracted energies from the continuum dispersion relation $E_{\vec{P}}=\sqrt{m_{\pi}^{2}+|\vec{P}|^{2}}$ are at most 5% for all momenta studied, increasing with increasing $|\vec{P}|$, but consistent with the expected size of lattice artifacts.

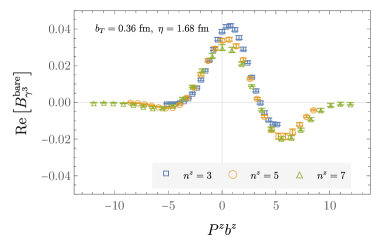
The ratio $\mathcal{R}_{\Gamma}$ defined in Eq. (11) is constructed for all Dirac structures $\Gamma$ and a range of operators with different staple widths and asymmetries, detailed in Table 1. As indicated, the number of measurements is varied for the different boost momenta, to partially compensate for the differences in statistical noise. All ratios are computed for sink times $t\in\{7,9,11,13\}$ and with all operator insertion times $\tau$ such that $0<\tau<t$. The fitting procedure used to determine $B^{\text{bare}}_{\Gamma}$ at each set of parameters is precisely the same procedure as detailed in Appendix A of Ref. Shanahan et al. (2020). Several examples of the fits in $t$ and $\tau$ used to extract the quasi beam functions are shown in Appendix A. An example of the resulting bare quasi beam functions, for particular choices of $b_{T}$ and $\eta$, is shown in Fig. 3. Additional examples are provided in Appendix B.

Computing the modified $\overline{\mathrm{MS}}$-renormalized quasi beam function $B^{\overline{\mathrm{MS}}}_{\Gamma}$ by Eq. (6) requires, in addition to the bare quasi beam functions, the $\mathrm{RI}^{\prime}\mathrm{/MOM}$ renormalization factor $Z^{\mathrm{RI}^{\prime}\mathrm{/MOM}}_{\mathcal{O}_{\gamma^{4}\Gamma}}$. This factor enters the calculation of the renormalized quasi beam function both through the renormalization itself (Eq. (7)) and in the computation of the factor $\tilde{R}$ (Eq. (9)). The calculation of the nonperturbative renormalization undertaken here follows closely the presentation of Ref. Shanahan et al. (2019).

The matrix $Z^{\text{$\mathrm{RI}^{\prime}\mathrm{/MOM}$}}_{\mathcal{O}_{\Gamma\Gamma^{\prime}}}$ is defined by the renormalization condition

$$Z_{q}^{-1}(p_{R})Z^{\text{$\mathrm{RI}^{\prime}\mathrm{/MOM}$}}_{\mathcal{O}_{\Gamma\Gamma^{\prime}}}(p_{R})\Lambda^{\mathcal{O}_{\Gamma^{\prime}}}_{\alpha\beta}(p)\big{|}_{p^{\mu}=p^{\mu}_{R}}=\Lambda_{\alpha\beta}^{\mathcal{O}_{\Gamma};\text{tree}}(p)\,,$$

(15)

where dependence on the lattice spacing is left implicit and $\Lambda^{\mathcal{O}_{\Gamma};(\text{tree})}$ denotes the bare (tree-level) amputated Green’s function of the operator $\mathcal{O}_{\Gamma}$ defined in Eq. (4) in an off-shell quark state in the Landau gauge:

$$\Lambda^{\mathcal{O}_{\Gamma}}(p)=S^{-1}(p)G^{\mathcal{O}_{\Gamma}}(p)S^{-1}(p)\,.$$

(16)

Here $S(p)$ is the quark propagator projected to momentum $p$:

	$\displaystyle S_{\alpha\beta}(p,x)$	$\displaystyle=\sum_{y}e^{-ip\cdot y}\langle q_{\alpha}(x)\bar{q}_{\beta}(y)\rangle,$		(17)
	$\displaystyle S_{\alpha\beta}(p)$	$\displaystyle=\frac{1}{V}\sum_{x}e^{ip\cdot x}S_{\alpha\beta}(p,x),$		(18)

and $G^{\mathcal{O}_{\Gamma}}$ denotes the non-amputated quark-quark Green’s function with one insertion of $\mathcal{O}_{\Gamma}$, which implicitly depends on the geometry of the staple-shaped Wilson line defining the operator:

	$\displaystyle G^{\mathcal{O}_{\Gamma}}_{\alpha\beta}(p)$	$\displaystyle=\ \frac{1}{V}\sum_{x,y,z}{\rm e}^{{\mathrm{i}}p\cdot(x-y)}\langle q_{\alpha}(x)\mathcal{O}_{\Gamma}(z+b,z)\bar{q}_{\beta}(y)\rangle,$
		$\displaystyle=\ \frac{1}{V}\sum_{z}\langle\!\gamma_{5}S^{\dagger}(p,\!b+z)\gamma_{5}\widetilde{W}(\eta;b+z,\!z)\frac{\Gamma}{2}S(p,\!z)\!\rangle_{\alpha\beta},$		(19)

where $V=L^{3}\times T$ is the lattice volume. The quark wavefunction renormalization $Z_{q}$ is defined as

		$\displaystyle Z_{q}(p_{R})S(p)\big{|}_{p^{2}=p_{R}^{2}}=S^{\text{tree}}(p)$
	$\displaystyle\implies$	$\displaystyle Z_{q}(p_{R})=\ \frac{1}{12}\text{Tr}\left[S^{-1}(p)S^{\text{tree}}(p)\right]\bigg{|}_{p^{2}=p_{R}^{2}}$		(20)
		$\displaystyle\hphantom{Z_{q}(p_{R})}=\ \frac{{\rm Tr}\left[{\rm i}\sum_{\lambda}\gamma_{\lambda}\sin(ap_{\lambda})S^{-1}(p)\right]}{12\sum_{\lambda}\sin^{2}(ap_{\lambda})}\bigg{|}_{p^{2}=p_{R}^{2}}.$

From Eq. (15), the matrix of $\mathrm{RI}^{\prime}\mathrm{/MOM}$ renormalization factors may be computed as

$$\left(Z^{\text{$\mathrm{RI}^{\prime}\mathrm{/MOM}$}}_{\mathcal{O}_{\Gamma\Gamma^{\prime}}}(p_{R})\right)^{-1}=\frac{\mathcal{V}^{\mathcal{O}_{\Gamma\Gamma^{\prime}}}(p)}{6e^{ip_{R}\cdot b}Z_{q}(p_{R})}\bigg{|}_{p^{\mu}=p^{\mu}_{R}},$$

(21)

where $b^{\mu}$ denotes the separation of the endpoints of the nonlocal operator $\mathcal{O}_{\Gamma}$, the projected vertex function is defined as

$$\mathcal{V}^{\mathcal{O}_{\Gamma\Gamma^{\prime}}}(p)\equiv\text{Tr}\left[\Lambda^{\mathcal{O}_{\Gamma}}(p)\Gamma^{\prime}\right],$$

(22)

and the replacement

$\displaystyle\text{Tr}\left[\Lambda^{\mathcal{O}_{\Gamma};\text{tree}}(p_{R})\Gamma^{\prime}\right]=6e^{ip_{R}\cdot b}\delta^{\Gamma\Gamma^{\prime}}$

(23)

has been made. It should be noted that since the operator $\mathcal{O}^{q}_{\Gamma}$ is nonlocal and frame dependent, different directions in $p_{R}^{\mu}$ constitute different renormalization schemes, related by finite renormalization factors. As such, $Z^{\text{$\mathrm{RI}^{\prime}\mathrm{/MOM}$}}_{\mathcal{O}_{\Gamma\Gamma^{\prime}}}$ depends on $p_{R}^{\mu}$ itself rather than only on its magnitude, which acts as the renormalization scale.

The complete $16\times 16$ matrix of $\mathrm{RI}^{\prime}\mathrm{/MOM}$ renormalization factors $Z^{\mathrm{RI}^{\prime}\mathrm{/MOM}}_{\mathcal{O}_{\Gamma\Gamma^{\prime}}}$ is computed for the same set of operator geometries defined in Table 1, on $n_{\text{cfg}}=50$ gauge field configurations. For all operator geometries with $\eta/a\in\{12,14\}$, the renormalization factors are computed for a range of four-momenta tabulated in Tab. 2, to enable an investigation of residual dependence on the renormalization scale (which would be canceled by an all-orders matching to the $\overline{\mathrm{MS}}$ scheme) and discretization artifacts. For operator geometries with $\eta/a=23$, only the four-momentum with $n^{\mu}=(12,12,12,12)$ is used. An example of the resulting $\mathrm{RI}^{\prime}\mathrm{/MOM}$ renormalization matrices is shown in Fig. 4, which displays a subset of the off-diagonal renormalization factors normalized relative to the diagonal components:

$\displaystyle\mathcal{M}^{\text{$\mathrm{RI}^{\prime}\mathrm{/MOM}$}}_{\mathcal{O}_{\Gamma\mathcal{P}}}\equiv$

$\displaystyle\frac{\text{Abs}[Z^{\text{$\mathrm{RI}^{\prime}\mathrm{/MOM}$}}_{\mathcal{O}_{\Gamma\mathcal{P}}}]}{\frac{1}{16}\sum_{i}\text{Abs}[Z^{\text{$\mathrm{RI}^{\prime}\mathrm{/MOM}$}}_{\mathcal{O}_{\Gamma_{i}\Gamma_{i}}}]}\,,$

(24)

computed for quark bilinear operators with straight Wilson lines and a particular choice of momentum.

The $\overline{\mathrm{MS}}$ renormalization factors are computed via Eq. (7) from the $\mathrm{RI}^{\prime}\mathrm{/MOM}$ renormalization matrices and the perturbative matching factor $\mathcal{R}^{\overline{\mathrm{MS}}}_{\mathcal{O}_{\gamma^{4}\Gamma}}$, calculated at next-to-leading order in continuum perturbation theory with dimensional regularization ($D=4-2\epsilon$) Constantinou et al. (2019); Ebert et al. (2020). In this work, the scale $\tilde{p}_{R}$ is set to 4.9 GeV. Examples of the resulting $\overline{\mathrm{MS}}$ renormalization factors are presented in Figs. 5 and 6. This renormalization is independent of $p_{R}$ up to discretization artifacts, two-loop perturbative matching corrections which are neglected here, and nonperturbative effects that vanish at asymptotically large $p^{2}_{R}$. While in principle one might fit to results generated at different $p_{R}$ values to constrain discretization effects, this is not feasible with the data generated here, and the covariance matrices for the nonlocal operators cannot be reliably estimated. The renormalization constants computed with $n^{\mu}=(12,12,12,12)$ are thus taken as best-estimates and used in the further analysis of the Collins-Soper kernel. For those operator structures where the $\mathrm{RI}^{\prime}\mathrm{/MOM}$ renormalization factors have been computed at other choices of $p_{R}$, this yields indistinguishable results for the Collins-Soper kernel compared with results obtained using the weighted averaging procedure over momenta which is employed in Ref. Shanahan et al. (2019). The components of $\mathcal{M}^{\text{$\mathrm{RI}^{\prime}\mathrm{/MOM}$}}_{\mathcal{O}_{\Gamma\mathcal{P}}}$ are of similar magnitude for both $\Gamma\in\{\gamma^{3},\gamma^{4}\}$, which is consistent with the conclusion of Ref. Ji et al. (2021) but is in contrast with the results of Refs. Constantinou et al. (2019); Green et al. (2020) which predict no mixing effects for $\Gamma=\gamma^{3}$ at ${\cal O}(a^{0})$. The quasi beam functions with both Dirac structures are thus treated on equal footing in this work.

Modified $\overline{\mathrm{MS}}$-renormalized quasi beam functions are computed via Eq. (6) from the bare quasi beam functions and $\overline{\mathrm{MS}}$ renormalization factors calculated as described in Secs. III.1 and  III.2; the uncertainties of the two components are combined in quadrature. While for clarity all equations in this section are expressed for renormalized quasi beam functions defined with the Dirac structure $\gamma^{4}$, both $B^{\overline{\mathrm{MS}}}_{\gamma^{4}}$ and $B^{\overline{\mathrm{MS}}}_{\gamma^{3}}$ are computed and analyzed independently.

The real and imaginary parts of the renormalized quasi beam functions should be symmetric and antisymmetric functions of $b^{z}$ respectively in the $\eta\rightarrow\infty$ limit. The numerical results obtained in this work, however, show significant departures from these expectations at finite $\eta$ as was also observed in the quenched calculation of Ref. Shanahan et al. (2019). The $b^{z}$-dependence of the asymmetry in the absolute value of the renormalized quasi beam functions is illustrated in Fig. 7a. This asymmetry can be understood as an incomplete cancellation of the Wilson-line self-energy correction proportional to $e^{-V(b_{T})\,b^{z}}$ between the $\overline{\mathrm{MS}}$ renormalization factor and the bare quasi beam function, where $V(b_{T})$ is the static quark-antiquark potential at distance $b_{T}$. Such an effect yields a $b^{z}$-dependent asymmetry proportional to $e^{-\Delta b^{z}}$, depending on an asymmetry parameter $\Delta=-V(b_{T})+V(b_{T}^{R})$. This is in fact a good model of the asymmetry observed in the numerical calculations of this work; fits of $|B^{\overline{\mathrm{MS}}}_{\gamma^{4}}(\mu,-b^{z},\vec{b}_{T},a,\eta,P^{z})|/|B^{\overline{\mathrm{MS}}}_{\gamma^{4}}(\mu,b^{z},\vec{b}_{T},a,\eta,P^{z})|$ (and the analogous expression constructed from $B^{\overline{\mathrm{MS}}}_{\gamma^{3}}$) to this functional form, fit separately for fixed values of $b_{T}$, $\eta$, and $P^{z}$, achieve acceptable goodness-of-fit with an average $\chi^{2}/\text{d.o.f.}=0.56$. These fits, and the resulting values of the asymmetry parameter $\Delta$, are illustrated in Fig. 7 and in Appendix B. Asymmetry-corrected modified $\overline{\mathrm{MS}}$-renormalized quasi beam functions are thus defined as

	$\displaystyle B^{\overline{\mathrm{MS}};\text{corr}}_{\gamma^{4}}(\mu,b^{z},$	$\displaystyle\vec{b}_{T},a,\eta,P^{z})=\ e^{\Delta(\vec{b}_{T},a,\eta,P^{z})|b^{z}|}$
	$\displaystyle\times\left(\text{Re}\vphantom{B^{\overline{\mathrm{MS}}}_{\gamma^{4}}}\right.$	$\displaystyle\!\!\left[B^{\overline{\mathrm{MS}}}_{\gamma^{4}}(\mu,|b^{z}|,\vec{b}_{T},a,\eta,P^{z})\right]$
	$\displaystyle+$	$\displaystyle\left.\text{sign}(b^{z})\,\text{Im}\!\!\left[B^{\overline{\mathrm{MS}}}_{\gamma^{4}}(\mu,|b^{z}|,\vec{b}_{T},a,\eta,P^{z})\right]\right).$		(25)

Here, the uncertainties in the factor $e^{\Delta|b^{z}|}$ and the quasi beam functions are added in quadrature and, after asymmetry correction, the more precise results for beam functions with $b^{z}>0$ (which involve shorter Wilson lines) are mirrored to $b^{z}<0$. An example of the modified $\overline{\mathrm{MS}}$-renormalized quasi beam functions before and after asymmetry correction is given in Fig. 8.

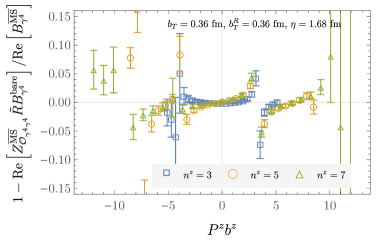
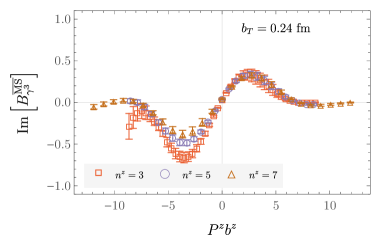
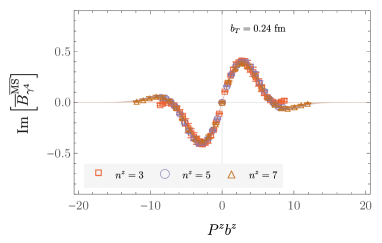
It is expected that the renormalized beam functions should be independent of the matching scale $b_{T}^{R}$. This expectation is satisfied within uncertainties for the numerical investigations of this work as illustrated in Fig. 9; for use in the calculation of the Collins-Soper kernel, a weighted average Aoki et al. (2020) over possible choices of $b_{T}^{R}$ in the window $a\ll b_{T}^{R}\ll\Lambda_{\text{QCD}}^{-1}$ is thus implemented, performed precisely as detailed in Appendix C of Ref. Shanahan et al. (2020). Similarly, the asymmetry-corrected renormalized quasi beam functions do not depend on $\eta$ within uncertainties, and the formal extrapolation to $\eta\rightarrow\infty$ is implemented with an analogous weighted average. The resulting averaged values of the asymmetry-corrected modified $\overline{\mathrm{MS}}$-renormalized quasi beam function are denoted by $\overline{B}^{\overline{\mathrm{MS}}}_{\gamma^{4}}(\mu,b^{z},b_{T},P^{z})$, and have no dependence on $\eta$ or $b^{R}_{T}$; the dependence on $a$ is also dropped in this notation, as a single lattice spacing is used in this numerical study. Figures showing $\overline{B}^{\overline{\mathrm{MS}}}_{\gamma^{4}}$ and $\overline{B}^{\overline{\mathrm{MS}}}_{\gamma^{3}}$ are provided in Appendix B. The contributions to these quantities from mixing between operators with different Dirac structures is generally found to be less than $10\%$; see Fig. 10 for an illustration. Additional examples are provided in Appendix B.

To determine the Collins-Soper kernel via Eq. (II) from the averaged asymmetry-corrected modified $\overline{\mathrm{MS}}$-renormalized quasi beam functions $\overline{B}_{\gamma^{4}}^{\overline{\mathrm{MS}}}$ and $\overline{B}_{\gamma^{3}}^{\overline{\mathrm{MS}}}$, defined in the previous section, requires a Fourier transform of the quasi beam functions in $b^{z}$. As is clear from Fig. 23, however, the $b^{z}$-range of the data is not sufficient for the tails of the quasi beam functions at large $|b^{z}|$ to decay to plateaus consistent with zero, particularly at the largest $b_{T}$ and smallest $P^{z}$ values used in this numerical study. As such, it is to be expected that a discrete Fourier transform (DFT) will have significant systematic uncertainties from the truncation of the data in $P^{z}b^{z}$; details of a DFT analysis of the quasi beam functions are presented in Appendix C. Instead, Fourier transforms are taken after fitting the quasi beam functions to functional forms that allow extrapolation in $b^{z}$. This approach trades the systematic uncertainties of a DFT for model-dependence in the fit form used to extrapolate the quasi beam functions. While this model-dependence is difficult to quantify rigorously, this approach allows the physical expectation that the quasi beam functions should decay smoothly at large $|b^{z}|$ to be incorporated (a DFT effectively models the beam functions as zero outside the $b^{z}$-range in which lattice QCD results are computed).

In particular, the quasi beam functions are modeled as a sum of polynomials in $b^{z}$ times Gaussian functions, which provide an appropriate basis, since it is expected that the quasi beam functions should be analytic functions of $b^{z}$ (the $b^{z}\to 0$ limit at fixed $b_{T}$ does not introduce additional divergences), and yield high-quality fits with few free parameters. Specifically, for each choice of $b_{T}$ and $P^{z}$, the real and imaginary parts of the quasi beam function $\overline{B}^{\overline{\mathrm{MS}}}_{\gamma^{4}}$ (and independently $\overline{B}^{\overline{\mathrm{MS}}}_{\gamma^{3}}$) are fit with even and odd functions of $b^{z}$ respectively, defined as

	$\displaystyle f_{\text{Re}}(\sigma,\{r_{n}\};b^{z})$	$\displaystyle=\text{exp}[-(b^{z})^{2}/(2\sigma^{2})]\sum_{n=0}^{n_{\text{max}}}r_{n}(b^{z})^{2n}$		(26)
	$\displaystyle f_{\text{Im}}(\sigma,\{r_{n}\};b^{z})$	$\displaystyle=\text{exp}[-(b^{z})^{2}/(2\sigma^{2})]\sum_{n=0}^{n_{\text{max}}}i_{n}(b^{z})^{2n+1}.$		(27)

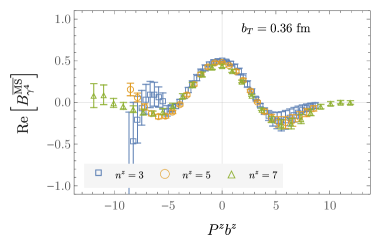
The value of $n_{\text{max}}$ is chosen to minimize the Akaike information criterion (AIC) Akaike (1974) and corresponds to $n_{\text{max}}\in\{2,3,4\}$ for all cases. The fits with these optimal values of $n_{\text{max}}$ are of high quality in all cases, with an average $\chi^{2}/\text{d.o.f.}=0.41$. The resulting models of the quasi beam functions are denoted $\hat{B}^{\overline{\mathrm{MS}}}_{\gamma^{4}}$ (and, correspondingly $\hat{B}^{\overline{\mathrm{MS}}}_{\gamma^{3}}$), and are illustrated in Fig. 11 (with further examples provided in Appendix B).

Finally, in terms of the models $\hat{B}^{\overline{\mathrm{MS}}}_{\gamma^{4}}$, the relation defining the Collins-Soper kernel in Eq. (II) is realized as

	$\displaystyle\hat{\gamma}^{q}_{\zeta}(\mu,b_{T};P_{1}^{z},P_{2}^{z},x)$	$\displaystyle\equiv\frac{1}{\ln(P^{z}_{1}/P^{z}_{2})}\ln\Biggr{[}\frac{C^{\mathrm{TMD}}_{\text{ns}}(\mu,xP_{2}^{z})}{C^{\mathrm{TMD}}_{\text{ns}}(\mu,xP_{1}^{z})}$
		$\displaystyle\!\times\!\frac{\int\!\mathrm{d}b^{z}e^{-ib^{z}\!xP_{1}^{z}}P_{1}^{z}\hat{B}^{\overline{\mathrm{MS}}}_{\gamma^{4}}(\mu,b^{z},b_{T},P_{1}^{z})}{\int\!\mathrm{d}b^{z}e^{-ib^{z}\!xP_{2}^{z}}\!P_{2}^{z}\hat{B}^{\overline{\mathrm{MS}}}_{\gamma^{4}}(\mu,b^{z},b_{T},P_{2}^{z})}\Biggr{]},$		(28)

which coincides with $\gamma^{q}_{\zeta}(\mu,b_{T})$ up to power corrections such as higher-twist corrections in the factorization formula for the quasi TMDPDF, and discretization artifacts, which introduce the dependence on $P_{1}^{z}$, $P_{2}^{z}$, and $x$. One approach to determine $\gamma^{q}_{\zeta}(\mu,b_{T})$ from $\hat{\gamma}^{q}_{\zeta}(\mu,b_{T};P_{1}^{z},P_{2}^{z},x)$ is to model, fit, and subtract, these various artifacts. However, the most straightforward models of these effects do not provide good fits to the numerical data of this study, as detailed in Appendix D. Instead, since the contamination in $\hat{\gamma}^{q}_{\zeta}$ will be different at each choice of $P_{1}^{z}$, $P_{2}^{z}$, and $x$, and the effects can be expected to be larger²²2The matching coefficient includes large logarithms of $xP^{z}_{i}$ at small $x$, while the quasi beam functions at $x\to 0$ and $x\to 1$ are sensitive to the long-range correlations in $b^{z}$ and are thus affected by the truncation of the data in $P^{z}b^{z}$. In addition, the power corrections are expected to be enhanced at small $x$. at large and small values of $x$ and at small values of $P^{z}$, the variation of $\hat{\gamma}^{q}_{\zeta}$ over these choices is used to define an estimate of the systematic uncertainty.

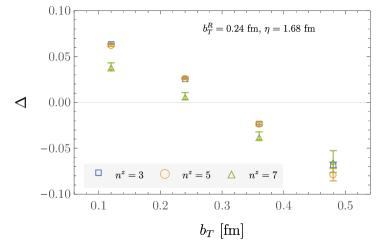
Precisely, a best value for the Collins-Soper kernel is determined from $\hat{\gamma}^{q}_{\zeta}$ via a multi-step procedure. First, the largest window of $x$ is determined for which the data for all choices of the pair $\{P_{1}^{z},P_{2}^{z}\}$ are consistent with a common constant value. In practice this region is defined as the largest window in which a constant fit to the data at a set of discrete $x$ points has a $\chi^{2}/\text{d.o.f.}\leq 1$. The central value and uncertainty are defined as the median and the 68% confidence interval of the union of the bootstrap data in that $x$ window, including all $\{P_{1}^{z},P_{2}^{z}\}$ pairs. The result of this procedure is robust to changes in the discretization of $x$, for sufficiently fine discretization scales (100 points spanning $0<x<1$ uniformly are used in the analysis presented). This procedure is performed separately for $\hat{\gamma}^{q}_{\zeta}$ determined from beam functions calculated with Dirac structures $\gamma^{4}$ and $\gamma^{3}$; examples of the resulting values are shown with $\hat{\gamma}^{q}_{\zeta}$ in Fig. 12, with the remainder presented in Appendix B. The central values of the independent calculations with Dirac structures $\gamma^{4}$ and $\gamma^{3}$ are averaged, and the average uncertainty is added in quadrature with half the difference between the central values obtained using each Dirac structure, to yield the final results of this work which are shown as a function of $b_{T}$ in Fig. 13, and are tabulated in Table. 3.

In addition to the approach followed here, there are a number of alternative methods of extracting the Collins-Soper kernel that have been proposed or employed in other studies, for example:

• •

  “LO”: The perturbative matching coefficient $C^{\mathrm{TMD}}_{\text{ns}}$ computed to leading-order (LO), instead of NLO, can be used in an analysis otherwise mirroring that presented here;

• •

  “Hermite/Bernstein”: As proposed in Ref. Shanahan et al. (2020), the $P^{z}b^{z}$-dependence of the quasi beam functions can be fit to models based on Hermite and Bernstein polynomial bases constructed to yield $x$-independent Collins-Soper kernels via Eq. (28), taking the LO value of the perturbative matching coefficient $C^{\mathrm{TMD}}_{\text{ns}}$;

• •

  “$b^{z}=0$”: An approximation of the Collins-Soper kernel can be computed with LO matching using only the quasi beam functions evaluated at $b^{z}=0$ (this approach does not require a Fourier transform in $b^{z}$):

  $$\hskip 25.60747pt[{\gamma}^{q}_{\zeta}(\mu,b_{T})]^{b^{z}=0}\equiv\frac{1}{\ln(P^{z}_{1}/P^{z}_{2})}\ln\Biggr{[}\frac{\overline{B}^{\overline{\mathrm{MS}}}_{\gamma^{4}}(\mu,0,b_{T},P_{1}^{z})}{\overline{B}^{\overline{\mathrm{MS}}}_{\gamma^{4}}(\mu,0,b_{T},P_{2}^{z})}\Biggr{]};$$

  (29)

• •

  “$b^{z}=0$, bare”: As proposed in Ref. Zhang et al. (2020), the same approach described for “$b^{z}=0$” can be followed, using bare quasi beam functions ${B}^{\text{bare}}_{\gamma^{4}}$ rather than renormalized quasi beam functions (i.e., neglecting operator mixing between different Dirac structures);

• •

  “$b^{z}=0/b_{T}=0$, bare”: As proposed in Ref. Li et al. (2021), a variation of the ‘$b^{z}=0$” approach can be used, approximating the Collins Soper kernel as

  	$\displaystyle\hskip 11.38109pt[{\gamma}^{q}_{\zeta}$	$\displaystyle(\mu,b_{T})]^{b^{z}=0/b_{T}=0}\equiv\frac{1}{\ln(P^{z}_{1}/P^{z}_{2})}$
  		$\displaystyle\times\ln\Biggr{[}\frac{{B}^{\text{bare}}_{\gamma^{4}}(0,b_{T},a,\eta,P_{1}^{z}){B}^{\text{bare}}_{\gamma^{4}}(0,0,a,\eta,P_{2}^{z})}{{B}^{\text{bare}}_{\gamma^{4}}(0,b_{T},a,\eta,P_{2}^{z}){B}^{\text{bare}}_{\gamma^{4}}(0,0,a,\eta,P_{1}^{z})}\Biggr{]}.$		(30)

Each of these methods can be followed using the quasi beam functions computed in this work; a comparison of the results is provided in Fig. 14. For the “LO” approach, the same procedure is followed to combine the results obtained using quasi beam functions with Dirac structures $\gamma^{3}$ and $\gamma^{4}$ as for the “NLO” method which yields the main results of this work. For the other approaches the results obtained with the two Dirac structures are not always consistent at one standard deviation, and are shown separately; for $b_{T}/a=4$ no results for the “Hermite/Bernstein” approach are shown with Dirac structure $\gamma^{3}$ as the model fits were of poor quality with $\chi^{2}/\text{d.o.f.}>2$. In the case of the “$b^{z}=0/b_{T}=0$, bare” approach, bare quasi beam functions with $\eta/a=14$, which is the largest extent studied in this work for all $P^{z}$, are used in the analysis.