Large-time behavior of solutions of parabolic equations on the real line with convergent initial data II: equal limits at infinity
Abstract
We continue our study of bounded solutions of the semilinear parabolic equation on the real line, where is a locally Lipschitz function on Assuming that the initial value of the solution has finite limits as , our goal is to describe the asymptotic behavior of as . In a prior work, we showed that if the two limits are distinct, then the solution is quasiconvergent, that is, all its locally uniform limit profiles as are steady states. It is known that this result is not valid in general if the limits are equal: . In the present paper, we have a closer look at the equal-limits case. Under minor non-degeneracy assumptions on the nonlinearity, we show that the solution is quasiconvergent if either , or and is a stable equilibrium of the equation . If and is an unstable equilibrium of the equation , we also prove some quasiconvergence theorem making (necessarily) additional assumptions on . A major ingredient of our proofs of the quasiconvergence theorems—and a result of independent interest—is the classification of entire solutions of a certain type as steady states and heteroclinic connections between two disjoint sets of steady states.
Key words: Parabolic equations on , quasiconvergence, entire solutions, chains, connecting orbits, zero number, spatial trajectories, Morse decompositions
1 Introduction and main results
1.1 Background
Consider the Cauchy problem
| (1.1) | ||||
| (1.2) |
where is a locally Lipschitz function on and We denote by or simply if there is no danger of confusion, the unique classical solution of (1.1), (1.2) and by its maximal existence time. If is bounded on , then necessarily that is, the solution is global. In this paper, we are concerned with the behavior of bounded solutions as . A basic question we specifically want to address is whether, or to what extent, the large-time behavior of bounded solutions is governed by steady states of (1.1).
If the initial data admits limits as then for all time the solution of (1.1), (1.2) admits limits as In other words, the function space
| (1.3) |
is invariant for (1.1). Continuing our study initiated in [29], we examine the large time behavior of bounded solutions in . More specifically, we are interested in the behavior of the solutions in bounded—albeit arbitrarily large—spatial intervals, as . For that purpose, we introduce the limit set of a bounded solution , denoted by or with , as follows:
| (1.4) |
Here the convergence is in the topology of , that is, the locally uniform convergence. By standard parabolic estimates, the trajectory of a bounded solution is relatively compact in This implies that is nonempty, compact, and connected , and it attracts the solution in (the metric space) :
If the limit set reduces to a single element , then is convergent: in as . Necessarily, is a steady state of (1.1). If all functions are steady states of (1.1), the solution is said to be quasiconvergent.
Convergence and quasiconvergence both express a relatively tame character of the solution in question, entailing in particular the property that approaches zero locally uniformly on as . In some cases, quasiconvergence can be established by means of energy estimates when bounded solutions in suitable energy spaces are considered (see [12], for example). However, when no particular rate of approach of to its limits at is assumed, energy techniques typically do not apply. Nonetheless, several quasiconvergence results are available for solutions in (see [33] for a general overview). These include quasiconvergence theorems of [23] for nonnegative functions with when —convergence theorems are available under additional conditions on , see [10, 11, 23]; or for generic , see [25]—and a theorem of [35] for functions satisfying or . An improvement over the latter quasiconvergence result was achieved in [29], where we proved that the condition alone, with no relations involving for , is already sufficient for the quasiconvergence of the solution if it is bounded.
It is also known that the -limit set of a bounded solution always contains at least one equilibrium [18, 19]. However, bounded solutions, even those in , are not always quasiconvergent (see [30, 32]). Moreover, as shown in [32], non-quasiconvergent solutions occur in (1.1) in a persistent manner: they exist whenever is a nonlinearity satisfying certain robust conditions (cp. (1.9) below). In view of these results, the following question arises naturally. Given , can one characterize in some way the initial data which yield quasiconvergence solutions? Our previous work [29] was our first step in addressing this question: we proved the quasiconvergence in the distinct-limits case: . In the present paper, we consider the case when the limits are equal: . We assume the nonlinearity to be fixed and satisfy minor nondegeneracy conditions (see the next section).
In our first main theorem, Theorem 1.1, we show that if , or if and is a stable equilibrium of the equation , then the solution of (1.1), (1.2) is quasiconvergent if bounded. In the examples of non-quasiconvergent solutions with , as given in [30, 32], is an unstable equilibrium of . Thus, our theorem shows that this is in fact necessary. Other two results, Theorems 1.3 and 1.4, give sufficient conditions for the quasiconvergence of the solution in the case that is an unstable equilibrium of the equation . A special case of the sufficient condition of Theorem 1.4 is the condition that has compact support and only finitely many sign changes. Theorem 1.3 has a somewhat surprising result saying that any element of whose range is not included in the minimal bistable interval containing is necessarily a steady state.
We give formal statements of these results in Subsection 1.3, after first formulating our hypotheses in Subsection 1.2. In Subsection 1.4, we give an outline of our strategy of proving the quasiconvergence theorems.
A quasiconvergence result closely related to our Theorem 1.1 has recently been proved by Risler. In [36], he considers the Cauchy problem for gradient reaction-diffusion systems on , where the initial data are assumed to converge at to stable homogeneous steady states contained in the same level of the potential function. Under certain generic conditions on the corresponding stationary system, he proves that bounded solutions of such Cauchy problems are quasiconvergent in a localized topology (in the companion paper [37], the global shape of such solutions at large times is investigated). His approach is variational, which has an advantage that it applies to gradient systems, as opposed to our techniques based on the zero number, which only apply to scalar equations. In the scalar case, our method seems to have some advantages. For example, it allows us to treat to some extent the case when the limit of the initial data at is unstable. Also, in principle, the method can be used under much less stringent nondegeneracy conditions (cp. Subsection 1.2) and, we believe, will eventually allow us to dispose of the nondegeneracy conditions altogether.
A key ingredient of our method of proof of the quasiconvergence theorems is a classification result for a certain type of entire solutions of (1.1), that is, solutions defined for all . Roughly speaking, the result shows that the entire solutions are either steady states or connections between two disjoint sets of steady states of (1.1) (see Sections 1.4 and 4 for details). Entire solutions play an important role in qualitative analysis of solutions of parabolic equations, as it can usually be proved that the large-time behavior of bounded solutions is governed by entire solutions. In our setting, for example, the -limit sets—or their generalized versions, as defined in Section 2.3—of bounded solutions of (1.1) consist of orbits of entire solutions. Entire solutions of (1.1) have been extensively studied and many different types of such solutions have been found. These include, in addition to steady states, spatially periodic heteroclinic orbits between steady states (see [14, 15, 34] for example), traveling waves and many types of “nonlinear superpositions” of traveling waves and other entire solutions (see [4, 5, 8, 20, 21, 27, 28] and references therein), as well entire solutions involving colliding pulses [24]. Unlike for equations on bounded intervals where rather general classification results for entire solutions are available (see [3, 15, 39] and references therein), no such general classification is currently in sight for the vast variety of entire solutions of (1.1). Our result classifying certain entire solutions as connections between two sets of steady state is a modest contribution in this area, exploring the asymptotic behavior of entire solutions as in the topology of .
1.2 Standing hypotheses
As above, is a locally Lipschitz function. We also assume the following nondegeneracy condition:
- (ND)
-
For each , is of class in a neighborhood of and
Our theorems can be proved under weaker conditions. To give an example of how (ND) can be relaxed, set
| (1.5) |
so zeros of are critical points of . The following nondegeneracy conditions can be considered in place of (ND).
- (ND1)
-
Each is locally a point of strict maximum or strict minimum for
- (ND2)
-
If are two consecutive local-maximum points of and then , are nondegenerate critical points of : is of class in a neighborhood of and
Relaxing (ND) to (ND1), (ND2) does not pose major problems in the proof of our results, but it would obscure the exposition a bit and would require modification of some standard results we refer to. Thus we decided to just work with (ND). All these nondegeneracy conditions are just technical and we believe our theorems can be proved by the same general method without them. Clearly, condition (ND) is generic with respect to “reasonable” topologies. Note, however, that we allow some nongeneric situations, for example, the existence of two consecutive local-maximum points of at which takes the same value. The nondegeneracy condition constrains considerably the complexity of possible phase portraits associated with equation for the steady states of (1.1):
| (1.6) |
This is mainly how the nondegeneracy condition is useful in this paper.
We will make another assumption on the nonlinearity. It concerns the behavior of for large values of and it can be assumed with no loss of generality. Indeed, our main quasiconvergence theorems deal with individual bounded solutions only. Thus we can modify freely outside the range of the given solution with no effect on the validity of the theorems. It will be convenient to assume that
- (MF)
-
is globally Lipschitz and there is such that for all with one has
Hypotheses (ND) and (MF) are our standing hypotheses on .
Each zero of is of course an equilibrium of the equation
| (1.7) |
Hypothesis (ND) implies in particular that any such equilibrium is either unstable from above and below, or asymptotically stable (this property would also be implied by (ND1)).
As mentioned above, in this paper we take , assuming that its limits at are equal. Without loss of generality, we assume the limits to be equal to zero:
| (1.8) |
We distinguish the following two cases:
1.3 Quasiconvergence theorems
If (S) holds, we have a general quasiconvergence theorem:
Theorem 1.1.
Remark 1.2.
We will show, more precisely, that any element of is a constant steady state, or a ground state at some level , or a standing wave of (1.1). See Section 2.2 for a description of the structure of steady states of (1.1) and the meaning of the terminology used here. We will also show that there is a single chain in the phase plane of containing the trajectories of all steady states (the definition of a chain is also given in Section 2.2). The same remarks apply to Theorem 1.4 below.
If (U) holds, then, as already noted in the introduction, a similar quasiconvergence does not hold in general: the references [30, 32] provide examples of bounded solutions of (1.1), (1.2) with which are not quasiconvergent. More specifically, such solutions exist whenever and belongs to a bistable interval of : there are such that
| (1.9) |
Whether the bistable nonlinearity is balanced in : , or unbalanced: , there always exists a continuous function such that , and the solution of (1.1), (1.2) is not quasiconvergent. Obviously, all limit profiles, stationary or not, of the solution take also values between , . One could naturally speculate that when the initial data are not constrained by the assumption , the behavior of the corresponding solutions can only get more complicated, with some nonstationary limit profiles possibly occurring outside the interval . Surprisingly perhaps, this turns out not to be the case. In our next theorem, we show that any limit profile whose range is not contained in is a steady state. Thus it is really the bistable interval which is “responsible” for the nonquasiconvergence of the solutions with , regardless of whether the range of is contained in or not.
Note that if (U) holds and , are the zeros of immediately preceding and immediately succeeding 0, respectively, assuming they exist, then the relations in (1.9) are satisfied.
Theorem 1.3.
A stronger version of this result will be given in Theorem 6.4 after some needed terminology has been introduced. Obviously, Theorem 1.3 implies that the solution is quasiconvergent if no function has its range in .
Another aspect of the examples of non-quasiconvergent solutions given in [30, 32] is that the solutions found there are always highly oscillatory in space: for all the function has infinitely many critical points and infinitely many zeros. This raises another natural question whether, in the case (U), spatially nonoscillatory solutions are always quasiconvergent. Here, by a spatially nonoscillatory solution we mean a solution satisfying the following condition
- (NC)
-
There is such that has only finitely many critical points.
A sufficient condition for (NC) in terms of is that there exist such that the function is monotone and nonconstant on each of the intervals , . For if this holds, then one shows easily, using the comparison principle, that for all with and all sufficiently small positive times . Consequently, by standard zero number results (cp. Section 2.1), has only a finite number of zeros for all .
Presently, we are able to prove the quasiconvergence assuming that (NC) holds together with the following technical condition:
-
(R) There are sequences , such that the following holds. For every there is such that the function has only finitely many zeros.
Remark 1.5(ii) below gives sufficient conditions for (R) in terms of .
Theorem 1.4.
Remark 1.5.
(i) If (R) is strengthened so as to say that has only finitely many zeros for every , then the quasiconvergence theorem holds—without any extra condition like (NC) on and without the nondegeneracy condition (ND) on —due to a result of [29] which we recall in Theorem 2.12 below. This in particular applies when for some the function has an odd (finite) number of zeros, all of them simple. Indeed, in this case has opposite signs for and and, consequently, for every one has if is large enough. Since the zeros of are isolated (cp. Section 2.1), there are only finitely many of them. Of course, it may easily happen for a function with that has only finitely many zeros if is sufficiently large, but has infinitely many of them if is sufficiently small. An example is any continuous function such that
where and .
(ii) Conditions (NC) and (R) are both satisfied if has compact support and only finitely many zeros in . More generally, they are satisfied if on and there is such that is monotone and nonconstant on each of the intervals , . Indeed, the validity of (NC) is verified in the remark following (NC). To show the validity of (R), take any . Then, the assumption on implies that and in the whole interval one has either or . The comparison principle applied to the function (cp. Section 2.4) shows that for all and . This also implies that for all , as the function is odd about Consequently, as in the previous remark (i), has only finitely many zeros for all . Similarly one shows that has only finitely many zeros if (in fact, with a little more effort one can show this for any ). Variations of these arguments show that (NC) and (R) are satisfied if on an interval and on an interval one has , (or , ).
1.4 Entire solutions and chains
Our strategy for proving the quasiconvergence theorems consists in careful analysis of a certain type of entire solutions of (1.1). By an entire solution we mean a solution of (1.1) defined for all (and ). If is well known (see Section 2.3 for more details) that for any there exists an entire solution of (1.1) such that and for all .
In analysis of such entire solutions we employ, as in several earlier papers starting with [31], a geometric technique involving spatial trajectories of solutions of (1.1). This technique, powered by properties of the zero number functional, often allows one to gain insights into the behavior of solutions of equation (1.1) (whose trajectories are in an infinite dimensional space) by examining their spatial trajectories, which are curves in . Specifically for any , we define
| (1.10) |
and refer to this set as the spatial trajectory (or orbit) of If , is the union of the spatial trajectories of the functions in :
| (1.11) |
Note that if is a steady state of (1.1), then is the usual trajectory of the solution of the planar system
| (1.12) |
associated with equation (1.6).
When considering an entire solution with , we want to constrain the locations that the spatial trajectories , , can occupy in relative to the locations of the spatial trajectories of steady states of (1.1). In this, the concept of a chain is crucial. By definition, a chain is any connected component of the set , where is the union of trajectories of all nonstationary periodic solutions of (1.12). Any chain consists of equilibria, homoclinic orbits, and, possibly, heteroclinic orbits of (1.12) (see Section 2.2). Our ultimate goal is to prove that the spatial trajectories , , are all contained in one chain. From this it follows, via a unique-continuation type result (cp. Lemma 2.9 below), that is a steady state of (1.1), which proves that consists of steady states, as desired.
To achieve our goal, we first show that if the spatial trajectories , , are not contained in one chain, then none of them can intersect any chain; and there exist two distinct chains , such that
| (1.13) |
Here , stand for the and -limit sets of ; is defined as in (1.4) and the definition of is analogous, with replaced by . We will also show that the set of all relevant chains, namely, the chains that can possibly intersect , is finite and ordered by a suitable order relation, and that the chains in (1.13) always satisfy in that relation. As a consequence, we obtain that the sets
corresponding to the chains with constitute a Morse decomposition for the flow of (1.1) in (see [9]). However, the existence of such a Morse decomposition (with at least two Morse sets) contradicts well-known recurrence properties of the flow in (cp. [9, 7, 17]). This contradiction shows that the spatial trajectories , , must in fact be contained in one chain, as desired.
The detailed proof following the above scenario, which we give below, is rather involved mainly because there are several different possibilities as to how the chains , in (1.13) can look like and how the spatial trajectories , , can fit into the structure of , . Even though the number of these possibilities is reduced considerably by the nondegeneracy condition (ND), the possibilities that still remain require special considerations and arguments.
We wish to emphasize that we prove (1.13) for a large class of entire solutions of (1.1), regardless of their containment in the -limit set of the solution of (1.1), (1.2), for any . Accordingly, we have striven to make Section 4, where the entire solutions are studied in detail, completely independent from the other parts of the paper. In particular, no reference is made in that section to the solution or its limit set . Thus the results there can be viewed as a contribution to the general understanding of entire solutions of (1.1). Relations (1.13) can be interpreted as a classification result, characterizing nonstationary entire solutions as connections between two different sets of steady states. We refer the reader to Section 4 for more details.
The rest of the paper is organized as follows. In Section 2, we collect preliminary results on the zero number, steady states of (1.1), entire solutions of (1.1) and their and -limit sets. We also recall there some results from earlier paper that are repeatedly used in the proofs of our main theorems. The proofs themselves comprise Sections 3 and 6. Section 4 is devoted to the classification of entire solutions, as mentioned above.
2 Preliminaries
In this section, we collect preliminary results and basic tools of our analysis. We first recall some well known properties of the zero-number functional and then examine trajectories of steady states of (1.1) in the phase plane, taking our standing hypotheses (ND), (MF) into account. Next we recall invariance properties of various limit sets of bounded solutions of (1.1). Finally, in Subsection 2.4 we state several important technical results concerning bounded solutions of (1.1).
2.1 Zero number for linear parabolic equations
In this subsection, we consider solutions of a linear parabolic equation
| (2.1) |
where and is a bounded measurable function. Note that if , are bounded solutions of (1.1), then their difference satisfies (2.1) with a suitable function . Similarly, and are solutions of such a linear equation. These facts are frequently used below, often without notice.
For an interval with we denote by the number, possibly infinite, of zeros of the function If we usually omit the subscript :
The following intersection-comparison principle holds (see [1, 6]).
Lemma 2.1.
Let be a nontrivial solution of (2.1) and with Assume that the following conditions are satisfied:
-
•
if then for all
-
•
if then for all
Then the following statements hold true.
-
(i)
For each all zeros of are isolated. In particular, if is bounded, then for all
-
(ii)
The function is monotone non-increasing on with values in
-
(iii)
If for some the function has a multiple zero in and then for any with one has
(2.2)
If (2.2) holds, we say that drops in the interval
Remark 2.2.
It is clear that if the assumptions of Lemma 2.1 are satisfied and for some one has then can drop at most finitely many times in ; and if it is constant on then has only simple zeros in for all In particular, if there exists such that is constant on and all zeros of are simple.
Using the previous remark and the implicit function theorem, we obtain the following corollary.
Corollary 2.3.
Assume that the assumptions of Lemma 2.1 are satisfied and that the function is constant on If for some one has then there exists a - function defined for such that and for all
The following result, which is a version of Lemma 2.1 for time-dependent intervals, is derived easily from Lemma 2.1 (cp. [2, Section 2]).
Lemma 2.4.
Let be a nontrivial solution of (2.1) and , where for . Assume that the following conditions are satisfied:
-
(c1)
Either or is a (finite) continuous function on (s,T). In the latter case, for all .
-
(c2)
Either or is a continuous function on (s,T). In the latter case, for all .
Then statements (i), (ii) of Lemma 2.1 are valid with , , replaced by , , , respectively; and statement (iii) of Lemma 2.1 is valid with all occurrences of , , replaced by , , respectively.
We will also need the following robustness lemma (see [10, Lemma 2.6]).
Lemma 2.5.
Let be a sequence of functions converging to in where is an open interval. Assume that solves a linear equation (2.1), , and has a multiple zero for some . Then there exist sequences , such that for all sufficiently large the function has a multiple zero at .
2.2 Phase plane of the stationary problem
In this subsection, we examine the trajectories of the solutions of equation (1.6). The first-order system
| (2.3) |
associated with (1.6) is Hamiltonian with respect to the energy
| (2.4) |
(with as in (1.5)). Thus, each orbit of (2.3) is contained in a level set of The level sets are symmetric with respect to the axis, and our extra hypothesis (MF) implies that they are all bounded. Therefore, all orbits of (2.3) are bounded and there are only four types of them: equilibria (all of which are on the axis), non-stationary periodic orbits (by which we mean orbits of nonstationary periodic solutions), homoclinic orbits, and heteroclinic orbits. Following a common terminology, we say that a solution of (1.6) is a ground state at level if corresponding solution of (2.3) is homoclinic to the equilibrium ; we say that is a standing wave of (1.1) connecting and if is a heteroclinic solution of (2.3) with limit equilibria and .
Each non-stationary periodic orbit is symmetric about the axis and for some one has
| (2.5) |
Let
The next lemma gives a description of the phase plane portrait of (2.3) with all the non-stationary periodic orbits removed. The following observations will be useful in its proof and at other places below. Let be an equilibrium of (2.3). Then and, by (ND), . Elementary considerations using the Hamiltonian show that if , then is not contained in the closure of any homoclinic or heteroclinic orbit of (2.3). On the other hand, if , then (MF) implies that is contained in the closure of a homoclinic or heteroclinic orbit contained in the halfplane as well as of another one contained in the halfplane .
Lemma 2.6.
The following two statements are valid.
-
(i)
Let be a connected component of Then is a compact set contained in a level set of the Hamiltonian and one has
where is the value of on and for some with Moreover, if and then is an equilibrium. If the points and lie on homoclinic orbits. If then and is an unstable equilibrium of (1.7).
-
(ii)
Each connected component of the set consists of a single orbit of (2.3), either a homoclinic orbit or a heteroclinic orbit.
Proof.
These results, except for the last two statements in (i) are proved in [23, Lemma 3.1] (and they are valid without the nondegeneracy condition (ND)). It is also proved there that the point is an equilibrium or it lies on a homoclinic orbit. We show that is not an equilibrium if . Indeed, assume it is. Then, in view of (ND) and the relation , there is a homoclinic or heteroclinic orbit of (2.3) (contained in ) having in its closure. Hence, necessarily, , and then it follows that is in the closure of another homoclinic or heteroclinic orbit contained in (see the remarks preceding the lemma). This contradicts the fact is a connected component of . Analogous arguments show that lies on a homoclinic orbit. For similar reasons, if , so is clearly an equilibrium, the relation would imply that is not a connected component of . Thus . ∎
The above Lemma motivates the following definitions. A chain is any connected component of We say that a chain is trivial if it consists of a single point.
If is a connected component of , let the set consisting of the closure of and the reflection of with respect to the axis. So is either the union of a homoclinic orbit and its limit equilibrium, or the union of two heteroclinic orbits and their common limit equilibria. We refer to as the loop associated with
Hypotheses (ND) and (MF) imply that has only finitely many zeros. Since any chain or loop contains an equilibrium, there is only a finite number of chains and loops. In particular, any chain is the union of finitely many loops. Also, any chain is a compact subset of and so their (finite) union, that is, the set , is compact. This implies that admits a unique unbounded connected component and all connected components of (as well itself) are open sets.
If is a chain, we denote by the union of all bounded connected components of Thus, is the union of the interiors of the loops, viewed as Jordan curves, contained in ; if consists of a single equilibrium (necessarily a center for (2.3)), . Since is clearly compact in the set is open. We also define The set is closed and equal to the closure of , except when consists of a single point, in which case . In a similar way we define the sets , , , , when is a loop and is a non-stationary periodic orbit.
The following lemma introduces two key concepts: the inner chain and the outer loop associated with a connected component of (see also Figure 1).
Lemma 2.7.
Let be any connected component of The following statements hold true.
-
(i)
The set is open.
-
(ii)
There exists a unique chain such that for all periodic orbits one has
-
(iii)
If is bounded, there exists a unique loop such that for all periodic orbits one has
-
(iv)
There is a zero of such that and for all periodic orbits
-
(v)
If are two distinct periodic orbits contained in then either or (thus, is totally ordered by this relation).
We refer to and as the inner chain and outer loop associated with ; we denote them by and if the correspondence to is to be explicitly indicated.
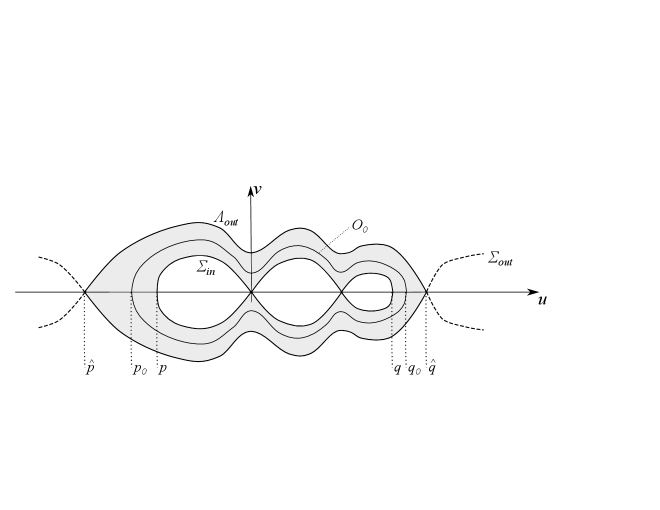
Proof of Lemma 2.7.
The openness of follows from the compactness of , as already mentioned above. This takes care of statement (i).
In the rest of the proof, we assume for definiteness that is bounded and prove statements (ii)-(v). The proof of statements (ii), (iv), (v) in the case that is the unique unbounded connected component of is similar and is omitted.
Fix any periodic orbit By (2.5), there are such that with and Define
In other words, is the maximal open interval containing such that . The existence of such an interval is guaranteed by the openness of . Note also that none of the points , is contained in . Indeed, if, say, , then a neighborhood of is contained in . By the definition of , this whole neighborhood would necessarily be contained in the connected component , from which we immediately get a contraction to the definition of . So, indeed, , in particular they are not equilibria of (2.3). Since there is no element of in , we have on and implies that on . In an analogous way, one finds a maximal interval containing such that , and proves that and on . A continuity argument shows that the union of all (periodic) orbits of (2.3) intersecting the segment is equal to the union of all orbits of (2.3) intersecting . We denote this union by . As distinct orbits of (2.3) do not intersect, it is clear that the periodic orbits contained in are nested in the sense that (v) holds with replaced by . (We will prove below that in fact , thereby proving statement (v).) Observe also that the points , can be approximated arbitrarily closely by one orbit contained in . This implies that they are in the same level set of the Hamiltonian, that is, , and also that in . One easily proves from this that the points , lie on the same chain which we denote by . Using Lemma 2.6 (and the fact that , are not equilibria), we can write:
| (2.6) |
Similarly one shows that , in , and the points , lie on the same chain, which we denote by . By Lemma 2.6,
for some , The inequality for actually holds in the strict sense: in , due to the previously established relation in and the strict monotonicity properties of in the intervals , . It follows that the set
| (2.7) |
is a loop contained in Clearly, , are distinct (hence disjoint) chains; in fact, they lie on two different level sets of the Hamiltonian .
It is obvious from the above constructions that for any periodic orbit we have
| (2.8) |
We next claim that
| (2.9) |
That is included in the set on the left has already been proved (cp. (2.8)); we prove the opposite inclusion. Take any . If lies on a periodic orbit, then that orbit intersects the -axis in the set (otherwise, in view of (2.6), (2.7) it would have to intersect one of the chain , , which is impossible), and hence . If does not lie on a periodic orbit, then it is contained in a chain disjoint from , and such a chain would also have to intersect the set . This is impossible, as this set is included in . Thus (2.9) is true.
From (2.9) it follows that is a connected component of , hence . As already noted above, this proves statement (v). Statements (iii) and (iv) follow from (2.8), (2.9). To prove statement (iv), take the minimum point of in . Recalling that , , we see that and it is a local minimum point of , hence and , due to (ND). Statement (v) clearly holds for this . ∎
The following lemma shows a relation between any two distinct chains.
Lemma 2.8.
-
(i)
If is any chain, then there is a connected component of such that is the inner chain associated with : .
-
(ii)
If , are any two distinct chains, then either , or , or else there are periodic orbits , such that and
(2.10)
Proof.
Since there are only finitely many chains, for any given chain there is a connected component of such that and the boundary of contains points of . It then follows from Lemma 2.7 that . This proves statement (i).
Let now , be any two distinct chains, and let , be the connected components of such that , . Pick periodic orbits , . By Lemma 2.7, inclusions (2.10) hold. Clearly, exactly one of the following possibilities occurs:
For the proof of statement (ii), it is now sufficient to prove that (a) implies that , and (b) implies . These being symmetrical cases, we only prove the former. Trivially, ; and Lemma 2.7(ii) gives . Thus, if (a) holds, which entails , then necessarily . ∎
2.3 Limit sets and entire solutions
Recall that the limit set of a bounded solution of (1.1), denoted by , or if the initial value of is given, is defined as in (1.4), with the convergence in . By standard parabolic estimates the trajectory of is relatively compact in This implies that is nonempty, compact, and connected in (the metric space) and it attracts the solution in the following sense:
| (2.11) |
It is also a standard observation that if there exists an entire solution of (1.1), that is, a solution defined for all , such that
| (2.12) |
We recall briefly how such an entire solution is found. By parabolic regularity estimates, are bounded on and are globally Hölder for any If in for some we consider the sequence , . Passing to a subsequence if necessary, we have in for some function this function is then easily shown to be an entire solution of (1.1). By definition, satisfies (2.12). Note that the entire solution is determined uniquely by ; this follows from the uniqueness and backward uniqueness for the Cauchy problem (1.1), (1.2).
Using similar compactness arguments, one shows easily that is connected in Hence, the set
is connected in . (Here, is as in (1.10).) Also, obviously, is connected in for all
If is a bounded entire solution of (1.1), we define its limit set by
| (2.13) |
Here, again, the convergence is in The -limit set has similar properties as the limit set: it is nonempty, compact and connected in as well as in , and for any there is an entire solution such that and for all . The connectivity property of implies that the set
is connected in
We will also employ a generalized notion of and -limit sets. Namely, if is a bounded entire solution, we define
| (2.14) | ||||
| (2.15) |
The convergence is in , but again one can take the convergence in without altering the sets , . These sets are nonempty, compact and connected in , and they have a similar invariance property as (cp. (2.12)). Also, by their definitions, the sets , are translation invariant as well. Further, the definitions and parabolic regularity imply that the sets
are connected and compact in We remark that the sets , are both connected (as noted above), but they are not necessarily compact in .
2.4 Some results from earlier papers
Several earlier results are used repeatedly in the forthcoming sections. We state them here for reference.
Throughout this subsection, we assume that (not necessarily in ), is the solution of (1.1), (1.2) and it is bounded.
In view of the invariance property of (see (2.12)), the following lemma gives a criterion for an element to be a steady state. This unique-continuation type result is proved in a more general form in [35, Lemma 6.10].
Lemma 2.9.
As already noted above, it is proved in [18] (see also [19]) that the -limit set of any bounded solution of (1.1) contains a steady state. For bounded entire solutions , the same is true for the -limit set due to its compactness and invariance properties (just apply the previous result to any entire solution with ). We state this in the following theorem.
Theorem 2.10.
In the next two results, we make use of the invariance of equation (1.1) under spatial reflections. For any consider the function defined by
| (2.16) |
Being the difference of two solutions of (1.1), is a solution of the linear equation (2.1) for some bounded function
The following lemma is an adaptation of an argument from [2, Proof of Proposition 2.1].
Lemma 2.11.
Let be a solution of (1.1) on , where is an open time interval, and let . Assume that for each the function has at least one zero and
is finite and depends continuously on . Then, for any satisfying the relations and , the function is of constant sign on the interval . If for some and , then is of constant sign on for all
Analogous statements hold for
Proof.
Pick any and set . Consider the function on the domain
Clearly, for all and, as is the last zero of , is of constant sign on . Since solves a linear parabolic equation (2.1), the maximum principle implies that is of constant sign on the whole domain , and the Hopf lemma yields . Since was arbitrary, is of constant sign on .
To prove the second statement, fix any and let . By the unboundedness assumption on , is a number in . Applying the result just proved, we obtain . Since was arbitrary, we obtain the desired conclusion. ∎
We next state a quasiconvergence result from our previous paper [29].
Theorem 2.12.
Assume that and one of the following conditions holds:
-
(i)
,
-
(ii)
there is such that for all one has
Then, is quasiconvergent.
If condition (i) is assumed, this is the content of the main theorem in [29]. In the proof of the theorem, we first proved that condition (i) and Lemma 2.1 imply that condition (ii) holds (this is actually the only place where condition (i) is used in the proof). As noted in [29, Remark 3.3], the quasiconvergence result holds if condition (i) is replaced by (ii) from the start.
The following result concerning various invariant sets for (1.1) is a variant of the squeezing lemma from [34]. This is an indispensable tool in our proofs.
Lemma 2.13.
Let be a bounded entire solution of (1.1) such that if is an unstable equilibrium of (1.7), then
| (2.17) |
for some Let be any one of the following subsets of
Assume that is a non-stationary periodic orbit of (2.3) such that one of the following inclusions holds:
| (i) , (ii) . |
Let be the connected component of containing . If (i) holds, then ; and if (ii) holds, then (in particular, is necessarily bounded in this case).
Proof.
We prove the result in the case (i) only, the proof in the case (ii) is analogous. To simplify the notation, let .
Take first . We go by contradiction: assume that Then there exists a periodic orbit such that for some By the hypotheses, and is a compact set. Using the compactness and the ordering of periodic orbits contained in as given in Lemma 2.7(v), we find the minimal periodic orbit with . Clearly,
| (2.18) |
Hence, there exist sequences such that
Let be a periodic solution of (1.6) with so that Consider the sequence of functions By parabolic estimates, upon extracting a subsequence, converges in to an entire solution of (1.1). Obviously, has a multiple zero at
We claim that Indeed, by Lemma 2.7(iv), there exists an unstable equilibrium of (1.7) such that Hence, there exists such that where is as in (2.17). Obviously, all zeros of are simple. Considering that converges uniformly on to and we see that cannot be identical to
Now, using Lemma 2.7(v), we find a sequence of periodic orbits such that , , for , and 222 Here and below, for , . There is a sequence of periodic solutions of (1.6) such that and in Then, the sequence of functions converges in to , which is an entire solution of a linear parabolic equation (2.1). Since has a multiple zero at and Lemma 2.5 implies that there exist such that the function has a multiple zero at Consequently,
| (2.19) |
However, since (2.19) contradicts (2.18). This contradiction concludes the proof of Lemma 2.13 in the case .
If is any of the sets , , , , then the conclusion follows from the previous case and the invariance properties of these sets. Indeed, consider for instance, the other cases being similar. For any there is an entire solution with for all and Then satisfies the hypotheses of the first case, and so is included in This is true for all hence ∎
Finally, we recall the following well known result concerning the solutions in (the proof can be found in [38, Theorem 5.5.2], for example).
Lemma 2.14.
Assume that . Then the limits
| (2.20) |
exist for all and are solutions of the following initial-value problems:
| (2.21) |
3 Spatial trajectories of entire solutions in
Throughout this section, we assume, in addition to the standing hypotheses (ND), (MF) on , that , , and the solution of (1.1), (1.2) is bounded. We reserve the symbol for this fixed solution.
Due to (2.21), the limits (2.20) are equal: , where is the solution of (1.7) with . This gives the first two statements of the following corollary; the last statement follows from Lemma 2.1.
Corollary 3.1.
Following the outline given in Section 1.4, we examine the elements of whose spatial trajectories are not contained in any chain. At the end, we want to show that no such elements of exist (an application of Lemma 2.9 then yields the desired quasiconvergence results). For that aim, we first examine the entire solutions through such elements . In Proposition 3.2 below, we expose a certain structure these entire solutions would necessarily have to have. Then, in Section 6, we show that that structure is incompatible with other properties of the -limit set.
Up to a point, we treat the cases (S) and (U) simultaneously. When (U) holds, we sometimes have to assume one or both of the extra conditions (NC), (R); we indicate when this is needed. The following notation will be used in the case (U): is the connected component of whose closure contains . Note that is well defined, for implies that is a center for (2.3).
Proposition 3.2.
Under the above hypotheses, assume that and let be the entire solution of (1.1) with Assume that , so that there exists a connected component of with
| (3.1) |
If (S) holds, or if (U) holds and , then the following statements are true.
-
(i)
The connected component satisfying (3.1) is unique, it is bounded, and
(3.2) -
(ii)
Let be the inner chain and the outer loop associated with as in Lemma 2.7. Then
(3.3)
If (U) holds and , then statement (i) is true if condition (NC) is satisfied, and statement (ii) is true if conditions (NC) and (R) are both satisfied.
Statement (i) is proved in the next subsection. Subsection 3.2 is devoted to the behavior at of and subsection 3.3 to additional properties when (U) holds. Statement (ii) is then proved in sections 4 and 5.
For the remainder of this section, we fix and denote by be the entire solution of (1.1) such that and for all Recall from Section 2.3 that there exists a sequence such that
| (3.4) |
3.1 No intersection with chains
In this subsection, we prove statement (i) of Proposition 3.2. The following result is a first step toward that goal.
Lemma 3.3.
Let be a nontrivial chain. If , then
| (3.5) |
(in particular, for all ). The result remains valid if one considers a loop in place of the chain
Proof.
Note that the second statement is a consequence of the first one; just consider the chain containing the loop and use the connectedness of the set .
Let be a nontrivial chain. We first show that the assumption implies
| (3.6) |
Assume for a contradiction that the intersections are both nonempty. The relation means that there is a steady state of (1.1) such that and has a multiple zero at some point . Using both assumptions and , together with the connectedness of and the fact that distinct chains are disjoint with positive distance, we find a periodic orbit such that Hence there is a steady state of (1.1) such that (so is nonconstant and periodic) and has a multiple zero at some Obviously, .
From , we infer that is either a ground state at some level , or a standing wave with some limits , or a constant steady state . We just consider the first possibility, the other two being similar. Assuming that is a ground state at level we first show that necessarily (and consequently is a stable equilibrium of (1.7), cp. Sect. 2.2). Indeed, the function is a nontrivial solution of a linear equation (2.1) and has a multiple zero at By (3.4), the sequence converges in to Therefore, by Lemma 2.5, there exist sequences such that for all sufficiently large the function has a multiple zero at In other words, has a multiple zero at Since and (due to the assumption ), Lemma 2.1 implies that for all Now, and , where (and is a stable equilibrium of (1.7)) and is a solution of (1.7). If for some (hence any) , then, by Lemma 2.1, . Thus, necessarily, , which shows that , as desired.
To conclude, we use the fact that belongs to , as does . Since is connected and we have either or Therefore, by Corollary 3.1, for all large enough . On the other hand, using Lemma 2.5 in a similar way as above, since has a multiple zero and we obtain that for all . This contradiction completes the proof of (3.6).
Using (3.6), the connectedness of , and the assumption we obtain that . The stronger statement (3.5) follows from this. Indeed, if (3.5) is not valid, then for some , we have and . At the same time, (otherwise, is a steady state, by Lemma 2.9, and then would contradict the assumption). Thus, . Applying what we have already proved to in place of , we obtain , a contradiction. The proof is now complete. ∎
The next result is analogous to the previous one, but the proof requires different arguments.
Lemma 3.4.
If is a nontrivial chain and , then
| (3.7) |
(in particular, for all ).
Proof.
It is sufficient to prove that . The stronger conclusion (3.7) follows from this by a similar argument as in the last paragraph of the previous proof.
We go by contradiction. Assume that and at the same time . Then, there is a solution of (1.6) with such that has a multiple zero at some Clearly, is either a ground state, or a standing wave, or a zero of which is the limit of some ground state or standing wave. In either case, is contained in a loop . To derive a contradiction, we choose a sequence of periodic solutions of (1.6) such that and in (the existence of such a sequence of periodic orbits is guaranteed by Lemma 2.7 and the fact that distinct chains are disjoint with positive distance). Then the sequence converges in to a solution of a linear equation (2.1). Since , we have that . Moreover, has a multiple zero at Hence, by Lemma 2.5, there exist , such that has a multiple zero. This means that , hence . Applying Lemma 3.3 to in place of , and taking in (3.5), we obtain a contradiction to the assumption that . ∎
In the next lemma, we deal with a trivial chain , that is, , where is an unstable equilibrium of (1.7).
Lemma 3.5.
Assume that is a trivial chain. If (so (U) holds), assume also that condition (NC) is satisfied. Then , which is the same as , unless .
Proof.
Assume that . If , then is a nontrivial solution of a linear equation. Hence, by Lemma 2.5, there is a sequence such that has a multiple zero for . Then by Lemma 2.1,
| (3.8) |
which is possible only if for all . Since is an unstable equilibrium of (1.7), this relation means that (U) holds and . However, in this situation assumption (NC) is in effect, which clearly contradicts (3.8). This contradiction shows that for it is necessary that . ∎
We are ready to complete the proof of Proposition 3.2(i).
Proof of Proposition 3.2(i).
We finish the subsection with a result ruling out some functions, including all nonconstant periodic steady states, from .
Lemma 3.6.
Let be a nonconstant periodic solution of (1.6) and . The following statements are valid.
-
(i)
If , then contains no function satisfying . In particular, does not contain itself and neither it contains any nonzero which is an unstable equilibrium of (1.7).
-
(ii)
If and either (S) holds, or (U) holds together with (NC), then .
Proof.
First we prove that . By Lemma 2.7(iv), there is such that is an unstable equilibrium of (1.7) and . Obviously, all zeros of are simple. Hence, if , then for some sequence . This is not possible, by Lemma 2.1, if . Neither is it possible if —which, due to the instability of , would mean that (U) holds—if (NC) holds, for Lemma 2.1 implies that is finite and bounded uniformly in . We have thus proved that statement (ii) holds, and also that if .
To complete the proof of statement (i), assume that . Suppose for a contradiction that contains a function satisfying .
First we find a contradiction if is a steady state of (1.1). Note that in this case, the assumption implies that either or is a shift of . If is a nonconstant periodic solution, we just use the result proved above with replaced by to obtain that . If is not a nonconstant periodic solution, then it is a constant, or a ground state, or a standing wave. In any case, one has as , where is an equilibrium of (2.3). Obviously, . This implies that . Clearly, all zeros of are simple. Since , there is a sequence such that . However, due to the assumption that , is not in the range of . So, by Lemma 4.4, is finite and uniformly bounded as , and we have a contradiction.
Next we derive a contradiction if is not a steady state and . Take the entire solution of (1.1) with . The assumption on implies that replacing by a suitable shift if necessary, has a multiple zero. We have , as . Also we know, cp. (3.4), that there is a sequence such that in . Therefore, by Lemma 2.5, there is a sequence such that has a multiple zero. Consequently, since , for all and this is a contradiction as in the previous case.
It remains to find a contradiction when and is not a steady state. In this case, there is a periodic orbit such that . Using the previous argument, with replaced by , we obtain a contradiction in this case as well.
Finally, if is an unstable equilibrium of (1.7), then, by (ND), . This implies that is a center for (2.3), hence any neighborhood of contains a periodic orbit of (2.3) satisfying . We can choose such a periodic orbit so that . Then, taking and using what we have already proved of statement (i) (with replaced by ), we conclude that . ∎
3.2 Existence of the limits at spatial infinity
In this subsection, we assume that is as in (3.1); and , , as in Proposition 3.2(ii). If (U) holds and , also assume that (NC) holds.
Recall that we have fixed and denoted by be the entire solution of (1.1) with . By Proposition 3.2(i), satisfies (3.2).
As a first step toward the proof of statement (ii) of Proposition 3.2, we show that the limits exist and, at least when are independent of .
Recall from Section 2.2 that , as any other chain, has the following structure:
| (3.9) |
for some . If , then is trivial: it reduces to a single equilibrium . Necessarily, is an unstable equilibrium of (1.7) in this case. If then and lie on (distinct) homoclinic orbits and
| (3.10) |
We define
| (3.11) |
These are well-defined finite quantities, as every chain contains equilibria (finitely many of them, by (ND)). Of course, if , then . Otherwise, , are contained in the interiors of distinct homoclinic loops. This implies that and
| (3.12) |
Also, the definition of , and (3.10) imply that , are unstable equilibria of (1.7).
In the following lemma, we relate and the limit (cp. Corollary 3.1).
Lemma 3.7.
The following statements hold:
-
(i)
If (that is, ), then necessarily () and so (U) holds and .
-
(ii)
If is a stable equilibrium of (1.7) or if (so that ), then
(3.13)
Proof.
Pick a periodic orbit such that , and let be a periodic solution of (1.6) with . Then, possibly after replacing by a suitable shift, has a multiple zero. By Lemma 3.6, . Applying Lemma 2.5, we find a sequence such that has a multiple zero, and then it follows from Lemma 2.1 that for all . Corollary 3.1 now tells us that must be in the range of . Hence, by the definition of
This and the definition of give
| (3.14) |
If , then , so , and is an unstable equilibrium of (1.7). By Corollary 3.1, and statement (i) is proved.
Remark 3.8.
We can now prove the existence of the limits
| (3.16) |
Lemma 3.9.
The limits (3.16) exist for all . Moreover, the following statements hold:
-
(i)
If (that is, is a nontrivial chain), then , are independent of , and their constant values, denoted by , , satisfy . Also, are stable equilibria of .
-
(ii)
If (that is, , condition (U) holds, and ), then is either independent of and its constant value satisfies , or it is a strictly monotone solution of (1.7) with and . The same is true for .
Proof.
From (3.2) we in particular obtain that cannot intersect the axis between and , or, in other words,
| (3.17) |
Assume now that for some one of the limits in (3.16), say the one at , does not exist:
Then there is a sequence of local-maximum points of and a sequence of local-minimum points of , such that , , and
| (3.18) |
In view of (3.17), we may also assume, passing to a subsequence if necessary, that either for all or for all . We assume the former, the latter can be treated similarly. Obviously, we also have
| (3.19) |
Observe that there is no zero of in , and the instability of implies in .
Pick so close to that also . Clearly, each of the functions and has infinitely many sign changes, which implies, by (3.4), that and as . The latter immediately gives contradiction if . Indeed, in this case , so condition (NC) is in effect, which implies, by Lemma 2.1, that is finite and bounded as . If , we employ the former. Take the solution of (1.7) with . Since in , we have as . The monotonicity of the zero number gives as for any . On the other hand, by (3.15), the function has only finitely many zeros, and by Lemma 2.1 we may fix such that all these zeros are simple. Then, since as and (3.15) holds, for all sufficiently large we have , which yields a contradiction.
Thus, (3.16) is proved, and parabolic estimates imply that also
| (3.20) |
It follows that for any the points are contained in . If for some the point is equal to an equilibrium of (2.3) in , then is independent of (as it is a solution of (1.7) and ). Otherwise, or and one shows easily (as for the solution above) that converges as to or , respectively. In this case, we also obtain that either or , which can hold only if .
3.3 Additional properties when (U) and (NC) hold
As in the previous subsection, we assume that is as in (3.1) and , , but here we specifically assume that (U) holds and . So is the trivial chain . We also assume that (NC) holds.
By Proposition 3.2(i), the entire solution satisfies
| (3.21) |
Lemma 3.11.
The following statements are valid.
-
(i)
There is a positive integer such that for all one has and all zeros of are simple.
-
(ii)
For any , the function has no positive local minima and no negative local maxima.
Proof.
First we prove that all zeros of are simple. Suppose for a contradiction that is multiple zero of for some . By parabolic regularity, since is Lipschitz, the function is bounded in for some . Therefore, by (3.4),
| (3.22) |
in . It now follows from Lemma 2.5, that there is a sequence such that has a multiple zero. Consequently, since , for all , in contradiction to (NC).
The simplicity of the zeros of for any is thus proved, and from (3.22) and (NC) it follows that the other statement in (i) is valid as well.
Take now such that the (finite) zero number is independent of for and all zeros of simple. Such exists due to (NC) and Lemma 2.1. Then, for , the zeros of are given by a -tuple , where are functions of .
Observe also that is finite for all . Since due to (U), itself is a solution of a linear equation (2.1). Therefore, making larger if necessary, we may assume that all zeros of are simple for . In particular, for , .
Let be any of the functions . Since is a simple zero of , it is a local minimum point of for all or a local maximum point of for all . Moreover, does not change sign on .
Assume now that is a positive local minimum of for some—hence any—. Since
the positivity and boundedness of imply that , where is the smallest positive zero of . For any function this clearly means that if has a positive local minimum , then . Applying this to , for any , we obtain, since , that can have no positive local minimum. Similarly one shows that does not have any negative local maximum. ∎
Under condition (R), the critical points of stay in a bounded interval:
Lemma 3.12.
Assume that, in addition to (U) and (NC), condition (R) holds. Then there is a constant such that for every the critical points of are all contained in . Moreover, the number of the critical points of and the number of its zeros are both (finite and) independent of .
Proof.
As in the previous proof, there is such that for all the zeros of are given by a -tuple , where are functions of . Let be any of the functions .
Take sequences , as in (R) and let , so has only finitely many zeros if is sufficiently large. Since is one of these zeros, Lemma 2.1 implies that for all sufficiently large one has . In particular, if is large enough. Since this holds for arbitrary , it follows that as one has either , or , or else stays in a bounded interval. Using this, (3.22), and the fact that the zeros of are all simple, we obtain that these zeros are contained in a bounded interval independent of . It follows from the simplicity and boundedness of the zeros of that their number is independent of .
As noted in the proof of Lemma 3.11, the function has only simple zeros, a finite number of them, for all sufficiently large . Using Lemma 2.5, similarly as in that proof, one shows that for any the zeros of are all simple. Also, their number is finite, as , and nonincreasing in . The only way the zero number can drop at some is that some of the zeros escape to or as . This clearly does not happen if or , respectively. On the other hand if , then for all , and in this case the zeros of are all greater than the minimal critical point of . A analogous remark applies in the case . Since the set of the critical points is always contained in , we obtain that is independent of . ∎
4 A classification of entire solutions with spatial trajectories between two chains
In the previous section, we considered entire solutions satisfying for all . We derived certain conditions any such solution would have to satisfy, see Proposition 3.2(i) and Lemma 3.9. In this section, we examine the entire solutions with the indicated properties and classify them in a certain way. Our classification in particular proves Proposition 3.2(ii) under the extra assumption that is a nontrivial chain. We stress, however, that no reference is made in this section to the solution or its limit set . Thus the results here are completely independent from the previous and forthcoming sections and can be viewed as contributions to the general understanding of entire solutions of (1.1).
Our assumptions throughout this section are as follows. We assume that the standing hypotheses (ND), (MF) on hold, is a bounded connected component of , and , . The next standing hypotheses delineates the class of entire solutions we consider:
- (HU)
Our main result in this subsection is following proposition concerning the case when is a nontrivial chain.
Proposition 4.1.
Under the above hypotheses, assuming also that is a nontrivial chain, the following alternative holds. Either is identical to a steady state with or else
| (4.3) |
and
| (4.4) |
An interpretation of this result is that any entire solution of (1.1) satisfying (4.1), (4.2) is either a steady state or a connection, in , between the following two sets of steady states:
Moreover, the connection always goes from to as time increases from to . Note that this result, in conjunction with Proposition 3.2(i) and Lemma 3.9, implies that statement (ii) of Proposition 3.2 holds under the extra assumption that is a nontrivial chain.
In the case when is a trivial chain, we do not have such a complete characterization of entire solutions satisfying (HU). We only prove some partial results in this case, which will be used in Section 5. For that, we will need the following additional assumption:
- (TC)
-
(Additional assumption in the case is a trivial chain). If is not a steady state, then for all the function has only simple zeros and and the number of its critical points is finite and bounded uniformly in .
In the next subsection, we prove several results valid in general, whether is trivial or nontrivial, assuming (TC) in the former case. Then, in Subsection 4.2, we examine in more detail the case when is nontrivial and prove Proposition 4.1.
The following notation will be used throughout this section.
Recall that (as any other chain) has the structure as in (3.9) for some . We define the values as in (3.11). They are unstable equilibria of (1.7). If is a trivial chain, then . If is nontrivial, then and (3.10), (3.12) hold.
As for , there are two possibilities:
- (A1)
- (A2)
To have a unified notation, we set
| (4.7) | ||||
Thus, if (A1) holds; and , if (A2) holds.
Also remember that if is any equilibrium of (2.3) contained in or in when is a nontrivial chain, then (cp. Section 2.2). This in particular applies to , in (A1), (A2).
4.1 Some general results
We assume the standing hypothesis for this section, as spelled out in the paragraph containing (HU). In case , we also assume the extra hypothesis (TC).
We start by recalling the following consequence of hypothesis (HU) (cp. Remark 3.10).
Corollary 4.2.
The following statements hold:
-
(i)
If is a nontrivial chain, are independent of and .
-
(ii)
If is a trivial chain and stands for or , then either is independent of and , or is a strictly monotone solution of (1.7) with and .
Next we prove the following basic dichotomy.
Lemma 4.3.
Either is identical to a steady state with , or else is not a steady state and (4.3) holds.
Proof.
The existence of the limits (4.2) implies that cannot be a nonconstant periodic steady state. Thus if (4.3) holds, cannot be any steady state.
Assume now that (4.3) does not hold. Then there exist and a steady state with such that has a multiple zero at . By connectedness of , or . For definiteness, we assume the former; the arguments in the latter case are analogous (and one does not need to deal with trivial chain in that case).
We want to show that . If is a trivial chain (hence ), this follows immediately from (TC), specifically from the assumption that has only simple zeros. Assume now that is a nontrivial chain. If , then is a nontrivial solution of a linear equation (2.1). Using Lemma 2.7 (and the fact that there are only finitely many chains), we find a sequence of periodic solutions of (1.6) such that and in . Applying Lemma 2.5, we find a sequence such that has a multiple zero. Consequently, , in contradiction to (4.1). This contradiction shows that, indeed, . ∎
Clearly, the inclusion (4.3) implies that
| (4.8) |
The following lemma shows in particular that if is not a steady state and is a nontrivial chain, then the number of critical points of is bounded uniformly in . If is a trivial chain, we have this by assumption, see (TC).
Lemma 4.4.
Assume that is a nontrivial chain. If is not a steady state, then the following statements are valid:
-
(i)
There are such that
(4.9) -
(ii)
Let or , and . Let , with , be any nodal interval of (that is, in and on ). Then has at most one critical point in and if such a critical point exists, it is nondegenerate.
Remark 4.5.
With and as in statement (ii), the number of critical points of in can be specified by elementary considerations. For example, has exactly one critical point in if , are both finite (and hence are two successive zeros of ). If , , , then either has exactly one critical point in and in this case or else in . The discussion in the other cases is similar.
Proof of Lemma 4.4.
By Lemma 4.3, (4.3) holds, and by Corollary 4.2, are independent of and contained in . These inclusions and (3.12) imply that . Therefore, the zero numbers are finite for all , and are nonincreasing in . We show that does not drop at any (the proof for is similar). By (4.8), all zeros of are simple, hence locally they are given by functions of . The only way can drop at is that one of these functions, say , is unbounded as . To rule this possibility out, we show that is uniformly bounded. Indeed, from (3.12) and the fact that we infer that is bounded from below by a fixed positive constant (independent of and ) whenever . Since, by parabolic estimates, is uniformly bounded, a bound on is found immediately upon differentiating the identity . This completes the proof of statement (i).
In the proof of statement (ii), we only consider the case of a bounded nodal interval , the other cases can be treated similarly. Also, we assume for definiteness that in , the case in being analogous. Suppose for a contradiction that has more than one critical point in or has a degenerate critical point there. From statement (i) and Remark 2.2 we infer that the function has a finite number (independent of ) of zeros, all of them simple. Using this and the implicit function theorem, we obtain the following. There are functions defined for all such that , , and, for any , is a nodal interval of : in , , . Considering the zero number of in (remembering that , due to the simplicity of the zeros), we infer from Lemma 2.4 that for all the function has at least two critical points in . Moreover, for , the critical points are all nondegenerate. Pick one of such , say . Due to (4.8), the value of at the critical points is greater than , which is greater than . Therefore, there is such that the function has at least three zeros. Let denote the solution of with . Then for all and Consider the function It solves a linear equation (2.1) and satisfies for all . Therefore, by Lemma 2.4, admits at least 3 zeros in . Take now a large enough negative so that . Using the fact that has at least 3 zeros in while in , we find a critical point at which takes a value in , which clearly contradict (4.8). This contradiction proves the conclusion of statement (ii). ∎
Corollary 4.6.
If and is the entire solution of (1.1) with (and for all ), then condition (HU) holds with replaced by . In particular, is not identical to any nonconstant periodic steady state.
Proof.
The inclusion for all follows from (4.1) and the fact that in the definition of , one can take the convergence in . We next show that the limits exist for every . A sufficient condition for this is that the zero number of is finite for all . This is verified easily using the fact—assumed in (TC) or proved in Lemma 4.4, depending on whether is trivial or not—that is finite and bounded from above by some constant independent of . Indeed, if for some , then we can find such that has at least simple zeros. Since , we obtain by approximation that has zeros for some , which is impossible. ∎
In the following lemma we establish a basic relation of to , .
Lemma 4.7.
Assume is not a steady state and let be any one of the sets , . Then the following statements are valid.
(Recall that and are the generalized limit sets of , as defined in Section 2.3.)
Proof of Lemma 4.7.
With the sequence as in (i), we may assume, passing to a subsequence if necessary, that
Let be the solution of (1.6) with , so . Consider the sequence of functions Up to a subsequence, it converges in to , an entire solution of (1.1). Clearly, , so has a multiple zero at . Now, unless , Lemma 2.5 implies that if is large enough, the function has a multiple zero for some . This would mean that , which is impossible by (4.3). Thus, necessarily, which yields the conclusion of statement (i).
We now prove the existence of a sequence with the above property and with . This is is trivial if is independent of and contained in , for in this case we have as for every . Similarly, the statement is trivial if . If is not constant (which may happen only if is a trivial chain, cp. Lemma 4.2), then again the statement is trivial and follows from the facts that as and either or (cp. Lemma 4.2). A similar argument applies if is not constant. It remains to consider the case when are both independent of and contained in , where where , . First we show the existence of a sequence satisfying (4.10). Suppose that no such sequence exists. Then there is such that
| (4.12) |
This implies that there is a periodic orbit , taken sufficiently close to (cp. Lemma 2.7) such that
In either case, Lemma 2.13 shows that
| (4.13) |
in contradiction to (4.3) (cp. Lemma 4.3). Thus there is a sequence satisfying (4.10). We claim that . Indeed, if not, then for a subsequence we have . Since is bounded, we have uniformly on . Consequently, by parabolic regularity, also uniformly on . Therefore, if and are sufficiently large. This implies, in view of (4.10), that the sequence is bounded and so, passing to a subsequence, we have . Using (4.10) and the convergence , we obtain , which is a contradiction to (4.3). This contradiction proves our claim and completes the proof of the first part of statement (ii). The last conclusion in (ii) follows immediately from statement (i) and the definition of the limit sets , . ∎
We next show that (4.4) holds if one of the zero numbers vanishes, that is, or . The following lemma is a stronger result, which partly also applies when is a trivial chain (in which case ). This lemma will be used at several other occasions below.
Lemma 4.8.
The following statements are valid (recall that , are defined in (4.7)).
-
(i)
If for some and is not a steady state, then (so, necessarily, ) and . Similarly, if for some and is not a steady state, then (so ) and .
-
(ii)
If for some and one has for all , then either or else . If for some and one has for all , then either or else .
-
(iii)
Assume that is a nontrivial chain. If , then ; and if , then .
Proof.
We only prove the first statements in (i) and (ii); the proofs of the other statements in (i) and (ii) are analogous and are omitted.
The statements in (iii) follow from (i) and the fact that if is a nontrivial chain, then there are no functions with satisfying or .
To prove (i), assume that is not a steady state and for some . By Lemma 4.3, (4.3) holds and, in particular, . By Lemma 4.7, the set contains a steady state with . Obviously, , hence, necessarily, (and ). Let be any periodic solution of (1.6) with , , and let be the minimal period of . Clearly, , in particular, . From we infer that there exist such that
| in . | (4.14) |
Consequently, in , where is the integer part of . This and the relations
yield, upon an application of the comparison principle, that in for all . Hence, for each we have in . We claim that, in fact,
| (4.15) |
Indeed, consider the set of all such that
We have shown above that . Suppose for a contradiction that . Then, clearly, , and using the compactness of in one shows easily that for some the inequality
| in | (4.16) |
is not strict. Let be the entire solution of (1.1) with and for all . The inclusion implies that in for all and from the assumption on it follows that
Therefore, by the strong comparison principle, the inequality in (4.16) is in fact strict and we have a desired contradiction. We have thus proved that . Similar arguments show that , hence . Now, given any and , take . Then and the fact that yields
This proves (4.15).
Clearly, taking the periodic solution with the maximum sufficiently close to , we can make as small as we like. Therefore, (4.15) implies that , as stated in Lemma 4.8.
Next we show that . We actually prove that implies that (which, of course, is a contradiction with the fact that is not a steady state). Note that in this argument we only use that the estimate holds for all sufficiently large negative , say for all , so the argument can be repeated in the proof of statement (ii) below. Assume that . As in the previous paragraphs, taking any periodic solution with and , we again obtain (4.14), but this time we can take and we can choose arbitrarily large. The comparison principle then implies in particular that in . Taking a sequence of periodic solutions with , we obtain . Consequently, is a steady state and , as claimed.
Take now an arbitrary and let be the entire solution of (1.1) with and for all . Obviously, inherits the relation from . If is not a steady state, then, by Corollary 4.6, what we have already proved above in this proof applies equally well to : (the latter relation is by compactness of in ). This is impossible as we have just proved, so has to be a steady state different from . Moreover, cannot be periodic (cp. Corollary 4.6), and therefore the relation implies . This shows that , completing the proof (i).
We now prove statement (ii). As already noted above, under the assumption of (ii), implies that . If , we can repeat the previous paragraph to show that . ∎
4.2 Nontrivial inner chain
In this subsection, we assume that is a nontrivial chain (and continue to assume the standing hypotheses formulated in the paragraph containing (HU)). By Corollary 4.2, the limits are independent of and contained in .
We distinguish the following cases of how can be included in :
-
(C1)
-
(C2)
-
(C3)
and ; or and .
We tackle these cases separately in the following subsections; in each of them, we prove that the conclusion of Proposition 4.1 holds. Some of the forthcoming results actually give a more specific description the and -limit sets than the general description given in (4.4).
4.2.1 Case (C1):
We first show that under condition (C1), converges in —not just in —to a steady state with . In particular, .
Lemma 4.9.
Assume (C1). Then the limit in exists and is more specifically described as follows.
-
(i)
If (so is a heteroclinic loop as in (A2)), then is a standing wave – a shift of or .
-
(ii)
If and is a heteroclinic loop as in (A2), then is identical to one of the constants , .
-
(iii)
If and is a homoclinic loop as in (A1), then is identical to the constant or to a shift of the ground state .
In all these cases, .
Proof.
If , then (cp. (A2)). Clearly, is a front-like solution in the sense that takes values between its limits , , at , . Since , statement (i) becomes a special case of a well-known convergence result [16, Theorem 3.1].
Under the assumptions of statement (ii), is equal to one of the constants , and . In this situation, the convergence stated in (ii) is also well-known and can be easily derived from [16, Theorem 3.1], see for example [30, Proof of Lemma 3.4].
Assume now that and is a homoclinic loop as in (A1). Clearly, and, since is the range of the ground state , in . Since also , we are in the setup of [23, Theorem 2.5] whose conclusion, translated to the present notation, is the same as the conclusion in (iii). ∎
The following lemma completes the proof of Proposition 4.1 in the case (C1).
Lemma 4.10.
Assume (C1). If is not a steady state, then .
Proof.
Let be as in Lemma 4.9: converges to uniformly as , hence, by parabolic estimates,
| (4.17) |
First of all we note that if is identical to one of the constants or (cp. statements (ii), (iii) in Lemma 4.9), then itself is identical to that constant. Indeed, we have either or for all large enough and consequently, by Lemma 4.4, for all . Our statement now follows directly from Lemma 4.8(ii). Thus, assuming that is not a steady state, we only need to consider the cases (i), (iii) in Lemma 4.9, and in the case (iii) we may assume that for some .
Case (iii) of Lemma 4.9 with . For definiteness, we also assume that (and this is the maximum of , cp. (A1)), the case being analogous. It follows from (4.17) and Lemma 4.4(i) that for all . Furthermore, by Lemma 4.4(ii) and Remark 4.5, has a unique critical point, the global maximum point.
By Lemma 4.7, the set contains a steady state with . The possibility is ruled out by uniform convergence (4.17) to , hence . Thus, there are sequences and such that
| in . | (4.18) |
We use this in the following conclusion. Fixing any periodic solution of (1.6) with the inclusion implies that has infinitely many simple zeros. Therefore, (4.18) and the monotonicity of the zero number imply that
| (4.19) |
We now use (4.19) to show that (hence no shift of is contained in , by the shift-invariance of ). We go by contradiction. Assume : for some sequences , we have
| (4.20) |
in . Observe that the monotonicity of in intervals not containing its unique critical point and the relations imply that the convergence in (4.20) is actually uniform. It then follows from parabolic estimates that the convergence takes place in . Consequently,
| (4.21) |
where is obviously finite (it is actually equal to 2, as one can easily verify). This contradiction to (4.19) proves our claim that no shift of is contained in . This means, by Lemma 4.7, that for some the maximum of stays below as . An application of Lemma 4.8(ii) gives , which is the desired conclusion.
Case (i) of Lemma 4.9. In this case is a standing wave. For definiteness, we assume that for some , where is the increasing standing wave connecting and (cp. (A2)); the case when is a shift of is analogous. From (4.17) and Lemma 4.4 we infer that and for all .
We first proceed similarly as in the previous case. By Lemma 4.7, the set contains a steady state with , and is ruled out by uniform convergence (4.17) to . Hence . Repeating almost verbatim the arguments involving (4.19) and (4.21) (just replace by and the relations by , ), one shows that no shift of is contained in . Obviously, by the monotonicity, no shift of can be contained in either.
We claim that none of the constants , is contained in . (We remark that both these constants are contained in , simply because .) Suppose, for example, that (the possibility is ruled out similarly). So there is a sequence such that locally uniformly. Pick a small so that . Define
| (4.22) |
and let be the solution of (1.1) emanating from at By [16], there exists such that converges uniformly to as On the other hand, by the assumption on and due to , for every there exists such that whenever . For any such , the comparison principle gives for all and Choosing and taking (so ), we obtain that for all . Taking , we obtain which is a contradiction proving our claim.
Note that a similar comparison argument gives the following. If there exist and a sequence such that for some one has for all , then there is such that for all . We show that this is impossible, thereby showing that
| (4.23) |
Indeed, by Theorem 2.10, contains a steady state of (1.1). It cannot be nonconstant and periodic due to the monotonicity of . As shown above, cannot be identical to any of the constants or any shift of . Therefore, This is not compatible with the relation , which would obviously follow from . Thus (4.23) is proved and it implies that for all . Similarly one shows that for all .
4.2.2 Case (C2):
Throughout this subsection, we assume that (C2) holds. We will also assume that the zero numbers are both positive:
| (4.24) |
This is the only case we still need to worry about, for Lemma 4.8(iii) shows that the conclusion of Proposition 4.1 holds if one of these zero numbers vanishes.
By (C2), are even numbers, in fact, if they are nonzero, they are both equal to 2:
Lemma 4.11.
Under conditions (4.24), we have
| (4.25) |
Proof.
Assume for a contradiction that (4.25) is false. Then, since are nonzero even numbers, we have (cp. Figure 2)
| (4.26) |

Recall that under condition (C2) the limits are in . By (4.8), whenever It follows that, assuming (4.26), the zero numbers are finite and greater than or equal to 2, and the zeros being counted are all simple. Moreover, between any two successive zeros of there are (two) zeros of either or . This implies that is bounded uniformly in . The same goes for . Thus, by the monotonicity of the zero number, are constant in for all sufficiently large negative , say for all . We define
These are well defined and continuous functions of for . As one checks easily, (4.26) implies that . Since , the function is not monotone on , nor it is such on Therefore, by Lemma 2.11, there exists such that
| (4.27) |
| (4.28) |
We consider the latter, the former is analogous. By Theorem 2.10, there is a steady state of (1.1) with . Using (4.27), (4.28) and taking into account that between any two successive zeros of the function achieves a value greater than or smaller than , we infer that Obviously, and is not a nonconstant periodic solution (see Corollary 4.6). Moreover, because of (4.27), there exist with such that These conditions on leave only one possibility for the steady state : for some where is the ground state at level as in (A1) (and, necessarily, is a homoclinic loop). We have thus shown that for some sequence
in . Notice that from (4.27) it follows that We show that this leads to a contradiction, which will complete the proof.
Let be any periodic solution of (1.6) with and let be the minimal period of Shifting , we may assume that Then on (otherwise, a shift of the graph of would be touching the graph of , which is impossible for two distinct solutions of (1.6)). Consequently, if is large enough, we have and
Moreover, since for all we have
Therefore, applying the comparison principle on , we obtain
This is true for all periodic solutions with the indicated properties. Taking a sequences of such periodic solution with —which entails and locally uniformly—we obtain that So as in contradiction to (C2). ∎

Assuming (4.24), the previous lemma shows that (4.25) holds for all . Lemma 4.4 now tells us that for every the function has exactly two critical points , , both nondegenerate, which are the global maximum and minimum points of , respectively. Since , we have
| (4.29) |
depending on whether or (cp. Figure 3). Similarly,
| (4.30) |
We next prove the conclusion of Proposition 4.1 in the case (C2) when is a homoclinic loop.
Lemma 4.12.
Proof.
For definiteness, we assume that —so is a ground state at level and is its maximum—the case is similar. We prove that for some
| (4.31) |
Once this is done, the desired conclusion follows immediately from Lemma 4.8(i).

We now treat the case when is a heteroclinic loop.
Lemma 4.13.
Proof.
With , as above, we only consider the case ; the arguments in the case are similar. Thus (cp. Figure 4)
| (4.32) | ||||
As in the proof of Lemma 4.11, we define
Clearly, for all , are defined and
| (4.33) |
(, may be equal, or ordered either way, depending on the relation between and ). Since is a simple zero of , it is a function of .
We split the rest of the proof into several steps.
It is sufficient to prove that the constants are not contained in . Indeed, if this holds, then does not contain any shifts of the standing waves either (by compactness and translation invariance of ). Consequently, by Lemma 4.7, and (4.34) follows upon an application of Lemma 2.13.
Assume, for a contradiction that (arguments to rule out the possibility are similar and are omitted). Clearly, since , the function is monotone neither on nor on Therefore, by Lemma 2.11, is bounded from below and from above as there is a constant such that
| (4.35) |
Since , there is a sequence such that, denoting , we have (and ). As in Lemma 4.7(i), passing to a subsequence if necessary, we obtain that the sequence of functions converges in to . Moreover, because of (4.33), (4.35), we have for all thus as
Let be any periodic solution of (1.6) with and , . Let be the minimal period of , so is the maximum of , and is the minimum of . Obviously, for all large enough , say for all , we have
Also, due to (4.35) and the convergence , we have, making larger if necessary,
Therefore, by the comparison principle, for ,
In particular, at , we obtain
Since , we obtain a contradiction to the fact that . This contradiction completes the proof of (4.34).
Step 2. We show that
| (4.36) |
Note that due to (4.32), in both cases and the solution satisfies the hypotheses of Theorem 2.12. So consists of steady states, and it does not contain non-constant periodic functions (cp. Corollary 4.6). So and it is connected. This gives (4.36).
Step 3. In this step we complete the proof of Lemma 4.13 by showing that . In view of (4.36), we just need to rule out the possibility
| (4.37) |
Assume it holds. We derive a contradiction. Pick a sufficiently small such that
Relation (4.37) in particular implies that for any there exists such that
| (4.38) |
By Step 1 and Lemma 4.7(ii), contains one of the constants (or a shift of one of the standing waves , and, consequently, also both constants ). We only consider the case , the case being similar. Hence, there is a sequence such that, denoting , we have
| (4.39) |
with the convergence in Clearly, (4.39), (4.38) imply that . We claim that necessarily Observe that, by (4.32) and (4.33),
| (4.40) | ||||
| (4.41) |
and Using the last relation and Lemma 2.11, we obtain the following monotonicity relations for all :
| (4.42) | ||||
| (4.43) |
From (4.41) and (4.39), it follows that there is such that for all . If for some it is also true that , then the relations and (4.42) give . This inequality can hold only for finitely many , due to (4.38), (4.39). Thus for all large enough we have , hence, since , it must be true that , as claimed.
Pick now a periodic solution of (1.6) with such that and . We shift such that . Let be the minimal period of . Thus we have
By (4.39), for large enough,
| (4.44) |
By (4.41), necessarily . We now show that for some large enough , the following must hold in addition to (4.44):
| (4.45) |
If this does not hold, then there exist arbitrarily large such that for some one has , where is either or . Since on (cp. (4.40)), it follows that . But, due to , we also have if is large enough; so, by (4.43), . This cannot be true for arbitrarily large , due to (4.38), so (4.45) must indeed hold for some, arbitrarily large, .
4.2.3 Case (C3): and
Our assumption in this subsection is that and . The case and is analogous and will be skipped.
For definiteness, we also assume that (hence ); the other possibility, , can be treated in an analogous way.
Lemma 4.14.
Under condition (C3), .
Proof.
Theorem 2.12 implies that is quasiconvergent, hence and contains only non-periodic steady states or constant steady states.
If is a heteroclinic loop, as in (A2), we choose a decreasing continuous function such that and . By the comparison principle, the corresponding solution of (1.1) satisfies for all . By [16, Theorem 3.1], the (front-like) solution converges in to a shift of the decreasing standing wave , say , as . This implies that for all , we have . Now, every is a steady state with . Therefore, implies that is identical to or to a shift of . In particular, .
If is a homoclinic loop, as in (A1), we have since we are assuming that and . The arguments here are similar as for the heteroclinic loop, but instead of a front-like solution, we compare to a solution which converges to a shift of the ground sate . For that, we find a continuous function with the following properties:
-
(s1)
is even and monotone nondecreasing in ;
-
(s2)
;
-
(s3)
for all sufficiently large ;
-
(s4)
the solution converges in to as .
Such a function is provided by [23, Theorem 2.6]. More specifically, take first a continuous function satisfying (s1)–(s3) and such that on the interval (so, in particular, ). According to Theorem 2.6 of [23], if is sufficiently large, then for some the function satisfies (s4) (the corresponding solution is a threshold solution in the terminology of [23]); it obviously satisfies (s1)–(s3) as well.
Since is decreasing for large , relations (s1)–(s3) imply that for a sufficiently large we have . Therefore, for all . As a consequence, taking into account that the difference of any two steady states (1.1) has only simple zeros, we have for all . Therefore, any is identical to or to a shift of . In particular, .
∎
Turning our attention to , we start with a preliminary lemma.
Lemma 4.15.
Assume (C3) holds. Then does not contain any function with .
Proof.
Recall that we are also assuming, without loss of generality, that and . Thus, and for all Using Lemma 4.4, we obtain that the function is decreasing to as , and monotone near , and the function has only finitely many zeros, all of them simple, with independent of .
We denote by the first zero of Since , the function is not monotone on . Therefore, by Lemma 2.11, there is such that
| (4.47) |
We distinguish the following two possibilities
-
(pi)
on ()
-
(pii)
on ()
Assume (pi). Then (4.47) implies that for all
| (4.48) |
and any function in has to satisfy this relation. In particular, the constant and any shift of (if is a heteroclinic loop) are ruled out from . It remains to rule out the constant , any shift of the ground state (if is a homoclinic loop), and any shift of (if is a heteroclinic loop). Take any of these functions, denoting it by , and assume for a contradiction that . By (4.48),
| (4.49) |
Take any periodic solution of (1.6) with , and . Obviously, there is such that We claim that
| (4.50) |
Due (4.48), this follows from the comparison principle if we can find a sequence such that the claim is valid for , . Note that the function , fixed as above, satisfies on . This is trivial if ; if is a shift of the ground state or the increasing standing wave, it follows from (4.49) (otherwise, a shift of the graph of we would be touching the graph at some point, which is impossible for two distinct solutions of (1.6)). Since , there is a sequence such that locally uniformly. This sequence, possibly after omitting a finite number of terms, has the desired property.
Thus, (4.50) has to hold for any periodic solution with the indicated properties. We now choose a sequence of such periodic orbits converging locally uniformly on to a shift of the ground state (if is a homoclinic loop) or a shift of (if is a heteroclinic loop). In either case, the relations (4.50) with , and , contradict the relations . This contradiction completes the proof if (pi) holds.
Now assume (pii). Then (4.47) implies that for all
Therefore, each function in has to satisfy this inequality, which shows that the following functions cannot be elements of : the constant , any shift of the ground state (if is a homoclinic loop), any shift of the increasing standing wave (if is a heteroclinic loop). Thus, we only need to show that if is a heteroclinic loop, then does not contain the constant or any shift of . The arguments for this are analogous to the arguments used in the case (pi) to show that does not contain the constant or any shift of and are omitted. ∎
We conclude this section by the following lemma, which, in conjunction with Lemma 4.14, shows that (4.4) holds in the case (C3) as well.
Lemma 4.16.
Assume (C3). Then
Proof.
Fix an arbitrary , we need to prove that . Let be the entire solution with . Then satisfies (HU) (cp. Corollary 4.6). Therefore, we may apply to the results concerning the -limit set already proved in this subsection and in the previous two subsections. Thus, if is not a steady state, then . This would mean—since by the invariance and compactness of —that contains a function with , in contradiction to Lemma 4.15. Therefore, has to be a steady state. It is not periodic (cp. Corollary 4.6) and is not contained in by Lemma 4.15. We are left with the desired option , completing the proof. ∎
5 Proof of Proposition 3.2 in the case
Proposition 4.1, proved in the previous section, implies that statement (ii) of Proposition 3.2 holds if . We now consider the case (and so ), assuming that conditions (U), (NC), (R) hold. We further assume that , is the entire solution of (1.1) with , and
| (5.1) |
We prove that
| (5.2) |
thereby completing the proof of Proposition 3.2 (note that is equivalent to ).
We use a similar notation as in the previous section:
| (5.3) | ||||
Thus, if (A1) holds; and , if (A2) holds, where conditions (A1), (A2) are as in Section 4 (cp. (4.5), (4.6)).
Recall from Lemmas 3.11, 3.12 that , are finite and independent of , all zeros of , are simple for all , and the zeros of are contained in an interval independent of . Further, has no positive local minima and no negative local maxima. This means that the zeros and critical points of alternate.
Clearly, one of the following possibilities occurs:
| ; ; and ; and ; and . | (5.4) |
We differentiate with respect to these four possibilities.
Next we show that is impossible. Assume it holds. Then has at least one zero contained between two successive critical points—hence contained in —for all . If , then the function assumes its positive global maximum in , at one of the local maxima. We claim that has to stay below for some Assume otherwise: then there exist sequences in and in such that converges to as and by Lemma 4.7(i), up to a subsequence, converges in to some steady state as with On the other hand, admits two critical points in where it takes opposite signs, which clearly contradicts the convergence to . Thus our claim is proved and Lemma 4.8(i) now implies that . This, however, is also prevented by the existence of a zero in and we have a contradiction. Similarly one shows that the relations lead to a contradiction. If or , then, by [16, Theorem 3.1], the (front-like) solution converges as to a standing wave of (1.1) in . But this implies that has no critical points in , and we have a contradiction again.
Now consider the case . We denote by , the critical point and the zero of , respectively. For definiteness, we assume that and in ; the other possibilities that can occur in the case can be treated similarly. It follows that is the point of positive maximum of First, we dispose of the possibility that is a homoclinic loop. Since and is the unique critical point of , we have in , in particular . Therefore, converges to a stable equilibrium of the equation as . In view (5.1), this equilibrium has to equal , which gives . So if is a homoclinic loop as in (A1), the ground state satisfies and . Using Lemma 4.7(i) and the facts that has two zeros while has only one and that with bounded, one shows easily that the global maximum of , namely , has to stay below for some . By Lemma 4.8(i), , which contradicts the relation . We may thus proceed assuming that is a heteroclinic loop, in particular , are zeros of . As above, if stays below for some , then Lemma 4.8(i) yields a contradiction. Thus, there is a sequence such that that and, then, by Lemma 4.7(i) and the fact that , up to some subsequence, in . Obviously, the sequence is unbounded. Pick any periodic solution of (1.6) with and . Let be the minimal period of . Then, for any large enough we have in . Since also in , the comparison principle gives in for all . Consequently,
| (5.5) |
since in (the only critical point of is in and it is the maximum point). Using (5.5) and taking admissible periodic solutions with (and , we obtain two conclusions. First, in as and, consequently, . Second, the sequence has to be bounded from below (otherwise (5.5) leads to , which is absurd). This implies that there is such that for all . Lemma 4.8(ii) now shows that , completing the proof of (5.2) in the case .
In the case and , we denote by the unique critical point of and assume for definiteness , so is the global maximum of . If , the arguments are analogous. Since , we have . The possibility can be treated in much the same way as the case (C1) with in Subsection 4.2.1: (5.2) holds in this case. Consider the opposite possibility, or . We assume, again just for definiteness, that the former holds. Then, since is a solution of , as and as . In particular, . If is a heteroclinic loop, it is easy to prove, using [16, Theorem 3.1] as in [30, Proof of Lemma 3.4] for example, that as , uniformly on . This, of course, is impossible when . Thus has to be a homoclinic loop, as in (A1), and the ground state satisfies and . We claim that there is such that for all . Indeed, otherwise, by Lemma 4.7(i) and the boundedness of , there is a sequence such that approaches a shift of the ground state in . This in conjunction with the property that as would imply that has more than one critical point if is large enough, a contradiction to . Thus, our claim is proved and Lemma 4.8(ii) now implies that . For the proof of (5.2), we now prove that . Once proved, this will yield a nonstationary periodic orbit of (2.3) such that from which (5.2) follows at once upon an application of Lemma 2.13. Assume for a contradiction that . Then Lemma 4.7(i) yields a sequence such that and in . This implies that given any periodic solution of (1.6) with one has as . On the other hand, since , picking near 0, so that , we obtain that for the zero number is finite and therefore bounded as increases to infinity. This contradiction completes the proof of (5.2) in the case and .
Finally, we deal with the case and . Clearly, are nonzero and have opposite signs. Assume for definiteness that . The assumption then means that everywhere. Being solutions of , converge to stable equilibria of this equation as . By (5.1), these equilibria have to be , : , . In particular, and is a heteroclinic loop. Using [16, Theorem 3.1], we obtain that the (front-like) solution approaches a shift of the increasing standing wave , as , uniformly on , so . We now claim that . If , , our claim can be proved by essentially the same arguments as those used in the case (C1) with in Subsection 4.2.1; see the proof of Lemma 4.10, the relevant part starts with “Case (i) of Lemma 4.9.” If , then as . This, in conjunction with the relation , implies that for any . Similarly, if , then for any . Thus, if and , we are done: . It remains to consider the possibility when exactly one of this inequalities holds, say and (the case and is analogous). If there is , , then contains the constant . To see this take the solution of (1.1) with and for all . Then, since , , we have in . The compactness of gives , as claimed. This, however, can be proven to be contradictory by the same comparison argument involving the function (4.22) as in the proof of Lemma 4.10. This shows that and completes the proof of (5.2) in the case , .
6 Morse decompositions and the proofs of the quasiconvergence results
In this section, we prove Theorems 1.1, 1.3, and 1.4, giving also a stronger and more precise version of Theorem 1.3, see Theorem 6.4 below. We prepare the proofs by recalling some results concerning Morse decompositions and chain recurrence.
Throughout this section, we assume that is as in (1.8)—specifically, and —and the solution of (1.1), (1.2) is bounded. In what follows, the -limit set of this solution, , is viewed as a compact subset of equipped with the induced topology (in which it is a compact metric space).
We start by recalling the following result of [13, Lemma 6.2]. Consider a bounded set in which is positively invariant for (1.1), meaning that implies that for all .
Lemma 6.1.
Let be a bounded set in which is positively invariant for (1.1). Equip with a metric from . Given any , there is such that for each the map is Lipschitz continuous with Lipschitz constant .
We now consider the solution flow on . For any , let be defined by , where is the entire solution of (1.1) with . As noted in Section 2.2, this entire solution is well (and uniquely) defined and satisfies for all . We claim that the family , , defines a flow on , that is,
-
(i)
is the identity on ,
-
(ii)
(,
-
(iii)
for each , the map is continuous.
Property (i) is obvious. The group property (ii) follows from the uniqueness of and the time-translation invariance of (1.1). The continuity of for follows from Lemma 6.1 applied to . Let now . Properties (i) and (ii) imply that is the inverse to the continuous map . Since is compact, the inverse is continuous, too.
Obviously, for any fixed , the map is continuous. In fact, the map is (jointly) continuous. This can be proved easily using Lemma 6.1, but the fact that the joint continuity follows from the separate continuity in and is a general property of flows (see [22, Section 8A]).
Next we note that the flow , , on is chain recurrent in the following sense. Let be a metric on compatible with the topology of . For any , , , there exist an integer , real numbers , and elements with such that
This chain recurrence property of the -limit set of solutions with compact orbits is well-known from [9, Sect. II.6.3], where it is proved for flows on compact metric spaces. For semiflows, including those generated by parabolic equations, proofs can be found in [7, Lemma 7.5], [26, Proposition 1.5], [17, Lemma 4.5]. Of course, the continuity result 6.1 is needed here, as the limit set is taken with respect to the topology of .
Finally, we recall that a Morse decomposition for is a system of mutually disjoint compact subsets of with the following properties:
-
(mi)
For , the set is invariant under : for all and .
-
(mii)
If and is the corresponding entire solution, then for some with one has and .
(Note that in our definition of , , we use the convergence in the topology of , and the same topology is used on .) The following result of [9, Theorem II.7.A] will be instrumental below. The chain recurrence property of the flow implies that if is a Morse decomposition for , then
| (6.1) |
In the proofs of our theorems, we build Morse decompositions for using chains of (2.3). Consider the system
| (6.2) |
of all chains of (2.3) with the property that (as noted in Section 2.2, conditions (ND), (MF) imply that there are only finitely many chains).
Given any two distinct chains , , we have, according to Lemma 2.8(ii), that either , or , or else there are periodic orbits , of (2.3) such that and , . For chains , intersecting , the last possibility is ruled out by Lemma 3.6(i). Thus, relabelling the chains in (1.13) if necessary, we may assume that
| (6.3) |
We will utilize Morse decompositions with Morse sets of the form
| (6.4) |
or
| (6.5) |
where is one of the chains (1.13). Let us prove first of all that these are compact subsets of .
Proof.
We prove the result for (6.4); the proof for (6.5) is similar and is omitted. Assume that , belong to the set (6.4) and in . This means, a priori, that in , but since is compact in (cp. Section 2.3), we also have in . Pick any . Then . Since the set is obviously closed in and , we obtain that . Since was arbitrary, we have proved that belongs to the set (6.4). ∎
We are ready to complete the proofs of our main theorems. In proving the quasiconvergence results, Theorems 1.1 and 1.4, our goal is to show that there is a chain of (2.3) such that
| (6.6) |
This inclusion implies, by Lemma 2.9, that consists of steady states of (1.1), and also gives an additional information that the spatial trajectories of the functions in are all contained in one chain.
Proof of Theorems 1.1, 1.4.
We use the chains in (6.2) to define the following sets
| (6.7) |
They are obviously mutually disjoint—as the chains (6.2) are such, cp. (6.3)—and by Lemma 6.2 they are compact in . Since the sets consist of steady states (cp. Lemma 2.9), they are invariant for . Take now an arbitrary , if there is any such , and let be the corresponding entire solution. By the definition of the sets (6.7) and (6.2), is not contained in any chain. Therefore, Proposition 3.2 tells us that—under the hypotheses of Theorem 1.1 or Theorem 1.4— there are two chains , such that and
| (6.8) |
(for , we take the chain containing the loop , with as in (3.3)). Since , the inclusions (6.8) imply that , for some ; and implies that . We have thus proved that is a Morse decomposition for the flow . From (6.1) and the connectedness of we now conclude that , that is, there is only one chain in (6.2) and (6.6) holds for that chain, as desired. ∎
Remark 6.3.
Hypotheses (R) of Theorem 1.4 is only needed in the proof of Proposition 3.2 in the case that (U) holds and is the connected component of whose closure contains (see Section 5). If this part of Proposition 3.2 could be proved under weaker or no conditions in place of (R), then the above proof would work without change.
We next state and prove a stronger version of Theorem 1.3. Recall from Section 3 that if (U) holds, Proposition 3.2 holds true for any connected component of distinct from .
Theorem 6.4.
Assume that (U) holds. If is such that is not contained in , then is a steady state of (1.1).
Obviously, Theorem 1.3 follows from this result.
Proof of Theorem 6.4.
Let be the outer loop associated with and let the the chain containing the loop . Note that .
We first consider the possibility that
| (6.9) |
This in particular implies that for . In this situation, one can almost verbatim repeat the previous proof to conclude that and consists of steady states. We only remark that if , then, due to condition (6.9), one has . Thus Proposition 3.2 applies to .
Now assume that
| (6.10) |
We distinguish the following two possibilities:
| (6.11) | ||||
| (6.12) |
The first one, (6.11), can actually be ruled out. Indeed, if (6.11) holds, Proposition 3.2 ensures that at least one of the chains (6.2) is disjoint from . Denoting by the number of such chains, we list those chains as
| (6.13) |
Here, the labels are chosen such that for (cp. (6.3)).
Consider the following subsets of :
| (6.14) | ||||
All these sets are nonempty by (6.11) and the definition of the sets . We claim that these sets constitute a Morse decomposition on . Clearly, the sets are mutually disjoint. By Lemma 6.2, they are compact in . The sets , , consist of steady states (cp. Lemma 2.9), hence they are invariant for . To prove the invariance of , take any with and let be the corresponding entire solution. If , then, by Lemma 3.3, —in particular —for all . Otherwise, and is a steady state, so holds trivially. Thus, the invariance of is proved.
Take now an arbitrary , if there is any such , and let be the corresponding entire solution. We have and is not contained in any chain. Applying Proposition 3.2 (with ), we obtain similarly as in the proof of Theorems 1.1, 1.4, that there are two chains , such that and
| (6.15) |
Arguing similarly as in the proof of Theorems 1.1, 1.4, we obtain from (6.15) that is a Morse decomposition for the flow , and so (6.1) holds. This time, however, since there are at least two Morse sets in (6.14), from (6.1) we obtain a contradiction to the connectedness of .
References
- [1] S. Angenent. The zero set of a solution of a parabolic equation. J. Reine Angew. Math., 390:79–96, 1988.
- [2] T. Bartsch, P. Poláčik, and P. Quittner. Liouville-type theorems and asymptotic behavior of nodal radial solutions of semilinear heat equations. J. Eur. Math. Soc., 13:219–247, 2011.
- [3] P. Brunovský and B. Fiedler. Connecting orbits in scalar reaction diffusion equations. II. The complete solution. J. Differential Equations, 81:106–135, 1989.
- [4] X. Chen and J.-S. Guo. Existence and uniqueness of entire solutions for a reaction-diffusion equation. J. Differential Equations, 212:62–84, 2005.
- [5] X. Chen, J.-S. Guo, and H. Ninomiya. Entire solutions of reaction-diffusion equations with balanced bistable nonlinearities. Proc. Roy. Soc. Edinburgh Sect. A, 136:1207–1237, 2006.
- [6] X.-Y. Chen. A strong unique continuation theorem for parabolic equations. Math. Ann., 311(4):603–630, 1998.
- [7] X.-Y. Chen and P. Poláčik. Gradient-like structure and Morse decompositions for time-periodic one-dimensional parabolic equations. J. Dynam. Differential Equations, 7(1):73–107, 1995.
- [8] Y.-Y. Chen, J.-S. Guo, H. Ninomiya, and C.-H. Yao. Entire solutions originating from monotone fronts to the Allen-Cahn equation. Phys. D, 378/379:1–19, 2018.
- [9] C. Conley. Isolated invariant sets and the Morse index, volume 38 of CBMS Regional Conference Series in Mathematics. American Mathematical Society, Providence, R.I., 1978.
- [10] Y. Du and H. Matano. Convergence and sharp thresholds for propagation in nonlinear diffusion problems. J. Eur. Math. Soc. (JEMS), 12(2):279–312, 2010.
- [11] Y. Du and P. Poláčik. Locally uniform convergence to an equilibrium for nonlinear parabolic equations on . Indiana Univ. Math. J., 64:787–824, 2015.
- [12] E. Feireisl. On the long time behaviour of solutions to nonlinear diffusion equations on . NoDEA Nonlinear Differential Equations Appl., 4(1):43–60, 1997.
- [13] E. Feireisl and P. Poláčik. Structure of periodic solutions and asymptotic behavior for time-periodic reaction-diffusion equations on . Adv. Differential Equations, 5:583–622, 2000.
- [14] B. Fiedler and P. Brunovský. Connections in scalar reaction diffusion equations with Neumann boundary conditions. In Equadiff 6 (Brno, 1985), volume 1192 of Lecture Notes in Math., pages 123–128. Springer, Berlin, 1986.
- [15] B. Fiedler and C. Rocha. Heteroclinic orbits of semilinear parabolic equations. J. Differential Equations, 125:239–281, 1996.
- [16] P. C. Fife and J. B. McLeod. The approach of solutions of nonlinear diffusion equations to travelling front solutions. Arch. Ration. Mech. Anal., 65(4):335–361, 1977.
- [17] J. Földes and P. Poláčik. Convergence to a steady state for asymptotically autonomous semilinear heat equations on . J. Differential Equations, 251:1903––1922, 2011.
- [18] T. Gallay and S. Slijepčević. Energy flow in extended gradient partial differential equations. J. Dynam. Differential Equations, 13:757–789, 2001.
- [19] T. Gallay and S. Slijepčević. Distribution of energy and convergence to equilibria in extended dissipative systems. J. Dynam. Differential Equations, 27:653–682, 2015.
- [20] J.-S. Guo and Y. Morita. Entire solutions of reaction-diffusion equations and an application to discrete diffusive equations. Discrete Contin. Dynam. Systems, 12:193–212, 2005.
- [21] F. Hamel and N. Nadirashvili. Entire solutions of the KPP equation. Comm. Pure Appl. Math., 52(10):1255–1276, 1999.
- [22] J. E. Marsden and M. McCracken. The Hopf bifurcation and its applications. Springer-Verlag, New York, 1976. With contributions by P. Chernoff, G. Childs, S. Chow, J. R. Dorroh, J. Guckenheimer, L. Howard, N. Kopell, O. Lanford, J. Mallet-Paret, G. Oster, O. Ruiz, S. Schecter, D. Schmidt and S. Smale, Applied Mathematical Sciences, Vol. 19.
- [23] H. Matano and P. Poláčik. Dynamics of nonnegative solutions of one-dimensional reaction-diffusion equations with localized initial data. Part I: A general quasiconvergence theorem and its consequences. Comm. Partial Differential Equations, 41(5):785–811, 2016.
- [24] H. Matano and P. Poláčik. An entire solution of a bistable parabolic equation on with two colliding pulses. J. Funct. Anal., 272:1956–1979, 2017.
- [25] H. Matano and P. Poláčik. Dynamics of nonnegative solutions of one-dimensional reaction-diffusion equations with localized initial data. Part II: The generic case. Comm. Partial Differential Equations, to appear.
- [26] K. Mischaikow, H. Smith, and H. R. Thieme. Asymptotically autonomous semiflows: chain recurrence and Lyapunov functions. Trans. Amer. Math. Soc., 347(5):1669–1685, 1995.
- [27] Y. Morita and H. Ninomiya. Entire solutions with merging fronts to reaction-diffusion equations. J. Dynam. Differential Equations, 18:841–861, 2006.
- [28] Y. Morita and H. Ninomiya. Traveling wave solutions and entire solutions to reaction-diffusion equations. Sugaku Expositions, 23:213–233, 2010.
- [29] A. Pauthier and P. Poláčik. Large-time behavior of solutions of parabolic equations on the real line with convergent initial data. Nonlinearity, 31(9):4423–4441, 2018.
- [30] P. Poláčik. Examples of bounded solutions with nonstationary limit profiles for semilinear heat equations on . J. Evol. Equ., 15:281–307, 2015.
- [31] P. Poláčik. Spatial trajectories and convergence to traveling fronts for bistable reaction-diffusion equations. In A. Carvalho, B. Ruf, E. Moreira dos Santos, S. Soares, and T. Cazenave, editors, Contributions to nonlinear differential equations and systems, A tribute to Djairo Guedes de Figueiredo on the occasion of his 80th Birthday, Progress in Nonlinear Differential Equations and Their Applications, pages 405–423. Springer, 2015.
- [32] P. Poláčik. Threshold behavior and non-quasiconvergent solutions with localized initial data for bistable reaction-diffusion equations. J. Dynamics Differential Equations, 28:605–625, 2016.
- [33] P. Poláčik. Convergence and quasiconvergence properties of solutions of parabolic equations on the real line: an overview. In Patterns of dynamics, volume 205 of Springer Proc. Math. Stat., pages 172–183. Springer, Cham, 2017.
- [34] P. Poláčik. Entire solutions and a Liouville theorem for a class of parabolic equations on the real line. Proc. Amer. Math. Soc., to appear.
- [35] P. Poláčik. Propagating terraces and the dynamics of front-like solutions of reaction-diffusion equations on . Mem. Amer. Math. Soc., to appear.
- [36] E. Risler. Global relaxation of bistable solutions for gradient systems in one unbounded spatial dimension. preprint.
- [37] E. Risler. Global behaviour of bistable solutions for gradient systems in one unbounded spatial dimension. preprint.
- [38] A. I. Volpert, V. A. Volpert, and V. A. Volpert. Traveling wave solutions of parabolic systems, volume 140 of Translations of Mathematical Monographs. American Mathematical Society, Providence, RI, 1994. Translated from the Russian manuscript by James F. Heyda.
- [39] M. Wolfrum. A sequence of order relations: encoding heteroclinic connections in scalar parabolic PDE. J. Differential Equations, 183:56–78, 2002.