Large Diamagnetism and Electromagnetic Duality in Two-dimensional Dirac Electron System

Dirac electron systems (DESs) such as bismuth and graphene can be described by the Dirac equation and provide a platform to realize physical properties rooted in relativistic quantum physics [1, 2]. One prominent property of DESs is their large orbital diamagnetism, which reaches a maximum when the chemical potential is in the mass gap, unlike Landau diamagnetism in metals. This orbital diamagnetism, which is theoretically argued to originate from the interband effect of magnetic fields, is observed in three-dimensional (3D) DESs including bismuth and antiperovskites [3, 4, 5, 6]. This mechanism also applies to two-dimensional (2D) systems. The diamagnetism was observed for mass-produced graphene flakes [7]. Here the random orientation of the flakes prevented separating the orbital diamagnetism agreeable with theory. Organic conductors have recently been found to realize 2D DESs with a bulk form such as $\alpha$-(BEDT-TTF)₂I₃ (BEDT-TTF = bis(ethylene)dithiotetrathiafulvalene) [8, 9, 10]; however, this is realized only under high pressure, limiting magnetic experiments and making it difficult to obtain the absolute value of the susceptibility using SQUID magnetometers.

The electric responses of 3D and 2D DESs show a sharp contrast. The uniform permittivity of bismuth is enhanced in accordance with its orbital diamagnetism [11, 12]. On the other hand, graphene has no enhancement in the permittivity, but rather shows exotic quantized optical conductance and minimum dc conductivity through Klein tunneling [2, 13, 14]. The organic conductor $\alpha$-(BEDT-TTF)₂I₃ also shows temperature-independent conductivity on the order of $e^{2}/h$ per sheet [15].

These magnetic and electric responses of DESs can be viewed as parallel to quantum electrodynamics (QED), a relativistic quantum field theory, in which two responses are unified due to the Lorentz covariance (space–time symmetry). Indeed, for 3D DESs, the large orbital diamagnetism and the enhanced permittivity can be explained by charge renormalization in a unified way, demonstrating an electromagnetic duality specified by the space–time symmetry of the Dirac equation [16]. In contrast to 3D DESs, permittivity enhancement due to charge renormalization is absent in 2D DESs [17], although they do exhibit a quantized conductance. The dependence of the charge renormalization on the dimensionality of the system raises the fundamental question of the existence and nature of the universal phenomena in DESs irrespective of the system dimension. Therefore, the two principal goals of the study of 2D DESs are to determine the behavior of the orbital diamagnetism and its relationship with quantized electric responses, and to clarify whether the two responses can be described by a unified theory. Observation of the orbital diamagnetism would resolve these questions, and in order to obtain absolute values of the magnetic susceptibility, a bulk-form single crystal at ambient pressure would be ideal.

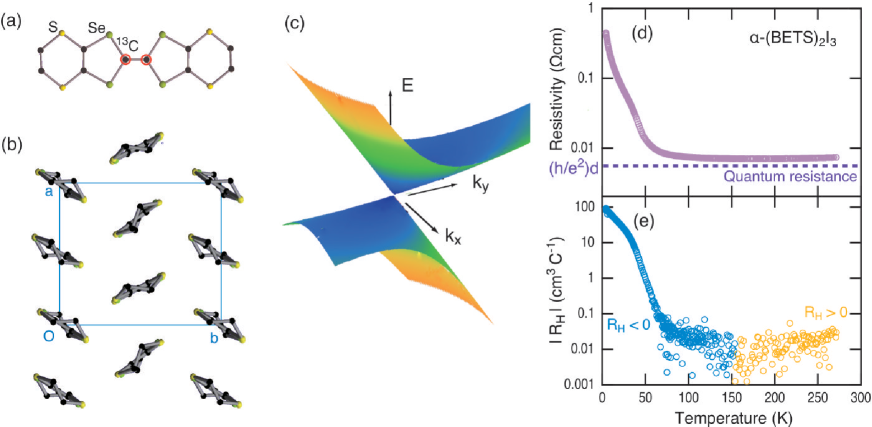
In this Letter, we demonstrate the magnetic and transport properties of a newly identified 2D DES organic conductor with a bulk form at ambient pressure, $\alpha$-(BETS)₂I₃ with a strongly anisotropic magnetic susceptibility $\chi$. We discriminated a large orbital diamagnetism ($\chi_{\mathrm{orb}}$) from a spin susceptibility ($\chi_{\mathrm{spin}}$) by changing the field direction. $\chi_{\mathrm{orb}}$ shows quantitative agreement with the theory for $T>50$ K, where the dc-conductivity ($\sigma_{\mathrm{dc}}$) per sheet is independent of temperature with the value of $e^{2}/h$. The $-T\chi_{\mathrm{orb}}$ scales with $\sigma_{\mathrm{dc}}$ in a wide temperature range, showing an electromagnetic duality specified by the space–time symmetry in DESs, corresponding to the Lorentz covariance in QED.

$\alpha$-(BETS)₂I₃ is composed of bis(ethylenedithio)tetraselenafulvalene (BETS) molecules that contain Se atoms (Fig. 1 (a)) [18, 19]. The structure is isomorphous with $\alpha$-(BEDT-TTF)₂I₃, as shown in Fig. 1 (b). The molecular orbital of BETS is spatially larger than that of BEDT-TTF, which yields uncorrelated electron characteristics and prevents the instabilities toward charge ordering or excitonic orders observed in $\alpha$-(BEDT-TTF)₂I₃ [20]. This noninteracting character enables us to extract the ideal physics of DES through theoretical and quantitative analysis.

The full relativistic first-principles calculation provides a Dirac-like linear dispersion with a mass gap of $\approx 2$ meV (Fig. 1 (c)) and an effective “speed of light” of $v\approx 5\times 10^{4}$ m/s [21, 22, 23, 24]. The resistivity above 50 K is nearly independent of temperature, as has also been observed in the high-pressure massless Dirac phase of $\alpha$-(BEDT-TTF)₂I₃ (Fig. 1 (d)). Here, Dirac electrons compensate for the temperature dependence of the mobility and the density of states [8], resulting in the temperature-independent resistivity corresponding to quantum sheet resistance, $(h/e^{2})d=4.6$ m$\Omega$ cm, where $d=17.8$ Å is the interplane distance using the value of the lattice constant along $c$.

The resistivity increases upon cooling below 50 K without a phase transition, consistent with the mass gap but does not follow an activated temperature dependence. The Hall coefficient ($R_{\mathrm{H}}$) is small above 50 K, and its sign changes at $T=150$ K from high-temperature positive (hole-like) values to low-temperature negative (electron-like) values, as shown in Fig. 1 (e). This indicates that the Fermi energy is in the mass gap but shifts slightly with temperature. At 150 K, the Fermi energy will be exactly at the midpoint of the gap.

We show in Fig. 2 (a) the magnetic susceptibilities $\chi_{a,b,c}$ for $H\parallel a,b,$ and $c$ (interplane direction). The susceptibility $\chi_{a}$, which nearly agrees with $\chi_{b}$, decreases linearly upon cooling below 150 K, consistent with Dirac-type linear dispersion. A possible in-plane anisotropy of $\chi$ originating from the tilting of the Dirac cone is negligible; therefore, we can consider that $\chi_{a,b}$ solely depends on the density of states and the electronic correlation is negligible. A detailed formula for the spin contribution to $\chi$ is given below using $\chi_{0}$, the spin susceptibility of 2D nonrelativistic electron gas with the interplane distance $d$.

where $m_{0}$ is the electron mass, $\Delta=m^{*}v^{2}$ is the mass gap, and $\beta=1/k_{B}T$. $\chi_{0}=\mu_{0}e^{2}/2\pi m_{0}d=1.57\times 10^{{-7}}$ in SI units, where $\mu_{0}$ is the vacuum permeability. The chemical potential $\mu$ is set to be zero for simplicity (see Ref. [21] for general $\mu$). In Fig. 2 (b), we plot $\chi_{\mathrm{spin}}$ using $\Delta=50$ K, which provides $m^{*}=\Delta/v^{2}=0.3m_{0}$ with the ab initio value of $v$, as well as the experimental $\chi_{\mathrm{spin}}^{\mathrm{(exp)}}=(\chi_{a}+\chi_{b})/2$, and find that this simple formula quantitatively reproduce the experiments.

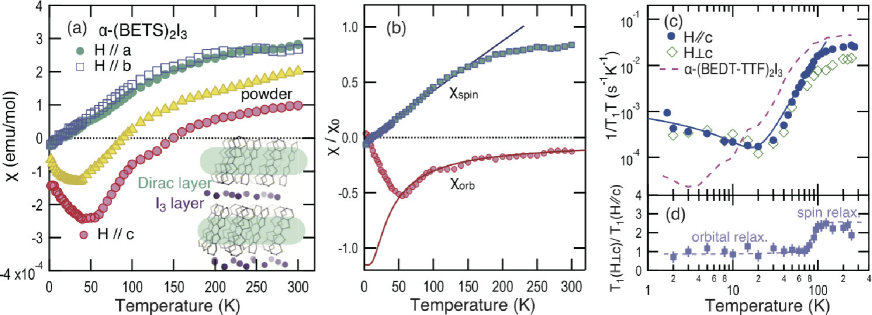
The magnetic susceptibility perpendicular to the conducting plane, $\chi_{c}$, is strongly suppressed and shows negative values below 150 K, which indicates an orbital diamagnetism, $\chi^{\mathrm{(exp)}}_{\mathrm{orb}}=\chi_{c}-\chi_{\mathrm{spin}}^{\mathrm{(exp)}}$, that emerges only along the $c$-direction. This diamagnetic $\chi_{\mathrm{orb}}$ was theoretically predicted for 2D DESs [25, 26]. In contrast to spins, which are conserved, the orbital currents that generate $\chi_{\mathrm{orb}}$ are not conserved. In general, the susceptibility of a non-conserved quantity has a contribution from high-energy bands, $\chi_{\mathrm{orb}}^{\mathrm{(exp)}}(\infty)$, which is independent of temperature and irrelevant to the Dirac band. We estimated $\chi_{\mathrm{orb}}^{\mathrm{(exp)}}(\infty)$ by fitting $\chi_{\mathrm{orb}}^{\mathrm{(exp)}}(T)$ for $T>100$ K with $\chi^{\mathrm{(exp)}}_{\mathrm{orb}}(T)=\mathrm{const}\times 1/T+\chi_{\mathrm{orb}}^{\mathrm{(exp)}}(\infty)$ (see below Eq. (3)). We plot in Fig. 2 (b) the temperature dependent component, $\chi_{\mathrm{orb}}(T)=\chi^{\mathrm{(exp)}}_{\mathrm{orb}}(T)-\chi^{\mathrm{(exp)}}_{\mathrm{orb}}(\infty)$.

For free electrons, a detailed formula for $\chi_{\mathrm{orb}}(T)$ in the presence of a mass gap is given by [27]

where the chemical potential $\mu$ is set to be zero (see Ref. [21] for general $\mu$). In Fig. 2 (b), we plot experimental and calculated $\chi_{\mathrm{orb}}$ obtained using Eq. (2) with the same parameters as those for $\chi_{\mathrm{spin}}$. We find quantitative agreements between the experimental and theoretical values as well as those for $\chi_{\mathrm{spin}}$ in the wide temperature range of $T>50$ K. Equation (2) shows a crossover at $T\approx\Delta/k_{B}$ and is approximated as

so that $\chi_{\mathrm{orb}}T$ = const is expected for $T\gtrsim\Delta/k_{\mathrm{B}}$.

The observed uncorrelated character of the 2D DES for $T>50$ K and the deviation of $\chi_{\mathrm{orb}}(T)$ from Eq. (2) are microscopically supported by ¹³C NMR. High-temperature Korringa-like $1/T_{1}T$ for $T>200$ K is significantly reduced following $1/T_{1}T\propto T^{\gamma}$ with $\gamma\approx 2$ for $30<T<100$ K as shown in Fig. 2 (c), which indicates a linear dispersion. Note that the observed $1/T_{1}T$ is five times smaller than that of $\alpha$-(BEDT-TTF)₂I₃, showing that the Dirac electrons in $\alpha$-(BETS)₂I₃ are relatively free of one-body renormalization of Coulomb repulsions [20]. The increase in $1/T_{1}T$ below 20 K indicates other emergent relaxation mechanisms. Fig. 2 (d) depicts the anisotropies of $1/T_{1}$, which we expect to be temperature-independent when the spin contribution $(1/T_{1})_{\mathrm{spin}}$ dominates $1/T_{1}$. The reduction of the anisotropy below 100 K, the onset temperature of the DES, coincides with that of $(1/T_{1})_{\mathrm{spin}}$. Since ¹³C does not couple with the electric field gradient, the most plausible source of the relaxation at low temperatures is the fluctuation of the orbital currents, which contributes to $1/T_{1}$ as $1/T_{1}=(1/T_{1})_{\mathrm{spin}}+(1/T_{1})_{\mathrm{orb}}$. Recent theories point out that $(1/T_{1})_{\mathrm{orb}}$ dominates $1/T_{1}$ in 3D Weyl materials [28, 29], but predict $(1/T_{1}T)_{\mathrm{orb}}\propto T$ for clean 2D DESs, which does not reproduce the experiments below 20 K [29]. Later, we will discuss a potential mechanism for the deviation related to $\chi_{\mathrm{orb}}$.

The correspondence between DES and QED relates Eq. (3) to the exotic quantized electric property in 2D DESs. In parallel to the Lorentz covariance in QED, we can show a duality between electric and magnetic responses in DES [21, 30, 31]. For $|\mu|\leq\Delta$ and $T=0$, the static magnetic susceptibility $\chi_{\mathrm{orb}}$ is given exactly as

where $c$ and $\varepsilon_{0}$ are the speed of light and vacuum permittivity, respectively [21]. Here, $\sigma(\omega)$ is the dynamical electrical conductivity, which originates only from interband electron–hole excitations. Thus, this duality relation indicates that dynamical vacuum fluctuations (the creation and annihilation of virtual electron–hole pairs), or the interband effect across the mass gap, necessarily generate the orbital diamagnetism $\chi_{\mathrm{orb}}<0$.

A dimensional analysis gives $\sigma(\omega)\propto(e^{2}/h)(\omega/v)^{D-2}$ for the massless limit of $\Delta\to 0$ in the $D$ dimensions. In three dimensions ($D=3$), Eq. (4) leads to a logarithmic divergence in $\chi_{\mathrm{orb}}$ for $\Delta\to 0$, which corresponds to the well-known ultraviolet divergence in the charge renormalization of QED [16]. In two dimensions ($D=2$), on the other hand, there is no charge renormalization [17]. The large diamagnetism $\chi_{\mathrm{orb}}\propto-1/\Delta$ in Eq. (3) is therefore free from charge renormalization but closely linked to the $\omega$-independent electrical conductivity for $\Delta\to 0$, where it takes a universal value of $\sigma_{0}=e^{2}/4\hbar d$ (quantized optical conductance) [32, 14]. (In Table 1, we summarize $\chi_{\mathrm{orb}}$ and $\sigma(\omega)$ as well as the permittivity $\varepsilon$ for 3D and 2D DESs.) More precisely, using a detailed formula for $\sigma(\omega)$ [32], we find that the duality relation, Eq. (4), expresses $\chi_{\mathrm{orb}}$ in terms of the universal constant $\sigma_{0}$ as

It is noteworthy that the conductivity unit $\sigma_{0}$ can be rewritten using the susceptibility unit $\chi_{0}$ as $\displaystyle\sigma_{0}=(\pi^{2}/Z_{0}\lambda_{e})\chi_{0}$, where $Z_{0}=\sqrt{\mu_{0}/\varepsilon_{0}}\approx 120\pi$ $\Omega$ is the impedance of free space and $\lambda_{e}=h/m_{0}c$ is the Compton wavelength, leading to the equivalence of Eqs. (3) and (5). This equivalence shows that $\chi_{\mathrm{orb}}$ scales with the universal electric conductance $\sigma_{0}d\approx e^{2}/h$ even for finite temperatures.

The dc conductivity $\sigma_{\mathrm{dc}}\equiv\alpha\sigma_{0}$ ($\alpha$ is of the order of $1$) is difficult to determine theoretically, depending on the characteristics of the disorder [33, 34, 35, 36]. $\alpha$ is naively given as $\alpha=8/\pi^{2}$ [37] for 2D massless Dirac electrons but remains under debate for $T\neq 0$. The experimentally obtained values of $\sigma_{\mathrm{dc}}$’s for organic DES, in contrast, are independent of temperature both for $\alpha$-(BETS)₂I₃ and $\alpha$-(BEDT-TTF)₂I₃; the $\sigma_{\mathrm{dc}}$ values are approximately equal to $\sigma_{\mathrm{dc}}=14$ k$\Omega^{-1}$m^-1, corresponding to $\alpha\approx 4/\pi^{2}$ [15].

We plot $-\chi_{\mathrm{orb}}T$ and $\sigma_{\mathrm{dc}}$, normalized by $\chi_{0}$ and $\sigma_{0}$, respectively, in Fig. 3, and find that these electromagnetic responses are scaled in a wide temperature range, as anticipated from Eq. (5). The observed electromagnetic duality manifests itself in the correspondence with the Lorentz covariance in QED. The interband effect across the mass gap in the presence of electromagnetic fields characterizes the physical properties.

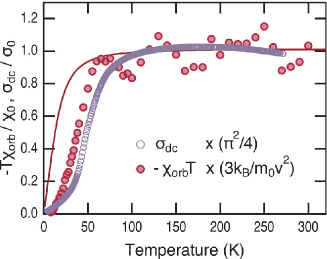
We now discuss potential sources for the deviation of $\chi_{\mathrm{orb}}(T)$ from Eq. (2), although Eq. (1) does reproduce $\chi_{\mathrm{spin}}(T)$ below 40 K. The most plausible source is a disorder in real materials, which raises a new problem related to the interaction of disorder and orbital currents in DESs. We found that the function $1/T_{1}T=aT^{2.5}+b\log(T^{*}/T)$ fits the $1/T_{1}T$, as shown in Fig. 2 (c). The logarithmic increase upon cooling below 20 K does not originate from the electronic correlation, which enhances $1/T_{1}T$ for the whole temperature range, and the crossing of the $1/T_{1}T$ curves of $\alpha$-(BETS)₂I₃ and $\alpha$-(BEDT-TTF)₂I₃ at $T\approx 10$ K suggests disorder effects on $(1/T_{1})_{\mathrm{orb}}$. A similar moderate increase of $1/T_{1}T$ is observed for a 3D Weyl system [38], which has been theoretically analyzed considering the effects of impurities or temperature-dependent chemical potential to $(1/T_{1})_{\mathrm{orb}}$ [39, 40]. Likewise, an observed increase in $1/T_{1}T$ for a noninteracting 3D DES with $\Delta\approx 15$meV, Bi_0.9Sb_0.1 [41], is closely related to our observation of the moderate increase in $1/T_{1}T$ below 20 K. A related phenomenon is also observed for the transport properties: namely, unconventional negative magnetoresistance with a field dependence of the form $1-\rho(B)/\rho_{0}\propto-\sqrt{B}$ [21]. These deviations from an ideal 2D DES are observed solely for the orbital-related properties at low temperatures, which suggests a new problem in disordered orbital physics in DESs. Surprisingly, despite the deviation of $\chi_{\mathrm{orb}}$ from Eq. (2) below 50 K, $\sigma_{\mathrm{dc}}$ approximately scales with $-\chi_{\mathrm{orb}}T$, thus maintaining the electromagnetic duality even at low temperatures where the effect of a disorder becomes crucial as shown in Fig. 3. This suggests a possible relationship between the effects of disorder on $\chi_{\mathrm{orb}}$ and $\sigma_{\mathrm{dc}}$, which results in a less disturbed electromagnetic duality.

In summary, we identified the organic conductor, $\alpha$-(BETS)₂I₃, as a 2D DES at ambient pressure through electric and magnetic measurements of $\sigma_{\mathrm{dc}}$, $R_{\mathrm{H}}$, $\chi_{\mathrm{spin}}$, and $1/T_{1}$ of ¹³C NMR. The latter two magnetic responses show negligible electronic correlation, enabling us to study an ideal characteristics of DES. We found orbital diamagnetism ($\chi_{\mathrm{orb}}$) only along the interplane direction. We demonstrate that the equation $T\chi_{\mathrm{orb}}=\mathrm{const}$ holds approximately for $T>50$ K and $\chi_{\mathrm{spin}}\propto T$, and that small shifts from the gapless DES are well reproduced by the theory using a unique parameter, $\Delta=m^{*}v^{2}$, the mass gap for the DES. We found a unified electromagnetic responses in which $-T\chi_{\mathrm{orb}}$ scales with $\sigma_{\mathrm{dc}}\approx e^{2}/hd$ in a wide temperature range, as shown in Fig. 3, consistent with an electromagnetic duality that is valid only within the relativistic framework.