Laplace Sum Rules in Quantum ChromoDynamics
Abstract
We shortly review some applications of the (inverse) Laplace (LSR) transform sum rules in Quantum ChromoDynamics (QCD) for extracting the fundamental QCD parameters (coupling constant , quark and gluon condensates) and the hadron properties (masses and decay constants). Links of LSR to some other forms of QCD spectral sum rules are also discussed. As prototype examples, we discuss in detail the and meson sum rules.
Keywords : QCD spectral sum rules, QCD coupling quark masses and condensates,
Hadron masses and couplings.
pacs:
11.55.Hx, 12.38.Lg, 13.20-Gd, 14.65.Dw, 14.65.Fy, 14.70.DI Introduction
Different spectral sum rules based on dispersion relations called current algebra sum rules have been used before QCD FURLAN . Among these, there are the Weinberg WEIN and Das-Mathur-Okubo (DMO) DMO sum rules which assume the asymptotic realizations of chiral and flavour symmetries to derive constraints on the vector and axial-vector mesons masses and couplings. One of the famous predictions from the Weinberg sum rules is the mass relation:
| (1) |
which is reproduced within the errors by the data.
Within the advent of QCD, corrections to these sum rules have been studied FNR ; DMOQCD ; GMONARISON in 1979-80. At about the same time, Shifman-Vainshtein and Zakharov (hereafter referred as SVZ) SVZa ; ZAKA 111For reviews, see e.g. the books SNB1 ; SNB2 , the reviews in SNB3 ; RRY ; BERTa ; REV and the recent ones in Refs.SNREV22 ; SNREV21 ; SNbc15 ., have introduced the QCD spectral sum rules which are the improvement of the usual dispersion relation obeyed by e.g. the hadron two-point function:
| (2) |
where mean subtraction constants polynomial in the momentum .
is a generic notation for a hadronic current:
– Quark bilinear local current for mesons. is any Dirac matrices which specify the quantum numbers of the corresponding meson state (and its radial excitations),
– Quark trilinear local current for baryons,
– Four-quark or diquark anti-diquark local current for molecules or tetraquark states,
– Pentaquark states,
– Gluon local currents for gluonia/glueball states,
– Quark-gluon local currents for hybrid states.
In the case of a meson bound state built from a quark and the anti-quark , the current reads:
| (3) |
where denotes any Dirac matrices which specify the quantum number of the associated hadron. for the vector, axial-vector, pseudoscalar and scalar currents which correspond respectively to the and scalar quarkonium mesons.
II The SVZ Borel/Laplace sum rules (LSR)
Besides the Shifman-Vainshtein-Zakharov (SVZ) (see Fig. 1) theoretical improvement of the perturbative QCD expression within the Operator Product Expansion (OPE) where quark and gluon condensates of higher and higher dimensions are supposed to approximate the non-perturbative QCD contributions which we shall discuss in the next section, the phenomenological success of QCD (spectral) sum rules or SVZ sum rules also comes from the improvement of the usual dispersion relation which is the bridge between the high-energy QCD expression and the measurable spectral function at low energy. In the example of the light isovector () vector current:
| (4) |
the spectral function is related to the Hadrons total cross-section via the optical theorem:
| (5) |

II.1 The form of the Laplace sum rules
This improvement has been achieved by working with large number of derivatives and large value of the momentum transfer but taking their ratio finite leading to the so-called SVZ Borel/Laplace or Exponential sum rules (LSR) and their ratios,222Non-relativistic version of this sum rule has been discussed by BELLa ; BERTa , while the inclusion of the PT correction to the QCD expression has shown that it has the property of an inverse Laplace transform in SNR SNR though the name LSR. :
| (8) | |||||
| (9) |
where is the LSR variable, is the hadronic threshold. Here is the threshold of the “QCD continuum” which parametrizes, from the discontinuity of the Feynman diagrams, the spectral function .
Thanks to the exponential weight and for moderate values of , the previous sum rule improvements enhance the low energy contribution to the spectral integral which is accessible experimentally.
II.2 The minimal duality ansatz (MDA)
In the often case where the data on the spectral function are not available, one usually parametrizes it via the minimal duality ansatz :
| (10) |
in order to predict the masses and couplings of the lowest ground state and in some case the ones of its radial excitations. depends on the dimension of the current, is the hadron decay constant normalized as 132 MeV. Its accuracy has been tested in various light and heavy quark channels where complete data are available SNB1 ; SNB2 and in the -pseudoscalar channel where an improved parametrization of the channel within chiral perturbation theory has been used BIJNENS . Within a such parametrization, the ratio of sum rules is used to extract the mass of the lowest ground state as it is equal to its square.
II.3 Hadron masses from the ratio of moments
Within the MDA parametrization, the ratio of sum rules is used to extract the mass of the lowest ground state as it is equal to its square:
| (11) |
However, this analysis cannot be done blindly without studying / checking the moments which in some cases can violate positivity of the specral integral for some values of the sum rule variables () though their ratio can lead to a positive number identified with the hadron mass squared.
II.4 Hadron mass-splittings from the double ratio of sum rule (DRSR) DRSR
The hadron and mass-splitting, like the one due to breakings, can be derived from the quantity:
| (12) |
provided that the optimal value: . A similar quantity can be used for the heavy quark moments.
III Link of LSR to some other sum rules
III.1 Local duality Finite Energy Sum Rules (FESR)
It has the form:
| (13) |
where is the degree of the sum rule. This sum rule has been used before QCD in Refs. LOGUNOV ; SAKURAI and within QCD in Refs. KRASNIKOV ; KATAEV ; LARIN .
This sum rule can be derived from LSR by using a small -expansion and by matching for a given its QCD and experimental side.
FESR can be used to fix the value of the QCD continuum threshold from its dual constraint with the mass and decay constant of the ground state FESR1 ; FESR2 . Contrary to LSR, FESR emphasizes the role of higher masses radial excitations to the integral. Therefore, it requires a good control of the high-energy part of the spectral function.
III.2 Gaussian Sum Rules
IV The SVZ - Operator Product Expansion (OPE)
According to SVZ, the Right Hand Side (RHS) of the two-point function can be evaluated in QCD within the Operator Product Expansion (OPE) provided that where MeV is the QCD scale for 3 flavours and is the heavy quark mass. In this way, it reads :
| (15) |
where, in addition to the usual perturbative QCD contribution (unit operator), one has added the ones due to non-perturbative gauge invariant quark and gluon condensates having a dimension which have been assumed to parametrize approximately the not yet under good control QCD confinement. are separated calculable Wilson coefficients in Perturbative (PT) QCD:
IV.1 The usual perturbative (PT) contribution
It corresponds to while the quadratic quark mass corrections enter via .
IV.2 The quark and gluon condensates
They contribute through the OPE. Up to , they are successively the :
– quark and gluon and ,
– mixed quark-gluon:
– four-quark and three-gluon: and .
– and so on.
IV.3 The condensates
The quark condensate and the part of the trace of the energy-momentum transfer : are known to be subtraction -independent where are the quark mass anomalous dimension and Callan-Symanzik -function.
– The condensate can be deduced from the well-known Gell-Mann, Oakes, Renner relation GMOR :
| (16) |
once the running light quark mass is known ( MeV are the pion mass and decay constant) or directly from light baryon sum rules DOSCHSN . With the value of the running quark masses given in Table 2 in Ref. SNREV22 , one can deduce the value of in this Table 2.
– The original value of the gluon condensate GeV4 of SVZ SVZa ; RRY has been claimed BELLa ; BERTa from charmonium sum rules and Finite Energy Sum Rule (FESR) for Hadrons FESR1 ; FESR2 to be underestimated. Recent analysis from Hadrons, -decay and charmonium confirm these claims with the present updated average (see the different determinations in Table 1 of SNparam ) :
| (17) |
IV.4 The quark-gluon mixed condensate
IV.5 The four-quark condensates
The renormalization of dimension-six condensates has been studied in SNTARRACH where it has been shown that these condensates mix under renormalization and then cannot be compatible with the vacuum saturation assumption used by SVZ. Its phenomenological estimate from -like decays SNTAU , Hadrons data LNT , -decay SOLA , FESR FESR1 ; FESR2 and baryon DOSCH sum rules, leads to the average :
| (19) |
indicating a huge violation of the vacuum saturation or factorization:
| (20) |
by a factor about 5.8.
IV.6 The condensate
It does not mix under renormalization and behaves as SNTARRACH , where is the first coefficient of the -function and is number of quark flavours. The first improvement of the estimate of the condensate was the recent direct determination of the ratio of the dimension-six gluon condensate over the dimension-four one using heavy quark sum rules with the value SNcb1 :
| (22) |
which differs significantly from the instanton liquid model estimate NIKOL2 ; SHURYAK ; IOFFE2 . This result may question the validity of the instanton result. Earlier lattice results in pureYang-Mills found: GeV2 GIACO such that it is important to have new lattice results for this quantity. Note however, that the value given in Eq. 22 might also be an effective value of all unknown high-dimension condensates not taken into account in the analysis of SNcb1 when requiring the fit of the data by the truncated OPE. We have seen in some examples SNREV21 ; SNREV22 that the effect of is a small correction at the stability region where the optimal results are extracted.
IV.7 Higher dimension condensates
Usually, the truncation of the OPE up to provides enough information for extracting the masses and couplings of the ground state hadrons with a good accuracy. In many papers, some classes of higher dimension terms up to 2D=12 ! are added in the OPE. However, it is not clear if such term gives the dominant contributions compared to the omitted ones having the same dimension. The size of these high-dimension condensates is not also under a good control due to the eventual violation of the vacuum saturation used for their estimate.
IV.8 Beyond the SVZ-OPE
V The different terminologies of the SVZ sum rules
V.1 The origin of the name: Borel sum rule from the OPE
Applying the operator in Eq. 9 to the QCD expression in Eq. 15, the OPE of the 1st moment becomes:
| (23) |
where the appearance of the factor in the OPE indicates the property of the Borel transform for the moment sum rule thus the name Borel sum rule. For this purpose, we recall that if we consider a function , its Borel transform is:
| (24) |
where the integration contour runs to the right of all the singularities of the function . Then, the inverse Borel transform reads:
| (25) |
Therefore, if
| (26) |
then :
| (27) |
The great advantage of this property is the improved convergence of the OPE for the Borel transform compared to the one of the original two-point function .
V.2 The origin of the name: Laplace sum rule (LSR) including corrections


In Ref. SNR , S. Narison and E. de Rafael (referred hereafter as SNR) 333The main idea comes from Prof. E. de Rafael as I was a student in that time. have remarked that working with the renormalization group resummed QCD expression including radiative corrections, the sum rule has instead a Laplace transform property from which all QCD expressions can be derived.
The Laplace transform sum rule (LSR) can be derived from the dispersion relation (Hilbert transform) in Eq. 2 from the useful formulae (see e.g. the Appendix of SNB1 ; SNB2 ) :
| (28) |
where is the (inverse) Laplace transform operator and :
| (29) |
with the useful properties:
| (30) |
In addition to previous formulae, the expression of the integral:
| (31) |
is useful for the treatment of the QCD continuum contribution to the LSR from the QCD spectral function as parametrized in Eq. 10.
VI The QCD expressions of the prototype meson and pion LSR
We illustrate the derivation of the Laplace sum rule in the case of the vector and pseudoscalar (divergence of the axial-vector) currents:
| (32) |
and the corresponding two-point functions and used in Ref. SNR for demonstrating (for the first time) the Laplace transform properties of the SVZ sum rule 444In these pedagogical examples, we shall limit to the perturbative QCD expression to order . Analysis including higher order terms can be found in SNe23 ; SNLIGHT . :
| (33) |
VI.1 The meson channel
As the corresponding two-point correlator is once substracted, it is convenient to work with its first derivative:
| (34) |
| (35) |
where for flavours. is superconvergent and obeys the homogeneous Renormalization Group Equation (RGE):
| (36) |
with the running parameters to order are (see e.g.FNR ; RUNDEC ; SNB1 ; SNB2 ):
| (37) |
where:
| (38) |
and are respectively the 1st and 2nd coefficients of the function and mass anomalous dimension. For quark flavours, they read:
| (39) |
Using the previous formulae of the Laplace transform into the QCD expressions of the corresponding two-point correlator, one can deduce the Laplace transform SNR ; SNB1 ; SNB2 :
| (40) | |||||
where the factor if one uses the vacuum saturation assumption for the four-quark condensate.
VI.2 The pion channel
The corresponding two-point function behaves as and is then twice substracted. Thererefore, its 2nd derivative is superficially convergent and obeys the RGE in Eq. 36. Taking the Laplace transform of , one obtains: SNR ; SNB1 ; SNB2 555For an updated expression including higher order contributions, see e.g. SNLIGHT .:
| (41) | |||||
VII Optimization procedure for the LSR
VII.1 The SVZ sum rule window
The second important step in the sum rule analysis is the extraction of the optimal result from the sum rule as, in principle, the Laplace sum rule (LSR) variable , the degree of moments and the QCD continuum threshold are free external variables. In their original work, SVZ have adjusted the values of and using some guessed contributions, for finding the sum rule window where the QCD continuum contribution is less than some input number while the ground state one is bigger than some input number and where, in this sum rule window, the OPE is expected to converge. The arbitrariness values of these numbers have created some doubts for non-experts on the results from the sum rules, in addition to the ones on the eventual non-correctness of the non-trivial QCD-OPE expressions. Unfortunately, many sum rules practitioners continue to use this inaccurate SVZ criterion.
VII.2 -stability from quantum mechanics and


VII.3 Examples of -stability from the and mesons


Hopefully, in the examples of harmonic oscillator in quantum mechanics and of the non-relativistic charmonium sum rules, Refs. BELLa ; BERTa have shown that the optimal information from the analysis for a truncated series is obtained at the minimum or inflexion point in of the approximate theoretical curves (see Figs 3 and 4). This optimal criterion corresponds to the (principle of minimum sensitivity of the physical parameters on the external sum rule variable ) and where the exact solution is reached when one adds more and more terms in the approximate series.
VII.4 and -stabilities
Later on, we have extended this -stability criterion to the continuum threshold variable 666In many papers, the optimal value is extracted at the lowest value of ! but the result still increases with the changes. and to the arbitrary Perturbative (PT) subtraction point 777One can also use the RGE resummed solution which is equivalent to take but in some case the value of is relatively large such that the OPE is not well behaved. A such choice of value is often outside the -stability region.. The lowest value of corresponds to the beginning of -stability while the -stability corresponds to a complete lowest ground state dominance in the spectral integral. In our analysis, we always consider the conservative optimal result inside this -region 888 is often identified to the mass of the 1st radial excitation which is a crude approximation as the QCD continuum smears all higher state contributions to the spectral function..
VII.5 Ground state versus the QCD continuum
For some low value of and large value of , one can have some flat curves or some (apparent) minimum in . Then, to check or/and to restrict the optimal region in this case, one also requests that the contribution of the ground state to e.g. the spectral integral (e.g. moment sum rule) is larger than the QCD continuum one. One can formulate this constraint in a more rigorous way as (see e.g. SNPC for some examples of applications) :
| (42) |
VIII Phenomenology of the -meson LSR
VIII.1 Lower bound on the -meson coupling from the lowest moment
We use the MDA parametrization of the spectral function and extract the -meson coupling 999Analysis using the complete Hadrons data can e.g. be found in Refs. LNT ; SNe23 . :
| (43) |
Using positivity of the spectral integral and evaluating the LSR at , SNR deduces the inequality to leading order of PT series 101010Notice that this inequality has been considered as an estimate in the original SVZ paper SVZa .:
| (44) |
We improve this bound by adding higher order terms in the PT series and including the contribution of the condensates up to dimension-six. We show the analysis in Fig.7 for different values of and . The condition is shown by the cyan curve where the lowest ground state dominates in the delimited right region. Optimal results are obtained for the sets from (0.5,1.5) to (1.1,3.0) in units of (GeV-2, GeV2). This leads to the improved lower bound at order :
| (45) |


VIII.2 The lowest moment using the Hadrons data
It is informative to compare the QCD prediction of with the one where the complete Hadrons data is used to estimate the spectral integral. This analysis has been done recently in Ref. SNe23 which we show in Fig. 8
One can observe that there is a good agreement with the experimental data. and the theory prediction using the previous sets of QCD parameters up to condensates.
VIII.3 from the lowest ratio of moments
Within MDA, one expects that the ratio of moments provides the mass squared of the -meson ground state. We show the analysis versus and for different values of in Fig. 9.

The optimal results are obtained for the sets from (0.5,1.2) to (1.2,3.0) in units of (GeV-2, GeV2). We obtain:
| (46) |
where the error comes mainly from the value of which we have taken in the conservative range from the beginning of stability until the -one.
One can restrict this range of value using the constraint from the first moment of FESR. It reads FESR1 ; FESR2 :
| (47) |
from which we deduce:
| (48) |
One should note that the low value of often chosen by many “QCD sum rules practitioners” to reproduce the value of the experimental mass or to extract the mass of the ground state does not coi ncide with the duality constraint from FESR. At the value of in Eq. 48, we obtain from the ratio of moments :
| (49) |
From the previous analysis, the ratio of moments reproduces within 10% the experimental meson mass.
VIII.4 QCD condensates from using Hadrons data
The ratio of moments has the advantage to be less sensitive to correction than the moment as the PT correction starts to order . It is then expected to be a good place for extracting the QCD condensates. This analysis has been initiated by Ref. LNT and revised recently in Ref. SNe23 . Using as input the value of the gluon condensate obtained from heavy quark sum rules SNparam ; SNREV22 ; SNREV21 given in Eq. 17, one obtains:
| (50) |
where the value of the four-quark condensate is in good agreement with the one in Eq. 19.
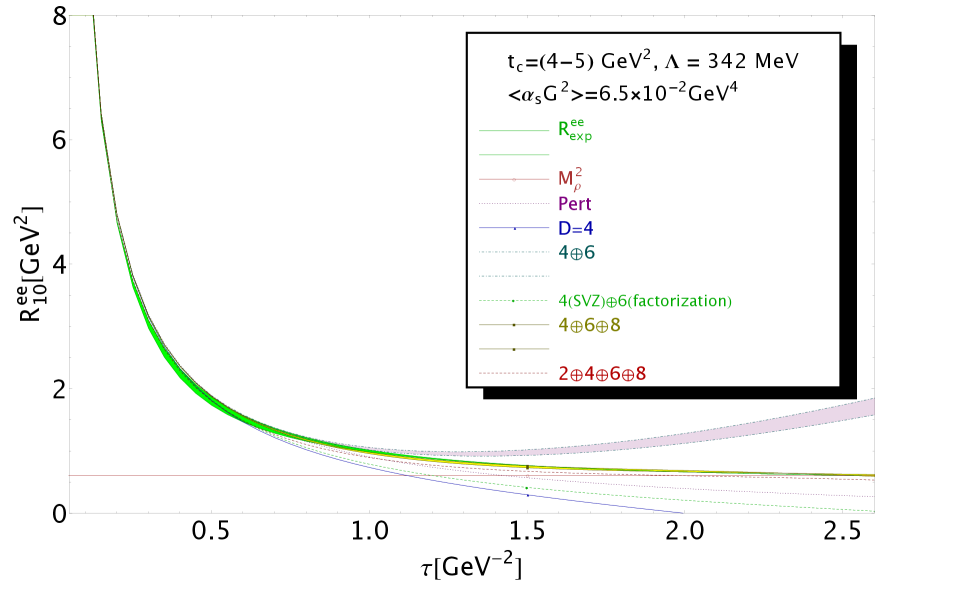
We show in Fig. 10 a comparison of the experimental expression of with the QCD prediction for different truncations of the OPE. One can notice a good agreement when the condensates up to dimension 6,8 are included.
IX Sum of light quark masses from the pion LSR
IX.1 Lower bound on
Using the pion sum rule, SNR has derived a lower bound on the RGI quark mass defined in Eq. 37 from the positivity of the spectral function and retaining the pion contribution. The results have been given for different values of the QCD scale . Given the present progress on the determination of , we show the new version of the figure given in Ref. SNR in Fig. 11 for different truncation of the PT series.

IX.2 Estimate of
One can transform the previous lower bound by introducing the QCD continuum for parametrizing the spectral function. Using the standard OPE, one obtains to order for the RGI and running masses evaluated at 2 GeV SNLIGHT 111111Extension of the analysis to some other channels are discussed in this paper.:
| (52) |
where one can notice that the main uncertainties and the size of the central value come from the parametrization of the spectral function (radial excitations choice of the QCD continuum threshold ). The error due to the way for truncating the PT series only affects slightly the total error (see e.g. KAHN ). These results agree with lattice calculations LATTLIGHT and from some other approaches quoted in PDG PDG .
X Some other applications of LSR
These applications have been already summarized in the recent short reviews SNREV21 ; SNREV22 where orginal references and some dedicated reviews can be found. They concern the :
Light baryons ligth quark states
Heavy quarks sector.
Heavy-light states.
So-called exotic states :
Glueballs / gluonia states.
Hybrids states.
Light , heavy-light , fully-heavy four-quark states.
Light , heavy-light , fully-heavy molecule states.
We plan to develop these different parts in a more extended review on QCD spectral sum rules.
Concluding remarks
LSR and (in general) QCD spectral sum rules (QSSR) are useful tools to tackle within a good approximation the properties of hadrons and for extracting the fundamental parameters of the QCD Lagrangian. If properly done, QSSR is a serious alternative or/and a supplement to the lattice QCD numerical simulations.
References
- (1) V. De Alfaro, S. Fubini, G. Furlan, C. Rossetti, Currents in hadron physics, North Holland Pub. Co. Amsterdam-London (1973).
- (2) S. Weinberg, Phys. Rev. Lett. 18 (1967) 507.
- (3) T. Das, V.S. Mathur, S. Okubo, Phys. Rev. Lett. 19 (1967) 470.
- (4) E.G. Floratos, S. Narison and E. de Rafael, Nucl. Phys. B155 (1979) 155 and references quoted therein.
- (5) S. Narison and E. de Rafael, Nucl. Phys B169 (1980) 253 and references quoted therein..
- (6) S. Narison, Z. Phys. C 22 (1984) 161.
- (7) M.A. Shifman, A.I. Vainshtein, V.I. Zakharov, Nucl. Phys. B147 (1979) 385; ibid, Nucl. Phys. B147 (1979) 448.
- (8) V.I. Zakharov, Int. J. Mod .Phys. A14, (1999) 4865.
- (9) S. Narison, QCD spectral sum rules, World Sci. Lect. Notes Phys. 26 (1989) 1.
- (10) S. Narison, QCD as a theory of hadrons, Cambridge Monogr. Part. Phys. Nucl. Phys. Cosmol. 17. (2004) 1-778 [hep-ph/0205006].
- (11) S. Narison, Phys. Rept. 84 (1982) 263; ibid, Riv. Nuovo Cim. 10N2 (1987) 1.
- (12) L.J. Reinders, H.R. Rubinstein, S. Yazaki, Phys. Reports 127 (1985) 1.
- (13) R.A. Bertlmann, Acta Phys. Austriaca 53, (1981) 305.
- (14) M.A. Shifman, Prog. Theor. Phys. Suppl. 131 (1998)1; P. Colangelo and A. Khodjamirian, hep-ph/0010175; E. de Rafael, hep-ph/9802448; F.J. Yndurain, Monographs in Physics, Springer-Verlag, New York (1999).
- (15) S. Narison,Nucl.Part. Phys. Proc.324-329 (2023) 94; ibid, 258-259 (2015) 189.
- (16) S. Narison, Nucl. Part. Phys. Proc.312-317 (2021) 87; ibid, 300-302 (2018) 153.
- (17) S. Narison, Nucl. Part. Phys. Proc. 309-311 (2020) 135; ibid 270-272 (2016) 143.
- (18) J.S. Bell, R.A. Bertlmann, Nucl. Phys. B177, (1981) 218; ibid, Nucl. Phys. B187, (1981) 285.
- (19) S. Narison, E. de Rafael, Phys. Lett. B103, (1981) 57.
- (20) J. Bijnens, J. Prades, E. de Rafael, Phys. Lett. B348 (1995) 226.
- (21) S. Narison, Phys. Lett. B210 (1988) 238; ibid, Phys. Lett. B337 (1994) 166.
- (22) A.A. Logunov, L.D. Soloviev, A.N. Tavkhelidze, Phys. Lett. B24 (1967) 181.
- (23) J.J. Sakurai, Phys. Lett. B46 (1973) 207.
- (24) K.G. Chetyrkin, N.V. Krasnikov, A.N. Tavkhelidze, Phys. Lett. B76 (1978) 83.
- (25) A.L. Kataev, N.V. Krasnikov, A.A. Pivovarov, Phys. Lett. B123 (1983) 93.
- (26) S.G. Gorishnii, A.L. Kataev, S.A. Larin, Phys. Lett. B135 (1984) 457.
- (27) R.A. Bertlmann, G. Launer and E. de Rafael, Nucl. Phys. B250, (1985) 61.
- (28) R.A. Bertlmann, C.A. Dominguez, M. Loewe, M. Perrottet and E. de Rafael, Z. Phys. C39 (1988) 231.
- (29) M. Gell-Mann, R.J. Oakes, B. Renner, Phys. Rev. 175 (1968) 2195.
- (30) H.G. Dosch, S. Narison, Phys. Lett. B417 (1998) 173.
- (31) S. Narison, Int. J. Mod. Phys. A33 (2018) no. 10, 185004; Addendum: Int. J. Mod. Phys. A33 (2018) no.10, 1850045.
- (32) S. Narison, R. Tarrach, Phys. Lett. B125 (1983) 217.
- (33) B.L. Ioffe, Prog. Part. Nucl. Phys. 56 (2006) 232; ibid, B188 (1981) 317; ibid, B191 (1981) 591.
- (34) H.G. Dosch, Non-Perturbative Methods (Montpellier 1985); Y. Chung et al.Z. Phys. C25 (1984) 151; H.G. Dosch, M. Jamin, S. Narison, Phys. Lett. B220 (1989) 251.
- (35) A.A. Ovchinnikov, A.A. Pivovarov, Yad. Fiz. 48 (1988) 1135.
- (36) S. Narison, Phys. Lett. B605 (2005) 319.
- (37) S. Narison, Phys. Lett. B673 (2009) 30.
- (38) G. Launer, S. Narison, R. Tarrach, Z. Phys. C26 (1984) 433.
- (39) C.A. Dominguez, J. Sola, Z. Phys. C40 (1988) 63.
- (40) S. Narison, Phys. Lett. B300 (1993) 293; ibid B361 (1995) 121.
- (41) S. Narison, Phys. Lett. B693 (2010) 559, erratum ibid, B705 (2011) 544; ibid, B706 (2012) 412; ibid, B707 (2012) 259.
- (42) S.N. Nikolaev, A.V. Radyushkin, Phys. Lett. B124 (1983) 243.
- (43) T. Schafer, E.V. Shuryak, Rev. Mod. Phys. 70 (1998) 323.
- (44) B.L. Ioffe, A.V. Samsonov, Phys. At. Nucl. 63 (2000) 1448.
- (45) A. Di Giacomo, Non-pertubative Methods, ed. Narison, World Scientific (1985); A. Di Giacomo, G.C. Rossi, Phys. Lett. B100 (1981) 481; M. D’Elia, A. Di Giacomo, E. Meggiolaro, Phys. Lett. B408 (1997) 315.
- (46) S. Narison, arXiv : 2306.14639 [hep-ph] (2023).
- (47) S. Narison, Phys. Lett. B707 (2012) 259.
- (48) S. Narison, Phys. Lett. B718 (2013) 1321; ibid, Nucl. Phys. (Proc.Suppl.) 234 (2013) 187.
- (49) R.M. Albuquerque, S. Narison, D. Rabetiarivony, arXiv : 2301.08199 (2023).
- (50) S. Narison, Phys. Lett. B738 (2014) 346 and references therein.
- (51) K.G. Chetyrkin, J.H. Kühn and M. Steinhauser,Comput. Phys. Comm 133 (2000) 43 and references therein.
- (52) L. Lellouch, E. de Rafael, J. Taron, Phys.Lett. B414(1997)195; C.A. Dominguez, E. de Rafael, Annals Phys. 174 (1987) 372; J. Bijnens, J. Prades, E. de Rafael, Phys. Lett. B348 (1995), 226.
- (53) S. Aoki et al., arXiv:1310.8555 [hep-lat] (2013).
- (54) M.S.A. Alam Khan, arXiv: 2306.10266 [hep-ph] (2023).
- (55) R.L. Workman et al. (Particle Data Group), Prog. Theor. Exp. Phys. 2022 (2022) 083C01.