Lamb dilatation and its hydrodynamic viscous flux in near-wall incompressible flows

The dynamics of an incompressible viscous Newtonian fluid can be well described by the Navier-Stokes (NS) equations:

	$\displaystyle\frac{\partial\bm{u}}{\partial t}+\bm{u}\bm{\cdot}\bm{\nabla}\bm{u}=-\bm{\nabla}\left(\frac{p}{\rho}\right)+\nu\nabla^{2}\bm{u},$		(1a)
	$\displaystyle\bm{\nabla}\bm{\cdot}\bm{u}=0,$		(1b)

where $\rho$ is the constant fluid density, $\bm{u}$ is the velocity and $p$ is the pressure. $\nu=\mu/\rho$ is the kinematic viscosity with $\mu$ being the dynamic viscosity. The body force potential has been combined into the pressure. Therefore, the body force does not exist explicitly in the following discussion.

The decomposition of the velocity gradient tensor $\bm{\nabla}\bm{u}$ gives the strain rate tensor $\bm{S}$ and the rotation tensor $\bm{A}$ as

$\displaystyle\bm{S}=\frac{1}{2}\left(\bm{\nabla}\bm{u}^{T}+\bm{\nabla}\bm{u}\right),~{}~{}\bm{A}=\frac{1}{2}\left(\bm{\nabla}\bm{u}^{T}-\bm{\nabla}\bm{u}\right).$

(2)

The rotation tensor $\bm{A}$ satisfies the relation $2\bm{A}\bm{\cdot}\bm{v}=\bm{\omega}\times\bm{v}$ for any vector $\bm{v}$ with $\bm{\omega}=\bm{\nabla}\times\bm{u}$ being the vorticity. The fluid enstrophy is defined as $\Omega\equiv\omega^{2}/2$.

In this paper, the no-slip and no-penetration boundary condition $\bm{u}_{\partial B}=\bm{0}$ is considered on a general stationary curved boundary surface $\partial B$ with the normal vector $\bm{n}$ directing from the wall to the fluid. A physical quantity with the subscript $\partial B$ denotes its value at the wall and $\bm{\nabla}_{\partial B}$ represents the tangential surface gradient operator. The surface Laplacian operator is denoted as $\nabla_{\partial B}^{2}\equiv\bm{\nabla}_{\partial B}\bm{\cdot}\bm{\nabla}_{\partial B}$. The surface curvature tensor is denoted as $\bm{K}=-\bm{\nabla}_{\partial B}\bm{n}$, whose trace $tr(\bm{K})$ is twice the mean surface curvature $H$, namely, $tr(\bm{K})=-\bm{\nabla}_{\partial B}\bm{\cdot}\bm{n}=2H=\kappa_{1}+\kappa_{2}$, where $\kappa_{1}$ and $\kappa_{2}$ represent the two principal curvatures of the surface. Obviously, $\bm{K}$ vanishes for a flat surface. Combined with proper boundary conditions, Eqs. (1a) and (1b) give a complete description for incompressible viscous flows.

Interestingly, in a small vicinity of the solid wall $\partial B$, applying the near-wall Taylor-series expansion to Eqs. (1a) and (1b) yields an explicit asymptotic solution of the NS system which uniquely relates the near-wall velocity $\bm{u}$ and pressure $p$ to the fundamental surface quantities (including skin friction $\bm{\tau}=\mu\bm{\omega}_{\partial B}\times\bm{n}$, surface pressure $p_{\partial B}$ and surface curvature tensor $\bm{K}$) as well as their temporal-spatial derivatives on the surface [33, 36, 35, 61]. Namely,

$\displaystyle\bm{u}=f_{1}\left(y;\bm{\tau},\bm{\nabla}_{\partial B}p_{\partial B},\bm{\nabla}_{\partial B}\bm{\cdot}\bm{\tau},\nabla_{\partial B}^{2}p_{\partial B},tr(\bm{K}),\cdots\right),$

(3)

$\displaystyle{p}=f_{2}\left(y;p_{\partial B},\bm{\nabla}_{\partial B}\bm{\cdot}\bm{\tau},\nabla_{\partial B}^{2}p_{\partial B},tr(\bm{K}),\cdots\right),$

(4)

where $y$ is the wall-normal coordinate measured from the surface in the fluid side. However, the physical and geometrical variables ($\bm{\tau}$, $p_{\partial B}$ and $\bm{K}$) are generally not independent but are coupled through the boundary enstrophy flux (BEF) $f_{\Omega}\equiv\mu[\partial\Omega/\partial n]_{\partial B}$, satisfying the exact relation [37, 38]

$\displaystyle\bm{\tau}\bm{\cdot}\bm{\nabla}_{\partial B}p_{\partial B}+\mu^{2}\bm{\omega}_{\partial B}\bm{\cdot}\bm{K}\bm{\cdot}\bm{\omega}_{\partial B}=\mu f_{\Omega}.$

(5)

The first term in Eq. (5) represents the non-linear coupling between the skin friction and the surface pressure gradient. The second term in Eq. (5) represents the interaction between the boundary vorticity and the surface curvature via the dynamic viscosity. The sum of these two contributions is physically balanced by the wall-normal diffusion of the enstrophy. Generally, the BEF is dominated by the $\bm{\tau}-p_{\partial B}$ coupling term when the surface curvature contribution is not significant. Since the enstrophy is usually created at the wall and then diffuses into the fluid, the BEF usually remains negative in most attached flows while its sign could be positive near the separation and attachment lines or isolated critical points [36, 35]. Of particular interest are small-Reynolds-number viscous flows where the surface curvature contribution cannot be neglected in the total BEF. The sign of the surface curvature contribution is obviously dependent on the surface type [38]. Proper modeling the BEF could realize the transformation between the footprints (skin friction and surface pressure) in an unified variational framework [36, 38].

The convective acceleration in Eq. (1a) can be decomposed as

$\displaystyle\bm{u}\bm{\cdot}\bm{\nabla}\bm{u}=\bm{\omega}\times\bm{u}+\bm{\nabla}\left(\frac{1}{2}u^{2}\right)\equiv\bm{L}+\bm{\nabla}K,$

(6)

where $K=u^{2}/2$ is the kinetic energy per unit mass. The cross product of the velocity and vorticity defines the Lamb vector $\bm{L}\equiv\bm{\omega}\times\bm{u}$, which represents the critical non-linear features of the viscous flows, while the kinetic energy potential gradient can be absorbed into the pressure gradient to form the stagnation enthalpy $h_{0}=p/\rho+u^{2}/2$ or the Bernoulli function [24, 9]. Using the incompressibility condition Eq. (1b) and the identity $\bm{\nabla}\times\bm{\omega}=\bm{\nabla}\times(\bm{\nabla}\times\bm{u})=-\nabla^{2}\bm{u}$, we recast Eq. (1a) as

$\displaystyle\frac{\partial\bm{u}}{\partial t}+\bm{L}=-\bm{\nabla}h_{0}-\nu\bm{\nabla}\times\bm{\omega}.$

(7)

The Lamb dilatation is defined as the divergence of the Lamb vector, namely $\vartheta_{L}\equiv\bm{\nabla}\bm{\cdot}\bm{L}$. Taking divergences of both sides of Eq. (7) yields a Poisson equation for the stagnation enthalpy $h_{0}$ where the Lamb dilatation $\vartheta_{L}$ (with a minus sign) acts as a source term, i.e., $\nabla^{2}h_{0}=-\vartheta_{L}$. Physically, a region with positive Lamb dilatation ($\vartheta_{L}>0$) implies a concentrated stagnation enthalpy, while a region with negative Lamb dilatation ($\vartheta_{L}<0$) implies a depleted stagnation enthalpy. Usually, straining motions tend to correspond to regions with positive Lamb dilatation, while vortical motions tend to correspond to regions with negative Lamb dilatation. Interaction between positive and negative regions of the Lamb dilatation will effect a time rate of change of momentum and thereby causes a distinct change in the overall flow dynamics [24]. In this sense, the spatial structure of the Lamb dilatation is directly related to the energy redistribution and momentum transfer between the flow regions with positive and negative Lamb dilatation.

By taking the curl of both sides of Eq. (7), the vorticity transport equation can be derived as

$\displaystyle\frac{\partial\bm{\omega}}{\partial t}=-\bm{\nabla}\times\bm{L}+\nu\nabla^{2}\bm{\omega}=-\bm{u}\bm{\cdot}\bm{\nabla}\bm{\omega}+\bm{\omega}\bm{\cdot}\bm{\nabla}\bm{u}+\nu\nabla^{2}\bm{\omega},$

(8)

where the convection, stretching and tilting effects on vorticity lines originate from the curl of the Lamb vector $\bm{\nabla}\times\bm{L}$.

Taking a cross product of the vorticity $\bm{\omega}$ with Eq. (7) and that of the velocity $\bm{u}$ with Eq. (8), Wu et al. [9] first obtained the transport equation for the Lamb vector,

$\displaystyle\frac{\partial\bm{L}}{\partial t}+\bm{u}\bm{\cdot}\bm{\nabla}\bm{L}=-\bm{L}\bm{\cdot}\bm{\nabla}\bm{u}+\bm{\nabla}h_{0}\times\bm{\omega}+\nu\nabla^{2}\bm{L}+\bm{q},$

(9)

where the left hand side of Eq. (9) represents the material derivative of the Lamb vector. In the right hand side of Eq. (9), the first term denotes the inviscid stretching and tilting effects of the $\bm{L}$-lines. The second term stands for the interaction between the gradient of the stagnation enthalpy $\bm{\nabla}h_{0}$ and the vorticity $\bm{\omega}$. Note that $\bm{\nabla}h_{0}\times\bm{\omega}=-2\bm{A}\bm{\cdot}\bm{\nabla}h_{0}=-2\lVert\bm{\nabla}h_{0}\rVert\bm{A}\bm{\cdot}\bm{n}_{0}$, where $n_{0}\equiv\bm{\nabla}h_{0}/\lVert\bm{\nabla}h_{0}\rVert$ is the unit normal vector of the isosurface of the stagnation enthalpy. Therefore, this term is determined by the magnitude of the stagnation enthalpy gradient and the increment of the unit normal vector $\bm{n}_{0}$ due to the rotational action exerted by the tensor $\bm{A}$. The third term represents the viscous diffusion of the Lamb vector. The last term $\bm{q}$ can be written as the divergence of a second-order tensor, namely,

$\displaystyle\bm{q}\equiv-2\nu\frac{\partial\bm{\omega}}{\partial x_{j}}\times\frac{\partial\bm{u}}{\partial x_{j}}=\nu\bm{\nabla}\bm{\cdot}\left(4\bm{S}\bm{\cdot}\bm{A}+\bm{\omega\omega}\right).$

(10)

Therefore, $\bm{q}$ can be interpreted as a viscous source. The detailed proof of Eq. (10) can be found in the appendix of our recent paper [62].

Using the following identities

$\displaystyle\bm{\nabla}\bm{\cdot}\left(\bm{u}\bm{\cdot}\bm{\nabla}\bm{L}\right)=\bm{\nabla}\bm{L}\bm{:}\bm{\nabla}\bm{u}^{T}+\bm{u}\bm{\cdot}\bm{\nabla}\vartheta_{L},$

(11)

$\displaystyle\bm{\nabla}\bm{\cdot}\left(\bm{L}\bm{\cdot}\bm{\nabla}\bm{u}\right)=\bm{\nabla}\bm{L}\bm{:}\bm{\nabla}\bm{u}^{T}+\bm{L}\bm{\cdot}\bm{\nabla}\left(\bm{\nabla}\bm{\cdot}\bm{u}\right)=\bm{\nabla}\bm{L}\bm{:}\bm{\nabla}\bm{u}^{T},$

(12)

$\displaystyle\bm{\nabla}\bm{\cdot}\left(\bm{\nabla}h_{0}\times\bm{\omega}\right)=-\bm{\nabla}h_{0}\bm{\cdot}\left(\bm{\nabla}\times\bm{\omega}\right),$

(13)

and taking the divergences of both sides of Eq. (9), we obtain the transport equation for the Lamb dilatation, i.e.,

$\displaystyle\frac{\partial\vartheta_{L}}{\partial t}+\bm{u}\bm{\cdot}\bm{\nabla}\vartheta_{L}=-2\bm{\nabla}\bm{L}\bm{:}\bm{\nabla}\bm{u}^{T}-\bm{\nabla}h_{0}\bm{\cdot}\left(\bm{\nabla}\times\bm{\omega}\right)+\nu\nabla^{2}\vartheta_{L}+\bm{\nabla}\bm{\cdot}\bm{q},$

(14)

where the left hand side of Eq. (14) represents the material derivative of the Lamb dilatation. In the right hand side of Eq. (14), the first term denotes the double contraction of the Lamb vector gradient and the transposed velocity gradient. The second term represents the coupling between the curl of the vorticity and the gradient of the stagnation enthalpy. The other two terms denote the viscous diffusion of the Lamb dilatation and the divergence of the viscous source term $\bm{q}$, respectively.

It should be noted that Hamman et al. [24] also reported another version for the transport equation of the Lamb dilatation, which read

	$\displaystyle\frac{\partial\vartheta_{L}}{\partial t}+\bm{u}\bm{\cdot}\bm{\nabla}\vartheta_{L}$	$\displaystyle=$	$\displaystyle-2\bm{\nabla}\bm{L}\bm{:}\bm{\nabla}\bm{u}^{T}-\bm{\nabla}h_{0}\bm{\cdot}\left(\bm{\nabla}\times\bm{\omega}\right)$		(15)
			$\displaystyle-\nu\lVert\bm{\nabla}\times\bm{\omega}\rVert^{2}+\nu\bm{u}\bm{\cdot}\nabla^{2}\left(\bm{\nabla}\times\bm{\omega}\right)-2\nu\bm{\omega}\bm{\cdot}\nabla^{2}\bm{\omega}.$

Here, we further prove the equivalence of Eqs. (14) and (15). First, we see that direct vector field analysis gives the following identity

$\displaystyle\nu\nabla^{2}\bm{\omega}\times\bm{u}+\nu\bm{\omega}\times\nabla^{2}\bm{u}=\nu\nabla^{2}\bm{L}+\bm{q}.$

(16)

Then, by taking divergences of both sides of Eq. (16), we have

$\displaystyle\nu\bm{\nabla}\bm{\cdot}(\nabla^{2}\bm{\omega}\times\bm{u})+\nu\bm{\nabla}\bm{\cdot}(\bm{\omega}\times\nabla^{2}\bm{u})=\nu\nabla^{2}\vartheta_{L}+\bm{\nabla}\bm{\cdot}\bm{q}.$

(17)

The first and the second terms in the left hand side of Eq. (17) can be evaluated as

	$\displaystyle\nu\bm{\nabla}\bm{\cdot}(\nabla^{2}\bm{\omega}\times\bm{u})$	$\displaystyle=$	$\displaystyle\nu\bm{u}\bm{\cdot}\bm{\nabla}\times\nabla^{2}\bm{\omega}-\nu\nabla^{2}\bm{\omega}\bm{\cdot}\bm{\nabla}\times\bm{u}$		(18)
		$\displaystyle=$	$\displaystyle\nu\bm{u}\bm{\cdot}\nabla^{2}(\bm{\nabla}\times\bm{\omega})-\nu\bm{\omega}\bm{\cdot}\nabla^{2}\bm{\omega},$

	$\displaystyle\nu\bm{\nabla}\bm{\cdot}(\bm{\omega}\times\nabla^{2}\bm{u})$	$\displaystyle=$	$\displaystyle\nu\nabla^{2}\bm{u}\bm{\cdot}\bm{\nabla}\times\bm{\omega}-\nu\bm{\omega}\bm{\cdot}\bm{\nabla}\times\nabla^{2}\bm{u}$		(19)
		$\displaystyle=$	$\displaystyle-\nu\lVert\bm{\nabla}\times\bm{\omega}\rVert^{2}-\nu\bm{\omega}\bm{\cdot}\nabla^{2}\bm{\omega}.$

Substituting Eq. (18) and (19) into Eq. (17) gives the following result:

$\displaystyle-\nu\lVert\bm{\nabla}\times\bm{\omega}\rVert^{2}+\nu\bm{u}\bm{\cdot}\nabla^{2}\left(\bm{\nabla}\times\bm{\omega}\right)-2\nu\bm{\omega}\bm{\cdot}\nabla^{2}\bm{\omega}=\nu\nabla^{2}\vartheta_{L}+\bm{\nabla}\bm{\cdot}\bm{q}.$

(20)

From Eq. (20), the equivalence between Eqs. (14) and (15) is proved.

On a general stationary curved wall, the terms $-\nabla h_{0}\bm{\cdot}\left(\nabla\times\bm{\omega}\right)$ and $-\nu\lVert\bm{\nabla}\times\bm{\omega}\rVert^{2}$ cancel out with each other because a natural reduction of the NS equations to the boundary gives a on-wall force balance equation, namely, $\rho^{-1}\left[\nabla p\right]_{\partial B}=\left[\nabla h_{0}\right]_{\partial B}=-\nu\left[\bm{\nabla}\times\bm{\omega}\right]_{\partial B}=\rho^{-1}\bm{\nabla}_{\partial B}p_{\partial B}+\rho^{-1}(\bm{\nabla}_{\partial B}\bm{\cdot}\bm{\tau})\bm{n}$. Although the total fluid acceleration on the wall is zero, the acceleration caused by either the pressure gradient or the viscous force is determined by the surface pressure gradient and the skin friction divergence. Additionally, applying the enstrophy transport equation on the wall, we have $\partial\Omega_{\partial B}/\partial t=\left[\nu\bm{\omega}\bm{\cdot}\nabla^{2}\bm{\omega}\right]_{\partial B}$. Combining these two results, Eq. (15) reduces to $\partial[\vartheta_{L}]_{\partial B}/\partial t=-2\partial\Omega_{\partial B}/\partial t$ at the wall. This identity obviously holds by taking time derivatives of both sides of Eq. (22).

Due to the velocity boundary condition $\bm{u}_{\partial B}=\bm{0}$, the Lamb vector $\bm{L}$ vanishes at the stationary wall and the boundary vorticity vector must be parallel to the tangent plane of the wall. However, once the vorticity is generated by virtue of the viscosity $\mu$ and surface pressure gradient $\bm{\nabla}_{\partial B}p_{\partial B}$ at the solid boundary and diffuses into the interior of the fluid, the spatial vortical structures rapidly become three-dimensionalized within a very limited distance away from the wall. Therefore, compared to the near-wall velocity and vorticity fields, a more compact and localized distribution of the Lamb vector will be observed slightly away from the wall. Indeed, the Lamb vector as the main aerodynamic force constituent is concentrated in a very thin layer (within about $10\%$ boundary-layer thickness) inside the boundary layer attached to the surface [1, 8]. This Lamb-vector maximum is the major contributor to the entire vortex force acting on an airfoil [1].

The sources and sinks of the Lamb vector can be well described by the Lamb dilatation $\vartheta_{L}$ [24]. The Lamb dilatation can be decomposed as the sum of a flexion product $\bm{u}\bm{\cdot}\bm{\nabla}\times\bm{\omega}$ and a non-positive part associated with the enstrophy $\Omega$, namely,

$\displaystyle\vartheta_{L}=\bm{\nabla}\bm{\cdot}\bm{L}=\bm{u}\bm{\cdot}\bm{\nabla}\times\bm{\omega}-2\Omega.$

(21)

Interestingly, different from the Lamb vector itself, the Lamb dilatation at the wall (i.e., $\left[\vartheta_{L}\right]_{\partial B}$) generally does not vanish. From Eq. (21), we have

$\displaystyle\left[\vartheta_{L}\right]_{\partial B}=-2\Omega_{\partial B},$

(22)

which implies that the non-positive Lamb dilatation at the wall is solely determined by the boundary enstrophy and thus the on-wall dissipation rate. A local maximum point of the boundary enstrophy must be a local minimum point of the boundary Lamb dilatation.

Like the BEF in Eq. (5), the wall-normal variation of the Lamb dilatation can be inferred from its boundary flux. For incompressible viscous flows, by applying the Gauss theorem, the volume integral of the viscous diffusion term $\mu\nabla^{2}\vartheta_{L}$ over a closed volume $B$ yields a surface integral of its viscous flux $\mu\bm{\hat{n}}\bm{\cdot}\bm{\nabla}\vartheta_{L}$ over the boundary surface $\partial B$, i.e.,

$\displaystyle\int_{B}\mu\nabla^{2}\vartheta_{L}dV=\oint_{\partial B}\mu\bm{\hat{n}}\bm{\cdot}\bm{\nabla}\vartheta_{L}dS,$

(23)

where $\hat{\bm{n}}$ represents the outward unit normal vector of the boundary surface. By analogy with the concept of BEF, we can introduce the boundary Lamb dilatation flux (BLDF) as

$\displaystyle f_{\vartheta_{L}}\equiv\mu\bm{n}\bm{\cdot}\left[\bm{\nabla}\vartheta_{L}\right]_{\partial B},$

(24)

which measures the diffusion rate of the Lamb dilatation through the boundary with the unit normal vector $\bm{n}=-\hat{\bm{n}}$ pointing from the boundary to the fluid.

For a general stationary curved surface, by performing wall-normal derivative to both sides of Eq. (21) and applying the resulting equation on the wall, we obtain

$\displaystyle f_{\vartheta_{L}}=-3\mu^{-1}\bm{\tau}\bm{\cdot}\bm{\nabla}_{\partial B}p_{\partial B}-2\mu\bm{\omega}_{\partial B}\bm{\cdot}\bm{K}\bm{\cdot}\bm{\omega}_{\partial B},$

(25)

Substituting Eq. (5) into Eq. (25) gives the exact relation between $f_{\vartheta_{L}}$ and $f_{\Omega}$:

$\displaystyle f_{\vartheta_{L}}=-3f_{\Omega}+\mu\bm{\omega}_{\partial B}\bm{\cdot}\bm{K}\bm{\cdot}\bm{\omega}_{\partial B}.$

(26)

As the first step of this theoretical study, we only consider flow past a stationary flat wall ($\bm{K}=\bm{0}$) in the present paper. Indeed, theoretical results for a stationary flat wall are relatively simple in mathematics, although the detailed derivation is not trivial as shown in Appendix A. Theoretical formulae for a stationary curved wall (and an arbitrarily moving and deforming wall) are much more complex due to the presence of the coupling terms among different kinematic, dynamic and geometric quantities, which will be further explored and reported in a separate paper. For example, skin friction on an deforming wall will include not only the surface-vorticity-induced contribution, but also the contribution from the additional vorticity caused by local angular velocity of the wall. These complex coupling mechanisms will be directly related to high-fidelity numerical topics, which cannot be thoroughly addressed in a single research.

Therefore, for a stationary flat wall, Eqs. (25) and (26) reduce to a concise relation between the BLDF and BEF:

$\displaystyle f_{\vartheta_{L}}=-3f_{\Omega}=-3\mu^{-1}\bm{\tau}\bm{\cdot}\bm{\nabla}_{\partial B}p_{\partial B}.$

(27)

Three comments are made here. Firstly, it is now clear that both the BLDF and BEF are determined by the nonlinear coupling mechanism between the skin friction $\bm{\tau}$ and the surface pressure gradient $\bm{\nabla}_{\partial B}p_{\partial B}$. The wall-normal diffusion of the Lamb dilatation is closely related to the boundary enstrophy generation and fundamental surface physical quantities.

Secondly, a negative BEF region ($f_{\Omega}<0$) must correspond to a positive BLDF region ($f_{\vartheta_{L}}>0$) for any instantaneous field in wall-bounded viscous flows, indicating a wall-normal increase of the Lamb dilatation inside a small vicinity of the wall. In fact, in a region of this kind, we have $[\partial\vartheta_{L}/\partial n]_{\partial B}=\mu^{-1}f_{\vartheta_{L}}>0$, which implies that $\vartheta_{L}$ increases monotonically with the wall-normal coordinate $y$ from its wall value $-2\Omega_{\partial B}$ in a small vicinity of the wall. According to the physical interpretation of the Lamb dilatation in Section II.2, these exists a trend to attenuate the vorticity bearing motion while to enhance the straining motion in negative BEF regions with the increasing wall-normal distance. In addition, the BEF remains negative in the sense of ensemble average [36, 35], which implies that the averaged BLDF should be positive, implying an increase of the Lamb dilatation along the wall-normal direction in a small vicinity of the wall. This analysis is consistent with the statistical results in a turbulent channel flow of $Re_{\tau}=590$ [24]: the mean Lamb dilatation increases from its negative minimum value at the wall till its positive maximum value is achieved at $y^{+}\approx 12$ and the mean Bernoulli function (stagnation enthalpy) transitions from a subharmonic (local energy depletion) to superharmonic (local energy concentration) state.

Thirdly, characteristic points in the BEF field that usually indicate local flow separation or attachment must also be those of the BLDF field. The BLDF provides a new physically-intuitive interpretation to the BEF because the Lamb dilatation has been shown as an effective structural indicator to coherent fluid motions and self-sustaining temporal-spatial interactions in the near-wall region [24, 31, 26].

As a direct application of Eq. (25), a new total aerodynamic force expression is presented based on the Lamb dilatation and the corresponding physical mechanism of pressure drag reduction is clearly elucidated.

Considering a two-dimensional body $B$ bounded by a closed surface $\partial B$, the curvature contribution vanishes because the vorticity is perpendicular to the plane. Under the continuity assumption, Eq. (22) implies that there always exists a small vicinity of the wall such that $\vartheta_{L}=-\lVert\vartheta_{L}\rVert\leq 0$. Therefore, if $\vartheta_{L}\neq 0$ holds for the region considered (extreme conditions are not included at present), Eq. (25) can be formally rewritten as

$\displaystyle\frac{dp}{ds}=-\frac{f_{\vartheta_{L}}}{3\left[\sqrt{\lVert\vartheta_{L}\rVert}\right]_{\partial B}}=\frac{2}{3}\mu\left[\frac{\partial\sqrt{\lVert\vartheta_{L}\rVert}}{\partial n}\right]_{\partial B},$

(28)

where $s$ is the arc length measured from a reference location $\bm{x}_{0}$ to the other location $\bm{x}$ on $\partial B$. Integrating Eq. (28) from $\bm{x}_{0}=\bm{x}(0)$ to $\bm{x}=\bm{x}(s)$ gives the surface pressure distribution,

$\displaystyle p_{\partial B}(\bm{x}(s))-p({\bm{x}_{0}})=\int_{0}^{s}\frac{2}{3}\mu\left[\frac{\partial\sqrt{\lVert\vartheta_{L}\rVert}}{\partial n}\right]_{\partial B}(s^{\prime})ds^{\prime},$

(29)

which is directly related to the wall-normal viscous diffusion of the square root of the Lamb dilatation along the skin friction line. Note that $\oint_{\partial B}\bm{n}ds=\bm{0}$ and the skin friction $\bm{\tau}=\mu\bm{\omega}_{\partial B}\times\bm{n}$, using Eq. (29) to eliminate the surface pressure, the total aerodynamic force can be evaluated as

	$\displaystyle\bm{F}$	$\displaystyle=$	$\displaystyle\oint_{\partial B}(-p_{\partial B}\bm{n}+\bm{\tau})ds$		(30)
		$\displaystyle=$	$\displaystyle-\frac{2}{3}\mu\oint_{\partial B}\left[\int_{0}^{s}\left[\frac{\partial\sqrt{\lVert\vartheta_{L}\rVert}}{\partial n}\right]_{\partial B}(s^{\prime})ds^{\prime}\right]\bm{n}(s)ds+\mu\oint_{\partial B}\bm{\omega}_{\partial B}(s)\times\bm{n}(s)ds.$

Physical interpretation of Eq. (30) is given as follows. On the one hand, it explicitly reveals the critical role of viscosity in generating the total force. Lift and drag must coexist as a result of the incompressible viscous flow over an airfoil. On the other hand, the lift force is mainly contributed by the first term due to the surface pressure integral while both the two terms can contribute to the drag force (including the pressure drag and skin friction drag). Therefore, balancing the positive and negative regions of the Lamb dilatation in the near-wall region gives the possibility to decrease the wall-normal variation of the near-wall Lamb dilatation and the magnitude of the wall-normal derivative of the square root of the Lamb dilatation, thereby reducing the pressure drag while the lift is sustained. Compared to the pressure drag reduction theory proposed by Hamman et al. [24], the present analysis provides a more natural and essential way to elucidate the physical mechanisms of pressure drag reduction and lift enhancement. It is noted that Liu et al. [64] gave a force formula similar to Eq. (30) based on the BEF. Therefore, both the BEF and BLDF are useful physical concepts in interpreting the origin of the aerodynamic force.

In this subsection, we simulate a 2D steady lid-driven square cavity flow at the Reynolds number $Re\equiv UL/\nu=1000$, where $U$ is the lid speed, $L$ is the cavity height and $\nu$ is the kinematic viscosity. $256\times 256$ uniform meshes are used in the simulation. The Mach number $Ma\equiv U/\sqrt{RT}$ is equal to $0.173$ such that the Knudsen number $Kn\equiv\sqrt{RT}\tau/L=Ma/Re$ is $0.000173$, where $\tau$ is the dimensional relaxation time. This sufficiently low Knudsen number implies that the flow is entirely at the continuum regime which can be described by the NS equations accurately. The variations of the velocity and pressure along the horizontal and vertical centerlines have been extensively used as the canonical benchmarks for numerical tests. However, to the authors’ knowledge, both the BLDF and the temporal-spatial evolution rate of the WNLDF at the bottom wall are not studied yet.

Fig. 1 shows the streamlines near the bottom wall. Due to interaction between the near-wall viscous flow and the bottom wall, distinct topological features can be observed at the bottom wall. The separation point $A$ and the attachment point $D$ correspond the two zero skin friction points, while $B$ and $C$ denote the local pressure minimum and maximum points, respectively. Eq. (22) implies that $\left[\sqrt{\lVert\vartheta_{L}^{*}\rVert}\right]_{\partial B}=\lVert\bm{\tau}^{*}\rVert=\lVert\bm{\omega}_{\partial B}^{*}\rVert$. Therefore, the zero points of the boundary Lamb dilatation are consistent with the zero points of skin friction field (or surface vorticity field), as shown in Fig. 2(a). Three local maximum points of the skin friction magnitude can also be observed in $OA$, $BC$ and $DE$, respectively.

In Fig. 2(b), the two zero skin friction points ($A$ and $D$) and the two pressure extreme points ($B$ and $C$) are just the four zero-crossing points of the BLDF. From Eq. (27), skin friction $\tau_{x}$ and surface pressure gradient $\partial p_{\partial B}/\partial x$ are coupled through the BLDF $f_{\vartheta_{L}}$, namely, $\tau_{x}\cdot\partial p_{\partial B}/\partial x=-\mu f_{\vartheta_{L}}/3$. Therefore, $f_{\vartheta_{L}}=0$ implies that $\tau_{x}=0$ or $\partial p_{\partial B}/\partial x=0$. The solutions of $\tau_{x}=0$ correspond to the two zero skin friction points ($A$ and $D$), while those of $\partial p_{\partial B}/\partial x=0$ correspond to the two pressure extreme points ($B$ and $C$). Positive BLDF is found in the main contact region between the primary vortex and the wall ($BC$), as well as the regions below the two small corner vortices. In constrast, the signs of the BLDF become negative in the regions $AB$ and $CD$. Positive (negative) BLDF indicates that the enhancement (attenuation) of the straining motion and the attenuation (enhancement) of the vortical motion along the wall-normal direction in a small vicinity of the wall.

Next, the temporal-spatial evolution rate of the WNLDF at the wall is discussed based on Eqs. (31) and (32). These expressions can be greatly simplified since the skin friction line is parallel to the surface pressure gradient line at the one-dimensional bottom wall. Fig. 3 displays different contributions to the wall-normal diffusion of $Q_{2}$. Since the global maximum point of the skin friction magnitude (denoted as $F$ where $d\tau_{x}/dx=0$) lies inside the region $BC$, we have $d\tau_{x}/dx<0$ and $d\tau_{x}/dx>0$ in the regions $AF$ and $FD$, respectively. Note that the coupling between the skin friction and the boundary enstrophy gradient is $Q_{21}=4\bm{\tau}\bm{\cdot}\bm{\nabla}_{\partial B}\Omega_{\partial B}=4\mu^{-2}\tau_{x}^{2}(d\tau_{x}/dx)$ and the skin friction divergence-boundary enstrophy coupling term is $Q_{22}=-4(\bm{\nabla}_{\partial B}\bm{\cdot}\bm{\tau})\Omega_{\partial B}=-2\mu^{-2}\tau_{x}^{2}(d\tau_{x}/dx)$. Therefore, the magnitude of $Q_{21}$ is twice that of $Q_{22}$. The sum of $Q_{21}$ and $Q_{22}$ gives $Q_{2}=2\mu^{-2}\tau_{x}^{2}(d\tau_{x}/dx)$, which has the same magnitude compared to $Q_{22}$ (with different sign) and $Q_{1}$. The variation of $Q_{2}$ mainly concentrates in the region between the two zero skin friction points. $Q_{2}$ is basically less than zero inside $AF$ while is greater than zero inside $FD$.

Fig. 3 shows different contributions to $Q_{3}$. $Q_{31}=-2(\bm{\nabla}_{\partial B}\bm{\cdot}\bm{\tau})\Omega_{\partial B}$ makes the primary contribution to $Q_{3}$, which is determined by the coupling between the skin friction divergence $\bm{\nabla}_{\partial B}\bm{\cdot}\bm{\tau}$ and the boundary enstrophy $\Omega_{\partial B}$. $Q_{32}$ and $Q_{33}$ represent the non-linear coupling between the spatial derivatives of the skin friction and those of the surface pressure. They demonstrate relatively small contributions compared to that from $Q_{31}$. Their contributions are mainly concentrated near the pressure maximum point $C$ and the zero skin friction point $D$ due to the relatively strong sweep motion induced by the primary vortex. Similar comparison is shown for $Q_{4}$ in Fig. 3. It is clear that the main contributions come from $Q_{47}=4\bm{\tau}\bm{\cdot}\bm{\nabla}_{\partial B}\Omega_{\partial B}=4\mu^{-2}\tau_{x}^{2}(d\tau_{x}/dx)$ and $Q_{48}=-4(\bm{\nabla}_{\partial B}\bm{\cdot}\bm{\tau})\Omega_{\partial B}=-2\mu^{-2}\tau_{x}^{2}(d\tau_{x}/dx)$. The obvious but relatively small variation of $Q_{41}$ are also observed around the pressure maximum point. Contributions from all the other terms are less significant. Fig. 3 illustrates different contributions to the temporal-spatial evolution rate of the WNLDF at the wall (i.e., $Q$). The variations of all the source terms show similar tendency that enhances the magnitude of $Q$ within the region $AD$.

Based on the above observation and analysis, the temporal-spatial evolution rate of the WNLDF at the wall (i.e., $Q$) is found to be predominantly contributed by $Q^{\prime}\equiv 10\bm{\tau}\bm{\cdot}\bm{\nabla}_{\partial B}\Omega_{\partial B}-10(\bm{\nabla}_{\partial B}\bm{\cdot}\bm{\tau})\Omega_{\partial B}$ and is less significantly influenced by the coupling effects between the spatial derivatives of skin friction and surface pressure gradient (dominated by $Q_{33}$ and $Q_{41}$, $Q^{\prime\prime}\equiv Q_{33}+Q_{41}$ denotes their sum). Comparison of $Q^{\prime}$, $Q^{\prime}+Q^{\prime\prime}$ and $Q$ on the bottom wall is demonstrated in Fig. 4. It is clear that $Q^{\prime}$ approximates $Q$ very well and the discrepancy near the peak regions could be further reduced by adding the coupling terms in $Q^{\prime\prime}$.

A single-phase incompressible turbulent channel flow is simulated at the frictional Reynolds number $Re_{\tau}=u_{\tau}H/\nu=180$. $H$ is the half channel height between the two no-slip flat walls. The domain size is $L_{x}\times L_{y}\times L_{z}=1800\times 299\times 600$ lattices with $x$, $y$ and $z$ being streamwise, wall-normal and spanwise directions, respectively. $u_{\tau}=\sqrt{\langle\tau_{x}\rangle/\rho_{0}}$ is the friction velocity and $y_{\tau}=\nu/u_{\tau}$ is the wall viscous length unit in the viscous sublayer, where $\langle\bm{\cdot}\rangle$ denotes the ensemble average. After the turbulence evolves into a statistically steady state, the pertubation force is switched off and the flow is only driven by a constant driving force $g$ in the streamwise direction, which is equivalent to a mean pressure gradient $\partial\langle p\rangle/\partial{x}=-\rho_{0}g$. Three hundred grid points are applied in the wall-normal direction with the first and the last points at the channel walls. In the following figures, a physical quantity with a superscript $+$ means the normalization by $u_{\tau}$ and $y_{\tau}$.

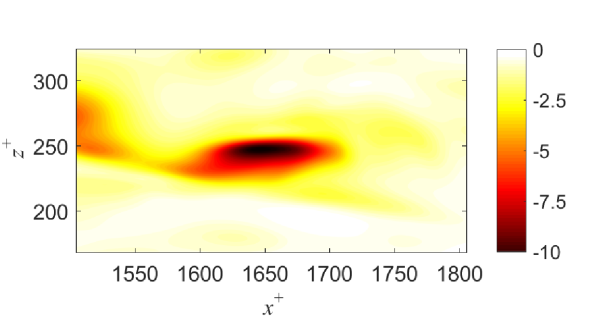
Previous studies show that strong wall-normal velocity events (SWNVEs) are responsible for high intermittency of the viscous sublayer, which are closely related to quasi-streamwise vortices and associated near-wall self-sustaining momentum transport processes [35, 44, 45]. The SWNVEs induce strong near-wall sweep and ejection events, which are usually accompanied by high skin friction magnitude and violent surface pressure fluctuation. In Fig. 5, the footprint of the quasi-streamwise vortice is identified by the skin friction divergence $\bm{\nabla}_{\partial B}\bm{\cdot}\bm{\tau}$, which is a critical surface quantity to characterize the topological features of the skin friction field [76, 62, 63]. According to the near-wall Taylor series expansion solution of the NS equations, the wall-normal velocity component is $u_{y}=-(2\mu)^{-1}(\bm{\nabla}_{\partial B}\bm{\cdot}\bm{\tau})y^{2}+O(y^{3})$. Therefore, positive skin friction divergence $(\bm{\nabla}_{\partial B}\bm{\cdot}\bm{\tau}>0)$ corresponds to the attachment lines due to sweep motions ($u_{y}<0$), while negative skin friction divergence $(\bm{\nabla}_{\partial B}\bm{\cdot}\bm{\tau}<0)$ corresponds to the separation lines due to ejection motions ($u_{y}>0$).

The Lamb dilatation captures the temporal-spatial evolution of local high- and low- momentum fluids, which is directly related to the turbulent mixing [24]. Relevant to the selected SWNVE, Fig. 6 shows the normalized snapshots of the Lamb dilatation $\vartheta_{L}$ at different wall-normal locations inside the viscous sublayer. On the wall, the boundary Lamb dilatation is determined by the boundary enstrophy, which is always non-positive and vorticity-dominated. Slightly away from the wall, the Lamb dilatation is determined by the competition between the flexion product $\bm{u}\cdot\bm{\nabla}\times\bm{\omega}$ and the enstrophy $-2\Omega$ such that both positive and negative Lamb dilatation centers can coexist. Positive flexion product are usually associated with the enhanced the straining motion and the depletion of the vortical motion. The flexion product increases rapidly with the increasing wall-normal distance and finally dominates the core pattern of the Lamb dilatation at the outer edge of the viscous sublayer. For example, in Fig. 6(d), positive and negative Lamb dilatation regions already coexist, among which the interaction and interference will drive the momentum and energy redistribution in the near-wall region. Normalized snapshots of the WNLDF $F_{\vartheta_{L}}$ are demonstrated in Fig. 7. High-magnitude positive and negative regions of $F_{\vartheta_{L}}$ are observed around the SWNVE. Particularly, the BLDF is plotted in Fig. 7(a), which is caused by the non-linear coupling between the skin friction and the surface pressure gradient. It is interesting to note that the pattern of $F_{\vartheta_{L}}$ rapidly changes even within the viscous sublayer, as the wall-normal distance increases. This distinct change should be directly related to sweep and ejection events induced by the quasi-streamwise vortice, and the concentrated wall-normal momentum transfer in this region.

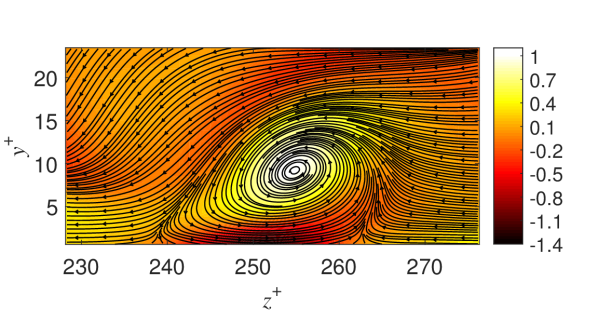
After briefly studying the basic features of near-wall Lamb dilatation and its wall-normal flux, by using Eqs. (31) and (32), the temporal-spatial evolution rate of the WNLDF at the bottom channel wall can be quantitatively evaluated with the information of surface quantities. In order to demonstrate the dominant mechanism to each source term, a line across the SWNVE along the spanwise direction (i.e., $x^{+}=1661.54$) is selected, as shown in Fig. 5. In Fig. 8, both $Q_{21}=4\bm{\tau}\bm{\cdot}\bm{\nabla}_{\partial B}\Omega_{\partial B}$ and $Q_{22}=-4(\bm{\nabla}_{\partial B}\bm{\cdot}\bm{\tau})\Omega_{\partial B}$ are of primary importance in determining the spatial distribution of $Q_{2}$. The positive peak region of $Q_{22}$ is partially counteracted and translated by $Q_{21}$. As shown in Fig. 8, $Q_{3}$ is mainly contributed by $Q_{31}=-2(\bm{\nabla}_{\partial B}\bm{\cdot}\bm{\tau})\Omega_{\partial B}$, namely, the coupling between the skin friction divergence and the boundary enstrophy. Other terms associated with the coupling between the temporal-spatial derivatives of the skin friction and the surface pressure only have negligible contributions to $Q_{3}$. As displayed in Fig. 8, $Q_{4}$ is mainly contributed by $Q_{47}=4\bm{\tau}\bm{\cdot}\bm{\nabla}_{\partial B}\Omega_{\partial B}$ and $Q_{48}=-4(\bm{\nabla}_{\partial B}\bm{\cdot}\bm{\tau})\Omega_{\partial B}$. Interestingly, $Q_{46}=2\mu^{-1}\bm{\tau}\bm{\cdot}\mathcal{L}_{\partial B}(\bm{\nabla}_{\partial B}p_{\partial B})$ mainly shows positive contribution to $Q_{4}$ and the positive peak region of $Q_{4}$ is mainly caused by $Q_{46}$. In addition, the contribution from $Q_{42}=6\mu^{-1}(\partial\bm{\tau}/\partial t)\bm{\cdot}\bm{\nabla}_{\partial B}p_{\partial B}$ can not be totally neglected in both the sweep and ejection sides of the SWNVE. In Fig. 8, the superposition of different source terms ($Q_{1}$, $Q_{2}$, $Q_{3}$ and $Q_{4}$) gives the total temporal-spatial evolution rate $Q$, which shows a high-magnitude negative peak in the region occupied by the SWNVE.

The preliminary exploration for the SWNVE implies that the temporal-spatial evolution rate of the WNLDF at the wall is mainly contributed by $Q^{\prime}\equiv 10\bm{\tau}\bm{\cdot}\bm{\nabla}_{\partial B}\Omega_{\partial B}-10(\bm{\nabla}_{\partial B}\bm{\cdot}\bm{\tau})\Omega_{\partial B}$ and is influenced by the coupling terms including $6\mu^{-1}(\partial\bm{\tau}/\partial t)\bm{\cdot}\bm{\nabla}_{\partial B}p_{\partial B}$ and $2\mu^{-1}\bm{\tau}\bm{\cdot}\mathcal{L}_{\partial B}(\bm{\nabla}_{\partial B}p_{\partial B})$. The sum of the latter two terms are denoted as $Q^{\prime\prime}$ for convenience. Fig. 9 plots the distribution of the dominant term $Q^{\prime}$, the sum of the dominant and the coupling terms $Q^{\prime}+Q^{\prime\prime}$ and the DNS result for the total evolution rate $Q$ along $x^{+}=1661.54$. It is clearly observed that $Q^{\prime}+Q^{\prime\prime}$ provides a very good approximation for $Q$. The discrepancy between the blue and red lines is therefore caused by the contribution from $Q^{\prime\prime}$. Furthermore, the dominant terms found in this turbulence case is very similar to those in the lid-driven cavity flow (see Section VII.1). This similarity can be intuitively understood, because for the two cases considered here, both the flow separation and attachment in the near-wall region are induced by a near-wall vortex interacting with the solid wall, which can be further evidenced from the streamlines in the $y-z$ plane (see Fig. 9 for a separation bubble-like structure).