Lagrangian dynamics and regularity of the spin Euler equation

The 3D incompressible Euler equation is

with $\boldsymbol{\nabla}\cdot\boldsymbol{u}=0$, where $\boldsymbol{u}$ is the velocity and $p$ the pressure.

By applying the spherical Clebsch mapping (Kuznetsov & Mikhailov, 1980), (1) is transformed into a Lagrangian form

Here, the spin vector $\boldsymbol{s}\in\mathbb{S}^{2}$ (Chern et al., 2016; Chern, 2017) is linked with a two-component wave function $\boldsymbol{\psi}=[\psi_{1},\psi_{2}]^{\mathrm{T}}\in\mathbb{S}^{3}$ by the Hopf fibration (Hopf, 1931)

with $\psi_{1}=a+\mathrm{i}b$, $\psi_{2}=c+\mathrm{i}d$ and the imaginary unit $\mathrm{i}$. Then, the velocity and vorticity $\boldsymbol{\omega}\equiv\boldsymbol{\nabla}\times\boldsymbol{u}$ can be re-expressed by $\boldsymbol{u}=a\boldsymbol{\nabla}b-b\boldsymbol{\nabla}a+c\boldsymbol{\nabla}d-d\boldsymbol{\nabla}c$ and

respectively, where $\varepsilon_{ijk}$ is the Levi–Civita symbol. Note that even though an arbitrary $\boldsymbol{\omega}$ in (4) may have no globally smooth spin vector due to vorticity nulls (Graham & Henyey, 2000) and unclosed vortex lines, a useful approximation can be obtained using the regularizer (Chern et al., 2017) and the Poincaré recurrence theorem (Poincaré, 1890).

We consider the quaternion form of the two-component wave function $\boldsymbol{\psi}=a+\boldsymbol{i}b+\boldsymbol{j}c+\boldsymbol{k}d$, where $a$, $b$, $c$ and $d$ are real-valued functions and $\{\boldsymbol{i},\boldsymbol{j},\boldsymbol{k}\}$ are the basis vectors of the imaginary part of the quaternion. The velocity and spin vector are then given by $\boldsymbol{u}=(\boldsymbol{\nabla}\mskip 1.5mu\overline{\mskip-1.5mu{\boldsymbol{\psi}}\mskip-1.5mu}\mskip 1.5mu\boldsymbol{i\psi}-\mskip 1.5mu\overline{\mskip-1.5mu{\boldsymbol{\psi}}\mskip-1.5mu}\mskip 1.5mu\boldsymbol{i}\boldsymbol{\nabla}\boldsymbol{\psi})/2$ and $\boldsymbol{s}=\mskip 1.5mu\overline{\mskip-1.5mu{\boldsymbol{\psi}}\mskip-1.5mu}\mskip 1.5mu\boldsymbol{i\psi}$, respectively, where $\mskip 1.5mu\overline{\mskip-1.5mu{\boldsymbol{\psi}}\mskip-1.5mu}\mskip 1.5mu$ denotes the quaternion conjugate of $\boldsymbol{\psi}$. Then, we derive

where $\boldsymbol{m}\equiv\boldsymbol{\nabla}\mskip 1.5mu\overline{\mskip-1.5mu{\boldsymbol{\psi}}\mskip-1.5mu}\mskip 1.5mu\cdot\boldsymbol{i}\boldsymbol{\nabla}\boldsymbol{\psi}$ is a pure quaternion (i.e. a vector in $\mathbb{R}^{3}$) and can be expanded as $\boldsymbol{m}=\boldsymbol{i}m_{1}+\boldsymbol{j}m_{2}+\boldsymbol{k}m_{3}$ with

Thus, we rewrite $\boldsymbol{u}\cdot\boldsymbol{\nabla}\boldsymbol{s}=\boldsymbol{s}\times\boldsymbol{m}$ with an effective field $\boldsymbol{m}=(m_{1},m_{2},m_{3})$.

In general, $\boldsymbol{m}$ cannot be represented solely in terms of $\boldsymbol{s}$, because the Hopf mapping is irreversible. Nevertheless, using the generalised Biot–Savart (BS) law, we can compute $\boldsymbol{s}\times\boldsymbol{m}$ at any point in $\mathbb{R}^{3}$ from the distribution of $\boldsymbol{s}$ under various boundary conditions, as illustrated in figure 1.

Substituting (5) into (2), we obtain the spin Euler equation

It is equivalent to the original incompressible Euler equation (1). In contrast to (2), (7) characterises the evolution of $\boldsymbol{s}$ by its precession about $\boldsymbol{m}$ rather than the convection with $\boldsymbol{u}$. The spin Euler equation (7) can be more suitable to study fluid dynamics from a Lagrangian perspective than its original form (1), because the isosurfaces of $s_{i},~{}i=1,2,3$ are vortex surfaces consisting of vortex lines (Yang & Pullin, 2010, 2011; Yang et al., 2023). From the Helmholtz theorem, the surfaces are material surfaces for all $t\geq 0$ in Euler flows.

Therefore, solving the spin Euler equation (7) is similar to a vortex method (Yang et al., 2021; Nabizadeh et al., 2022; Xiong et al., 2022) for simulating ideal flows. Since the primary variable $\boldsymbol{s}$ of (7) is a unit vector, the simulation of the spin Euler equation could avoid issues of numerical blowup.

In particular, the spin Euler equation contains the inherent Lagrangian vortex dynamics via level sets of $s_{i}$ (i.e. vortex surfaces). This can facilitate the regularity analysis of the Euler equation, similar to the level set representation of $\boldsymbol{\omega}$ (Constantin, 2001a, b; Deng et al., 2005).

It is also interesting that the spin Euler equation (7) can be considered as the Landau–Lifshitz equation

without a damping term (Landau & Lifshitz, 1935), which is used to analyse magnetodynamic processes in magnetic materials, and is generally referred to as the Heisenberg model (Lakshmanan & Porsezian, 1990; Porsezian & Lakshmanan, 1991; Kamppeter et al., 2001). The Landau–Lifshitz equation plays an important role in elucidating magnetisation dynamics, analogous to the role of the NS equation in fluid dynamics.

The mean spin of electrons, i.e. the magnetisation (or spin vector) $\boldsymbol{s}$ at the macroscopic scale, determines the unit volume magnetic dipole moment in magnetic crystals. A continuous function $\boldsymbol{s}(\boldsymbol{x},t)$ describes the macroscopic magnetisation dynamics in the limit of vanishing lattice partition size, if the angle between the spin vectors of neighbouring lattice atoms in a crystal is sufficiently small (Heisenberg, 1928). This resembles the continuum assumption in fluid mechanics, but unlike isotropic fluids, most crystal structures are anisotropic.

In (8), $\boldsymbol{H}_{\mathrm{eff}}$ is the effective magnetic field, corresponding to (minus) the $L^{2}$-derivative of the magnetic energy of the material with respect to $\boldsymbol{s}$. This implies a deep connection between the ideal flow and magnetic material. The spin Euler equation has $\boldsymbol{H}_{\mathrm{eff}}=\boldsymbol{m}$, where the magnetic energy of a material is replaced by the total kinetic energy of a fluid. Therefore, the ideal flow might be physically interpreted as a specific magnetic material by (7). As sketched in figure 2, the magnetisation (or spin) $\boldsymbol{s}$ in (3) at each point in space precesses around the effective magnetic field $\boldsymbol{m}$ in (6).

The similarity and difference between the spin Euler equation (7) and the isotropic Heisenberg spin system widely used in modelling magnetic crystals are discussed in Appendix A.

Next, we discuss the regularity of the spin Euler equation. By taking the double inner-product of $\boldsymbol{\nabla}\boldsymbol{s}$ and the gradient of (7), and multiplying $p|\boldsymbol{\nabla}\boldsymbol{s}|^{2(p-1)}$, we obtain

where $p\geq 1$ is a constant, and the vector product of the second-order tensor $\boldsymbol{\nabla}\boldsymbol{m}$ and the vector $\boldsymbol{s}$ is defined as $\boldsymbol{\nabla}\boldsymbol{m}\times\boldsymbol{s}\equiv\varepsilon_{ljk}\p_{i}m_{j}s_{k}\boldsymbol{e}_{i}\boldsymbol{e}_{l}$ with the basis $\{\boldsymbol{e}_{1},\boldsymbol{e}_{2},\boldsymbol{e}_{3}\}$. Using the identity $\boldsymbol{s}\cdot\rmDelta\boldsymbol{s}=-|\boldsymbol{\nabla}\boldsymbol{s}|^{2}$ for the unit vector $\boldsymbol{s}$, we have

Integrating (9) over an unbounded domain $\mathcal{D}$ or a domain bounded by solid wall boundaries and using (10) yield

where the Neumann boundary condition $\p\boldsymbol{s}/\p n|_{\p\mathcal{D}}=\boldsymbol{0}$ is imposed on the solid wall boundary. Applying the Hölder inequality to (11) yields

Here, the $L^{p}$-norm of a function $f$ is defined as

We estimate the upper bound of $\|\boldsymbol{\omega}\|_{p}$ in terms of $\|\boldsymbol{\nabla}\boldsymbol{s}\|_{{2p}}$. From (4), using $|\boldsymbol{s}|=1$ and basic inequalities, we obtain

so that

Then, we estimate the upper bound of $\|\boldsymbol{m}\|_{1}$ in terms of $\|\boldsymbol{\nabla}\boldsymbol{s}\|_{{2}}$ and $\|\rmDelta\boldsymbol{s}\|_{\infty}$. Substituting (14) into (6), we have

so that

Integrating (17) over the domain $\mathcal{D}$ yields

By virtue of the Sobolev–Poincaré inequality (Moffatt & Tsinober, 1992),

holds, with a positive constant $C_{\omega}$ independent of $\boldsymbol{u}$. Combining (10), (15), (18) and (19), we derive

Finally, substituting (20) into (12) and applying the Hölder inequality, we have

where $\mu(\mathcal{D})$ is the finite measure of domain $\mathcal{D}$. Integrating (21) over time yields

for $p=1$, with a constant $C_{s}=\exp\left(\|\boldsymbol{\nabla}\boldsymbol{s}(\cdot,0)\|_{2}^{2}\right)$, and

for $p>1$.

As the Hölder inequality leads to

we have

where $C_{p}(t)=\sqrt{6}t^{1/(p+1)}+\sqrt{2}C_{\omega}$ is a finite coefficient when $t<\infty$. Using (15), (22) and (25), the $L^{1}$-norm of the vorticity can be estimated by

Moreover, using (15), (23) and (25), the $L^{p}$-norm ($p>1$) of the vorticity can be estimated by

From (26) and (27), we obtain a sufficient condition for bounded $\|\boldsymbol{\omega}\|_{p}$ as

Note that it is straightforward to deduce the special case of (28) with $p=2$ from (14) using the BKM theorem (Beale et al., 1984).

In summery, we obtain a non-blowup condition (28) of the spin Euler equation (which is equivalent to the original Euler equation), which guarantees a bounded $\|\boldsymbol{\omega}\|_{p}$. It implies that, if the solution loses regularity beyond a certain time, the Laplacian of the spin vector must grow unbounded. The transport equation and the estimation of the norm of $\rmDelta\boldsymbol{s}$ are further discussed in Appendix B.

The DNS of the spin Euler equation (7) is carried out to investigate Lagrangian dynamics of ideal flows listed in table 1, and to validate the non-blowup criterion (28). To illustrate the Lagrangian vortex dynamics, figure 4 shows the top view of the isosurface of $s_{1}=0.5$ (i.e. vortex surface) for the trefoil knot at $t^{*}=0$, 0.9 and 1.8. Note that isosurfaces of $s_{2}$ and $s_{3}$ can show similar structures (Tao et al., 2021), and the isosurfaces of $|\boldsymbol{\omega}|$ (not shown) fail to capture the complete vortex tube as visualised by $s_{1}$ (as discussed in Xiong & Yang, 2019; Shen et al., 2023) .

Near the three crossings of the initial vortex knot, adjacent parts of the vortex tube are nearly orthogonal. Driven by the self-induced velocity with the BS law, the vortex tube and vortex lines are stretched and twisted. The adjacent parts of the vortex knot approach each other, and they are progressively flattened and rolled up, instead of undergoing the vortex reconnection in viscous flows (Yao & Hussain, 2022). The regions with large vorticity magnitude $|\boldsymbol{\omega}|$ are rapidly stretched into spiral sheets with strong twist.

In figure 4, the evolving vortex surfaces and lines preserve their initial mapping to the red circle and cyan points on $\mathbb{S}^{2}$, respectively, due to the Lagrangian nature of the spin Euler equation. Namely, the vortex topology is preserved in ideal flows. In addition, figure 5 shows the top view of the isosurface of $s_{1}=0.5$ for the Hopf link at $t^{*}=0$, 0.88, and 2.19. The structural evolution is similar to that of the trefoil knot.

Figure 6 plots the contour of $|\boldsymbol{\omega}|$ on the $x$–$y$ plane at $z=2.55$ and on the $y$–$z$ plane at $x=3.24$ for the trefoil knot, along with the contour lines of $s_{1}$. These planes intersect the point with the largest $|\boldsymbol{\omega}|$, so their contours show the most intense swirling motion. In figure 6(b), ‘vorticity pancakes’ (Brachet et al., 1992) form in the regions of large $|\boldsymbol{\omega}|$ among highly stretched and curved vortex surfaces. These structures appear when the vortex surfaces approach each other and undergo strong deformation. The formation of the high-vorticity region within sheet-like structures was observed in the collapse of vortex pairs (e.g. Pumir & Siggia, 1990; Kerr, 1993) and TG and KP flows (Yang & Pullin, 2010). Furthermore, we observe the energy spectra with the $k^{-3}$ scaling (not shown) in the evolution of the trefoil knot and Hopf link, consistent with the result for the collision of two Lamb dipoles in Orlandi et al. (2012).

In the highly symmetric MTG flow, a finite-time singularity may not exhibit according to the theoretical analysis (Constantin et al., 1996). Figure 7 plots the evolution of the isosurfaces of $s_{1}=0.8$ (red) and $s_{1}=-0.8$ (blue) for the MTG flow. A pair of vortex blobs are compressed and flattened into pancakes. Since the vortex surface is compressed in a quasi-2D configuration, preserving the smoothness $\boldsymbol{\nabla}(\boldsymbol{\omega}/|\boldsymbol{\omega}|)$ of the vorticity direction (Constantin et al., 1996), the MTG flow does not exhibit a finite time singularity, even though the vorticity grows rapidly (Brachet et al., 1992).

The comparison of the two types of ideal flows implies that the Euler equation cannot form a singularity in a 2D process. Constantin et al. (1996) proved that if $\boldsymbol{u}$ remains uniformly bounded and $\boldsymbol{\omega}/|\boldsymbol{\omega}|$ stays $C^{1}$, then no singularity can occur. In other words, the vorticity must change its direction very rapidly to form a potential singularity. Note that if a singularity occurs at a vorticity null for all $t^{*}<t_{b}^{*}$ (e.g. Elgindi, 2021), the vorticity direction becomes discontinuous at the time of singularity. The MTG flow vortex lines near the vorticity nulls maintain a quasi-2D smooth shape, which contradicts the necessary blowup conditions. Hence, the MTG flow does not exhibit finite-time singularities. By contrast, the trefoil knot or Hopf link have large vortex-line curvature in figures 4(c) and 5(c) with a rapid change in the vorticity direction.

We apply (28) to the three ideal flows to test the non-blowup criterion based on the spin Euler equation, and compare our criterion to the BKM criterion (Beale et al., 1984) by examining growth rates of the maximum vorticity and Laplacian spin vector. Before $t^{*}=T_{\mathcal{R}}$, $\|\boldsymbol{\omega}\|_{\infty}$ increases by a factor of about 16 for the trefoil knot and the Hopf link in figure 8. Both $\|\boldsymbol{\omega}\|_{\infty}$ and $\|\rmDelta\boldsymbol{s}\|_{\infty}$ exhibit the nearly double-exponential growth for the trefoil knot and Hopf link. The double-exponential growth of $\|\boldsymbol{\omega}\|_{\infty}$ is consistent with the results in Hou & Li (2007) and Kerr (2013). As the number of grid points increases (up to $1536^{3}$), the growth rate of $\|\rmDelta\boldsymbol{s}\|_{\infty}$ appears to remain constant for the trefoil knot and Hopf link.

The present criterion has some advantages that $\ln\ln\|\rmDelta\boldsymbol{s}\|_{\infty}$ grows more slowly than $\ln\ln\|\boldsymbol{\omega}\|_{\infty}$ (4–6 times slower), and exhibits better convergence with the mesh resolution. Therefore, $\rmDelta\boldsymbol{s}$ can be resolved more easily than $\boldsymbol{\omega}$ with the same numerical accuracy. Moreover, the duration of the linear stage for $\ln\ln\|\rmDelta\boldsymbol{s}\|_{\infty}$ exceeds that for $\ln\ln\|\boldsymbol{\omega}\|_{\infty}$ by more than a factor of five.

The highly symmetric MTG flow shows no evidence of a finite time singularity. The profile of $\ln\ln\|\rmDelta\boldsymbol{s}\|_{\infty}$ in figure 8(f) clearly bends downward before $t^{*}=T_{\mathcal{R}}$ with $N^{3}=1024^{3}$. The growth rate of $\|\rmDelta\boldsymbol{s}\|_{\infty}$ is weaker than double exponential, whereas the growth of $\|\boldsymbol{\omega}\|_{\infty}$ remains double exponential in figure 8(c) when $t^{*}<T_{\mathcal{R}}$. Therefore, the criterion based on $\rmDelta\boldsymbol{s}$ can effectively identify the flows that are unlikely to develop a finite-time singularity.

As the double-exponential growth is bounded in a finite time $t$, we have

with constants $c_{1}$ and $c_{2}$. According to the non-blowup condition (28), the Euler equation can avoid singularity formation in finite time for the double-exponential growth of $\|\rmDelta\boldsymbol{s}\|_{\infty}$.

We highlight the major difference between (28) and the BKM criterion, and explain why $\|\rmDelta\boldsymbol{s}\|_{\infty}$ grows more slowly than $\|\boldsymbol{\omega}\|_{\infty}$. Figure 9 plots the trajectories of $\arg\max|\boldsymbol{\omega}|$ and $\arg\max|\rmDelta\boldsymbol{s}|$ colour-coded by $t^{*}$ and their projections on the $x$–$y$ plane for the trefoil knot and Hopf link. The trajectories of $\arg\max|\boldsymbol{\omega}|$ and $\arg\max|\rmDelta\boldsymbol{s}|$ starting from the same locations do not collapse, implying that the present criterion is distinct from the BKM criterion.

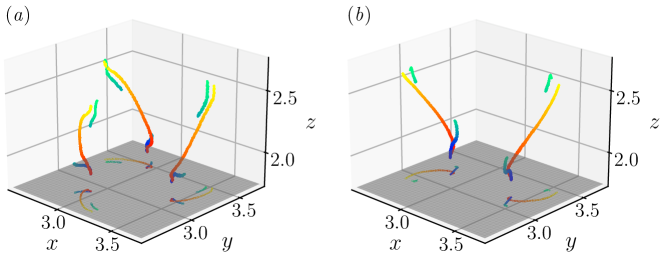
The continuous trajectory of $\arg\max|\rmDelta\boldsymbol{s}|$ is more tractable than the discontinuous one of $\arg\max|\boldsymbol{\omega}|$ in figure 9. Figure 10 illustrates the $z$-coordinates of the maximum $|\boldsymbol{\omega}|$ and $|\rmDelta\boldsymbol{s}|$, the Lagrangian trajectory of particles which locate at the position of the maximum values at $t^{*}=0$, and the evolution of the centroid positions $z_{c}=\int_{s_{1}\geq 0}z\operatorname{d\!}V\big{/}\int_{s_{1}\geq 0}\operatorname{d\!}V$ of the trefoil knot and Hopf link. We find that $\arg\max|\rmDelta\boldsymbol{s}|$ remains continuous over time and moves at a constant speed in the $z$-direction in both flows, which is close to the Lagrangian velocity of the particle at the location of $\arg\max|\rmDelta\boldsymbol{s}|$ (or $\arg\max|\boldsymbol{\omega}|$) at $t^{*}=0$. This implies that the maximum $|\rmDelta\boldsymbol{s}|$ could have some Lagrangian nature.

By contrast, $\arg\max|\boldsymbol{\omega}|$ exhibits a sharp jump at $t^{*}=1.26$ for the trefoil knot and $t^{*}=1.98$ for the Hopf link. The speed of $\arg\max|\boldsymbol{\omega}|$ in the $z$-direction is close to that of the centroid of the vortex at early times. During the surge of $|\boldsymbol{\omega}|$, it jumps to a value close to $\arg\max|\rmDelta\boldsymbol{s}|$ (marked in dashed box in figure 10).

We examine the correlation and distribution of the values of $|\rmDelta\boldsymbol{s}|$ and $|\boldsymbol{\omega}|$, normalised by their respective maxima, for the trefoil knot at $t^{*}=1.8$ and the Hopf link at $t^{*}=2.19$. The scatter plots in figure 11 shows a low positive correlation between $|\rmDelta\boldsymbol{s}|/\|\rmDelta\boldsymbol{s}\|_{\infty}$ and $|\boldsymbol{\omega}|/\|\boldsymbol{\omega}\|_{\infty}$, with correlation coefficients of $\rho=0.675$ for the trefoil knot and $\rho=0.627$ for the Hopf link. Therefore, the criterion based on $\rmDelta\boldsymbol{s}$ in (28) has a notable statistical difference from that based on $\boldsymbol{\omega}$.

The probability density function (PDF) of the normalised values of $|\rmDelta\boldsymbol{s}|$ and $|\boldsymbol{\omega}|$ for the trefoil knot at $t^{*}=1.8$ and the Hopf link at $t^{*}=2.19$ is shown in figure 12. For both configurations, the PDF profiles of $|\rmDelta\boldsymbol{s}|/\|\rmDelta\boldsymbol{s}\|_{\infty}$ are smoother than those of $|\boldsymbol{\omega}|/\|\boldsymbol{\omega}\|_{\infty}$, and they obey a Pareto distribution (Arnold, 2015) with the $-2$ power law except for very large values, indicating that the extreme values at a few locations can dominate norms of $\rmDelta\boldsymbol{s}$ and $\boldsymbol{\omega}$.