KREUTZ SUNGRAZERS: SUMMARY OF RECENT MODELING AND ORBITS OF THE SOHO OBJECTS
Abstract
I summarize and streamline the results of recent modeling of the orbital evolution and cascading fragmentation of the Kreutz sungrazers. The model starts with Aristotle’s comet — the progenitor whose nucleus is assumed to be a contact binary — splitting near aphelion into the two lobes and concludes with the SOHO dwarf objects as the end products of the fragmentation process. The Great March Comet of 1843, a member of Population I, and the Great September Comet of 1882, a member of Population II, are deemed the largest surviving masses of the lobes. I establish that the Kreutz system consists currently of nine populations, one of which — associated with comet Pereyra — is a side branch of Population I. The additions to the Kreutz system proposed as part of the new model are the daylight comets of AD 363, recorded by the Roman historian Ammianus Marcellinus, and the Chinese comets of September 1041 and September 1138, both listed in Ho’s catalogue. The comets of 363 are the first-generation fragments, the latter — together with the Great Comet of 1106 — the second-generation fragments. Attention is directed toward the populations’ histograms of perihelion distance of the SOHO sungrazers and the plots of this distance as a function of the longitude of the ascending node. Arrival of bright, naked-eye Kreutz sungrazers in the coming decades is predicted.
Subject headings:
comets general: Kreutz sungrazers; comets individual: 372 BC, X/363, X/1041, X/1106 C1, X/1138, C/1843 D1, C/1882 R1, C/1965 S1; methods: data analysis1. Introduction
Recent introduction of a new model for the orbital evolution of the Kreutz system of sungrazing comets (Sekanina 2021a; hereafter referred to as Paper 1) was necessitated by significant developments in the past 15 years, which made major parts of the previous models, including the two-superfragment model (Sekanina 2002; Sekanina & Chodas 2004), obsolete. Among the developments, the most important event was the arrival of the naked-eye sungrazer Lovejoy (C/2011 W3), whose orbit defied Marsden’s (1989) expanded classification of the Kreutz comets into three populations — or subgroups in his terminology — I, II, and IIa. Sekanina & Chodas (2012) referred to comet Lovejoy as a member of a new population — III, a designation adopted in Paper 1.
The new model is based on two stipulations, not employed in the earlier models. One is the progenitor in shape of a contact binary, consisting of two lobes of comparable dimensions connected with a neck. The progenitor’s splitting into the separate lobes (and, simultaneously or subsequently, the neck) is much more plausible than the breakup of a nearly spherical nucleus into two halves through its center, the scenario tolerated in the two-superfragment model (Sekanina & Chodas 2004); the contact binary also emerges as an apparently rather common figure among cometary nuclei and Kuiper Belt objects (e.g., Sierks et al. 2015; Stern et al. 2019).
My second stipulation was that most of the surviving mass of Lobe I was contained in the Great March Comet of 1843 or C/1843 D1, the intrinsically brightest known fragment of Population I, and most of the surviving mass of Lobe II in the Great September Comet of 1882 or C/1882 R1, intrinsically the brightest known fragment of Population II. The orbital distance that separated the two masses, gradually increasing with time, was in the 19th century equivalent to a time difference of merely 39.5 yr in perihelion time, a measure of the young age of the Kreutz system. This constraint effectively eliminated all scenarios that involved 5th century comets as members of the Kreutz system because they would have implied orbital periods much too short to fit the arrival times of the two 19th century’s spectacular sungrazers.
Another recent development was the detection in Paper 1 of as many as nine populations of sungrazers that are making up the Kreutz system. This major result was obtained by processing Marsden’s gravitational orbital elements of the SOHO Kreutz sungrazers (Section 2) and is understood in the context of cascading fragmentation: the initial breakup was followed by a number of events of secondary splitting. The account and results of the new model are below summarized and streamlined with the aim to benefit the reader.
The problem of systematic trends in the gravitational orbital elements of the SOHO sungrazers was explored in great detail on several particular objects by Sekanina & Kracht (2015). The most troublesome were the systematic positional deviations of the SOHO sungrazers’ lines of apsides from the fixed position of the line of apsides of the naked-eye Kreutz comets. The deviations, apparent in the plots of the inclination and perihelion latitude against the longitude of the ascending node, were shown to be effects of the normal component of the nongravitational acceleration, while a set of select data of higher accuracy in Paper 1 revealed the structure of the system of SOHO Kreutz sungrazers to be much more complex than earlier thought. A further, not yet fully examined test, a potential relationship between the longitude of the ascending node and the perihelion distance, is a subject of the present paper.

2. Nominal Orbital Elements of the SOHO
Dwarf Sungrazers
Marsden computed sets of approximate parabolic gravitational orbital elements for more than 1500 Kreutz sungrazers detected in the coronagraphic images of the SOHO space observatory between 1996 and 2010. The orbits are mostly in Marsden & Williams (2008), for the objects that arrived during 2008–2010 in a number of Minor Planet Circular issues. I refer to these sets of elements as nominal to distinguish them from the sets of true elements. The difference is significant, as the SOHO sungrazers were subjected to an appreciable sublimation-driven force ignored by Marsden. The magnitude of this acceleration, pointing — as already noted — essentially in the direction normal to the orbital plane, was in extreme cases nearly comparable to the Sun’s gravitational acceleration. The computation of the true orbit was time consuming, because the parameter of the normal component of the nongravitational acceleration has to be determined iteratively by forcing the standard position of the line of apsides, as illustrated by Sekanina & Kracht (2015) for several particular SOHO Kreutz sungrazers.
It was inconceivable to compute the true orbits for all 1500 SOHO comets. Instead, I chose to exploit the implications of the dependence of the nominal perihelion latitude, , on the nominal longitude of the ascending node, , presented for the 1500 SOHO Kreutz sungrazers in Figure 1. The reason for the great deal of noise that the figure exhibits is Marsden’s computation of the nominal orbits from astrometric positions derived from measurements of all images, taken with the C2 as well as C3 coronagraphs on board the SOHO spacecraft. Because the pixel size of the C3 coronagraph is about five times larger than the pixel size of the C2 coronagraph, an obvious way to improve the quality of the plot was to restrict the data set to the objects whose nominal orbits were computed exclusively from the C2 images. The 193 select SOHO sungrazers are listed in Table 1 and the plot of their latitude against nodal longitude is presented in Figure 2.
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/b396cca9-3dcf-4f82-b252-a0ab9b64b19b/x2.png)
It is well known that an overwhelming majority of the SOHO dwarf sungrazers belongs to Population I. This turns out as well to be the case for the subset of these objects with the orbits derived exclusively from the data based on the C2 coronagraphic images. Since the purpose of the exercise in Paper 1 was to obtain a data set of the highest possible quality, I included only those sungrazers of Population I whose orbits were derived from at least 12 astrometric observations. As I was unaware of Populations Pe and Pre-I at the time of this selection process, their sets were subjected to the same constraint. On the other hand, I did suspect the existence of Population Ia, and with the aim to increase the number of its members in the plot, I relaxed the constraint for this population from the minimum of 12 observations down to 10. The numbers of members in all the other populations in Table 1 were considerably lower and the minimum of observations for them was further relaxed to five; I deemed all orbits based on fewer than five observations too uncertain to include in the data set.
The plot of the 193 nominal values of as a function of in Figure 2, reproduced from Paper 1, shows that the data points line up along the straight lines
| (1) |
where is the constant true perihelion latitude, is the true longitude of the ascending node for the given population of sungrazers, and is the slope, which equals . Equation (1) serves to compute from the nominal values of and for SOHO sungrazers:
| (2) |
The values of the other true angular elements — the argument of perihelion, , and inclination, , follow from the values of , , and the true perihelion longitude, :
| (3) |
where for the Kreutz sungrazers , , , and . These and all other angular elements are in this paper referred to the J2000 equinox.
It was the plot presented here in Figure 2, on which the existence of the nine populations of the Kreutz system was first recognized in Paper 1. Added to the already known Populations I, II, IIa, and III were — in the order of the decreasing nodal longitude — Pre-I, Pe (apparently a branch of Population I associated with comet Pereyra, C/1963 R1, rather than with the Great March Comet of 1843), Ia, IIIa, and IV.
In order to improve clarity of Figure 2, the crowded areas around Population I are redrawn in greater detail in Figure 3. The sets of true orbital elements averaged over all members from Table 1 are listed for all nine populations in the columns dwarfs in Table 2, also reproduced from Paper 1. Where available, the orbit of the associated brightest known naked-eye Kreutz sungrazer is listed in the column main. For Population Ia the orbit shown in the column model refers to the progenitor, as derived in Paper 1.
The remarkable feature of Table 2 is a relatively uniform step in the true longitude of the ascending node between the neighboring populations. The average size of this step, near 10∘ (except for Population Pe), is significantly greater than the minor differences between the columns main (or model) and dwarfs. From the SOHO dwarf sungrazers of Table 1, supported by the naked-eye, Solwind (P78-1), and Solar Maximum Mission (SMM) objects, strong evidence has been assembled to support a new investigation of the process of cascading fragmentation of the Kreutz system’s progenitor.

3. Nuclear Splitting: Separation Velocities and Perturbed Orbits of
Fragments.
Populations and Clusters
Cometary nuclei fragment by a variety of forces. Sungrazers split at or near perihelion by the Sun’s tidal force. This mechanism was in the past so popular that until recently all sungrazers were thought to break up exclusively in the immediate proximity of the Sun, in spite of the fact that efforts to explain the orbital evolution of the Kreutz system in this fashion met with formidable difficulties and were never successful.

On the other hand, it is well known that comets fairly often split far from the Sun and planets, and there is no reason why the sungrazers should do otherwise. Some 20 years ago I proposed (Sekanina 2002) that a Kreutz comet can fragment at any point of its orbit about the Sun and that the fragmentation process has cascading nature. This is of key importance because it turns out that the new orbit, in which a fragment ends up after breaking off from its sungrazing parent, depends dramatically on the orbital location of the event. When the breakup occurs at or near perihelion, the fragment’s separation velocity — possibly of rotational origin and typically not exceeding a few meters per second — affects almost exclusively the period of the orbit, the difference compared to the parent’s orbit reaching as much as several hundred years; the aphelion distance does of course change accordingly. On the other hand, when the breakup takes place near aphelion (say, about 160 AU from the Sun), significantly affected are (i) the angular elements by the normal component of the separation velocity, shifting by 10∘ or more in the nodal longitude; and (ii) the perihelion distance by the transverse component, changing by a few tenths of the solar radius, so that the fragment’s perihelion point may get below the surface of the photosphere.
Conversely, it is impossible for a Kreutz fragment to end up in an orbit whose period differs from the orbit of its parent by more than a few months following an event occurring at or close to aphelion; and it is equally impossible for a fragment to end up in an orbit whose angular elements and perihelion distance differ from those of its parent by any nontrivial amounts in an event taking place at or close to perihelion.
Fragments generated by tidal disruption of a sungrazer are expected to end up in orbits with dramatically different periods even if they should acquire no differential momenta at breakup. This is so because, in general, the centers of mass of the fragments are at the time of their birth located at slightly different heliocentric distances (Figure 4) but have the same orbital velocity: the fragment farther from the Sun has to get into a greater orbit, with a longer period. If the heliocentric distance of the parent sungrazer at the time of fragmentation is (at or near perihelion) and the difference in the radial distances between a fragment and the parent is , the fragment’s orbital period, , is related to the parent’s orbital period, , by (Sekanina & Kracht 2022; hereafter referred to as Paper 2)
| (4) |
where the orbital periods are in years, while and are in AU. For example, a fragment separating at perihelion from a sungrazer whose perihelion distance is 1.5 and orbital period 750 yr ends up in an orbit whose orbital period is almost exactly 900 yr when the fragment’s center of mass at breakup is 5 km farther from the Sun than the parent’s center of mass. This effect is marginal or trivial for all comets other than sungrazers.
Another peculiar property of the Kreutz sungrazers is their anomalously low orbital velocity at aphelion, of about 20 m s-1, very unusual at less than 200 AU from the Sun. As a result, a separation velocity of a few meters per second could cause a fragment’s orbital velocity to differ by more than 10 percent from the parent’s, a sizable relative change that implies a major orbit transformation. And if fragmentation events should be distributed randomly in time, their occurrence at large heliocentric distance is strongly favored.
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/b396cca9-3dcf-4f82-b252-a0ab9b64b19b/x5.png)
From the preceding it follows that fragments given birth in breakups in close proximity of perihelion became members of the same population but different clusters, whereas products of fragmentation events in proximity of aphelion became members of the same clusters but different populations. The Great September Comet of 1882 and comet Ikeya-Seki (C/1965 S1) present an example of two members of the same population that arrived at perihelion 83 yr apart, while the sungrazers Pereyra (C/1963 R1), Ikeya-Seki, and White-Ortiz-Bolelli (C/1970 K1) offer an example of three members of the same cluster that arrived at perihelion within seven years of one another, but belonged to Populations Pe, II, and IIa, respectively.
The bottom line is that the spread among the SOHO Kreutz sungrazers in the longitude of the ascending node (a total of 66∘) and in the other true angular elements, apparent from Table 2, can under no circumstances be explained by recurring fragmentation at or near perihelion. On the other hand, it was shown in Paper 1 — and is briefly reviewed below — that the contact-binary model offers a self-consistent solution to the problem, fitting the observed data on the Kreutz system.
4. The Contact-Binary Model
The main features of the model are chronologically summarized in the following subsections, which describe issues related, respectively, to (i) the pre-split progenitor; (ii) the primary (initial) breakup into the two lobes (and the neck); (iii) secondary fragmentation of the lobes; (iv) the arrival of the first-generation fragments to perihelion; (v) the arrival of the second- and third-generation fragments to perihelion; (vi) tidal fragmentation and dispersal of fragments, including the SOHO dwarf sungrazers; and (vii) the big picture — issues behind the major overhaul of the old hypotheses and the model properties that withstood the challenges of new evidence.
4.1. The Progenitor
The ultimate parent — the progenitor — of the Kreutz system in the recently introduced model was Aristotle’s comet. The time of its appearance is usually given as (ca.) 372 BC (e.g., Seargent 2009), but by combining all pieces of information available and weeding out obvious errors, I believe that the perihelion time of the comet — if it indeed was a Kreutz sungrazer — should be known with accuracy better than 1 month.
It has to be remembered that the Greek year started with the month Hekatombaion on the day of the first full moon after the summer solstice,
usually early July in our calendar. After 683 BC it was customary to identify
the year by the name of the Athens’ annual chief magistrate, called eponymous archon.111See, e.g.,
https://www.hellenicaworld.com/Greece/History/
en/ArchonsOfAthens.html.
A parallely defined time scale was of course given by the Olympiad and its
year (from 1 to 4); for example, the year starting in July 373 BC and extending
through the end of June 372 BC was the 4th year of the 101st Olympiad, during
which Asteius was the archon at Athens. Next came the 1st year of the 102nd
Olympiad, with Alcisthenes as archon.
The principal source of data on Aristotle’s comet was his Meteorologica 1.6 (translated by E. W. Webster), where the object is mentioned twice, in consecutive paragraphs. In the first Aristotle says that “the great comet, which appeared at the time of the earthquake in Achaea and the tidal wave, rose due west.” In the next paragraph the text continues by repeating that “the great comet we mentioned before appeared to the west in winter in frosty weather …, in the archonship of Asteius.”

The last sentence offers a tight constraint on the time. A Kreutz sungrazer is seen (after sunset) in the west from Europe only when perihelion occurs in February or later.222Comet C/1887 B1 (perihelion on 11 January) was reported only from the southern hemisphere, C/1880 C1 (perihelion on 28 January) possibly also from China (Strom 2002); neither from Europe. On the other hand, frosty weather in Greece seldom extends into March (except in the mountains). For a Kreutz sungrazer, Aristotle’s account alone shows that it was at perihelion (and under observation) in February or (early) March. Asteius’ archonship means the year was 372 BC.
Before I address the time relationship of the Achaea earthquake, I compare Aristotle’s description with the story written by Diodorus Siculus about three centuries later. In his Bibliotheca Historica 15.50 (translated by C. H. Oldfather) Diodorus says that “[w]hen Alcisthenes was archon at Athens …and the Eleians celebrated the 102nd Olympiad …, a divine portent foretold the loss of [Lacedaemonians’] empire; for there was seen in the heavens during the course of many nights a great blazing torch which was named from its shape a ‘flaming beam,’ and a little later …the Spartans were defeated in a great battle and irretrievably lost their supremacy.”
The first part of this text is in glaring contradiction to Aristotle’s account, which obviously ought to be preferred. Yet, one should ask why the conflict? The answer appears to be furnished by the rest of Diodorus’ narrative. The reference is to the Battle of Leuctra, which was fought on 6 July 371 BC and which Spartans lost to Boeotians led by Thebans. Moving the sighting of the comet forward by one year, it was by that amount of time closer to the time of the battle, preceding it by 4–5 months rather than 16–17 months. That of course made the comet a much more relevant portent. How convenient! This sort of “adjustment” was unfortunately no exception among some ancient historians. In any case, Diodorus offered no good reason for correcting Aristotle!
Now on the issue of the time that Aristotle assigned to the Achaean cataclysmic earthquake that engulfed the city-states of Helike (submerged by a tsunami) and Boura (collapsed and caved in). The universally adopted time for the earthquake has been the winter of 373 BC (e.g., Katsonopoulou 2017), which depends in part on an equally universally adopted statement that the earthquake occurred two years before the Battle of Leuctra. Given that the battle was in the summer and the earthquake in the winter, the statement makes no sense. The two events must have been either 1 or 2 years apart. Since both Diodorus and Pausanias claimed that at the time of the earthquake Asteius was the archon at Athens, it was the winter of 373/372 BC; in the previous year the archon at Athens was Socratides. This allows one to state explicitly that the earthquake was apparently in December (or possibly late November) 373 BC rather than January or February 373 BC. If Aristotle’s statement that the comet appeared at the time of the earthquake was meant to suggest that the two events occurred in the same winter, under the same archon at Athens, then it was factually correct. With Diodorus’ time of the comet’s appearance discredited, the uncertainty of the perihelion time indeed is clearly less than 1 month, and the comet was with high probability observed during the months of Anthesterion and/or Elaphebolion of the 4th year of the 101st Olympiad.
The contact-binary model is insensitive to the perihelion time of Aristotle’s comet, for which a standard date of 371.0 was adopted in Paper 2. This implied an orbital period of 735 yr, while the perihelion distance amounted to approximately 1.46 , fairly close to the working model in Table 2, and the longitude of the ascending node came out to be about 345.4, almost 10∘ less than assumed for the working model. The line of apsides has been holding remarkably steady over the period of 24 centuries: in 372 BC the perihelion longitude was 282.38, the perihelion latitude +35.51.
4.2. The Primary (Initial) Breakup
This is of course the point of ultimate importance — the birth of the Kreutz system. At issue is the origin of the sizable gap between the orbits of Populations I and II, or, more specifically, between the orbits of the Great March Comet of 1843 and the Great September Comet of 1882 — nearly 20∘ in the nodal longitude, 0.5 in the perihelion distance, etc. Early on — shortly after 1882 — it was suspected that the orbital motions of the sungrazers could have been affected differently by drag in the solar corona (e.g., Elkin 1883), which was thought might explain the gap. Besides, both the 1843 and 1880 sungrazers were measured only after perihelion.
The orbital gap was recognized as a serious problem once Kreutz (1891) found that the preperihelion observations of the single nucleus and the post-perihelion observations of the nuclear fragments of the 1882 sungrazer could readily be linked, ruling out a perceptible effect of the solar corona. However, little was done until Marsden’s (1967, 1989) thorough investigation of the orbital gap in terms of a long-term influence of the indirect planetary perturbations. Though ingenious, this hypothesis required highly nonrandom perturbations acting over long periods of time, a scenario that is contrary to evidence, as shown below.

Unlike a gradual buildup of minor contributions, the scenario proposed to explain the orbital gap between the 1843 and 1882 sungrazers in the context of the contact-binary model in Paper 1 was by a brief event in which the progenitor split into the two lobes it consisted of, with the connecting neck possibly as a third fragment. To simplify the matter, a scenario of overall symmetry, with the spherical lobes of equal size and density, was adopted. The modeled event was assumed to have occurred at aphelion on 30 December 5 BC and at about 163 AU from the Sun, which implies the Kreutz system’s age of almost exactly two millennia. A schematic representation at the instant of the breakup is in Figure 5; in the view from the Sun the progenitor rotated counterclockwise along the axis directed toward the Sun. The rotation velocity measured at each lobe’s center of mass was the separation velocity, which, added vectorially with the progenitor’s orbital velocity, determined the lobe’s orbital velocity and upcoming orbit. The three angular elements were affected by the normal component of the separation velocity, the perihelion distance by the transverse component, which also had a marginal influence on the next perihelion time in the sense that the fragment subjected to a transverse separation velocity in the direction of the orbital velocity should arrive at perihelion days later.
In the initial breakup, Lobe I, the protofragment of Population I, separated from Lobe II, the protofragment of Population II, in line with the stipulations that the Great March Comet of 1843 was the largest surviving mass of Lobe I and the Great September Comet of 1882 the largest surviving mass of Lobe II.
The working model, updated in Sekanina (2022; hereafter referred to as Paper 3), shows the relevant separation velocity of Lobe I had a normal component of 1.80 m s-1 and a transverse component of 1.86 m s-1, the opposite for Lobe II. The respective corrections to the progenitor’s orbit for Lobes I and II were +7.3 and 5.7 in the argument of perihelion; +9.0 and 7.1 in the longitude of the ascending node; +1.0 and 1.4 in the inclination; 0.23 and +0.27 in the perihelion distance; and 1.31 day and +1.56 day in the time of the next perihelion passage (Section 4.4). Accordingly, the difference Lobe II minus Lobe I was predicted to have amounted to 13.0 compared to 13.2 in Table 2 in the argument of perihelion; and 16.1 compared to 16.0 in the longitude of the ascending node. The differences of 2.4 in the inclination and +0.50 in the perihelion distance have been fitted perfectly.

Similarly well was fitted the simulated orbital solution to the progenitor’s fragmentation, derived by numerically integrating the orbits of the 1843 and 1882 sungrazers in Paper 2. In this solution as well as in the woking model, the neck connecting the two lobes was assumed to have acquired no extra velocity at the breakup, continuing to move in the orbit of the progenitor before splitting. This motion is characterized in Table 2 by the orbital elements of Population Ia in the column model. Since there is no major, naked-eye sungrazer known to move in the orbit of Population Ia and since the deviations between the model and dwarfs sets of elements in Table 2 are fairly sizable, it is possible that the neck remained attached to one of the two lobes after the initial breakup (probably Lobe I) and separated from it later.
The radial component of the separation velocity was assumed to be zero in both the working model (Papers 1 and 3) and the simulated orbital solution (Paper 2). This component affects the next perihelion time much more significantly than the transverse component; for a fragmentation event at aphelion an increase in the radial velocity by 0.1 m s-1 would move the next perihelion time by 5.2 days.
The final point in this subsection concerns the dependence of fragments’ orbits on the distance of the fragmentation event from aphelion. The choice of aphelion was conditioned on the fact that the separation velocity needed is always a minimum. The rate of increase in the velocity needed to achieve the same effect 130 years before or after aphelion (150 AU from the Sun) is 10 percent in the argument of perihelion and the longitude of the ascending node, 5 percent in the inclination, and 8 percent in the perihelion distance. The rate varies at an accelerated rate, the numbers at 230 years before or after aphelion (120 AU from the Sun) being, respectively, 40 percent, 23 percent, and 32 percent. At a zero radial separation velocity, the change in the next perihelion time increases by about 2 days when the fragmentation event is moved from aphelion to 230 years before perihelion, but decreases by about 1 day when it is moved to 230 years after perihelion. In general, the fragmentation solutions are found to vary insignificantly over a time scale of a century or so from the aphelion time.
4.3. Secondary Fragmentation of the Lobes (and Neck)
The dwarf Kreutz sungrazers in Populations I, II, and possibly Ia, are explained as fragmentation end products of the major surviving masses of, respectively, Lobes I, II, and perhaps the neck. But what about the dwarf sungrazers in the other populations?
Given the cascading nature of the fragmentation process, the chance was that the separated lobes continued to split. And because of the nature of fragmentation far from the Sun, one can reasonably expect that the secondary events took place under essentially the same conditions as the primary breakup, except for decreasing dimensions of the objects.
The sequence of proposed fragmentation events is presented in a pedigree chart in Figure 6, copied from Paper 3. They are expected to have occurred — in the depicted order from the top down — in the aphelion region of the progenitor’s orbit. The exception was Fragment Pe, a precursor of comet Pereyra, which apparently separated from Lobe I later, at about 70 AU on the way to perihelion. In line with the proposed classification of the Kreutz system, it is contemplated that, repeatedly, a parent fragment split into two fragments, one of which containing most mass became a new parent fragment only to split again. The fragments in the heavy boxes in Figure 6 were on the way to their first perihelion and are in the following referred to as the first-generation fragments.
Figure 6 shows that fragmentation proceeded in the direction of decreasing true nodal longitude for both lobes. At the end of the Lobe II sequence, Precursor III split into Fragment III (whose existence is supported by comet Lovejoy C/2011 W3 and by Population III dwarf comets) and Precursor IIIa, which in the final documented fragmentation step split into Fragments IIIa and IV. The total separation velocities of the five fragments from IIa to IV were, respectively, 3.5 m s-1, 3.3 m s-1, 3.2 m s-1, 4.4 m s-1, and 4.6 m s-1 (Paper 3). Lobe I fragmented less profusely. Its main product was Fragment I, others were Fragment Pre-I, whose derived separation velocity was 1.5 m s-1 and, centuries later, Fragment Pe, separating with a velocity of 2.4 m s-1. Given that the separation velocities were essentially constant, the parent fragments were progressively spun up, as their dimensions were getting smaller.
4.4. First-Generation Fragments at Perihelion
in AD 363
One trait of Aristotle’s comet that made it an attractive candidate for the Kreutz progenitor was its timing: the period of time between its appearance and the appearance of the Great Comet of 1106 (X/1106 C1), a likely Kreutz sungrazer, was almost exactly twice the presumed orbital period of the Great March Comet of 1843, whose previous return to perihelion the 1106 comet was believed to portray. The weak point of this argument had been the absence of a related event halfway between 372 BC and AD 1106, most probably in the decade of AD 360–370. Already in the aftermath of the 1882 sungrazer’s appearance, this problem was noticed by Hall (1883), who proposed a link between Aristotle’s comet, a missing comet in AD 368, and the comets of 1106 and 1843. Similarly, the two superfragments were predicted by Sekanina & Chodas (2004) to pass perihelion one week apart in AD 356. The perihelion return of two or more sungrazers around this time has become an indispensable condition, following a postulated near-aphelion fragmentation event.
Because of its confused presentation in the literature, I had long dismissed a note written in the treatise Res Gestae by Ammianus Marcellinus, a prominent Roman historian of the 4th century AD, that in the year 363 “in broad daylight comets were seen” (Rolfe 1940) from Antioch on the Orontes, the capital of the Syrian Province of the Roman Empire. For example, Ramsey (2007) refers to this event as the “Jovian comet” and dates it August–September 363. Ho (1962), whose catalogue comprises only Far Eastern sources, says (under #173) that a po (tailless) comet was seen between August 26 and September 23 first in Virgo (near Vir and Vir) and then it entered Hercules, Aquila, etc., so it could under no circumstances have been a sungrazer; also, in August–September it was not a daytime comet. Only after reading about Ammianus’ account in the carefully researched book by Seargent (2009), in which he actually suggested that this may have been a case of Kreutz sungrazers, it became clear to me that the Chinese comet in Ho’s catalogue had nothing in common with the event commented on by Ammianus. And although the historian offered no dates, his narrative suggests that the observation was most probably made in the course of November 363. Most significantly, the text specifically says comets rather than a comet and the daylight sighting implies that the comets were extraordinarily luminous, probably around apparent magnitude 10 or brighter and located near the Sun both in the sky and in space. This must have been an unprecedented, spectacular celestial show that, as far as I know, was never to be witnessed again!
The brief comment by Ammianus provokes a number of questions. Why the sighting was not reported by anyone else? Why not by the Chinese? Can one be sure that the timing of the sighting of the comets as a portent was not manipulated in relation to historical events? What has been Ammianus’ professional reputation? How many comets were seen? And over what period of time?
Some of these questions can be answered more or less fully, some partially, and some not at all. First, the work of Ammianus has generally been praised (e.g., Matthews 2008); he almost certainly was the top Roman historian of his time, was knowledgeable in natural sciences, and his description of the earthquake and tsunami of AD 365 in Alexandria has been deemed factually accurate.
On the other hand, Ammianus was a protagonist of paganism and believed in omens and portents. Because of these tendencies, he greatly preferred emperor Julian to Jovian, even though he served under both. If Ammianus should have manipulated the date of sighting of the comets (as Diodorus had in the case of the comet of 372 BC), he would have moved the event to early 363 to present it as a portent of the forthcoming death, in June 363, of his beloved pagan emperor Julian, rather than the pro-Christian Jovian. He did not.
If the Chinese had observed the daytime event in AD 363, they would have recorded it as sun-comets to use Strom’s (2002) terminology. At first sight, the absence of a Chinese account is surprising. However, Strom, who examined the statistics of the sun-comets in the Chinese annals, discovered that the sightings were strongly concentrated in the summer months in spite of summer monsoon. Besides, there was only one sun-comet record before 1539. The lack of corroboration of Ammianus’ account from China may not be too unexpected after all.
It is unfortunate that Ammianus failed to provide more information on the daylight comets. One can only speculate about their number and the period of time involved. Based on the working model in Paper 3, which consisted of 10 sizable fragments whose perihelion times in AD 363 spanned 4.4 days, one can guess that up to 70 percent of the fragments could have been above the naked-eye detection threshold at the most favorable time, as illustrated in Figure 7.
Once the first-generation fragments reached perihelion in AD 363, the tidal fragmentation began to multiply the numbers and thereby to make the structure of the Kreutz system much more complex. To offer the potential evolutionary path for any individual sungrazer requires the knowledge of a rather accurate set of its orbital elements, including the period. Unfortunately, this information is available for only a few Kreutz comets.

4.5. Second- and Third-Generation Fragments
In the continuing story of the computer simulated evolution of the Kreutz system in Paper 2, Fragment I — the largest fragment of Lobe I — broke at the 363 perihelion into at least two subfragments. The largest piece, whose orbital motion was closely simulated, ended up in a slightly changed orbit with a period of 742.2 yr and returned to perihelion as the Great Comet of 1106. With very minor orbital changes at this perihelion it then completed another revolution about the Sun to return as the Great March Comet of 1843.
Similarly, Fragment II — the largest fragment of Lobe II — appears to have split tidally at perihelion in 363 into a number of subfragments. The largest subfragment entered a weakly modified orbit with a period of 774.7 yr and returned to perihelion as a Chinese comet of 1138, #403 in Ho’s (1962) catalogue. As modeled in Paper 2, the comet suffered at least two breakups in 1138, the last one — presumably hours after perihelion — producing the famous pair of the Great September Comet of 1882 and Ikeya-Seki of 1965. A comprehensive orbital reanalysis of component A of Ikeya-Seki in Paper 2 was instrumental in establishing beyond doubt that this comet previously appeared in the late 1130s, decades after the arrival of the Great Comet of 1106. This result is in excellent agreement with Marsden’s (1967) computation of the previous appearance of the brightest nucleus of the 1882 sungrazer and in line with his conclusion that the two comets separated from a shared parent at perihelion in the 12th century.
Having split off from Precursor I on the way to the 363 perihelion (Figure 6), Fragment Pe was presumed to have likewise undergone an event of tidal fragmentation in AD 363, one of its subfragments having returned to perihelion in early August 1041. According to Hasegawa & Nakano (2001), this comet — a suspected Kreutz sungrazer — was observed in China and Korea from the beginning of September 1041 on, its celestial path resembling that of the Chinese comet of 1138. Comet Pereyra of 1963 was proposed in Paper 1 as one of the fragments of the 1041 comet.
The second-generation fragments — the comets of 1041, 1106, and 1138 — and the third-generation fragments — the bright 1843 and 1882 sungrazers, Pereyra, and Ikeya-Seki — complete the set of members of the Kreutz system, whose orbital evolution was successfully simulated in Paper 2 starting with the progenitor two millennia ago. Although the orbital period is also known with high accuracy for comet Lovejoy, C/2011 W3 (Sekanina & Chodas 2012), a sungrazer associated with Population III, it was not possible to link this object with any obvious candidate of the Kreutz system in the past. For other naked-eye sungrazers of the 19th and 20th centuries, the orbital period was not determined: White-Ortiz-Bolelli of 1970 (associated with Population IIa), the Great Southern Comet of 1880 (C/1880 C1), the Great Southern Comet of 1887 (C/1887 B1), and of course the eclipse comet of 1882 (X/1882 K1) — all associated with Population I or Pe. Populations Pre-I, Ia, IIIa, and IV are related to no known naked-eye Kreutz sungrazer.
The sets of orbital elements for the progenitor, the lobes, and the fragments of the three generations, as derived in Paper 2, are summarized here in Table 3. Listed for the progenitor are both the heliocentric elements at perihelion in 372 BC and the barycentric elements at the time of the aphelion breakup in 5 BC.
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/b396cca9-3dcf-4f82-b252-a0ab9b64b19b/x10.png)
4.6. Tidal Fragmentation and Random Dispersal
of Fragments
The events of tidal fragmentation at perihelion are extremely powerful in their ability to randomly disperse the fragments in time and space. I present a few examples to illustrate the magnitude of these effects on the orbital period, governed by a shift of the center of mass along the radius vector, , expressed by Equation (4) in Section 3.
The first case is the evolution of the well-behaving Great March Comet of 1843 and its Population I precursors. Fragment I did apparently break up into a number of subfragments at the 363 perihelion, the most sizable of which became the Great Comet of 1106, whose center of mass shifted merely by km. This indicates that should Fragment I have not split, it would have reached perihelion in AD 1139. This negative shift of the 1106 comet must have been balanced by positive shifts of greater magnitudes for smaller naked-eye fragments due to arrive at perihelion at least a century later. The comet of 1232, a Kreutz candidate according to Hasegawa & Nakano (2001), is a case in point.
Much more complicated was the evolution of the Great September Comet of 1882 and its precursors. Fragment II must have broken into a larger number of subfragments than Fragment I. The center-of-mass shift of the Chinese comet of 1138, the putative parent to the 1882 sungrazer and Ikeya-Seki, was formally computed to equal 5.25 km, which implies that should Fragment II have not split in AD 363, it would have passed perihelion in AD 1237. However, the computed shift value is affected by the separation of Ikeya-Seki and the 1882 comet; the correct value should be closer to zero and compensated by larger positive shifts of smaller naked-eye sungrazers in the 14th and possibly even the 15th centuries; one of Hasegawa & Nakano’s (2001) Kreutz suspects, the comet of 1381, is the example of a plausible candidate. And, significantly, some of the Population II objects should be due for another return to perihelion by the mid-21st century.
The center of mass of a fragment of the comet of 1041 needed km to fit the motion of comet Pereyra, as otherwise it would have returned to perihelion in AD 1744. One or more bright siblings of comet Pereyra, perhaps of comparable size and prominence, may have arrived in the 17th century, such as, say, C/1668 E1 and/or C/1695 U1.
The ultimate case of this kind of orbit dispersal has been documented by the statistics of the dwarf sungrazers’ motions, especially those imaged by the SOHO coronagraphs. Since the overwhelming majority of the SOHO dwarf Kreutz comets belongs to Population I, I focus in the following on this particular set.
Because the SOHO dwarf sungrazers are known to never survive perihelion, their age cannot exceed one revolution about the Sun and the time of their birth could not predate the perihelion time of the Population I parent, the Great Comet of 1106. I assume that these 10-meter-or-so sized fragments were released at perihelion (in AU) from all over the comet’s nucleus of diameter with zero velocity, undergoing the same dispersion process as the major fragments. At a bulk density of 0.5 g cm-3 the mass of a fragment is about grams. I further assume that the rate of release, measured by the number of dwarf sungrazers returning to perihelion per year, varies as the surface area of the parent nucleus. For a perihelion breakup, Equation (4) shows that an infinitesimal increase of in a fragment’s orbital period (in yr) is invoked by a differential center-of-mass shift (in AU) along the radius vector of
| (5) |
For yr, Equation (5) offers a range of radial shifts of all fragments with the period near that arrive at perihelion per year. These fragments come from a ring area of the surface whose center-of-mass shift along the radius vector from the nuclear center of the parent comet, , is related to the comet’s orbital period, , by
| (6) |
The size of an infinitesimal surface area is
| (7) |
where is the angle, measured from the nuclear center, that the line connecting it with any point of the ring made with the plane normal to the radius vector and . Equation (7) now becomes
| (8) |
Now about the recent influx of the SOHO sungrazers: Let the annual rate of their arrivals at a reference time be , coming from an area , and let their orbital period be . Let the number of SOHO-like sungrazers released from the whole surface of the comet’s nucleus in 1106 be . Since the number is assumed to be proportional to the surface area, I have at the reference time with help of Equation (8)
| (9) |
where is a constant of proportionality. The total population has to equal
| (10) |
and, eliminating ,
| (11) |
Here and are in AU, in yr. If the nucleus of the 1106 comet was, say, 50 km across, the shift relative to the center of mass varied from 25 km to +25 km. The comet’s orbital period equaled 737 yr (= 1843–1106) and the perihelion distance amounted to 0.005342 AU (Table 3). The shortest orbital period of the fragments, corresponding to a shift of 25 km was 270 yr, the longest, corresponding to +25 km, 79,000 yr. The stream of the SOHO sungrazers is thus predicted to have begun in the late 14th century and will go on for another nearly 80 thousand years. The last objects of the stream will reach nearly 3700 AU from the Sun at aphelion.
Let us take the year 2010 as the reference time. The rate of arriving sungrazers and sunskirters in the decade around that year equaled about 200 yr-1, the Kreutz comets made about 85 percent of the total, and Population I alone contributed, judging from Table 1, a little more than 50 percent of all Kreutz members. I take the rate of Population I members to equal yr-1. Their orbital period averaged 2010–1106 = 904 yr, so that the ratio and the total number of the Kreutz SOHO sungrazers in Population I comes out to be approximately 300,000. Their total mass is less than 1014 grams over the nearly 80 thousand years, the mass of a subkilometer-sized cometary nucleus, a trivial fraction of the expected mass of the 1106 comet.
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/b396cca9-3dcf-4f82-b252-a0ab9b64b19b/x11.png)
4.7. The Big Picture: Issues Behind the Major Overhaul and Features Shared
In Section 1 I already commented on some of the important developments in the past 15 years that made the introduction of a new model imperative. However, the contact-binary model is not merely an update of the two-superfragment model (Sekanina & Chodas 2004), it works on a conceptually higher level. While the two-superfragment model was by and large ad hoc in its approach, the contact-binary model has features of a pyramidal construct. The 2004 model focused on the relationships among eight bright, naked-eye sungrazers only, optimizing the locations of fragmentation events in order that the separation velocities stay as low as possible. This effort was not entirely successful, because the values near 6–7 m s-1 were common and the initial breakup of the progenitor into the two superfragments required that they detached at 8 m s-1. The model also used the incorrect premise that the Great Comet of 1106 was a member of Population II, whose fragments included both comet Pereyra and White-Ortiz-Bolelli, thus eliminating Populations Pe and IIa. Aristotle’s comet did not fit the progenitor and no serious effort was made to incorporate the SOHO sungrazers; they were added only in part 2 of the investigation (Sekanina & Chodas 2007).
On the other hand, the contact-binary model skillfully integrates the data on the naked-eye and SOHO dwarf members of the Kreutz system. The greatly expanded number of populations, whose existence is established by evidence from the SOHO sungrazers, is shown to be the result of a stochastic process of cascading fragmentation rather than ad hoc breakup events and the separation velocities are kept below 5 m s-1. The progenitor is equated with Aristotle’s comet and the SOHO sungrazers are logically presented as the end products of the same process. The orbital correlations between the naked-eye and coronagraphic sungrazers are documented in the five cases when the former is known. The model also profits from the refined orbit determination of the 1843 sungrazer (Sekanina & Chodas 2008), in which the planetary perturbations and relativistic effect were included, unlike in Kreutz’s (1901) set of elements.
A remarkable feature of the contact-binary model is an outward appearance of
some of its features as chance events that at first sight would not pass the
skeptic’s approval. Because of it, the model may look somewhat vulnerable,
but it is not. A good example is the case of the daylight comets in AD 363.
The actual amount of information provided by Ammianus Marcellinus may look
rather flimsy, yet it was enough to Seargent (2009) to immediately evoke the
Kreutz sungrazers based solely on the circumstances of observation. Yet, much
more was involved, as this virtually unique event was highly significant
diagnostically for three reasons:
(i) it was in line with the prediction by a generic model of nontidal
fragmentation that, following the disruption of the progenitor sungrazer
(Aristotle’s comet) at large heliocentric distance, its remains should at the
subsequent perihelion appear as a swarm of nearly- simultaneously
arriving fragments;
(ii) its timing was amazing — almost exactly midway between the appearances
of Aristotle’s comet and the Great Comet of 1106; and
(iii) it implied an orbital period of about 740 years, consistent with
the period of the Great March Comet of 1843, which itself fits the
pattern!
Then there was the issue of the missing second predecessor (a “sibling” of the Great Comet of 1106) to the two 19th century major Kreutz sungrazers, which was still missing when I was writing Paper 1! It was on a hunch that a novel method was developed in Paper 2, which, against all odds, was successful in establishing the time of the previous perihelion appearance of comet Ikeya-Seki (i.e., its parent comet) with a high degree of confidence. It came as a surprise that Ikeya-Seki could under no circumstances derive from the 1106 comet. Rather, the computed date in late 1139 agreed, with the uncertainty of 2 years, with April 1138, the time of the previous appearance of the brightest nucleus of the Great September Comet of 1882, Ikeya-Seki’s more massive twin, which happened to be determined — and promptly dismissed as inaccurate — by Marsden (1967).
As if not enough, this surprise was followed by the detection of a plausible candidate in Ho’s (1962) catalogue, whose estimated perihelion time occurred at most five months after the date derived by Marsden. And — to crown the achievement — the sets of orbital elements of the 1882 comet and Ikeya-Seki integrated back to 1138 agreed much better with one another than when integrated back to 1115 by Marsden, as seen in Table 4 reproduced from Paper 2.
Could all coincidences in the preceding paragraphs be fortuitous? Not in my opinion.
Other points of contention exist between the alternative version of the two-superfragment model (Sekanina & Chodas 2007) and the contact-binary model. One is the relationship of sungrazers in a cluster. In the 2007 paper we considered that “the sungrazers in one cluster are more closely related to one another than to the sungrazers in the other cluster,” a problem resolved by the contact-binary model (Section 3). To accommodate the 17th century and earlier clusters, the range of searched arrival times of the first-generation fragments was broadened in the 2007 paper and the comets of February 423 and February 467 were regarded as possible Kreutz sungrazers, referring to Hasegawa & Nakano (2001) and to England (2002) as the sources to argue the choice.
It is ironic that in the context of the contact-binary model the two 5th century comets are no longer Kreutz suspects at a time when the second object, in AD 467, was suggested to be an attractive candidate, according to Martínez et al. (2022). Fortunately, the scope of tidal-fragmentation scenarios is wide enough that a sungrazer can move in a Kreutz-like orbit without being a Kreutz sungrazer. This is particularly true for a fragment that separated from the progenitor near perihelion before the Kreutz system’s birth. The comet of 467 could have separated from Aristotle’s comet at perihelion in 372 BC, in which case the orbital elements of the two objects would have been essentially identical, with the exception of their periods: 735 yr for Aristotle’s comet, 838 yr for the comet of 467.
Having described the issues that were behind the major model overhaul necessitating the introduction of the contact binary, I now list four features shared by both the two-superfragment model and the new model. The first feature is apparent from the models’ names, which imply that fragmentation began with an event involving two objects: the two superfragments in the former hypothesis versus the two lobes of the contact binary in the latter. The second shared feature is the stipulation that the events responsible for the birth of the fragments took place at very large heliocentric distance, which implies that the fragments were to pass the subsequent perihelion nearly simultaneously, in a swarm — the point already referred to above. The third shared feature is the process of cascading fragmentation, employed in the 2007 investigation. And the last feature, in line with the third, is the young age of the Kreutz system, close to two millennia, the difference between the two models amounting to less than 20 percent. Both models predict that more brilliant, naked-eye sungrazers should arrive at perihelion in the coming decades.
5. Perihelion Distances of the SOHO
Dwarf Sungrazers
In the context of the contact-binary model, the orbital work on the dwarf sungrazers detected in the SOHO coronagraphic images focused in Paper 1 almost exclusively on the longitude of the ascending node, especially the relationship between the nominal values derived by Marsden and the population-diagnostic true values. Very little attention was directed toward the distribution of perihelion distances among the 193 objects of Table 1. This shortcoming is being rectified in this section.
The problem with the perihelion distances of the dwarf Kreutz comets is — unlike with the nodal longitudes — the absence of an obvious algorithm for converting Marsden’s nominal values to true values, accounting for the major nongravitational effects. The several dwarf sungrazers investigated in detail by Sekanina & Kracht (2015) showed that, as a rule, the true perihelion distances of these objects were closer to the solar radius than their nominal values. A safe conclusion could be made about those among the comets that were subjected to relatively minor nongravitational effects and whose nominal nodal longitudes were close to the true nodal longitudes. As expected, their true and nominal perihelion distances differed very little. In any case, plots of the perihelion distance as a function of the nodal longitude should provide a fitting line of attack.

This method of inquiry was used in the only attempt in Paper 1 to find out whether an investigation of perihelion distances could contribute meaningfully to the study of the Kreutz system’s structure. The attempt concerned the 24 members of Population IIa listed in Table 1 and the conclusion, seen from Figure 8 adapted from Paper 1, was the clear discrimination of the perihelion-distance distribution into two distinct subpopulations. The upper part is a plot of the nominal perihelion distance as a function of the nominal nodal longitude, while the lower part is a histogram of the nominal perihelion distances. The main set of 18 objects had perihelia between 1.4 and 2.0 and on the plot of the nominal nodal longitude against the nominal perihelion distance this subpopulation covers a continuous area that includes comet White-Ortiz-Bolelli. A subpopulation IIa, which was introduced in Paper 1 to offer an alternative birth scenario for comet Lovejoy, blends as part of this main set. The remaining six sungrazers, referred to in Paper 1 as Population IIa, have perihelia between 1 and 1.2 , which are in Figure 2 distinguished from the rest of Population IIa by special symbols. The difference between the perihelion distances of the subpopulation IIa⋆ and comet White-Ortiz-Bolelli, 0.7 or more, implies a transverse component of the separation velocity in excess of 5 m s-1. The meaning of this result is unclear, potentially indicating that the fragmentation process was even more complex.

It should be pointed out that a general pattern on the plots for the Kreutz dwarf sungrazers, of the type displayed in Figure 8, is affected by the planetary perturbations and subjected to two categories of major effects: (i) the process of cascading fragmentation, resulting in ever smaller dimensions of the SOHO objects; and (ii) the outgassing-driven nongravitational acceleration, causing the problems with the line of apsides. Either effect is capable on its own to lead to the ultimate disintegration of the objects shortly before perihelion.
The fragmentation events, proceeding throughout the orbit, influence the orbital elements because of the accumulating separation-velocity effects: in the nodal longitude because of the normal component, in the perihelion distance owing to the transverse component. The result in the plot of is a trend in Figure 8 along a tilted line with an average slope of , which is apparent among the data points at . On the other hand, the nongravitational effect in the out-of-plane direction (see Table 4 of Sekanina & Kracht 2015), affects the angular elements, the nodal line in particular. The trend in the plot should be along a line with , which is apparent in the figure among the data points at . The gap in the perihelion distance between 1.2 and 1.4 could be the product of a major fragmentation event that has not been accounted for by the present model.
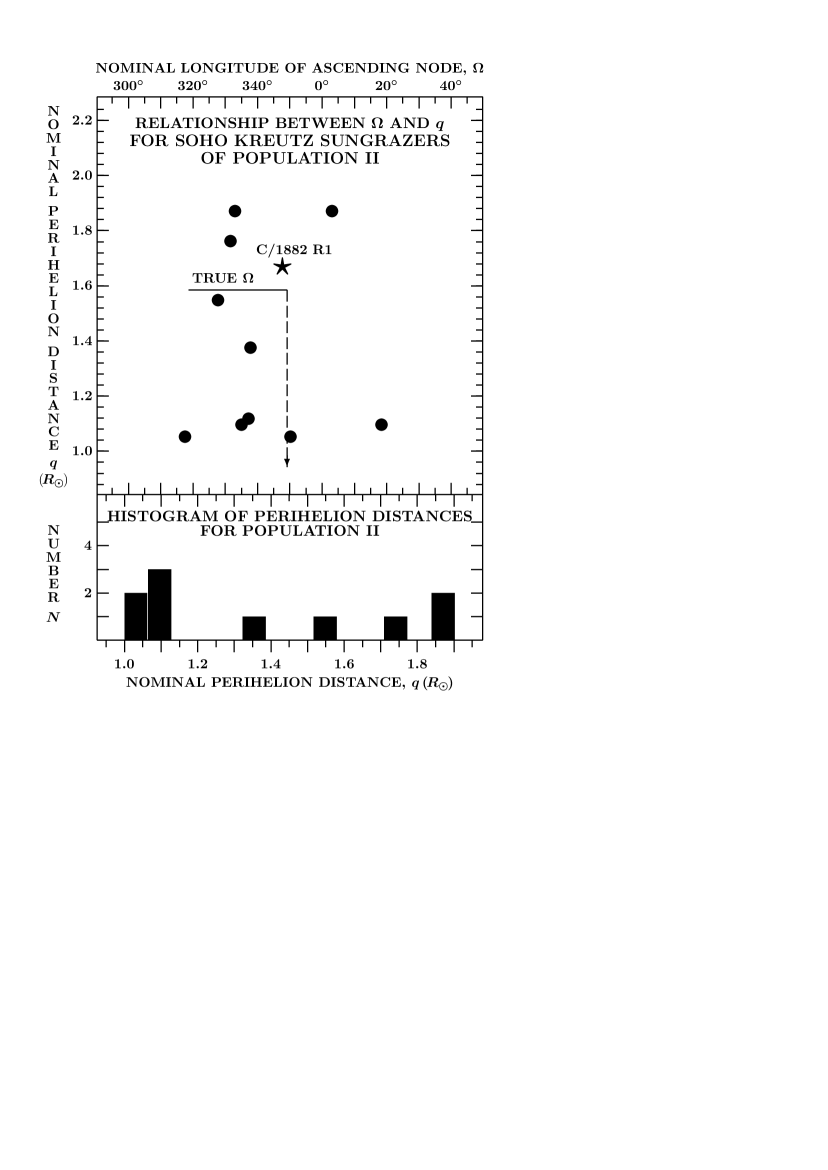
The next task is to examine the relations and the perihelion-distance distributions of the other populations. I employ the same technique as in Paper 1 and start with the most extensive Population I. Its histogram in Figure 9 resembles that of Population IIa in Figure 8 in that it also exhibits two peaks, but differs from it by the enormity of the peak just above the photosphere, whose position coincides with the perihelion distance 1.17 of the Great March Comet of 1843; the relationship between this comet and Population I is unquestionable. A second sharp but much smaller peak is located near 1.55 , otherwise the distribution is rather flat.

Since the difference, , between the nominal value of the longitude of the ascending node for a dwarf sungrazer, , and the presumed parent comet’s value, ,
| (12) |
can serve in a first approximation as a proxy parameter that measures the magnitude of the normal component of the nongravitational acceleration of the dwarf comet, the cumulative distribution of should offer further information on the process that governs the dispersal of fragments and complement the results offered by the relation. For Population I the log-log plot of the cumulative distribution is presented in Figure 10, in which (I) is the number of the population’s dwarf sungrazers, whose values of exceed or equal the plotted limit. At high values of [or low numbers (I)] the curve is a straight line showing that
| (13) |
strongly resembling the distribution of the nongravitational parameters for a set of long-period comets, presented in Figure 2 of Sekanina (2021b) and displaying at large values of a variation of . This similarity strengthens a conclusion that the distribution of the SOHO sungrazers of Population I was dominated by sublimation effects, with a lesser contribution from cascading fragmentation.
The relation and the histogram of nominal perihelion distances for Population Pe are exhibited in Figure 11. The features resemble those of Population I in Figure 9, with the exception of the significantly narrower range of the nominal nodal longitudes, with 20∘–25∘ of the true longitude, suggesting larger objects.


Figure 12 displays the distribution of nominal perihelion distances among the SOHO dwarf comets belonging to Population Ia. Given the unclear history of this population, but some connection to the contact binary’s neck, the histogram of nominal perihelion distances is of particular interest. The results are stunning, as, contrary to expectation, the distribution displays only a single peak positioned still closer to the surface of the photosphere than the peak of Population I.
To examine more closely the meaning of the unexpected result, the cumulative distribution of the differential nodal longitude is compared in Figure 10 with the cumulative distribution of Population I. The two distributions are clearly very different. While Population I follows at large s the relation (13), the curve of Population Ia is there considerably steeper, running way above Population I when normalized. Figure 13 reveals the nature of the difference between the two distributions: replacing the power law by an exponential law suggests that the rate of growth in the number of fragments varies with their number,
| (14) |
or
| (15) |
where (Ia) = 33 is the total number of Population Ia fragments. From Figure 13, deg-1. The proportionality between the number of fragments and the rate of growth in their number is of course an obvious property of colliding particles: the more of them there are, the more they keep running into one another. Given that the values for Population Ia were computed with the progenitor model’s value of .8 and that the corresponding value of the model’s perihelion distance was 1.40 , it is remarkable to see in Figure 12 the fairly crowded area of the nominal nodal longitudes near on the one hand and a major deficit of the SOHO sungrazers with the nominal perihelion distances near the model’s perihelion distance on the other hand. The process of fragmentation appears to be very efficient in dispersing the fragments’ perihelion distances away from the parent’s value. And again, there appears to be a class of fragments with their perihelia just above the surface of the photosphere.
Figures 14 and 15 exhibit the relation between the nominal nodal longitude and the nominal perihelion distance as well as the latter’s histogram for, respectively, Populations II and III. Because of the smaller numbers of sungrazers detected in these populations, they provide less reliable results than Populations I and Ia. However, indications are that once again there are peaks near 1.1 , which of course is more surprising for Population II. On the plot of Figure 15 comet Lovejoy is just on the outskirts of a clump of SOHO sungrazers.
The three remaining populations — Pre-I, IIIa, and IV — have fewer than ten members each in the collected set and their nominal perihelion distances are summarized in Table 5. To the extent that the statistics can at all be deemed meaningful, the same peak near 1.1 is again recognized. RMSD is the root-mean-square deviation.
In summary, the relationships and distributions involving the nominal perihelion distances of the SOHO dwarf sungrazers appear to suggest that the process of fragmentation may have been even more complex than is implied by the contact-binary model. Overwhelming evidence points to the detection of excess numbers of the SOHO sungrazers with the nominal perihelion distances near 1.1 in apparently every population, regardless of the perihelion distance of the bright, naked-eye sungrazer, when known to be associated. Given that a fragment released from its parent with a separation velocity, whose transverse component is directed against the parent’s orbital velocity, ends up in an orbit with a smaller perihelion distance, excessive numbers of the SOHO sungrazers in such orbits may be surprising only in the populations derived from Lobe II, which separated from the progenitor with a positive transverse velocity (Figure 5). Since both positive and negative directions are possible, the perihelion-distance histograms could imply a preferential fragmentation mode. On the other hand, one conclusion that the convoluted relationship between the nominal and true values of perihelion distance allows is that the amount of information conveyed by the distribution of the nominal perihelion distances may be rather limited and should not be overrated.

6. Conclusions
This paper has two objectives. One is to summarize and streamline the recently introduced contact-binary model for the Kreutz sungrazer system, whose details were developed and verified by direct orbit integration in three papers — 1, 2, and 3 (see the list of references). This summary aims primarily at making the presentation of the model more reader-friendly, but was also necessitated by new information added stepwise in between the three papers. A striking example is the derived birth place of the Great September Comet of 1882 and comet Ikeya-Seki, an issue that was not tackled until Paper 2, which happened to be completed last.
The contact-binary model begins with Aristotle’s comet as the adopted progenitor of the Kreutz system, presumably a body of formidable size, perhaps 100 km or more across. The model assumes that the comet’s nucleus consisted of two masses, referred to as the lobes (and connected by a narrower neck), which eons ago merged into a single object at a very low relative velocity.
Whereas the data analysis dictated that the narrative of Papers 1 to 3 proceed from an account of more recent fragmentation episodes, involving the surviving pieces of the progenitor, to earlier events, involving more substantial masses, this summary offers an account of the sequence of fragmentation events in their chronological order, again to the benefit of the reader.
The initial and most fundamental of these episodes — the birth of the Kreutz system — was the progenitor’s breakup into the two lobes (plus the neck) near aphelion, at 160 AU from the Sun. Perhaps a product of material fatigue, this event must have occurred at large heliocentric distance — an absolutely essential condition ensuring that a very modest separation velocity should suffice to open up a sizable gap between the orbits of Lobes I and II, equaling nearly 20∘ in the longitude of the ascending node and about 0.5 in the perihelion distance, while keeping the apsidal directions almost perfectly aligned. Splitting near the Sun could never explain the orbital disparity of this magnitude.

The initial breakup was followed, still near aphelion, by events of secondary fragmentation, as the lobes (especially Lobe II) continued to break up, thus generating precursors of the nine populations, whose existence was established in Paper 1. The most massive surviving fragment of Lobe I did eventually become the Great March Comet of 1843 of Population I, the most massive fragment of Lobe II — the Great September Comet of 1882 of Population II. The smaller fragments of Lobe I became the precursors of Populations Pre-I and Pe, the smaller fragments of Lobe II became the precursors of Populations IIa, III, IIIa, and IV. The surviving mass of the neck may have separated from one of the two lobes (probably Lobe I) a little later to become the precursor of Population Ia.
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/b396cca9-3dcf-4f82-b252-a0ab9b64b19b/x20.png)
TABLE 5
Because near-aphelion fragmentation of the progenitor and its lobes was affecting the orbital periods quite insignificantly, the first-generation fragments were predicted to have arrived at perihelion in the late 4th century AD nearly simultaneously. Magnificent in appearance, they must have presented an awesome sight, consistent with Ammianus’ brief, yet fitting comment on the daylight comets in AD 363 (accompanied by an eloquent and more elaborate narrative on comets generally). The inevitable side effects of the sudden arrival of a swarm of massive comets at sungrazing perihelion were numerous events of tidal splitting, in the aftermath of which the nearly identical orbital periods of the first-generation fragments were abruptly replaced by widely-scattered orbital periods of the second-generation fragments. These enormous changes may have been products of acquired separation velocities, or of radial shifts in the positions of the centers of mass on the order of a few kilometers, requiring no separation velocities whatsoever. Only the most massive of the fragments, whose centers of mass were moved by very small, subkilometer-sized shifts, ended up in orbits with periods close to the parent’s. The best example was the fragment that eventually became the Great March Comet of 1843. While the first-generation fragment of Population I had an orbital period of 735 yr and the population’s second-generation fragment — the Great Comet of 1106 — a period of 742 yr, the 1843 sungrazer itself ended up in an orbit with a period of 737 yr, a remarkably uniform motion from generation to generation.
Because of the large scatter in the orbital periods, the second-generation fragments were returning to perihelion at very different times. One can be more specific only in the cases in which the orbital period of a third-generation fragment is known with fairly high accuracy, a rather rare occasion. Next to Population I, a solution could be charted for Population II, whose second-generation fragment appears to have been the Chinese comet of 1138, as established in Paper 2 from the data on comet Ikeya-Seki, a third-generation fragment, and its famous twin, the spectacular 1882 sungrazer. A different evolutionary path was found for comet Pereyra, whose likely previous appearance was the comet discovered in September of 1041 rather than the Great Comet of 1106. The pedigree of comet Lovejoy could not be determined; for other naked-eye Kreutz sungrazers the history of orbital evolution is unclear because their orbital periods are unknown. However, the Great Southern Comet of 1887 is likely to be a fragment of the Great Southern Comet of 1880, which in turn appears to be a fragment of the Great Comet of 1106.
On the premise that the mechanism responsible for the dispersal of the naked-eye Kreutz sungrazers in time and space likewise applied to the dwarf members seen in the coronagraphic images of the space observatories, the SOHO spacecraft in particular, one can get some interesting estimates for the streams of these dwarf objects. For the currently dominant Population I, derived from the Great Comet of 1106, I estimate the total number of dwarf sungrazers at 300,000 and the duration of the stream (nearly equal to the maximum orbital period) at 80,000 yr, even though the rate should be dropping dramatically with time: in 3000 yr from now it should be about 1/10th the current rate. Of course by that time the 1843 sungrazer will have passed perihelion four or five times, presumably resupplying the stream. One cannot rule out the possibility that the stream will strengthen with time until the source is exhausted. By comparison, the poor showing of the Population II stream of dwarf sungrazers is disappointing.
The second objective of this paper is the examination of one aspect of the motions of the SOHO dwarf sungrazers that was just barely touched upon in Papers 1 to 3. Broadly, this problem concerns their gravitational orbits derived by Marsden, which, useless when unprocessed, contain important information that has allowed the detection of the nine populations discriminating in terms of the longitude of the ascending node. More specifically, the unsettled problem involves the nominal perihelion distances, which were deemed very poorly determined (and published to merely two decimals) by Marsden, but potentially of a diagnostic value for continuing classification efforts. A limited study of this kind in Paper 1 bore only on Population IIa, leading to a possible further expansion of the fragmentation process beyond the presented scenario of the contact-binary model.
The extended investigation of the distribution of the nominal perihelion distances and their relation to the nominal nodal longitudes for a select subset of the SOHO dwarf sungrazers, presented in this paper for the first time, does not unfortunately provide much information about the subject. The primary result is the acknowledgment of an essentially universal peak in the histograms of the nominal perihelion distances at about 1.1 , suggesting a potential preference for fragments released with a negative transverse component of the separation velocity. However, given Marsden’s skepticism about the poor quality of his determination of the SOHO sungrazers’ perihelion distances, one cannot rule out that these data may provide no or very little useful information.
In summary, the contact-binary model offers the picture of a very different
and more complex, though better organized, Kreutz system than was provided
by the two-superfragment model (Sekanina & Chodas 2004, 2007). The primary
reason for the refinements is the considerable amount of highly relevant
information that has been accumulated over the past 15 years, unavailable
when the two-superfragment model was being developed. Yet it is appropriate
to emphasize that the two models also have features in common that discriminate
them from the earlier models of the Kreutz system: the number of initial
fragments limited to two; a very large distance from the Sun at birth;
cascading fragmentation; and young age. Both models predict that another
cluster of bright Kreutz sungrazers is to arrive at perihelion in the
coming decades. And we are still waiting for the first naked-eye members
of Populations Pre-I, Ia, IIIa, and IV.
This research was carried out at the Jet Propulsion Laboratory, California
Institute of Technology, under contract with the National Aeronautics and
Space Administration.
REFERENCES
-
Elkin, W. L. 1883, Astron. Nachr., 104, 281
-
England, K. J. 2002, J. Brit. Astron. Assoc., 112, 13
-
Hall, M. 1883, Observatory, 6, 233
-
Hasegawa, I., & Nakano, S. 2001, Publ. Astron. Soc. Japan, 53, 931
-
Ho, P.-Y. 1962, Vistas Astron., 5, 127
-
Katsonopoulou, D. (ed.) 2017, Helike V: Ancient Helike and Aigia- leia. Athens: Helike Society, 310pp
-
Kreutz, H. 1891, Publ. Sternw. Kiel, 6
-
Kreutz, H. 1901, Astron. Abhandl., 1, 1
-
Marsden, B. G. 1967, AJ, 72, 1170
-
Marsden, B. G. 1989, AJ, 98, 2306
-
Marsden, B. G., & Williams, G. V. 2008, Catalogue of Cometary Orbits 2008, 17th ed. Cambridge, MA: Minor Planet Center/ Central Bureau for Astronomical Telegrams, 195pp
-
Martínez, M. J., Marco, F. J., Sicoli, P., & Gorelli, R. 2022, Icarus, 384, 115112
-
Matthews, J. 2008, The Roman Empire of Ammianus. Ann Arbor: Michigan Classical Press, 608pp
-
Ramsey, J. T. 2007, J. Hist. Astron., 38, 175
-
Rolfe, J. C. 1940, The Roman History of Ammianus Marcellinus, Book XXV. https://penelope.uchicago.edu/Thayer/E/Roman/ Texts/Ammian/25.html
-
Seargent, D. 2009, The Greatest Comets in History: Broom Stars and Celestial Scimitars. New York: Springer Science+Business Media, LLC, 260pp
-
Sekanina, Z. 2002, ApJ, 566, 577
-
Sekanina, Z. 2021a, eprint arXiv:2109.01297 (Paper 1)
-
Sekanina, Z. 2021b, eprint arXiv:2109.11120
-
Sekanina, Z. 2022, eprint arXiv:2202.01164 (Paper 3)
-
Sekanina, Z., & Chodas, P. W. 2004, ApJ, 607, 620
-
Sekanina, Z., & Chodas, P. W. 2007, ApJ, 663, 657
-
Sekanina, Z., & Chodas, P. W. 2008, ApJ, 687, 1415
-
Sekanina, Z., & Chodas, P. W. 2012, ApJ, 757, 127 (33pp)
-
Sekanina, Z., & Kracht, R. 2015, ApJ, 801, 135 (19pp)
-
Sekanina, Z., & Kracht, R. 2022, eprint arXiv:2206.10827 (Paper 2)
-
Sierks, H., Barbieri, C., Lamy, P. L., et al. 2015, Science, 347, a1044
-
Stern, S. A., Weaver, H. A., Spencer, J. R., et al. 2019, Science, 364, 9771
-
Strom, R. 2002, Astron. Astrophys., 387, L17