Kramers Fulde-Ferrell state and superconducting spin diode effect
Abstract
We study a novel equal-spin pairing state with opposite center of mass momentum for each spin polarization. This state, dubbed a Kramers Fulde-Ferrell (KFF) state, respects time-reversal symmetry and can be realized in a one-dimensional system with spin-orbit coupling and nearest neighbor attraction. We find that the KFF state supports nonreciprocal spin transport for both bulk superconductor and Josephson junctions. In addition to the spin Josephson diode effect, the charge transport is controlled by intriguing dynamics of bound states whose transitions can be manipulated by the length of the KFF superconductor. The KFF state is relevant for embedded quantum structures in monolayer Fe-based superconductors and dissipationless superconducting spintronics.
I Introduction
Recent experimental observations of the diode effect in superconductors [1, 2, 3, 4] and Josephson junctions (JJ) [5, 6, 7, 8, 9] have stimulated the research of nonreciprocal transport properties in superconducting (SC) systems. Following the proposal of SC diode effect [10], the so-called Josephson state has been extensively studied [11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23] as a possible mechanism to realize nonreciprocal transport in JJs. More recently, many theoretical proposals [24, 25, 26, 27, 28, 29, 30, 31] have been put forward for SC diode in bulk superconductors. In particular, the finite-momentum pairing Flude-Ferrell-Larkin-Ovchinnikov state [32, 33] is believed to provide a physical mechanism, since the order parameter of Fulde-Ferrell (FF) state can directly generate a difference in the critical current along and against the direction of q, leading to SC diode effect [28, 27]. The FF order, also known as helical superconductivity, can be realized in noncentrosymmetric superconductors with spin-orbit coupling (SOC) and time reversal symmetry breaking fields [34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47].
So far, the study of SC diode effect focused on the nonreciprocity of charge transport. One may wonder if there exists a similar nonreciprocal property in spin transport in certain SC systems. From the symmetry point of view, SC diode effect in charge transport, where critical currents in opposite directions have different magnitudes, requires the system to break both inversion and time-reversal () symmetry, since the charge current operator changes sign under either inversion or . While the spin current operator changes sign under inversion, it is invariant under . Thus, the nonreciprocity in spin transport only requires breaking inversion symmetry and can be realized in invariant superconductors.
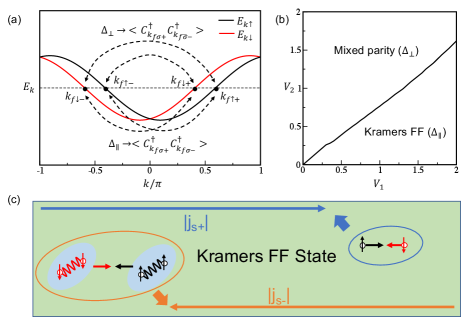
In this article, we propose a novel SC state that can realize nonreciprocal spin transport. This state has equal-spin pairing and a FF type of order parameter , with opposite Cooper pair center of mass momentum for opposite spin polarizations as shown schematically in Fig. 1(a). We term this SC state as a Kramers FF (KFF) state since symmetry is maintained. Such FF state has pairing field with only one Q vector in each pairing channel, which is translational invariant unlike the Larkin-Ovchinnikov state also known as the pair density wave state, where the pairing field has both Q and vectors in each channel so that the pairing order parameters varies in space. We demonstrate that the KFF state can be realized in a meanfield theory of a concrete model describing a spin-orbit coupled chain with nearest neighbor attractions as illustrated in Fig. 1(a,b). The nonzero Q pairing across the Fermi points in Fig. 1(a) is enabled by the SOC split bands. We study the condition to realize the nonreciprocal spin transport where the critical spin current along positive and negative directions are unequal in magnitude for both bulk SC state and Josephson junction structures. Moreover, we find intriguing properties and rich phases in the charge transport across JJs of the KFF state, which can be realized by simply changing the length of the SC chain. Similar pairing state was also studied in the two dimensional honeycomb system where the valley degree of freedom plays the role of spin here [48].
This article is organized as follows. We start with the introduction of our model Hamiltonian and meanfield formulation for the KFF state in Sec. II. In Sec. III, we discuss the nonreciprocal spin transport for the bulk SC with KFF order, which is followed by the discussion of the hidden inversion symmetry that is related to the nonreciprocal spin transport in Sec. IV Then we study the transport properties of the Josephson junction structure constructed from the KFF state in Sec. V and discuss various phases realized in the charge transport across JJs of the KFF state in Sec. VI. We finalize the discussion in Sec. VII.
II Formulation
II.1 Model Hamiltonian
We first consider a one-dimensional (1D) spin-orbit coupled chain with nearest neighbor attraction described by the Hamiltonian
| (1) |
where are hopping parameters up to the 2nd neighbor ( and ) and describes a nearest neighbor SOC. In 1D, SOC leaves a conserved spin quantum number which is taken to be the spin quantization axis along the chain direction. The nearest neighbor attraction responsible for SC order can be decomposed into equal-spin and opposite-spin pairing channels as
| (2) |
where the first term corresponds to the attraction between the electrons with the same spin and the second term corresponds to the attraction between the electrons with opposite spins and is the number of sites. If we further define the two pairing operators in equal-spin and opposite-spin channels as
| (3) |
Eq. 2 can be written as
| (4) |
where these two terms correspond to the pairing channels with equal and opposite spin respectively and here we denote the attraction in these two channels as and . While in the original model in Eq. (1), we consider here a more general model where the effective attraction and can be different. The equal-spin pairing can be induced in embedded quantum structures in high-Tc superconductors due to spatial symmetry breaking [49], such as along the atomic line defects in monolayer FeTeSe [50]. Then the total Hamiltonian becomes
| (5) |
where
| (6) |
is the band dispersion with
| (7) |
which determines the positions of the Fermi points.
II.2 Meanfield decoupling
From the structure of Fermi points shown in Fig. 1(a), we can solve the model in Eq. (5) within a meanfield approximation assuming the following meanfield ansatz
| (8) |
Here, in equal-spin pairing channel, electrons with up (down) spin pair into the FF state with a nonzero center of mass momentum Q(-Q). The resulting Kramers doublet ensures that symmetry is preserved. In opposite-spin pairing channel, electrons with up and down spins form zero-momentum pairs, which is in general a mixture of -wave and -wave pairing depending on the phase . Specifically, corresponds to -wave pairing and corresponds to -wave pairing, while other values give rise to a mixed parity state.
After the meanfield decoupling, the meanfield Hamiltonian can be written as
| (9) |
In the Nambu basis , Eq. 9 can be written as
| (10) |
with
| (11) |
This meanfield Hamiltonian can be solved self-consistently for a fixed chemical potential and various values of and with the self-consistent equations
| (12) |
and the ground state is determined by the states with the lowest free energy density which also determines the value of and .
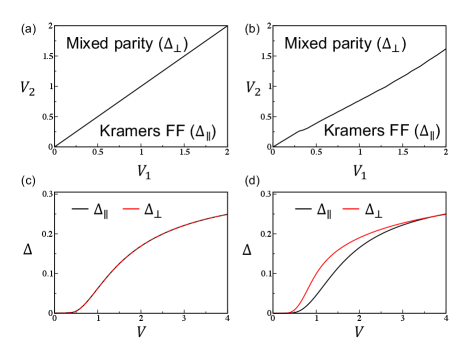
We perform the calculation with a general set of parameter and the obtained meanfield phase diagram in Fig. 1(b) shows that the novel KFF state is a more stable ground state than the mixed parity state when is larger than . We thus focus on the KFF state driven by equal-spin pairing and investigate its many intriguing properties. A more detailed analysis of the meanfield phase diagram as well as the behavior of the order parameters are shown in Appendix. A. The detailed calculation for the mixed parity state is also shown in Appendix. E.
III Nonreciprocal spin transport and Spin diode effect in bulk KFF state
The meanfield Hamiltonian in KFF state becomes
| (13) |
which can be written in the Nambu basis as
| (14) |
where,
| (15) |
is block diagonal in spin space, leading to the eigenenergy as
| (16) |
and we have due to the symmetry. Then the free energy density at zero temperature can be calculated as
| (17) |
where the Heaviside step function. The order parameter for a given can be determined self-consistently by minimizing with respect to , leading to the self-consistency equation
| (18) |
The optimal value can be further determined by minimizing with respect to , i.e., . Because the latter is directly related to the spin current carried by the KFF state (see Appendix. B) , the ground state with optimized does not carry any net spin current since . When the KFF state is driven out of equilibrium into a state with , a nonzero applied spin current is realized. Throughout the remaining text, we define the charge and spin currents in units of and unity, respectively. Since the spin current carrying state has equal but opposite center of mass momentum for Cooper pairs in opposite spin channels, the charge current always vanishes due to symmetry. The critical spin currents in and directions are determined by the maximum and minimum values of sustained by the SC state according to and . When , the SC state enables nonreciprocal spin transport as shown in Fig. 1(c).
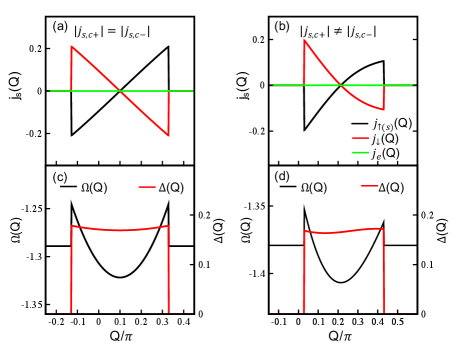
We performed meanfield calculations using two sets of parameters. In the first case, we set and obtain analytically that the ground state has , consistent with the SOC split bands where electrons pair across the Fermi points in the same spin sector, giving rise to finite Cooper pair momenta with more details shown in Appendix. C. The zero temperature free energy in Eq. (17) and the current density from its momentum derivative are calculated numerically and plotted in Figs. 2(a, c) as a function of . The critical spin currents are determined by the maximum and minimum values of the spin current density. Fig. 2(c) shows that the two critical momenta at which the spin current reaches critical values coincide with the two momenta where the SC order parameter vanishes. In this case with , we find that the critical spin currents , as shown in Fig. 2(a), and the spin transport is reciprocal. The absence of nonreciprocal spin transport turns out to be due to a hidden inversion symmetry when .
IV Hidden inversion symmetry
To demonstrate the hidden inversion symmetry, we can perform a local gauge transformation , corresponding to in momentum space. Then the meanfield Hamiltonian Eq. 13 becomes
| (19) |
Since in the absence of , , we can see that in the new basis, the only inversion breaking term owing to the spin-orbit coupling , is cancelled if . In other words, when , the inversion symmetry can be recovered in the new basis, where the meanfield Hamiltonian becomes
| (20) |
The transformed Hamiltonian describes two spin-degenerate -wave Kitaev chains [51] with inversion symmetry in each spin sector. It is precisely this hidden inversion symmetry that forbids the nonreciprocal property of spin current, since this hidden inversion symmetry changes the sign of the current operator , while keeping the total Hamiltonian invariant, which guarantees a one to one correspondence between the positive and negative current, such that and have to have the same magnitude.
In the case with finite , the dispersion of the noninteracting Hamiltonian reads , and then the Fermi momentum no longer have a closed form and the sum of the two Fermi momentum belonging to the same spin polarization is incommensurate in general. Here, we can immediately see that the gauge transformation above can not recover the inversion symmetry as above, since now , and the inversion breaking phase of the two cosine function and cannot be cancelled by simultaneously, so that there is no hidden inversion symmetry that forbids the presence of the nonreciprocal spin transport. Therefore, the transformed model describes the two p-wave Kitaev chains with complex hoppings, which are time-reversal counterparts of each other but not identical and can be written in the real space as
| (21) |
Indeed, the results shown in Fig. 2(b) confirms that critical spin currents are nonreciprocal with and along and directions, respectively. As a result, a spin current satisfying flows as dissipationless supercurrent in the negative direction since , but can only be transported as a dissipative normal current in the positive direction since . This SC spin diode effect is shown schematically in Fig. 1(c).
V Josephson junctions
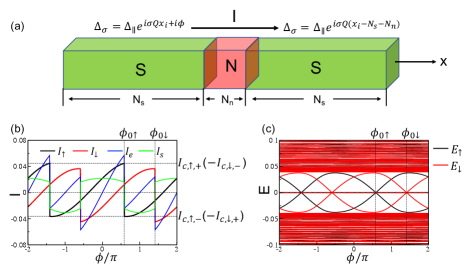
We next study the transport properties of Josephson chains consisting of a normal metal sandwiched between two KFF superconductors depicted in Fig. 3(a) with more detailed setups shown in Appendix. D. We consider the general case with nonzero in the KFF state.
V.1 Spin Diode effect with spin-independent phase bias
We first study the transport properties of JJ with spin-independent phase bias . The Josephson currents can be calculated by the formula
| (22) |
where is the free energy of the system [52]. The results for both spin components and total charge and spin currents are shown in Fig. 3(b). Due to symmetry, the spin-dependent critical currents satisfy such that charge current is reciprocal . In contrast, the critical current for each spin is asymmetric, i.e. , giving rise to nonreciprocal Josephson spin currents and the SC spin diode effect.
V.2 Spin diode effect in the Josephson junction with spin phase
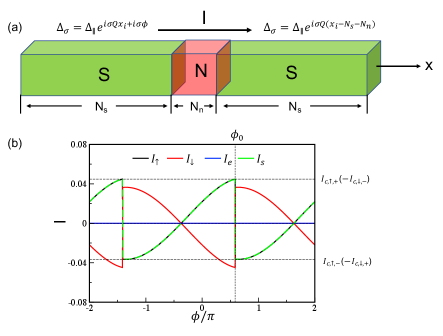
The spin diode effect with nonreciprocal spin current by applying a spin-dependent phase bias known as the spin phase [53] is obvious. The spin phase was first introduced in Ref. 53. In the current case, we consider the spin phase in the direction, which corresponds to the spin-dependent phase bias applied to the Josephson junction. We consider the same parameter set as that shown in Fig. 3 and the resulting current phase relation is shown in Fig. 4. Here, since the spin phase still respects the symmetry, the current for the opposite spin polarization are always equal in magnitude and opposite in the direction, i.e., , so that the total charge current always vanishes and the total spin current , which is nonreciprocal as long as the hidden inversion symmetry is broken by finite . The nonreciprocal spin current of the Josephson junction with spin phase is inherited from the nonreciprocal spin transport of the bulk KFF state.
VI Length controlled phase transitions in charge transport
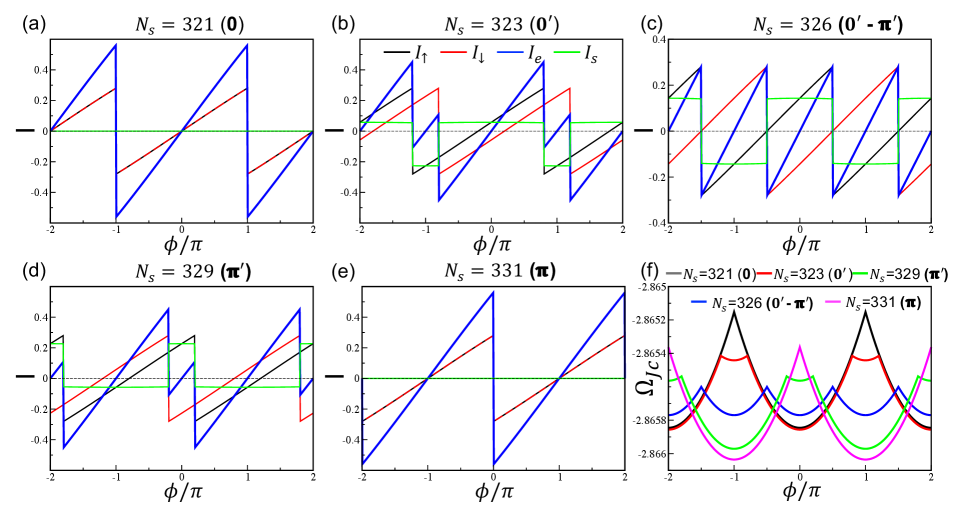
An intriguing feature in Fig. 3(b) is the phase difference between Josephson currents in two spin sectors, which is clearly revealed in the energy spectrum plotted in Fig. 3(c). Apart from the continuum states outside the SC gap, there are eight in-gap states. Among them, four are at exactly zero energy, corresponding to two pairs of Majorana zero modes (one for each spin) located at the two ends of the chain due to -wave nature of the KFF state [51], which do not contribute to Josephson current. The other four in-gap states are Andreev bound states of the S-N-S junction. For junctions made of conventional superconductors, the energies of the bound states cross at [54], corresponding to zero modes trapped by -junction [55]. In the current KFF JJs, the energy spectrum of the bound states for two spin species shifts in opposite directions as shown in Fig. 3(c). As a result, the phase bias where the bound states cross zero shifts from to , where the Josephson current jumps due to branch switching as shown in Fig. 3(b).
Such phase differences have a great impact on charge transport. The charge current crosses zero at both and with positive slopes, indicating the free energy of the junction reaches a local minimum at both and . This state is called a or state depending on the momentum of the global minimum. It was studied previously in JJs where two superconductors are coupled through an Anderson impurity [56] or a magnetic quantum dot [57]. Here, these remarkable states are realized in -invariant systems due to the novel KFF SC order. Remarkably, we find that distinct Josephson junction states (, , and ) can all be realized by tuning the phase shift, which can be easily achieve by changing the length of the SC region. The definition of these states are listed in Table. 1.
The dependence of the phase shift on the length of the SC region can be understood by performing a local gauge transformation that maps the KFF JJ onto a Kitaev JJ consisting of two spin-degenerate -wave Kitaev chains subject to spin-dependent phase bias as shown in Appendix. D. If we further assume the Josephson current for the Josephson chain consisting of two spin degenerate -wave Kitaev chains with phase bias as which is identical for the two spin species due to the spin degeneracy, we can then immediately get the Josephson current for each spin species as , i.e., the Josephson current is shifted from the current of the transformed junction by a phase (mod ) so that the relative phase difference of the current between the two spin species is (mod ). Various Josephson junction states can be realized by tuning from 0 to through the length . This relation is verified numerically in Figs. 5(a-e) for and . Any combination of and can produce similar results as long as covers the range . We also calculate the total free energy of the system for different and indeed observe transitions between all these states controlled by as shown in Fig. 5(f). Specifically, for =321 (331), there is only one global minimum located at and the system is in state. For =323 (329), the free energy has a global minimum at and a local minimum at so that the system is in () state. The transition between the two states is reached at , where and .
Interestingly, in this case with only nearest neighbor hopping , the charge current acquires a period of in phase instead of as in conventional Josephson current at the critical point (), which can also be understood in the gauge transformed basis. In this case with , the phase bias becomes and we thus have , from which we can get . Then we can derive a new relation for the total charge current as
so that the charge current acquires a period of instead of . The spin current then acquires a minus sign when progressing phase, so that its period is still .
The realization of diverse Josephson junction states by simply controlling the length of the superconductor is an intriguing property. It originates from the opposite nonzero momentum of Cooper pairs in each spin sector in the novel KFF state. The quantum interference of relative phase shifted pairing functions with opposite spin polarization leads to rich phases and physical phenomena.
| State label | Distribution of minimums of the free energy |
|---|---|
| global minimum at | |
| global minimum at and local minimum at | |
| global minimum at both and | |
| global minimum at and local minimum at | |
| global minimum at |
VII Discussion
We reported the theoretical discovery of a novel time-reversal invariant, finite momentum pairing Fulde-Ferrell state – the KFF state. The concrete effective 1D model we used to realize the KFF state and its many unprecedented properties is intimately connected to the novel physics observed at the atomic line defect (ALD) in monolayer iron-based superconductor Fe(Te,Se), where zero-energy bound states emerge at both ends of the ALD with no signatures of symmetry breaking [50]. The missing atoms cause inversion symmetry breaking and induces Rashba SOC. It was shown that significant equal-spin triplet pairing can be induced by coherent quantum mechanical processes along such a Rashba ALD embedded in 2D unconventional superconductors [49]. This makes it plausible for materializing the effective 1D model with significant equal-spin triplet pairing to generate the KFF state. More recently, evidence for finite momentum pair density wave order has been observed in monolayer Fe(Te,Se) along one-dimensional domain walls [58]. The experimental evidence suggests time-reversal symmetry is preserved, which makes the KFF state a plausible candidate in addition to the Larkin-Ovchinnikov state.
The most remarkable of the KFF state is that, in the presence of broken inversion symmetry, it supports nonreciprocal spin supercurrent in both bulk superconductor and JJ. In contrast to nonreciprocal charge transport in SC systems which requires breaking both inversion and symmetry, nonreciprocal SC spin transport only requires breaking inversion symmetry. This is because the spin current operator is invariant under time-reversal, such that systems with positive and negative spin current are unrelated by the operation. This is true regardless of whether the system respects the symmetry or not, making it free of the constraint by the Onsager relation. We thus propose a novel SC spin diode effect as a potential new frontier for using spins to make dissipationless electronic devices in SC spintronics. While future work is clearly needed which is outside the scope of the current paper, we point out that the unique properties of the KFF state make it plausible for possible realizations in JJs consisting of a ferromagnetic barrier. The exchange field of the barrier favors spin-triplet pairing and has very little effect on the critical current of equal-spin triplet pairing such as in the KFF state, resulting in the slow decay of the critical current with increasing barrier length. Both effects have been demonstrated experimentally [59, 60]. In turn, detecting the nonreciprocal spin transport together with the slow decay of the critical current with the barrier length can serve as the smoking gun evidence for the KFF state.
Acknowledgements.
We thank Kun Jiang for helpful discussions. YZ is supported in part by National Natural Science Foundation of China (NSFC) Grants No. 12004383, No. 12074276 and No 12274279. ZW is supported by the U.S. Department of Energy, Basic Energy Sciences, Grant No. DE FG02-99ER45747.Appendix A More detailed results from the meanfield calculation
We perform the calculation with two sets of parameters, which are shown in Fig. 6. As shown in Fig. 6, the ground states with finite pairing are either the KFF states with order parameters solely condensed in the equal-spin pairing channel or the mixture of and wave pairing states whose order parameters are solely condensed in the opposite-spin pairing channel and no mixed states with the coexistence of the order in both channels are found as the ground states except along the phase boundary of the two states where these two states are degenerate. This means that we can consider the two pairing channels separately, which further simplifies the meanfield Hamiltonian and is helpful for us in studying the properties of each state.
Appendix B Derivation of the spin current for the KFF state
As shown in the main text, the meanfield Hamiltonian purely in the equal-spin pairing channel can be written as
| (23) |
which can be further simplified in the Nambu basis as
| (24) |
with
| (25) |
In order to derive the expression for the spin current, let’s consider the free energy density of the KFF state at finite temperature T, which is given as
| (26) |
with
| (27) |
The current operator for each spin species in the system studied is defined as
| (28) |
Next, from Eq. 25 we have
| (29) |
and then we further have
| (30) |
which means
| (31) |
Then the current for each spin species can be calculated as
| (32) |
where is the Fermi distribution function. Here, the operator is the density current, from which we can define the charge current operator as and the operator for the spin current carrying spin polarization in direction as . Therefore, we can conveniently define the unit for the charge and spin current as and 1, so that both currents can be written in a similar format. We finally arrive at the expression for the spin current with spin up polarization as
| (33) |
This means the ground state with the optimized value of does not carry any net spin current as expected, since , and when a spin current is applied to the KFF state, the state with a different value of , satisfying is realized. Then the critical spin current for the positive and negative directions are determined by the maximum and minimum values of sustained by the superconducting state, which can be defined as and . Moreover, due to the presence of symmetry, , which means , such that the charge current always vanishes in the KFF state as expected and .
Appendix C Determining the optimized Q for KFF state
We first consider a simpler case with only nearest neighbor hopping, i.e. . In this case, the dispersion of the noninteracting Hamiltonian becomes with and , which determines the Fermi momentum as
| (34) |
Then the quasiparticle energy Eq. 16 becomes
| (35) |
and from Eq. 17 and the symmetry, we have the free energy density at zero temperature as
| (36) |
which leads to the expression for the spin current as
| (37) |
We can easily see that when , , then we have . Therefore, the ground state is characterized by the momentum , which is also consistent with the Fermi surface of the noninteracting Hamiltonian, where the electrons around the two Fermi points within the same spin species pair together, giving rise to a finite Cooper pair momentum . We numerically calculate the zero temperature free energy as well as the current density as shown in Fig. 2(a, c) of the main text, which indeed confirms that the free energy density reaches the minimum at and the critical spin currents are determined by the maximum and minimum values of the spin current density.
Appendix D The relation between the phase difference and
To study the transport properties of the Josephson chain, we consider the system consisting of two superconductors with KFF order sandwiching a normal metal in between as shown in Fig. 3(a) of the main text. By setting the lattice constant to 1, this Josephson chain can be described by the tight-binding Hamiltonian , where
| (38) |
| (39) |
describe the two SC regions on the left and right sides,
| (40) |
describes the normal metal region in the middle and
| (41) |
| (42) |
correspond to the coupling between the normal metal region and the left and right SC region, with the phase bias between the two SCs. Then the Josephson currents can be calculated by the formula
| (43) |
with the n-th eigenvalue for at the phase bias and the Fermi distribution function.
Next, we demonstrate the dependence of the relative phase difference on the length of the superconducting region . Let us consider a simpler case with only nearest neighbor hopping on the superconducting region. We first perform a local gauge transformation
| (44) |
then each term in Hamiltonian becomes
| (45) |
| (46) |
| (47) |
| (48) |
| (49) |
We can see that , and are unchanged in the new basis, and if we further use the relation for the KFF state , the phase factors of the hopping in Eq. 45, 46 disappear, and and then describe the spin degenerate p-wave Kitaev chains with superconducting phase and , which means describes the Josephson chain consisting of two spin degenerate -wave Kitaev chains with phase bias for spin species . If we further assume the Josephson current for the Josephson chain consisting of two spin degenerate -wave Kitaev chains with phase bias as which is identical for the two spin species due to the spin degeneracy, we can then immediately get the Josephson current for each spin species as , i.e., the Josephson current is shifted from the current of the transformed junction by a phase (mod ) so that the relative phase difference of the current between the two spin species is (mod ). We verify this relation numerically in Fig. 5 of the main text where we take the parameters as , , , , , which leads to and . For =321, 323, 326, 329 and 331 which leads to the phase difference varying from 0 to , is shifted by , , , and , which is consistent with the results shown in Fig. 5(a-e) of the main text. Various Josephson junction states including , , , and junction states can be realized by tuning from 0 to . The definition of these states is listed in Table. 1 of the main text.
Moreover, if the second neighbor hopping is finite, after the gauge transformation of Eq. 44, Eq. 45,46 acquire extra term as the 2nd neighbor hopping. Now, since the relation no longer holds, neither this phase nor the phase of in Eq. 45,46 can be gauged away, the transformed model no longer describes the Josephson chain consisting of two spin degenerate p-wave Kitaev chains, but rather two spin dependent p-wave Kitaev chains with complex hopping parameters that are time-reversal counterparts of each other, so that the time-reversal symmetry is not broken.
Appendix E channel (mixture of and wave pairing state)
If we consider the meanfield Hamiltonian purely in the opposite-spin pairing channel, then the meanfield Hamiltonian becomes
| (50) |
which can be further simplified in the Nambu basis as
| (51) |
with
| (52) |
Diagonalizing , and considering the relation owing to the symmetry, we can get
| (53) |
Then the free energy density at zero temperature can be calculated as
| (54) |
with the Heaviside step function. Therefore, for a given value of , the order parameter can be determined self-consistently by minimizing , with respect to , leading to the self-consistent equation
| (55) |
The value of can be further determined by minimizing with respect to , which is equivalent to have . From Eq. 53 and Eq. 54, we have
| (56) |
If we further consider the case with , then we have
| (57) |
Apparently, when with integer n, the denominator of the integral is even in k while the numerator is odd in k, so that this integral vanishes, which means reaches extremum when and which one (odd n or even n) is the minimum depends on the details of the parameters. We note that when the free energy reaches a minimum at , the energy spectrum becomes which is identical to the spectrum of the KFF state if .
References
- Ando et al. [2020] Fuyuki Ando, Yuta Miyasaka, Tian Li, Jun Ishizuka, Tomonori Arakawa, Yoichi Shiota, Takahiro Moriyama, Youichi Yanase, and Teruo Ono, “Observation of superconducting diode effect,” Nature 584, 373–376 (2020).
- Bauriedl et al. [2021] Lorenz Bauriedl, Christian Bäuml, Lorenz Fuchs, Christian Baumgartner, Nicolas Paulik, Jonas M. Bauer, Kai-Qiang Lin, John M. Lupton, Takashi Taniguchi, Kenji Watanabe, Christoph Strunk, and Nicola Paradiso, “Supercurrent diode effect and magnetochiral anisotropy in few-layer NbSe2,” arXiv e-prints , arXiv:2110.15752 (2021), arXiv:2110.15752 [cond-mat.supr-con] .
- Shin et al. [2021] Jeacheol Shin, Suhan Son, Jonginn Yun, Giung Park, Kaixuan Zhang, Young Jae Shin, Je-Geun Park, and Dohun Kim, “Magnetic Proximity-Induced Superconducting Diode Effect and Infinite Magnetoresistance in van der Waals Heterostructure,” arXiv e-prints , arXiv:2111.05627 (2021), arXiv:2111.05627 [cond-mat.supr-con] .
- Lin et al. [2022] Jiang-Xiazi Lin, Phum Siriviboon, Harley D. Scammell, Song Liu, Daniel Rhodes, K. Watanabe, T. Taniguchi, James Hone, Mathias S. Scheurer, and J. I. A. Li, “Zero-field superconducting diode effect in small-twist-angle trilayer graphene,” Nature Physics 18, 1221–1227 (2022).
- Wu et al. [2022] Heng Wu, Yaojia Wang, Yuanfeng Xu, Pranava K. Sivakumar, Chris Pasco, Ulderico Filippozzi, Stuart S. P. Parkin, Yu-Jia Zeng, Tyrel McQueen, and Mazhar N. Ali, “The field-free josephson diode in a van der waals heterostructure,” Nature 604, 653–656 (2022).
- Baumgartner et al. [2022a] Christian Baumgartner, Lorenz Fuchs, Andreas Costa, Simon Reinhardt, Sergei Gronin, Geoffrey C. Gardner, Tyler Lindemann, Michael J. Manfra, Paulo E. Faria Junior, Denis Kochan, Jaroslav Fabian, Nicola Paradiso, and Christoph Strunk, “Supercurrent rectification and magnetochiral effects in symmetric josephson junctions,” Nature Nanotechnology 17, 39–44 (2022a).
- Baumgartner et al. [2022b] C Baumgartner, L Fuchs, A Costa, Jordi Picó-Cortés, S Reinhardt, S Gronin, G C Gardner, T Lindemann, M J Manfra, P E Faria Junior, D Kochan, J Fabian, N Paradiso, and C Strunk, “Effect of rashba and dresselhaus spin–orbit coupling on supercurrent rectification and magnetochiral anisotropy of ballistic josephson junctions,” Journal of Physics: Condensed Matter 34, 154005 (2022b).
- Pal et al. [2022] Banabir Pal, Anirban Chakraborty, Pranava K. Sivakumar, Margarita Davydova, Ajesh K. Gopi, Avanindra K. Pandeya, Jonas A. Krieger, Yang Zhang, Mihir Date, Sailong Ju, Noah Yuan, Niels B. M. Schröter, Liang Fu, and Stuart S. P. Parkin, “Josephson diode effect from cooper pair momentum in a topological semimetal,” Nature Physics 18, 1228–1233 (2022).
- Díez-Mérida et al. [2023] J. Díez-Mérida, A. Díez-Carlón, S. Y. Yang, Y. M. Xie, X. J. Gao, J. Senior, K. Watanabe, T. Taniguchi, X. Lu, A. P. Higginbotham, K. T. Law, and Dmitri K. Efetov, “Symmetry-broken josephson junctions and superconducting diodes in magic-angle twisted bilayer graphene,” Nature Communications 14, 2396 (2023).
- Hu et al. [2007] Jiangping Hu, Congjun Wu, and Xi Dai, “Proposed design of a josephson diode,” Phys. Rev. Lett. 99, 067004 (2007).
- Buzdin [2008] A. Buzdin, “Direct coupling between magnetism and superconducting current in the josephson junction,” Phys. Rev. Lett. 101, 107005 (2008).
- Yokoyama et al. [2013] Tomohiro Yokoyama, Mikio Eto, and Yuli V. Nazarov, “Josephson current through semiconductor nanowire with spin–orbit interaction in magnetic field,” Journal of the Physical Society of Japan 82, 054703 (2013).
- Yokoyama et al. [2014] Tomohiro Yokoyama, Mikio Eto, and Yuli V. Nazarov, “Anomalous josephson effect induced by spin-orbit interaction and zeeman effect in semiconductor nanowires,” Phys. Rev. B 89, 195407 (2014).
- Dolcini et al. [2015] Fabrizio Dolcini, Manuel Houzet, and Julia S. Meyer, “Topological josephson junctions,” Phys. Rev. B 92, 035428 (2015).
- Szombati et al. [2016] D. B. Szombati, S. Nadj-Perge, D. Car, S. R. Plissard, E. P. A. M. Bakkers, and L. P. Kouwenhoven, “Josephson 0-junction in nanowire quantum dots,” Nature Physics 12, 568–572 (2016).
- Assouline et al. [2019] Alexandre Assouline, Cheryl Feuillet-Palma, Nicolas Bergeal, Tianzhen Zhang, Alireza Mottaghizadeh, Alexandre Zimmers, Emmanuel Lhuillier, Mahmoud Eddrie, Paola Atkinson, Marco Aprili, and Hervé Aubin, “Spin-orbit induced phase-shift in bi2se3 josephson junctions,” Nature Communications 10, 126 (2019).
- Alidoust and Linder [2013] Mohammad Alidoust and Jacob Linder, “-state and inverted fraunhofer pattern in nonaligned josephson junctions,” Phys. Rev. B 87, 060503 (2013).
- Bobkova et al. [2016] I. V. Bobkova, A. M. Bobkov, Alexander A. Zyuzin, and Mohammad Alidoust, “Magnetoelectrics in disordered topological insulator josephson junctions,” Phys. Rev. B 94, 134506 (2016).
- Alidoust and Hamzehpour [2017] Mohammad Alidoust and Hossein Hamzehpour, “Spontaneous supercurrent and phase shift parallel to magnetized topological insulator interfaces,” Phys. Rev. B 96, 165422 (2017).
- Alidoust et al. [2018] Mohammad Alidoust, Morten Willatzen, and Antti-Pekka Jauho, “Strain-engineered majorana zero energy modes and josephson state in black phosphorus,” Phys. Rev. B 98, 085414 (2018).
- Alidoust [2020] Mohammad Alidoust, “Critical supercurrent and state for probing a persistent spin helix,” Phys. Rev. B 101, 155123 (2020).
- Alidoust et al. [2021] Mohammad Alidoust, Chenghao Shen, and Igor Žutić, “Cubic spin-orbit coupling and anomalous josephson effect in planar junctions,” Phys. Rev. B 103, L060503 (2021).
- Halterman et al. [2022] Klaus Halterman, Mohammad Alidoust, Ross Smith, and Spencer Starr, “Supercurrent diode effect, spin torques, and robust zero-energy peak in planar half-metallic trilayers,” Phys. Rev. B 105, 104508 (2022).
- Misaki and Nagaosa [2021] Kou Misaki and Naoto Nagaosa, “Theory of the nonreciprocal josephson effect,” Phys. Rev. B 103, 245302 (2021).
- He et al. [2022] James Jun He, Yukio Tanaka, and Naoto Nagaosa, “A phenomenological theory of superconductor diodes,” New Journal of Physics 24, 053014 (2022).
- Yuan and Fu [2022] Noah F. Q. Yuan and Liang Fu, “Supercurrent diode effect and finite-momentum superconductors,” Proceedings of the National Academy of Sciences 119, e2119548119 (2022).
- Daido et al. [2022] Akito Daido, Yuhei Ikeda, and Youichi Yanase, “Intrinsic superconducting diode effect,” Phys. Rev. Lett. 128, 037001 (2022).
- Davydova et al. [2022] Margarita Davydova, Saranesh Prembabu, and Liang Fu, “Universal josephson diode effect,” Science Advances 8, eabo0309 (2022).
- Scammell et al. [2022] Harley D Scammell, J I A Li, and Mathias S Scheurer, “Theory of zero-field superconducting diode effect in twisted trilayer graphene,” 2D Materials 9, 025027 (2022).
- Zhang et al. [2022] Yi Zhang, Yuhao Gu, Pengfei Li, Jiangping Hu, and Kun Jiang, “General theory of josephson diodes,” Phys. Rev. X 12, 041013 (2022).
- Souto et al. [2022] Rubén Seoane Souto, Martin Leijnse, and Constantin Schrade, “Josephson diode effect in supercurrent interferometers,” Phys. Rev. Lett. 129, 267702 (2022).
- Fulde and Ferrell [1964] Peter Fulde and Richard A. Ferrell, “Superconductivity in a strong spin-exchange field,” Phys. Rev. 135, A550–A563 (1964).
- Larkin and Ovchinnikov [1965] A.I. Larkin and Yu.N. Ovchinnikov, “Nonuniform state of superconductors,” Sov. Phys. JETP 20, 762 (1965).
- Smidman et al. [2017] M Smidman, M B Salamon, H Q Yuan, and D F Agterberg, “Superconductivity and spin–orbit coupling in non-centrosymmetric materials: a review,” Reports on Progress in Physics 80, 036501 (2017).
- Gor’kov and Rashba [2001] Lev P. Gor’kov and Emmanuel I. Rashba, “Superconducting 2d system with lifted spin degeneracy: Mixed singlet-triplet state,” Phys. Rev. Lett. 87, 037004 (2001).
- Barzykin and Gor’kov [2002] Victor Barzykin and Lev P. Gor’kov, “Inhomogeneous stripe phase revisited for surface superconductivity,” Phys. Rev. Lett. 89, 227002 (2002).
- Agterberg [2003] D.F. Agterberg, “Novel magnetic field effects in unconventional superconductors,” Physica C: Superconductivity 387, 13–16 (2003), proceedings of the 3rd Polish-US Workshop on Superconductivity and Magnetism of Advanced Materials.
- Dimitrova and Feigel’man [2003] O. V. Dimitrova and M. V. Feigel’man, “Phase diagram of a surface superconductor in parallel magnetic field,” Journal of Experimental and Theoretical Physics Letters 78, 637–641 (2003).
- Kaur et al. [2005] R. P. Kaur, D. F. Agterberg, and M. Sigrist, “Helical vortex phase in the noncentrosymmetric ,” Phys. Rev. Lett. 94, 137002 (2005).
- Agterberg and Kaur [2007] D. F. Agterberg and R. P. Kaur, “Magnetic-field-induced helical and stripe phases in rashba superconductors,” Phys. Rev. B 75, 064511 (2007).
- Dimitrova and Feigel’man [2007] Ol’ga Dimitrova and M. V. Feigel’man, “Theory of a two-dimensional superconductor with broken inversion symmetry,” Phys. Rev. B 76, 014522 (2007).
- Samokhin [2008] K. V. Samokhin, “Upper critical field in noncentrosymmetric superconductors,” Phys. Rev. B 78, 224520 (2008).
- Yanase and Sigrist [2008] Youichi Yanase and Manfred Sigrist, “Helical superconductivity in non-centrosymmetric superconductors with dominantly spin triplet pairing,” Journal of the Physical Society of Japan 77, 342–344 (2008).
- Michaeli et al. [2012] Karen Michaeli, Andrew C. Potter, and Patrick A. Lee, “Superconducting and ferromagnetic phases in oxide interface structures: Possibility of finite momentum pairing,” Phys. Rev. Lett. 108, 117003 (2012).
- Sekihara et al. [2013] Takayuki Sekihara, Ryuichi Masutomi, and Tohru Okamoto, “Two-dimensional superconducting state of monolayer pb films grown on gaas(110) in a strong parallel magnetic field,” Phys. Rev. Lett. 111, 057005 (2013).
- Houzet and Meyer [2015] Manuel Houzet and Julia S. Meyer, “Quasiclassical theory of disordered rashba superconductors,” Phys. Rev. B 92, 014509 (2015).
- Yuan and Fu [2021] Noah F. Q. Yuan and Liang Fu, “Topological metals and finite-momentum superconductors,” Proceedings of the National Academy of Sciences 118, e2019063118 (2021).
- Lee et al. [2019] Kyungmin Lee, Tamaghna Hazra, Mohit Randeria, and Nandini Trivedi, “Topological superconductivity in dirac honeycomb systems,” Phys. Rev. B 99, 184514 (2019).
- Zhang et al. [2021] Yi Zhang, Kun Jiang, Fuchun Zhang, Jian Wang, and Ziqiang Wang, “Atomic line defects and topological superconductivity in unconventional superconductors,” Phys. Rev. X 11, 011041 (2021).
- Chen et al. [2020] Cheng Chen, Kun Jiang, Yi Zhang, Chaofei Liu, Yi Liu, Ziqiang Wang, and Jian Wang, “Atomic line defects and zero-energy end states in monolayer fe(te,se) high-temperature superconductors,” Nature Physics 16, 536–540 (2020).
- Kitaev [2001] A Yu Kitaev, “Unpaired majorana fermions in quantum wires,” Physics-Uspekhi 44, 131–136 (2001).
- Beenakker [1991] C. W. J. Beenakker, “Universal limit of critical-current fluctuations in mesoscopic josephson junctions,” Phys. Rev. Lett. 67, 3836–3839 (1991).
- Mao and Sun [2022] Yue Mao and Qing-Feng Sun, “Spin phase regulated spin josephson supercurrent in topological superconductor,” Phys. Rev. B 105, 184511 (2022).
- Golubov et al. [2004] A. A. Golubov, M. Yu. Kupriyanov, and E. Il’ichev, “The current-phase relation in josephson junctions,” Rev. Mod. Phys. 76, 411–469 (2004).
- Sauls [2018] J. A. Sauls, “Andreev bound states and their signatures,” Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 376, 20180140 (2018).
- Rozhkov and Arovas [1999] A. V. Rozhkov and Daniel P. Arovas, “Josephson coupling through a magnetic impurity,” Phys. Rev. Lett. 82, 2788–2791 (1999).
- Siano and Egger [2004] F. Siano and R. Egger, “Josephson current through a nanoscale magnetic quantum dot,” Phys. Rev. Lett. 93, 047002 (2004).
- Liu et al. [2022] Yanzhao Liu, Tianheng Wei, Guanyang He, Yi Zhang, Ziqiang Wang, and Jian Wang, “Discovery of a pair density wave state in a monolayer high-Tc iron-based superconductor,” arXiv e-prints , arXiv:2209.04592 (2022), arXiv:2209.04592 [cond-mat.supr-con] .
- Robinson et al. [2010] J. W. A. Robinson, J. D. S. Witt, and M. G. Blamire, “Controlled injection of spin-triplet supercurrents into a strong ferromagnet,” Science 329, 59–61 (2010).
- Khaire et al. [2010] Trupti S. Khaire, Mazin A. Khasawneh, W. P. Pratt, and Norman O. Birge, “Observation of spin-triplet superconductivity in co-based josephson junctions,” Phys. Rev. Lett. 104, 137002 (2010).