Knowledge Cross-Distillation for Membership Privacy
Abstract
A membership inference attack (MIA) poses privacy risks for the training data of a machine learning model. With an MIA, an attacker guesses if the target data are a member of the training dataset. The state-of-the-art defense against MIAs, distillation for membership privacy (DMP), requires not only private data for protection but a large amount of unlabeled public data. However, in certain privacy-sensitive domains, such as medicine and finance, the availability of public data is not guaranteed. Moreover, a trivial method for generating public data by using generative adversarial networks significantly decreases the model accuracy, as reported by the authors of DMP. To overcome this problem, we propose a novel defense against MIAs that uses knowledge distillation without requiring public data. Our experiments show that the privacy protection and accuracy of our defense are comparable to those of DMP for the benchmark tabular datasets used in MIA research, Purchase100 and Texas100, and our defense has a much better privacy-utility trade-off than those of the existing defenses that also do not use public data for the image dataset CIFAR10.
1 Introduction
1.1 Background
Machine learning (ML) has been extensively used in various aspects of society [dlsurvey]. We have seen great improvements in areas such as image recognition and natural language processing. 00footnotetext: The authors are alphabetically ordered.
However, in the recent years, it has been reported that the privacy of the training data can be significantly undermined by analyzing ML models. Since, in most applications, privacy-sensitive data are used as the training data for the models, protecting the privacy of the training data is crucial for getting approval from data providers or essentially society.
Following the growing concern for privacy in society worldwide, many countries and regions are introducing regulations for data protection, e.g., the General Data Protection Regulation (GDPR) [GDPR], California Consumer Privacy Act (CCPA) [CCPA], and Health Insurance Portability and Accountability Act (HIPAA) [HIPAA]. Moreover, guidelines and regulations designed specifically for trustworthiness in artificial intelligence (AI) and ML are under discussion [EU-Guideline].
Membership Inference Attacks: One of the most fundamental attacks against the privacy of a ML model is the membership inference attack (MIA) [shokri2017membership, nasr2018machine, salem2019ml, song2020systematic, DBLP:conf/sp/NasrSH19, DBLP:conf/ccs/SongSM19, choo2020label, veale2018algorithms, yeom2018privacy, DBLP:journals/corr/abs-2103-07853, sablayrolles2019white], where an attacker guesses whether the given target data is in the training data of a ML model.
MIAs are dangerous because they reveal the information of individual pieces of data rather than the trend of the whole population of training data. For instance, consider an ML model for inferring a reaction to some drug from a cancer patient’s morphological data. An MIA attacker who knows the victim’s data and has access rights to the ML model can know whether the victim has cancer or not, although the victim’s data itself do not directly contain this information.
Another reason that MIAs are dangerous is that they can be executed through legitimate access to ML models only, meaning that they cannot be prevented by the conventional security methods such as data encryption and access control [shokri2017membership].
Defense against MIAs: The current state-of-the-art defense against MIAs is Distillation for Membership Privacy (DMP) [shejwalkar2021membership]. It can protect even against various state-of-the-art MIA attacks [song2020systematic, DBLP:conf/sp/NasrSH19, choo2020label], which the previous defenses [nasr2018machine, jia2019memguard] cannot protect against very well, and its success comes from the “semi-supervised assumption” that a defender can obtain public unlabeled data. Specifically, DMP exploits a knowledge transfer technique [hinton2015distil]; a defender trains an ML model using their own private data, feeds public data to the ML model to obtain the outputs of them, and trains another ML model using the public data and the corresponding outputs. Such indirect usage of private data makes knowledge distillation-based methods highly effective in protecting the privacy of private data.
However, in many domains of ML applications, public data are scarce due to the sensitive nature of the data, e.g., financial and medical data. To overcome this, utilization of synthetic data is proposed [shejwalkar2021membership] as well. However, this method decreases accuracy [shejwalkar2021membership] due to the decrease in data quality.
1.2 Our Contributions
In this paper, we propose a novel knowledge distillation-based defense that uses only private data for model training.
Our contributions are as follows.
-
–
We propose a novel MIA defense called knowledge cross-distillation (KCD)111After we submitted our work to PETS 2022 Issue 2, Tang et al. [tang2021mitigating] published a concurrent and independent work similar to ours in arXiv.. Unlike the state-of-the-art defense, DMP, it does not require any public or synthetic reference data to protect ML models. Hence, KCD allows us to protect the privacy of ML models in areas where public reference data are scarce.
-
–
For the benchmark tabular datasets used in MIA research, Purchase100 and Texas100, we empirically show that the privacy protection and accuracy of KCD are comparable to those of DMP even though KCD does not require public or synthetic data, unlike DMP.
-
–
For the image dataset CIFAR10, we empirically show that the accuracy of KCD is comparable to that of DMP, and KCD provides a much better privacy-utility trade-off than those of other defenses that do not require public or synthetic reference data.
1.3 Other Related Works
We focus only on related works that are directly related to our contributions. See Hu et al. [DBLP:journals/corr/abs-2103-07853] for a comprehensive survey of MIAs.
Membership Inference Attacks: One of the earliest works considering MIAs is by Homer et al. [homer2008resolving], and MIAs were introduced in the ML setting in a seminal work by Shokri et al. [shokri2017membership]. A series of MIA attacks, which is now called the neural network-based attack, was proposed by Shokri et al. [shokri2017membership] and was studied in detail by Salem et al. [salem2019ml] and Truex et al. [8634878]. Later, a new type of MIA attack, the metric-based attack, was proposed by Yeom et al. [yeom2018privacy] and studied by Song et al. [DBLP:conf/ccs/SongSM19], Salem et al. [salem2019ml], and Leino et al. [DBLP:conf/uss/LeinoF20]. Then, Song et al. [song2020systematic] summarized and improved upon them and proposed the state-of-the art metric-based attack as well.
Choo et al. [choo2020label] and Li et al. [DBLP:journals/corr/abs-2007-15528] independently and concurrently succeeded in attacking neural networks in a label-only setting, where an attacker can get only labels as outputs of a target neural network, while the attackers of other known papers require confidence scores as the outputs of it. Nasr et al. [DBLP:conf/sp/NasrSH19] proposed an MIA attack in a white-box setting, where an attacker can obtain the structure and parameters of the target neural network.
Known Defenses: MIAs can be mitigated using one known method, differential privacy [10.1007/11787006_1, DBLP:conf/eurocrypt/DworkKMMN06], which is a technique for guaranteeing worst-case privacy by adding noise to the learning objective or model outputs. However, defenses designed to protect against MIAs specifically have better privacy-utility trade-offs. Three MIA-specific defenses were proposed: AdvReg by Nasr et al. [nasr2018machine], MemGuard by Jia et al. [jia2019memguard], and DMP [shejwalkar2021membership].
An important technique for protecting MLs against MIAs is knowledge transfer [hinton2015distil]. Using this technique, PATE by Papernot et al. [DBLP:conf/iclr/PapernotAEGT17, DBLP:conf/iclr/PapernotSMRTE18] achieved DP, Cronos [chang2019cronus] by Chang et al. protected ML from an MIA in a federated learning setting, and DMP [shejwalkar2021membership] achieved a higher privacy-utility trade-off by removing public data with low entropy.
Currently, DMP is the best defense in the sense of the privacy-utility trade-off. However, it requires public data. Other known defenses, AdvReg and MemGuard, have an advantage in that they do not require public reference data.
2 Preliminaries
2.1 Machine Learning
An ML model for a classification task is a function parameterized by internal model parameters. It takes a -dimensional real-valued vector as input and outputs a -dimensional real-valued vector . The output has to satisfy and . Each is called a confidence score. Its intuitive meaning is the likelihood of belonging to class . The is called a predicted label (or predicted class).
An ML model is trained using a training dataset , where is a data point, and is a one-hot vector reflecting the true class label of . In the training procedure, the model parameters of are iteratively updated to reduce the predetermined loss , which is the sum of errors between the prediction and true label . For inference, takes input and outputs as a prediction.
The accuracy of for dataset is the ratio between the number of elements satisfying . Here, and are the -th component of and , respectively. The training accuracy and testing accuracy of are for the training and testing datasets, respectively. Here, testing dataset is a dataset that does not overlap with the training dataset. The generalization gap of is the difference between training and testing accuracies.
2.2 Membership Inference Attack (MIA)
MIA is an attack in which an attacker attempts to determine whether given data (called target data) are used for training a given ML model (called a target model). In the discussion of MIAs, the training data of the target model are called member data, and non-training data are called non-member data.
There are two types of MIAs, white-box and black-box [shokri2017membership, DBLP:conf/sp/NasrSH19]. Attackers of the former can take as input the model structure and model parameters of the target model. Attackers of the latter do not take them as input but are allowed to make queries to the target model and obtain answers any number of times. A black-box MIA can be divided into the two sub-types, MIA with confidence scores and label-only MIA [choo2020label]. Attackers of the former can obtain confidence scores as answers from the target model but attackers of the latter can obtain only predicted labels as answers.
In all types of MIAs, the attackers can take the target data and prior knowledge as inputs. Intuitively, the prior knowledge is what attackers know in advance. What type of prior knowledge an adversary can obtain depends on the assumed threat model. An example of prior knowledge is a dataset sampled from the same distribution as the training data of the target model, not overlapping with the training data. Another example is a portion of the training data. The prior knowledge we focused in this study is described in Section 4.3. The attack accuracy of an attacker for an MIA is the probability that they will succeed in inferring whether target data are member data. As in the all previous papers, the target data are taken from member data with a probability of .
One of the main factor causing MIA risks is overffiting of an ML model on the training (member) data. The member data can be distinguished from non-member data [yeom2018privacy, salem2019ml] depending on whether it is overfitted to the target model, e.g. by checking whether the highest confidence score of output of the target model is more than a given threshold.
2.3 Distillation for Membership Privacy (DMP)
DMP [shejwalkar2021membership] is a state-of-the-art defense method against MIAs that leverages knowledge distillation [hinton2015distil]. Distillation was originally introduced as a model compression technique that transfers the knowledge of a large teacher model to a small student model by using the output of a teacher model obtained on unlabeled reference dataset. DMP needs public reference dataset disjoint from the training dataset to train ML models with membership privacy.
The training algorithm of DMP is given in Algorithm 1. Here, is the loss function. First, DMP trains a teacher model using a private training dataset (Step 1). is overfitted to and therefore vulnerable to MIA. Next, DMP computes the soft labels of each peice of data of public reference dataset and lets be the set of (Step 2). Finally, to obtain a protected model, DMP trains a student model using the dataset (Step 3). has MIA resistance because it is trained without direct access to the private . Note that DMP uses with the same architecture as .
The authors of DMP [shejwalkar2021membership] proposed three different ways of achieving the desired privacy-utility tradeoffs:
-
–
increasing the temperature of the softmax layer of ,
-
–
removing reference data with high entropy predictions from ,
-
–
decreasing the size of the reference dataset.
All of the above changes reduce MIA risks but also the accuracy of and vice versa. When we use the second or third way to tune DMP, we select samples from the reference dataset and use them as in Step 2.
3 Our Proposed Defense
In this section, we propose a new defense that can protect ML from MIAs without using a reference dataset.
3.1 Idea
The starting point with our approach is DMP [shejwalkar2021membership]. That is, we train a teacher model using a training dataset , compute soft labels to of public reference dataset , train a student model using , and, finally, use for inference. DMP can mitigate MIAs as described in Section 2.3.
The problem with DMP is that it requires a public reference dataset, which may be difficult to collect in privacy-sensitive domains [shejwalkar2021membership]. A naïve idea to solve this problem is to use the original as a reference dataset. However, our experiment shows that this approach does not sufficiently mitigate the MIA risk (see Section LABEL:subsec:Discussions). The main problem of the naïve idea is that data of the reference dataset is member data of . Therefore, results in overfitting on and the confidence score is close to the one-hot vector of the true label. Hence, trained on results again in overfitting on , which can be exploited by an MIA.
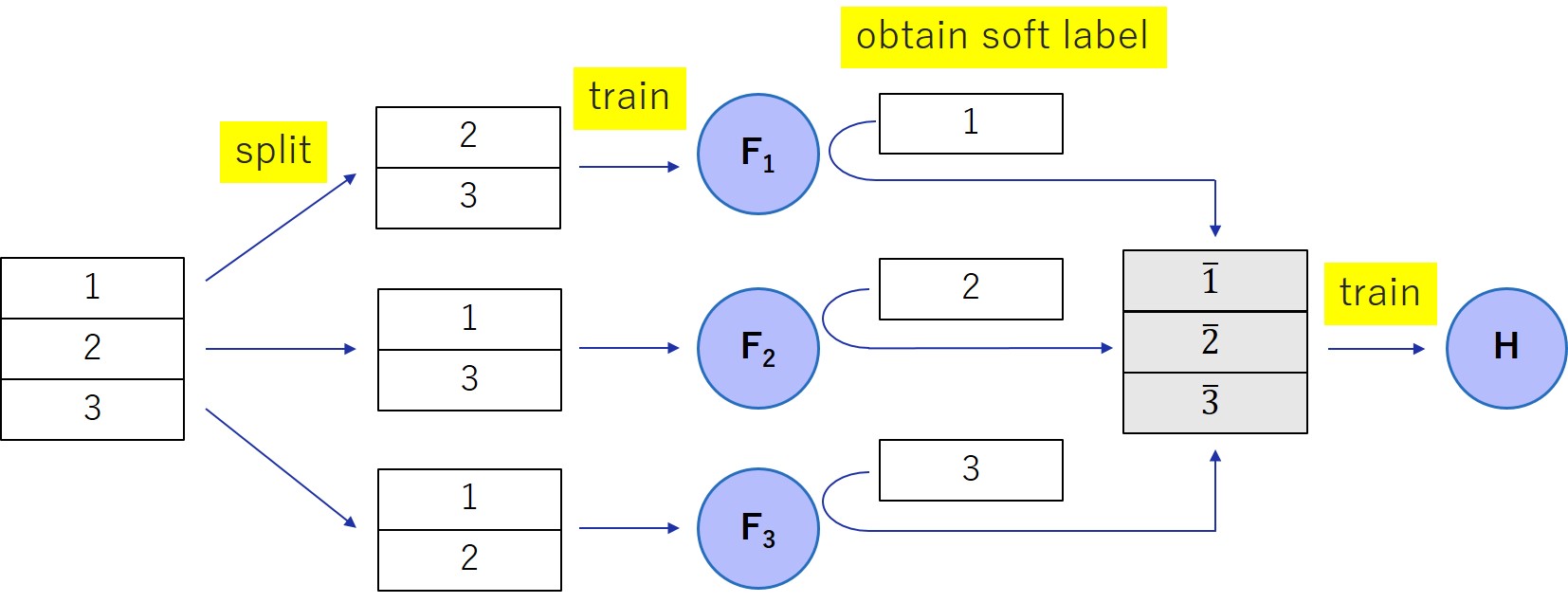
Our proposed defense, denoted by knowledge cross-distillation (KCD) is designed to overcome the above problem. We divide the training dataset into parts, leave one part as a reference dataset, and train a teacher using the remaining parts. To increase the accuracy of KCD, we prepare teachers as well and repeat the above procedure for each teacher by changing the reference part. Finally, we use each reference part to distill the knowledge of each corresponding teacher into a single . Our defense solves the problem of the naïve idea because none of the remaining parts of the training dataset are used to train the teacher model.
3.2 Description
The training algorithm of the our proposed defense, KCD, is given in Algorithm 2 and is overviewed in Figure 1. Here, , and are models with the same structure as that of the model that we want to protect222Although we use the term “distillation,” we use teacher and student models with the same structure as in DMP [shejwalkar2021membership]. This is because we are not concerned about the size of the resulting model.. is the loss function.
In Algorithm 2, we divide training dataset into disjoint subsets with almost the same size, such that holds333 denotes a disjoint union of sets (Step 1). Then, for , we train the teacher model using the dataset but exclude (Step 2-4). Let be the dataset that is obtained by adding soft labels to (Step 5). Finally, we train a student model using the dataset to minimize the combined loss function with hyperparameter (Step 6).
Our loss function comprises two terms; the first term is the loss for soft labels , and the second is the loss for the true label . The hyperparameter can tune the privacy-utility trade-off of KCD. In fact, if , our defense protects the privacy of the training data due to the reason mentioned in Section 3.1. If , KCD becomes the same as the unprotected ML.
Note that our privacy-utility trade-off based on cannot be directly applied to the known knowledge distillation-based defenses, DMP [shejwalkar2021membership] and Cronus [chang2019cronus], because the public reference datasets for these defenses do not have the true labels and loss for the predicted scores and true labels cannot be computed.
| (1) |
4 Experimental Setup
We conducted our experiments using the following datasets and model architectures as in the previous studies [shokri2017membership, nasr2018machine, jia2019memguard, choo2020label, DBLP:conf/sp/NasrSH19, shejwalkar2021membership, song2020systematic].
4.1 Datasets
CIFAR 10: This is a typical benchmark dataset used for evaluating the performance of image-classification algorithms [Krizhevsky09]. It contains RGB images. Each image is composed of pixels and labeled in one of classes.
Purchase100: This is a benchmark dataset used for MIAs. It is based on a dataset provided by Kaggle’s Acquire Valued Shoppers Challenge [Purchase100]. We used a processed and simplified one by Shokri et al. [shokri2017membership]. The dataset has records with binary features, each of which represents whether the corresponding customer purchased an item. The data are clustered into classes representing different purchase styles, and the classification task is to predict which one of the classes an input is in.
Texas100: This is also a benchmark dataset used for MIAs. It is based on the hospital discharge data [Texas100] from several health facilities published by the Texas Department of State Health Services and was processed and simplified by Shokri et al. [shokri2017membership]. It contains the 100 most frequent procedures that patients underwent. The dataset has records with binary features of patients, such as the corresponding patient’s symptoms and genetic information. The classification task is to predict which one of the procedures a patient for a piece of an input data underwent.
4.2 Model Architectures
Wide ResNet-28: For CIFAR 10, we used the same model architecture as in a previous study [choo2020label], i.e., Wide ResNet-28.
Purchase and Texas classifiers: For Purchase 100 and Texas 100, we used fully connected NNs with Tanh activation functions. We used the same layer sizes as in a previous study [nasr2018machine], i.e., layer sizes .
4.3 Setting of MIA
As in the previous studies of MIAs [nasr2018machine, DBLP:conf/sp/NasrSH19], we consider a strong setting where the attackers know the non-member dataset and a subset of the member dataset of the target model as prior knowledge. (This subset of the member dataset does not contain the target data, of course). This setting is called supervised inference [DBLP:conf/sp/NasrSH19].
One may think that the supervised inference setting seems too strong as a real setting. However, the shadow model technique [shokri2017membership] allows an attacker to achieve supervised inference virtually [DBLP:conf/sp/NasrSH19]. A shadow model is an ML model that is trained by an attacker to mimic a target ML model. The attacker then knows the training data of the shadow model as in the supervised inference setting since the attacker trains it.
4.4 MIAs for Evaluations
We conducted comprehensive experiments for three types of MIA: black-box MIA with confidence score, black-box MIA with only labels, and white-box MIA.
4.4.1 Black-box MIA with confidence score (BB w/score)
These are attacks such that the attackers know the confidences scores as outputs of the target model. There are two sub-types of these attacks.
NN-based attack: This is a type of black-box MIA using an NN, called attack classifier . Specifically, the attacker knows a set of non-member data and a subset of member data as their prior knowledge, as mentioned in Section 4.3. They send these data to the target model and obtain their confidence scores as answers. Using these data, the answers, and the knowledge of whether these data are members, they train . Finally, they infer the membership status of the target data by taking their label and confidence score as input to . There are two known NN-based attacks [shokri2017membership, salem2019ml]. The difference between them is whether the attacker trains an attack classifier for each label class; the original attack by Shokri et al. [shokri2017membership] uses one classifier per each class and a simplified attack by Salem et al. [salem2019ml], called ML Leaks Adversary 1, uses only one common attack classifier for all classes.
In our experiments, we executed the attack ML Leaks Adversary 1 [salem2019ml] since it is simpler and “has very similar membership inference” [salem2019ml] to that of Shokri et al. [shokri2017membership].
Metric-based attack: This is a type of black-box MIA that directly uses the fact that the confidence score of the target data differs depending on whether is a member. Specifically, an attacker computes a value , called a metric, and infers as a member if satisfies a given condition (e.g., greater than a given threshold). There are five known attacks of this type: Top 1, correctness, confidence, entropy, and m-entropy attacks (Table LABEL:tab:metric-based), where Top 1 was proposed in [salem2019ml], and the other four were proposed in [song2020systematic] by generalizing or improving known metric-based attacks [yeom2018privacy, DBLP:conf/ccs/SongSM19, salem2019ml, DBLP:conf/uss/LeinoF20, salem2019ml, song2020systematic].
In our experiments, we executed all five metric-based attacks [salem2019ml, song2020systematic] mentioned above.
| Name | Condition |
|---|---|
| Top 1 | |
| Correctness | |
| Confidence | |
| Entropy | |
| Modified Entropy |