Kerr magnon assisted asymptotic stationary photon-phonon squeezing

Hybrid quantum systems consisting of collective spin excitations in ferromagnetic crystals have recently attracted intensive attention [1, 2, 3, 4, 5, 6]. They offer promising avenues for advancements in quantum computing [7], quantum communication [8], and quantum sensing [9]. Similar to cavity-QED [10] and cavity optomechanics [11], cavity magnomechanics [12, 13, 14] developed rapidly as an alternative candidate for quantum information processing in both theoretical and experimental aspects. In particular, a cavity magnomechanical system comprises a single-crystal yttrium iron garnet (YIG) sphere inside a microwave cavity. The magnon mode arises from excitations of the collective angular momentum within the magnetic-material sphere, coupling with the cavity photon through magnetic dipole interaction and coupling with the sphere deformation phonon mode via magnetostrictive force. Typical applications based on such hybrid system include quantum entanglement [15, 16] and steering [17, 18], quantum squeezed states [19, 20, 21], and quantum memory [22, 23, 24].

Two-mode squeezed states (TMSS), also named Einstein-Podolsky-Rosen (EPR) states, are crucial in quantum computation [25], information [26], teleportation [27], and metrology [28]. Bosonic TMSS can be generated by mixing two single-mode squeezed states on a beam splitter [29] or via a nonlinear interaction [30, 31] such as spontaneous parametric down conversion [32]. A nondegenerate optical parametric amplifier is often used to generate optical TMSS [33, 34, 35]. Cavity optomechanics [11] provides an alternative model for creating optical [36, 37, 38] or mechanical [39, 40] TMSS. In addition, TMSS are well established in thermal gases [41], Bose-Einstein condensates of ultracold atoms [42, 43, 44, 45], spin ensembles in cavities [46, 47, 48, 49], antiferromagnet magnons [50], and superconducting circuits based on Josephson junctions [51, 52].

In this work, we propose an approach to generate photon-phonon TMSS in the cavity magnomechanics [12, 13, 14] on account of the fundamental interest in a level-resolved process. The squeezing generation is governed by an effective Hamiltonian that describes photon-phonon squeezing interaction, assisted by magnon through exploiting strong or even ultrastrong magnon-photon and magnon-phonon interactions. Inspired by the earlier method, which applies to the condition of avoided level crossing in the energy diagram [53, 54], we propose an intriguing method to confirm the effective Hamiltonian with level attractions. The method uses the diagonalization of the Liouvilian superoperator of the whole system. It can be extended to arbitrary bosonic systems, such as cavity optomechanics [11] and cavity optomagnomechanics [55], to evaluate the two-mode squeezing induced by virtual processes.

Such a two-mode squeezing naturally leads to entanglement without reservoir engineering. Under the constraint of the stable condition, the maximum logarithmic negativity [56] (a standard quantification of entanglement) is smaller than $\ln 2\sim 0.69$, by which the squeezing level cannot go beyond $3$ ${\rm dB}$ below the vacuum limit. However, by analyzing the system’s dynamic behavior within the open-quantum-system framework, we find that the stability of the Gaussian system, i.e., the covariance matrix (CM) becomes invariant under time evolution, is a sufficient but not necessary condition for the stationary generation of TMSS. We find that the asymptotic stationary TMSS can be obtained in unstable evolutions, displaying an enhanced squeezing level exceeding the stable limit. Environmental noises alter the optimized quadrature operator of two-mode squeezing while simultaneously providing TMSS an asymptotic stationary property. The coupling between two modes can influence the squeezing level, but it does not destroy the squeezing stationarity, even if it is beyond the stability threshold [32] of the CM. Through analysis of the system’s dynamical process, we found that strong coupling essentially implies strong and stationary quantum entanglement.

The rest of this work is organized as follows. In Sec. II, we introduce a hybrid cavity magnomechanical system and provide an effective Hamiltonian for photon-phonon squeezing mediated by the magnon. In Sec. III, we confirm the effective Hamiltonian by comparing the effective coupling strength and energy shift with numerical results obtained by diagonalization of the system’s Liouvilian superoperator. Section IV phenomenologically analyzes the generation process of the photon-phonon TMSS by the quantum Langevin equation. We find that the asymptotic stationary two-mode squeezing can be obtained even in an unstable dynamic regime. Finally, we discuss the experimental feasibility and summarize the work in Sec. V.

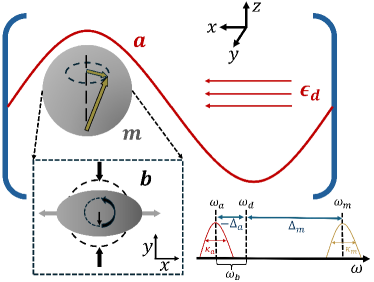
Consider a hybrid cavity magnomechanical system as shown in Fig. 1, where a YIG sphere is inserted into a three-dimensional microwave cavity. The system is constituted by the microwave-mode photons, the magnons provided by the YIG sphere, and the vibrational modes (phonons) of the sphere. The magnons are coupled to photons via the Zeeman interaction and to phonons by the magnetostrictive interaction. The hybrid system has been experimentally realized in recent works [12, 13]. The whole system Hamiltonian thus reads ($\hbar\equiv 1$)

	$\displaystyle H_{s}$	$\displaystyle=\omega_{a}a^{\dagger}a+\omega_{m}m^{\dagger}m-K_{m}m^{\dagger}mm^{\dagger}m+\omega_{b}b^{\dagger}b$		(1)
		$\displaystyle+g_{ma}(a^{\dagger}m+am^{\dagger})+g_{mb}m^{\dagger}m(b+b^{\dagger})$
		$\displaystyle+\epsilon_{d}(a^{\dagger}e^{-i\omega_{d}t}+ae^{i\omega_{d}t}),$

where $a(a^{\dagger})$, $m(m^{\dagger})$, and $b(b^{\dagger})$ are the annihilation (creation) operators of the photon mode, the magnon of the ground Kittel mode [1], and the phonon mode with transition frequencies $\omega_{a}$, $\omega_{m}$, and $\omega_{b}$, respectively. The magnon-mode frequency is $\omega_{m}=\gamma h$, where $\gamma$ is the gyromagnetic ratio and $h$ is the external bias magnetic field. Thus, it can be appropriately tuned by the external magnetic field. $K_{m}$ is the nonlinear coefficient for the Kerr effect due to the ensued magnetocrystalline anisotropy, which can be either positive or negative by adjusting the crystallographic axis of the YIG sphere along the bias magnetic field and is inversely proportional to the volume of the YIG sphere. The Kerr effect cannot be neglected when the magnon excitation number is sufficiently large [13, 57]. $g_{ma}$ is the phonon-magnon coupling strength, entering into the strong-coupling regime. The single-magnon magnomechanical coupling strength $g_{mb}$ is typically small, considering the large frequency mismatch between the magnon and the phonon modes, yet it can be compensated by a strong drive. The last term in Eq. (1) describes the external driving of the photon mode, where $\epsilon_{d}$ is the Rabi frequency and $\omega_{d}$ is the driving frequency.

The magnon mode under strong diving is assumed to have a large expectation value $|\langle m\rangle|\gg 1$, which allows us to linearize the system dynamics. Following the standard linearization approach [11, 15], the whole system Hamiltonian turns into

	$\displaystyle H$	$\displaystyle=\Delta_{a}a^{\dagger}a+\Delta^{\prime}_{m}m^{\dagger}m+\omega_{b}b^{\dagger}b+g\cosh r(am^{\dagger}+a^{\dagger}m)$		(2)
		$\displaystyle+g\sinh r(ame^{-i\theta}+a^{\dagger}m^{\dagger}e^{i\theta})$
		$\displaystyle+Ge^{r}(me^{-i\frac{\theta}{2}}+m^{\dagger}e^{i\frac{\theta}{2}})(b+b^{\dagger}),$

where $\Delta^{\prime}_{m}=\Delta_{m}/\cosh(2r)$ is the magnon-number-dependent frequency detuning ($\Delta_{m}=\omega_{m}-\omega_{d}-2K$ and $K=K_{m}|\langle m\rangle|^{2}$). $r$ is the squeezing parameter induced by the linearization of the Kerr effects and $\tanh(2r)=2K/\Delta_{m}$. $g=g_{ma}$ for simplicity, $G=g_{mb}|\langle m\rangle|$ is the effective magnomechanical coupling strength. $\theta$ is a phase associated with $\langle m\rangle=|\langle m\rangle|e^{i\theta/2}$. The details can be found in Appendix A.

At the large detuning regime, i.e., $g\cosh r,g\sinh r,Ge^{r}\ll|\Delta^{\prime}_{m}-\omega_{b}|,|\Delta^{\prime}_{m}-\Delta_{a}|$, and under the near-resonant condition $\Delta_{a}=-\omega_{b}+\delta$, we can extract an effective Hamiltonian describing the photon-phonon squeezing by perturbative theory [53, 54]. The effective Hamiltonian is found to be

$$H_{\rm eff}=g_{\rm eff}(e^{i\frac{\theta}{2}}a^{\dagger}b^{\dagger}+e^{-i\frac{\theta}{2}}ab),$$

(3)

where the effective coupling strength

$$g_{\rm eff}=-gGe^{r}\left(\frac{\sinh r}{\Delta^{\prime}_{m}-\omega_{b}}+\frac{\cosh r}{\Delta^{\prime}_{m}+\omega_{b}}\right),$$

(4)

and the energy shift

$$\delta=\frac{G^{2}e^{2r}+g^{2}\cosh^{2}r}{\Delta^{\prime}_{m}+\omega_{b}}+\frac{G^{2}e^{2r}+g^{2}\sinh^{2}r}{\Delta^{\prime}_{m}-\omega_{b}}.$$

(5)

The details can be found in Appendix B. The phase $\theta$ specifies the squeezing quadrature operator but does not affect the squeezing level. Therefore, we set $\theta=\pi$ in the following contents for simplicity and with no loss of generality. The corresponding squeezing operators can be written as

$$X(t)=\frac{1}{\sqrt{2}}[X_{a}(t)+X_{b}(t)],$$

(6)

where $X_{o}=(o+o^{\dagger})/\sqrt{2},o=a,b$. When the initial state is a vacuum state, its variance turns into $\Delta X(t)=\langle X^{2}(t)\rangle-\langle X(t)\rangle^{2}=e^{2g_{\rm eff}t}/2$ under the time-evolution of Hamiltonian (3) [32, 40]. Obviously, the quadrature operator $X$ is squeezed when $g_{\rm eff}<0$.

In this section, we check the applicability range of the effective Hamiltonian in Eq. (3) in terms of the coupling strengths and Kerr parameters. In previous works [53, 54], a method about diagonalizing the whole system Hamiltonian was employed to confirm the effective Hamiltonian constructed by virtual transitions. This method relies on a precondition that the energy splitting at the avoided level crossing point exactly equals twice the effective coupling strength, making it applicable only if the eigenenergy diagram exhibits avoided level crossings. Inspired by this method, we propose an interesting method to validate the two-mode squeezing effective Hamiltonian (3) that the energy diagram lacks avoided level crossings.

Under the evolution of the whole system Hamiltoian (2), the time-evolved quadrature operators in the Heisenberg picture can be written as

$$\dot{u}(t)=i[H,u(t)]=i\mathcal{L}u(t),$$

(7)

where $u(t)=[X_{a}(t),Y_{a}(t),X_{b}(t),Y_{b}(t),X_{m}(t),Y_{m}(t)]^{T}$ is the vector of quadrature operators, and $X_{o}=(o+o^{\dagger})/\sqrt{2},Y_{o}=(o-o^{\dagger})/i\sqrt{2},o=a,b,m$. $\mathcal{L}$ represents the Liouvilian superoperator,

$\displaystyle\mathcal{L}=-i\begin{bmatrix}0&\Delta_{a}&0&0&0&g_{+}\\ -\Delta_{a}&0&0&0&g_{-}&0\\ 0&0&0&\omega_{b}&0&0\\ 0&0&-\omega_{b}&0&0&-G_{r}\\ 0&g_{+}&G_{r}&0&0&\Delta^{\prime}_{m}\\ g_{-}&0&0&0&-\Delta^{\prime}_{m}&0\end{bmatrix},$

(8)

where $g_{\pm}=g\sinh r\pm g\cosh r$ and $G_{r}=2Ge^{r}$. The Heisenberg equation (7) can be seen as a discrete Schrödinger equation, where $u(t)$ is conceptualized as an effective operator wave function [58]. The superoperator $\mathcal{L}$ then can be analogously regarded as the whole system Hamiltonian, and its diagonalization values are the system’s eigenvalues.

We now analyze the distinct phenomenon observed in the energy diagram of the Liouvilian superoperator at two-mode squeezing. Rotating the effective Hamiltonian (3) at $\theta=\pi$ into the lab frame, it turns into

$$H_{\rm ab}=\Delta_{a}a^{\dagger}a+\omega_{b}b^{\dagger}b+g_{\rm eff}(ia^{\dagger}b^{\dagger}-iab).$$

(9)

The corresponding Heisenberg equation is

$$\dot{u}^{\rm eff}(t)=i[H_{\rm ab},u^{\rm eff}(t)]=i\mathcal{L}_{\rm ab}u^{\rm eff}(t),$$

(10)

where $u^{\rm eff}(t)=[X_{a}(t),Y_{a}(t),X_{b}(t),Y_{b}(t)]^{T}$. Four eigenvalues of the Liouvbilian superoperator $\mathcal{L}_{\rm ab}$ can be derived as

	$\displaystyle E_{\pm}$	$\displaystyle=\frac{\omega_{b}-\Delta_{a}\pm\sqrt{(\omega_{b}+\Delta_{a})^{2}-4g_{\rm eff}^{2}}}{2},$		(11)
	$\displaystyle E^{\prime}_{\pm}$	$\displaystyle=-E_{\mp}.$

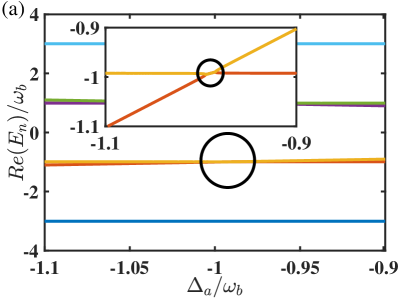
As the detuning $\Delta_{a}$ gradually approaches $-\omega_{b}$, the real parts of the eigenvalues $E_{\pm}$ ($E^{\prime}_{\pm}$) progressively converge, while the imaginary parts simultaneously increase splitting. Until $\Delta_{a}=-\omega_{b}$, the real parts of $E_{\pm}$ ($E^{\prime}_{\pm}$) become identical, while the imaginary parts reach their extreme values of $\pm g_{\rm eff}$. Then, in the energy-level diagram of the whole superoperator $\mathcal{L}$ with $\Delta_{a}$ as the variable, one can analyze the specific phenomenon, i.e., the level attractions of the real parts and the maximal splittings of the imaginary parts, to demonstrate the two-mode squeezing interaction.

We plot the energy levels (complete real and partial imaginary parts) in Fig. 2(a) and (b), where the eigenvalues $\{E_{n}\}$ are obtained by the standard numerical diagonalization on the whole system superoperator $\mathcal{L}$ in Eq. (8). Fig. 2(a) shows the real parts of all six eigenvalues. The lowest and highest correspond to magnon mode and are independent of photon-phonon squeezing. For the middle four eigenvalues, two level attractions appear simultaneously as the detuning frequency of photon $\Delta_{a}$ approaches (but does not exactly equal) the opposite frequency of phonon $-\omega_{b}$. One is highlighted in the dark circle, with the inset further emphasizing this level attraction. The imaginary parts of the two typical eigenvalues (red and orange lines) are illustrated in Fig. 2(b). As the real parts of the two eigenvalues gradually converge, their imaginary parts progressively increase, reaching a maximum absolute value $|g_{\rm eff}|$ at $\Delta_{a}=-\omega_{b}+\delta$. The shift $\delta$ is induced by the mutual interaction between the photon (phonon) and the magnon.

The maximal splitting $|g_{\rm eff}|$ of the imaginary parts of the two eigenvalues [see Fig. 2(b)] is presented in Figs. 3(a) and 3(c) as a function of the original coupling strengths $g$ and $G$ in Eq. (2), respectively. The result given by the analytical expression in Eq. (4) is compared to that evaluated by the numerical simulation over the superoperator $\mathcal{L}$ in Eq. (8). Blue dots and purple squares represent the numerical results at parameters $r=0$ and $r=0.25$, respectively. The red solid and black dashed lines are the analytical results at $r=0$ and $r=0.25$, respectively. In Fig. 3(a), the analytical $g_{\rm eff}$ do match well with their numerical results for the coupling strength $g\leq 0.3\omega_{b}$, regardless of whether $r$ is $0$ or $0.25$. The valid range has entered the ultrastrong coupling regime, $g/\omega_{b}\geq 0.1$ [59]. As $r$ increases to $0.25$, the effective coupling $g_{\rm eff}$ is significantly amplified. That can enhance the photon-phonon squeezing level in the following discussion. The value distinguished by the black box corresponds to Fig. 2 (b). In Fig. 3(c), $g_{\rm eff}$ is valid at the range of $G/\omega_{b}\leq 0.3$ when $r=0$. As $r$ increases to $0.25$, the valid range reduces to $G/\omega_{b}\leq 0.24$. Similarly, the energy shift $\delta$ in Eq. (5) can also be justified by Figs. 3(b) and 3(d). We check the same range of $g$ and $G$ as in Figs. 3(a) and 3(c). In Fig. 3(b), the analytical $\delta$ shows a slight deviation from the numerical results, but this deviation gradually decreases as $g$ and $r$ increase. In Fig. 3(d), it is found that the energy shift $\delta$ is valid at $G/\omega_{b}\leq 0.3$, whatever the parameters $r$ is $0$ or $0.25$.

Using the effective Hamiltonian (3), one can generate naturally and directly the photon-phonon TMSS. In this section, we will take the open-quantum-system framework to discuss the dynamics of TMSS generation and explain why the asymptotic two-mode squeezing can be obtained even in an unstable dynamical regime. Under the standard assumptions, i.e., Markovian approximation and structure-free environment at zero temperature, the dynamics of the quantum system are governed by the quantum Langevin equation (QLE), written in a matrix form

$$\dot{u}^{\rm eff}(t)=A_{\rm eff}u^{\rm eff}(t)+n^{\rm eff}(t),$$

(12)

where $u^{\rm eff}(t)$ is the same as Eq. (10). The transition matrix $A_{\rm eff}(t)$ is

$\displaystyle A_{\rm eff}=\begin{bmatrix}-\kappa_{a}&0&g_{\rm eff}&0\\ 0&-\kappa_{a}&0&-g_{\rm eff}\\ g_{\rm eff}&0&-\kappa_{b}&0\\ 0&-g_{\rm eff}&0&-\kappa_{b}\end{bmatrix}$

(13)

where $\kappa_{a}$ and $\kappa_{b}$ are the decay rates of the modes $a$ and $b$, respectively. $n^{\rm eff}(t)=[X^{in}_{a}(t),Y^{in}_{a}(t),X^{in}_{b}(t),Y^{in}_{b}(t)]^{T}$ is the vector of Gaussian noise operators, and $X^{in}_{o}=(o_{in}+o^{\dagger}_{in})/\sqrt{2},Y^{in}_{o}=(o_{in}-o^{\dagger}_{in})/i\sqrt{2},o=a,b$. $a_{in}$ and $b_{in}$ are characterized by their covariance functions: $\langle o_{in}(t)o^{\dagger}_{in}(t^{\prime})\rangle=[N_{o}+1]\delta(t-t^{\prime})$ and $\langle o^{\dagger}_{in}(t)o_{in}(t^{\prime})\rangle=N_{o}\delta(t-t^{\prime})$, where $N_{o}$ is the mean population of mode $o$ at the thermal equilibrium state.

By virtue of the QLE in Eq (12), the system evolution can be completely characterized by a $4\times 4$ covariance matrix (CM) $V^{\rm eff}(t)$. The dynamics of the CM $V^{\rm eff}(t)$ satisfies

$$\dot{V}^{\rm eff}(t)=A_{\rm eff}V^{\rm eff}(t)+V^{\rm eff}(t)A_{\rm eff}^{T}+D^{\rm eff}.$$

(14)

The entries of $V^{\rm eff}(t)$ are defined as

$$V^{\rm eff}_{ij}(t)=\frac{\langle u^{\rm eff}_{i}(t)u^{\rm eff}_{j}(t)+u^{\rm eff}_{j}(t)u^{\rm eff}_{i}(t)\rangle}{2},$$

(15)

where $u^{\rm eff}_{i}(t)$ is the $i$-term of $u^{\rm eff}(t)$ and $i=1,2,3,4$. $D^{\rm eff}=Diag[\kappa_{a}(2N_{a}+1),\kappa_{a}(2N_{a}+1),\kappa_{b}(2N_{b}+1),\kappa_{b}(2N_{b}+1)]$ is the diffusion matrix, which is defined through $D^{\rm eff}_{ij}(t)=\langle n^{\rm eff}_{i}(t)n^{\rm eff}_{j}(t)+n^{\rm eff}_{j}(t)n^{\rm eff}_{i}(t)\rangle/2$. In the stable condition, the CM is invariant under time evolution, i.e, $\dot{V}^{\rm eff}=0$ in Eq. (14), which requires $g^{2}_{\rm eff}<\kappa_{a}\kappa_{b}$.

Assume the photon and phonon are both in vacuum states initially, which can be realized by precooling them to their respective ground states [60]. Then the initial CM can be written as $V^{\rm eff}(0)=I_{4}/2$, $I_{4}$ is an identity matrix with four dimensions. With this condition, the non-zero matrix elements in $V^{\rm eff}(t)$ can be solved as

	$\displaystyle V^{\rm eff}_{11}(t)$	$\displaystyle=C_{+}(1-\sin\varphi)e^{(\Omega-\kappa_{a}-\kappa_{b})t}-C_{0}\cos\varphi e^{-(\kappa_{a}+\kappa_{b})t}$		(16)
		$\displaystyle+C_{-}(1+\sin\varphi)e^{-(\Omega+\kappa_{a}+\kappa_{b})t}+c_{a};$
	$\displaystyle V^{\rm eff}_{33}(t)$	$\displaystyle=C_{+}(1+\sin\varphi)e^{(\Omega-\kappa_{a}-\kappa_{b})t}+C_{0}\cos\varphi e^{-(\kappa_{a}+\kappa_{b})t}$
		$\displaystyle+C_{-}(1-\sin\varphi)e^{-(\Omega+\kappa_{a}+\kappa_{b})t}+c_{b};$
	$\displaystyle V^{\rm eff}_{13}(t)$	$\displaystyle=C_{+}\cos\varphi e^{(\Omega-\kappa_{a}-\kappa_{b})t}-C_{0}\sin\varphi e^{-(\kappa_{a}+\kappa_{b})t}$
		$\displaystyle-C_{-}\cos\varphi e^{-(\Omega+\kappa_{a}+\kappa_{b})t}+c,$

and $V^{\rm eff}_{22}(t)=V^{\rm eff}_{11}(t),V^{\rm eff}_{44}(t)=V^{\rm eff}_{33}(t),V^{\rm eff}_{24}(t)=-V^{\rm eff}_{13}(t)$. The parameters are defined as

	$\displaystyle\Omega$	$\displaystyle=\sqrt{4g^{2}_{\rm eff}+(\kappa_{a}-\kappa_{b})^{2}},\quad\tan\varphi=\frac{\kappa_{a}-\kappa_{b}}{2g_{\rm eff}},$		(17)
	$\displaystyle C_{\pm}$	$\displaystyle=\pm\frac{\kappa_{+}\mp\sin\varphi\kappa_{-}}{4[\Omega\mp(\kappa_{a}+\kappa_{b})]}+\frac{1}{4},\quad C_{0}=\frac{\cos\varphi\kappa_{-}}{2(\kappa_{a}+\kappa_{b})},$
	$\displaystyle\kappa_{\pm}$	$\displaystyle=\kappa_{a}(2N_{a}+1)\pm\kappa_{b}(2N_{b}+1).$

And

	$\displaystyle c_{o}$	$\displaystyle=N_{o}+\frac{1}{2}+\frac{g_{\rm eff}}{\kappa_{o}}c,\quad o=a,b$		(18)
	$\displaystyle c$	$\displaystyle=\frac{g_{\rm eff}\kappa_{a}\kappa_{b}(N_{a}+N_{b}+1)}{(\kappa_{a}\kappa_{b}-g^{2}_{\rm eff})(\kappa_{a}+\kappa_{b})}.$

which also exactly equal to the matrix elements $V^{\rm eff}_{11}$, $V^{\rm eff}_{33}$, and $V^{\rm eff}_{13}$ in the stable regime, obtained by setting $\dot{V}^{\rm eff}=0$ in Eq. (14). These stable CM elements are the asymptotic values as $t\to\infty$.

With the CM definition in Eq. (15) and its solution in Eq. (16), the variance of the quadrature operator $X$ in Eq. (6) can be derived as

	$\displaystyle\Delta X(t)$	$\displaystyle=\frac{1}{2}[V^{\rm eff}_{11}(t)+V^{\rm eff}_{33}(t)+2V^{\rm eff}_{13}(t)]$		(19)
		$\displaystyle=(1+\cos\varphi)C_{+}e^{(\Omega-\kappa_{a}-\kappa_{b})t}-\sin\varphi C_{0}e^{-(\kappa_{a}+\kappa_{b})t}$
		$\displaystyle+(1-\cos\varphi)C_{-}e^{-(\Omega+\kappa_{a}+\kappa_{b})t}+C,$

where

$\displaystyle C$

$\displaystyle=\frac{1}{2}(N_{a}+N_{b}+1)\frac{\kappa_{a}\kappa_{b}(2g_{\rm eff}+\kappa_{a}+\kappa_{b})}{(\kappa_{a}\kappa_{b}-g^{2}_{\rm eff})(\kappa_{a}+\kappa_{b})}.$

(20)

In the stable regime, $g^{2}_{\rm eff}<\kappa_{a}\kappa_{b}$, one can demonstrate that the exponent factor $\Omega-\kappa_{a}-\kappa_{b}$ in Eq. (19) is negative through the definition of $\Omega$ in Eq. (17). That leads to $\Delta X(\infty)=C$, consistent with the result obtained by $\dot{V}^{\rm eff}(t)=0$. When the photon decay rate is larger than the phonon decay rate, i.e., $\kappa_{a}>\kappa_{b}$, the minimal value of $C$ can be obtained as

$$C_{\rm min}=\frac{1}{2}(N_{a}+N_{b}+1)\frac{\kappa_{a}}{\kappa_{a}+\kappa_{b}}$$

(21)

at $g_{\rm eff}=-\kappa_{b}$. Even at the zero temperature, $N_{a}=N_{b}=0$, the minimum $C_{\rm min}>0.25$. The value $0.25$ corresponds to the upper bound of the squeezing level, $S=3$dB, under the stable condition. The squeezing level $S$ in the decibel unit is defined by $S=-10\log_{10}(\Delta X/\Delta X_{zp})$, where $\Delta X_{zp}=0.5$ is the standard fluctuation in the zero-point level. The decay rates satisfy $\kappa_{a}\gg\kappa_{b}$ in the recent cavity magnomechanical system [12], resulting in $C_{\rm min}\approx 0.5$ even when $N_{a}=N_{b}=0$. That implies that $X$ cannot be squeezed under stable conditions in this specific experimental platform.

It the unstable regime, $g^{2}_{\rm eff}>\kappa_{a}\kappa_{b}$, all the CM elements $V^{\rm eff}_{11}$, $V^{\rm eff}_{33}$, and $V^{\rm eff}_{13}$ in Eq. (16) exhibit exponential divergence due to the exponential factor $\Omega-\kappa_{a}-\kappa_{b}>0$. These are clearly illustrated by their respective numerical results, shown by a blue-solid line, a red-dashed line, and a black dash-dotted line in Fig. 4(a). The corresponding variance $\Delta X(t)$ in Eq. (19) is depicted by a blue solid line in Fig. 4(b). One can observe that it initially decreases until it reaches its minimum value $\Delta X(\tau)$, where the moment $\tau$ can be analytically determined by setting the derivation $\dot{\Delta X}(\tau)=0$. After reaching its minimum, $\Delta X(t)$ increases exponentially, and $\Delta X(\infty)\to+\infty$.

However, both the CM and the variance $\Delta X(t)$ instabilities do not imply nonstationary TMSS. To find a stationary TMSS with a higher squeezing level, we define a general two-mode squeezing operator $X_{\phi}=\cos\phi X_{a}+\sin\phi X_{b}$, where $\phi$ is an angle to optimize. With the CM elements (16), its variance $\Delta X_{\phi}=\langle X_{\phi}^{2}\rangle-\langle X_{\phi}\rangle^{2}$ can be described as

	$\displaystyle\Delta X_{\phi}(t)$	$\displaystyle=\cos^{2}\phi V^{\rm eff}_{11}(t)+\sin^{2}\phi V^{\rm eff}_{33}(t)+\sin(2\phi)V^{\rm eff}_{13}(t)$		(22)
		$\displaystyle=C_{+}(1-\sin\tilde{\varphi})e^{(\Omega-\kappa_{a}-\kappa_{b})t}-C_{0}\cos\tilde{\varphi}e^{-(\kappa_{a}+\kappa_{b})t}$
		$\displaystyle+C_{-}(1+\sin\tilde{\varphi})e^{-(\Omega+\kappa_{a}+\kappa_{b})t}+C_{\phi},$

where $\tilde{\varphi}=\varphi-2\phi$ and $C_{\phi}=\cos^{2}\phi c_{a}+\sin^{2}\phi c_{b}+\sin(2\phi)c$, $c_{a},c_{b},c$ are constants in Eq. (18).

From Eq. (22), one can find that the exponential divergence term of $\Delta X_{\phi}(t)$ can be canceled at an optimized angle $\tilde{\varphi}=\pi/2$, i.e., the angle $\phi$ satisfies

$$\tan(2\phi)=-\cot(\varphi)=\frac{2g_{\rm eff}}{\kappa_{b}-\kappa_{a}}.$$

(23)

Specifically, $\Delta X_{\phi}(t)=\Delta X(t)$ at $\kappa_{a}=\kappa_{b}$. Under this optimized angle, $\Delta X_{\phi}(t)$ turns into

$$\Delta X_{\phi}(t)=\frac{1}{2}+2C_{-}e^{-(\Omega+\kappa_{a}+\kappa_{b})t}-2C_{-},$$

(24)

which shows an asymptotic stationary squeezing over a long evolution, i.e., $\Delta X_{\phi}(\infty)$ equals to

$$\Delta X_{\phi}(\infty)=\frac{\Omega\kappa_{+}+(\kappa_{a}-\kappa_{b})\kappa_{-}}{2\Omega(\Omega+\kappa_{a}+\kappa_{b})}.$$

(25)

Given the definition of $\Omega$ in Eq. (17), it follows that $\Delta X_{\phi}(\infty)$ decreases as well as the two-mode squeezing enhances as $g_{\rm eff}$ increases.

In Fig. 4 (b), we plot the variance $\Delta X_{\phi}(t)$ using the effective Hamiltonian by blue dash-dotted line. After a long time evolution $\omega_{b}t\geq 450\approx 1.5\tau$, it tends to stabilize a certain value of $0.05$, and the corresponding squeezing level $S$ is about $10$dB below vacuum fluctuation, which is larger than the upper bound $3$dB in the stable condition.

We also simulate the logarithmic negativity (LN) to quantify the photon-phonon squeezing (EPR entanglement), which is defined as

$$E_{N}=\rm{Max}\left[0,-\frac{1}{2}\rm{ln}\left\{2[\mathcal{P}-(\mathcal{P}^{2}-4\det V^{\rm eff})^{1/2}\right\}\right].$$

(26)

$V^{\rm eff}=[V_{a},V_{ab};V^{T}_{ab},V_{b}]$, with $V_{a}$, $V_{b}$, and $V_{ab}$ being the $2\times 2$ blocks of $V^{\rm eff}$, and $\mathcal{P}\equiv\det V_{a}+\det V_{b}-2\det V_{ab}$. Then, the time-dependent LN can be derived as

$$E_{N}(t)=\rm{Max}\{0,-\rm{ln}\left[\eta\left(1-\sqrt{1+\delta^{\prime}}\right)\right]\}.$$

(27)

where $\eta=V^{\rm eff}_{11}(t)+V^{\rm eff}_{33}(t)$ and $\delta^{\prime}=\{4[V^{\rm eff}_{13}(t)]^{2}-4V^{\rm eff}_{11}(t)V^{\rm eff}_{33}(t)\}/\eta^{2}$. In the unstable dynamical regime $g^{2}_{eff}>\kappa_{a}\kappa_{b}$, using the solutions in Eq. (16), one can demonstrate that $\delta^{\prime}\to 0$ when $t\to\infty$. With the Taylor expansion $\sqrt{1+\delta^{\prime}}\approx 1+\delta^{\prime}/2$ up to the first order of $\delta^{\prime}$, one can finally obtain the LN at infinity

$$E_{N}(\infty)=-\ln[2\Delta X_{\phi}(\infty)].$$

(28)

The above results obtained by the effective Hamiltonian in Eq. (3) can be further confirmed by the whole system’s dynamics. Similar as Eq. (14), using the full Hamiltonian $H$ (2), the dynamics of the whole system CM $V(t)$ is determined by

$$\dot{V}(t)=AV(t)+V(t)A^{T}+D.$$

(29)

The entries of $V(t)$ are defined as $V_{ij}(t)=\langle u_{i}(t)u_{j}(t)+u_{j}(t)u_{i}(t)\rangle/2,(i,j=1,2,...6)$, where $u(t)$ is shown in Eq. (7). The transition matrix $A=i\mathcal{L}+\tilde{A}$, where $\mathcal{L}$ is the superoperator in Eq. (8) and $\tilde{A}=Diag[-\kappa_{a},-\kappa_{a},-\kappa_{b},-\kappa_{b},-e^{2r}\kappa_{m},-e^{2r}\kappa_{m}]$. The magnon decay rate is exponentially enlarged due to the Kerr effect, i.e., it turns into $e^{2r}\kappa_{m}$ [61]. $D=Diag[\kappa_{a}(2N_{a}+1),\kappa_{a}(2N_{a}+1),\kappa_{b}(2N_{b}+1),\kappa_{b}(2N_{b}+1),e^{2r}\kappa_{m}(2N_{m}+1),e^{2r}\kappa_{m}(2N_{m}+1)]$ is the matrix of noises covariance. Then, the dynamics of $\Delta X(t)$ and $\Delta X_{\phi}(t)$ can be obtained by numerically calculating the CM $V(t)$,

	$\displaystyle\Delta X(t)$	$\displaystyle=\frac{1}{2}[V_{11}(t)+V_{33}(t)+2V_{13}(t)],$		(30)
	$\displaystyle\Delta X_{\phi}(t)$	$\displaystyle=\cos^{2}\phi V_{11}(t)+\sin^{2}\phi V_{33}(t)+\sin(2\phi)V_{13}(t).$

The initial condition is $V(0)=I_{6}/2$, and $I_{6}$ is a six-dimensional identity matrix.

Numerical results are shown in Figs. 4(a) and (b). All of the matrix elements in Fig. 4(a), $V_{11}(t)$, $V_{33}(t)$, and $V_{13}(t)$, along with the variances in Fig. 4(b), $\Delta X(t)$ and $\Delta X_{\phi}(t)$ obtained using Eq. (29) do match well with the corresponding results via the effective Hamiltonian (3).

We also numerically analyze the asymptotic stationary LN, $E_{N}(\infty)$, using the whole system dynamics to evaluate our protocol. For the whole system, the $E_{N}$ is defined by replacing the $V^{\rm eff}$ in Eq. (26) with $V(1:4,1:4)$ in Eq. (29). Besides, we approximate $E_{N}(\infty)$ by evaluating the value at a sufficient long time, specifically $E_{N}(\infty)=E_{N}(2\tau)$, where $\tau$ is the moment when $\Delta X(t)$ in Eq. (19) reaches its minimum, as shown in Fig. 4 (b).

In Fig. 5(a), we illustrate the $E_{N}(\infty)$ in the parameter space of coupling strengths $g$ and $G$. One can observe that a high entanglement LN can be obtained when the coupling strengths $g$ and $G$ are increased. The LN $E_{N}(\infty)$ is greater than $2.5$ for the coupling strengths $g,G\geq 0.2\omega_{b}$. In Fig. 5(b), we present $E_{N}(\infty)$ in the parameter space defined by magnon detuning $\Delta_{m}$ and the parameter $r$. A low entanglement regime $E_{N}(\infty)\leq 0.5$ around $\Delta_{m}\approx\omega_{b}$ is observed, and the low-region enhances with increasing $r$, which is attributed to the invalidity of the effective Hamiltonian constructed in perturbation condition (3). For a fixed $r$, as $|\Delta_{m}-\omega_{b}|$ increases, $E_{N}(\infty)$ generally increases first and then decreases. A larger $|\Delta_{m}-\omega_{b}|$ allows a broader range of $r$ to achieve a high LN. An optimal parameter space $E_{N}(\infty)\geq 2$ exists at $\Delta_{m}\leq 3.5\omega_{b},r\geq 0.15$. From these findings, we conclude that our protocol significantly enhances the asymptotic stationary LN, $E_{N}$, from the previously reported values of approximately $0.1-0.3$ [15]. It can also exceed the maximum theoretical value at the stable regime, i.e., $0.69$ [36].

Our protocol is primarily centered on the cavity magnomechanical system, focusing on constructing the magnon-assisted photon-phonon squeezing via precise modulating of the driving pulse frequency in the photon mode. The parameters required are feasible in recent experiments. The phonon frequency is about $10\rm{MHz}$, with a decay rate close to $\kappa_{b}\sim 10^{-5}\omega_{b}$ [12, 13]. The transition frequency of microwave photon is around $10\rm{GHz}$, with a high quality $Q_{a}\sim 10^{5}-10^{7}$, corresponding to the decay rate $\kappa_{a}\sim 10-1000\kappa_{b}$. The magnon decay rate, $\kappa_{m}\sim 1\rm{MHz}\sim 1000\kappa_{b}$, is challenging to reduce further due to intrinsic damping [2]. However, its impact on our protocol is insignificant as the magnon primarily serves as an interface. At a low temperature $T\sim 10\rm{mK}$, both the photon and magnon excitation numbers approach zero, while the phonon number $N_{b}\approx 10$ when $\omega_{b}=10\rm{MHz}$. The magnon Kerr effect has been experimentally demonstrated in this hybrid system [13], which can be enhanced by reducing the YIG sphere’s volume [57]. In addition to the cavity magnomechanics, our protocol can be extended to other bosonic systems to generate TMSS entangled by two indirectly coupled Gaussian models. For instance, we can utilize a mechanical interface to realize the microwave-optical photon squeezing state [62, 63] or generate a photon-magnon squeezed state [55]. Hence, our scheme presents an extendable framework to create TMSS, which will be widely applied in quantum information processing and quantum metrology using bosonic systems.

In summary, we have presented a protocol for achieving photon-phonon two-mode squeezing in the cavity magnomechanics, where the magnon in the YIG sphere is coupled to both microwave photons and the mechanical vibration modes in the same sphere. Our protocol offers significant advantages in terms of solid controllability within the system, and the Kerr effect of magnon can further enhance the squeezing level. This magnon-assisted protocol relies on the two-mode squeezing effective Hamiltonian for coupling photons and phonons. We apply an interesting method by diagonalizing the whole system’s Liouvilian superoperator to numerically confirm the validity range of the effective Hamiltonian, which is beneficial in shedding light on more physics in the specific case. In the open-quantum-system framework, we derive the process for generating TMSS with the effective Hamiltonian. Our analysis demonstrates that the asymptotic stationary TMSS with high squeezing levels can be achieved even in an unstable dynamic regime. Our work provides an important implementation of TMSS generation in a solid system under realistic noises. It extends the application of cavity magnomechanics as a promising hybrid platform for quantum information processing.

We acknowledge financial support from the National Science Foundation of China (Grant No. 12404405) and the Science Foundation of Hebei Normal University of China (Grant No.13114122).