figurec

Over the past few years, the higher-order topological insulator (TI), as an overlooked intriguing topological phase, has inspired great research interests 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 ; 9 ; 10 ; TI1 ; TI2 ; TI3 ; TI4 ; TI5 ; TI6 ; TI7 ; TI8 ; TI9 ; TI10 ; TI11 . Different to conventional or the first-order TI, the higher-order band topology of m-dimensional nth-order TI is characterized by gapless states at (m-n)-dimensional boundary 1 , greatly enriching the fundamental knowledge of bulk-boundary correspondence in topological materials. Currently, there are three different physical mechanisms that have been proposed to realize the SOTI. The first is breathing-lattice mechanism, which can induce a nontrivial gap by lifting the band degeneracy between two folded Dirac bands 11 ; 12 . This type of 2D SOTI has been experimentally confirmed in a variety of artificial lattices 13 ; 14 , including the acoustic 15 ; 16 , photonic 17 and elastic 18 systems. The second is double-band-inversion mechanism, which can induce a nontrivial gap by inverting the bands with opposite parity twice 19 . This type of 3D SOTI has been experimentally confirmed in very few electronic materials, including the Bi 20 , Td-WTe₂ 21 and Bi₄Br₄ 22 . The third is in-plane Zeeman-field mechanism, which can induce a nontrivial gap by breaking the helical Dirac edge or surface states of the first-order TI 23 ; 24 ; 25 ; 26 ; 27 . This type of SOTI is a magnetic SOTI that has not been experimentally confirmed yet. Nowadays, it’s emergent to search more SOTI candidates in natural materials for accelerating the experimental detection.

As a fast-booming field, the TI research in electron is also extended to phonon in recent years 28 ; 29 ; 30 ; 31 ; 32 . Since phonon is boson without spin-orbital coupling (SOC), the well-known SOC mechanism for opening the nontrivial gap of electronic TI 33 is invalid for phononic TI. Due to such a discrepancy between phonon and electron, so far, there is no report for the phononic and electronic TI in the same system. One notices that SOC is prerequisite for the first-order TI, but not necessary for the higher-order TI 13 ; 14 . The breathing-lattice mechanism provides a simple strategy to design electronic SOTI without SOC and phononic SOTI in the same framework, making a chance to realize them simultaneously. Recently, Kekulé lattice, as one of the breathing-lattices, is successfully created by intercalating Li atoms in graphene 34 . However, it is still a challenging task to realize an intrinsic Kekulé lattice without external modifications, because this breathing order is not an energy-favorable configuration in most natural materials. Additionally, from the symmetry perspective, the vibration basis of a phonon Hamiltonian can be viewed as $p$ orbital 35 , so the out-of-plane and in-plane phonon bands should be comparable to $p_{z}$ and $p_{x,y}$ electron bands in Kekulé lattice. This feature has already been observed in previous model calculations 12 ; 30 ; 35 ; 36 , indicating the carbon-based Kekulé lattice to be an ideal platform to study both phononic and electronic SOTI.

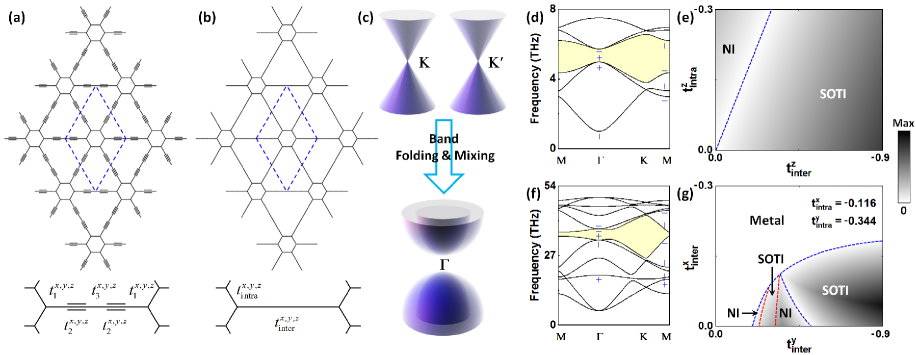
In this work, starting from the 2D graphdiyne, an electronic SOTI proposed recently 37 ; 38 , it is further identified to be a phononic SOTI by density-functional tight-binding calculations 39 , demonstrating the coexistence of 2D phononic and electronic SOTI in one natural material. Firstly, we show the equivalence between Kekulé lattice and graphdiyne, and map out a topological phase diagram for both out-of-plane and in-plane modes, where an anomalous topological phase transition without closing the bulk gap is found for the in-plane modes. Then, the edge termination dependent topological edge and corner states are investigated systematically, where the robust topological corner states can be either inside or outside the bulk gap, showing tunable energies by local corner potential. Lastly, the unique interplay between phononic and electronic topological corner states is revealed by exploring the electron-phonon coupling (EPC), where an enhanced EPC is achieved for phonon with even mirror symmetry coupled to electron spatially localized at the same corner.

The atomic structure of 2D graphdiyne is shown in Fig. 1(a), which constitutes benzene rings connected with alkyne unites 40 . If we focus on the carbon atoms in benzene rings only, it is equivalent to a Kekulé lattice, as shown in Fig. 1(b). Following the two-band analysis for graphyne 41 , the indirect phonon hopping between two vertex carbons through C-C single-bond (labeled as $t_{1}$ and $t_{3}$) and C$\equiv$C triple-bond (labeled as $t_{2}$) can be simplified to an effective inter-cell hopping for both out-of-plane ($z$) and in-plane ($x,y$) force constant as $t_{\rm{inter}}=t_{1}^{2}t_{3}/t_{2}^{2}$ SI , as shown in Fig. 1(a) and 1(b). From this kind of view, the phononic band topology of graphdiyne will be captured by the Kekulé lattice, which is supported by our numerical calculations later. Physically, the band gap of Kekulé lattice is induced by folding $\rm K$ and $\rm K^{\prime}$ Dirac cone to $\Gamma$ point, and mixing them together through different inter-cell ($t_{\rm{inter}}^{x,y,z}$) and intra-cell ($t_{\rm{intra}}^{x,y,z}$) hopping 13 ; 31 , as shown schematically in Fig. 1(c). In principles, this gap opening mechanism is applicable to both out-of-plane and in-plane phonon bands. However, the previous model of phononic and electronic SOTI are only limited in out-of-plane mode 42 and $p_{z}$ orbital 12 , without considering the possibility of in-plane mode and $p_{x},p_{y}$ orbital.

To fill out the missing region and fully understand the topological physics of SOTI in Kekulé lattice, the decoupled out-of-plane and in-plane phonon bands are calculated separately, as shown in Fig. 1(d) and 1(f), where even/odd parity is labeled as $+/-$ at time-reversal-invariant-momenta (TRIM) $\Gamma$ and M points. The quadrupole moment ($q_{12}$) is used as a topological invariant to distinguish the 2D SOTI 12 ; 43 , which is nontrivial (or trivial) for $q_{12}=1/2$ (or $0$) if the number of subbands with opposite parity between $\Gamma$ and M below the bulk gap is 2,6,10 $\cdot\cdot\cdot$ (or 4,8,12 $\cdot\cdot\cdot$) SI . Clearly, there are only two subbands satisfy this rule below the light-yellow colored gap in Fig. 1(d) and 1(f), exhibiting a 2D SOTI phase for both out-of-plane and in-plane modes. Furthermore, the topological phase diagram is mapped out to show the parameter dependence of phononic SOTI. For the out-of-plane modes described by $t_{\rm{inter}}^{z}$ and $t_{\rm{intra}}^{z}$, the phase transition between SOTI and normal insulator (NI) is characterized by closing the bulk gap at $t_{\rm inter}^{z}$=$t_{\rm intra}^{z}$ (blue-dashed line), as shown in Fig. 1(e). The SOTI exists in space for $t_{\rm inter}^{z}$ larger than $t_{\rm intra}^{z}$, which is the same to the electronic SOTI with $p_{z}$ orbital 12 . However, the phase diagram is more complex for the in-plane modes described by $t_{\rm{inter}}^{x,y}$ and $t_{\rm{intra}}^{x,y}$. Besides the metallic phase without global gap, there are two different types of phase transition between SOTI and NI, companied with (blue-dashed line) and without (red-dashed line) closing the bulk gap, as shown in Fig. 1(g). The appearance of such an anomalous phase transition without closing the bulk gap can be attributed to the special definition of quadrupole moment. Different to the $Z_{2}$ index that accounts for the number of subbands with odd parity at TRIM 44 , the quadrupole moment only accounts for the number of subbands with opposite parity between different TRIM 12 . Hence, the sequence of subbands below the bulk gap is meaningless in $Z_{2}$ index but meaningful in quadrupole moment, which can induce an anomalous higher-order topological phase transition without closing the bulk gap.

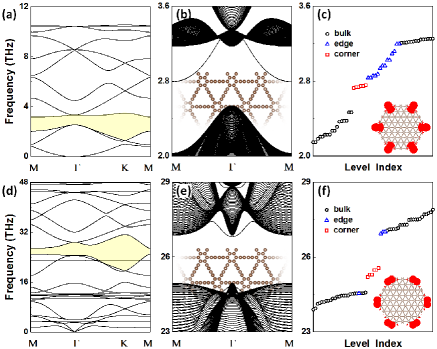
After establishing the universal phononic phase diagram of Kekulé lattice, its material realization in 2D graphdiyne is studied directly. From the bulk aspect, the out-of-plane phonon bands of graphdiyne are shown in Fig. 2(a), where the lowest six subbands are comparable to the Kekulé lattice bands shown in Fig. 1(d). Focusing on the light-yellow colored gap, we found that its quadrupole moment is $q_{12}=1/2$ SI , showing a nontrivial bulk topology for 2D SOTI. From the edge aspect, the out-of-plane phonon bands of graphdiyne nanoribbon are shown Fig. 2(b), where the edge is terminated by benzene ring connected with two carbon atoms (inset of Fig. 2(b)). There is one edge state inside the bulk gap connected with the upper bulk bands, showing the character of gapped topological edge state for 2D SOTI. From the corner aspect, the discrete out-of-plane phonon levels of hexagonal graphdiyne cluster are shown in Fig. 2(c). There are six almost degenerate corner states (red cube) inside the bulk gap, just below the discrete edge states (blue triangle). The spatial distribution of them is localized at six corners (inset of Fig. 2(c)), showing the character of in-gap topological corner state for 2D SOTI. Combining these three characters, the 2D phononic SOTI is identified in the out-of-plane modes of graphdiyne.

Moreover, the higher-order topology for the in-plane modes of graphdiyne is also describable by the Kekulé lattice. As shown in Fig. 2(d), the main feature of in-plane phonon bands of graphdiyne is comparable to the twelve-band Kekulé lattice (Fig. 1(f)), where a quantized quadrupole moment ($q_{12}=1/2$) is obtained in the light-yellow colored gap SI . For the graphdiyne nanoribbon (inset of Fig. 2(e)), there are one pair of gapped topological edge states inside the bulk gap, as shown in Fig. 2(e). For the hexagonal graphdiyne cluster, there are six spatially localized in-gap topological corner states inside the bulk gap, as shown in Fig. 2(f) and its inset. Thus, the 2D phononic SOTI is identified in the in-plane modes of graphdiyne.

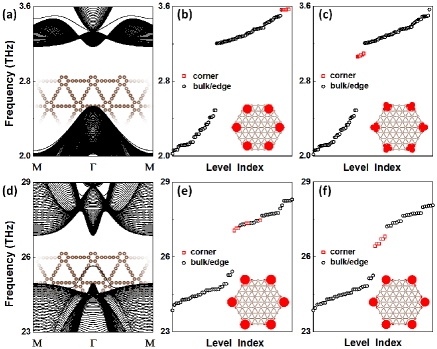
The in-gap topological corner states provide a smoking gun signature to identify the 2D phononic SOTI. However, the nontrivial bulk topology only guarantees the existence of corner states, but doesn’t restrict their energies 45 , namely, the corner states may either inside or outside the bulk gap. Additional symmetry is needed to pin them inside the bulk gap, such as chiral or particle-hole symmetry 45 . But these symmetries are not necessary to protect the 2D SOTI, which may be broken in different edge configurations. To investigate the termination dependence of topological corner states in graphdiyne, four more edges are considered, all showing the similar features (see Fig. S1 SI ). For the edge terminated by bare benzene ring (inset of Fig. 3(a)), the out-of-plane phonon bands of graphdiyne nanoribbon are shown in Fig. 3(a). Compared to Fig. 2(b), the edge state is pushed upward to the bulk bands, while one lower edge state appears with slightly splitting from the bulk bands. The corresponding discrete out-of-plane phonon levels of hexagonal graphdiyne cluster are shown in Fig. 3(b). Compared to Fig. 2(c), the six corner states (red cube) are pushed upward to the bulk levels, but they are still spatially localized at six corners (inset of Fig. 3(b)). Furthermore, if a small local corner potential is added to the corner region, these localized corner states can be pushed back to the bulk gap again, as shown in Fig. 3(c). Experimentally, this local perturbation method has already been used to detect the topological corner states buried in the bulk states 46 , making it easier to distinguish the higher-order topological phase in different conditions. For the in-plane modes, the energies of edge and corner states also depend on edge terminations, which are tunable by local corner potential, as shown in Fig. 3(d)-(f). Hence, our results demonstrate the robust existence of phononic topological corner states in graphdiyne cluster with different edge configurations, providing more convenience to realize them in the experiment.

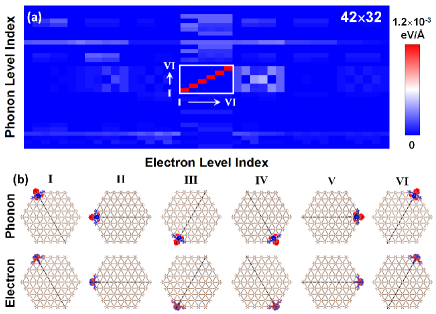
Since the phononic and electronic topological corner states coexist in graphdiyne, the EPC is further calculated to reveal the unique interplay between topological phonon and electron. The EPC ($\Xi_{\nu}^{n}$) between one electron state ($n$) and one phonon mode ($\nu$) is defined as $\Xi_{\nu}^{n}=\langle\psi_{n}|\Delta H_{\nu}|\psi_{n}\rangle$ 47 ; SI , where $|\psi_{n}\rangle$ is the electron eigenstate with index $n$ at equilibrium configuration, and $\Delta H_{\nu}$ is the variation of electron Hamiltonian induced by phonon mode $\nu$. Before performing the numerical calculations, we first make a qualitative analysis about this EPC. Based on the definition of $\Delta H_{\nu}$, one can see that its non-zero elements are limited in the space where the phonon mode $\nu$ is non-zero. Similarly, the non-zero elements of $|\psi_{n}\rangle$ are also limited in the space where the electron eigenstate $n$ is non-zero. Therefore, the degree of overlapping between these two spaces will determine the intensity of EPC. This indicates that the enhanced EPC may be achieved for phononic and electronic corner states localized at the same corner. Moreover, there are three in-plane mirror planes in graphdiyne, so the phonon mode has either even or odd mirror symmetry. Our two-atom model analysis shows that the EPC will be canceled by the phonon mode with odd mirror symmetry, which is irrelevant to the symmetry of electron state SI . This indicates that the enhanced EPC may be achieved for phononic corner states with even mirror symmetry only.

To check this analysis, the coupling between 42 electron states around Fermi-level (see Fig. S2 SI ) and 32 out-of-plane phonon modes around nontrivial gap (Fig. 2(c)) are calculated, as shown in Fig. 4(a). The EPC between six phononic and electronic corner states (labeled as I to VI) are highlighted in the while rectangular region, including 36 elements. The spatial distribution of the phononic and electronic corner states are shown in Fig. 4(b), exhibiting even mirror symmetry. Obviously, if the phonon and electron are localized at the same corner, the EPC is large (red color), otherwise, it is small (blue color). Moreover, the EPC between electron states and in-plane phonon modes (Fig. 2(f)) are also calculated. In this case, all phononic corner states have odd mirror symmetry, and no enhanced EPC is observed for phonon and electron localized at the same corner (see Fig. S3 SI ). These features are consistent with our qualitative analysis. Consequently, a unique selectivity of space and symmetry in EPC is revealed for the topological corner states.

In summary, we demonstrate the coexistence of 2D phononic and electronic SOTI in graphdiyne, and discover a distinctive EPC between phononic and electronic topological corner states. Our results extend the higher-order topological physics in Kekulé lattice and introduce an exotic platform to explore the interplay between higher-order topological phonon and electron, which will draw immediate experimental attentions.

This work was supported by National Natural Science Foundation of China (Grant No. 12174369, 11774325 and 21603210), National Key Research and Development Program of China (Grant No. 2017YFA0204904), and Fundamental Research Funds for the Central Universities. We thank Supercomputing Center at USTC for providing the computing resources.