3.6cm3.6cm3.6cm3.6cm
Jordan mating is always possible for polynomials
Abstract.
Suppose and are two post-critically finite polynomials of degree and respectively and suppose both of them have a finite super-attracting fixed point of degree . We prove that one can always construct a rational map of degree
by gluing and along the Jordan curve boundaries of the immediate super-attracting basins. The result can be used to construct many rational maps with interesting dynamics.
Key words and phrases:
2010 Mathematics Subject Classification:
Primary: 37F45; Secondary: 37F10, 37F301. Introduction
Polynomial mating was an operation proposed by Douady and Hubbard to understand the dynamics of rational maps. Very roughly speaking, for two post-critically finite polynomials and of degree with both the Julia sets being connected, we may glue and along the Julia sets to get a topological map . We say and are matable if is a branched covering map of the two sphere to itself, and moreover, is topologically conjugate to some rational map. Noting that the Julia set is the boundary of the immediate super-attracting basin of the infinity, the idea can be naturally extended to the situation of rational maps. Suppose and are two post-critically finite rational maps both of which have a simply connected immediate super-attracting basin of degree such that there are no other critical orbits which intersect the immediate basins. Then one may construct a topological map by gluing and along the attracting basin boundaries and then copy this gluing for all the pre-images of the attracting basins. As in the case of polynomial mating, we say and are matable if is a branched covering of the two sphere to itself, and moreover, is topologically conjugate to some rational map .
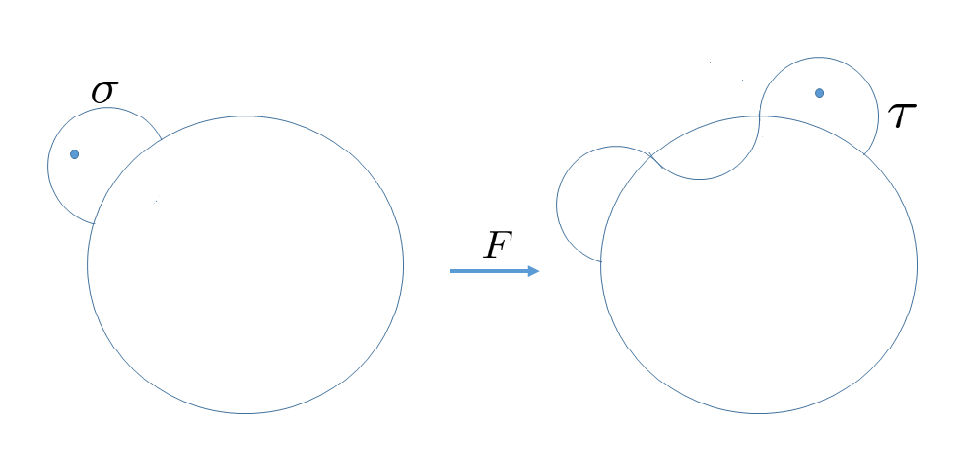
A particularly important case is that both the super-attracting basins are Jordan domains (Noting that all bounded immediate attracting basins of polynomials are Jordan domain [4]). In this case, no pinching happens when gluing and along the Jordan boundary and the topological map is always a branched covering of the two sphere to itself. Let us describe this topological construction as follows. Let and denote the two Jordan super-attracting basins and be there complements respectively. Let and be the holomorphic isomorphism which conjugate and to . Then for each ,
| (1.1) |
is a homeomorphism which reverses the orientation. We can extend it to a homeomorphism of the sphere so that it maps to and maps to . Now we glue and by identifying the points and . It is clear that is a topological two sphere. Define
by setting
| (1.2) |
Since by assumption no other critical orbits of and enter into and respectively, the way of extending dose not affect the combinatorially equivalent class of . In the case that has no Thurston obstruction, we have a rational map which is combinatorially equivalent to (One can actually prove that is topologically conjugate to ). Unlike the usual mating, whose Julia sets is the disjoint union of and with those points in a ray equivalent class being identified, the Julia set of contains infinitely many copies of and . To get , one may start from , and then iteratively fill the pre-images of and by copies of and respectively. To make a distinction with the usual mating, we call such mating a Jordan mating.
In contrast to the usual mating, for which there exist cubic polynomials which are topologically matable but not matable [6], Jordan mating is always possible for two polynomials. We will actually prove a stronger result.
Definition.
For , let denote the family of all post-critically finite rational maps which have a marked immediate super-attracting basin which is a Jordan domain and of degree such that all the other critical orbits do not intersect .
Main Theorem.
Let . Suppose such that at least one of them is a polynomial. Then and can be mated into a rational map of degree
with and being the degrees of and respectively. In particular, Jordan mating is always possible for polynomials.
Since the topological map in our case is always a branched covering of the sphere to itself, all we need to do is to show that has no Thurston obstructions. up to now there is no general way to check if a given topological map has Thurston obstructions or not, although many tools and ideas haven been developed[1][3][6][7][8]. The idea of our proof is to associate each non-peripheral curve a quantity which is monotonically increasing as we iterate the topological map. This property will lead us to get a Levy cycle from an irreducible Thurston obstruction. We then show that such a Levy cycle can be deformed into a Levy cycle of the rational map , which is a contradiction. Our argument relies essentially on the assumption that one of the two rational maps is a polynomial.
Question 1.
Is the Jordan mating always possible for rational maps in ?
2. Examples
In this section we give two examples of Jordan mating. Let be a cubic polynomial which has a degree two super-attracting fixed point at the origin so that the other finite critical point belongs to the boundary of the super-attracting basin, and moreover, . Let be a cubic polynomial which has a a degree two super-attracting fixed point at the origin so that the other finite critical point belongs to the boundary of the super-attracting basin, and moreover, . Let be a post-critically finite cubic rational map so that it has a degree two super-attracting fixed point at and the Julia set is a Sierpinski carpet.



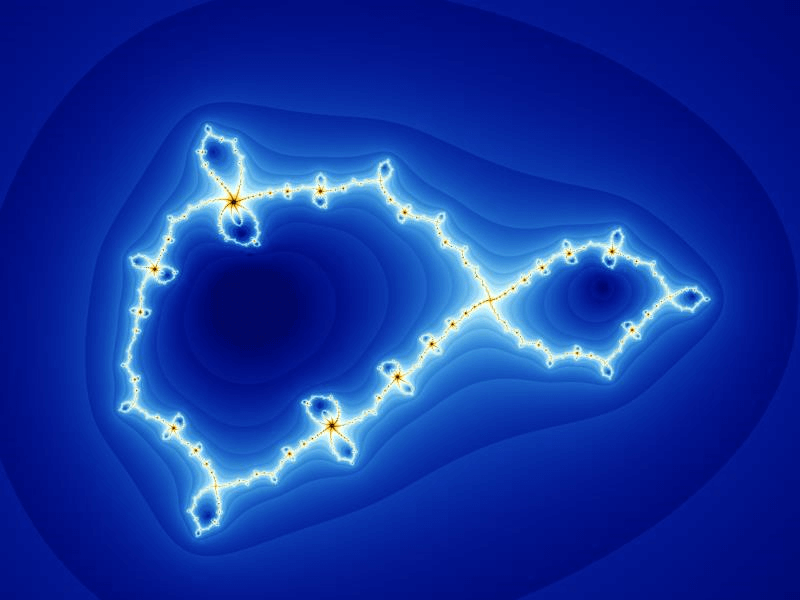

3. Proof of the main theorem
The reader may refer to [2] [5] for the details of the Thurston’s theory for characterization of post-critically finite rational maps. Throughout the paper we use , , , and to denote the Riemann sphere, the complex plane, the puncture complex plane, the unit circle and the unit disk respectively. Assume that with being a polynomial. Then there are ways to glue and along the boundary of the marked attracting basin, see (1.1). Let be one of such topological maps. All we need to do is to show that has no Thurston obstructions. We may identify the boundaries of the two marked immediate attracting basins with . We may assume that is given by , and up to combinatorial equivalence, outside and inside . When a post-critical point belongs to the forward orbit of some critical point of , we write , and similarly, if it belongs to the forward orbit of some critical point of , we write . In particular, we have
Suppose is a non-peripheral curve of . In the following we only concern those so that . By homotopy rel we may assume that is a finite set. Then consists of finitely many curve segments. Let be any of such curve segments. We call of type P (polynomial type) if it is outside , otherwise, we call it of type R (rational type). Let be the arc so that and is homotopic to rel in . Let be the union of and the bounded domain bounded by and .
Lemma 3.1.
Suppose is non-peripheral curve in and is a non-peripheral component of . Suppose is a type P curve segment of and . Then there is some type P curve segment of such that .
Proof.
By assumption the orbit of the critical points of which belongs to does not enter . So . Since the action of on the outside of is given by the polynomial , the image of is bounded whose boundaries is a subset of the union of and finitely many curve segments of type P and R of . Since , it follows that there is some type P curve segment of so that . ∎
For and a non-peripheral curve in , let denote the set of all the type P curve segments of so that . Let denote the number of the elements in . Let
where is taken over all non-peripheral curves which are homotopic to in . We need more notations.
-
•
Let denote the set of periodic points in .
-
•
Let denote the class of non-peripheral curves so that there is with and let denote the class of other non-peripheral curves.
-
•
Let denote the class of non-peripheral curves so that holds for any .
Lemma 3.2.
There is some large such that for any , if is a non-peripheral component of , then .
Proof.
Since every critical point of is eventually periodic, we have an integer such that for all . Take an arbitrary and let be a non-peripheral component of . If , then there would be a type P curve segment of , say , such that . By applying Lemma 3.1 times, we would have some type P curve segment of , say , such that . This implies that which contradicts the assumption that .
∎
Now suppose has an obstruction. Then by [5] has a canonical Thurston, say , which consists of all homotopy classes of the non-peripheral curves whose length go to zero as we iterate the Thurston pull back induced by . We claim that . Let us prove the claim. Suppose . Then must be -stable by Lemma 3.1. Since the length of every curve in goes to zero as we iterate the Thurston pull back, the transformation matrix associated to must have an eigenvalue . By the definition of , one can deform the curves in so that it is a stable family of and with the same transformation matrix. This is a contradiction because has no obstruction. This, together with Lemma 3.2, implies that . We thus have
Lemma 3.3.
If there is an obstruction for , then there must be one which consists of curves in whose length go to zero as we iterate the Thurston pull back induced by .
Lemma 3.4.
Let be a non-peripheral curve. Let . Then
where the sum is taken over all the non-peripheral components of . In particular,
Proof.
Let
where the union is taken over all the non-peripheral components of . We may introduce an order in : if and only if . Similarly we introduce an order in by setting if and only if .
Now for each , as in the proof of Lemma 3.1, has at least one component in . Let denote the maximal one among these elements. It is sufficient to show that
But this follows from the polynomial property: as we make larger, the polynomial image of will become larger, and therefore, will become strictly larger. See Figure 7 for an illustration. ∎
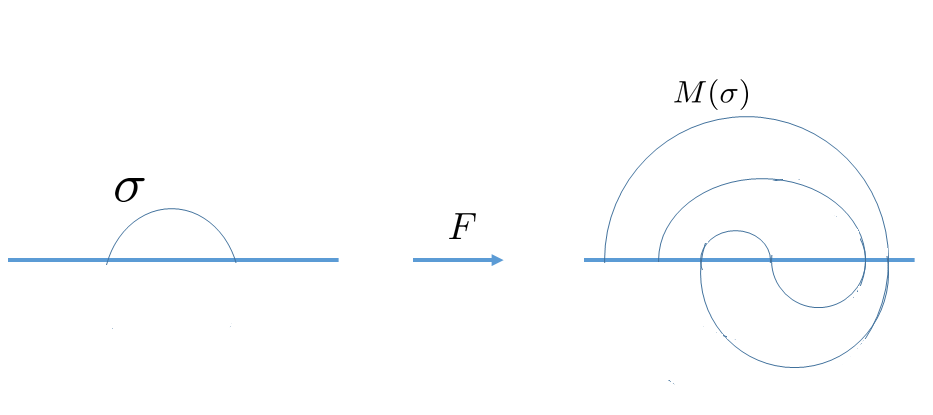
Corollary 3.5.
Suppose is a non-peripheral curve and is a non-peripheral component of . Then for any , we have
Now let us prove the main theorem. Suppose has an obstruction and let be an obstruction guaranteed by Lemma 3.3. We may assume that it is an irreducible one. That is, for any , there is an such that is homotopic to a component of . Now let us prove is a Levy cycle.
Claim: for each , there exists exactly one non-peripheral component of . Suppose this were not true. Then we would have two non-peripheral components of and two sequence:
| (3.1) |
and
| (3.2) |
where is homotopic to some component of , , and is homotopic to some component of , . Since , we have some such that . Let such that . Let be the period of the . Repeating (3.1) times,
Apply Corollary 3.5 to the above sequence, we get
which implies that
Similarly, we may repeat (3.2) times and then apply Corollary 3.5, we get
which implies that
But by Lemma 3.4 and , we also have
This implies that . This contradicts the assumption that . The Claim has been proved.
Now for any non-peripheral curve , let denote the number of the type P curve segments of and let
where is taken over all the non-peripheral curves which are homotopic to . From the claim above, it follows that must be a Levy cycle for . Let so that
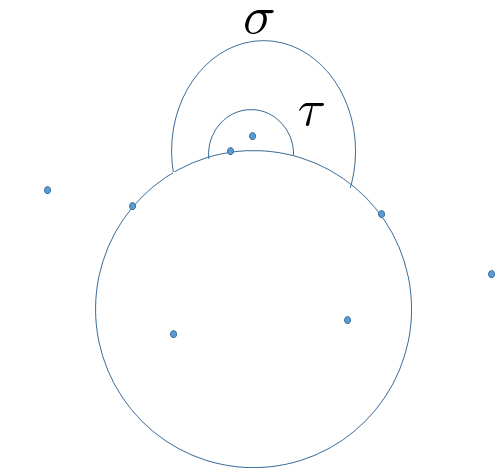
and for , is the unique non-peripheral component of . Since the image of a type P curve segment contains at least one type P curve segment, we must have
So all type P curve segments of , , are non-trivial in the sense that . So for any type P curve segment of , there is a type P curve segment which is homotopic to (Figure 8 illustrates the meaning that two type P curve segments are homotopic), such that is mapped homeomorphically to some type P curve segment of . We thus get a cycle of type P curve segments , with , such that for each , there is a type P curve segment which is homotopic to so that is a homeomorphism. Since is post-critically finite which expands the orbifold metric, it follows that contains exactly one point in , say , which lies in , and moreover, is a periodic cycle. But one may then deform each into a small neighborhood of . In this way becomes into a Levy cycle of . This is impossible. The proof of the main theorem is completed.
The author would like to thank Fei Yang who provides all the computer generating pictures in the paper.
References
- [1] B. Bielefeld, Y. Fisher, and J. Hubbard, The classification of critically preperiodic polynomials, J. Amer. Math. Soc. 5 (1992), no. 4, 721–762.
- [2] A. Douady and J. Hubbard, A proof of Thurston’s topological characterization of rational functions, Acta Math. 171 (1993), no. 2, 263–297.
- [3] M. Rees, Realization of matings of polynomials as rational maps of degree two, manuscript, 1986.
- [4] P. Roesch and Y. Yin, The boundary of bounded polynomial Fatou components, C. R. Math. Acad. Sci. Paris 346 (2008), no. 15-16, 877–880.
- [5] K. Pilgrim, Canonical Thurston obstructions, Adv. Math. 158 (2001), no. 2, 154–168.
- [6] M. Shishikura and L. Tan, A family of cubic rational maps and matings of cubic polynomials, Experiment. Math. 9 (2000), no. 1, 29–53.
- [7] L. Tan, Matings of quadratic polynomials, Ergodic Theory Dynam. Systems 12 (1992), no. 3, 589–620.
- [8] D. P. Thurston, A positive characterization of rational maps, Ann. Math. 192 (2020), no. 1, 1–46.