Joint Stabilization and Regret Minimization through Switching in Over-Actuated Systems (extended version)
Abstract
Adaptively controlling and minimizing regret in unknown dynamical systems while controlling the growth of the system state is crucial in real-world applications. In this work, we study the problem of stabilization and regret minimization of linear over-actuated dynamical systems. We propose an optimism-based algorithm that leverages possibility of switching between actuating modes in order to alleviate state explosion during initial time steps. We theoretically study the rate at which our algorithm learns a stabilizing controller and prove that it achieves a regret upper bound of .
keywords:
Adaptive Control, Regret Bound, Model-Based Reinforcement Learning, Over-Actuated Systems, Online-Learning.1 Introduction
The past few years have witnessed a growing interest in an online learning-based Linear Quadratic (LQ) control, in which an unknown LTI system is controlled while guaranteeing a suitable scaling of the regret (defined as the average difference between the closed-loop quadratic cost and the best achievable one, with the benefit of knowing the plant’s parameters) over a desired horizon .
Table 1 summarizes the regret’s scaling achieved by several recent works in the literature (Abbasi and Szepesvári (2011); Mania et al. (2019); Cohen et al. (2019); Lale et al. (2020a)). As can be seen, the bounds scale like , but also include an exponential term in (the dimension of the plant’s state plus inputs) when an initial stabilizing controller is unavailable. Recently, Chen and Hazan (2021) have shown that this dependency is unavoidable in this setting, at least for an initial exploration time period, by providing a matching lower bound. On closer inspection, this undesirable dependency stems from an exponential growth of the system’s state during the initial period of learning, which eventually contributes a term like that appearing on the last row of Table 1. Apart from negatively impacting regret, this transient state growth can also be damageable if, e.g., the linear plant to be controlled is in fact the linearization of a nonlinear process around some particular equilibrium, and the state can be driven outside the neighborhood of this equilibrium where the linearization is adequate.
A natural idea to try and partially alleviate this effect in over-actuated systems is to reduce the ambient dimension during the initial period by employing only a subset of all available actuators, before potentially switching to a different mode to simultaneously learn and control the plant. The goal of this paper is to show that this approach yields the desired result (a lower bound on the plant’s state and the regret than in the presence of all actuators) and to provide a rigorous proof of the achieved bound (where is number of actuators during initial exploration). We note that, while the idea is conceptually simple, obtaining these rigorous guarantees is not completely straightforward, and requires a revisit of the tools of Lale et al. (2020a) to overcome a potential challenge: ensuring that, at the end of the period when a strict subset of actuators is used, all entries of the B-matrix (including those corresponding to unused actuators) are sufficiently well-learned for the closed-loop to become stable and the regret to remain appropriately bounded. This can only be achieved by adding additional exploratory noise with respect to the approach of Lale et al. (2020a) and results in an additional linear term in the regret bound.
| Algorithm | Regret | * |
|---|---|---|
| Abbasi and Szepesvári (2011) | No | |
| Mania et al. (2019) | Yes | |
| Cohen et al. (2019) | Yes | |
| Lale et al. (2020a) | No |
* requirement for initial stabilizing controller.
While this idea of leveraging over-actuation can generally be applied to any model-based type of online learning algorithms presenting the exponential scaling mentioned above, we focus on the special kind of methods based on “Optimism in the Face of Uncertainty (OFU)”.
OFU type of algorithms, which couple estimation and control design procedures, have shown their ability to outperform the naive certainty equivalence algorithm. Campi and Kumar (1998) propose an OFU based approach to address the optimal control problem for LQ setting with guaranteed asymptotic optimality. However, this algorithm only guarantees the convergence of average cost to that of the optimal control in the limit but does not provide any bound on the measure of performance loss in finite time. Abbasi and Szepesvári (2011) propose a learning-based algorithm to address the adaptive control design of LQ control system in finite time with worse case regret bound of with exponential dependence in dimension. Using -regularized least square estimation, they construct a high-probability confidence set around unknown parameters of the system and designed an algorithm that optimistically plays with respect to this set. Along this line, many works attempt to get rid of the exponential dependence with further assumption, e.g. highly sparse dynamics (see Ibrahimi et al. (2012)) or access to a stabilizing controller (see Cohen et al. (2019)). Furthermore, Faradonbeh et al. (2020) propose an OFU-based learning algorithm with mild assumptions and regret. This class of algorithms was extended by Lale et al. (2020b, 2021) to LQG setting where there is only partial and noisy observations on the state of system. In addition, Lale et al. (2020a) propose an algorithm with more exploration for both controllable and stabilizable systems.
The remainder of the paper is organized as follows: Section 2 reviews the preliminaries, assumptions and presents the problem statement and formulation. Section 3 overviews the proposed initial exploration (IExp), stabilizing OFU (SOFUA) algorithms and discusses in detail how to choose best actuating mode for the initial exploration purpose. Furthermore, in Section 3 the performance analysis (state norm upper-bound and regret bound) is given while leaving the details of the analysis to Section 6 and technical theorems and proofs of analysis to Section 7. Numerical experiments are given in Section 4. Finally, Section 5 summarizes the paper’s key contributions.
2 Assumptions and Problem Formulation
Consider the following linear time invariant dynamics and the associated cost functional given by:
| (1a) | ||||
| (1b) | ||||
where the plant and input matrices and are initially unknown and have to be learned and is controllable. and represent known and positive definite matrices. denotes process noise, satisfying the following assumption.
Assumption 1
There exists a filtration such that
for some ;
are component-wise sub-Gaussian, i.e., there exists such that for any and
The problem is designing a sequence of control inputs such that the regret defined by
| (2) |
achieves a desired specification which scales sublinearly in . The term in (2) where denotes optimal average expected cost. For LQR setting with controllable pair we have , where is the unique solution of discrete algebraic riccati equation (DARE) and the average expected cost minimizing policy has feedback gain of
While the regret’s exponential dependency on system dimension appears in the long-run in Abbasi and Szepesvári (2011) the recent results of Mania et al. (2019) on the existence of a stabilizing neighborhood, makes it possible to design an algorithm that only exhibits this dependency during an initial exploration phase (see Lale et al. (2020a)).
After this period, the controller designed for any estimated value of the parameters is guaranteed to be stabilizing and the exponentially dependent term thus only appears as a constant in overall regret bound. As explained in the introduction, this suggests using only a subset of actuators during initial exploration to even further reduce the guaranteed upperbound on the state.
In the remainder of the paper, we pick the best actuating mode (i.e. subset of actuators) so as to minimize the state norm upper-bound achieved during initial exploration and characterize the needed duration of this phase for all system parameter estimates to reside in the stabilizing neighborhood. This is necessary to guarantee both closed loop stability and acceptable regret, and makes it possible to switch to the full actuation mode.
Let be the set of all columns, () of . An element of its power set is a subset of columns corresponding to a submatrix of and mode . For simplicity, we assume that i.e., that the first mode contains all actuators. Given this definition we write down different actuating modes dynamics with extra exploratory noise as follows
| (3) |
where is controllable.
The associated cost with this mode is
| (4) |
where is a block of which penalizes the control inputs of the actuators of mode .
We have the following assumption on the modes which assists us in designing proposed strategy.
Assumption 2
(Side Information)
-
1.
There exists and such that for all modes where
is controllable, .
-
2.
There are known positive constants , , such that ,
(5) and
(6) for every mode .
By slightly abusing notation, we drop the superscript label for the actuating mode 1 (e.g. , , and ). It is obvious that .
Note that the item (1) in Assumption 2 is typical in the literature of OFU-based algorithms (see e.g., Abbasi and Szepesvári (2011); Lale et al. (2020a)) while (2) in fact always holds in the sense that and are always bounded (see e.g., Abbasi and Szepesvári (2011); Lale et al. (2020a)). The point of (2), then, is that upper-bounds on their suprema are available which can in turn be used to bound regret explicitly. The knowledge of these bounds does not affect Algorithms 1 and 2 but their value enters Algorithm 3 for determination of the best actuating mode and the corresponding exploration duration. In that sense ”best actuating mode” should be understood as ”best given the available information”.
Boundedness of ’s implies boundedness of with a finite constant (see Anderson and Moore (1971)), (i.e., ). We define . Furthermore, there exists such that .
Recalling that the set of actuators of mode is , we denote its complement by (i.e. ). Furthermore, we denote the complement of control matrix by .
If some modes fail to satisfy Assumption 2 they can simply be removed from the set without affecting algorithm or the derived guarantees.
3 Overview of Proposed Strategy
In this section, we propose an algorithm in the spirit of that first proposed by Lale et al. (2020a) which leverages actuator redundancy in the ”more exploration” step to avoid blow up in the state norm while minimizing the regret bound. We break down the strategy into two phases of initial exploration, presented by Algorithm (IExp), and optimism (Opt), given by SOFUA algorithm.
The IExp algorithm, which leverages exploratory noise, is deployed in the actuating mode for duration to reach a stabilizing neighborhood of the full-actuation mode and alleviate state explosion while minimizing regret.
Afterwards, Algorithm 2 which leverages all the actuators comes into play. This algorithm has the central confidence set, given by the Algorithm 1, as an input. The best actuating mode that guarantees minimum possible state norm upper-bound and initial exploration duration is determined by running Algorithm 3 at the subsection 3.3.
3.1 Main steps of Algorithm 1
3.1.1 Confidence Set Contruction
In IExp phase we add an extra exploratory Gaussian noise to the input of all actuators even those not in actuators set of mode . Assuming that the system actuates in an arbitrary mode , the dynamics of system, used for confidence set construction (i.e. system identification), is written as
| (7) |
in which and , and where, if and , the vector is constructed by only keeping the entries of corresponding to the index set of elements in . Note that (7) is equivalent to (3) but separates used and unused actuators.
By applying self-normalized process, the least square estimation error, can be obtained as:
| (8) |
with regularization parameter . This yields the -regularized least square estimate:
| (9) |
where and are matrices whose rows are and , respectively. Defining covariance matrix as follows:
it can be shown that with probability at least , where , the true parameters of system belongs to the confidence set defined by (see 17):
| (10) |
After finding high-probability confidence sets for the unknown parameter, the core step is implementing Optimism in the Face of Uncertainty (OFU) principle. At any time , we choose a parameter such that:
| (11) |
Then, by using the chosen parameters as if they were the true parameters, the linear feedback gain is designed. We synthesized the control on (7) where . The extra exploratory noise with is the random “more exploration” term.
As can be seen in the regret bound analysis, recurrent switches in policy may worsen the performance, so a criterion is needed to prevent frequent policy switches. As such, at each time step the algorithm checks the condition to determine whether updates to the control policy are needed where is the last time of policy update.
3.1.2 Central Ellipsoid Construction
Note that (10) holds regardless of the control signal . The formulation above also holds for any actuation mode, being mindful that the dimension of the covariance matrix changes. Even while actuating in the IExp phase, by applying augmentation technique, we can build a confidence set (which we call the central ellipsoid) around the parameters of the full actuation mode thanks to extra exploratory noise. For , this simply can be carried out by rewriting (7) as follows:
| (12) |
where and is constructed by augmentation as follows
| (13) |
By this augmentation, we can construct the central ellipsoid
| (14) |
which is an input to Algorithm 2 and used to compute IExp duration.
3.2 Main steps of Algorithm 2
The main steps of Algorithm 2 are quite similar to those of Algorithm 1 with a minor difference in confidence set construction. Algorithm 2 receives , , and from Algorithm 1, using which for we have
and the confidence set is easily constructed.
The following theorem summarizes boundedness of state norm when Algorithm 1 and 2 are deployed.
Theorem 3
-
1.
The IExp algorithm keeps the states of the underlying system actuating in any mode bounded with the probability at least during initial exploration, i.e.,
(15) for all modes .
-
2.
For we, with probability at least , have where
(16)
From parts (1) and (2) of Theorem 3 we define the following good events:
| (17) |
and
| (18) |
in which
| (19) |
where both the events are used for regret bound analysis and the former one specifically is used to obtain best actuating mode for initial exploration.
3.3 Determining the Optimal Mode for IExp
We still need to specify the best actuating mode for initial exploration along with its corresponding upperbound . Theorem 5 specifies . First we need the following Lemma.
Lemma 4
At the end of initial exploration, for any mode the following inequality holds
| (20) |
where is given as follows
| (21) |
with,
in which stands for initial exploration duration of actuating in mode . Furthermore, if we define
| (22) |
then for , holds with probability at least .
The proof is provided in Appendix 7.
Theorem 5
Suppose Assumptions 1 and 2 hold true. Then for a system actuating in the mode during initial exploration phase, the following results hold true
-
1.
where is indicator function of set and
(23) with
where
in which holds with probability least .
-
2.
The best actuating mode for initial exploration is,
(24) -
3.
The upper-bound of state norm of system actuating in the mode during initial exploration phase can be written as follows:
(25) for some finite system parameter-dependent constant .
Remark 6
While optimization problem (24) cannot be solved analytically because itself depends on , it can be determined using Algorithm 3.
3.4 Regret Bound
Recall (2), the regret for the proposed strategy (IExp+
SOFUA) can be defined as follows:
| (26) |
where for and for .
An upper-bound for is given by the following theorem which is the next core result of our analysis.
4 Numerical Experiment
In this section, we demonstrate on a practical example how the use of our algorithms successfully alleviates state explosion during the initial exploration phase. We consider a control system with drift and control matrices to be set as follows:
We choose the cost matrices as follows:
The Algorithm 3 outputs the exploration duration and best actuating mode for initial exploration with corresponding control matrix and
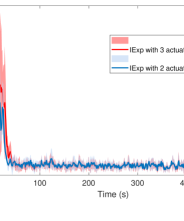
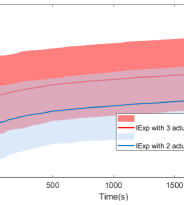
It has graphically been shown in Abbasi-Yadkori (2013) that the optimization problem (11) is generally non-convex for . Because of this fact, we decided to solve optimization problem (11) using a projected gradient descent method in Algorithm 1 and 2, with basic step
| (27) |
where for and for . is the gradient of with respect to . is the confidence set, is Euclidean projection on and finally is the step size. Computation of gradient as well as formulation of projection has been explicited in Abbasi-Yadkori (2013), similar to which we choose the learning rate as follows:
We apply the gradient method for 100 iterations to solve each OFU optimization problem and apply the projection technique until the projected point lies inside the confidence ellipsoid. The inputs to the OFU algorithm are , , , , and we repeat simulation times.
As can be seen in Fig. 1, the maximum value of the state norm (attained during the initial exploration phase) is smaller when using mode than when all actuators are in action.
Regret-bound for both cases is linear during initial exploration phase, however SOFUA guarantees regret for .
5 Conclusion
In this work, we proposed an OFU principle-based controller for over-actuated systems, which combines a step of ”more-exploration” (to produce a stabilizing neighborhood of the true parameters while guaranteeing a bounded state during exploration) with one of ”optimism”, which efficiently controls the system. Due to the redundancy, it is possible to further optimize the speed of convergence of the exploration phase to the stabilizing neighborhood by choosing over actuation modes, then to switch to full actuation to guarantee an regret in closed-loop, with polynomial dependency on the system dimension.
A natural extension of this work is to classes of systems in which some modes are only stabilizable. Speaking more broadly, the theme of this paper also opens the door to more applications of switching as a way to facilitate learning-based control of unknown systems, some of which are the subject of current work.
References
- Abbasi and Szepesvári (2011) Abbasi, Y. and Szepesvári, C. (2011). Regret bounds for the adaptive control of linear quadratic systems. In Proceedings of the 24th Annual Conference on Learning Theory, 1–26.
- Abbasi-Yadkori (2013) Abbasi-Yadkori, Y. (2013). Online learning for linearly parametrized control problems. UAlberta.
- Anderson and Moore (1971) Anderson, B.D. and Moore, J.B. (1971). Linear Optimal Control [by] Brian DO Anderson [and] John B. Moore. Prentice-hall.
- Bertsekas (2011) Bertsekas, D.P. (2011). Dynamic programming and optimal control 3rd edition, volume ii. Belmont, MA: Athena Scientific.
- Campi and Kumar (1998) Campi, M.C. and Kumar, P. (1998). Adaptive linear quadratic gaussian control: the cost-biased approach revisited. SIAM Journal on Control and Optimization, 36(6), 1890–1907.
- Chen and Hazan (2021) Chen, X. and Hazan, E. (2021). Black-box control for linear dynamical systems. In Conference on Learning Theory, 1114–1143. PMLR.
- Cohen et al. (2019) Cohen, A., Koren, T., and Mansour, Y. (2019). Learning linear-quadratic regulators efficiently with only sqrt(t) regret. International Conference on Machine Learning, 1300–1309.
- Faradonbeh et al. (2020) Faradonbeh, M.K.S., Tewari, A., and Michailidis, G. (2020). Optimism-based adaptive regulation of linear-quadratic systems. IEEE Transactions on Automatic Control, 66(4), 1802–1808.
- Ibrahimi et al. (2012) Ibrahimi, M., Javanmard, A., and Roy, B.V. (2012). Efficient reinforcement learning for high dimensional linear quadratic systems. In Advances in Neural Information Processing Systems, 2636–2644.
- Lale et al. (2020a) Lale, S., Azizzadenesheli, K., Hassibi, B., and Anandkumar, A. (2020a). Explore more and improve regret in linear quadratic regulators. arXiv preprint arXiv:2007.12291.
- Lale et al. (2020b) Lale, S., Azizzadenesheli, K., Hassibi, B., and Anandkumar, A. (2020b). Regret bound of adaptive control in linear quadratic gaussian (lqg) systems. arXiv.
- Lale et al. (2021) Lale, S., Azizzadenesheli, K., Hassibi, B., and Anandkumar, A. (2021). Adaptive control and regret minimization in linear quadratic gaussian (lqg) setting. In 2021 American Control Conference (ACC), 2517–2522. IEEE.
- Mania et al. (2019) Mania, H., Tu, S., and Recht, B. (2019). Certainty equivalence is efficient for linear quadratic control. Advances in Neural Information Processing Systems, 32.
6 Analysis
In this section, we dig further and provide a numerical experiment and rigorous analysis of the algorithms, properties of the closed-loop system, and regret bounds. The most technical results, proofs and lemma can be found in the Appendix.
6.1 Stabilization via IExp (proof of Theorem 3. (1))
This section attempts to upper-bound the state norm during initial exploration phase. We carry out this part regardless of which mode has been chosen for initial exploration.
During the initial exploration the state recursion of system actuating in mode is written as follows:
| (28) |
where . The state update equation can be written as follows:
| (29) |
where
| (30) |
and
| (31) |
By propagating the state back to time step zero, the state update equation can be written as:
| (32) |
Recalling Assumptions 2 we have
| (33) |
Now, by assuming it yields
| (34) |
On the other hand, we have
| (35) |
which results in
| (36) |
where in second term from right hand side we applied the fact that (see Assumption 2).
Now applying Lemma 18 and union bound argument one can write
| (37) |
where stands for the number of actuators of an actuating mode and similarly any subscripts and superscripts denotes the actuating mode .
The policy explicited in Algorithm 1 keeps the states of the underlying system bounded with the probability at least during initial exploration which is defined as the ”good event”
| (38) |
A second ”good event” is associated with the confidence set for an arbitraty mode defined as:
| (39) |
6.2 Determining the exploration time and best mode for IExp
6.2.1 Exploration duration
Given the constructed central confidence set , we aim to specify the time duration that guarantees the parameter estimate resides within stabilizing neighborhood. For this, we need to lower bound the smallest eigenvalue of co-variance matrix . The following lemma adapted from Lale et al. (2020a), named persistence of excitation during the extra exploration, provides this lower bound.
Lemma 8
For the initial exploration period of we have
| (40) |
with probability at least where , , and
for any and such that .
The following lemma gives an upper-bound for the parameter estimation error at the end of time which will be used to compute the minimum extra exploitation time .
Lemma 9
Suppose assumption 1 and 2 holds. For having additional exploration leads to
| (41) |
The proof is straightforward. First, a confidence set around the true but unknown parameters of the system is obtained which is given by (10). Then applying (40) given by Lemma 8 completes the proof.
There is one more step to obtain the extra exploration duration, which is obtaining an upper-bound for the right hand side of (41). Performing such a step allows us to state the following central result.
6.2.2 Best Actuating mode for initial exploration
Given the side information and s for all actuating modes , using the bound (6.1), we aim to find an actuating mode that provides the lowest possible upperbound of state at first phase. This guarantees the state norm does not blow-up while minimizing the regret. The following lemma specifies the best mode to reach this goal. Theorem 5 gives best actuating mode for IExp and its corresponding duration.
6.3 Stabilization via SOFUA (proof of Theorem 3. (2))
After running the IExp algorithm for (or ) noting that the confidence set is tight enough and we are in the stabilizing region, Algorithm 2 which leverages all the actuators comes into play. This algorithm has the central confidence set given by the Algorithm 1 as an input. The confidence ellipsoid for this phase is given as follows:
| (42) |
where
| (43) |
and
| (44) |
Now, we can define the good event for time
| (45) |
Now, we are ready to upperbound the state norm.
SOFUA keeps the states of the underlying system bounded with probability at least . In this section, we define the ”good event” for .
Noting that for the algorithm stops applying the exploratory noise , the state dynamics is written as follows: dynamics
| (46) |
where
With controllability assumption for the , if the event holds then for all . Then starting from state one can write
| (47) |
By applying union bound argument on the second term from right hand side of (47) and using the bound (25), it is straight forward to show that
where
| (48) |
For we have . Now the ”good event” is defined by
| (49) |
in which
| (50) |
.
6.4 Regret Bound Analysis
6.4.1 Regret decomposition
From definition of regret, one can write
| (51) |
Applying Bellman optimality equation (see Bertsekas (2011)) for LQ systems actuating in any mode , one can write
where for and for and with slight abuse of notation . In third equality we applied the dynamics and used the martingale property of process noise .
Now taking summation up to time and redefining gives
| (52) | |||
| (53) | |||
| (54) |
where
| (55) |
| (56) |
and
| (57) |
with for , and when for which we drop the corresponding super/sub scripts abusively.
Recalling optimal average cost value formula and taking into account that the extra exploratory noise is independent of process noise , for duration that system actuates in the mode , the term is decomposed as follows
| (58) |
From given side information (6) (Assumption 2), one can write
| (59) |
which results in
| (60) |
Combining (59) with (54) and (51) for both controllable settings under the events for and for (and for stabilizable setting with its corresponding events) the regret can be upper-bounded as follows:
| (61) |
where
| (62) |
The term given by (62) which is direct effect of extra exploratory noise on the regret bound has same upper-bound for both controllable and stabilizable settings which is given by following lemma.
Lemma 10
The following subsequent sections gives rest of upperbounds.
Lemma 11
(Bounding ) On the event for and for , with probability at least for the term is upper-bounded as follows:
| (64) |
for some problem dependent coefficients .
Proof follows as same steps as of Lale et al. (2020a), with only difference that exploration phase is performed through actuating in the mode with corresponding number of actuators .
The following lemma upper-bounds the term .
Lemma 12
(Bounding ) On the event for and for , it holds true that the term defined by (56) is upper-bounded as
| (65) |
in which
The proof can be found in Appendix 7
Lemma 13
(Bounding ) On the event for and for , the term defined by (57) has the following upper bound:
| (66) |
Putting Everything Together, gives the overall regret bound which holds with probability at least . This bound has been summarized by Theorem 7.
7 Appendix
7.1 Technical Theorems and Lemmas
Lemma 14
(Norm of Sub-gaussian vector) For an entry-wise subgaussian vector the following upper-bound holds with probability at least
Lemma 15
(Self-normalized bound for vector-valued martingales Abbasi and Szepesvári (2011)) Let be a filtration, be a stochastic process adapted to and (where is the th element of noise vector ) be a real-valued martingale difference, again adapted to filtration which satisfies the conditionally sub-Gaussianity assumption (Assumption 2.4) with known constant . Consider the martingale and co-variance matrices:
then with probability of at least , we have,
| (67) |
Given the fact that for controllable systems solving DARE gives a unique stabilizing controller, in this section we go through an important result from literature that show there is a strongly stabilizing neigborhood around the parameters of a system. This means that solving DARE for any parameter value in this neighborhood gives a controller which stabilizes the system with true parameters.
Lemma 16
(Mania et al. Mania et al. (2019)) There exists explicit constants and
in which and such that for any , we have
| (68) |
where is infinite horizon performance of policy applied on .
Lemma 16 implicitly says that for any estimates residing within stabilizing neighborhood, the designed controller, applied on true system, is stabilizing.
7.2 Confidence Set Construction
The following theorem gives the confidence set for initial exploration phase and actuating mode . Central confidence set and confidence set of actuating mode 1 can be similarly constructed.
Theorem 17
From (9) we have:
| (70) |
where and are matrices whose rows are and , respectively. and on the other hand considering the definition of , and whose rows are ,…, the dynamic of system can be written as
which leads to
Noting definition it yields
| (71) |
For an arbitrary random covariate we have,
| (72) |
By taking norm on both sides one can write,
| (73) |
where in last inequality we applied the (from Assumptions 2 and LABEL:Assumption3) and teh fact that .
Using Lemma 15, is bounded from above as
| (74) |
By arbitrarily choosing and plugging it into (73) it yields
and since , the statement of Theorem 17 holds true.
Lemma 18
(Abbasi and Szepesvári (2011)) For any and we have that
| (75) |
where is a set of finite number of times, with maximum cardinality , occurring between any time interval such that is not well controlled in those instances (see Lemma 17 and 18 of Abbasi and Szepesvári (2011) for more details).
During initial exploration, while the system actuate in an arbitrary mode it constructs the central ellipsoid by using augmentation technique. The following lemma gives an upper-bound for the determinant of co-variance matrix of mode , and that of central ellipsoid (for central ellipsoid ).
Lemma 19
Let the system actuate in an arbitrary mode and applies extra exploratory noise . Further assume that the central ellipsoid is constructed by applying augmentation technique. Then with probability at least the determinant of the co-variance matrix ( denotes the central ellipsoid) is given by
| (76) |
where .
we can write
In second inequality, we applied AM-GM inequality and in the third inequality we apply the property . Furthermore, . Given one can write:
| (77) |
where holds with probability least . This completes the proof of (20). Proof of the second statement of lemma is given in Lale et al. (2020a).
7.3 Proofs of Lemma 4 and Theorem 5
(Proof of Lemma 4). The proof directly follows by plaguing the upper-bound of into Lemma 9.
In second inequality we applied AM-GM inequality and in the third inequality we apply the property . Furthermore, . Given which holds with probability at least one can write:
| (78) |
This completes the proof of (20). Proof of the second statement of lemma is given in Lale et al. (2020a).
(Proof of Theorem 5) Given (6.1), we first upper-bound the term . First, we can write
| (79) |
which results in
| (80) |
where and . On the other hand, given the definition of one can write:
| (81) |
Combining the results give:
| (82) | ||||
| (83) |
We also have
where
One can simply rewrite as follows:
where
and
with to be defined as follows
Given the fact that . Then by having nonzero initial state then by defining we have the following upper-bound for
Then we can upper bound as follows
Hence, the state norm is bounded as follows:
By elementary but tedious calculations one can show
An upper bound for the third term in the right hand side is given by applying Lemma 4. Letting and results in
By applying elementary calculations, it yields
where
Using the property which holds and letting , one can write
By elementary calculations first statement of the lemma is shown. The proofs of statements 2 and 3 are immediate and we skip them for the sake of brevity.
7.4 Proofs of Regret Bound Analysis Section
(Proof of Lemma 12) Note that except the times instances that there is switch in policy, most terms in RHS of (56) vanish. Denote covariance matrices of central ellipse and actuating mode by and respectively, and suppose at time steps the algorithm changes the policy. Therefore, it yields for and for . This results in
| (84) | ||||
| (85) |
where and are number of switches in policy while actuating in the mode and fully actuating mode respectively. On one hand where
| (86) | ||||
| (87) |
in which we applied the bound
| (88) |
Using (84) is upper-bounded by
| (89) |
On the other hand we have where
| (90) | ||||
| (91) |
Furthermore,
| (92) |
with probability at least together with upper-bounds of state norm in both initial exploration and optimism parts yields
| (93) |
Considering (40) we have
| (94) |
now applying results in
| (95) |
Considering switch from IExp to SOFUA that can cause switch in the policy, the total number of switch in policy is . Now, applying bounds of state norm for and complete proof. The following lemma adapts the proof of Abbasi and Szepesvári (2011) to our setting which will be useful in bounding .
Lemma 20
Let , for both and , then one can write
| (97) |
For one can write
| (98) | ||||
| (99) | ||||
| (100) | ||||
| (101) |
where is the last time that policy change happened. We applied Cauchy-Schwartz inequality in (98). The inequality (99) follows from the Lemma 11 in Abbasi and Szepesvári (2011). Furthermore, applying the update rule gives (100) and finally (101) is obtained using the property for .
Now, for we have
which in turn is written
| (102) |
where in the second inequality we applied the Lemma 10 of Abbasi and Szepesvári (2011).
For the algorithm applies an extra exploratory noise, we still have same decomposition (97) with . However, to upper-bound we need to some algebraic manipulation which is substituting in terms of . Bringing this into mind, by following similar steps as of (98-101) it yields
where . Applying this result gives
| (103) |
where in first inequality we applied (79) and (92). Similar to (102) in the second inequality we applied the Lemma 10 of Abbasi and Szepesvári (2011). Combining (102) and (103) completes proof.
(Proof of Lemma 13)) In upper-bounding the term we skip a few straight forward steps which can be found in Abbasi and Szepesvári (2011) and Lale et al. (2020a) and write
| (104) | |||
| (105) |
where in the inequalities (104) and (105) we applied (103) and (102) (from the Lemma 20 ) respectively. The remaining step is following upper-bounds
where
| (106) |
and in the second inequality we applied (94). Considering the definitions of , and we can easily notice the statement of lemma holds true.