Joint Radio Frequency Fingerprints Identification via Multi-antenna Receiver

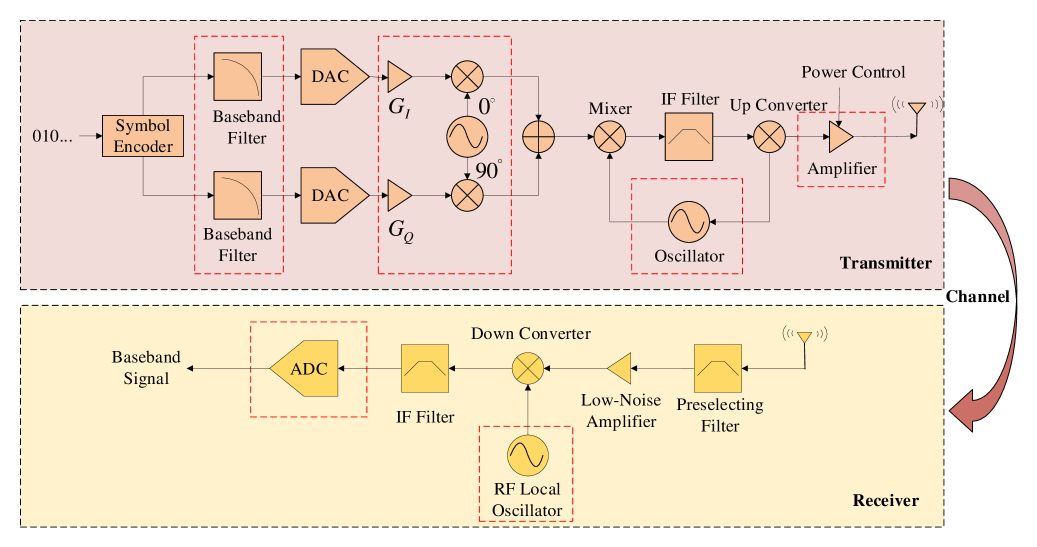
Fig. 1 depicts a typical end-to-end transceiver link and shows the source of both the emitter and receiver distortions highlighted with red dashed lines. As shown in this figure, the distortions experienced by the transmitted signal at the emitter include filter distortions, I/Q imbalance, spurious tones, and power amplifier nonlinearities. With reference to [21] and [23], the specific mathematical models for these distortions are given as follows.

• 1)

  Transmit shaping filter distortion:

  We denote the $n$th transmitted symbol after constellation mapping as $S_{n}$, and the symbol interval is $T_{s}$. Subsequently, $S_{n}$ passes through transmit shaping filter. Considering the inevitable filter distortions due to the limited precision during the manufacturing process, the actual transmit shaping filter is written as

  $$\widetilde{g}_{t}(t)=g_{t}(t)\otimes\upsilon(t),$$

  (1)

  where $\otimes$ stands for the convolution, $g_{t}(t)$ is assumed to be the ideal transmit shaping filter, and $\upsilon(t)$ denotes the filter distortion. The Fourier transform form of $\upsilon(t)$ is as follows:

  $$\Upsilon(f)=A_{\Upsilon}(f)e^{j\Phi_{\Upsilon}(f)},$$

  (2)

  where $A_{\Upsilon}(f)$ and $\Phi_{\Upsilon}(f)$ denote the amplitude distortion and phase distortion of the filter, respectively. Current literature generally uses the second-order Fourier series model to characterize these two distortions [21], such that

  $$A_{\Upsilon}(f)=\rho_{0}+\rho_{1}\rm{cos}(\frac{2\pi\it{f}}{\it{T_{A}}}),$$

  (3)

  $$\Phi_{\Upsilon}(f)=2\pi q_{0}f+q_{1}\rm{sin}(\frac{2\pi\it{f}}{\it{T}_{\rm{\Phi}}}),$$

  (4)

  where $\rho_{i}$, $q_{i}$, $i=0,1$, $T_{A}$, $T_{\Phi}$ are the parameters of the Fourier series. With the filter in (1), the transmission symbols after filter shaping can be written as

  $$s(t)=\sum_{n=-\infty}^{\infty}\widetilde{g}_{t}(t-nT_{s})S_{n}.$$

  (5)

• 2)

  I/Q distortion:

  We denote the in-phase and quadrature components of $s(t)$ in (5) by $s_{I}(t)$ and $s_{Q}(t)$, respectively. The imbalance between $s_{I}(t)$ and $s_{Q}(t)$ caused by the modulator is called I/Q distortion, which is mainly manifested as a gain mismatch and quadrature error, then the signal in (5) changes into

  	$\displaystyle x(t)$	$\displaystyle=G_{I}s_{I}(t)e^{j(2\pi ft+\zeta/2)}+G_{Q}s_{Q}(t)e^{j(2\pi ft-\zeta/2)}$		(6)
  		$\displaystyle=\alpha s(t)e^{j2\pi ft}+\beta s^{*}(t)e^{j2\pi ft},$

  where $G_{I}$ and $G_{Q}$ represent the gain mismatches of these two components, $\zeta$ denotes the quadrature error, and $(\cdot)^{*}$ stands for conjugate operation. To facilitate the following discussion, we define

  $$\begin{cases}\alpha=\frac{1}{2}(G+1)\rm{cos}(\frac{\zeta}{2})+\frac{\it{j}}{2}(\it{G}-\rm{1})\rm{sin}(\frac{\zeta}{2})\\ \beta=\frac{1}{2}(G-1)\rm{cos}(\frac{\zeta}{2})+\frac{\it{j}}{2}(\it{G}+\rm{1})\rm{sin}(\frac{\zeta}{2}).\\ G=G_{I}/G_{Q}\\ \end{cases}$$

  (7)

• 3)

  Spurious tone:

  Affected by oscillators and other active devices, DC offset commonly exists in the signal. The presence of DC offset will result in harmonic components, which we refer to as spurious tone. Considering the impact of spurious tone, the signal in (6) becomes

  $$x^{(1)}(t)=x(t)+\sum_{i=1}^{C}c_{i}e^{j2\pi(f+f_{\zeta,i})t},$$

  (8)

  where $C$ is the number of harmonic components, $c_{i}$ and $f_{\zeta,i}$ are the amplitude and frequency offset of the $i$th harmonic component, respectively. It is worth noting that when $f_{\zeta,i}=0$ and $c_{i}\neq 0$, the $i$th harmonic component is also known as carrier leakage.

• 4)

  Power amplifier nonlinearities:

  The nonlinearity of the power amplifier causes distortions in both the amplitude and phase of the signal. We express these nonlinear distortions by the Taylor series [19]. Considering a Taylor series of order $B$, the distorted signal in (8) further becomes

  $$x^{(2)}(t)=\sum_{i=0}^{B}b_{i}(x^{(1)}(t))^{2i+1},$$

  (9)

  where $b_{i}$ is the $i$th coefficient of the Taylor polynomial.

In this subsection, we consider the case of single antenna reception for simplicity. This discussion can be extended to multi-antenna reception easily, which will be described in detail in the next subsection. The channel attenuation is denoted by $h(t)$ and the additive white Gaussian noise (AWGN) is defined as $w(t)$, then the signal received by the antenna is

In the aspect of receiver distortions, we concentrate on the phase noise caused by the oscillator, as well as the sampling jitter and quantization error caused by the ADC, which have a greater impact on the received signal compared with other hardware modules [23]. These receiver distortions are modeled as follows.

• 1)

  Phase noise:

  Assume a phase-locked loop (PLL) is used at the receiver side for phase synchronization. As a typical signal frequency tracker, PLL has the advantages of high output stability and continuously adjustable phase, etc. However, it inevitably produces phase noise, under the impact of which the output signal of PLL is given as:

  $$y^{(1)}(t)=h(t)x^{(2)}(t)e^{-j(2\pi f^{\prime}t+\theta(t))}+\hat{w}(t)e^{-j(2\pi f^{\prime}t)},$$

  (11)

  where

  $$\hat{w}(t)=w(t)e^{-j\theta(t)},$$

  (12)

  $f^{\prime}$ is the local oscillator frequency and $\theta(t)$ denotes its phase noise. Similar to most studies, e.g., [21, 23], we model the phase noise as a Wiener process as follows:

  $$\theta(t)=\frac{1}{2\pi\chi}\frac{d\theta(t)}{dt}+c(t),$$

  (13)

  where $\chi$ is the 3 dB bandwidth of the phase noise power spectrum and $c(t)$ is the noise obeying the standard Gaussian distribution.

• 2)

  Sampling jitter:

  Sampling jitter means the deviation of the sampling point from the optimal position when the signal is downsampled by the ADC. In the presence of sampling jitter, the signal in (11) changes into

  $$y^{(2)}(n)=y^{(1)}(nT+\delta(n)T),$$

  (14)

  where $n$ denotes the $n$th sampling point, $T$ is the sampling period and $T\ll T_{s}$, and $\delta(n)$ denotes the relative sampling jitter, which is a random process, and $|\delta(n)|\ll 1$.

• 3)

  Quantization error:

  The signal is quantized after sampling, and the quantization error is usually modeled as additive noise in the case of uniform quantization. The quantized version of (14) is written as:

  $$y(n)=y^{(2)}(n)+\bigtriangleup(n),$$

  (15)

  where $\bigtriangleup(n)$ denotes the quantization error at the $n$th sampling point. If quantization accuracy is $\epsilon$ and the dynamic range is $[-V,V]$, then $\bigtriangleup(n)$ obeys a uniform distribution within the interval $[-2^{-\epsilon}V,2^{-\epsilon}V]$ with a variance of $2^{-2\epsilon}V^{2}/3$.

To summarize, based on (9) to (15), when the effects of the emitter distortions, channel, and receiver distortions are considered, the down-converted signal at the receiver is expressed as (16) written at the top of next page, where the second equation is the simplified form of (16) since sampling jitter does not affect the distribution of $\hat{w}(nT)$.

Based on the single-antenna reception model in the previous subsection, this subsection extends it to a multi-antenna reception scenario. Assuming an uplink multi-antenna received RFF system model consists of $M$ single-antenna IoT devices and a $N$-antenna receiver, each antenna of which is equipped with an independent oscillator.

Suppose that multiple emitters adopt orthogonal access technology to communicate with the receiver, thus this paper does not consider the interference among multiple emitters. According to the previous subsections, the down-converted signal at the $i$th antenna is established as:

where

$(k,n)$ represents the $n$th sample in the $k$th frame. $h_{i}(k,n)$ is the channel fading coefficient between the emitter and the $i$th antenna of the receiver, $\theta_{i}(k,n)$ represents the phase noise of the $i$th antenna at the receiver side, $\delta(k,n)$ denotes the sampling jitter, $\bigtriangleup_{i}(k,n)$ indicates the quantization error at the $i$th antenna, $\hat{w}_{i}(k,n)$ is the AWGN at the $i$th antenna, and $x_{m}^{(2)}(k,nT+\delta(n)T)$ in the form of (9) for the $m$th emitter.

As mentioned in the previous subsection, the antenna oscillator inevitably generates phase noise. Fortunately, it is reasonable to assume the phase noise remains constant within a single frame while varies frame-by-frame in this paper [24, 25]. Meanwhile, we assume a slow fading channel, so $h_{i}(k,n)$ remains constant within a signal frame. Based on these two assumptions, we define $h_{i}(k)\triangleq h_{i}(k,n)$ and $\theta_{i}(k)\triangleq\theta_{i}(k,n)$ for any $n$, and the model in (18) is further simplified as

The MI between the emitted signal and the received signal reflects their information similarity. In this paper, the larger the MI is, the less the emitter signal is affected by channel noise and receiver distortions. Based on this fact, we first estimate the MI between the emitter signal and the received signal at each antenna. Then the weight of the received signal at each antenna is set to be proportional to its corresponding MI. Finally, the RFFI result is obtained as the weighted voting of all classification results predicted from received signals.

In this subsection, we calculate the MI between the emitter signal and the received signal by taking one receiving antenna as an illustration, which can be extended to other antennas easily. For simplicity, the subscript $i$ of the $i$th antenna in the subsequent discussion is ignored. Based on the previous analysis, we know that the emitter signal $x^{(2)}(t)$ undergoes channel fading $h(t)$, AWGN $w(t)$, and receiver distortions before completing the classification. To facilitate subsequent analysis, we define

Firstly, with the definition in (22), we transform the signal in (10) into the frequency domain and get

where $\bf{Z}(\it{f})$, $\mathbf{G}(\it{f})$, and $\mathbf{W}(\it{f})$ are the expressions in frequency domain of $z(t)$, $g(t)$, and $w(t)$, respectively. According to [26], the MI between $\mathbf{G}(\it{f})$ and $\bf{Z}(\it{f})$ is calculated as

where $\sigma_{g}^{2}$ and $\sigma_{w}^{2}$ are the variance of $g(t)$ and $w(t)$, respectively. The function $\mathcal{H}(\cdot)$ implements entropy calculation.

Consider a special case of (24), i.e., no receiver distortion $d(t)$ exists. In this case, $\sigma_{y}^{2}=\sigma_{z}^{2}$, where $\sigma_{y}^{2}$ represents the variance of $y(t)$. Then the special case of above equation is

Note that (25) is only an ideal case, which does not exist in practical systems. To measure the quality of the received signal, we calculate the difference between (24) and (25) as follows,

where $\sigma_{h}^{2}$ and $\sigma_{x^{\rm{(2)}}}^{\rm{2}}$ indicate the variance of $h(t)$ and $x^{(2)}(t)$ in (10), respectively. In practical applications, $\sigma_{w}^{2}$ and $\sigma_{h}^{2}$ can be derived by some Signal to Noise Ratio (SNR) estimation techniques [27, 28, 29], and channel coefficient estimation techniques[30, 31]. Additionally, $\sigma_{x^{(2)}}^{2}$ can also be estimated based on the received pilots.

Obviously, a smaller $\bigtriangleup I$ indicates fewer distortions at the receiver. Based on this fact, we define the weight of $y_{i}(t)$ as,

where $\bigtriangleup I_{i}$ represents the MI difference at the $i$th receiving antenna in the form of (26).

We use $s\it{{}_{i}}$ to denote the classification result of $y_{i}(t)$. Then the weighted voting of all results is implemented based on their corresponding weights in (27), and the final RFFI result can be obtained.

Though the MIWS described in the previous subsection realizes the reduction of the negative impact of channel noise and receiver distortions through diversity gain, a more direct way is to eliminate these negative effects. Thus, this subsection proposes DFS to filter out the channel noise and receiver distortions when the number of receiving antennas is sufficiently large.

If not specifically mentioned, the following derivations are given for single-frame signal, thus we omit the label $k$. By defining $\phi_{i}=h_{i}e^{-j\theta_{i}}$, the overall system model in (21) is rewritten as

To improve the quality of $y_{i}(n)$, DFS attempts to filter out the adverse factors, i.e., $\phi_{i}$, $\bigtriangleup_{i}(n)$, and $\hat{w}_{i}(n)$.

First, by considering all the sampling points of all antennas, (28) is converted into the matrix form

where

$\Delta\in\mathbb{R}^{\it{N}\times L}$ with the $n$th element of the $i$th row being $\bigtriangleup_{i}(n)$, $\bf{\hat{W}}\in\mathbb{R}^{\it{N}\times L}$ with the $n$th element of the $i$th row being $\hat{w}_{i}(n)$, and $L$ is the number of sampling points in a frame.

The basic idea of DFS is to recover the matrix $\bf{\Xi}$ from $\bf{Y}$, and then recover $\bf{\hat{x}}$ based on its relationship with $\bf{\Xi}$ given in (32). In doing so, the impacts of $\bf{\Phi}$, $\Delta$, and $\bf{\hat{W}}$ are expected to be eliminated.

To better illustrate the statistical properties of the received signals, the matrix $\bf{Y}$ is rewritten as (33) shown at the top of the next page,

where

It should be noted that $\bf{\bigtriangleup}_{\it{i}}\it{(j)}$ and $\hat{w}_{i}(j)$ follow the uniform and Gaussian distribution, respectively. Both of them have a mean of 0. Hence, the mean of $v_{ij}$ is 0. Based on this property, we calculate the mean of each row of the matrix in (33) to obtain

where $\bf{Y}_{\it{i},.}$ denotes the $i$th row of the matrix $\bf{Y}$ in (33),

and $\mathcal{E}(\bf{u})$ calculates the mean of the vector $\bf{u}$. Based on (35), it is easy to obtain

Next, we reconstruct the $l$th row of $\bf{\Xi}$ from $\bf{Y}$, the processes of which apply to the other rows of $\bf{\Xi}$ as well. By multiplying the $j$th row of (33) by ${\phi_{l}}/{\phi_{j}}$ with $j=1,2,...,N$, which has been obtained by (35) and (37), the matrix in (33) becomes (38).

With the derived $\widetilde{\bf{Y}}^{(l)}$ in (38), by calculating its column mean, we get

where $\mathcal{E}_{c}(\bf{U})$ calculates the column mean of the matrix $\bf{U}$. It is worth noting that $\mathcal{E}_{c}(\widetilde{\bf{Y}}^{(l)})$ is exactly the $l$th row of $\bf{\Xi}$, which is denoted as $\bf{\Xi}_{\it{l},\cdot}$. Following the above procedures, we are able to recover all the rows of $\bf{\Xi}$ by varying the value of $l$ from 1 to $N$ in order.

By observing $\bf{\Xi}$, we find that directly separating it into $\bf{\Phi}$ and $\bf{\hat{x}}$ without any prior knowledge of $\bf{\hat{x}}$ is impossible. Fortunately, by defining $\rm{\hat{\it{x}}_{\it{m}}(1)}$ as the first symbol of this frame, we have

where

It is obvious that $\widetilde{\bf{x}}$ is highly correlated with $\bf{\hat{x}}$.

Since $\widetilde{\bf{x}}$ retains all the information of $\bf{\hat{x}}$, it is reasonable to use $\widetilde{\bf{x}}$ rather than $\bf{\hat{x}}$ as the signal for the subsequent RF feature extraction and classification without affecting the performance of RFFI.

We find that in (35) and (39) the calculation of the mean is implemented. However, in practical scenarios, it can only be approximated by averaging. To ensure the effect of filtering out channel noise and receiver distortions, $L$ and $N$ should be large enough. Generally, $L$ is sufficiently large in practical applications. Therefore, the filtering ability of DFS mainly depends on the value of $N$, and their relationship will be analyzed in detail in Section IV.

The previous analysis has suggested the larger $N$ is, the smaller the difference between the averaging result and the actual mean 0. When $N$ is sufficiently large, this difference will be definitely very small. At this moment, even if we further increase $N$, the difference will converge and thus no significant performance enhancement will appear. We call such phenomenon of DFS as performance saturation. To alleviate this problem when the number of receiving antennas is large, this subsection proposes GDFWS that divides all antennas into several groups to avoid the appearance of saturation phenomenon.

Fig. 3 illustrates the overall structure of GDFWS, where signals received by all antennas are divided into four groups for illustration. In this figure, $N_{1}=N/2$, and $N_{2}=N/2+1$. First, DFS is applied in each group to filter out channel noise and receiver distortions. Then, the obtained $\widetilde{x}_{i}(t),i\in{1,2,3,4}$ are delivered to the feature extraction module and weight calculation module, where the former extracts RF features that are subsequently fed into the classification module to obtain classification results $\bf{s}\in\mathbb{R}^{\rm{1}\times\it{N}}$, and the later calculates their respective weights $\bf{\omega}\in\mathbb{R}^{\rm{1}\times\it{N}}$. Finally, the classification result $\bf{s}$ and its corresponding weight $\bf{\omega}$ are sent into the weighted voting module to obtain the final RFFI result.

Obviously, GDFWS enjoys the advantages of both MIWS and DFS in terms of diversity gain and adverse factors elimination. Meanwhile, the above structure can be easily extended to the case of multiple groups, where the number of antennas in each group is smaller than the one when DFS exhibits performance saturation.

According to the produces of RFF, we describe the settings of the simulation experiments in this paper from five aspects in turn: emitters, channel, receiver, RF feature extraction methods, and classifiers, the detail of which are as follows.

• 1)

  The settings of emitters:

  	$\rm{T_{1}}$	$\rm{T_{2}}$	$\rm{T_{3}}$	$\rm{T_{4}}$	$\rm{T_{5}}$
  $\rho_{0}$	1	1	1	1	1
  $\rho_{1}$	0.03	0.06	0.085	0.073	0.040
  $T_{A}$	4	4	4	4	4
  $q_{0}$	1	1	1	1	1
  $q_{1}$	0.0302	0.0295	0.0290	0.0310	0.0313
  $T_{\Phi}$	4	4	4	4	4
  $G$	0.998	1.0056	1.0102	0.9992	0.9982
  $\zeta$	-0.018∘	0.0175∘	0.012∘	0.003∘	0.024∘
  $c_{1}$	0.0013+0.0082j	0.0015+0.0072j	0.0011+0.0068j	0.0017+0.009j	0.002+0.0065j
  $c_{2}$	0.0082	0.0075	0.0070	0.0087	0.0090
  $f_{\zeta,1}$	0	0	0	0	0
  $f_{\zeta,2}$	0.0129	0.0132	0.0123	0.0135	0.0119
  $b_{1}$	1	1	1	1	1
  $b_{3}$	0.3	0.6	0.01	0.4	0.08

  The RF signal is generated according to the emitter distortion model described in Section II. It should be noted that we assume the number of harmonic components in (8) and the order of the Taylor series in (9) both are 2. We consider 5 emitters with the distortion parameters provided in Table IV, where the E and P are abbreviations for Emitters and Parameters, respectively, and $\rm{T_{1}}$ to $\rm{T_{5}}$ labels for emitter 1 to emitter 5. The modulation mode of the RF signal is QPSK, with the oversampling factor $T/T_{s}=10$, $1/T_{s}=10^{6}$ MHz, and the signal center frequency is 1GHz. A frame consists of 128 symbols, wherein 32 symbols carry pilots.

• 2)

  The settings of channel:
  AWGN channel is considered in our experiments, so the channel fading coefficients $h_{i}(k)$ in (21) is set to be 1. Nonetheless, the following experimental conclusions also apply to the case where the channel coefficients are random.

• 3)

  The settings of the receiver:
  The receiver distortions are generated according to the receiver distortion model described in Section II. The distortion parameters of sampling jitter and quantization errors are set as follows: $\delta(n)=0.003$, $V=1$, $\epsilon=16$. The parameter $\chi$ in (13) for phase noise varies to show its influence on RFFI accuracy.

• 4)

  RF feature extraction methods:
  Two classical RF feature extraction methods, i.e., least mean square (LMS)-based feature extraction [33] and intrinsic time-scale decomposition (ITD)-based feature extraction [21], are used in our experiments. The LMS-based feature extraction method updates its filter weights recursively based on some criteria until convergence, then uses its converged weight vector as features. The ITD-based feature extraction method first decomposes the signal by ITD and then calculates the skewness and kurtosis of each decomposed signal as the feature vector.

• 5)

  Classifiers:
  Currently, there have been many successful classifiers applied to RFFI. However, since classifiers are not the focus of our paper, we choose the typical multi-classification SVM for RFF classification.

In the following experiments, the number of training frames and testing frames for each emitter is 200 and 100, respectively. Each experiment result is obtained by averaging over 1000 trials. We use ORS to represent the original scheme without distortion filtering and the weighted voting operation, which is used as a benchmark for the proposed schemes.

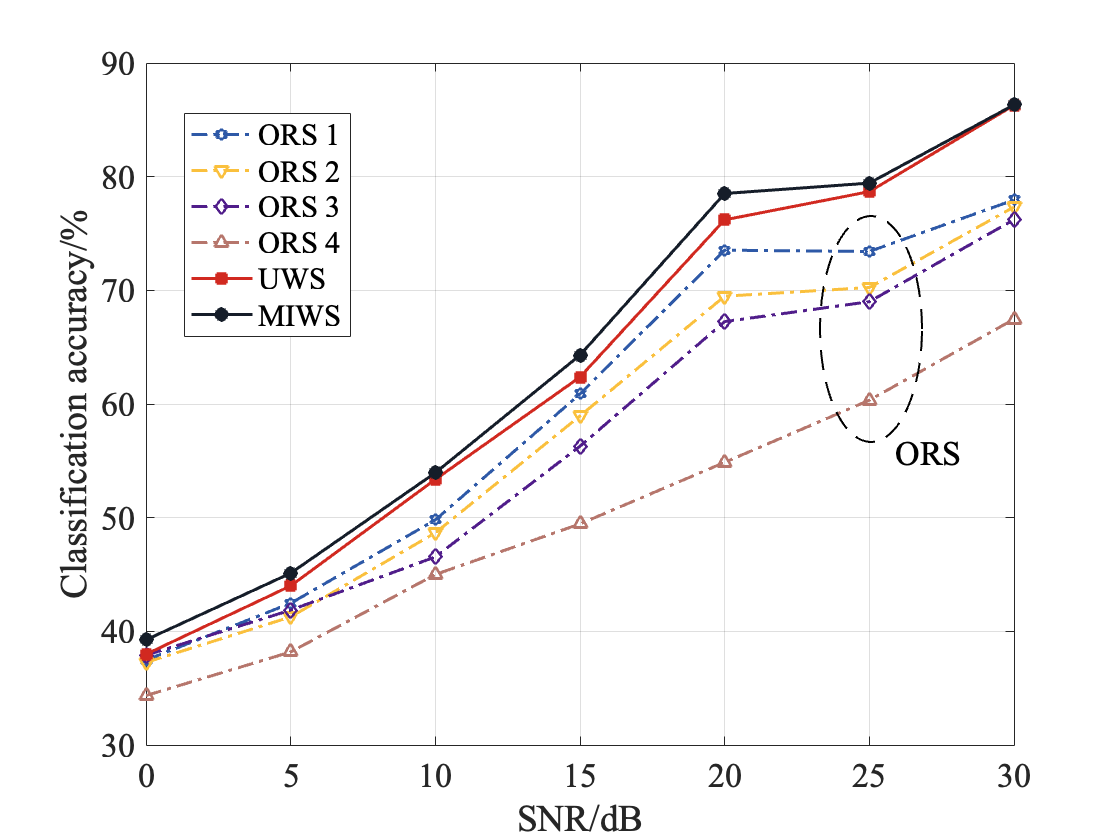
Fig. 4 depicts the results of RFFI accuracy with varying SNR for MIWS, where five emitters are present, the ITD-based feature extraction method is adopted, and the receiver is equipped with four antennas with $\chi$ of 0.001, 0.01, 0.1, 1, respectively. In this figure, UWS stands for the scheme of equally weighting the signals received by each antenna, while ORS $i$ represents the scheme that directly uses the signals at the $i$th receiving antenna without any distortion filtering or weighting operation. It is noteworthy that the results of each ORS in this figure reveal that the larger the $\chi$, the lower the recognition accuracy, which indicates that the ITD-based feature extraction method is sensitive to the phase noise at the receiver. Furthermore, the experimental results indicate that both MIWS and UWS outperform the ORS of each antenna, while the performance of MIWS is better than that of UWS, which highlights the benefit of setting weights according to MI.

Fig. 5 depicts the results of RFFI accuracy with varying SNR for MIWS, where the LMS-based feature extraction method is employed, and the other settings are the same as those in Fig. 4. Unlike the ORS with significant differences in Fig. 4, the ORS of each antenna maintains similar RFFI accuracy when $\chi$ varies in this figure. This observation suggests that the ITD-based feature extraction method is sensitive to phase noise at the receiver, whereas the LMS-based feature extraction method is robust to it. Therefore, there is no significant difference in the performance of MIWS and UWS when the LMS-based feature extraction method is applied. We also note that both MIWS and UWS enjoy a 10% accuracy gain when compared with ORS, thereby confirming the benefit of weighting when multiple received versions are configurated.

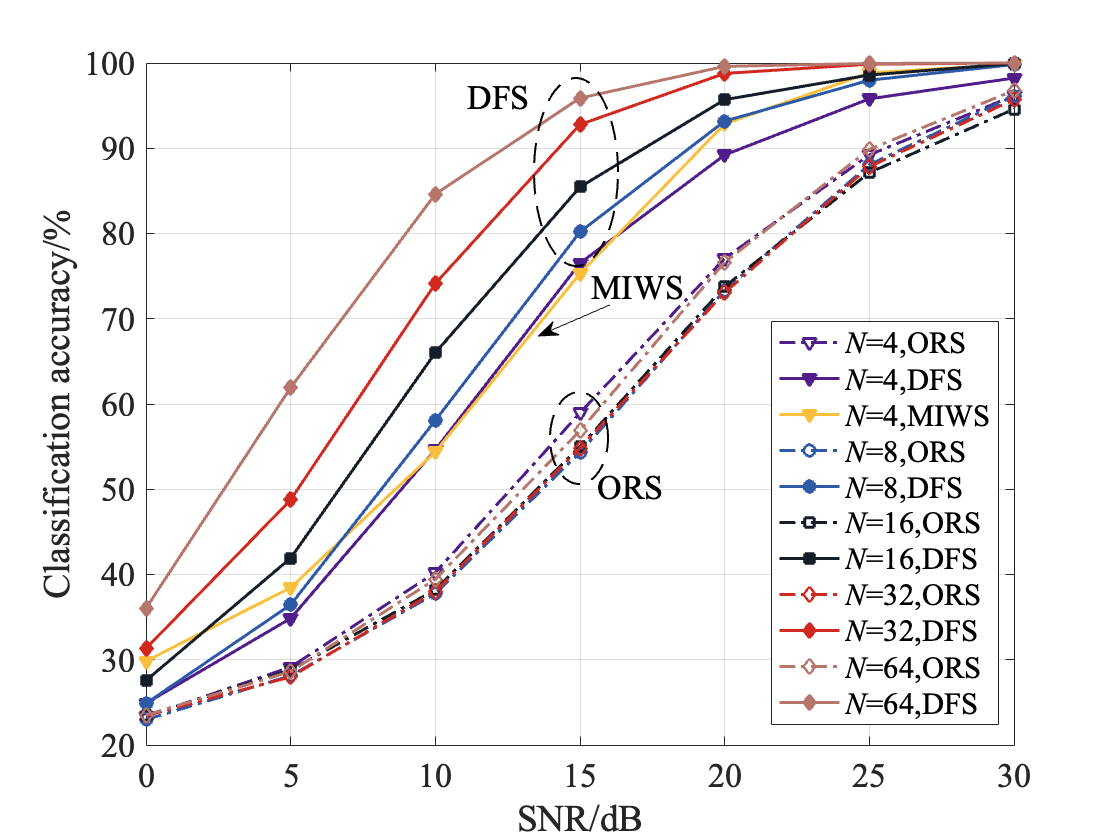
Fig. 6 shows the RFFI results of DFS, where the LMS-based feature extraction method is adopted with $M=5$ and $\chi=0.01$ for all receiver antennas. As can be seen from this figure, the superiority of DFS over ORS becomes increasingly apparent as $N$ increases. Such phenomenon that DFS outperforms ORS in terms of RFFI accuracy demonstrates that DFS can effectively filter out channel noise and receiver distortions. Moreover, there are two noteworthy points: 1) when $N=4$, DFS performs worse than MIWS, suggesting that MIWS is more appropriate when $N\leq 4$; 2) when SNR$=$0dB, the performance gain of DFS over ORS is not obvious, whereas when SNR$>$15dB, such gain becomes more significant for different $N$s, indicating that the level of the performance gain of DFS with respect to ORS is related to the SNR. These two observations are consistent with the statements in Section IV.

Fig. 7 and Fig. 8 show the RFFI accuracy versus receiving phase noise when using the ITD-based RF feature extraction method. The former varies SNR with $N=8$, and the latter varies $N$ with SNR$=15$dB. As seen from these two figures, the larger the $\chi$, the worse the RFFI accuracy of ORS. In contrast, DFS shows its stability and robustness under different $\chi$, which indicates that DFS filters out receiver phase noise effectively. Fig. 8 illustrates that the performance of DFS becomes better with the increasing number of receiving antennas, which remains consistent with the conclusion of Fig. 6.

Figure 9 provides the performance of BDFWS in comparison with DFS when the LMS-based RF feature extraction method is employed. The receiving antennas are evenly divided into four groups, and the other settings are consistent with those in Fig. 6. When SNR$\geq$10 dB and $N=256$ or $N=512$, GDFWS with weighted voting outperforms DFS. However, when SNR$<$10 dB, performance saturation does not appear in DFS, thus its performance is comparable with that of GDFWS. Moreover, when $N=128$, the overall performance of GDFWS is inferior to that of DFS, which suggests that GDFWS is unsuitable for scenarios where $N\leq 128$. Overall, the results presented in this figure demonstrate the effectiveness of GDFWS with weighted voting in scenarios where $N>128$ and SNR$\geq$10 dB when compared with DFS, the finding of which is consistent with the theoretical analysis presented in Section IV.