Joint Device Selection and Power Control for Wireless Federated Learning

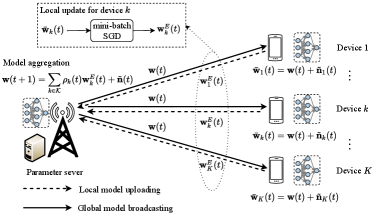
We consider a wireless FL system, as shown in Fig. 1, where one PS coordinates a set of $K$ terminal devices $\mathcal{K}=\{1,\cdots,K\}$ through wireless channels to cooperatively train a shared ML model (e.g., DNN), denoted by $\mathbf{w}\in\mathbb{R}^{d}$ of dimension $d$. Each terminal device $k\in\mathcal{K}$ collects its own labeled training data, and constitutes a local data set $\mathcal{D}_{k}=\{(\mathbf{x}_{k,i},y_{k,i})\}_{i=1}^{D_{k}}$ with $D_{k}=|\mathcal{D}_{k}|$ data samples, where $\mathbf{x}_{k,i}\in\mathbb{R}^{n}$ is the $i$-th input data with $n$ dimensions and $y_{k,i}\in\mathbb{R}$ is the labeled output corresponding to $\mathbf{x}_{k,i}$. Then, the total training data set is given as $\mathcal{D}=\bigcup_{k\in\mathcal{K}}\mathcal{D}_{k}$ of size $D=|\mathcal{D}|=\sum_{k=1}^{K}D_{k}$.

Though the PS has no access to the data samples distributed at the terminal devices due to the privacy concern, the goal of training a global model $\mathbf{w}$ can be achieved by solving the following distributed learning problem

where $q_{k}=D_{k}/D$ is the fraction of data samples for device $k$ and $F_{k}(\mathbf{w})$ is the local loss function defined as

with $\mathcal{L}(\mathbf{w};(\mathbf{x}_{k,i},y_{k,i}))$ being an empirical sample-wise loss function defined by the learning task that quantifies the loss of the model $\mathbf{w}$ for sample $(\mathbf{x}_{k,i},y_{k,i})$.

For the implementation of FL algorithms, the system solves the distributed learning problem (1) in an iterative fashion following the widely used broadcasting-computation-aggregation (BCA) principle, which involves the following three steps in each iteration: $1)$ the PS broadcasts a global model $\mathbf{w}$ to the terminal devices; $2$) terminal device $k$ updates the global model $\mathbf{w}$ to a local model $\mathbf{w}_{k}\in\mathbb{R}^{d}$ after several local learning iterations based on its local data samples; $3)$ the PS aggregates $\mathbf{w}_{k}$’s to generate a new global model $\mathbf{w}$. In the following, we discuss the considered wireless FL algorithm.

This paper considers the scenario where both the downlink and uplink communications are performed in the analog manner and the quasi-static fading channel model is adopted, i.e., both the downlink and uplink channels remain unchanged during each communication round (corresponding to one FL iteration containing all the three BCA steps) and are independent across different communication rounds following the Rayleigh distribution. Specifically, at the $t$-th communication round, the three steps of the wireless FL algorithm are described as follows:

• (1)

  Broadcasting: In this step, the PS broadcasts the vector $\mathbf{u}_{\rm dl}(t)=p_{s}(t)\mathbf{w}(t)$ to terminal devices, containing the information of the global model $\mathbf{w}(t)$ and with the downlink transmit power value $p_{s}(t)$ satisfying

  $$\|\mathbf{u}_{\rm dl}(t)\|_{2}^{2}=\|p_{s}(t)\mathbf{w}(t)\|_{2}^{2}\leq P_{\rm max}^{\rm dl}(t),$$

  (3)

  where $P_{\rm max}^{\rm dl}(t)$ is the downlink transmit power budget at the $t$-the round. Hence, the received vector at the $k$-th terminal device is given as

  	$\displaystyle\mathbf{v}_{k}(t)$	$\displaystyle=h_{k}^{\rm dl}(t)\mathbf{u}_{\rm dl}(t)+\mathbf{n}_{k}(t)$		(4)
  		$\displaystyle=h_{k}^{\rm dl}(t)p_{s}(t)\mathbf{w}(t)+\mathbf{n}_{k}(t),$

  where $h_{k}^{\rm dl}\in\mathbb{C}$ is the complex-valued downlink channel coefficient between the PS and terminal device $k$, and $\mathbf{n}_{k}(t)\in\mathbb{C}^{d}$ is the independent identically distributed (i.i.d.) CSCG noise vector following the distribution $\mathcal{CN}(0,\sigma_{d}^{2}\mathbf{I})$ with $\sigma_{d}^{2}$ being the downlink noise power. With perfect knowledge of $p_{s}(t)$ and the CSI of the downlink channels, terminal device $k$ estimates the global model by descaling the received signal $\mathbf{v}_{k}$, i.e.,

  $$\bar{\mathbf{w}}_{k}(t)=\frac{a_{k}(t)}{p_{s}(t)h_{k}^{\rm dl}(t)}\mathbf{v}_{k}(t)=\mathbf{w}(t)+\tilde{\mathbf{n}}_{k}(t),$$

  (5)

  where $\bar{\mathbf{w}}_{k}(t)$ is the estimated global model for terminal device $k$ at the $t$-th round, $a_{k}(t)$ is the selection indicator for the device $k$ at the $t$-th round ($a_{k}(t)=1$ implies that the device $k$ is selected to participate in the training at the $t$-th round, and otherwise, $a_{k}(t)=0$), and $\tilde{\mathbf{n}}_{k}(t)=\frac{a_{k}(t)}{p_{s}(t)h_{k}^{\rm dl}(t)}\mathbf{n}_{k}(t)$ is the equivalent noise at the device $k$. Then, terminal device $k$ sets its current local model to $\mathbf{w}_{k}(t)=\bar{\mathbf{w}}(t)$.

• (2)

  Local Model Update: In this step, terminal device $k$ updates its local model $\mathbf{w}_{k}(t)$ by minimizing its local objective (2) via a local optimization algorithm, e.g., the mini-batch stochastic gradient descent (SGD) method, based on its collected data set $\mathcal{D}_{k}$. When implementing the mini-batch SGD algorithm, the local dataset $\mathcal{D}_{k}$ at the device $k$ is divided into several mini-batch with size $B$, and the device runs $E$ SGD iterations with each SGD iteration corresponding to one mini-batch. At the $\tau$-th SGD iteration, $\tau\in\{1,\cdots,E\}$, the local model is updated as

  $$\mathbf{w}_{k}^{\tau}(t)=\mathbf{w}_{k}^{\tau-1}(t)-\eta_{t}\nabla F_{k}(\mathbf{w}_{k}^{\tau-1}(t);\mathcal{B}_{k}^{\tau}(t)),$$

  (6)

  where $\eta_{t}$ is the learning rate at the $t$-th round, $\mathcal{B}_{k}^{\tau}(t)$ is a mini-batch with size $|\mathcal{B}_{k}^{\tau}(t)|=B$ and its data points being independently and uniformly chosen from $\mathcal{D}_{k}$, and $\nabla F_{k}(\mathbf{w}_{k}^{\tau-1}(t);\mathcal{B}_{k}^{\tau}(t))\in\mathbb{R}^{d}$ is the stochastic gradient of the local loss function with respect to (w.r.t.) the $(\tau-1)$-th model parameter $\mathbf{w}_{k}^{\tau-1}(t)$ and randomly sampled mini-batch $\mathcal{B}_{k}^{\tau}(t)$, i.e.,

  	$\displaystyle\nabla F_{k}$	$\displaystyle(\mathbf{w}_{k}^{\tau-1}(t);\mathcal{B}_{k}^{\tau}(t))$		(7)
  		$\displaystyle=\frac{1}{B}\sum_{\xi_{k,i}^{\tau}(t)\in\mathcal{B}_{k}^{\tau}(t)}\nabla\mathcal{L}(\mathbf{w}_{k}^{\tau-1}(t);\xi_{k,i}^{\tau}(t)),$

  with $\xi_{k,i}^{\tau}(t)$ being the $i$-th training data in mini-batch $\mathcal{B}_{k}^{\tau}(t)$. The initial local model parameter at device $k$ before training is set as $\bar{\mathbf{w}}(t)$ in (5), i.e., $\mathbf{w}_{k}^{0}(t)=\bar{\mathbf{w}}_{k}(t)$. After $E$ SGD iterations, the local model parameter at device $k$ is updated as $\mathbf{w}_{k}^{E}(t)$.

• (3)

  Model Aggregation: In this step, the terminal devices upload their updated local model parameters $\mathbf{w}_{k}^{E}(t)$’s to the PS, and the PS aggregates the received local models to generate a new global model. For the uplink transmissions of $\mathbf{w}_{k}^{E}(t)$’s, the terminal devices transmit their local model parameters concurrently through AirComp by exploiting the waveform superposition nature of the wireless MAC channel, since the information of interest at the PS for aggregation is just the weighted summation of the local model parameters. Specifically, the updated model parameter $\mathbf{w}_{k}^{E}(t)$ at the device $k$ is multiplied with a pre-processing factor $\beta_{k}(t)$, which is given as

  $$\beta_{k}(t)=\frac{a_{k}(t)p_{k}(t)(h_{k}^{\rm up}(t))^{H}}{|h_{k}^{\rm up}(t)|^{2}},$$

  (8)

  where $p_{k}(t)$ is the uplink transmit power value at device $k$, $h_{k}^{\rm up}(t)$ is the complex uplink channel coefficient from device $k$ to the PS. With perfect CSI of the uplink channels, the received vector $\mathbf{v}(t)$ at the PS is given as

  	$\displaystyle\mathbf{v}(t)$	$\displaystyle=\sum_{k\in\mathcal{K}}h_{k}^{\rm up}(t)\beta_{k}(t)\mathbf{w}_{k}^{E}(t)+\mathbf{n}(t)$		(9)
  		$\displaystyle=\sum_{k\in\mathcal{K}}a_{k}(t)p_{k}(t)\mathbf{w}_{k}^{E}(t)+\mathbf{n}(t),$

  where $\mathbf{n}(t)\in\mathbb{C}^{d}$ is the i.i.d. CSCG noise vector following the distribution $\mathcal{CN}(0,\sigma_{u}^{2}\mathbf{I})$. In this paper, the uplink transmit power values at the devices satisfy the following two types of constraints: For the individual uplink transmit power constraint at each device, the transmit power value of device $k$ is supposed to satisfy

  $$\|\beta_{k}(t)\mathbf{w}_{k}^{E}(t)\|_{2}^{2}\leq P_{\rm max}^{k}(t),$$

  (10)

  where $P_{\rm max}^{k}(t)$ is the individual power budget at the $t$-th round of device $k$; for the sum uplink transmit power constraint over all devices, the transmit power values of the devices are supposed to satisfy

  $$\sum_{k=1}^{K}\|\beta_{k}(t)\mathbf{w}_{k}^{E}(t)\|_{2}^{2}\leq P_{\rm tot}(t),$$

  (11)

  where $P_{\rm tot}(t)$ is the sum power budget at the $t$-th round of all the participated devices.

  The PS scales the received signal $\mathbf{v}(t)$ with a factor $1/\zeta(t)$ to aggregate and update the global model parameter as

  		$\displaystyle\mathbf{w}(t+1)$		(12)
  	$\displaystyle=$	$\displaystyle\frac{\mathbf{v}(t)}{\zeta(t)}=\frac{1}{\zeta(t)}\sum_{k\in\mathcal{K}}a_{k}(t)p_{k}(t)\mathbf{w}_{k}^{E}(t)+\frac{1}{\zeta(t)}\mathbf{n}(t),$

  where $\zeta(t)$ is set as the summation of all the products $a_{k}(t)p_{k}(t)$, i.e., $\zeta(t)=\sum_{k=1}^{K}a_{k}(t)p_{k}(t)$, with perfect knowledge on all $a_{k}(t)$ and $p_{k}(t)$ at the PS. Hence, based on (9) and (12), the model aggregation is given as¹¹1The proposed model aggregation scheme requires perfect CSI about both the downlink and uplink channels. Nevertheless, our design and analysis can be extended to the case with imperfect CSI, and the impact of imperfect CSI will be studied for future work.

  $$\mathbf{w}(t+1)=\sum_{k\in\mathcal{K}}\rho_{k}(t)\mathbf{w}_{k}^{E}(t)+\tilde{\mathbf{n}}(t),$$

  (13)

  where $\rho_{k}(t)=\frac{a_{k}(t)p_{k}(t)}{\sum_{j\in\mathcal{K}}a_{j}(t)p_{j}(t)}$ is the weight of $\mathbf{w}_{k}^{E}(t)$ for aggregation satisfying $\sum_{k=1}^{K}\rho_{k}(t)=1$ and $\tilde{\mathbf{n}}(t)=\frac{\mathbf{n}(t)}{\sum_{j\in\mathcal{K}}a_{j}(t)p_{j}(t)}$ is the equivalent noise.

As mentioned in Remark 1, when practically implementing the wireless FL algorithm, not all devices are able to participate the training over the whole time. Hence, when considering both the downlink and uplink communications between the PS and the terminal devices, we need to develop an efficient device selection scheme while guaranteeing the convergence of the considered algorithm.

First, we make the following standard assumptions that are commonly adopted in the convergence analysis of the BCA-type FL algorithms [30, 23, 24, 15, 31].

Based on the global model broadcasting in (5), the mini-batch local SGD (6) and (7), and the proposed adaptive reweighing model aggregation scheme (13), the PS updates the global model at the $(t+1)$-th round as

where $(a)$ follows the local mini-batch SGD iterations in (6), $(b)$ is to due to $\mathbf{w}_{k}^{0}(t)=\bar{\mathbf{w}}_{k}(t)$, and $(c)$ follows (5) and $\sum_{k\in\mathcal{K}}\rho_{k}(t)=1$.

Define the local model difference $\Delta\mathbf{w}_{k}(t)$ as

and define the virtual noisy global model $\tilde{\mathbf{w}}(t)$ as

Thus, we can further rewrite $\mathbf{w}(t+1)$ as

We first present the following lemmas and their proofs that are used in the proof of Theorem 1.

The proofs of Lemma 2, 3, 4 follow the same ideas in [15], [31], [33], with a slight modification according to the problem that we consider. Now, we present the main convergence analysis results in the following theorem.

As mentioned in Remark 3, by properly choosing the learning rate $\eta_{t}\leq\frac{1}{20EL}$ to guarantee the convergence of the proposed wireless FL algorithm, the optimality gap between the expected and optimal global loss values derived in (1) becomes

which determines the performance of the algorithm when converges and needs to be minimized. Specifically, with instantaneous CSI in each round, we minimize the performance gap $G(t)$ over the device selection indicator $a_{k}(t)$, downlink transmit power value $p_{s}(t)$ and uplink transmit power value $p_{k}(t)$ round by round. Besides, we ignore the constant terms $(a)$ and $(b)$ in $G(t)$ that is related to the gradient variance and data heterogeneity, and focus on minimizing the sum of terms $(c)$ and $(d)$ in $G(t)$, since the goal of this paper is to minimize the impact of the downlink and uplink wireless communications on the convergence of the considered wireless FL algorithm. Hence, by dropping the notation $t$ for simplicity, we can formulate the following performance gap minimization problem as

where $\mathbf{a}=[a_{1},\cdots,a_{K}]$, $\mathbf{p}=[p_{1},\cdots,p_{k}]$, (32b) denotes the feasible set of the selection indicators, and (32c) is the downlink transmit power constraint with $\bar{P}_{\rm dl}=P_{\rm max}^{\rm dl}/\|\mathbf{w}\|_{2}^{2}$. For the individual power constraint, $\mathcal{P}$ in (32d) is given as

which is the matrix-vector form of (10), with $\mathbf{Q}_{k}\in\mathbb{R}^{K\times K},k=1,\cdots,K$, being a diagonal matrix with $[\mathbf{Q}_{k}]_{k,k}=\frac{\|\mathbf{w}_{k}^{E}\|_{2}^{2}}{|h_{k}^{\rm up}|^{2}}$ and all other entries being zero; for the sum power constraint, $\mathcal{P}$ in (32d) is given as

which is the matrix-vector form of (11), with $\mathbf{Q}_{0}=\mathtt{diag}\left(\frac{\|\mathbf{w}_{1}^{E}\|_{2}^{2}}{|h_{1}^{\rm up}|^{2}},\cdots,\frac{\|\mathbf{w}_{K}^{E}\|_{2}^{2}}{|h_{K}^{\rm up}|^{2}}\right)\in\mathbb{R}^{K\times K}$.

In this section, we propose a joint device selection and power control algorithm to solve problem (32). Obviously, the formulated optimization problem (32) is a typical MIP problem, where the difficulty for solving this problem is the binary selection variables $\mathbf{a}$ and the non-convex objective function (32a).

However, we could replace the device selection $\mathbf{a}$ with the uplink transmit power value $\mathbf{p}$, based on the observation that the selection indicator $\mathbf{a}$ is always coupled with uplink transmit power value $\mathbf{p}$, and independent of the downlink transmit power value $p_{s}$, as shown in (32). Hence, the device is selected only when its uplink transmit power value $p_{k}$ is positive. Thus, we can drop the selection indicator $\mathbf{a}$ in (32a) and (32d) and its associated constraint (32b). Besides, to minimize the objective function (32a), the constraint (32c) should be met with equality, i.e., $p_{s}^{2}=\bar{P}_{\rm dl}$, since (32a) monotonically decreases with $p_{s}^{2}$. Hence, problem (32) can be equivalently transformed as

For the individual uplink power constraint case, $\mathcal{P}_{0}$ is given as

and for the sum uplink power constraint case, $\mathcal{P}_{0}$ is given as

By rearranging the objective function (35a) in the matrix-vector form, problem (35) is equivalent to

where $\mathbf{\Theta}=\mathtt{diag}(\mathbf{\theta})\in\mathbb{R}^{K\times K}$ with $\mathbf{\theta}=[\theta_{1},\cdots,\theta_{K}]\in\mathbb{R}^{K}$ and $\theta_{k}=\frac{d\sigma_{d}^{2}L(1+2\eta E+4\eta^{2}E^{2}L^{2})}{(1-4\eta^{2}E^{2}L^{2})\bar{P}_{\rm dl}|h_{k}^{\rm dl}|^{2}}$. Now, problem (38) is a typical QCRQ minimization problem. It has been proved in [36] that with the given constraint (35b) for both the individual and sum uplink power constraint cases (36) and (37), the QCRQ problem (38) can be equivalently rewritten as the following homogeneous version by introducing a real auxiliary variable $s$ with $\mathbf{y}=s\mathbf{p}$, i.e.,

where for the individual uplink power constraint case, $\mathcal{Y}$ in (39c) is given as

and for the sum uplink power constraint case, $\mathcal{Y}$ in (39c) is given as

Though problem (39) is still non-convex, it can be approximated by its SDR [37]. First, we make the change of variables $\mathbf{z}=(\mathbf{y}^{T},s)^{T}$, and rewrite (39) as

where $\tilde{\mathbf{\Theta}}$ and $\mathbf{C}$ are given as