ItôWave: Itô Stochastic Differential Equation Is All You Need For Wave Generation

Itô SDE is a very natural model that can realize the transformation between different data distributions. The general Itô SDE is as follows

for $0\leq t\leq T$, where $\mathbf{f}(\cdot,t)$ is the drift coefficient, $g(t)$ is the diffusion coefficient, $\mathbf{W}$ is the standard Wiener process. Let $p(\mathbf{x}(t))$ be the density of the random variable $\mathbf{X}(t)$. This SDE (3) changes the initial distribution $p(\mathbf{x}(0))$ into another distribution $p(\mathbf{x}(T))$ by gradually adding the noise from the Wiener process $\mathbf{W}$. In this work, $\mathbf{x}(t)\in\mathbb{R}^{d}$, and $p(\mathbf{x}(0))$ is to denote the data distribution of wave in ItôWave. $p(\mathbf{x}(T))$ is an easy tractable distribution (e.g. Gaussian) of the latent representation of the wave signal corresponding to the conditional mel spectrogram. If this stochastic process $\mathbf{x}(t)$ can be reversed in time, then the corresponding target waveform of the conditional mel spectrogram can be generated from a simple latent distribution.

Actually the reverse-time diffusion process is the solution of the following corresponding reverse-time Itô SDE [9]

for $0\leq t\leq T$, where $p(\mathbf{x}(t))$ is the distribution of $\mathbf{X}(t)$, $\overline{\mathbf{W}}$ is the standard Wiener process in reverse-time. The solution of this reverse-time Itô SDE (7) can be used to generate wave data from a tractable latent distribution $p(\mathbf{x}(T))$. Therefore, it can be seen from (7) that the key to generating wave with SDE lies in the calculations of $\nabla_{\mathbf{x}}\log p(\mathbf{x}(t))$ $(0\leq t\leq T)$, which is always called score function [10, 11] of the data.

In this work, a neural network $\mathfrak{S}_{\theta}$ is used to approximate the score function, where $\theta$ denotes the parameters of the network. The input of the network $\mathfrak{S}_{\theta}$ includes time $t$, $\mathbf{x}(t)$, and conditional input mel spectrograms $\mathbf{m}$ input in ItôWave. The expected output is $\nabla_{\mathbf{x}(t)}\log p(\mathbf{x}(t))$. The objective of score matching is [10]

Generally speaking, in the low-density data manifold area, the score estimation will be inaccurate, which will further lead to the low quality of the sampled data [11]. If the wave signal is contaminated with a very small scale noise, then the contaminated wave signal will spread to the entire space $\mathbb{R}^{d}$ instead of being limited to a small low-dimensional manifold. When using perturbed wave signal as input, the following denoising score matching (DSM) loss [12, 11]

is equal to the loss (8) of a non-parametric (e.g. Parzen windows densiy) estimator [12]. This DSM loss is used in this paper to train the score prediction network. If we can accurately estimate the score $\nabla_{\mathbf{x}(t)}\log p(\mathbf{x}(t))$ of the distribution, then we can generate wave sample data from the original distribution.

It should be noted that in the experiment we found that the choice of training loss is very critical. For ItôWave, the $\mathcal{L}2$ loss is more appropriate than $\mathcal{L}1$ loss.

Generally the transition densities $p(\mathbf{x}(t)|\mathbf{x}(0))$ and the score $\nabla_{\mathbf{x}(t)}\log p(\mathbf{x}(t)|\mathbf{x}(0))$ in the DSM loss are difficult to calculate, but for linear SDE, these values have close formulas [13].

Empirically it is found that different types of linear SDE for different audio generation tasks, e.g. the variance exploding (VE) SDE [14] is much suitable for wave generation. VE SDE is of the following form

where $\sigma_{0}=0.01<\sigma_{1}$.

Then the differential equation satisfied by the mean and variance of the transition densities $p(\mathbf{x}(t)|\mathbf{x}(0))$ is as follows

Solving the above equation, and choose $\sigma_{1}$ makes $2\log\frac{\sigma_{1}}{\sigma_{0}}=1$, we get the transition density of this as

The score of the VE linear SDE is

The prior distribution $p(\mathbf{x}(T))$ is a Gaussian

thus $\log p(\mathbf{x}(T))=-\frac{d}{2}\log(2\pi\sigma_{1}^{2})-\frac{1}{2\sigma_{1}^{2}}\left\lVert\mathbf{x}(T)\right\rVert^{2}$.

Based on subsections 2.1 and 2.2, we can get the training procedure of the score networks based on general SDEs, as shown in Algorithm 1.

After we get the optimal score network $\mathfrak{S}_{\theta_{*}}$ through loss minimization, thus we can get the gradient of log value of the distribution probability density of the wave with $\mathfrak{S}_{\theta_{*}}(\mathbf{x}(t),t,\mathbf{m})$. Then we can use Langevin dynamics or the reverse-time Itô SDE (7) to generate the wave corresponding to the specific mel spectrogram $\mathbf{m}$. The reverse-time SDE (7) can be solved and used to generate target audio data. Assuming that the time schedule is fixed, the discretization of the diffusion process (3) is as follows

since $d\mathbf{W}$ is a wide sense stationary white noise process [15], which is denoted as $\mathbf{\xi}(\cdot)\sim\mathcal{N}\left(\mathbf{0},\mathbf{I}\right)$ in this paper.

The corresponding discretization of the reverse-time diffusion process (7) is

In this paper, we use the strategy of [14], which means that at each time step, Langevin dynamics is used to predict first, and then reverse-time Itô SDE (30) is used to revises the first predicted result.

The generation algorithm of wave based on VE linear SDE is as follows

It was found that although the score network model does not have as strict restrictions on the network structure as the flow model [16, 7, 17], not all network structures are suitable for score prediction.

The structure of ItôWave’s score prediction network $\mathfrak{S}_{\theta}(\mathbf{x}(t),t,\mathbf{m})$ is shown in Figure 1. The input is the wave to be generated, and the conditional input has mel spectrogram and time $t$. The output is the score at time $t$. All three types of input require preprocessing processes. The preprocessing of the wave is through a convolution layer; the preprocessing of mel spectrogram is based on the upsampling by two transposed convolution layers. After all inputs are preprocessed, they will be sent to the most critical module of $\mathfrak{S}_{\theta}(\mathbf{x}(t),t,\mathbf{m})$, which is of several serially connected dilated residual blocks. The main input of the dilated residual block is the wave, and the step time condition and mel spectrogram condition will be input into these dilated residual blocks one after another, and added to the feature map after the transformation of the wave signal. Similarly, there are two outputs of each dilated residual block, one is the state, which is used for input to the next residual block, and the other is the final output. The advantage of this is the ability to synthesize information of different granularities. Finally, the outputs of all residual blocks are summed and then pass through two convolution layers as the final output score.

The data set we use is LJSpeech [18], a single female speech database, with a total of 24 hours, 13100 sentences, randomly divided into 13000/50/50 for training/verification/testing. The sampling rate is 22050. In the experiment, for mel spectrogram, the window length is 1024, hop length is 256, the number of mel channels is 80. We use the same Adam [19] training algorithm for ItôWave. We have done quantitative evaluations based on mean opinion score (MOS) with other state-of-the-art methods on ItôWave. We compared with WaveNet [1], WaveGlow [7], Diffwave [20], and WaveGrad [21]. All experiments were performed on a GeForce RTX 3090 GPU with 24G memory.

In order to verify the naturalness and fidelity of the synthesized voice, we randomly select 40 from 50 test data for each subject, and then let the subject give the synthesized sound a MOS score of 0-5.

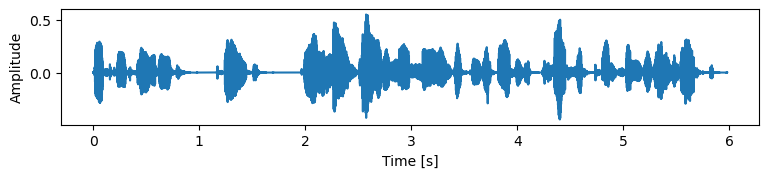
For ItôWave, the original mel spectrogram of the test set was used as the condition input to the score estimation network. ItôWave uses 30 residual layers. For the comparison methods,

The results are shown in Table 1, and you can see that ItôWave scores the best. It has approached the true value of ground truth. As shown in Figure 2, we can see how ItôWave gradually turns white noise into meaningful wave.