Isotopic analysis of 295 MeV proton scattering off ^204,206,208Pb for improvement of neutron densities and radii

The theoretical densities of Pb isotopes, which are used as inputs for nucleon-nucleus folding potentials in Pb$(p,p)$ calculations, are obtained via the RHB and SHFB calculations of spherical nuclei using the computational codes named DIRHB Nikšić et al. (2014) and HFBRAD Bennaceur and Dobaczewski (2005), respectively. For the former, the DD-ME2 Lalazissis et al. (2005) and DD-PC1 Nikšić et al. (2008) interactions are used; in this paper, these are simply denoted by me2 and pc1, respectively. For the latter case, the SKM* Bartel et al. (1982) and SLy4 Chabanat et al. (1998) interactions are used. Note that the parameter sets of these structure models were adjusted to globally fit the binding energies and rms charge radii in wide mass-number regions that include ${}^{40}\textrm{Ca}$ and ${}^{208}\textrm{Pb}$.

The experimental neutron densities of the Pb isotopes used in this paper are those of Refs. Zenihiro et al. (2010); Zenihiro (2011), which were extracted by fitting the Pb$(p,p)$ data at 295 MeV using the RIA calculation with the ddMH model, which was called medium-modified RIA calculation in the original paper. The neutron-density distribution is written in a sum-of-Gaussians (SOG) form and called the SOG-fit density in the present paper. The experimental proton densities are taken from Ref. Zenihiro et al. (2010); they were obtained by unfolding the nuclear charge distribution determined by electric elastic scattering data De Vries et al. (1987).

Figures 1(a)-(c) show proton ($\rho_{p}$) and neutron ($\rho_{n}$) densities of ${}^{204}\textrm{Pb}$, ${}^{206}\textrm{Pb}$, and ${}^{208}\textrm{Pb}$, and Fig. 1(d) shows $4\pi r^{2}\rho_{p}$ and $4\pi r^{2}\rho_{n}$ of ${}^{208}\textrm{Pb}$. The theoretical densities of the RHB (me2 and pc1) and SHFB (SKM* and SLy4) calculations and the experimental SOG-fit density are shown. The proton scattering at $E_{p}=295$ MeV is a sensitive probe of the surface-neutron density around the peak position of $4\pi r^{2}\rho_{n}$ at $r\sim 6$ fm, but it is insensitive to the inner densities. Therefore, the SOG-fit neutron densities of Pb isotopes have large uncertainties in the $r<4$ fm region as shown by the error envelopes (filled area). Theoretical neutron densities depend upon structure models, but each model yields similar neutron densities between ${}^{204}\textrm{Pb}$, ${}^{206}\textrm{Pb}$, and ${}^{208}\textrm{Pb}$. Comparing the theoretical model and SOG-fit neutron densities in the surface region, the me2 model shows the best agreement with the SOG-fit density, whereas other theoretical models show disagreements; $4\pi r^{2}\rho_{n}(r)$ obtained by the pc1, SKM*, and SLy4 models exhibits a peak position that is slightly shifted outward compared with the SOG-fit and me2 densities. This peak-position shift causes deviation of the $(p,p)$ cross sections from the data at backward angles, as discussed later in Sec. II.2.

Figure 2(a) shows the theoretical and experimental values of $r_{p}$ and $r_{n}$, whereas Fig. 2(b) shows the values of $\Delta r_{np}$. All theoretical models show smooth changes of $r_{p}$ and $r_{n}$ as the mass number $A$ increases from ${}^{204}\textrm{Pb}$ to ${}^{208}\textrm{Pb}$. The $A$ dependence of $r_{p}$ is quite similar between different models and is consistent with the experimental data. As for the neutron radii, the $r_{n}$ and $\Delta r_{np}$ change smoothly with the same slope as $A$ increases in all theoretical models, meaning that the $A$ dependence is approximately model independent though the absolute $r_{n}$ values are model dependent. Compared with the smooth changes of the theoretical $r_{n}$ and $\Delta r_{np}$ values, the $r_{n}$ values of the SOG-fit density seem to show a different $A$ dependence—in particular, an enhancement of $r_{n}$ and $\Delta r_{np}$ at $A=208$ from ${}^{206}\textrm{Pb}$ to ${}^{208}\textrm{Pb}$. However, this is not definite due to the large experimental errors that arise mainly from uncertainty in the internal neutron densities extracted from the $(p,p)$ data.

Proton elastic scattering at $E_{p}=295$ MeV is calculated using RIA with the ddMH model (a modified MH model proposed by Sakaguchi et al. Sakaguchi et al. (1998) by introducing density-dependent $\sigma$- and $\omega$-meson masses and coupling constants of the relativistic Love-Franey (RLF) $NN$ interaction of the original MH model Horowitz (1985); Murdock and Horowitz (1987)). The density dependence is considered as “medium effects” of the effective $NN$ interaction, which includes various many-body effects in proton elastic scattering such as the Pauli blocking and multistep processes, in addition to the medium effects of meson properties. The RIA calculation with the ddMH model is performed in the default case, and that with the MH model is also performed in an optional case.

The parameter set of the density dependence used in this paper is the same as that used to analyze Pb$(p,p)$ and Ca$(p,p)$ at $E_{p}=295~{}$MeV in Refs. Zenihiro et al. (2010, 2018). This parameter set is the latest version calibrated to fit the updated data for $p+^{58}\textrm{Ni}$ at $E_{p}=295~{}$MeV and can well reproduce the ${}^{40}\textrm{Ca}(p,p)$ data at $E_{p}=295~{}$MeV Zenihiro et al. (2018). In the RIA framework with the MH and ddMH models, the proton-nucleus potentials are calculated by folding the vector and scalar densities of target nuclei with the meson-exchange $NN$ interaction. As the input target densities, the proton $(\rho_{p}(r))$ and neutron $(\rho_{n}(r))$ densities are used for the proton and neutron vector densities, whereas $0.96\rho_{p}(r)$ and $0.96\rho_{n}(r)$ are used for the proton and neutron scalar densities, respectively; this prescription of the scalar densities was adopted in Ref. Zenihiro et al. (2010) to fit the ddMH model to the ${}^{58}\textrm{Ni}(p,p)$ data and applied to the Pb$(p,p)$ analysis. Note that, in the RHB calculations, the scalar densities can be obtained without such an approximation, but give only a minor correction to the Pb$(p,p)$ reactions at this energy. We adopt the prescription of the scalar densities for all models consistently with the calibration of the ddMH model.

The cross sections and analyzing powers of Pb$(p,p)$ at 295 MeV obtained by the RIA calculation with the ddMH model are shown in Figs. 3 and 4, respectively, and the Rutherford ratio of the cross sections are shown in Fig. 5. In the results obtained using the pc1, SKM*, and SLy4 densities, dip and peak positions in the diffraction pattern deviate from the experimental data, in particular, at backward angles, in which the dip (peak) positions shift to forward angles because of the slight outward shift of the $4\pi r^{2}\rho_{n}(r)$ peak position compared with the SOG-fit and me2 densities. The me2 result agrees better with the data than those of other theoretical densities, but a slight deviation from the data still remains. Therefore, the dip interval in the diffraction pattern is sensitive to the $4\pi r^{2}\rho_{n}(r)$ peak position, but does not necessarily correspond to the neutron radius $r_{n}$. For instance, the SKM* density has a smaller value of $r_{n}$ than the SOG-fit density, but it gives a shrunk diffraction pattern of the $(p,p)$ cross sections consistent with the outward shift of the $4\pi r^{2}\rho_{n}(r)$ peak, indicating an expansion of the nuclear size probed by proton scattering.

To show reaction model dependence, the results obtained using the MH model with the SOG-fit and me2 densities are shown in Figs. 4 and 5 in comparison with the results of the ddMH model. The dip interval of the cross sections depends upon the effective $NN$ interaction in the reaction model; compared with the ddMH results, the diffraction pattern of the MH model deviates forward, indicating that the range of the effective $NN$ interaction in the MH model is slightly longer than that in the ddMH model.

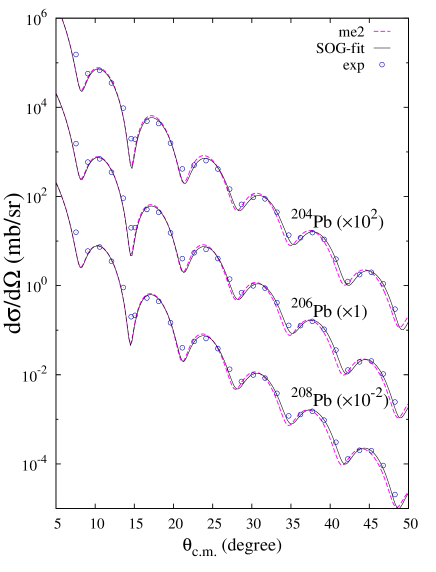
As shown in the results, the calculated $(p,p)$ cross sections at 295 MeV are sensitive to differences between input neutron densities at the nuclear surface, and depend upon the effective $NN$ interaction used in the nucleon-nucleus folding potential. However, in each model, the results for a series of isotopes from ${}^{204}\textrm{Pb}$ to ${}^{208}\textrm{Pb}$ are quite similar and deviation from the experimental data occurs systematically for the three isotopes. To see the isotopic similarities, the results of Pb isotopes are compared in Fig. 6 for densities and Fig. 7 for the Rutherford ratio of the cross sections on a linear scale. For each result of the SOG-fit, me2, pc1, SKM*, SLy4, MH-SOG-fit, and MH-me2, the isotopic difference between ${}^{204}\textrm{Pb}$, ${}^{206}\textrm{Pb}$, and ${}^{208}\textrm{Pb}$ in the cross sections is small because surface densities in the $r\gtrsim 6$ fm region of the three isotopes approximately coincide,. even in the linear plot of the Rutherford ratio (Fig. 7). These isotopic systematics are useful for a model-independent analysis of proton elastic scattering.

By considering ${}^{208}\textrm{Pb}$ as the reference nucleus, the isotopic density and radius differences and cross-section ratio are calculated for each model in the present isotopic analysis. The isotopic density and radius differences are respectively given as

where $\rho_{n(p)}({}^{A}\textrm{Pb}^{A};r)$ and $r_{n(p)}(^{A}\textrm{Pb})$ are the neutron(proton) density and rms radius of ${}^{A}\textrm{Pb}$. The isotopic cross-section ratio is given as

with differential cross sections in the center-of-mass frame. It is trivial that, even in the case of $\rho_{p,n}(^{A}\textrm{Pb};r)\propto\rho_{p,n}({}^{208}\textrm{Pb};r)$, $R(\sigma;\theta)$ is not constant because of normalization of the target densities used for the folding potential and kinematical effects in the reaction.

Experimental values of $R(\sigma;\theta_{\textrm{c.m.}})$ are obtained using the $(p,p)$ cross section data at approximately the same angles in a series of Pb isotopes by omitting isotopic differences in the transformation from the laboratory frame to the center-of-mass frame, which is negligibly small in this mass-number region.

The isotopic radius differences $D(r_{n})$ and $D(r_{p})$ are nothing but the relative radii of ${}^{A}\textrm{Pb}$, measured from ${}^{208}\textrm{Pb}$. The theoretical values of $D(r_{n})$ and $D(r_{p})$ are shown in Fig. 8 together with the experimental $D(r_{n})$ of the SOG-fit density and the $D(r_{p})$ values Zenihiro et al. (2010). The theoretical results of RHB (me2 and pc1) and SHFB (SKM* and SLy4) calculations are consistent and show linear dependences of $D(r_{n})$ and $D(r_{p})$ upon the neutron-number difference $N-126$ because of the isotopic systematics of $r_{n}$ and $r_{p}$ as discussed previously. The theoretical values of the isotopic proton radius difference, $D(r_{p})=-0.02$ fm for ${}^{204}\textrm{Pb}$ and $D(r_{p})=-0.01$ fm for ${}^{206}\textrm{Pb}$, agree well with the experimental values reduced from the charge radii. For the isotopic neutron radius difference, the theoretical values are independent from structure models as $D({}^{204}\textrm{Pb};r_{n})\approx-0.04$ fm and $D({}^{206}\textrm{Pb};r_{n})\approx-0.02$ fm. They are contained in the experimental errors extracted from the $(p,p)$ data at 295 MeV, but deviate from the experimental best-fit values $D(r_{n})=-0.055$ fm for ${}^{204}\textrm{Pb}$ and $D(r_{n})=-0.040$ fm for ${}^{206}\textrm{Pb}$ of the SOG-fit neutron density.

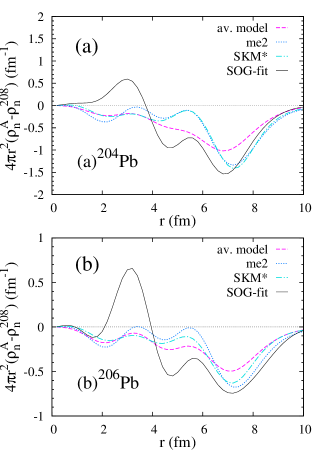
The isotopic neutron-density differences in ${}^{204}\textrm{Pb}$ and ${}^{206}\textrm{Pb}$ of the SOG-fit, me2, and SKM* densities are shown in Fig. 9. The one-neutron hole densities of the $3p_{1/2}$ and $2f_{5/2}$ orbits in ${}^{208}\textrm{Pb}$ of the me2 density are shown for comparison. In the me2 and SKM* densities, $4\pi r^{2}D(\rho_{n})$ shows a remarkable reduction of the surface density in the $6\lesssim r\lesssim 8$ fm region from ${}^{208}\textrm{Pb}$ to ${}^{206}\textrm{Pb}$ because of the dominant $(3p_{1/2})^{-2}$ and $(3p_{3/2})^{-2}$ contributions, but contains the paring effect and other higher-order effects beyond perturbation such as ${}^{208}\textrm{Pb}$-core shrinkage. Compared with the enhanced amplitude of $4\pi r^{2}D(\rho_{n})$ at the surface, the amplitude in the internal region is relatively small and shows almost no specific character except for a small oscillation of the $3p$-hole component. The SOG-fit density shows a $4\pi r^{2}D(\rho_{n})$ surface amplitude similar to the theoretical densities in the $6\lesssim r\lesssim 8$ fm region, but a strange behavior occurs in the $2\lesssim r\lesssim 4$ fm region—that is, a sharp peak with an opposite sign. Since the proton elastic scattering at 295 MeV is insensitive to this internal region, this sharp peak may be an artifact that accidentally occurred in the SOG fitting under the condition of total neutron-number conservation. However, this artifact in the internal region causes a sudden increase of $r_{n}$ from ${}^{206}\textrm{Pb}$ to ${}^{208}\textrm{Pb}$ as understood by the relationship between $D(\rho_{n})$ and $D(r_{n})$ given in Eq. (2). Another difference between the SOG-fit and theoretical densities is seen in the $4\lesssim r\lesssim 6$ fm region.

The isotopic cross-section ratios $R(\sigma)$ of ${}^{204}\textrm{Pb}$ and ${}^{206}\textrm{Pb}$ to ${}^{208}\textrm{Pb}$ are calculated by the ddMH model using the SOG-ft and theoretical densities. Figure 10 compares the results obtained using the SOG-fit, me2, and SKM* densities, with the experimental values. The result calculated with the original MH model using the me2 density is also compared to see the dependence on the effective $NN$ interaction in the reaction models. The isotopic cross-section ratio shows an oscillating behavior that reflects the diffraction pattern of the cross sections; the dip positions of $R(\sigma)$ correspond to the dip angles of the ${}^{A}\textrm{Pb}(p,p)$ cross sections, whereas the peak positions of $R(\sigma)$ correspond to the dip angles of the ${}^{208}\textrm{Pb}(p,p)$ cross sections. In principle, the oscillation amplitude of $R(\sigma)$ is sensitive to the size difference between isotopes. The size shrinkage of ${}^{A}\textrm{Pb}$ from ${}^{208}\textrm{Pb}$ expands the diffraction pattern of $\sigma({}^{A}\textrm{Pb})$, shifting the dip positions slightly to backward angles as compared with $\sigma({}^{208}\textrm{Pb})$. This shift that originates in the nuclear size shrinkage increases the amplitude in one cycle of the oscillation of $R(\sigma)$. Comparing different model calculations the oscillation interval of $R(\sigma)$ depends upon the structure and reaction models because of the model dependence of the dip positions of $\sigma$ as shown in Fig. 5; however, the oscillation amplitude of $R(\sigma)$ is similar between different models.

To see more details of the oscillation amplitude, $R(\sigma)$ is plotted for yhr rescaled angles $\theta^{*}_{\textrm{c.m.}}=(\theta^{\textrm{SOG}}_{\textrm{5th}}/\theta^{\textrm{cal}}_{\textrm{5th}})\theta_{\textrm{c.m.}}$ so as to adjust the fifth peak angle ($\theta^{\textrm{SOG}}_{\textrm{5th}}$) of the ${}^{208}\textrm{Pb}(p,p)$ cross sections of SOG-fit with that ($\theta^{\textrm{theor}}_{\textrm{5th}}$) of the other calculations. The $\theta^{*}_{\textrm{c.m.}}$-plots of $R(\sigma)$ for ${}^{204}\textrm{Pb}$ and ${}^{206}\textrm{Pb}$ are shown in Figs. 10(c) and (d), respectively. After rescaling the angles, the model dependence of $R(\sigma)$ becomes small except for the $\theta^{*}>42^{\circ}$ region as expected from that the isotopic neutron-density differences $D(\rho_{n})$ in the surface region being similar between various theoretical densities and the SOG-fit density. This result indicates that a model-independent discussion is possible in isotopic analysis using the rescaled angles $\theta^{*}$.

Compared with the experimental $R(\sigma)$ obtained from the $(p,p)$ cross section data, the $R(\sigma)$s calculated using the theoretical and SOG-fit densities slightly overshoot the experimental oscillation amplitude for ${}^{204}\textrm{Pb}$ and ${}^{206}\textrm{Pb}$ as shown by the $\theta^{*}$-plots in Figs. 10(c) and (d), respectively.

As discussed previously, isotopic similarities are found in the neutron density and $(p,p)$ cross sections in a series of Pb isotopes, indicating that isotopic differences can be described by a perturbative treatment based on the ${}^{208}\textrm{Pb}$ core. By assuming a ${}^{208}\textrm{Pb}$ core and hole contributions, I introduce a model (called the hole model in this paper) for the neutron densities of ${}^{204}\textrm{Pb}$ and ${}^{206}\textrm{Pb}$ and discuss the connection between $D(\rho_{n})$ and $R(\sigma)$.

The hole-model neutron densities of ${}^{204}\textrm{Pb}$ and ${}^{206}\textrm{Pb}$ are expressed using two parameters for the neutron-hole contribution and size scaling of the ${}^{208}\textrm{Pb}$-core as

where ${\cal N}_{0}$ is the normalization factor for the total neutron number, $\rho^{\textrm{s.p.}}_{3p_{1/2}}$ is the neutron single-particle density of the $3p_{1/2}$ orbit in the ${}^{208}\textrm{Pb}$-core, $s$ is the $r$-scaling factor of the core-size shrinkage, which is given by the scaling parameter $\delta_{s}$, and $h$ is a model parameter for the $3p_{1/2}$-hole contribution. Note that $h$ does not necessarily equal the actual neutron $3p_{1/2}$-hole number but is a parameter of the effective hole number for the $3p_{1/2}$-orbit contribution to neutron density. For the no-scaling ($\delta=0$) case, the hole model neutron density $\rho_{n}({}^{A}\textrm{Pb};r)$ is approximately written as

meaning that the total hole contribution is approximated by the $3p_{1/2}$-hole contribution and an overall reduction in the total neutron density, which contains contributions from other orbits. With this expression of two parameters, $h$ for the effective $3p_{1/2}$-hole number and $\delta_{s}$ for the size shrinkage, the hole model can simulate the densities of various configurations such as the $(2f_{5/2})^{-h}$ configuration and also describe “equivalent” neutron densities to other theoretical densities that reproduce $R(\sigma)$. Examples of the hole model neutron densities equivalent to the $(2f_{5/2})^{-h}$ configuration and the me2 density are demonstrated in Appendix A.

In the present hole-model analysis, the hole-model density is used only for the neutron densities of ${}^{204}\textrm{Pb}$ and ${}^{206}\textrm{Pb}$ but the proton part is unchanged from the original proton densities of ${}^{204}\textrm{Pb}$ and ${}^{206}\textrm{Pb}$. For the parameter $h$ of the effective $3p_{1/2}$-hole number, the hole-model densities with $h=0$, 0.5, $\ldots,$ 2 are used and labeled as $(\textrm{0h},\delta_{s})$, $(\textrm{0.5h},\delta_{s})$, $\cdots$, $(\textrm{2h},\delta_{s})$, respectively.

I first perform isotopic analysis using the hole model with the ${}^{208}\textrm{Pb}$-core and $3p_{1/2}$-orbit densities obtained by the me2 calculation to clarify the correspondence of $R(\sigma)$ to $D(\rho_{n})$ and $D(r_{n})$. Then, I perform the hole-model analysis using the SOG-fit ${}^{208}\textrm{Pb}$-core and the me2 $3p_{1/2}$-orbit densities to obtain optimized parameter sets $h$ and $\delta_{s}$ of the hole model by fitting the experimental $R(\sigma)$ obtained by the Pb$(p,p)$ cross section data at 295 MeV.

The isotopic neutron-density difference $D(\rho_{n})$ and the isotopic cross-section ratio $R(\sigma)$ for ${}^{206}\textrm{Pb}$ obtained using the hole-model density with the me2-core are shown in Fig. 11. The 0h, 1h, and 2h results corresponding to the $3p_{1/2}$-hole numbers $h=0$, 1, and 2 in the range of $-0.2\%<\delta_{s}<0$ (0.2–0% core shrinkage) are illustrated by the yellow, pink, and blue-colored areas, respectively. The oscillation amplitude of $R(\sigma)$ depends upon the size-scaling parameter $\delta_{s}$; it becomes larger as ${}^{206}\textrm{Pb}$ size shrinks from the ${}^{208}\textrm{Pb}$ core. The increase of $h$ (the effective $3p_{1/2}$-hole number) changes the surface behavior of $D(\rho_{n})$; it reduces and enhances the surface amplitude of $4\pi r^{2}D(\rho_{n})$ in the $r\lesssim 7$ fm and 7$\lesssim r\lesssim$ regions, respectively, as expected from the hole density $\rho^{\textrm{s.p.}}_{3p_{1/2}}$ (Fig. 9(c)). This change in $4\pi r^{2}D(\rho_{n})$ increases $R(\sigma)$.

Let me now discuss each effect of the size scaling and increase of $h$ upon $R(\sigma)$ via changes in $D(\rho_{n})$ and $D(r_{n})$ in greater detail. First, I shall discuss the size-scaling effect by changing only $\delta_{s}$ of the 0h (no-hole) case of ${}^{206}\textrm{Pb}$. The results are shown in Figs. 12 and 13. Figures 12(a), (b), and (c) show $4\pi r^{2}D(\rho_{n})$, $\rho_{n}(r)$, and $4\pi r^{2}\rho_{n}(r)$ for $-1\%\leq\delta_{s}\leq 0\%$, respectively. Figures 13(a) and (b) show the results of $\sigma$ and $R(\sigma)$, respectively. For a clear visualization, $\rho_{n}(r)$ and $4\pi r^{2}\rho_{n}(r)$ in an extreme case of $\delta_{s}=-3\%$ are shown in Figs. 12(d) and (e), respectively. As the size shrinks from $\delta_{s}=0\%$ to $-1\%$, $\rho_{n}(r)$ increases in the $r<6$ fm region and decreases in the $r>6$ fm region (Figs. 12(b) and (d)); therefore, the peak position of $4\pi r^{2}\rho_{n}(r)$ shifts inwardly (Figs. 12(c) and (e)). The inward shift of the $4\pi r^{2}\rho_{n}(r)$ peak causes an outward shift of the diffraction pattern of the cross section (Fig. 13(a)) and enhances the oscillation amplitude of $R(\sigma)$, which monotonically increases as $\delta_{s}$ decreases (Fig. 13(b)). This indicates that the oscillation amplitude of $R(\sigma)$ is a sensitive measure of the shrinkage of ${}^{206}\textrm{Pb}$ relative to ${}^{208}\textrm{Pb}$.

Next, I discuss the $3p_{1/2}$-hole contribution effects, which provide a nontrivial change of the density shape in the surface region. The density and cross sections obtained for the two-hole (2h) case are compared with those for the no-hole case in Figs. 12 and 15, respectively; to eliminate the size changing effect, I choose $\delta_{s}$ independently for the 0h and 2h cases so that approximately the same $D(r_{n})$ values will be given in the two cases as $D(r_{n})\approx-0.024$ fm for ${}^{206}\textrm{Pb}$ and $D(r_{n})\approx-0.046$ fm for ${}^{204}\textrm{Pb}$. The densities of ${}^{206}\textrm{Pb}$ are shown in Fig. 12, the results of the ${}^{206}\textrm{Pb}(p,p)$ cross sections are shown in Figs. 12(a) and (b), and those for ${}^{204}\textrm{Pb}(p,p)$ cross sections are presented in Fig. 15(c). Figures 12(d) and (e) display $\rho_{n}({}^{208}\textrm{Pb})-10\times D(\rho_{n})$ with 10 times enhanced $D(\rho_{n})$ to show the difference between the 0h and 2h densities more clearly. The dominant effect of the $3p_{1/2}$-hole contribution is an enhancement of the surface density in the 5 fm$<r<$7 fm region around the peak position of $4\pi r^{2}\rho_{n}(r)$, whereas the contribution to the tail density in the $r>7$  fm region is relatively small (Fig. 12 (a),(c), and (e)). This density change by the $3p_{1/2}$-hole contribution globally raises the cross sections of ${}^{206}\textrm{Pb}$ (Fig. 15(a)); therefore, it causes an upward shift of the isotopic cross-section ratio $R(\sigma)$ without changing its angular dependence (Fig. 15(b)). Note that, the parallel shift of $R(\sigma)$ with increasing $h$ is obtained only when $D(r_{n})$ is kept constant. The same analysis is performed for ${}^{204}\textrm{Pb}$, and a qualitatively consistent result is obtained (Fig. 15(c)).

In Figs. 15 (b) and (c), the $R(\sigma)$ obtained using the hole-model density is compared with that obtained using the me2 and SKM* densities. The me2(SKM*) density gives $D(r_{n})=-0.023$ fm ($-0.022$ fm) for ${}^{206}\textrm{Pb}$ and $-0.044$ fm ($-0.045$ fm) for ${}^{204}\textrm{Pb}$, which are consistent with the $D(r_{n})$ values of the hole-model density presented herein. The oscillation amplitude of $R(\sigma)$ is almost consistent between the hole-model, me2, and SKM* densities, meaning that it is determined by $D(r_{n})$ independently from details of model densities.

The present analyses of $\delta_{s}$ and $h$ dependences indicate the clear correspondence of $R(\sigma)$ to $D(\rho_{n})$ and $D(r_{n})$. Namely, the oscillation amplitude of $R(\sigma)$ is a good measure to determine the isotopic neutron radius difference $D(r_{n})$, whereas deviation of the center value of the oscillation from $R=1$ is a sensitive probe to the surface shape of the isotopic neutron-density difference $D(\rho_{n})$.

Using the SOG-fit core density, the hole-model analysis is performed in a similar way to Sec. IV.2 for the me2-core density, and qualitatively consistent results are obtained. The $R(\sigma)$ result obtained by the RIA+ddMH calculation with the hole-model (SOG-core) density is shown in Fig. 16. Figures  16(a) and (b) show the $\delta_{s}$ and $h$ dependences of $R(\sigma)$ for ${}^{206}\textrm{Pb}$, and Figs. 16(c) and (d) show the results for ${}^{204}\textrm{Pb}$. For ${}^{206}\textrm{Pb}$, the hole-model density with (0h,$-0.7\%$) (which has $D(r_{n})=-0.040$ fm, same as the SOG-fit density) overshoots the oscillation amplitude of the experimental $R(\sigma)$ (see the red line in Fig. 16(a)). This indicates that the value $D(r_{n})=-0.040$ fm of the SOG-fit density for ${}^{206}\textrm{Pb}$ may be too large; similarly, the hole-model density of ${}^{204}\textrm{Pb}$ with (0h,$-1\%$) has $D(r_{n})=-0.057$ fm, which is almost the same as the SOG-fit density, but seems to overshoot the oscillation amplitude of the experimental $R(\sigma)$ (see the red line in Fig. 16(c)), meaning that the value of $D(r_{n})=-0.057$ fm for ${}^{204}\textrm{Pb}$ is unlikely.

The optimal parameter set of $h$ and $\delta_{s}$ is sought for the hole model to fit the experimental $R(\sigma)$. First, I choose the favored parameter sets among the 0h densities, (0h,$-0.2\%$) with $D(r_{n})=-0.011$ fm for ${}^{206}\textrm{Pb}$ and (0h,$-0.4\%$) with $D(r_{n})=-0.023$ fm for ${}^{204}\textrm{Pb}$, to reproduce the slope in one cycle of the oscillation amplitude of the experimental $R(\sigma)$; then, I change the effective hole number $h$, maintaining the optimal $D(r_{n})$ values. The calculated $R(\sigma)$ obtained using the 0h, 1h, and 2h densities with $D(r_{n})\approx-0.01$ fm ($-0.02$ fm) for ${}^{206}\textrm{Pb}$ (${}^{204}\textrm{Pb}$) is shown in Fig. 16(b) (Fig. 16(d)). Finally, the (1h,$-0.01\%$) density with $D(r_{n})=-0.012$ fm is obtained as an optimized solution for ${}^{206}\textrm{Pb}$, which describes the experimental $R(\sigma)$, and an optimized set (1h,$-0.03\%$) with $D(r_{n})=-0.023$ fm is obtained for ${}^{204}\textrm{Pb}$. The $R(\sigma)$ values calculated using the optimized solutions are shown by solid lines in Figs. 16 (b) and (d).

To discuss the uncertainty in determining $D(r_{n})$ from the experimental $R(\sigma)$, I calculate the $\chi^{2}$ values of $R(\sigma)$ for the hole model. In the present analysis of $R(\sigma)$, the angular resolution of the experimental $(p,p)$ cross section data is not taken into account, but it can have crucial effects at the forward and dip angles of the cross sections. Therefore, $\chi^{2}$ is calculated using a total of 17 datapoints in a “safe” region by eliminating seven datapoints at the forward angles and five at the dip angles. In Fig. 17, the $\chi^{2}$ values obtained for $h=\{0,0.5,\ldots,2\}$ and $\delta_{s}=\{0\%,0.1\%,\cdots-1.0\%\}$ are plotted as functions of $D(r_{n})$.

The results for ${}^{204}\textrm{Pb}$ and ${}^{206}\textrm{Pb}$ of the hole model with the SOG-fit core are shown in Figs. 17(a) and (b). The absolute values of the calculated $\chi^{2}$ are meaningless because the experimental errors of $R(\sigma)$ are estimated by assuming independent errors of the ${}^{A}\textrm{Pb}$ and ${}^{208}\textrm{Pb}$ cross sections though the $A$-independent systematic errors should be removed. To roughly estimate the uncertainty, I here adopt a criterion for the acceptable $\chi^{2}$ range as less than three times the minimum value $\chi^{2}_{\textrm{min}}$ as $\chi^{2}\lesssim 3\chi^{2}_{\textrm{min}}$. From the acceptable ranges of this criterion, which are shown by dotted lines in the figures, $D(r_{n})=-0.03$–$-0.006$ fm for ${}^{206}\textrm{Pb}$ and $D(r_{n})=-0.05$–$-0.006$ fm for ${}^{204}\textrm{Pb}$ are obtained. The $\chi^{2}$ values for the SOG-fit density are $\chi^{2}=14$ for ${}^{206}\textrm{Pb}$ and $\chi^{2}=52$ for ${}^{204}\textrm{Pb}$, which exceed the acceptable range because the systematics between the Pb isotopes was not taken into account in the fitting of Ref. Zenihiro et al. (2010).

For the hole model with the me2 core, the $\chi^{2}$ values are calculated using rescaled angles $\theta^{*}$, and the results obtained for ${}^{204}\textrm{Pb}$ and ${}^{206}\textrm{Pb}$ are shown in Figs. 17(c) and (d), respectively. The results of the me2 core are almost consistent with those of the SOG-fit core meaning that the present hole-model analysis of $R(\sigma)$ can obtain $D(r_{n})$ values almost independently from the adopted ${}^{208}\textrm{Pb}$-core density. In Table 1, the values of $D(r_{n})$ and $\chi^{2}$ obtained by the hole models (SOG-fit and me2 ${}^{208}\textrm{Pb}$ cores) are summarized in comparison with those of the SOG-fit and me2 densities of the Pb isotopes.

As mentioned previously, the SOG-fit density overshoots the oscillation amplitude of the experimental $R(\sigma)$. The reason for this failure in reproducing $R(\sigma)$ is that the fitting was performed independently for each isotope without taking the isotopic systematics into account. From the SOG-fit density, I reconstruct the improved neutron densities of Pb isotopes that can describe experimental $R(\sigma)$ as follows. First, the neutron density of ${}^{206}\textrm{Pb}$ is obtained by averaging three densities of ${}^{206}\textrm{Pb}$, ${}^{206}\textrm{Pb}$, and ${}^{206}\textrm{Pb}$ given by the SOG-fit density to avoid a risk from uncertainty of the SOG-fit density in the internal region. Next, the neutron densities of ${}^{208}\textrm{Pb}$ and ${}^{204}\textrm{Pb}$ are constructed to reproduce the $D(\rho_{n})$ of the best solution of the hole model. The density of the Pb isotopes obtained with these procedures is called the “averaged-model” density. In Fig. 18, the averaged-model density is shown in comparison with the SOG-fit and me2 densities. The averaged-model density is similar to the SOG-fit density. The $D(\rho_{n})$s of the averaged model, SOG-fit, and me2 densities are compared in Fig. 19. Note that the $D(\rho_{n})$ of the averaged model is tuned to fit the $R(\sigma)$ data in the hole-model analysis. The surface peak shape of $4\pi r^{2}D(\rho_{n})$ in the $6~{}\textrm{fm}\lesssim r\lesssim 8~{}\textrm{fm}$ region is similar between three kinds of densities; however, a difference is found in the internal $r\lesssim 5~{}\textrm{fm}$ region, to which $(p,p)$ at 295 MeV is insensitive. The flopping behavior of $4\pi r^{2}D(\rho_{n})$ found in the SOG-fit density disappears in the averaged-model density, which shows a smooth behavior in the internal region similar to theoretical densities such as the SKM* density, rather than the SOG-fit density.

Pb$(p,p)$ at 295 MeV is calculated using RIA+ddMH with the averaged-model density. The results of $R(\sigma)$, $\sigma$, and $A_{y}$ are shown in Figs. 22, 20, and 21, respectively, and compared with those obtained with the SOG-fit and me2 densities. $R(\sigma)$ is significantly improved by the averaged-model density compared with other densities because $D(\rho_{n})$ is tuned to fit the $R(\sigma)$ data. Moreover, the averaged-model density successfully describes the cross sections and analyzing powers in a quality almost equivalent to the SOG-fit density.

In Fig. 23, the neutron radius ($r_{n}$) and skin thickness ($\Delta r_{np}$) obtained by the present averaged model are shown in comparison with the experimental and theoretical values. The averaged model yields smooth changes of $r_{n}$ and $\Delta r_{np}$ in a series of Pb isotopes from ${}^{204}\textrm{Pb}$ to ${}^{208}\textrm{Pb}$. The values are within the experimental errors of the SOG fitting extracted from the $(p,p)$ data at 295 MeV. It is difficult to quantitatively discuss the systematic errors of the present result because the angular resolutions and systematic errors of the experimental data are not taken into account in the present analysis. In Fig. 23, I present a rough estimation of the error range of $r_{n}$ for ${}^{208}\textrm{Pb}$ using the acceptable range $D(r_{n})=-0.03\sim-0.006$ fm obtained by hole-model analysis and the $r_{n}$ value of ${}^{206}\textrm{Pb}$ of the averaged model.