Isospin Mixing and the Cubic Isobaric Multiplet Mass Equation in the Lowest Quintet
Abstract
The Isobaric Multiplet Mass Equation (IMME) is known to break down in the first isospin quintet. In this work we combine high-resolution experimental data with state-of-the-art shell-model calculations to investigate isospin mixing as a possible cause for this violation. The experimental data are used to validate isospin-mixing matrix elements calculated with newly developed shell-model Hamiltonians. Our analysis shows that isospin mixing with non-analog states contributes to the IMME breakdown, making the requirement of an anomalous cubic term inevitable for the multiplet.
If nuclear isospin were a conserved quantity, the members of an isobaric multiplet would be -fold degenerate. However, it is known Benenson and Kashy (1979) that this degeneracy is broken by two-body charge-dependent interactions, which can be described at tree-level as the sum of an isoscalar, isovector and isotensor operator of rank 2. To first order, the energy spacings between the multiplet members can be obtained from the expectation value of the charge-dependent perturbation. On applying the Wigner-Eckart theorem to the perturbing Hamiltonian, the mass splittings are described by the isobaric multiplet mass equation (IMME) Wigner (1958); Weinberg and Treiman (1959)
| (1) |
where each member of the multiplet is characterized by its isospin projection .
The general success of the IMME over a large mass range made it a reliable tool to address a variety of research problems. For example, it was used to test recent advances in nuclear theory Holt et al. (2013); Ormand et al. (2017); Martin et al. (2021), map the proton dripline Ormand (1997), identify candidates for two-proton radioactivity Dossat et al. (2005); Blank and Borge (2008), search for physics beyond the standard model Adelberger et al. (1999), infer rapid proton capture () nuclear reaction rates relevant for studies of novae and x-ray bursts Wrede et al. (2009); Richter and Brown (2013); Ong et al. (2017), assess global nuclear mass model predictions Liu et al. (2011) and constrain calculations relevant for CKM unitarity tests Hardy and Towner (2015).
In this context, the lowest isospin quintet for (with spin and parity ) is an interesting case. The decay of 32Ar, the most proton-rich member of the quintet was previously used for searches of exotic scalar Adelberger et al. (1999) and tensor Araujo-Escalona et al. (2020) weak interactions as well as for benchmarking isospin symmetry breaking (ISB) corrections Bhattacharya et al. (2008) important for obtaining a precise value of , the up-down element of the CKM quark-mixing matrix Hardy and Towner (2015). In fact, the quintet is one of the most extensively studied and precisely measured multiplets to date Triambak et al. (2006); Kwiatkowski et al. (2009); Kankainen et al. (2010); Blaum et al. (2003); Signoracci and Brown (2011); Lam et al. (2013). It remains an anomalous case, for which the IMME breaks down significantly MacCormick and Audi (2014). A satisfactory fit to the measured masses is only obtained with an additional cubic term, with keV (c.f. Table 1). This is the smallest and most precisely determined violation of the IMME observed so far. Unlike other multiplets, where apparent violations of the IMME were resolved through subsequent measurements Herfurth et al. (2001); Pyle et al. (2002); Gallant et al. (2014); Glassman et al. (2015); Zhang et al. (2012); Su et al. (2016), the anomaly has persisted over several years, despite high-precision remeasurements of ground state masses Kwiatkowski et al. (2009); Kankainen et al. (2010); Shi et al. (2005) as well as excitation energies Triambak et al. (2006); Pyle et al. (2002). A recent compilation MacCormick and Audi (2014) showed the quintet to be a unique case, in which the value for a cubic fit yields 95% probability that it is the correct model to describe the data. Since there are no known fundamental reasons that preclude a cubic IMME term, it is interesting that the magnitude of the extracted coefficient for this case agrees well with theoretical estimates that used a simple nonperturbative model Henley and Lacy (1969) or a three-body second-order Coulomb interaction Bertsch and Kahana (1970), both of which allow a non-vanishing cubic term, with . Alternatively, the role of isospin-mixing with non-analog states was also theoretically investigated in the recent past Signoracci and Brown (2011); Lam et al. (2013).
We delve into the above aspect here, via an analysis of high-resolution experimental data and a comparison with calculations that use recently developed shell model Hamiltonians Magilligan and Brown (2020). For the former, we mainly rely on data from a previous 32Ar decay experiment at CERN-ISOLDE Adelberger et al. (1999), that acquired -delayed protons from unbound states in the daughter 32Cl ( keV) with high resolution (full widths at half maximum of keV). The primary goal of the ISOLDE experiment was to search for scalar currents in the weak interaction, by determining the angular correlation () for the decay, via a precise analysis of the shape of the superallowed -delayed proton peak Adelberger et al. (1999). Part of the proton spectrum is shown in Fig. 1.
The high resolution nature of the ISOLDE data allow an identification of potential isospin admixtures to the isobaric analog state (IAS) in 32Cl. The nature of each transition is encoded in the shapes of the proton groups, which would be different if the transitions were Fermi ( ), with or Gamow-Teller ( ), with .
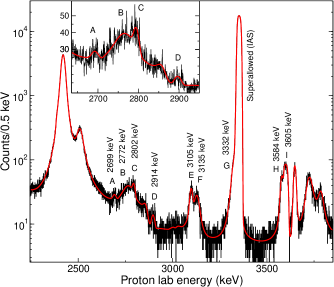
We analyzed these data using the R-matrix formalism described in Refs. Barker (1971); Warburton (1986). In the analysis, the proton peaks were grouped as or depending on whether the proton emission left the residual 31S nucleus in its ground state or any of its first three excited states at 1249, 2234 and 3077 keV (see Fig. 9 in Ref. Bhattacharya et al. (2008)). Interference was allowed between all levels that had the same quantum numbers, transition type (Fermi or Gamow-Teller), and final states in 31S. The R-matrix fits folded in the detector response function and lepton recoil effects (described in Ref. Adelberger et al. (1999)), and were parameterized using various values for the daughter 32Cl states and associated coefficients. The fits yielded relative intensities, 32Cl excitation energies and intrinsic widths. They were repeated for different values of , spin-parity combinations and , assignments for the daughter levels to obtain best agreement with experimental data. A few important features of the analysis are described below.
Peaks C, E and H were assumed to be from the group. These assignments were based on data reported by independent 32Ar -delayed proton- coincidence measurements Bhattacharya et al. (2008); Blank et al. (2021). We observe that a reasonably a good R-matrix fit is attained (Fig. 1) with the parameters listed in Table 2. The fit assumes that peak B arises from a Fermi transition, while the others (apart from peak I) are exclusively from Gamow-Teller decays. Based purely on values from independent fits, peak I could be either from a Fermi or Gamow-Teller decay.
| Peak | Group | 32Ar decay Adelberger et al. (1999) | ||||
|---|---|---|---|---|---|---|
| (keV) | (keV) | (%) | (keV) | |||
| A | 0.23(3) | |||||
| B | 1 | 0.8(1) | … | |||
| C | 5721(4) | 0.10(3) | … | |||
| D | 0.20(3) | 4584(5) | ||||
| E | 0.14(2) | .. | ||||
| F | 0.26(3) | 4815(5) | ||||
| G | 0.49(6) | 5020(5) | ||||
| H | 0.25(3) | … | ||||
| I | or 1 | 0.45(4) | … | |||
| = 0.80 | ||||||
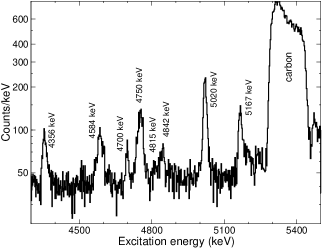
We compared these results with data that were independently obtained at the MLL tandem accelerator facility in Garching, Germany. The experiment used 300 enA of 33 MeV ions, incident on a g/cm2-thick natural ZnS target. The tritons exiting the target were momentum analyzed using the high-resolution Q3D magnetic spectrograph Löffler et al. (1973); Dollinger and Faestermann (2018). A sample triton spectrum in the energy range of interest is shown in Fig. 2. These data provided an important confirmation of the assignments for peaks A, D, F and G in our R-matrix analysis. Additionally, since the charge-exchange reaction predominantly populates , levels at forward angles 111This assumes no anomalous isospin-mixing mechanisms within 32S., the states observed at these energies in both 32Ar decay and the reaction can be ruled out as sources of isospin impurity. This comparative analysis leaves only the 4443 and 5302 keV levels (c.f. Table 2) as potential admixed states. We find from the decay data that the intensity for the latter is around 1.2 times larger than its group. In comparison, the intensity for the IAS is roughly 80 times smaller than the . This is due to the low penetrability of protons from the IAS. The above discrepancy makes it highly unlikely for the 5302 keV state to have spin-parity , which rules it out as a source of isospin mixing.
We next used the measured -delayed proton intensities in Table 2, together with shell model calculations of isospin mixing to investigate the matter further. For the latter we used newly developed isospin non-conserving (INC) USDC and USDI interactions, described extensively in Ref. Magilligan and Brown (2020). The INC parameters in the new USD Hamiltonians were obtained from a fit to several mirror displacement energies and stringently tested via a comparison with experimental data Magilligan and Brown (2020). The isospin-mixing matrix elements calculated with these Hamiltonians were robustly validated Magilligan and Brown (2020) with results from independent high-precision 31,32Cl decay experiments Bennett et al. (2016); Melconian et al. (2011, 2012), where large isospin-mixing in the daughter 31,32S states were observed. More recently, such calculations were used together with a 32Ar decay measurement Blank et al. (2021), that acquired valuable proton-gamma coincidence data, albeit with lower proton energy resolution. Ref. Blank et al. (2021) identified two possible sources of isospin mixing at 4799 and 4561 keV. However, their measured proton branches were significantly lower than calculated values. We show below that the higher-resolution ISOLDE data justifies ruling out these proposed levels, while providing a viable alternative for the admixed state, which is consistent with both theory predictions as well as experimental observations.
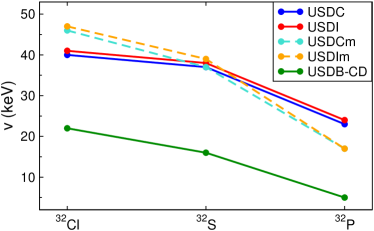
Our shell model calculations show that the isospin mixing within the members of the quintet occurs primarily with a single state, located few hundred keV below the IAS in each isobar. The results are summarized in Table 3, which lists the energy differences () between the admixed and states for each nucleus, and the calculated isospin-mixing matrix element () for 32Cl. The evaluated mixing matrix elements for each of the three nuclei are plotted in Fig. 3. We note that the mixing matrix elements obtained with the older USDB-CD interactions Ormand and Brown (1989) are nearly a factor of two smaller than the ones obtained with the newer interactions, for all three isobars. This is consistent with previous observations for 31,32Cl decay Magilligan and Brown (2020).
| Interaction | (keV) | (keV) | ||
|---|---|---|---|---|
| 32Cl | 32S | 32P | 32Cl | |
| USDC | -226 | -186 | -237 | 40 |
| USDI | -308 | -266 | -326 | 41 |
| USDCm | -324 | -239 | -293 | 46 |
| USDIm | -405 | -321 | -383 | 47 |
| USDB-CD | -440 | -378 | -427 | 22 |
| Expt (this work) | -603 | |||
The predicted level in 32Cl can be identified by obtaining an experimental value of from the data in Fig. 1 and Table 2. For two-state mixing, is simply
| (2) |
where the ratio in the square bracket is the (Fermi) strength to the admixed state, relative to the superallowed decay. This is easily determined from the measured values in Table 2, the ratio of calculated phase-space factors, a small ISB correction Bhattacharya et al. (2008) and the contribution to the total superallowed intensity. On applying this prescription to the only candidate level at 4443 keV, we obtain a keV, in excellent agreement with the calculations. The results in Table 3, together with our aforementioned observations and the experimental values listed in Table 2 allow a credible identification of the 4443 keV level as the predicted admixed state. The discrepancy between theory and experiment for should not be surprising, given the 150 keV root-mean-square (rms) deviation for energies in USD interactions Magilligan and Brown (2020).
We next investigated additional cubic () and quartic () terms to the IMME due to such isospin mixing. One can determine the exact solutions for the and coefficients by modifying Eq. (1) to incorporate such terms, such that
| (3) | ||||
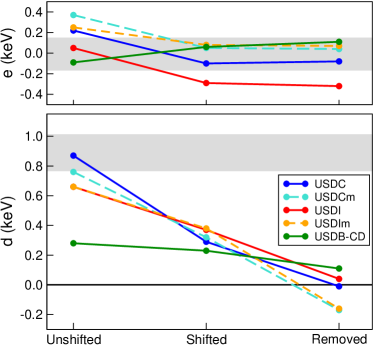
where the are isobar masses in the quintet. The results for and using the calculated values of and are shown in Fig. 4, and labeled as “unshifted”. We repeated these evaluations by shifting the states in 32Cl, 32S and 32P by the amount needed to reproduce our experimentally determined 603 keV energy difference in 32Cl. The same was used for the three isobars due to the lack of similar experimental information for 32S and 32P. The shifts were accomplished by adding a term to the Hamiltonian that shifts the states relative to the others, without changing the isospin-mixing. As evident in Fig. 4, the shifts mildly affect the coefficient (due to changes in the mixing with the IAS in 32S), but significantly decrease the calculated coefficient to – keV for the new interactions.
The single-state contributions from and levels are
| (4) | ||||
where is the shift in each IAS due to two-state mixing. Thus, one can remove the mixing contribution for further investigation (labeled as “removed” in Fig. 4). We observe that on doing so, the extracted coefficients are mostly consistent with zero. The negative coefficient from the USDI calculation is due to mixing with a state in 32S. However such mixing would not explain the non-zero coefficient required for the quintet, as evident from Eq. (4).
The above analysis validates the contention that isospin mixing with predicted levels necessitates a small cubic term for the multiplet. Our extracted coefficients for the “shifted” calculations from different USDC and USDI Hamiltonians agree reasonably well with one another, but are smaller than the experimental value keV, from Table 1.
| Interaction | Proton emission amplitudes | |||
| (shifted calculation) | (%) | |||
| USDC | 0.011 | 0.022 | 0.21 | 0.55 |
| USDI | 0.011 | 0.031 | 0.19 | 0.58 |
| USDCm | 0.0052 | 0.031 | 0.21 | 0.15 |
| USDIm | 0.0043 | 0.031 | 0.19 | 0.70 |
| USDB-CD | 0.0024 | 0.017 | 0.21 | 0.15 |
| (keV) | 990 | 17.5 | 590 | |
| (keV) | 0.0182(5)a | 0.000233(7)a | 77(15)b | |
| 0.0041(1)a | 0.0035(1)a | 0.34(4)b | ||
a From Ref. Bhattacharya et al. (2008).
b This work, using data from Ref. Adelberger et al. (1999).
As further tests of our calculations, we also evaluated amplitudes for isospin-forbidden proton emission from the two admixed levels in 32Cl and the effect of the isospin mixing on the superallowed Fermi decay of 32Ar. Unlike the energy shift of the IAS in 32Cl, which is predominantly from isospin mixing with the predicted 0 state below the IAS, isospin-forbidden proton emission from the IAS depends on mixing with a large number of states in 32Cl and isospin mixing within 31S, which is dominated by mixing of the lowest state into its ground state.
We calculated proton widths for and transitions from the admixed state and the IAS in 32Cl. The widths were evaluated using the simple expression
| (5) |
where the factor is a center-of-mass correction Dieperink and de Forest (1974), the are the shell model spectroscopic factors, and are single-particle proton widths. Similar to Ref. Signoracci and Brown (2011), the were calculated from + scattering on potentials obtained with an energy-density functional calculation with the Skx Skyrme-type interaction Alex Brown (1998). On the other hand, the measured proton widths Bhattacharya et al. (2008) for the IAS are known to be eV and eV for the and protons respectively. Together with the calculated single-particle proton decay widths, we use these results to obtain experimental values for the decay amplitudes . These are simply determined from the relation . The results for are shown in Table 4 and compared with theory predictions, obtained using the ‘shifted’ calculations.222For example, for the shifted USDCm calculation, the calculated amplitude can be decomposed as = 0.0041 (0; ) 0.0159 (0; ) 0.0009 (0; ) 0.0009 (all other ) (31S; ) = 0.0052. The USDC result has a larger amplitude, mainly due to a 50% smaller destructive contribution from the state in 31S. We observe reasonable agreement between theory and experiment, except for the transition, whose calculated amplitudes are found to be much larger.
Finally, we also provide isospin-symmetry-breaking (ISB) corrections for 32Ar 32Cl superallowed Fermi decay, due to the isospin-mixing in 32Cl. The superallowed strength is reduced by a factor , where is the total ISB correction Hardy and Towner (2015). Such corrections play a critical role in testing the unitarity of the CKM matrix and placing important constraints on beyond the standard model (BSM) physics Hardy and Towner (2015). The ISB correction is generally expressed as a sum of two separate contributions, Bhattacharya et al. (2008), from configuration mixing and a overlap mismatch between the parent and daughter radial wavefunctions. The former are known to quite model dependent as they are very sensitive to the details of their calculation Hardy and Towner (2015). Our calculated results for (from the mixing in 32Cl) are listed the final column of Table 4. It may be noted that for the shifted USDCm and USDIm calculations, which show best agreement with the measured amplitude, we obtain = 0.15% and 0.70% respectively. From a previous evaluation of Bhattacharya et al. (2008), these yield and , in agreement with the experimentally extracted value, Bhattacharya et al. (2008).
In summary, we used high-resolution experimental data to validate newly-developed shell model calculations of isospin mixing in 32Cl. This analysis is used to investigate the observed IMME violation in the first quintet. We show that isospin mixing with shell-model-predicted states below the IAS necessarily result in a break down of the IMME, leading to the requirement of a small cubic term. However, this alone cannot explain the magnitude of the experimental coefficient in Table 1. Experimental investigations of intruder levels, isospin-mixing in 32S and 32P, continuum coupling of the proton unbound states in 32Cl, and further mass measurements may be useful in this regard.
Our observations pertaining to 32Ar 32Cl superallowed Fermi decay may also be useful to benchmark theory calculations Bhattacharya et al. (2008) of model-dependent ISB corrections that are important for top-row CKM unitarity tests Hardy and Towner (2015). This is particularly relevant in light of recent evaluations of radiative corrections Seng et al. (2018) that show an apparent violation of CKM unitarity at the level Seng et al. (2021).
Acknowledgements.
We thank Eric Adelberger and Gordon Ball for insightful and illuminating discussions. This work was partially supported by the National Research Foundation (NRF), South Africa under Grant No. 85100, the U.S. National Science Foundation under Grant No. PHY-1811855 and the U.S. Department of Energy under Grants No. DE-SC0017649 and DE-FG02-93ER40789. P.A. acknowledges funding from the Claude Leon Foundation in the form of a postdoctoral fellowship.References
- Benenson and Kashy (1979) W. Benenson and E. Kashy, Rev. Mod. Phys. 51, 527 (1979).
- Wigner (1958) E. P. Wigner, in Proceedings of the Robert A. Welch Foundation Conferences on Chemical Research, Houston, Vol. 1, edited by W. O. Milligan (The Robert Welch Foundation, 1958, 1958) p. 88.
- Weinberg and Treiman (1959) S. Weinberg and S. B. Treiman, Phys. Rev. 116, 465 (1959).
- Holt et al. (2013) J. D. Holt, J. Menéndez, and A. Schwenk, Phys. Rev. Lett. 110, 022502 (2013).
- Ormand et al. (2017) W. E. Ormand, B. A. Brown, and M. Hjorth-Jensen, Phys. Rev. C 96, 024323 (2017).
- Martin et al. (2021) M. S. Martin, S. R. Stroberg, J. D. Holt, and K. G. Leach, Phys. Rev. C 104, 014324 (2021).
- Ormand (1997) W. E. Ormand, Phys. Rev. C 55, 2407 (1997).
- Dossat et al. (2005) C. Dossat et al., Phys. Rev. C 72, 054315 (2005).
- Blank and Borge (2008) B. Blank and M. Borge, Progress in Particle and Nuclear Physics 60, 403 (2008).
- Adelberger et al. (1999) E. G. Adelberger et al., Phys. Rev. Lett. 83, 1299 (1999).
- Wrede et al. (2009) C. Wrede, J. A. Caggiano, J. A. Clark, C. M. Deibel, A. Parikh, and P. D. Parker, Phys. Rev. C 79, 045808 (2009).
- Richter and Brown (2013) W. A. Richter and B. A. Brown, Phys. Rev. C 87, 065803 (2013).
- Ong et al. (2017) W.-J. Ong et al., Phys. Rev. C 95, 055806 (2017).
- Liu et al. (2011) M. Liu, N. Wang, Y. Deng, and X. Wu, Phys. Rev. C 84, 014333 (2011).
- Hardy and Towner (2015) J. C. Hardy and I. S. Towner, Phys. Rev. C 91, 025501 (2015).
- Meng Wang and W. J. Huang and F.G. Kondev and G. Audi and S. Naimi (2021) Meng Wang and W. J. Huang and F.G. Kondev and G. Audi and S. Naimi, Chinese Physics C 45, 030003 (2021).
- Bhattacharya et al. (2008) M. Bhattacharya, D. Melconian, A. Komives, S. Triambak, A. García, E. G. Adelberger, B. A. Brown, M. W. Cooper, T. Glasmacher, V. Guimaraes, P. F. Mantica, A. M. Oros-Peusquens, J. I. Prisciandaro, M. Steiner, H. E. Swanson, S. L. Tabor, and M. Wiedeking, Phys. Rev. C 77, 065503 (2008).
- Triambak et al. (2006) S. Triambak, A. García, E. G. Adelberger, G. J. P. Hodges, D. Melconian, H. E. Swanson, S. A. Hoedl, S. K. L. Sjue, A. L. Sallaska, and H. Iwamoto, Phys. Rev. C 73, 054313 (2006).
- Endt (1998) P. Endt, Nuclear Physics A 633, 1 (1998).
- Araujo-Escalona et al. (2020) V. Araujo-Escalona, D. Atanasov, X. Fléchard, P. Alfaurt, P. Ascher, B. Blank, L. Daudin, M. Gerbaux, J. Giovinazzo, S. Grévy, T. Kurtukian-Nieto, E. Liénard, G. Quéméner, N. Severijns, S. Vanlangendonck, M. Versteegen, and D. Zákoucký, Phys. Rev. C 101, 055501 (2020).
- Kwiatkowski et al. (2009) A. A. Kwiatkowski, B. R. Barquest, G. Bollen, C. M. Campbell, D. L. Lincoln, D. J. Morrissey, G. K. Pang, A. M. Prinke, J. Savory, S. Schwarz, C. M. Folden, D. Melconian, S. K. L. Sjue, and M. Block, Phys. Rev. C 80, 051302 (2009).
- Kankainen et al. (2010) A. Kankainen, T. Eronen, D. Gorelov, J. Hakala, A. Jokinen, V. S. Kolhinen, M. Reponen, J. Rissanen, A. Saastamoinen, V. Sonnenschein, and J. Äystö, Phys. Rev. C 82, 052501 (2010).
- Blaum et al. (2003) K. Blaum, G. Audi, D. Beck, G. Bollen, F. Herfurth, A. Kellerbauer, H.-J. Kluge, E. Sauvan, and S. Schwarz, Phys. Rev. Lett. 91, 260801 (2003).
- Signoracci and Brown (2011) A. Signoracci and B. A. Brown, Phys. Rev. C 84, 031301 (2011).
- Lam et al. (2013) Y. H. Lam, N. A. Smirnova, and E. Caurier, Phys. Rev. C 87, 054304 (2013).
- MacCormick and Audi (2014) M. MacCormick and G. Audi, Nuclear Physics A 925, 61 (2014).
- Herfurth et al. (2001) F. Herfurth, J. Dilling, A. Kellerbauer, G. Audi, D. Beck, G. Bollen, H.-J. Kluge, D. Lunney, R. B. Moore, C. Scheidenberger, S. Schwarz, G. Sikler, J. Szerypo, and I. Collaboration, Phys. Rev. Lett. 87, 142501 (2001).
- Pyle et al. (2002) M. C. Pyle, A. García, E. Tatar, J. Cox, B. K. Nayak, S. Triambak, B. Laughman, A. Komives, L. O. Lamm, J. E. Rolon, T. Finnessy, L. D. Knutson, and P. A. Voytas, Phys. Rev. Lett. 88, 122501 (2002).
- Gallant et al. (2014) A. T. Gallant, M. Brodeur, C. Andreoiu, A. Bader, A. Chaudhuri, U. Chowdhury, A. Grossheim, R. Klawitter, A. A. Kwiatkowski, K. G. Leach, A. Lennarz, T. D. Macdonald, B. E. Schultz, J. Lassen, H. Heggen, S. Raeder, A. Teigelhöfer, B. A. Brown, A. Magilligan, J. D. Holt, J. Menéndez, J. Simonis, A. Schwenk, and J. Dilling, Phys. Rev. Lett. 113, 082501 (2014).
- Glassman et al. (2015) B. E. Glassman, D. Pérez-Loureiro, C. Wrede, J. Allen, D. W. Bardayan, M. B. Bennett, B. A. Brown, K. A. Chipps, M. Febbraro, C. Fry, M. R. Hall, O. Hall, S. N. Liddick, P. O’Malley, W. Ong, S. D. Pain, S. B. Schwartz, P. Shidling, H. Sims, P. Thompson, and H. Zhang, Phys. Rev. C 92, 042501 (2015).
- Zhang et al. (2012) Y. H. Zhang et al., Phys. Rev. Lett. 109, 102501 (2012).
- Su et al. (2016) J. Su, W. Liu, N. Zhang, Y. Shen, Y. Lam, N. Smirnova, M. MacCormick, J. Wang, L. Jing, Z. Li, Y. Wang, B. Guo, S. Yan, Y. Li, S. Zeng, G. Lian, X. Du, L. Gan, X. Bai, Z. Gao, Y. Zhang, X. Zhou, X. Tang, J. He, Y. Yang, S. Jin, P. Ma, J. Ma, M. Huang, Z. Bai, Y. Zhou, W. Ma, J. Hu, S. Xu, S. Ma, S. Chen, L. Zhang, B. Ding, Z. Li, and G. Audi, Physics Letters B 756, 323 (2016).
- Shi et al. (2005) W. Shi, M. Redshaw, and E. G. Myers, Phys. Rev. A 72, 022510 (2005).
- Henley and Lacy (1969) E. M. Henley and C. E. Lacy, Phys. Rev. 184, 1228 (1969).
- Bertsch and Kahana (1970) G. Bertsch and S. Kahana, Physics Letters B 33, 193 (1970).
- Magilligan and Brown (2020) A. Magilligan and B. A. Brown, Phys. Rev. C 101, 064312 (2020).
- Barker (1971) F. C. Barker, Australian Journal of Physics 24, 771 (1971).
- Warburton (1986) E. K. Warburton, Phys. Rev. C 33, 303 (1986).
- Blank et al. (2021) B. Blank, N. Adimi, M. Alcorta, A. Bey, M. J. G. Borge, B. A. Brown, F. de Oliveira Santos, C. Dossat, H. O. U. Fynbo, J. Giovinazzo, H. H. Knudsen, M. Madurga, A. Magilligan, I. Matea, A. Perea, K. Sümmerer, O. Tengblad, and J. C. Thomas, Eur. Phys. J. A 57, 28 (2021).
- Löffler et al. (1973) M. Löffler, H. Scheerer, and H. Vonach, Nuclear Instruments and Methods 111, 1 (1973).
- Dollinger and Faestermann (2018) G. Dollinger and T. Faestermann, Nuclear Physics News 28, 5 (2018).
- Bennett et al. (2016) M. B. Bennett, C. Wrede, B. A. Brown, S. N. Liddick, D. Pérez-Loureiro, D. W. Bardayan, A. A. Chen, K. A. Chipps, C. Fry, B. E. Glassman, C. Langer, N. R. Larson, E. I. McNeice, Z. Meisel, W. Ong, P. D. O’Malley, S. D. Pain, C. J. Prokop, H. Schatz, S. B. Schwartz, S. Suchyta, P. Thompson, M. Walters, and X. Xu, Phys. Rev. Lett. 116, 102502 (2016).
- Melconian et al. (2011) D. Melconian, S. Triambak, C. Bordeanu, A. García, J. C. Hardy, V. E. Iacob, N. Nica, H. I. Park, G. Tabacaru, L. Trache, I. S. Towner, R. E. Tribble, and Y. Zhai, Phys. Rev. Lett. 107, 182301 (2011).
- Melconian et al. (2012) D. Melconian, S. Triambak, C. Bordeanu, A. García, J. C. Hardy, V. E. Iacob, N. Nica, H. I. Park, G. Tabacaru, L. Trache, I. S. Towner, R. E. Tribble, and Y. Zhai, Phys. Rev. C 85, 025501 (2012).
- Ormand and Brown (1989) W. E. Ormand and B. A. Brown, Nuclear Physics A 491, 1 (1989).
- Dieperink and de Forest (1974) A. E. L. Dieperink and T. de Forest, Phys. Rev. C 10, 543 (1974).
- Alex Brown (1998) B. Alex Brown, Phys. Rev. C 58, 220 (1998).
- Seng et al. (2018) C.-Y. Seng, M. Gorchtein, H. H. Patel, and M. J. Ramsey-Musolf, Phys. Rev. Lett. 121, 241804 (2018).
- Seng et al. (2021) C.-Y. Seng, D. Galviz, W. J. Marciano, and U.-G. Meißner, “An update on and from semileptonic kaon and pion decays,” (2021), arXiv:2107.14708 [hep-ph] .