∎
e1e-mail: [email protected] \thankstexte2e-mail: [email protected] \thankstexte3e-mail: [email protected] \thankstexte4e-mail: [email protected] \thankstexte5e-mail: [email protected] \thankstexte6e-mail: [email protected]
Isoscaling in central Sn+Sn collisions at 270 MeV/u
Abstract
Experimental information on fragment emissions is important in understanding the dynamics of nuclear collisions and in the development of transport model simulating heavy-ion collisions. The composition of complex fragments emitted in the heavy-ion collisions can be explained by statistical models, which assume that thermal equilibrium is achieved at collision energies below 100 MeV/u. Our new experimental data together with theoretical analyses for light particles from Sn+Sn collisions at 270 MeV/u, suggest that the hypothesis of thermal equilibrium breaks down for particles emitted with high transfer momentum. To inspect the system’s properties in such limit, the scaling features of the yield ratios of particles from two systems, a neutron-rich system of and a nearly symmetric system of , are examined in the framework of the statistical multifragmentation model and the antisymmetrized molecular dynamics model. The isoscaling from low energy particles agree with both models. However the observed breakdown of isoscaling for particles with high transverse momentum cannot be explained by the antisymmetrized molecular dynamics model.
1 Introduction
During a collision involving heavy-ions at energies well above the Coulomb barrier, nuclear matter is driven through very different configurations. In the early stages, violent collisions between its constituents take place, causing matter to be heated up. If these collisions occur above the production thresholds, sub-atomic particles such as pions, for instance, may be produced StockR_PR_1986_135_259 ; SengerPeter_PPNP_2004_53_1 ; OnoAkira_PPNP_2019_105_139_HIC_dynamics ; IkenoNatsumi_PRC_2016_93_044612_AMD_SnSn300 ; HongJun_PRC_2014_90_024605 . Many particles are ejected in this pre-equilibrium stage XuHM_PRC_1994_50_1659 , carrying away an appreciable amount of energy from the system. At the same time, the relative collective motion between the colliding nuclei leads to the compression of nuclear matter and densities higher than the saturation density found in the core of normal nuclei such as lead IkenoNatsumi_PRC_2016_93_044612_AMD_SnSn300 ; BorderieB_PPNP_2019_105_82_Phase_Transition_Nuclei .
Dynamical treatments WolterHermann_PPNP_2022_125_103962 have been developed to study such early stages. The density, the isospin configuration, and the temperatures attained by the system are sensitive to the physics input parameters employed by the models WolterHermann_PPNP_2022_125_103962 ; XuHM_PRC_1994_50_1659 ; LiBaoAn_PRL_1997_78_1644 ; TanWP_PRC_2001_64_051901 ; JhangG_SpiRIT_PLB_2021_813_136016_pion_ratio . Therefore, important information on the Nuclear Equation of State (EOS) may be provided by these dynamical approaches. Determining the input parameters of the models using experimental observables is of particular interest, as some of them are closely related to the rate of equilibration of the system, providing deeper insight into the dynamics of the collisions.
After pre-equilibrium emission, a freeze-out configuration is reached and many fragments including protons and neutrons are emitted XuHM_PRC_1994_50_1659 . Its behaviors can be described both by dynamical OnoAkira_PPNP_2019_105_139_HIC_dynamics ; WolterHermann_PPNP_2022_125_103962 and statistical models BondorfJP_PR_1995_257_133_SMM ; DasCB_PR_2005_406_1 ; BotvinaAS_EPJA_2006_30_121 ; BorderieB_PPNP_2019_105_82_Phase_Transition_Nuclei . In the former case, it appears as a result of the dynamical path taken by the system. In the case of statistical models, a freeze-out configuration is assumed. In both cases, most of the excited fragments predicted by the models would decay before detection and, therefore, a de-excitation treatment BotvinaAS_NPA_1987_475_663 ; TanWP_PRC_2003_68_034609_ISMM must be applied before comparing theoretical predictions with the experimental data. Consequently, important vestiges of the freeze out configuration may be blurred by the de-excitation process.
In this context, the nuclear isoscaling phenomenon TsangMB_MSU_PRC_2001_64_054615_isoscaling_SMM_EES ; TsangMB_MSU_PRL_2001_86_5023_isoscaling_experiment , first reported in Ref. XuHS_MSU_PRL_2000_85_716_isoscaling for Sn+Sn reactions at 50 MeV/u, is a very useful tool as the ratios of yields from two different reactions (which differ mainly in the isospin composition) is weakly affected by the fragment de-excitation process TsangMB_MSU_PRC_2001_64_054615_isoscaling_SMM_EES , retaining information on the system’s configuration right after the violent stages of the reaction. Particularly, under certain conditions TsangMB_MSU_PRC_2001_64_054615_isoscaling_SMM_EES ; SouzaSR_PRC_2009_80_044606_isoscaling_symmetryenergy ; RamiF_PRL_2000_84_1120_FOPI_Isospin_tracing , it may be related to the symmetry energy, which makes this observable specially relevant to investigations on the nuclear EOS. The isoscaling analysis considers the ratio:
| (1) |
where and stand for the yields of species , observed in two similar reactions “1” and “2” , where and respectively denote the neutron and proton numbers of the isotope. It has been found that this ratio follows a simple scaling law TsangMB_MSU_PRL_2001_86_5023_isoscaling_experiment ; TsangMB_MSU_PRC_2001_64_054615_isoscaling_SMM_EES
| (2) |
where and are the scaling parameters and C is a normalization constant. By convention, reaction 2 is chosen to have a larger isospin asymmetry compared with that of reaction 1.
This scaling property can be derived in the framework of the grand-canonical ensemble TsangMB_MSU_PRC_2001_64_054615_isoscaling_SMM_EES . From it, simple relationships between the neutron and proton chemical potentials, and , respectively, and the scaling parameters are obtained:
| (3) |
and
| (4) |
In these expressions, symbolizes the temperature at the freeze-out configuration and the superscripts () represent reactions “1” or “2”.
Although the formal derivation is based on the grand-canonical ensemble, the isoscaling property is also found in nearly all statistical models TsangMB_MSU_PRC_2001_64_041603_isoscaling_condition , including versions of the Statistical Multifragmentation Model (SMM) which employ the micro-canonical and canonical ensembles SouzaSR_PRC_2009_80_044606_isoscaling_symmetryenergy . It has also been observed in the Antisymmetrized Molecular Dynamics (AMD) model OnoAkira_SpiRIT_PRC_2003_68_051601_isoscaling_AMD . Calculations based on the molecular dynamics approach DorsoCO_PRC_2006_73_044601 seem to indicate that the isoscaling may be observed even when the system has not yet attained thermal equilibrium. Furthermore, recent experimental results suggest that the parameters and are sensitive to the mechanisms responsible for fragment production. These results call for further investigations on the nuclear isoscaling property.
Many experimental studies GeraciE_LNS_NPA_2004_732_173_isoscaling_experiment ; TrautmannW_2006_nuclex_0603027_isoscaling_ALADIN_INDRA ; FableQ_Arxiv_2022_2202_13850_CaCa_INDRA ; WuenschelS_TAMU_PRC_2009_79_061602_isoscaling_experiment ; YoungsM_TAMU_NPA_2017_962_61_isoscaling_experiment have investigated the isoscaling property in different systems at different bombarding energies. A close relationship between the parameter and the symmetry energy coefficient has been pointed out in Ref. TsangMB_MSU_PRC_2001_64_054615_isoscaling_SMM_EES . More specifically, denoting by and the atomic and mass numbers of the -th source, one has:
| (5) |
This property has been examined in several theoretical SouzaSR_PRC_2009_80_044606_isoscaling_symmetryenergy ; BotvinaAS_JINR_PRC_2002_65_044610_isoscaling_ion_induce and experimental TrautmannW_2006_nuclex_0603027_isoscaling_ALADIN_INDRA ; FableQ_Arxiv_2022_2202_13850_CaCa_INDRA ; WuenschelS_TAMU_PRC_2009_79_061602_isoscaling_experiment ; YoungsM_TAMU_NPA_2017_962_61_isoscaling_experiment works. Studies found that the isoscaling parameter and the difference between the two sources are related WuenschelS_TAMU_PRC_2009_79_061602_isoscaling_experiment , and different isoscaling tendencies between the projectile-like fragments and the emitted fragments exist YoungsM_TAMU_NPA_2017_962_61_isoscaling_experiment . The INDRA-GSI collaboration extended this investigation to relativistic collision energies for carbon induced reactions on Sn isotopes LeFevreA_PRL_2005_94_162701_INDRA_Alladin .
In this work, we extend earlier investigations at low incident energies of Sn+Sn reactions to a collision energy (270 MeV/u). We concentrate on central mid-rapidity events, with impact parameters fm. The scaling properties are studied as a function of the transverse momentum.
2 Experiment
The SRIT experiment was performed at the Radioactive Isotope Beam Factory (RIBF) at RIKEN. The primary beams of 238U and 132Xe impinged on the Be target to produce secondary beams of and respectively, at 270 MeV/u. The beams bombarded on the isotopically enriched and targets with areal density of and , respectively. Four reactions with different neutron-to-proton ratios, , of the total system were measured: , , , and . In this work, we focus mainly on the most and least neutron rich systems.
Charged particles produced in the reactions were detected with the SAMURAI Pion Reconstruction and Ion-Tracker Time Projection Chamber (SRIT-TPC) ShaneR_SpiRIT_NIMA_2015_784_513_spirittpc ; TangwancharoenS_SpiRIT_NIMA_2017_853_44_TPCGatingGrid ; BarneyJ_SpiRIT_RSI_2021_92_063302_spirittpc installed inside the SAMRURAI dipole magnet OtsuH_NIMB_2016_376_175_SAMURAIMagnet with a magnetic field of 0.5 T. The effective volume of the TPC is 1344 mm 864 mm 530 mm, and the target was placed at 15 mm upstream of the entrance window, resulting in an angular coverage of with respect to the beam axis in the laboratory frame. Description of the associated trigger arrays located on the side and downstream of the TPC used to select central events can be found in Refs. LaskoP_NIMA_2017_856_92_KATANA ; KanekoM_NIMA_2022_1039_167010_KyotoArray . The Generic Electronics for TPCs (GET) was employed to read out the track signals. The analysis software SRITROOT JhangGenie_SpiRIT_JKPS_2016_69_144_SpiRITROOT ; LeeJW_SpiRIT_NIMA_2020_965_163840_SpiRITROOT was developed for the track reconstruction of the charged particles. Detailed performance of the TPC and GET electronics as well as the software analysis codes have been published in BarneyJ_SpiRIT_RSI_2021_92_063302_spirittpc ; JhangGenie_SpiRIT_JKPS_2016_69_144_SpiRITROOT ; IsobeT_SpiRIT_NIMA_2018_899_43_GET_electronics ; LeeJW_SpiRIT_NIMA_2020_965_163840_SpiRITROOT . Other technical issues including space charge correction and extending the dynamic range of the TPC electronics can be found in TsangCY_SpiRIT_NIMA_2020_959_163477_space_charge ; EsteeJ_SpiRIT_NIMA_2019_944_162509_tpcdynamicrange .
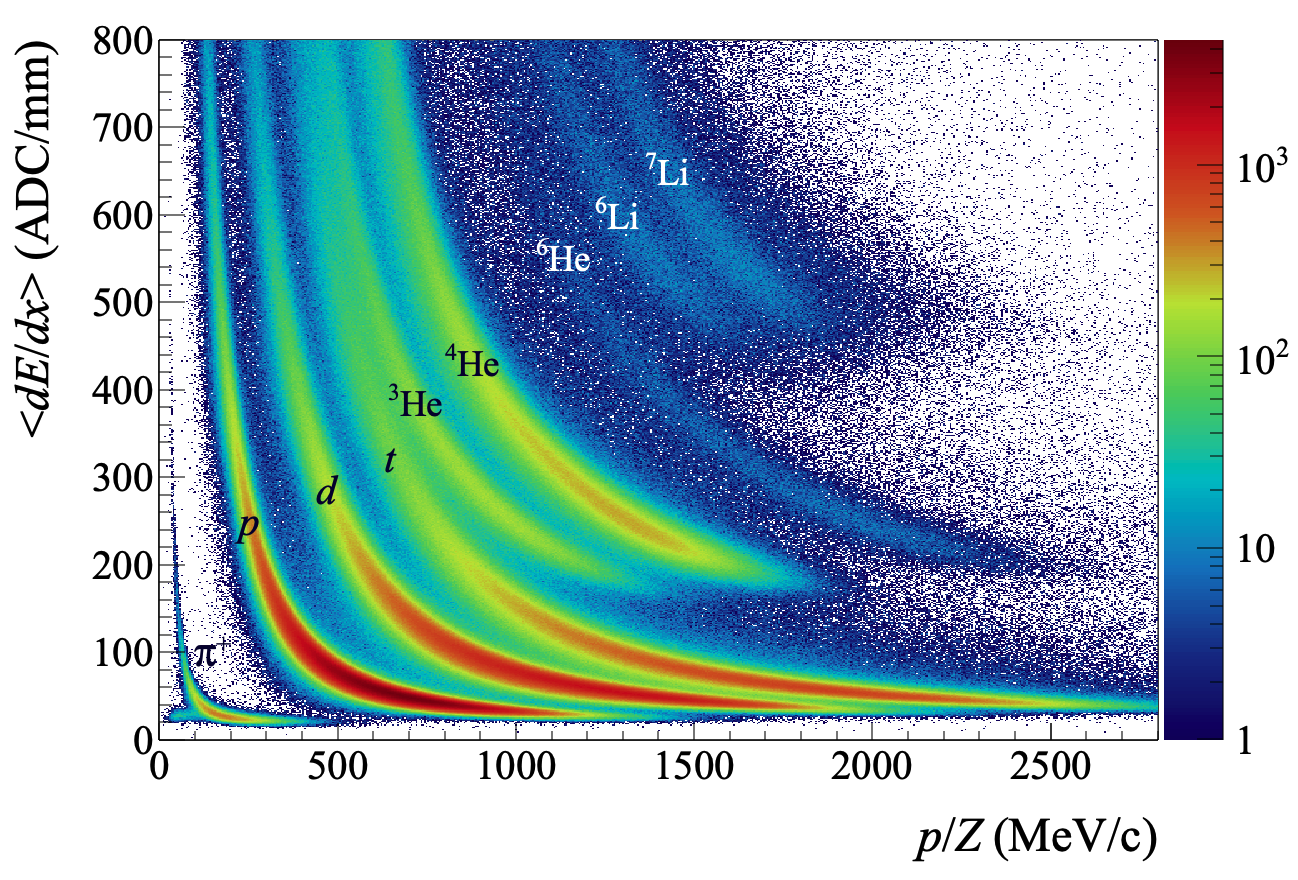
The cuboid-shaped SRIT TPC lacks the azimuthal symmetry. In this work, we mainly analyze the data at the azimuthal angles, , and where the tracks are longest and the track quality is generally much better. The TPC efficiencies arising from the detector performance are determined by the track embedding method AndersonM_NIMA_2003_499_659_STARTPC using events generated from Monte Carlo simulations and GEANT-4. The reconstructed rigidity momentum/charge, and the mean energy loss per unit length were provided for each track. The resolution of the reconstructed momentum and for single tracks is 1.6% and 4.6 %, respectively EsteeJustinBrian_phdthesis_MichiganStateUniversity_2020 . The particle identification (PID) is obtained using the correlation plot of magnetic rigidity, , and energy loss, , of the detected particles, as shown in Fig. 1. Isotopes of , , , , 4He, , , and can be clearly identified. However, below 600 MeV/, the and PID lines merge. In this study, we mainly focus on particles in the mid-rapidity range 0 - 0.4 with where is the rapidity of the particle and is center-of-mass rapidity of the nucleon-nucleon system. Since the mid-rapidity gate eliminates tritons below 1000 MeV/, contamination from in triton spectra is minimal. On the other hand, contamination from triton in the 3He spectra has to be determined.
Some physics results regarding the symmetry energy constraints from the SRIT experiments have been published. Charged pion multiplicities and ratios were published in Ref. JhangG_SpiRIT_PLB_2021_813_136016_pion_ratio and Ref. EsteeJ_SpiRIT_PRL_2021_126_162701_pion_ratio . Ref. KanekoM_SpiRIT_PLB_2021_822_136681_Z1particles_AMD focused on =1 particles and comparisons of the rapidity distributions with the AMD modelsOnoAkira_PTP_1992_87_1185_AMD ; OnoAkira_PPNP_2019_105_139_HIC_dynamics . This paper provides a more comprehensive study than Ref. KanekoM_SpiRIT_PLB_2021_822_136681_Z1particles_AMD and focuses on the transverse momentum spectra and yield ratios obtained from light charged fragments, specifically , , , 3He and 4He.
To select central collisions, we assume the impact parameters increase monotonically with the charged particle multiplicity CavataC_PRC_1990_42_1760_reduced_impact_parameter ; BarneyJonathanElijah_phdthesis_MichiganStateUniversity_2019 . Very central collision events ( 1.5 fm) similar to those analyzed in Ref. KanekoM_SpiRIT_PLB_2021_822_136681_Z1particles_AMD are chosen for this work. The difference between this work and Ref. KanekoM_SpiRIT_PLB_2021_822_136681_Z1particles_AMD for the rapidity spectra in 0 - 0.4 (Fig. 2) is within 3 %. The charge multiplicity selection in both works is different. Indeed, events with multiplicities equal or more than 57 and 56 charged particles, for 132Sn+124Sn and 108Sn+112Sn respectively, are chosen in this work, while 56 and 55 are used in Ref. KanekoM_SpiRIT_PLB_2021_822_136681_Z1particles_AMD . In both cases, the impact parameter gates of ( 1.5 fm) is chosen. In this work, is defined to be the experimental of 7.52 fm in and 7.13 fm in while in Ref. KanekoM_SpiRIT_PLB_2021_822_136681_Z1particles_AMD , =10 fm is defined by the sum of the radii for the projectile and target. These slight differences in the multiplicity gates do not affect the results of both works. The total statistics is increased as the tracks from both the left and right side of the TPC is used in the present work, whereas only the tracks in the right side of the TPC is used in Ref. KanekoM_SpiRIT_PLB_2021_822_136681_Z1particles_AMD . These are the main reasons for the 3 % discrepancy. In any case, the isocaling ratios are unaffected by the slight discrepancies in the spectra.
Fig. 1 shows a typical PID plot of the charged particles obtained in the 132Sn+124Sn collisions. The heavier clusters with A 5 nuclei such as , , are not included in the current analysis due to lack of statistics. To standardize the PID conditions, the center and width of of the PID line for each particle are fitted with the empirical Bethe-Bloch formula with Gaussian widths. Only tracks having PID probability larger than ( for ) and width of are selected for the analysis.
The overall systematic uncertainties are estimated from the variations of track multiplicity, track quality LeeJW_SpiRIT_NIMA_2020_965_163840_SpiRITROOT and PID quality cuts TsangChunYuen_phdthesis_MichiganStateUniversity_2022 . In the region 400 MeV/c, the statistical errors are smaller than systematic errors which are about 5% and 2% for the absolute yield and yield ratios, respectively. Outside of this region the statistic and systematic uncertainties increase with to exceed 15%. The error bars shown in this work include both the systematic and statistical errors.
3 Particle Spectra


The experimental rapidity and transverse momentum spectra for =1 and 2 particles are shown in Fig. 2 and Fig. 3, respectively, for the neutron rich system (black circles) and the nearly symmetric system, (red squares). The data in both left and right panels in each figure are the same. Comparison of the data to the two different parameter sets of the AMD models, shown by solid (left panels) and dashed (right panels) lines, will be discussed in details later.
In all cases, the rapidity spectra show peaking near or at suggesting high degree of stopping. The slight asymmetry observed around for all particles is due to the inefficiencies in the TPC to detect target rapidity particles which are generally low in energy and emitted at backward angles in the laboratory frame. In the case of , the PID contamination from tritons is significant and the spectra peak is located slightly off . For the analysis, we assume the spectra is symmetric at and only include data in - .
At mid rapidity, except for proton and isotopes, more particles, , and are produced in the neutron-rich systems. The same observation is also seen in Fig. 3 for particles with MeV/. On the contrary, more high energy particles including the neutron rich tritons, with MeV/, are produced from the nearly symmetric system than the neutron-rich one. This is surprising as one would expect that neutron-rich systems would produce more neutron-rich isotopes at all energies. One explanation could be that high energy particles are produced in a dynamical and non-equilibrium environment and that the hot participant zone is rather neutron deficient.
4 Yield Ratios and Isoscaling
It has been shown that isoscaling occurs only when the two systems have nearly the same temperature TsangMB_MSU_PRC_2001_64_041603_isoscaling_condition . Since the absolute temperature cannot be directly measured, we use the established isotope thermometers based on the double ratio of hydrogen and helium species
| (6) |
to examine the relative temperature increase with particle energy in both reactions:
| (7) |
We note that the isotope temperature can be derived in the grand-canonical ensemble AlbergoS_INCA_1985_89_1 and it is found to be independent of ratio of the source in low energy collisions KundeGJ_PLB_1998_416_56_HHeTemperature .
The upper panel of Fig. 4 displays the H-He temperature evaluated from Eq. (7). The for both neutron rich (solid circles) and the near-symmetric (open squares) systems are nearly the same for low energy particles. The temperatures increases slowly from around 8 MeV to 10 MeV with increasing . Above 280 MeV/, temperatures start to increase dramatically. Furthermore, the temperatures of the two systems begin to differ. Above 400 MeV/ the temperature of the near-symmetric system is higher than that of the neutron rich system. The increasing differences in temperatures with indicates that the Sn+Sn collisions studied here (with incident energy of 270 MeV/u) do not form fully equilibrated systems.
The increase in H-He temperature as a function of the surface velocity of the particles, has been observed in Refs. WangJ_PRC_2005_72_024603 ; BougaultR_JPG_47_025103 . In previous work, a drop of the temperature is also observed at very high velocity. We do not see the drop. This could be a consequence of the dramatic decrease of the cross-sections for above 280 MeV/.

Next, we focus on the spectral ratio of isotope yields of the =1 and 2 particles, observed in the and systems. These are shown in the lower panel of Fig. 4 as a function of . The dotted lines connect data points providing visual guidance to the trends of the data for each particle. The vertical dashed line at MeV/ marks the approximate region when the temperatures of the two systems start to differ.
The isotope ratios plotted to the left of the dashed line show isoscaling characteristics. In each (, 0 and 1) group, values are nearly constant as a function of . Moreover, 3He behave like protons () with ratio value smaller than 1, and 4He behave similarly to deuterons () with higher ratio value than protons. The tritons () have the highest ratio values as expected from isoscaling.
The ratios for the five particles with 280 MeV/ are plotted as a function of and , in the left panels of Fig 5. The three parameters , and are simultaneously fitted and the resulting isoscaling fits are shown as lines in the figure. The two fitted lines of the data for the isotopes with = 1 and 2 are shown separately in the top left panel, where the slopes of the lines represent the fit parameter = 0.29. The three fitted lines for the isotones with = 0, 1 and 2 are shown on the bottom left panel as a function of and the slopes represent the fit parameter = -0.23. In the absence of Coulomb, protons and neutrons should behave similarly and one would expect and to have similar values but opposite signs. This has been observed in most of the previous studies of isoscaling. In this case, the magnitude of the value is larger than the value. The isoscaling ratios obtained from these fits are plotted as solid horizontal lines in the bottom panel of Fig. 4 to the left of the vertical dashed line.
In contrast, except for protons, for high energy isotopes shown on the right side of the vertical dashed line decreases with . Furthermore, the lines from different isotopes cross over each other. In the case of particles (triton and 4He), falls off suddenly above 280 MeV/ with the largest drop exhibited by tritons. This reflects the sharper drop in the and 4He particle spectra at the high energy. The right panels of Fig. 5 show the ratios plotted as a function of and in the range of MeV/. values for t, and 4He have nearly the same values leading to the breakdown of isoscaling. The lines connecting the isotope (upper right panel) and isotone (lower right panel) data points serve only to guide the eye and provide a contrast trends of the values between fragments with low (left panels) and high (right panels) transverse momentum.
It is also interesting to note that is less than 1 for all high energy isotopes. For isotopes with MeV/, 0.5 for t, 3He and 4He, i.e. 50% less tritons are produced from the neutron-rich system of than that from the system. So far there is no explanation for the surprising result.

5 Model Comparisons
The isoscaling ratios of the = 1 and 2 particles, obtained from the experimental yields measured in the and systems, are shown in Fig. 6. In each panel, data are compared to the models; SMM (horizontal lines in the top panel), AMD and AMD (hatched bands in the middle and bottom pannels, respectively).
5.1 Statistical Multifragmentation Model
In order to check the extent to which the isoscaling properties observed experimentally may be understood in a scenario in which a thermal equilibrated source is formed and undergoes a prompt breakup, we employ the canonical version of the SMM model described in Refs. SouzaSR_NPA_2019_989_69_ISMM ; TanWP_PRC_2003_68_034609_ISMM . Many different sources contribute to the actual data whereas a single source is employed in the calculation due to the computational effort needed to generate a source distribution. The model assumes a breakup volume three times larger than that of the source at normal density, and breakup temperature MeV. The mass and atomic numbers of the decaying source associated with the 132Sn+124Sn system are and , whereas and are used in the case of the 108Sn+112Sn system. These values have been selected in order to obtain a good agreement with the measured ratios. Different source compositions lead to slightly different values and, therefore, those adopted in this work should be seen as average values. The predicted isotope ratios are shown as horizontal solid lines in the top panel of Fig. 6.

5.2 Asymmetrized Molecular Dynamics Model
In Ref. KanekoM_SpiRIT_PLB_2021_822_136681_Z1particles_AMD , the AMD model OnoAkira_PTP_1992_87_1185_AMD ; OnoAkira_PPNP_2019_105_139_HIC_dynamics has been employed to describe the rapidity distributions of = 1 particles (top six panels in Fig. 2). The time evolution of the system is calculated by AMD until fm/. The productions of light charged particles and their properties are almost determined at this primary stage. The employed version of AMD considers the process of cluster formation in the final state of every two-nucleon collision as , where each scattered nucleon () may form a cluster with a surrounding particle(s) . Clusters in the configuration are considered for . A formed cluster may be broken later, e.g., when a nucleon in the cluster is scattered by some other particle. The important model parameters include the medium effects on two-nucleon collision cross sections and cluster correlations. A set of parameters was chosen in Ref. OnoAkira_JPSCP_2020_32_010076_AMD_IMSigmaNN for a reasonable reproduction of the FOPI data of central Xe + CsI collisions at 250 MeV/nucleon ReisdorfW_FOPI_NPA_2010_848_366_HICsystematics ; AndronicA_PRC_2003_67_034907 , paying attention to the yields of light charged particles and heavier fragments, and a kind of stopping observable of various particle species. (The stopping observable is expressed as with transverse and longitudinal momentum components, and , in the center-of-mass frame.) This parametrization of Ref. OnoAkira_JPSCP_2020_32_010076_AMD_IMSigmaNN is called AMD here.
For the present systems of Sn + Sn collisions, the rapidity distributions predicted by AMD are shown in the right panels of Fig. 2. The calculated distribution looks more transparent than the data and underestimates the yields of deuterons and especially that of tritons in the mid-rapidity region. To reduce this discrepancy in the rapidity distributions in Ref. KanekoM_SpiRIT_PLB_2021_822_136681_Z1particles_AMD , another parametrization by adopting larger in-medium cross sections is chosen, so that the rapidity distributions become much narrower as shown in the left panels of Fig. 2. In addition, agreement with the triton multiplicity was improved by modifying the phase space so that the bound phase space for the relative coordinate between a two-nucleon pair and another nucleon becomes approximately KanekoM_SpiRIT_PLB_2021_822_136681_Z1particles_AMD . We label this parameter set as AMD. A persistent observed problem is that the yield ratio is always underestimated, either by AMD or AMD.
In the present work, we adopt the Skyrme SLy4 effective interaction, which corresponds to a soft symmetry energy with the slope parameter MeV. The calculation of stiff symmetry energy with MeV was also analyzed in Ref. KanekoM_SpiRIT_PLB_2021_822_136681_Z1particles_AMD . However, only the soft symmetry energy case is shown here since the data seems to have a better agreement with the soft symmetry energy case. The interaction with soft symmetry energy overestimates the deuteron binding energy and consequently may overestimate the deuteron yield PiantelliS_PRC_2019_99_064616 . However, such an effect of the binding energy or the bound phase space is largely canceled out when the double ratio is taken between two systems KanekoM_SpiRIT_PLB_2021_822_136681_Z1particles_AMD .
In Fig. 3, the spectra predicted by the AMD and AMD are depicted by the solid lines (left panels) and dotted lines (right panels) respectively. For proton and deuteron, the overall shapes and absolute yields are well explained with both AMD and AMD. On the other hand, for clusters with , the shapes of the spectra change significantly when the in-medium cross sections are increased from AMD to AMD, and the spectra extend to high in AMD compared to the experimental data. The change from AMD to AMD is understood as a natural consequence of the increased to reduce and increase . To reproduce the experimental data of both the rapidity and distributions, both and of clusters need to be reduced, in particular for tritons.This is not possible by only changing in AMD. (The enhanced production of isotope yields from the AMD parameterizations in Fig. 2 suggests that adjusting the in-medium cluster correlations may also be needed.)
For the low energy particles with MeV/, the behaviour of is qualitatively explained by both AMD and AMD. The predicted values are shown as bands in the middle and bottom panels of Fig. 6. The widths of the bands represent statistical uncertainties. The predicted for all particles except proton show slightly lower values. Similar to SMM, the of tritons shows the largest difference in the model comparisons. Furthermore, the ratios for tritons from AMD(S) underestimate the data more than the results from AMD(F).
An emergence of isoscaling in the AMD calculation is not trivial, because AMD does not assume any equilibrium state, and the fragments are produced within a rapidly evolving system OnoAkira_SpiRIT_PRC_2003_68_051601_isoscaling_AMD . However, during the dynamical evolution, clusters are repeatedly created and broken by the microscopic processes explained above, and therefore a situation similar to a chemical equilibrium may be realized before particles stop interacting. The isoscaling observed in AMD is consistent with such a picture, at least qualitatively. The precise values of may depend on the details of the model ingredients. In the present calculation, all clusters with the configuration () are considered, including the dineutron and diproton correlations. When the strength of dinucleon correlation is varied, a test calculation shows that the composition of nucleons and clusters is affected. However, the steep drop of of clusters at high down to in the experimental data seems to be difficult to explain by a minor modification of the present AMD model. Direct information on free neutrons can be an important clue to solve this puzzle. It is available in the calculated results but is not shown in the present paper.
6 Summary and Conclusion
In summary, the isoscaling phenomenon of hydrogen and helium isotopes in and reactions at beam energy of 270 MeV/u is presented as a function of . Isoscaling phenomenon up to MeV/ is found but breaks down for cluster particles with MeV/. The systems are found to form a thermal equilibrium not throughout the system but locally, which is evident from the increasing trend of H-He isotope ratio temperature with increasing . The isoscaling can be qualitatively explained by both the SMM and AMD models. When the yield spectra and isoscaling are compared to the predictions from the dynamical model AMD with two different parameter sets, we do not find any preference in increasing the default values of as observed in earlier study of Z=1 particles. While isoscaling breaks down for MeV/ particles in the data, the isoscaling trend in AMD persist. Most intriguely, the high-momentum clusters are suppressed in the neutron-rich system compared to the more symmetric system suggesting the non-equilibrium nature of the emission process especially for the high energy particles.
Acknowledgement
The authors would like to thank Prof. Pawel Danielewicz for many fruitful discussions. This work was supported by the U.S. Department of Energy, USA under Grant Nos. DE-SC0021235, DE-NA0003908, DE-FG02-93ER40773, DE-FG02-93ER40773, DE-SC0019209, DE-SC0015266, DE-AC02-05CH11231, U.S. National Science Foundation Grant No. PHY-1565546, the Robert A. Welch Foundation (A-1266 and A-1358), the Japanese MEXT, Japan KAKENHI (Grant-in-Aid for Scientific Research on Innovative Areas) grant No. 24105004, JSPS KAKENHI Grants Nos. JP17K05432, JP19K14709 and JP21K03528, the National Research Foundation of Korea under grant Nos. 2018R1A5A1025563 and 2013M7A1A1075764, the Polish National Science Center(NCN) under contract Nos. UMO-2013/09/B/ST2/04064, UMO-2013/-10/M/ST2/00624, Computing resources were provided by FRIB, the HOKUSAI-Great Wave system at RIKEN, and the Institute for Cyber-Enabled Research at Michigan State University. S.R. Souza acknowledges partial support from CNPq, CAPES, FAPERJ and the use of the supercomputer Lobo Carneiro, where part of the calculations have been carried out. This work has been done as part of the project INCT-Física Nuclear e aplicações, projeto No. 464898/2014-5.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: The data can be available on request sent to the corresponding author.]
References
- (1) R. Stock, Particle production in high energy nucleus-nucleus collisions, Phys. Rep. 135 (1986) 259, https://www.sciencedirect.com/science/article/pii/0370157386901341.
- (2) Peter Senger, Particle production in heavy-ion collisions, Progress in Particle and Nuclear Physics 53 (2004) 1, https://doi.org/10.1016/j.ppnp.2004.02.005.
- (3) Akira Ono, Dynamics of clusters and fragments in heavy-ion collisions, Progress in Particle and Nuclear Physics 105 (2019) 139, https://doi.org/10.1016/j.ppnp.2018.11.001.
- (4) Natsumi Ikeno, Akira Ono, Yasushi Nara et al., Probing neutron-proton dynamics by pions, Phys. Rev. C 93 (2016) 044612, https://doi.org/10.1103/PhysRevC.93.044612.
- (5) Jun Hong and P. Danielewicz, Subthreshold pion production within a transport description of central Au + Au collisions, Phys. Rev. C 90 (2014) 024605, https://doi.org/10.1103/PhysRevC.90.024605.
- (6) H. M. Xu, W. G. Lynch, and P. Danielewicz, Residue temperatures in intermediate energy nucleus-nucleus collisions, Phys. Rev. C 50 (1994) 1659, https://doi.org/10.1103/PhysRevC.50.1659.
- (7) B. Borderie and J. D. Frankland, Liquid-Gas phase transition in nuclei, Progress in Particle and Nuclear Physics 105 (2019) 82, https://doi.org/10.1016/j.ppnp.2018.12.002.
- (8) Hermann Wolter, Maria Colonna, Dan Cozma, Pawel Danielewicz, Che Ming Ko, Rohit Kumar, Akira Ono, ManYee Betty Tsang, Jun Xu, Ying-Xun Zhang et al., Transport model comparison studies of intermediate-energy heavy-ion collisions, Progress in Particle and Nuclear Physics, 125 (2022) 103962, https://doi.org/10.1016/j.ppnp.2022.103962.
- (9) Bao-An Li, C. M. Ko, and Zhongzhou Ren, Equation of State of Asymmetric Nuclear Matter and Collisions of Neutron-Rich Nuclei, Phys. Rev. Lett. 78 (1997) 1644, https://doi.org/10.1103/PhysRevLett.78.1644.
- (10) W. P. Tan, B.-A. Li, R. Donangelo, C. K. Gelbke, M.-J. van Goethem, X. D. Liu, W. G. Lynch, S. Souza, M. B. Tsang, G. Verde, A. Wagner and H. S. Xu , Fragment isotope distributions and the isospin dependent equation of state, Phys. Rev. C 64 (2001) 051901, https://doi.org/10.1103/PhysRevC.64.051901.
- (11) G. Jhang, J. Estee, J. Barney, G. Cerizza, M. Kaneko, J. W. Lee, W. G. Lynch, T. Isobe, M. Kurata-Nishimura, T. Murakami et al., Symmetry energy investigation with pion production from Sn+Sn systems, Phys. Lett. B 813 (2021) 136016, https://doi.org/10.1016/j.physletb.2020.136016.
- (12) J. P. Bondorf, A. S. Botvina, A. S. Iljinov, I. N. Mishustin and K. Sneppen, Statistical multifragmentation of nuclei, Phys. Rep. 257 (1995) 133, https://doi.org/10.1016/0370-1573(94)00097-M.
- (13) C. B. Das, S. Das Gupta, W. G. Lynch and A. Z. Mekjian, M. B. Tsang, The thermodynamic model for nuclear multifragmentation, Phys. Rep. 406 (2005) 1, https://doi.org/10.1016/j.physrep.2004.10.002.
- (14) A. S. Botvina and I. N. Mishustin, Statistical description of nuclear break-up, Eur. Phys. J. A 30 (2006) 121, https://doi.org/10.1140/epja/i2005-10316-7.
- (15) A. S. Botvina, A. S. Iljinov, I. N. Mishustin, J. P. Bondorf, R. Donangelo and K. Sneppen, Statistical simulation of the break-up of highly excited nuclei, Nucl. Phys. A 475 (1987) 663, https://doi.org/10.1016/0375-9474(87)90232-6.
- (16) W. P. Tan, S. R. Souza, R. J. Charity, R. Donangelo, W. G. Lynch, and M. B. Tsang, Isospin effects in nuclear multifragmentation, Phys. Rev. C 68 (2003) 034609, https://doi.org/10.1103/PhysRevC.68.034609.
- (17) M. B. Tsang, C. K. Gelbke, X. D. Liu, W. G. Lynch, W. P. Tan, G. Verde, H. S. Xu, W. A. Friedman, R. Donangelo, S. R. Souza et al., Isoscaling in statistical models, Phys. Rev. C 64 (2001) 054615, https://doi.org/10.1103/PhysRevC.64.054615.
- (18) M. B. Tsang, W. A. Friedman, C. K. Gelbke, W. G. Lynch, G. Verde, and H. S. Xu, Isotopic Scaling in Nuclear Reactions, Phys. Rev. Lett. 86 (2001) 5023, https://doi.org/10.1103/PhysRevLett.86.5023.
- (19) H. S. Xu, M. B. Tsang, T. X. Liu, X. D. Liu, W. G. Lynch, W. P. Tan, A. Vander Molen, G. Verde, A. Wagner, H. F. Xi et al., Isospin Fractionation in Nuclear Multifragmentation, Phys. Rev. Lett. 85 (2000) 716, https://doi.org/10.1103/PhysRevLett.85.716.
- (20) S. R. Souza, M. B. Tsang, B. V. Carlson, R. Donangelo, W. G. Lynch, and A. W. Steiner, Temperature effects in nuclear isoscaling, Phys. Rev. C 80 (2009) 044606, https://doi.org/10.1103/PhysRevC.80.044606.
- (21) F. Rami, Y. Leifels, B. de Schauenburg, A. Gobbi, B. Hong, J. P. Alard, A. Andronic, R. Averbeck, V. Barret, Z.Basrak et al. (FOPI Collaboration), Isospin Tracing: A Probe of Nonequilibrium in Central Heavy-Ion Collisions, Phys. Rev. Lett. 84 (2000) 1120, https://doi.org/10.1103/PhysRevLett.84.1120.
- (22) M. B. Tsang, W. A. Friedman, C. K. Gelbke, W. G. Lynch, G. Verde, and H. S. Xu, Conditions for isoscaling in nuclear reactions, Phys. Rev. C 64 (2001) 041603, https://doi.org/10.1103/PhysRevC.64.041603.
- (23) Akira Ono, P. Danielewicz, W. A. Friedman, W. G. Lynch, and M. B. Tsang, Isospin fractionation and isoscaling in dynamical simulations of nuclear collisions, Phys. Rev. C 68 (2003) 051601, https://doi.org/10.1103/PhysRevC.68.051601.
- (24) C. O. Dorso, C. R. Escudero, M. Ison, and J. A. López, Dynamical aspects of isoscaling, Phys. Rev. C 73 (2006) 044601, https://link.aps.org/doi/10.1103/PhysRevC.73.044601.
- (25) E. Geraci, M. Bruno, M. D’Agostino, E. De Filippo, A. Pagano, G. Vannini, M. Alderighi, A. Anzalone, L. Auditore, V. Baran et al., Isoscaling in central 124Sn+64Ni, 112Sn+58Ni collisions at 35 A MeV, Nucl. Phys. A 732 (2004) 173, https://doi.org/10.1016/j.nuclphysa.2003.11.055.
- (26) W. Trautmann, A.S. Botvina, J. Brzychczyk, A. Le Fevre, P. Pawlowski, C. Sfienti, and the ALADIN, and INDRA collaborations, Isoscaling and the symmetry energy in spectator fragmentation, International Workshop on Multifragmentation and Related Topics (IWM 2005), https://doi.org/10.48550/arxiv.nucl-ex/0603027.
- (27) Q. Fable, A. Chbihi, M. Boisjoli, J.D. Frankland, A. Le Févre, N. Le Neindre, P. Marini, G. Verde, G. Ademard, L. Bardelli et al., Experimental study of the 40,48Ca+ 40,48Ca reactions at 35 MeV/nucleon, Phys. Rev. C 106 (2022) 024605, https://link.aps.org/doi/10.1103/PhysRevC.106.024605.
- (28) S. Wuenschel, R. Dienhoffer, G.A. Souliotis, S. Galanopoulos, Z. Kohley, K. Hagel, D. V. Shetty, K. Huseman, L. W. May, S.N. Soisson et al., Isoscaling of fragments with from reconstructed quasiprojectiles, Phys. Rev. C 79 (2009) 061602, https://doi.org/10.1103/PhysRevC.79.061602.
- (29) M. Youngs, A.B. McIntosh, K. Hagel, L. Heilborn, M. Huang, A. Jedele, Z. Kohley, L.W. May, E. McCleskey, A. Zarrella, S.J. Yennello, Observation of different isoscaling behavior between emitted fragments and residues, Nucl. Phys. A 962 (2017) 61, https://doi.org/10.1016/j.nuclphysa.2017.03.009.
- (30) A.S. Botvina, O. V. Lozhkin, and W. Trautmann, Isoscaling in light-ion induced reactions and its statistical interpretation, Phys. Rev. C 65 (2002) 044610, https://link.aps.org/doi/10.1103/PhysRevC.65.044610
- (31) A. Le Fèvre, G. Auger, M.L. Begemann-Blaich, N. Bellaize, R. Bittiger, F. Bocage, B. Borderie, R. Bougault, B. Bouriquet, J.L. Charvet, A. Chbihi, it et al., INDRA and ALADIN Collaborations, Isotopic Scaling and the Symmetry Energy in Spectator Fragmentation, Phys. Rev. Lett. 94 (2005) 162701, https://link.aps.org/doi/10.1103/PhysRevLett.94.162701
- (32) R. Shane, A. B. McIntosh, T. Isobe, W. G. Lynch, H. Baba, J. Barney, Z. Chajecki, M. Chartier, J. Estee, M. Famiano et al., SRIT: A time-projection chamber for symmetry-energy studies, Nucl. Instrum. Methods Phys. Res., Sect. A 784 (2015) 513, https://doi.org/10.1016/j.nima.2015.01.026.
- (33) S. Tangwancharoen, W. G. Lynch, J. Barney, J. Estee, R. Shane, M. B. Tsang, Y. Zhang, T. Isobe, M. Kurata-Nishimura, T. Murakami et al., A gating grid driver for time projection chambers, Nucl. Instrum. Methods Phys. Res., Sect. A 853 (2017) 44, https://doi.org/10.1016/j.nima.2017.02.001.
- (34) J. Barney, J. Estee, W. G. Lynch, T. Isobe, G. Jhang, M. Kurata-Nishimura, A. B. McIntosh, T. Murakami, R. Shane, S. Tangwancharoen et al., The SRIT time projection chamber, Rev. Scientific Inst. 92 (2021) 063302, https://doi.org/10.1063/5.0041191.
- (35) H. Otsu, S. Koyama, N. Chiga, T. Isobe, T. Kobayashi, Y. Kondo, M. Kurokawa, W. G. Lynch, T. Motobayashi, T. Murakami et al., SAMURAI in its operation phase for RIBF users, Nucl. Instrum. Methods Phys. Res., Sect. B 376 (2016) 175, https://doi.org/10.1016/j.nimb.2016.02.056.
- (36) P. Lasko, M. Adamczyk, J. Brzychczyk, P. Hirnyk, J. Łukasik, P. Pawłowski, K. Pelczar, A. Snoch, A. Sochocka, Z. Sosin et al., KATANA - A charge-sensitive triggering system for the SRIT experiment, Nucl. Instrum. Methods Phys. Res., Sect. A 856 (2017) 92, https://doi.org/10.1016/j.nima.2017.03.006.
- (37) M. Kaneko, T. Murakami, K. Miwa, T. Shiozaki, J. Barney, G. Cerizza, J. Estee, T. Isobe, G. Jhang, M. Kurata-Nishimura et al., Multiplicity trigger detector for the SRIT experiment, Nucl. Instrum. Methods Phys. Res., Sect. A 1039 (2022) 167010, https://doi.org/10.1016/j.nima.2022.167010.
- (38) Genie Jhang, Jon Barney, Justin Estee, Tadaaki Isobe, Masanori Kaneko, Mizuki Kurata-Nishimura, Giordano Cerizza, Clementine Santamaria, Jung Woo Lee, Paweł Lasko et al., Beam commissioning of the SRIT time projection chamber, J. Korean Phys. Soc. 69 (2016) 144, https://doi.org/10.3938/jkps.69.144.
- (39) J.W. Lee, G. Jhang, G. Cerizza, J. Barney, J. Estee, T. Isobe, M. Kaneko, M. Kurata-Nishimura, W. G. Lynch, T. Murakami et al., Charged particle track reconstruction with SRIT Time Projection Chamber, Nucl. Instrum. Methods Phys. Res., Sect. A 965 (2020) 163840, https://doi.org/10.1016/j.nima.2020.163840.
- (40) T. Isobe, G. Jhang, H. Baba, J. Barney, P. Baron, G. Cerizza, J. Estee, M. Kaneko, M. Kurata-Nishimura, J. W. Lee et al., Application of the Generic Electronics for Time Projection Chamber (GET) readout system for heavy Radioactive isotope collision experiments, Nucl. Instrum. Methods Phys. Res., Sect. A 899 (2018) 43, https://doi.org/10.1016/j.nima.2018.05.022.
- (41) C. Y. Tsang, J. Estee, R. Wang, J. Barney, G. Jhang, W. G. Lynch, Z. Q. Zhang, G. Cerizza, T. Isobe, M. Kaneko et al., Space charge effects in the SRIT time projection chamber, Nucl. Instrum. Methods Phys. Res., Sect. A 959 (2020) 163477, https://doi.org/10.1016/j.nima.2020.163477.
- (42) J. Estee, W. G. Lynch, J. Barney, G. Cerizza, G. Jhang, J. W. Lee, R. Wang, T. Isobe, M. Kaneko, M. Kurata-Nishimura et al., Extending the dynamic range of electronics in a Time Projection Chamber, Nucl. Instrum. Methods Phys. Res., Sect. A 944 (2019) 162509, https://doi.org/10.1016/j.nima.2019.162509.
- (43) M. Anderson, J. Berkovitz, W. Betts, R. Bossingham, F. Bieser, R. Brown, M. Burks, M. Calderón de la Barca Sánchez, D. Cebra, M. Cherney et al., The STAR time projection chamber: a unique tool for studying high multiplicity events at RHIC, Nucl. Instrum. Methods Phys. Res., Sect. A 499 (2003) 659, https://doi.org/10.1016/S0168-9002(02)01964-2.
- (44) Justin Brian Estee, CHARGED PION EMISSION FROM NEUTRON-RICH HEAVY ION COLLISIONS FOR STUDIES ON THE SYMMETRY ENERGY, Ph.D thesis, Michigan State University (2020)
- (45) J. Estee, W. G. Lynch, C. Y. Tsang, J. Barney, G. Jhang, M. B. Tsang, R. Wang, M. Kaneko, J. W. Lee, T. Isobe et al., Probing the Symmetry Energy with the Spectral Pion Ratio, Phys. Rev. Lett. 126 (2021) 162701, https://doi.org/10.1103/PhysRevLett.126.162701.
- (46) M. Kaneko, T. Murakami, T. Isobe, M. Kurata-Nishimura, A. Ono, N. Ikeno, J. Barney, G. Cerizza, J. Estee, G. Jhang et al., Rapidity distributions of Z=1 isotopes and the nuclear symmetry energy from Sn+Sn collisions with radioactive beams at 270 MeV/nucleon, Phys. Lett. B 822 (2021) 136681, https://doi.org/10.1016/j.physletb.2021.136681.
- (47) Akira Ono, Hisashi Horiuchi, Toshiki Maruyama, Akira Ohnishi, Antisymmetrized Version of Molecular Dynamics with Two-Nucleon Collisions and Its Application to Heavy Ion Reactions, Progress of Theoretical Physics 87 (1992) 1185, https://doi.org/10.1143/ptp/87.5.1185.
- (48) C. Cavata, M. Demoulins, J. Gosset, M.-C. Lemaire, D. L’Hôte, J. Poitou, and O. Valette, Determination of the impact parameter in relativistic nucleus-nucleus collisions, Phys. Rev. C 42 (1990) 1760, https://doi.org/10.1103/PhysRevC.42.1760.
- (49) Jonathan Elijah Barney, CHARGED PION EMISSION FROM 112SN+124SN AND 124SN+112SN REACTIONS WITH THE SRIT TIME PROJECTION CHAMBER, Ph.D thesis, Michigan State University (2019)
- (50) Chun Yuen Tsang, CONSTRAIN NEUTRON STAR PROPERTIES WITH SRIT EXPERIMENT, Ph.D thesis, Michigan State University (2022)
- (51) S. Albergo, S. Costa, E. Costanzo and A. Rubbino, Temperature and free-nucleon densities of nuclear matter exploding into light clusters in heavy-ion collisions, Nuovo Cimento Soc. Ital. Fis., A 89 (1985) 1, https://doi.org/10.1007/BF02773614.
- (52) G. J. Kunde, S Gaff, C. K. Gelbke, T Glasmacher, M. J. Huang, R. Lemmon, W. G. Lynch, L. Manduci, L. Martin, M. B. Tsang et al., Isospin independence of the H-He double isotope ratio “thermometer”, Phys. Lett. B 416 (1998) 56, https://doi.org/10.1016/S0370-2693(97)01344-0.
- (53) J. Wang, R. Wada, T. Keutgen, K. Hagel, Y. G. Ma, M. Murray, L. Qin, A. Botvina, S. Kowalski, T. Materna et al., Tracing the evolution of temperature in near Fermi energy heavy ion collisions, Phys. Rev. C 72 (2005) 024603, https://doi.org/10.1103/PhysRevC.72.024603.
- (54) R Bougault, E Bonnet, B Borderie, A Chbihi,J D Frankland, E Galichet, D Gruyer, M Henri,M La Commara, N Le Neindre et al., Equilibrium constants of hydrogen and helium isotopes at low nuclear densities, J. Phys. G 47 (2020) 025103, https://doi.org/10.1088/1361-6471/ab56ba.
- (55) S. R. Souza, B. V. Carlson, and R. Donangelo, Post breakup dynamical evolution of fragments produced in nuclear multifragmentation, Nucl. Phys. A 989 (2019) 69, https://doi.org/10.1016/j.nuclphysa.2019.05.017.
- (56) Akira Ono, Impacts of Cluster Correlations on Heavy-Ion Collision Dynamics, JPS Conf. Proc. 32, 010076 (2020), https://doi.org/10.7566/JPSCP.32.010076.
- (57) W. Reisdorf, A. Andronic, R. Averbeck, M. L. Benabderrahmane, O. N. Hartmann, N. Herrmann, K. D. Hildenbrand, T. I. Kang, Y. J. Kim, M. Kiš et al., Systematics of central heavy ion collisions in the 1A GeV regime, Nucl. Phys. A 848 (2010) 366, https://doi.org/10.1016/j.nuclphysa.2010.09.008.
- (58) A. Andronic, W. Reisdorf, N. Herrmann, P. Crochet, J.P. Alard, V. Barret, Z. Basrak, N. Bastid, G. Berek, R. Čaplar, et. al., FOPI-Collaboration, Directed flow in Au+Au, Xe+CsI, and Ni+Ni collisions and the nuclear equation of state, Phys. Rev. C 67 (2003) 034907, https://link.aps.org/doi/10.1103/PhysRevC.67.034907.
- (59) S. Piantelli, A. Olmi, P. R. Maurenzig, A. Ono, M. Bini, G. Casini, G. Pasquali, A. Mangiarotti, G. Poggi, A. A. Stefanini et al., Comparison between calculations with the AMD code and experimental data for peripheral collisions of at 38 MeV/nucleon, Phys. Rev. C 99 (2019) 064616, https://doi.org/10.1103/PhysRevC.99.064616.