Ion temperature effects on plasma flow in the magnetic mirror configuration
Abstract
Effects of finite ion temperature on plasma flow in the converging-diverging magnetic field, the magnetic mirror, or equivalently, magnetic nozzle configuration, are studied using a quasineutral paraxial two-fluid MHD model with isothermal electrons and warm magnetized ions. The ion acceleration was studied with an emphasis on the role of the singularity at the sonic point transition. It is shown that the regularity of the sonic point defines a global solution describing plasma acceleration from subsonic to supersonic velocity. Stationary accelerating solutions were obtained and compared with the time dependent dynamics, confirming that the solutions of the time-dependent equations converge to the stationary solutions and therefore are stable. The effects of the ion pressure anisotropy were analyzed using the Chew-Golberger-Low model and its generalization. It is shown that the mirror force (manifested by the perpendicular ion pressure) enhances plasma acceleration. The role of ionization and charge exchange on plasma flow acceleration have been investigated.
I Introduction
Plasma flow in the magnetic mirror configuration (magnetic nozzle) plays an important role in a number of devices, such as magnetic mirrors used in fusion research and devices for electric propulsion in space. In plasma propulsion, the magnetic nozzle configuration is employed to convert the plasma thermal energy into the ion kinetic energy, thus generating thrust KaganovichPoP2020 ; LongmierPSST2011 . In open mirror fusion devices, the expanding magnetic field of the divertor (expander region) is used to spread the energy over the larger area to reduce the wall heat loads onofri2017magnetohydrodynamic . Plasma flow in the edge region of the divertor tokamak also experiences acceleration to supersonic velocities due to the combined effects of plasma pressure and inhomogeneous magnetic field BufferandPPCF2014 ; KirkPPCF2003 ; GhendrihPPCF2011 . Various aspects of plasma flow and acceleration in the magnetic mirror configurations have been studied. General framework of plasma flow and acceleration in the MHD approximation was formulated in Ref. morozov1980steady, , and subsequently used to study plasma detachment HooperAIAA1993 , acceleration mechanisms and propulsion efficiency AhedoPoP2010 ; MerinoPoP2016 . The role of the magnetic nozzle in the conversion of plasma thermal energy to supersonic flow was demonstrated experimentally InutakePST2004 ; InutakePPCF2007 . The MHD models were used to study the supersonic acceleration in the scrape-off-layer (SOL) of tokamak edge in Refs. GoswamiPoP2014, ; TogoCPP2018, ; TogoNF2019, . Ion pressure anisotropy and related mirror force effects on the plasma flow in the SOL were considered and the predictions of the isotropic and anisotropic pressure models were compared for specific conditions of the advanced divertors in fusion systems in Refs. TogoCPP2018, ; TogoNF2019, . The emphasis of this paper is on the role of the sonic point transition in the formation of the accelerating potential in plasma with anisotropic ion pressure and including atomic processes such as ionization and charge exchange.
It is well known that in the quasineutral approximation the ion inertia and finite temperature will result in the appearance of the sonic point singularity at the point where the local ion velocity is equal to the ion sound speed . It has recently been emphasized SmolyakovPoP2021 that the conditions at the sonic point in the nozzle region where the magnetic field has the maximum are critical for the existence of the smooth accelerating solution such that the resulting plasma flow is uniquely defined in the whole converging-diverging region, i.e. in the whole range from sub-sonic, , to super-sonic, , velocities. Such smooth accelerating solution is formed by the ambipolar potential supported by the electron pressure gradient. Here we study how the addition of the ion pressure, its anisotropy in particular, the effects of the mirror force, and some dissipative processes modify the conditions for the formation of a smooth accelerating potential. These results are of interest for fusion devices application TogoNF2019 ; onofri2017magnetohydrodynamic as well as for propulsion devices where a large ion temperature is expected LongmierPSST2011 .
The basic model equations are presented in Section II. The Section III discusses general features of the sonic point singularity and ion acceleration with finite ion pressure. Plasma acceleration for cold ions is reviewed in Section IV. The Section V presents the results of the solution of the stationary and dynamic (time-dependent) equations for the base case with anisotropic pressure. The Section VI analyzes modifications due to the ionization and charge-exchange collisions. The summary and discussions are presented in Section VII.
II Basic model
In our model, electrons are considered in the massless isothermal approximation,
| (1) |
The ions are described by the two-pressure Chew-Golberger-Low (CGL) model chew1956boltzmann in the form
| (2) |
| (3) |
where and are the perpendicular and parallel ion pressure, respectively. The standard CGL model is generalized here to include the sink terms , due to dissipation related to ionization and charge-exchange. We consider a problem in the paraxial approximation so that the total fluid time derivative for ions is , where is the ion parallel velocity, , and represents a unit vector in the direction of the magnetic field.
In the paraxial approximation, the ion continuity and momentum equations take the form
| (4) |
| (5) |
The effects of anisotropic pressure are included in the momentum equation with anisotropic pressure tensor , ,. and where describe the ionization source/sink effects.
In the context of the plasma flow and acceleration along the open magnetic field lines, the anisotropic MHD equations were considered in Refs. zawaideh1986generalized, ; GuoPoP2014, . Similar equations also follow from the drift-kinetic SmolyakovPoP2010 or gyro-fluid equations SnyderPoP1997 ; RobertsonPoP2016 . In simulations of plasma flow in the SOL tokamak regions, the fluid models with additional source/sink terms in the density, momentum, and energy equations as well as model approximations for the heat fluxes and relaxation terms were used TogoNF2019 . In this paper, our emphasis is on the ion pressure effects, thus we use the standard adiabatic CGL equations chew1956boltzmann modified with the model sink terms and to model the effects of ionization and charge-exchange on the ion pressure evolution, cf. Eqs. (2) and (3).
In general, ionization contributes to the density, ion momentum and pressure evolution, while the charge exchange affects the ion momentum and pressure evolution. In the context of fusion and electric propulsion, the ionization by electron impact is most relevant. The ionization coefficients depend on the neutral species, neutral density, electron temperature and electron density, while charge-exchange coefficients depend on the ions/neutral density and their energy. Thus the ionization and charge-exchange effects may have complex profile dependencies depending on the particular situation and plasma parameters. In this study we are interested in the main parametric trends due to the ionization and charge exchange. Thus, we use a simplified model HelanderPoP1994 ; NgPoP2007 where the effects of ionization and charge exchange are represented by two constant coefficients and . The coefficient corresponds to the ionization, while the coefficient in the ion momentum equation describes the total effects of ionization and charge-exchange. In this study we neglect the heat flux effects in the energy (pressure evolution) as well as any possible ionization heating terms LehnertNF1971 and only the pressure ”decay” terms are included with the same coefficient for and . In the expanded form, the full system of equations including ionization and charge-exchange effects is then written in the form similarly to Ref. onofri2017magnetohydrodynamic, :
| (6) |
| (7) |
| (8) |
| (9) |
We have to note that here we do not consider the plasma source region but focus on plasma acceleration in the magnetic mirror region, . Thus, effects of ionization and charge exchange, represented by the and coefficients in the continuity, momentum, and pressure equations, are the model approximations for the ionization and charge-exchange effects in the magnetic mirror, while the plasma source is assumed for .
Before we proceed with the general case, we consider general conditions for the existence of accelerating solution and describe plasma acceleration for cold and warm ions in the absence of ionization and charge-exchange effects.
III The sonic point singularity and plasma acceleration
In this section we consider a general condition for the existence of the global stationary accelerating solution in the absence of ionization and charge-exchange but taking into account anisotropic ion pressure. Setting , for the stationary case one can obtain from (1 - 9) the following equation for the ion velocity
| (10) |
This equation has to be solved simultaneously with equations (8) and (9) for and . In equation (10), is the plasma velocity normalized to the speed of sound with respect to the electron velocity . Such normalization is convenient because is constant and uniform. It is important to note that for warm anisotropic ions, the actual sound velocity includes the parallel ion temperature, . This is reflected in the modification of the sonic point singularity in equation (10), which occurs at a point where the ion velocity is equal to the local ion sound velocity, . We note that the expression used for sound speed in some papers TogoNME2019 ; TogoNF2019 is incorrect and thus misrepresents the location of the transition point.
Equation (10) describes two mechanisms of the ion acceleration: the electric field and the mirror force due to the perpendicular ion pressure. The electric field is supported by the electron pressure gradient in Eq. (1), so this mechanism comes from the electron thermal energy. The approximation of isothermal electrons used here assumes an infinite source of electron energy. In practice, electrons can experience cooling along the flow LittlePRL2016 ; MerinoPSST2020 and thus their temperature is not constant. Semi-empirically, this can be described by a general polytropic equation of state for electrons, . The ion acceleration due to the electron pressure with was considered previously SmolyakovPoP2021 (not included here for simplicity).
An additional contribution to the ion acceleration comes from the ion perpendicular pressure (energy), manifested by the term on the right hand side of (10), and is the result of the mirror force. As it will be discussed below, the effect of the ion parallel pressure modifies the location of the sonic point in Eq. 10 but the impact on the ion velocity is not significant due to the fast decrease of the ion pressure related to the decrease of plasma density along the nozzle and strong density dependence in the CGL equation for .
In general, acceleration in the magnetic mirror configuration is similar to the Laval nozzle acceleration. The ion acceleration by the electric field is supported by the density drop. In subsonic region, for , the ion inertia can be neglected and the acceleration occurs kinematically due to the effective area cross-section decrease as a result of the magnetic field rise, . Effectively, in this regime for , the density gradient is small and the acceleration simply follows from the flow conservation: , under constant density.
Equation (10) exhibits the singularity at , the point where the ion flow resonates with the ion sound mode. A global smooth accelerating solution can be obtained by regularizing the sonic point at the point where , which therefore requires the condition
| (11) |
Expanding the left and right sides of (10) near the singular point and using equation (11) one obtains the expression for the derivative near
| (12) | |||||
This expression illustrates that the condition , i.e. maximum of the magnetic field, for , is required for the existence of a smooth (regular) solution. Note that condition (12), for , also allows the decelerating solution with .
Equation (12) shows that there are no regular solutions in case of the minimum of the magnetic field suggesting the possibility of shock solutions. Various dissipative effects however may affect the singularity and allow the flow with at the sonic point. For example, ionization and charge-exchange modify the regularity condition as shown below in Section VI, Eq. (20). More generally, the singularities may be resolved by collisional MirnovNF1972 ; SkovorodinPPR2012 and finite Debye length PekkerSovJPP1984 effects allowing the flows in complex non-monotonic magnetic field geometries. The finite Debye length effects may also result in formation of the double layers at the singular points.
IV The accelerating potential for the case of cold ions
In this section we overview the case of cold ions providing a simple illustration of the global properties of the accelerating potential formed by the converging-diverging magnetic field configuration. For , Eq.(10) can be integrated ManheimerIEEE2001 ; FruchtmanPoP2012 resulting in the implicit equation for the ion velocity in the form
| (13) |
Here at and the integration constant was chosen so the solution becomes regular at where .
Generally, acceleration of the magnetized plasma in the magnetic nozzle is analogous to the gas flow in Laval nozzle. It is also similar to the problem of the solar wind acceleration when the effective nozzle is created by the spherical expansion and the gravity force ParkerAJ1958 . The exact solution for equation (13) can be written SmolyakovPoP2021 in terms of the Lambert function which appears in various fields including numerous plasma physics applications DubinovJPP2005 ; RaimbaultPoP2007 ; DubinovPoP2022 . The solution for spherically expanding solar wind can also be written with the Lambert function CranmerAJP2004 .
In the limit of , from Eq.(13) one can obtain two asymptotic solutions: and . These asymptotics correspond to two branches of the regular solution, respectively, in the converging and diverging parts of the nozzle. The singularity at , where the ion flow velocity is equal to , can be removed if . This condition corresponds to the smooth matching of two branches in Eq.(13) fixing the value of the velocity derivative at the sonic point. Expanding Eq. (13) near gives the expression for the velocity derivative , cf. with Eq. (12)
| (14) |
Here, for illustration, we consider the magnetic field mirror with Gaussian profile, , giving a mirror ratio at both ends, and . Several cases with different widths were considered by changing , as shown in Fig. 1a.




As it is shown in Figs. 1b-1c, changing the profile of the magnetic field under the constant mirror ratio modifies the velocity, density and potential profiles but the values at and remain the same. The plasma density is normalized to the value at : Equation (13) shows that the local value of the plasma velocity is defined by the local value of the magnetic field. It is important to note that this solution has a global character defined by the regularization condition at the sonic point, , which for cold plasma occurs at the point of the maximum magnetic field, where . The condition for the regular (smooth) solution at the sonic point defines the velocity derivative at this point, therefore fixing the velocity profile globally. Changing the values of the mirror ratio modifies the velocities at and but the value at the maximum remains equal to , as shown in Fig. 2. Note that different values of the mirror ratio were considered by changing the value of both and . The values of were adjusted as to ensure that the magnetic field with different R values would overlap at , i.e. to have the same derivative at . Increase of the mirror ratio leads to the decrease of the initial velocity , and increase of the exit velocity at , . The plasma velocity at the nozzle exit only depends on the mirror ratio R (regardless of the details of the magnetic field profile), and has weak logarithmic divergence for .

V Effect of the anisotropic ion temperature on plasma flow
In this Section, we present the global regular solutions for plasma flow with finite (and anisotropic) ion pressure for the magnetic field profile similar to the C-2U device onofri2017magnetohydrodynamic ; BinderbauerAIP2016 shown in Fig. 3. The global solutions are considered in the region . The mirror ratios were and at the left, , and the right, , ends of the nozzle, respectively. The magnetic field setup is described in more detail in the Appendix. The left side of the simulation region represents the transition to the plasma source at .
The magnetic geometry used in this paper considers only one side of a typical magnetic mirror system like C-2U. This region has to be matched with the central source (plasma production and heating) region. Similar configurations are used in propulsion applications with the mirror only on one side. It is assumed in our study that the source region is at . An important result of our study is the observation that plasma velocity is fixed globally by the condition at the singular point, so that the value of the velocity at cannot be arbitrary. The matching of the accelerating region (as studied here) with the source region is outside of the scope of this paper. However, some comments are provided in Section VII.
The numerical solution of stationary equations (10) and (1 - 9) are obtained by the integration from the the proximity of the sonic point, , in both and directions. The initial conditions for the parameters , , , and are obtained from the Taylor series expansion near . Across the entire nozzle electrons were assumed to be isothermal with . At the left end of the nozzle it was assumed that with the density , however all results can be represented in dimensionless units by being normalized to their respective values at .

.
The shooting method was used to achieve the final solution with isotropic ion pressure, at the left end of the nozzle, which corresponds to the beginning of Region A in Fig. 3.
Similarly to the case of cold ions, plasma acceleration occurs in the regions with the finite gradient of the magnetic field. The perpendicular ion pressure enhances the ion acceleration according to equation (12). The parallel ion pressure shifts the sonic point which is now defined by Eq. (10). However, the parallel pressure decreases fast with distance, so the effects of the finite parallel pressure on the location of the singular point is weak for our parameters.
An interesting observation that can be seen from Fig. 4b is that for a finite ion temperature there is a region where the density is increasing with distance, contrary to
the case of cold ions, where the density is always monotonically decreasing in regions of non-constant magnetic field. A similar behavior is observed for the potential, with the small increase with distance being displayed in Fig. 4f.
The perpendicular plasma pressure follows the increase of the magnetic field related to the conservation of the adiabatic invariant as . The dependence of on are shown in Fig. 4e. The decrease of in the outer region is related to strong plasma density dependence in the CGL equation of state for and density decrease due to plasma acceleration.
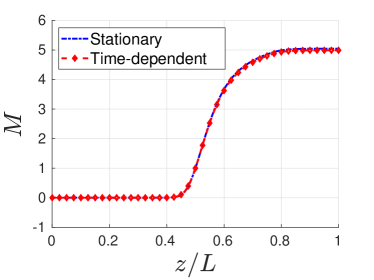





The perpendicular ion temperatures were changed to study the effect of perpendicular temperature at the nozzle entrance . Three additional cases were studies with , , and , while and remained the same. For the initial anisotropic ion pressure state at , the finite perpendicular ion temperature increases the velocity of the accelerated ions as shown in Fig. 5 and displayed in Table I.
Plasma temperatures can be lower in some laboratory devices MakrinichPoP2009 , e.g. and . The ion temperatures with will resemble the profiles of the cold ion case. Since, the speed of sound has been normalized as , the lower values of will result in a lower absolute values of the velocities. The ion temperatures profiles will qualitatively remain similar, e.g. as in Fig. 4.
| 200 | 400 | 6.41 | |
| 200 | 200 | 5.04 | |
| 200 | 100 | 0.01 | 4.18 |
| 200 | 50 | 0.06 | 3.66 |

Steady-state solutions of stationary equations obtained by the shooting method were compared with the time-dependent solutions obtained as a solution of the initial value problem for equations (6 - 9), presented in the Appendix with additional details. We have verified that the solution of the time-dependent equations converge well to the stationary solution obtained by the shooting method, as shown in figures 4a, 4b, 4c and 4d. The characteristic time was and each time interval was given as a multiple of . Each time step in the simulation was equivalent to . The evolution of the time-dependent problem towards the stationary solution is shown in Fig. 6 for the successive moments in time with the lowest and the stationary solution value being reached at . This exercise demonstrates that the stationary accelerating solutions are stable and therefore dynamically accessible in the initial value problem.

VI Ionization and Charge-Exchange Effects
In this section we consider the ion flow taking into account ionization and charge-exchange effects. These effects are important in fusion applications due to presence of neutrals in the mirror region. Effects of neutrals were also considered in propulsion applications MakrinichPoP2009 ; FruchtmanJPhysD2017 ; FruchtmanIEEE2011 . Depending on the application, neutral density and therefore ionization and charge-exchange coefficients may vary in a rather wide range lieberman2005principles ; onofri2017magnetohydrodynamic ; BinderbauerAIP2016 ; MakrinichPoP2009 . To estimate possible effects at various conditions, here we use a generic form of the sink terms and with various values of and in normalized form , from low to large values. We have used the values of as the length of the nozzle and as the speed of sound BinderbauerAIP2016 giving for and with the dimensional values of and , respectively. The ionization and charge-exchange coefficients are and , where is the density of neutral atoms, and typical rates janev1987collision and . For our parameters above, it gives for the values in the range the neutral density , and for – the values . Note that at lower boundaries of these values the collisional effects are not significant. Therefore, our parameters cover a wide range of typical densities observed in experiments BinderbauerAIP2016 and also extend to the low collisionalities typical for space propulsion applications. It should be noted however that generally in applications the density of neutral atoms is not constant while we assumed the constant and uniform profile. Therefore, our results should be understood as a parametric study towards revealing the main trends.
For the applications in Ref. BinderbauerAIP2016, the lowest value of the ion cyclotron frequency is remaining larger than the collisional frequencies, therefore justifying the use of the MHD approximation and assumption of magnetized ions. The problem of detachment HooperAIAA1993 ; BreizmanPoP2008 that occurs for space propulsion applications with lower values of the magnetic field is not considered in our paper.
In dimensionless form the stationary equations describing ion dynamics have the form
| (15) |
| (16) |
| (17) |
| (18) |
| (19) |
The plasma parameters here are normalized to their respective values at the left end of the nozzle such that , , , , , and . For the sake of convenience all the primes on parameters will be dropped and it will be assumed that n, , , , , , , and represent normalized quantities.
Additional terms in Eq. (18) due to the ionization and charge-exchange effects modify the regularization condition at the sonic point. The sonic point is still defined by condition 11. However the location of the sonic point, where the right hand side of equation (18) is zero, is shifted from the position of the maximum magnetic field at Expanding near the point, where both sides of Eq. (18) equal zero, we obtain for the following equation
| (20) |
where
| (21) |
| (22) |
| (23) |
Here and are the normalized values of the parallel and perpendicular temperatures at the sonic point, which no longer occurs at but is shifted to the right. The shift in the location of the sonic is directly affected by the value of that is in turn affected by the values of and . Thus, higher values of and will have a more profound effect on and will indirectly shift the sonic point further away from its initial position at . Similar to Section V, we obtain stationary solutions for equations (15) - (19) using the shooting method as described in Section III and compare these solutions with the solution of the initial value problem given by equations (1) - (9). Again, it has been confirmed that time-dependent solutions converge well to the stationary solutions after some relaxation.
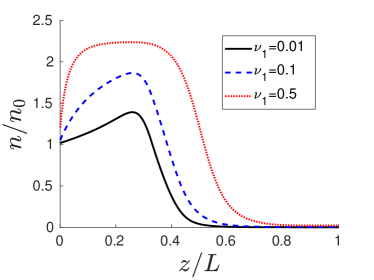
There are several features introduced by ionization and charge-exchange effects. One is a non-monotonous behavior of plasma density with the increase due to the ionization, which is especially noticeable in the region of flat magnetic field before any substantial acceleration occurs. This behavior is more pronounced for higher ionization values, as indicated in Fig. 8d. Related to the density behavior, the potential also shows a non-monotonous increase in the region to the left of the maximum of the magnetic field as shown in Fig. 7e.
Another effect introduced by the dissipative terms, is the modification of the perpendicular pressure profile so that it does not follow the increase in the magnetic field. The latter effect is much reduced by dissipation so the perpendicular pressure profile may become similar to the parallel pressure with almost monotonous decrease throughout the whole region, and both the parallel and perpendicular pressure having very similar profiles with and as displayed in Figures 7c and 7d. With the above noted modifications, the resulting velocity has a significantly larger value at the left boundary, , compared with the case in the absence of charge-exchange and ionization, and a lower final acceleration value on the exit side of the nozzle. The reduction in the final value of acceleration is greater for higher charge-exchange values as shown in Fig. 7a but also in the case of ionization alone as shown in Fig. 8a. One has to note also that the presence of the dissipative terms due to the ionization and charge-exchange results in the shift of the position of the sonic point so it is no longer at the magnetic field maximum, as described by equation (20).
The effect of charge-exchange has been further studied for various values of as shown in Table II and Figures 7a, 7b, 7c, 7d and 7e. In Table II, the values of and represent the value of the Mach number at the and ends of the nozzle respectively. Further increase in results in the non-monotonous behavior of the plasma velocity in the outer region, namely Region C, where the magnetic field is almost flat, between and , see Fig. 7a. The width of the region with the density increase on the left side of the mirror is also increasing with as shown in Fig. 7b. The characteristic increase in the perpendicular pressure so well pronounced for , is smoothed out by finite values of and eventually disappears for large values of as shown in Fig. 7d. A similar behavior is observed for and when only ionization is present, with the decrease being more pronounced for higher values of as shown in Fig. 8b and Fig. 8c respectively. An interesting observation is that the density curve corresponding to , is below the curve corresponding to in the Region A where the magnetic field is constant. A larger charge-exchange value would result in a greater drag force on the ions, reducing the Mach number and resulting in a higher plasma density. It could be possible that when the rate of ionization is equal to the rate of charge-exchange, as is the case for , the neutrals that formed in the region of constant magnetic field as a result of charge-exchange are themselves ionized, thus enhancing ionization and resulting in a greater increase in plasma density. The same effect is seen for the parallel pressure in Fig. 7c and this effect is likely a result of the behavior of the plasma density. The reduction of the velocity at the exit side, corresponding to the end of Region C, is consistent with the lower overall drop in the electrostatic potential as shown in Fig. 7e and displayed in Table II.
| 0 | 3.32 | -4.77 | ||
| 0.1 | 0.024 | 3.217 | -4.6 | |
| 0.35 | 0.054 | 2.981 | -4.21 | |
| 1.0 | 0.071 | 2.564 | -3.83 | |
| 1.44 | 0.077 | 2.348 | -3.77 | |
| 1.85 | 0.127 | 2.145 | -3.71 |








VII Discussion and conclusions
The flow of plasma in a magnetic nozzle was studied in the paraxial approximation using fluid MHD model with fully magnetized ions and anisotropic pressure. Stiffness of the global acceleration profile, which is fully defined by the regularization condition at the sonic point, is one of the most important results of this manuscript. The unique accelerating solution starts with a finite (and fixed) value at the entrance of the magnetic mirror. This solution continues through the sonic point to the diverging region where the ion velocity becomes supersonic. Plasma acceleration occurs as a result of an ambipolar electrostatic potential drop formed in the magnetic mirror, converting finite plasma pressure into the ion kinetic energy. We have shown that the finite perpendicular ion temperature increases the finite ion velocity in the exit region due to the effect of the mirror force. The finite (accelerated) value of the plasma velocity is defined by the electron and ion temperatures and the magnetic mirror aspect ratio. It is important to note that CGL theory is collisionless and the additional ion acceleration due to the perpendicular pressure is a result of the mirror force.
In many applications plasmas are collisionless but coupling of plasma flow with neutrals was noted as an important factor for some fusion onofri2017magnetohydrodynamic ; NgPoP2007 and plasma thruster applications FruchtmanJPhysD2017 ; WachsPSST2020 ; TakahashiAPL2016 . We have studied how the ionization and charge-exchange processes reform the accelerating potential impeding the plasma flow. We have shown that the ionization and charge-exchange shift the position of the sonic point from the maximum magnetic field, reduce plasma acceleration, and may result in non-monotonous behavior of plasma density and electrostatic potential.
We have obtained solutions of stationary equations with the shooting method. We have also performed simulations of time-dependent equations as an initial value problem therefore proving the stability of the obtained stationary solutions.
Similarly to Refs. MerinoPSST2018, ; AhedoPSST2020, , our model is a paraxial approximation which considers the radial variations only in the main order. Though such one-dimensional models are often a good approximation for a full two-dimensional dynamics FruchtmanPoP2012 , two-dimensional effects are expected to be important AhedoPoP2010 for large diameter systems.
In general ion kinetic effects are important for low density collisionless plasma as in Refs. BinderbauerAIP2016, ; onofri2017magnetohydrodynamic, . One of the related limitations of the current study is the use of the standard collisionless two-pressure CGL model which neglects the ion heat fluxes. Further work is required to include heat fluxes either with extended two-pressure models and/or with full kinetic theory AhedoPSST2020 ; MartinezPoP2011 . It is expected that the addition of heat fluxes will result in flattening of the parallel and perpendicular temperature profiles along the entire magnetic nozzle, thus resulting in higher Mach number at the exit point. These effects require further studies. It would be interesting to implement kinetic closures SnyderPoP1997 for the heat flux as proposed in Refs. GuoPoP2014, . The kinetic ion model would also be required to describe the possible ion trapping and demagnetization effects for very low values of the magnetic field in the expander region. We have assumed fully magnetized ions and did not consider the detachment problem which may not be critical for fusion application, but would need to be analyzed for space propulsion applications BreizmanPoP2008 .
It is expected that electron cooling and trapped electrons in the region of the diverging magnetic field (expander) are important MerinoPSST2018 ; WethertonPoP2021 ; SkovorodinPPR2019 . Here, we have focused on ion dynamics and for simplicity assumed isothermal Boltzmann electrons. Effects of general polytropic equation of state for electrons with can be included similarly as in Ref. SmolyakovPoP2021, .
The obtained global solutions do not allow for arbitrary values of plasma velocity at the entrance point of the mirror region and also fully determine the plasma velocity at the mirror exit (fixed by the mirror ratio). The uniqueness of the accelerating solutions will therefore provide the constraints on the matter and energy outflow through the magnetic nozzle (mirror). These effects were not previously considered either in the context of open mirror or propulsion applications. These results raise interesting questions of how the plasma solutions in the source region can be matched to the mirror. Such a solution will require the full analysis of the matter and energy balance, in particular, electron and energy fluxes. Neither of fluid model approximations used here, such as isothermal electrons with infinite electron heat conductivity, nor the ion CGL model which neglects the ion heat fluxes are fully adequate for this purpose. Collisionless regimes of interest for most applications also require kinetic analysis. The adjustment (matching) of plasma source with the magnetic nozzle constraints will occur via partial particle reflections and particle mixing in the source (that have to be described kinetically), possibly enhanced, in part, by non-stationary fluctuations that will occur in regimes when stationary fluid solutions do not exist. It is expected that in general the magnetic nozzle constraints discussed in this paper will reduce plasma losses through the mirror compared to the standard estimates based on the collisional transitions between trapped and passing (loss cone) regions MirnovNF1972 . The particle reflections and mixing will likely smooth out the non-monotonous features in the potential that exist in fluid models in some regimes thus increasing the plasma density in the confinement region. The kinetic analysis of such effects is outside of the scope of the present paper and is left for future studies. It is also important to note that additional drag due to interactions with neutrals (such as charge-exchange interactions) can increase the total thrust and thus be beneficial for the electric propulsion applications as shown experimentally and theoretically MakrinichPoP2009 ; FruchtmanIEEE2011 .
Acknowledgements.
This work was supported in part by NSERC Canada and the U.S. Air Force Office of Scientific Research FA9550-15-1-0226 and FA9550-21-1-0031. Computational resources were provided by Compute Canada. The authors thank the investors of TAE Technologies and the entire TAE Team for their support.Data availability
Data generated in this study is available from the authors upon reasonable request.
References
- [1] Igor D. Kaganovich, Andrei Smolyakov, Yevgeny Raitses, Eduardo Ahedo, Ioannis G. Mikellides, Benjamin Jorns, Francesco Taccogna, Renaud Gueroult, Sedina Tsikata, Anne Bourdon, Jean-Pierre Boeuf, Michael Keidar, Andrew Tasman Powis, Mario Merino, Mark Cappelli, Kentaro Hara, Johan A. Carlsson, Nathaniel J. Fisch, Pascal Chabert, Irina Schweigert, Trevor Lafleur, Konstantin Matyash, Alexander V. Khrabrov, Rod W. Boswell, and Amnon Fruchtman. Physics of EB discharges relevant to plasma propulsion and similar technologies. Physics of Plasmas, 27(12):120601, 2020.
- [2] B. W. Longmier, E. A. Bering, M. D. Carter, L. D. Cassady, W. J. Chancery, F. R. C. Diaz, T. W. Glover, N. Hershkowitz, A. V. Ilin, G. E. McCaskill, C. S. Olsen, and J. P. Squire. Ambipolar ion acceleration in an expanding magnetic nozzle. Plasma Sources Science & Technology, 20(1):015007, 2011.
- [3] M Onofri, P Yushmanov, S Dettrick, D Barnes, K Hubbard, and T Tajima. Magnetohydrodynamic transport characterization of a field reversed configuration. Physics of Plasmas, 24(9):092518, 2017.
- [4] H. Bufferand, G. Ciraolo, G. Dif-Pradalier, P. Ghendrih, P. Tamain, Y. Marandet, and E. Serre. Magnetic geometry and particle source drive of supersonic divertor regimes. Plasma Physics and Controlled Fusion, 56(12):122001, 2014.
- [5] A. Kirk, W. Fundamenski, J. W. Ahn, and G. Counsell. Parallel sol transport in mast and jet: the impact of the mirror force. Plasma Physics and Controlled Fusion, 45(8):1445–1463, 2003.
- [6] P. Ghendrih, K. Bodi, H. Bufferand, G. Chiavassa, G. Ciraolo, N. Fedorczak, L. Isoardi, A. Paredes, Y. Sarazin, E. Serre, F. Schwander, and P. Tamain. Transition to supersonic flows in the edge plasma. Plasma Physics and Controlled Fusion, 53(5):054019, 2011.
- [7] AI Morozov and LS Solov’ev. Steady-state plasma flow in a magnetic field. pages 1–103. Springer, 1980.
- [8] E. B. Hooper. Plasma detachment from a magnetic nozzle. Journal of Propulsion and Power, 9(5):757–763, 1993.
- [9] E. Ahedo and M. Merino. Two-dimensional supersonic plasma acceleration in a magnetic nozzle. Physics of Plasmas, 17(7):073501, 2010.
- [10] M. Merino and E. Ahedo. Fully magnetized plasma flow in a magnetic nozzle. Physics of Plasmas, 23(2):023506, 2016.
- [11] M. Inutake, K. Yoshino, S. Fujimura, H. Tobari, T. Yagai, Y. Hosokawa, R. Sato, K. Hattori, and A. Ando. Production of a high-mach-number plasma flow for an advanced plasma space thruster. Plasma Science & Technology, 6(6):2541–2545, 2004.
- [12] M. Inutake, A. Ando, K. Hattori, H. Tobari, T. Makita, M. Shibata, Y. Kasashima, and T. Komagome. Generation of supersonic plasma flows using an applied-field mpd arcjet and icrf heating. Plasma Physics and Controlled Fusion, 49(5A):A121–A134, 2007.
- [13] Rajiv Goswami, Jean-François Artaud, Frédéric Imbeaux, and Predhiman Kaw. Numerical study of transition to supersonic flows in the edge plasma. Physics of Plasmas, 21(7):072510, 2014.
- [14] S. Togo, D. Reiser, P. Borner, M. Sakamoto, N. Ezumi, and Y. Nakashima. Benchmarking of b2 code with a one-dimensional plasma fluid model incorporating anisotropic ion pressures on simple mirror configurations. Plasma and Fusion Research, 13:3403022, 2018.
- [15] S. Togo, T. Takizuka, D. Reiser, M. Sakamoto, N. Ezumi, Y. Ogawa, K. Nojiri, K. Ibano, Y. Li, and Y. Nakashima. Self-consistent simulation of supersonic plasma flows in advanced divertors. Nuclear Fusion, 59(7):076041, 2019.
- [16] A. I. Smolyakov, A. Sabo, P. Yushmanov, and S. Putvinskii. On quasineutral plasma flow in the magnetic nozzle. Physics of Plasmas, 28(6):060701, 2021.
- [17] GF Chew, ML Goldberger, and FE Low. The boltzmann equation and the one-fluid hydromagnetic equations in the absence of particle collisions. Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, 236(1204):112–118, 1956.
- [18] Emad Zawaideh, Farrokh Najmabadi, and Robert W Conn. Generalized fluid equations for parallel transport in collisional to weakly collisional plasmas. The Physics of fluids, 29(2):463–474, 1986.
- [19] Zehua Guo, Xian-Zhu Tang, and Chris McDevitt. Parallel heat flux and flow acceleration in open field line plasmas with magnetic trapping. Physics of Plasmas, 21(10):102512, 2014.
- [20] A. I. Smolyakov and X. Garbet. Drift kinetic equation in the moving reference frame and reduced magnetohydrodynamic equations. Physics of Plasmas, 17(4):042105, 2010.
- [21] P. B. Snyder, G. W. Hammett, and W. Dorland. Landau fluid models of collisionless magnetohydrodynamics. Physics of Plasmas, 4(11):3974–3985, 1997.
- [22] S. Robertson. A reduced set of gyrofluid equations for plasma flow in a diverging magnetic field. Physics of Plasmas, 23(4):043513, 2016.
- [23] P. Helander, S. I. Krasheninnikov, and P. J. Catto. Fluid equations for a partially-ionized plasma. Physics of Plasmas, 1(10):3174–3180, 1994.
- [24] Sheung-Wah Ng and A. B. Hassam. Neutral penetration in centrifugally confined plasmas. Physics of Plasmas, 14(10):102508, 2007.
- [25] B. Lehnert. Rotating plasmas. Nuclear Fusion, 11(5):485–533, 1971.
- [26] S. Togo, T. Takizuka, D. Reiser, M. Sakamoto, Y. Ogawa, N. Ezumi, K. Ibano, K. Nojiri, Y. Li, and Y. Nakashima. Characteristics of plasma flow profiles in a super-x-divertor-like configuration. Nuclear Materials and Energy, 19:149–154, 2019.
- [27] J. M. Little and E. Y. Choueiri. Electron cooling in a magnetically expanding plasma. Physical Review Letters, 117(22):225003, 2016.
- [28] Mario Merino, Pablo Fajardo, Gabriel Giono, Nickolay Ivchenko, Jon-Tomas Gudmundsson, Stephane Mazouffre, Dimitry Loubere, and Kathe Dannenmayer. Collisionless electron cooling in a plasma thruster plume: experimental validation of a kinetic model. Plasma Sources Science & Technology, 29(3):035029, 2020.
- [29] V. V. Mirnov and D. D. Ryutov. Gas-dynamic description of a plasma in a corrugated magnetic-field. Nuclear Fusion, 12(6):627–636, 1972.
- [30] D. I. Skovorodin and A. D. Beklemishev. Plasma outflow from a corrugated trap in the kinetic regime. Plasma Physics Reports, 38(3):202–206, 2012.
- [31] M. S. Pekker. Particle scattering by potential jumps in a tandem mirror with a thermal barrier. Sov. J. Plasma Physics, 10(11):33–35, 1984.
- [32] W. M. Manheimer and R. F. Fernsler. Plasma acceleration by area expansion. Ieee Transactions on Plasma Science, 29(1):75–84, 2001.
- [33] A. Fruchtman, K. Takahashi, C. Charles, and R. W. Boswell. A magnetic nozzle calculation of the force on a plasma. Physics of Plasmas, 19(3):033507, 2012.
- [34] E. N. Parker. Dynamics of the interplanetary gas and magnetic fields. Astrophysical Journal, 128(3):664–676, 1958.
- [35] Alexander E. Dubinov and Irina D. Dubinova. How can one solve exactly some problems in plasma theory. Journal of Plasma Physics, 71(05):715, 2005.
- [36] J. L. Raimbault, L. Liard, J. M. Rax, P. Chabert, A. Fruchtman, and G. Makrinich. Steady-state isothermal bounded plasma with neutral dynamics. Physics of Plasmas, 14(1):013503, 2007.
- [37] Alexander E. Dubinov. Mathematical tricks for pseudopotentials in the theories of nonlinear waves in plasma. Physics of Plasmas, 2022.
- [38] Steven R. Cranmer. New views of the solar wind with the lambert w function. American Journal of Physics, 72(11):1397–1403, 2004.
- [39] M. W. Binderbauer, T. Tajima, M. Tuszewski, L. Schmitz, A. Smirnov, H. Gota, E. Garate, D. Barnes, B. H. Deng, E. Trask, X. Yang, S. Putvinski, R. Andow, N. Bolte, D. Q. Bui, F. Ceccherini, R. Clary, A. H. Cheung, K. D. Conroy, S. A. Dettrick, J. D. Douglass, P. Feng, L. Galeotti, F. Giammanco, E. Granstedt, D. Gupta, S. Gupta, A. A. Ivanov, J. S. Kinley, K. Knapp, S. Korepanov, M. Hollins, R. Magee, R. Mendoza, Y. Mok, A. Necas, S. Primavera, M. Onofri, D. Osin, N. Rath, T. Roche, J. Romero, J. H. Schroeder, L. Sevier, A. Sibley, Y. Song, L. C. Steinhauer, M. C. Thompson, A. D. Van Drie, J. K. Walters, W. Waggoner, P. Yushmanov, K. Zhai, and T. A. E. Team. Recent breakthroughs on c-2u: Norman’s legacy. In T. Tajima and M. Binderbauer, editors, Physics of Plasma-Driven Accelerators and Accelerator-Driven Fusion, volume 1721 of AIP Conference Proceedings, page 030003, 2016.
- [40] G. Makrinich and A. Fruchtman. Experimental study of a radial plasma source. Physics of Plasmas, 16(4):043507, 2009.
- [41] A. Fruchtman. Neutral gas depletion in low temperature plasma. Journal of Physics D-Applied Physics, 50(47):473002, 2017.
- [42] A. Fruchtman. The thrust of a collisional-plasma source. Ieee Transactions on Plasma Science, 39(1):530–539, 2011.
- [43] M. Lieberman and A. Lichtenberg. Principles of plasma discharges and materials processing. (Wiley-Blackwell, 2005).
- [44] Ratko K Janev, William D Langer, Douglass E Post, and Kenneth Evans. Elementary Processes in Hydrogen-Helium Plasmas. (Springer, 1987).
- [45] B. N. Breizman, M. R. Tushentsov, and A. V. Arefiev. Magnetic nozzle and plasma detachment model for a steady-state flow. Physics of Plasmas, 15(5):057103, 2008.
- [46] B. Wachs and B. Jorns. Background pressure effects on ion dynamics in a low-power magnetic nozzle thruster. Plasma Sources Science & Technology, 29(4):045002, 2020.
- [47] K. Takahashi, Y. Takao, and A. Ando. Neutral-depletion-induced axially asymmetric density in a helicon source and imparted thrust. Applied Physics Letters, 108(7):074103, 2016.
- [48] M. Merino, J. Maurino, and E. Ahedo. Kinetic electron model for plasma thruster plumes. Plasma Sources Science and Technology, 27(3):035013, 2018.
- [49] E. Ahedo, S. Correyero, J. Navarro-Cavallé, and M. Merino. Macroscopic and parametric study of a kinetic plasma expansion in a paraxial magnetic nozzle. Plasma Sources Science and Technology, 29(4):045017, 2020.
- [50] Manuel Martinez-Sanchez and Eduardo Ahedo. Magnetic mirror effects on a collisionless plasma in a convergent geometry. Physics of Plasmas, 18(3):033509, 2011.
- [51] B. A. Wetherton, A. Le, J. Egedal, C. Forest, W. Daughton, A. Stanier, and S. Boldyrev. A drift kinetic model for the expander region of a magnetic mirror. Physics of Plasmas, 28(4):042510, 2021.
- [52] D. I. Skovorodin. Influence of trapped electrons on the plasma potential in the expander of an open trap. Plasma Physics Reports, 45(9):799–804, 2019.
Appendix A Magnetic field profile
To study the effects of finite ion temperature we employed a mirror magnetic field. To simplify numerical calculations, the magnetic field was described by three different functions in regions A, B, and C: the region A, from to 0.33, with , (T); the region B from 0.33 to 0.77 with where is the magnetic field at the maximum at ; the regions C from 0.77 to 1 with (T). The functions , , and are chosen to have and continuous across the boundaries and .
Appendix B Time-dependent equations
The solutions of the stationary equations were verified with the initial value simulations of the time-dependent equations. In the absence of charge-exchange and ionization they have the following form:
| (24) |
| (25) |
| (26) |
| (27) |
Here, with the exception of , and , all quantities are expressed in dimensionless units. The diffusive coefficients had the following values: , , and .
Note that while the profiles of the density and pressure are fully determined by the global solution, the absolute values have free normalization parameters. Plasma parameters are normalized to their respective values at the left end of the nozzle such that , , , , , and . (For the sake of convenience all the primes on parameters will be dropped and it will be assumed that n, , , , , , and represent normalized quantities).
The values for the diffusion coefficients were small in comparison to the other terms in the equation and thus their addition did not affect the physics of the problem. For instance, for a value of , and the condition holds.
When ionization and charge-exchange effects were included in the model, the time-dependent equations had the form
| (28) |
| (29) |
| (30) |
| (31) |
The diffusion coefficients were dimensionless and had the following values: , , and .
Similar to the values of , the values of were small and did not affect the physics of the problem. For instance for , and the condition is true and the addition of the parameters did not affect the physics of the problem.
The time-dependent equations describing the flow of plasma were solved in BOUT++. In the BOUT++ simulations, was displaying oscillatory behavior in region A of the nozzle. These oscillations were damped as increased and the time-dependent value of approached the stationary solution value.