Ion acceleration at two collisionless shocks in a multicomponent plasma

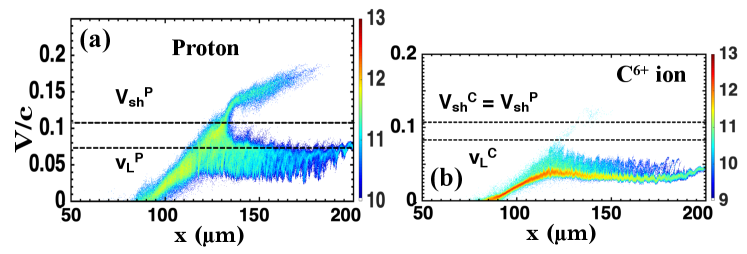
Figure 2 shows the phase-space of protons and C⁶⁺ ions at $a_{0}$ = 3.35. A significant population of protons satisfy Eq. (1) and as result are accelerated at the collisionless shock [Fig. 2(a)]. In comparison, relatively few C⁶⁺ ions are reflected by the same collisionless shock, as this requires $V_{sh}^{\rm C}$ = $V_{sh}^{\rm P}$ [Fig. 2(b)]. The lower threshold velocity for carbon ions, $v_{L}^{\rm C}$ is slightly larger than $v_{L}^{\rm P}$ as the charge-to-mass ratio, $Z_{i}/A_{i}$, is a factor of two smaller for C⁶⁺. Furthermore, because of the smaller $Z_{i}/A_{i}$, the expansion velocity $v_{0}^{\rm C}$ driven by $E_{\rm TNSA}$ in the upstream region is lower than equivalent process for protons. This causes $v_{0}^{\rm C}$ to drop below $v_{L}^{\rm C}$. This is illustrated in Fig. 2(b) which highlights how few C⁶⁺ ions are accelerated. Indeed, some of the energetic C⁶⁺ ions in Fig. 2(b) likely originate early in time from the laser interaction at the front surface of the plasma. We conclude that a negligible number of C⁶⁺ ions are accelerated via the CSA mechanism for $a_{0}=3.35$.

Simulations at low-intensity ($a_{0}=3.35$) generate a single-shock. At higher intensity, a key finding is the appearance of two distinct collisionless shocks. Figure 3 shows results at $a_{0}=10$, and Fig. 3(a) illustrates the longitudinal electrostatic field $E_{x}$, averaged over the y-axis, and potential $\phi$ at $t=3.0~{}\mathrm{ps}$. Large amplitude changes in $E_{x}$ and $\phi$ are present at two different longitudinal positions. Large changes in the normalized proton and C⁶⁺ ion densities are indicated, respectively, by the dotted ($x\approx 112~{}\rm\mu m$) and solid ($x\approx 126~{}\rm\mu m$) vertical lines in Fig. 3(b). Figure 3(c) shows how the normalized ion populations have evolved 1 ps later at $t=4.0~{}\rm ps$. It is clear that the position of the jump in proton and C⁶⁺ ion densities are different.

Multiple shock structures are seen in the phase-space and velocity spectra in the first and second columns, respectively, of Fig. 4. The three sets of data are for single-component H, single-component C, and multicomponent $\rm C_{2}H_{3}Cl$ plasmas at $t=4.0~{}\rm ps$. The positions of the shock fronts highlighted in Figs. 4(c) and 4(e) are at the same longitudinal locations as the jumps in $n_{\rm H}/n_{cr}$ and $n_{\rm C}/n_{cr}$ identified in Fig. 3(c). A large number of protons and some of the C⁶⁺ ions have velocities greater than $v_{L}^{i}$ and so CSA increases the velocity of these ions to $2V_{sh}^{i}-v_{L}^{i}$. In the $\rm C_{2}H_{3}Cl$ plasma, collisionless shocks associated with the protons and separately with the C⁶⁺ ions accelerate the protons and C⁶⁺ ions to different velocities. Figures 4(c) and 4(e) indicate that the multicomponent $\rm C_{2}H_{3}Cl$ plasma develops, in the expanding upstream, a broad velocity distribution within the proton and C⁶⁺ ion populations. This is driven by an electrostatic ion two-stream instability (EITI) that arises from the velocity differences between the proton population with $Z_{i}/A_{i}=1$, and the heavier C⁶⁺ ions with $Z_{i}/A_{i}=0.5$. We refer to this as heavy-ion EITI or HI-EITI Kumar et al. (2019). We find that the HI-EITI decelerates some upstream protons, while it accelerates some C⁶⁺ ions with velocities below $v_{L}^{\rm C}$ to velocities that exceed this lower threshold, and thereby increases the population of C⁶⁺ ions available for CSA Kumar et al. (2019). Furthermore, the CSA reflected-ion population, which moves at high velocity, causes an additional EITI with the slower moving expanding plasma that forms the upstream. We refer to this as reflected-ion EITI or RI-EITI Kumar et al. (2019). Overall, RI-EITI accelerates the slower upstream expanding ions towards higher velocity and promotes some ions, both protons and C⁶⁺ ions, with velocities below $v_{L}^{i}$ to velocities above the lower threshold. This further increases the ion population available for CSA Kumar et al. (2019). In a multicomponent $\rm C_{2}H_{3}Cl$ plasma, both RI-EITI and HI-EITI play essential roles in enabling the acceleration of C⁶⁺ ions.

In the previous Section, the multiple-shock (proton shock and C⁶⁺-ion shock) formation is described in a multicomponent $\rm C_{2}H_{3}Cl$ plasma at $a_{0}=10$, and protons and C⁶⁺ ions are reflected and accelerated by each shock once. In this Section, we illustrate C⁶⁺-ion acceleration is a double-step process with reflections at each shock in a multicomponent $\rm CH$ plasma at $a_{0}=10$.

Figures 5 show the phase-space for protons [Fig. 5(a)] and C⁶⁺ ions [Fig. 5(b)] in a $\rm CH$ plasma at $a_{0}=10$ and $t=4.0~{}\rm ps$. We see that in this $\rm CH$ plasma, the high-mass C⁶⁺ ions are reflected and accelerated twice; first at the C⁶⁺ ion-shock ($x\approx 143~{}\rm\mu m$) and second at the proton-shock ($x\approx 177~{}\rm\mu m$) to the velocity $V/c=0.23$. This is a clear observation of double-step multiple-shock acceleration of high-mass C⁶⁺ ions in a multicomponent plasma. This double-step shock acceleration of C⁶⁺ ions is clearly seen in Fig. 5 but not in a $\rm C_{2}H_{3}Cl$ plasma [Fig. 4]. This is caused by a slightly faster proton-shock velocity of $V_{sh}^{\rm P}/c=0.22$ in a $\rm CH$ plasma compared with $V_{sh}^{\rm P}/c=0.20$ in a $\rm C_{2}H_{3}Cl$ plasma. As a result, in a $\rm CH$ plasma $V_{sh}^{\rm P}$ is larger than the velocity of the pre-accelerated C⁶⁺ ions, which are reflected and accelerated by the C⁶⁺-ion shock and likely originated from the laser interaction at the front surface of the plasma early in time. This results in the second acceleration of C⁶⁺ ions by the proton-shock. In the case of a $\rm C_{2}H_{3}Cl$ plasma, $V_{sh}^{\rm P}$ is nearly equal to the velocity of the pre-accelerated C⁶⁺ ions, and the second acceleration of C⁶⁺ ions is not observed.

Furthermore, the respective deceleration and acceleration of expanding proton and C⁶⁺ ion populations, as a result of HI-EITI, are more apparent in a $\rm CH$ plasma compared with a $\rm C_{2}H_{3}Cl$ plasma.

Simulations show the formation of two collisionless shocks at $a_{0}\geq 10$, and CSA of a significant number of C⁶⁺ ions in multicomponent plasmas. This is qualitatively different from simulations at $a_{0}=3.35$ which show, see in Fig. 2(b), a single shock. To understand the importance of increasing $a_{0}$, we extend our numerical investigation of CSA to $a_{0}=20$ and $33$ in a $\rm C_{2}H_{3}Cl$ plasma. These simulations confirm the existence of two collisionless shocks and indicate that the Mach number depends on $a_{0}$.

In Fig. 6(a) we compare, at $t=4.0~{}\rm ps$, the upstream electron energy distributions for different $a_{0}$ and fit these with two-dimensional-relativistic (2D-relativistic) Maxwellian functions. The distributions at $a_{0}=10$, $20$, and $33$ are described by a two-temperature fit representing a bulk population and an energetic tail, while at $a_{0}$ = 3.35 the distribution is described by a single temperature. The bulk and tail Maxwellian components are shown for $a_{0}=33$. Figure 6(b) shows an $a_{0}$ power-law dependence for temperatures associated with the bulk and high-energy parts of the electron distributions. The fitted electron temperatures do not depend on the target material, as the laser intensity and the electron densities are not material dependent but determined by $a_{0}$ Kumar et al. (2019).

The shock velocity $V_{sh}^{i}$ and the mean velocity $v_{m}^{i}$ of the expanding ions for all values of $a_{0}$ are higher in single-component H and C plasmas, compared with a multicomponent $\rm C_{2}H_{3}Cl$ plasma. Furthermore, the difference between $V_{sh}^{i}$ and $v_{m}^{i}$, $v_{df}^{i}=V_{sh}^{i}-v_{m}^{i}$, increases with $a_{0}$ as a power-law except at the highest intensity, where $a_{0}$ = 33, which results from significant-levels ion reflection depleting or dissipating the collisionless shock Liseykina et al. (2015).

Figures 7(a) and 7(b) represent the shock velocity ($V^{i}_{sh}$) and the mean velocity ($v^{i}_{m}$), respectively, of the expanding protons and C⁶⁺ ions as a function of $a_{0}$ in a single-component H plasma, single-component C plasma, and $\rm C_{2}H_{3}Cl$ plasmas. The proton and C⁶⁺-ion $V_{sh}^{i}$ and $v_{m}^{i}$ are always larger for the single-component H plasma and single-component C plasma compared with the multicomponent $\rm C_{2}H_{3}Cl$ plasma, and follow the trend $V^{\rm P}_{\rm H}>V^{\rm P}_{\rm C_{2}H_{3}Cl}>V^{\rm C}_{\rm C}>V^{\rm C}_{\rm C_{2}H_{3}Cl}$ for all laser intensities. Here superscripts P and C denote protons and C⁶⁺ ions, respectively, with different plasmas indicated by subscripts. The ordering of velocities results from differences in the average charge-to-mass ratio $\langle Z\rangle/\langle A\rangle$, that is as $V^{i}_{sh}$ and $v^{i}_{m}$ are predominantly determined by the ion-acoustic velocity ($c^{i}_{s}$) and velocity of ions due to $E_{\rm TNSA}$, respectively. Differences in the hole-boring velocity, which depends on $\sqrt{\langle Z\rangle/\langle A\rangle}$, explains why $V^{\rm P}_{\rm H}>V^{\rm P}_{\rm C_{2}H_{3}Cl}$ and $V^{\rm C}_{\rm C}>V^{\rm C}_{\rm C_{2}H_{3}Cl}$ Kumar et al. (2019). As a result, the shock velocity in a single-component H plasma (with $\langle Z\rangle/\langle A\rangle$ = 1) is larger than that in $\rm C_{2}H_{3}Cl$ ($\langle Z\rangle/\langle A\rangle$ = 0.48), and shock velocity for C⁶⁺ ion in a single-component C plasma ($\langle Z\rangle/\langle A\rangle$ = 0.50) is larger than that in $\rm C_{2}H_{3}Cl$.

Ion-acoustic waves are excited in proton and C⁶⁺ ion populations and using the bulk electron temperatures $T_{e}$ to derive an ion-acoustic velocity, $c_{s}^{i}=\sqrt{(Z_{i}/A_{i})T_{e}/m_{p}}$, we find that the associated Mach numbers, $M^{i}=v_{df}^{i}/c_{s}^{i}$, scale as a power law in $a_{0}$. The ion-acoustic velocities for protons ($c_{s}^{\rm P}$) and C⁶⁺ ions ($c_{s}^{\rm C}$) are calculated using the bulk temperature of the plasma. The upstream bulk temperatures in a single-component H plasma, single-component C plasma, and multicomponent $\rm C_{2}H_{3}Cl$ plasma are the same, as a result the $c_{s}^{i}$ depends on the $\sqrt{\langle Z\rangle/\langle A\rangle}$. This is shown in Fig. 7(c). The $c_{s}^{i}$, indicated by the solid lines, scale with $a_{0}$ as a power-law. The difference between the shock velocity and mean velocity of the expanding ions, i.e., $v_{df}^{i}=V_{sh}^{i}-v_{m}^{i}$, is shown in Fig. 7(d) and increases as a power-law with $a_{0}$ except at $a_{0}$ = 33.

The ratio between the $v_{df}^{i}$ and $c_{s}^{i}$ yields the Mach number $M^{i}=v_{df}^{i}/c_{s}^{i}$, this is shown in Fig. 7(e). In comparison with $M^{\rm P}$, the Mach number for protons, $M^{\rm C}$, the Mach number for C⁶⁺ ions, has a strong scaling with $a_{0}$. Notice in multicomponent $\rm C_{2}H_{3}Cl$, $M^{\rm C}<1$ for $a_{0}$ = 3.35, and no shock is associated with the C⁶⁺ ions. Furthermore, $M^{\rm P}$ in a single-component H plasma decreases with $a_{0}$, this occurs as $v_{m}^{\rm P}$ scales faster with $a_{0}$ than $V_{sh}^{\rm P}$, causing a slow scaling of $v_{df}^{\rm P}$ compared with $c_{s}^{\rm P}$ as $a_{0}$ increases.

For $a_{0}$ = 33 shock dissipation, driven by ion reflection, becomes more pronounced. This reduces the shock velocity Liseykina et al. (2015). Evidence for this is seen in Fig. 7(d) of $v_{df}^{i}$ and in Fig. 7(e) of $M^{i}$ which illustrate a power-law trend for $a_{0}=3.35$, $10$, and $20$ up to the end of the simulations at $t=4.0$ ps. Simulations at $a_{0}=33$ show significant shock dissipation from $t\approx 2.5$ ps. For $a_{0}=3.35$, $10$, and $20$, shock velocities increase exponentially with time until $t=4.0~{}\rm ps$, in contrast, for $a_{0}=33$, the shock velocity increases to $t<2.5~{}\rm ps$ then dissipates, which results in low Mach numbers at $a_{0}=33$ for single- and multicomponent plasmas Liseykina et al. (2015).

The temporal variation of shock positions ($X_{sh}$) in a single-component H plasma and a multicomponent $\rm C_{2}H_{3}Cl$ plasma for $a_{0}$ = 3.35 are shown in Fig. 8(a). The derivative $dX_{sh}/dt$ gives the shock velocity $V_{sh}$. Since there is an exponential drop in the density at the rear-side of the target, $V_{sh}$ increases exponentially as a function of time for all target materials. For $a_{0}$ = 3.35 [see Fig. 8(a)], 10, and 20, $X_{sh}$ and $V_{sh}$ rise exponentially with time. Comparing this to Fig. 8(b), we see that at $a_{0}$ = 33 the temporal evolution of $X_{sh}$ and $V_{sh}$ for protons and C⁶⁺ ions in a multicomponent $\rm C_{2}H_{3}Cl$ plasma is slower. Indeed, the time dependencies of $X_{sh}$ and $V_{sh}$ are best represented by third- and second-order polynomials, respectively. This slower temporal evolution results from enhanced ion reflection at the shock which increases shock dissipation Liseykina et al. (2015).

Figures 9(a) and 9(b) show how the energy $E$ and the number of reflected ions at the peak of the energy distribution $dN/dE$ depend on $a_{0}$. In the $\rm C_{2}H_{3}Cl$ plasma there are no C⁶⁺-associated shocks at $a_{0}=3.35$ as $M^{\rm C}<1$. The energies of the reflected ions are always larger in single-component H or C plasma when compared with multicomponent $\rm C_{2}H_{3}Cl$ plasma [Fig. 9(a)]. This is a feature of smaller $V_{sh}^{i}$ and amplitude of $\phi$ in the multicomponent $\rm C_{2}H_{3}Cl$ compared with the single-component H or C plasma as shown in Fig. 4.

Figures 10(a) and 10(b) show the spatial profile of electrostatic potentials $\phi$ in a multicomponent $\rm C_{2}H_{3}Cl$ plasma and a single-component H plasma, respectively, at $t=$ 2.5 (blue curve) and 4.0 ps (red curve) for $a_{0}=3.35$. The vertical lines indicate the position of the shock fronts. These highlight that $\phi$ is smaller in a multicomponent $\rm C_{2}H_{3}Cl$ plasma compared to a single-component H plasma. The smaller $\phi$ is a result of a lower $\langle Z\rangle/\langle A\rangle$ plasma. In a single-component H plasma, the gradient $d\phi/dx$ is large. This potential jump is associated with the shock and is necessary for ion acceleration. It is produced by a charge separation between electrons and ions. This feature is not observed in the multicomponent $\rm C_{2}H_{3}Cl$ plasma because the charge separation between electrons and ions is smeared out over a larger volume by the heavier C and Cl ions, as a result the amplitude and gradient associated with $\phi$ are smaller.

Our PIC results indicate that $V_{sh}$ is smaller at lower $\langle Z\rangle/\langle A\rangle$, this is explained by recognising that the hole-boring velocity Robinson et al. (2009)

determines the velocity of the piston driving the collisionless shock. Given that $a_{0}$ and $n_{e}$ are same for all target materials, $V_{HB}$ has relative dependence on only $\sqrt{\langle Z\rangle/\langle A\rangle}$, maximizing $V_{sh}$ when $\langle Z\rangle/\langle A\rangle$ is largest, i.e., for a single-component H plasma.

For the multicomponent $\rm C_{2}H_{3}Cl$ plasma at $a_{0}>3.35$ the flux of the reflected protons and C⁶⁺ ions is higher [see Fig. 9(b)]. It is important to note that more protons are accelerated in multicomponent plasma as $v_{L}^{\rm P}$ is lower in comparison with the single-component H plasma. For C⁶⁺ ion acceleration, HI-EITI, which is present only in a multicomponent plasma, broadens the velocity distribution of the expanding C⁶⁺ ions towards higher velocity. This results in more C⁶⁺ ions being available for CSA in comparison to single-component C plasmas.

These results confirm our earlier observation Kumar et al. (2019) that only proton collisionless shocks were observed in multicomponent plasmas at $a_{0}$ = 3.35. In this work Mach numbers $M$ = 1.6 - 1.7 were calculated with a critical Mach number needed for the proton reflection and CSA. These values were derived using ion-acoustic velocities based on a $\langle Z\rangle/\langle A\rangle$, where $\langle Z\rangle$ and $\langle A\rangle$ are the respective averages of $\langle Z_{i}\rangle$ and $\langle A_{i}\rangle$ across all ion species in a plasma. Here, we use ion-specific ion-acoustic velocities to describe the two collisionless shocks. For protons $c_{s}^{\rm P}$ determines the Mach number $M^{\rm P}$ of a proton collisionless shock, and ions satisfying the reflection condition given by Eq. (1) are accelerated even when the Mach number is less than $M_{\rm cr}$ defined in Ref. Kumar et al. (2019).