Involution Matrix Loci and Orbit Harmonics
Abstract.
Let be the affine space of complex matrices with coordinate ring . We define graded quotients of which carry an action of the symmetric group by simultaneous permutation of rows and columns. These quotient rings are obtained by applying the orbit harmonics method to matrix loci corresponding to all involutions in and the conjugacy classes of involutions in with a given number of fixed points. In the case of perfect matchings on with even, the Hilbert series of our quotient ring is related to Tracy-Widom distributions and its graded Frobenius image gives a refinement of the plethysm .
1. Introduction
Let be a list of variables and let be the polynomial ring over these variables. If is a finite locus of points in affine -space, we have the vanishing ideal
| (1.1) |
and an identification of vector spaces. The method of orbit harmonics replaces by its associated graded ideal ; we have an isomorphism
| (1.2) |
where the quotient is a graded -vector space. If is stable under the action of a finite matrix group , then (1.2) is an isomorphism of -modules, where is a graded -module.
Geometrically, orbit harmonics corresponds to linearly deforming the reduced locus to a scheme of multiplicity supported at the origin. This deformation is shown schematically in the picture below for a locus of six points in the plane which is stable under the group generated by reflections in the lines.
Orbit harmonics has seen applications to presenting cohomology rings [GP], Macdonald theory [Griffin, HRS], cyclic sieving [OR], Donaldson-Thomas theory [RRT], and Ehrhart theory [RR]. When the locus has favorable ‘organization’ and interesting symmetries, the quotient often has nice properties. One expects algebraic properties of to be governed by combinatorial properties of .
Let be an matrix of variables. Consider the affine space of complex matrices with coordinate ring . The application of orbit harmonics to finite matrix loci was initiated by Rhoades [RhoadesViennot]. He considered the locus of permutation matrices. Since forms a group, this permutation matrix locus carries an action of by left and right multiplication. Algebraic properties of are governed by longest increasing subsequences in and the Schensted correspondence. Liu extended [Liu] this work to the locus of -colored permutation matrices.
In this paper we consider matrix loci which do not form a group, but are closed under permutation matrix conjugation. We consider the locus
| (1.3) |
of involutions (or matchings). For with , we have the sublocus
| (1.4) |
of matchings with fixed points. If is even, we write
| (1.5) |
for the set of perfect matchings (or fixed-point-free involutions). The loci and are closed under the conjugation action of the permutation matrix group . The quotients and are therefore graded -modules. Our results on these modules are as follows.
- •
-
•
We show (Theorem 3.3) that admits a basis of monomials indexed by matchings where
is the squarefree product of upper triangular variables indexed by 2-cycles in .
-
•
We describe the graded -module structure of each of the orbit harmonics quotient rings and ; see Theorems 3.5, LABEL:thm:conjugacy-module-character.
In the case of , the graded structure in the last bullet point has an especially nice form. For even, the conjugation action of on perfect matchings is well-known to have Frobenius image
| (1.6) |
where is the plethysm of Schur functions and the sum is over partitions with only even parts. The graded refinement of this character weights this sum according to the length of the first row of , viz.
| (1.7) |
where is a grading variable; see Theorem 4.4. The Hilbert series of is (up to renormalization) the distribution of the longest decreasing subsequence statistic on fixed-point-free involutions in ; see Corollary 4.6. Baik and Rains proved [BR] that the limit as of this Hilbert series arises in random matrix theory as a flavor of the Tracy-Widom distribution (up to renormalization and reversal).
The rest of the paper is organized as follows. In Section 2 we give background material on the orbit harmonics deformation, symmetric functions, and -representation theory. In Section 3 we prove our results on the matrix locus of all involutions in . In Section 4 we turn to the perfect matching locus . Section 5 is the most technical part of the paper; it computes the graded -structure of . We close in Section LABEL:sec:Conclusion with some conjectures and open problems.
2. Background
2.1. Orbit Harmonics
Let be a finite locus of points in affine -space. As in the introduction, the vanishing ideal is given by
| (2.1) |
Multivariate Lagrange interpolation gives the identification of vector spaces
| (2.2) |
where is the space of all functions . If is stable under the action of a finite matrix group , the ideal is also -stable and (2.2) is an isomorphism of -modules.
Given a nonzero polynomial , write , where is homogeneous of degree and . Let be the top degree homogeneous part of , that is, . Given an ideal , the associated graded ideal of is the homogeneous ideal
| (2.3) |
Remark 2.1.
Given a generating set of an ideal , we have a containment of homogeneous ideals in , but this containment is strict in general.
The identification of ungraded -vector spaces in Equation (2.2) extended to a vector space isomorphism
| (2.4) |
Since is a homogeneous ideal, has the additional structure of a graded -vector space. If is stable under the action of a finite matrix group , we may regard (2.4) as an isomorphism of ungraded -modules, where has the additional structure of a graded -module.
We will need a slightly more refined statement than the isomporphism (2.4). If is a graded vector space and , we write . In particular, we write for the vector space of polynomials in of degree . If is an ideal, we have a subspace . The following result is standard; see e.g. [RhoadesViennot, Lem. 3.15].
Lemma 2.2.
Suppose is an ideal and . Let be a set of homogeneous polynomials which descends to a vector space basis for . Then descends to a vector space basis of .
Now suppose is a finite locus which is stable under the action of a finite matrix group . For , the subspace is -stable, as is the ideal . The quotient is therefore an ungraded -module. The following result refines the isomorphism (2.4).
Lemma 2.3.
Suppose a finite locus is stable under the action of a finite matrix group . For , we have an isomorphism of ungraded -modules
Lemma 2.3 is well-known in orbit harmonics theory, but we include a proof for the benefit of the reader.
Proof.
Let be a set of homogeneous polynomials which descends to a vector space basis of . Lemma 2.2 says that also descends to a vector space basis of the quotient
Fix a matrix . Write where denotes the elements in of homogeneous degree . One checks that
-
•
the representing matrix for on is block diagonal with respect to the stratification ,
-
•
the representing matrix for on is block triangular with respect to the stratification , and
-
•
the diagonal blocks of the above two matrices coincide.
By the above three bullet points, the -modules and have the same composition series. Since is a finite group, the group algebra is semisimple and we have , as desired. ∎
The above proof works over any field in which the order of is nonzero. For arbitrary fields , the -modules and have the same composition series (i.e. these modules are Brauer-isomorphic).
2.2. The Schensted Correspondence
Let be a positive integer. A partition of is a sequence of non-decreasing positive integers such that . We write to say that is a partition of .
Let . A Young diagram of shape is the diagram obtained by placing boxes in the -th row. Below on the left is a Young diagram of shape .
{ytableau}& {ytableau} 1 & 3 6 7 2 5 4
A standard Young tableaux of shape is a bijective filling of into the boxes of the Young diagram of shape , such that the entries are increasing across rows and down columns. Above on the right is a standard Young tableaux of shape . We write to denote the collection of standard Young tableau of shape .
The Schensted correspondence [Schensted] is a bijection
| (2.5) |
which associates each permutation with a pair of standard Young tableau of the same shape. The Schensted correspondence is usually described by an insertion algorithm, which can be found in [Sagan].
Remark 2.4.
One important fact about the Schensted correspondence is that if corresponds to the pair of tableau , then corresponds to the pair of tableau . In particular, if is an involution, the pair of tableau that corrsponds to will have the form .
2.3. Representation Theory of
We write for the graded algebra of symmetric functions in an infinite variable set over the ground field . For example, the power sum symmetric function of degree is given by . It is well known that is an algebraically independent generating set .
Bases of the graded piece of are indexed by partitions . For example, the power sum basis is defined by for . We will also need the Schur basis .
A symmetric function is Schur-positive if the coefficients in its -expansion satisfy . If we define by
if and only if is Schur-positive.
Furthermore, if is some property that partitions may or may not have and , we define the truncation by
| (2.6) |
Here is 1 if a statement is true and 0 otherwise. The truncation operator will typically be used to restrict the first row lengths of a partition, e.g. or .
In addition to its usual multiplication, the graded ring carries an additional binary operation called plethysm. If and , we defined by
| (2.7) |
Since is an algebraically independent generating set of , the rules
| (2.8) |
for all and all scalars uniquely define a symmetric function for all . For more details on plethysm, see Macdonald’s book [Macdonald].
Irreducible representations of the symmetric group over are in one-to-one correspondence with partitions . If is a partition, write for the corresponding irreducible -module. If is any finite-dimensional -module, there are unique multiplicities so that . The Frobenius image of is the symmetric function
| (2.9) |
obtained by replacing each irreducible with the corresponding Schur function . For example, the trivial representation corresponds to the Schur function indexed by the one-part partition . If is a graded -module, we define the graded Frobenius image by
| (2.10) |
More generally, if is a graded vector space, the Hilbert series of is
| (2.11) |
Given , we have an embedding by letting permute the first letters of and letting permute the last letters. If is an -module an is an -module, the tensor product is naturally an -module. The induction product of and is
| (2.12) |
Induction product of representations corresponds to multiplication of symmetric functions; we have (see e.g. [Macdonald, Sagan])
| (2.13) |
For , the wreath product is the subgroup of generated by
-
•
the -fold direct product permuting elements of the sets
independently, as well as
-
•
products of transpositions of the form
for which interchange two of the above sets ‘wholesale’.
One way to visualize the group is as follows. Fill the entries of an grid with the numbers in English reading order. For example, if and we have the following figure.
The group is the subgroup of generated by permutations which either permute entries within rows or interchange rows wholesale. We have embeddings and ; the images of these embeddings generate .
If is an -module and is an -module, we have a -module with underlying vector space
| (2.14) |
and group action determined by
| (2.15) |
Plethysm of symmetric functions relates to this construction via
| (2.16) |
See [Macdonald] for a textbook treatment of this fact. We will only use this construction when both and are trivial modules; we note the combinatorial interpretation of the relevant symmetric function .
Lemma 2.5.
For , let be the family of set partitions of consisting of blocks, each of size . The symmetric group acts on ; let be the corresponding permutation module. The -module has Frobenius image
Proof.
It is not hard to see that so that is the Frobenius image of the coset representation
| (2.17) |
On the other hand, there is a natural correspondence between set partitions in and cosets in which is equivariant with respect to . ∎
In particular, if is even, Lemma 2.5 implies that the Frobenius image of the action of on the set of perfect matchings on is . It is an extremely difficult open problem to determine the -expansion for arbitrary . However, if is even it is known that
| (2.18) |
is the multiplicity-free sum over all where has all even parts.
We will need a standard result on symmetrizers acting on -irreducibles. Let and consider the embedding where acts on the first letters. This induces an embedding of group algebras . We let be the element which symmetrizes with respect to , i.e.
| (2.19) |
If is an -module, the element acts as an operator on . The following result characterizes when annihilates irreducible -modules.
Lemma 2.6.
Let . For a partition , we have if and only if .
Lemma 2.6 is standard, but we include a proof for the convenience of the reader.
Proof.
For any -module , it is not hard to check that
| (2.20) |
Therefore, we have
| (2.21) |
which is true if and only if the trivial representation occurs with positive multiplicity in the restriction . The Branching Rule for -modules (see e.g. [Macdonald, Sagan]) states that where the direct sum is over partitions obtained by removing an outer corner of . Iterating, we see that (2.21) holds if and only if . ∎
3. The Matching Locus
As in the introduction, we consider the locus of permutation matrices corresponding to involutions. The symmetric group acts on by conjugation:
| (3.1) |
The corresponding action of on is
| (3.2) |
The ideal is homogeneous and -stable.
3.1. Matching monomial basis
In order to study the ring , it will be useful to have an explicit generating set of its defining ideal . It will turn out that such a generating set is as follows.
Definition 3.1.
Let be the ideal generated by
-
•
all sums of variables in a single row,
-
•
all sums of variables in a single column,
-
•
all products of variables in a single row,
-
•
all products of variables in a single column, and
-
•
all diagonally symmetric differences of variables.
Here .
We aim to show that as ideals in . One of these containments is straightforward.
Lemma 3.2.
We have .
Proof.
As , it consists of all symmetric and matrices with exactly one in each row and column. For , the following polynomials are contained in (and in fact generate) the ideal :
-
•
-
•
,
-
•
,
-
•
,
-
•
,
-
•
.
Note that the top degree homogeneous part of these polynomials are exactly the generators of , so the proof is complete. ∎
As explained in Remark 2.1, the top degree components of a given generating set of do not in general suffice to generate . In order to show that we have generating in the context of Lemma 3.2, we show that the quotient has vector space dimension at most . Recall from the introduction that if is a matching, the matching monomial is the product over all variables for which .
Theorem 3.3.
The set of matching monomials descends to a vector space basis of .
Proof.
We show that descends to a spanning set of the vector space . This will establish that
| (3.3) |
where the first equality follows from the orbit harmonics isomorphism (2.4), the second equality is the definition of , the following inequality is a consequence of Lemma 3.2, and the last inequality is our spanning claim. This chain of (in)equalities will then show that and that descends to a basis of .
It remains to show that descends to a spanning set of . Consider a monomial in the variable set . We want to show that lies in the span of modulo . Write
| (3.4) |
for some . Since and for all we may assume that
the monomial is squarefree, and every variable which appears in satisfies .
We call a monomial in satisfying this condition triangular. We induct on the number of factors of the triangular monomial which satisfy .
First assume that , so that for all . If there exist with then so that certainly lies in the span of modulo . Similarly, we are done if there exist with . If there exist with , then using , we have
| (3.5) |
so that in this case, as well. We may therefore assume that the indices are distinct so that is the reduced cycle form of an involution . By definition, we have which completes the base case.
If the triangular monomial contains the variable for some . We may use the congruences
| (3.6) |
to rewrite modulo as the summation of triangular monomials of the same degree, but with one fewer variable on the main diagonal. By induction, we see that lies in the span of . ∎
For example, if we have the matching monomial basis of given by
where the bars indicate separation by degree. We record the generating set of derived obtained in the above proof. It is precisely the set of highest degree components of the ‘natural’ generating set of shown in the proof of Lemma 3.2.
Proposition 3.4.
We have .
3.2. Module structure
The basis of in Theorem 3.3 is closed under the action of . This is not a common property for ‘nice’ bases of quotient rings with group actions. Thanks to this special property, we may easily compute the graded -structure of .
Theorem 3.5.
The graded Frobenius image of is given by
Proof.
The explicit graded decomposition of into irreducibles is easily obtained from Equation (2.18), Theorem 3.5, and the Pieri Rule
| (3.10) |
where the sum is over partitions of such that and the difference of Young diagrams consists of boxes, no two of which share a column. For example, if we have
The Hilbert series of is an easy consequence of Theorem 3.3. Recall the double factorial .
Corollary 3.6.
The Hilbert series of is given by
Proof.
Apply Theorem 3.3 and count matching monomials by degree. ∎
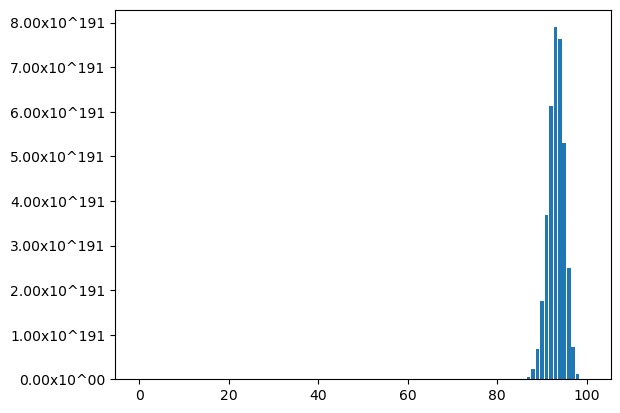
In Figure 1, we give the histogram of when . The horizontal axis corresponds to degrees , and the height of each bar represents the corresponding .
4. The Perfect Matching Locus
In this section, assume is even. We consider the locus
of perfect matchings (or fixed-point-free involutions) inside . Our study of is more indirect than our study of . In particular, the authors do not know an explicit basis of .
4.1. -annihilation
As in the case of , it will be useful to understand the defining ideal of . This ideal will turn out to have the following generating set.
Definition 4.1.
Assume is even. Let be the ideal
We will show that as ideals in . As in the case of , one containment is straightforward.
Lemma 4.2.
For even we have .
Proof.
Since we have and therefore . Furthermore, we have for since the involutions in have no fixed points. ∎
Theorem 3.3 gives bounds on the degrees of the quotient ring by the ideal in Definition 4.1. Recall that acts on -modules by symmetrization with respect to the first letters.
Lemma 4.3.
Let and assume is even. The symmetrizer annihilates the degree part of the ring whenever . In particular, if and an irreducible -module appears in , we have .
Proof.
The second statement follows from the first part and Lemma 2.6. We prove the first statement as follows.
Since , by Theorem 3.3 the set of matching monoimals descends to a spanning set of . Therefore it suffices to show that
where has -cycles and .
Write and let . We have that
| (4.1) |
where denotes equality up to a scalar multiple, and the summation is over all functions with the convention if . The verification of (4.1) uses the fact that each diagonal variable , each row product , and each column product lie in . We want to show that
| (4.2) |
Let . We calculate
| (4.3) |
with the convention if , where the is true modulo because each row sum and each column sum lies in and the congruence holds because each row product and column product lies in .
In order to prove Equation (4.2), it remains to show
| (4.4) |
Note that the set has cardinality
| (4.5) |
Every function indexing the sum in (4.4) is therefore not an injection. This given, Equation (4.4) follows from the fact that each diagonal variable , each row product and each column product lie in . ∎
4.2. Module structure
Lemma 4.3 gives a bound on the irreducible representations appearing in . This bound allows us to deduce the graded Frobenius image of from that of .
Theorem 4.4.
For even, the graded Frobenius image of is given by
Proof.
Definition 4.1 and Lemma 4.2 imply that . Therefore, we have graded -equivariant surjections
| (4.6) |
By Theorem 3.5 and the Pieri Rule, any irreducible appearing in will have . Thus, any appearing in and will also satisfy . On the other hand, Lemma 4.3 says that each appearing in satisfies , hence each Specht module appearing in should also satisfy . It follows that
every irreducible appearing in satisfies .
The reasoning in Theorem 4.4 did not directly show that . We deduce this equality of ideals using some symmetric function theory.
Proposition 4.5.
We have .
Proof.
Recall the symmetric function operators and introduced in Section 2. For any , we claim that
| (4.9) |
where means that is Schur-positive. Indeed, by Pieri’s Rule and Equation (2.18),
| (4.10) |
where the sum is over all ordered pairs consisting of
-
•
an even partition , and
-
•
a horizontal strip of size where , such that
-
•
Since , the Pieri Rule forces , so that each appearing in (4.10) satisfies . Thus each column of contains a box of , which means that each part of equals some part of or . Therefore is even and is uniquely determined by . Hence the claimed inequality (4.9) holds.
Theorem 3.5 gives a combinatorial formula for the Hilbert series of . If is a permutation, a decreasing subsequence of length is a sequence of indices such that . We write
| (4.13) |
for the longest possible length of a decreasing subsequence of . It is a famous result of Baik, Deift, and Johansson [BDJ] that the distribution of the statistic on converges to the Tracy-Wildom distribution, after appropriate rescaling. Restricting to the set of fixed-point-free involutions gives the Hilbert series of , up to reversal.
Corollary 4.6.
Assume that is even. The Hilbert series of is given by
| (4.14) |
Proof.
We recall several standard facts about the Schensted correspondence. Suppose satisfies .
-
(1)
We have . In particular, we have if and only if .
-
(2)
The statistic equals the length of the first column of (or ).
-
(3)
If , the number of fixed points of equals the number of columns in of odd length.
From these facts, for any we have
| (4.15) |
where is the conjugate partition obtained from interchanging the rows and columns of . Since , we are done by Theorem 4.4. ∎
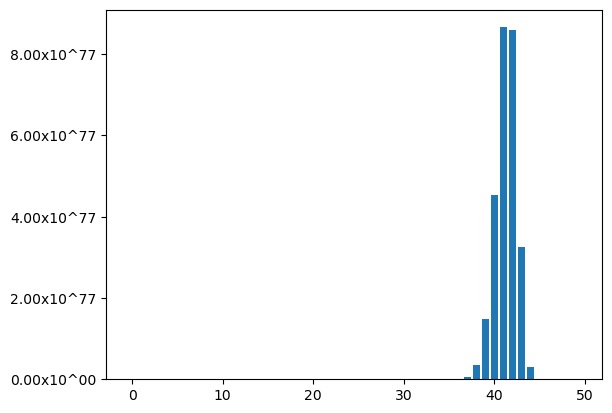
The asymptotics of the distribution in Corollary 4.6 may be derived from work of Baik and Rains [BR, Thm. 3.1]. After rescaling, the distribution of on converges to the GOE distribution of random matrix theory as . Figure 1 gives the histogram of when . The horizontal axis corresponds to degrees , and the height of each bar represents the corresponding .
5. Conjugacy classes of involutions
For with , we have the following subset of the locus of all involution permutation matrices:
| (5.1) |
The set of matrices forms a single orbit under the conjugation action of , and can be identified with permutations of cycle type . We have the disjoint union . Our study of will be more indirect and involved than our study of or ; we will calculate the graded -structure of in Theorem LABEL:thm:conjugacy-module-character after many lemmas. The added difficulties in studying are the lack of an explicit basis for this quotient ring (as in Theorem 3.3 for ) and the failure of -operator annihilation to determine (as it did in the proof of Theorem 4.4 for ).
5.1. Some symmetric function results
This subsection proves technical results on Schur expansions which will assist in our analysis of . This material should probably be skipped on a first reading and returned to as needed.
These technical results require some notation. If is a polynomial in , we write for the coefficient of in . Similarly, if is a symmetric function expressed in the Schur basis, we write for the coefficient of . Finally, if we write for the remainder of modulo . The next lemma describes the Schur expansion of the ungraded Frobenius image of .
Lemma 5.1.
For each , write where , and let . Then
| (5.2) |
with the convention .
Proof.
By Pieri’s Rule and Equation (2.18), we have
| (5.3) |
One the other hand,
| (5.4) |
We show that
| (5.5) |
Indeed, if we let
| (5.6) |
and
| (5.7) |
we have a map given by
| (5.8) |
It remains to show that is a bijection as follows.
First, we show that is well-defined, i.e. . In fact, if , since we have
| (5.9) |
Therefore
| (5.10) |
which forces
| (5.11) |
Since
| (5.12) |
we have so that is well-defined.
Next, we claim that is injective. Indeed, for any tuple , Equation (5.9) implies that each entry is determined by . The injectivity of follows.
Finally, we show that is surjective. Let and set for . We claim that . Given , since
| (5.13) |
we have
| (5.14) |
In addition,
| (5.15) |
Furthermore, we have
| (5.16) |
We conclude that , and we have . Therefore, the map is a bijection, Equation (5.5) holds, and the proof is complete. ∎
Our second lemma is an identity of symmetric functions. Roughly speaking, it stratifies the Schur expansion of according to the length of the first row.
Lemma 5.2.
If we have the identity of symmetric functions
| (5.17) |
Proof.
For any , we claim that
| (5.18) |
| (5.19) |
For Equation (5.18), fix such that and write where . Let for . Consider the polynomial given by
| (5.20) |
Observe that the coefficient sequence of is palindromic. Since , we have . Therefore
| (5.21) |
The palindromicity of yields
| (5.22) |
Equation (5.18) follows from Equation (5.22) and Lemma 5.1. The proof of Equation (5.19) is similar to that of Equation (5.18) and omitted.
Our final symmetric function lemma is an equality (5.25) of two sums involving Schur function plethysms. The right hand side is the Frobenius image of the -module . The terms of the left hand side involve the Frobenius images of the submodules , but are truncated by the length of the first row.
Lemma 5.3.
We have the identity of symmetric functions
| (5.25) |
5.2. The ideal
We want to understand the defining ideal of . As in the case of (Lemma 3.2), some elements of are not difficult to obtain.
Definition 5.4.
In other words, the ideal is generated by together with the diagonal sum and any product of variables on the diagonal. The analog of Lemma 3.2 is as follows.
Lemma 5.5.
We have .
Unlike in the case of or , we do not have in general. We leave finding an explicit generating set of as an open problem.
Proof.
Since , we need only show that the diagonal sum and the product lie in for . Indeed, we have and therefore . Furthermore, if we have and therefore . ∎
We want to show that certain degrees of the graded -module are annihilated by the symmetrization operator . This will be done in Lemma LABEL:lem:conjugacy-module-annihilation below. In order to prove Lemma LABEL:lem:conjugacy-module-annihilation we require two technical results; the first is as follows.
Lemma 5.6.
Fix consisting of pairs of integers in and suppose satisfies . For each function , at least one of the two following statements is true.
-
•
There exist integers such that for all .
-
•
There exist integers such that .
Proof.
We prove this lemma by contradiction. Assume that neither of the two statements holds. Since the first statement does not hold, we have
| (5.36) |
Define by
| (5.37) |
Then , , and the restriction of to is injective. Since the second statement does not hold, we have
| (5.38) |
We compute
| (5.39) |
where the first equality is justified by (5.38), the second equality uses , the third equality holds because is injective, the fourth equality holds because , the strict inequality holds because , and the weak inequality uses . But (5.39) implies , which is a contradiction. ∎
For we have the symmetrization operator over . We use Lemma 5.6 to show that the images of certain matching monomials under lie in the ideal .
Lemma 5.7.
Suppose . Let be a matching with matched pairs. For with we have .
The proof of Lemma 5.7 is involved, but worth it. It will enable us to fruitfully apply Lemma 2.6 to the ring .
Proof.
We prove this lemma by induction on