Investigation of Numerical Dispersion with Time Step of The FDTD Methods: Avoiding Erroneous Conclusions
Abstract
It is widely thought that small time steps lead to small numerical errors in the finite-difference time-domain (FDTD) simulations. In this paper, we investigated how time steps impact on numerical dispersion of two FDTD methods including the FDTD(2,2) method and the FDTD(2,4) method. Through rigorously analytical and numerical analysis, it is found that small time steps of the FDTD methods do not always have small numerical errors. Our findings reveal that these two FDTD methods present different behaviours with respect to time steps: (1) for the FDTD(2,2) method, smaller time steps limited by the Courant-Friedrichs-Lewy (CFL) condition increase numerical dispersion and lead to larger simulation errors; (2) for the FDTD(2,4) method, as time step increases, numerical dispersion errors first decrease and then increase. Our findings are also comprehensively validated from one- to three-dimensional cases through several numerical examples including wave propagation, resonant frequencies of cavities and a practical engineering problem.
Index Terms:
finite-difference time-domain method, high order methods, numerical dispersion, time stepI Introduction
The finite-difference time-domain (FDTD) method is one of the most widely used numerical methods to solve the practical electromagnetic problems, like scattering from electrically large and multiscale objects [1, 2, 3], integrated circuits [4, 5, 6, 7], electromagnetic compatibility (EMC) [8, 9, 10], electromagnetic interference (EMI) [11, 12, 13], due to its easy implementation, robustness, strong capability of handling complex media and highly efficient parallel computation [14, 15].
However, the accuracy of the FDTD methods can be affected by several factors, such as numerical dispersion, mesh size, staircase errors, time steps, and so on. Numerical dispersion is one of the main factors that must be taken into consideration in FDTD methods, which implies that wavenumber of electromagnetic waves in the Yee’s grid does not linearly depend on frequency. Numerical dispersion of the FDTD method and its variations, like high order FDTD methods [16, 18, 17], the alternatively-direction-implicit (ADI) FDTD methods [19, 20], the locally 1-D (LOD) FDTD methods [21], are extensively investigated in a substantial literature [22, 23, 25, 28, 24, 27, 26]. Most of them focus on investigation of the relationship between numerical dispersion and propagation angles both in and , mesh size, spatial distributions. Effects of time steps on numerical dispersion of the explicitly marching FDTD methods are seldom studied since one might think that it is relative simple and small time steps can reduce numerical dispersion. It is more common for the implicitly unconditionally stable FDTD methods to numerically discuss numerical dispersion with respect to time steps [19, 20, 21, 29], since the Courant-Friedrichs-Lewy (CFL) condition is removed and large time steps are possible. It is found that for certain implicit FDTD methods, like the ADI-FDTD method and the LOD-FDTD method, numerical dispersion indeed decreases with smaller time steps [19, 20, 21, 29].
Then, several approaches to minimize numerical dispersion are proposed to obtain more accurate results without significantly increasing computational costs. One simple but suboptimal option is to use fine enough grid in the FDTD simulations. It indeed increases the accuracy [30], however, inevitably with significantly increasing computational resources in terms of memory and CPU time since quite small mesh has to be used to capture fine geometric features, like wires and slots. Another type is to use optimized updating coefficients or artificial anisotropy in the time-marching formulations [31, 32, 33, 34, 35]. In essence, through minimize numerical dispersion of different FDTD methods, the accuracy can be greatly improved without decreasing mesh sizes. Last but not least, high order finite-difference schemes are used to approximate the partial differential derivatives in the temporal and/or spatial domain [16, 18, 17], which show that significant accuracy improvement can be obtained.
It is easy to take for granted that a smaller time step leads to smaller numerical dispersion errors (NDEs) and then more accurate results in the FDTD simulations since
| (1) |
It is obvious that a larger would have larger approximation errors as shown in (1). One may erroneously conclude that to obtain acceptable numerical results in the FDTD simulations, a small time step is much preferred. As shown in [19, 20, 21, 29], although the implicit updating methods are unconditionally stable, time steps can not be arbitrarily large if high accurate results are required. Otherwise, numerical dispersion can severely degenerate the accuracy and even totally unacceptable. It implies that long simulation time has been inevitable because of small time steps used in the FDTD methods. Therefore, large time step and small NDE seem to be contradictive. However, is it really true? In this paper, we would report several findings upon effects of time steps in two classic FDTD methods upon numerical dispersion. Our findings reveal that smaller time steps do not always necessarily decrease numerical dispersion. On the contrary, it may lead to larger errors. Numerical dispersion of two typical FDTD methods including the FDTD(2,2) method and the FDTD(2,4) method are analytically and numerically studied in terms of various time steps. Then, we discussed optimal time steps for those methods with minimized numerical dispersion.
This paper is organized as follows. In Section II, the analytical numerical dispersion relationships of the two FDTD methods are briefly summarized. In Section III, effects of time steps of the two FDTD methods upon numerical dispersion are analytically investigated and then NDEs are discussed. In Section IV, numerical studies upon numerical dispersion are carried out to validate our analytical analysis. In Section V, several numerical examples including wave propagation, resonant frequencies of cavities and a practical engineering problem further validate our findings. At last, we draw some conclusions in Section VI.
II Numerical Dispersion Formulations for
Two FDTD Methods
II-A Numerical Dispersion of the FDTD(2, 2) Method
Without loss of generality, a homogenous, lossless, isotropic medium and uniform mesh is considered in our study. Therefore, the analytical numerical dispersion of the FDTD(2,2) method [30] can be expressed as
| (2) |
where , , are numerical wavenumbers in the , and direction, respectively, and are the azimuth and zenith angles, is the numerical wavenumber of electromagnetic waves in the Yee’s grid, , and are mesh sizes in the , and direction, respectively. denotes the angular frequency and is the time step.
To obtain stable numerical solutions for the explicit FDTD (2,2) method, time steps must satisfy the CFL condition [30], expressed as
| (3) |
For convenience in our following derivation, is defined as
| (4) |
where is the maximum time step defined by the CFL condition in (3).
II-B Numerical Dispersion Relationship of the FDTD(2,4) Method
The analytical numerical dispersion of the FDTD(2,4) method [30] is written as
| (5) |
Then, the CFL condition for the FDTD(2,4) method [30] is expressed as
| (6) |
III Analytical Analysis of Numerical Dispersion of the FDTD Methods
In this section, we theoritically discuss effects of time steps on numerical dispersion of the two FDTD methods. All the subscripts of and are suppressed for brevity.
III-A The FDTD(2,2) Method
Remark 1: , .
Since the explicit expression of can not be directly obtained from (2), the parameter scanning method [36, 37] is used to study the relationship between and . We scanned , with other possible parameters in (2). This above statement always holds true. Although it is not mathematically rigorous, it should be enough for practical applications and our analysis. Here, we plot the maximum with GHz, = = = m. Both , are scanned and the maximum is obtained as shown in Fig. 1. It can be easy to find that when satisfies the CFL condition, namely , is always larger than .

Lemma 1: For the FDTD(2,2) method,
| (8) |
Proof: Since the explicit expression of is not available, the implicit differentiation [38] is resorted to investigating the derivative of with respect to defined in (4). For convenience of derivations, the following symbols are defined as
| (9) |
and
| (10) |
Therefore, (2) is separated into LHS and RHS two parts. We first consider LHS. By assuming uniform mesh used in the simulations, , and substituting and (4) into LHS, we obtain
| (11) |
where is the count of sampling cells per wavelength, defined as . For practical simulations, should be satisfied to obtain acceptable accurate results [30].
With some mathematical manipulations, the derivative of LHS with respect to is obtained as
| (12) |
where . Since ,
| (13) |
Then, let’s check the sign of in (12). By taking its derivative, we get
| (14) |
Since is a continous function, , and , we get
With a similar manner, the derivative of RHS can be expressed as
| (17) |
where , where is the numerical phase velocity in the Yee’s grid, and
| (18) |
with , , and .
(a)
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/78cd263e-fc19-468f-bd95-b70d53fcfb56/three.jpg)
(b)
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/78cd263e-fc19-468f-bd95-b70d53fcfb56/second.jpg)
(c)
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/78cd263e-fc19-468f-bd95-b70d53fcfb56/third.jpg)
To further investigate signs of (18), we divide its domain into several parts based on signs of their function values of each term. Note that the function domain is and . Therefore, we divide them into several parts to check their signs. The detailed results are summarized in Table I. Table I (a)-(c) correspond to three terms in (18). To better illustrate it, we take term1 in (18) as an example. When and , it is evidently that . Note that , then . Therefore, we have and , which implies that term1 is positive when and . The remaining situations can be obtained with similar manners. To sum them up, we can obtain the following inequality
| (19) |
| (20) |
Evidently, Lemma 1 is analytically proved and we can further analyze effect of time steps on the NDE of the FDTD(2,2) method.
From Remark 1 and Lemma 1, we can easily find that the numerical wavenumber monotonically decreases as in the FDTD(2,2) method increases. When time steps grow larger and are bounded by (3), the numerical phase velocity of electromagnetic waves is closer to its physical counterpart , and then NDE caused by the numerical dispersion would be relatively smaller. Therefore, the NDE reaches its minimum value when gets its maximum value defined by (3).
With similar procedures, we can investigate effects of time steps upon numerical dispersion for the FDTD(2,4) method.
III-B The FDTD(2,4) Method
Remark 2: , we have , , .
Lemma 2: For the FDTD(2,4) method,
| (21) |
From Remark 2 and Lemma 2, the NDE firstly decreases as the of the FDTD(2,4) method get larger. When , the NDE becomes larger. Therefore, the NDE reaches its minimum value at .
IV Numerical Analysis of Numerical Dispersion of the FDTD Methods
IV-A The FDTD(2, 2) Method
To comprehensively investigate the numerical dispersion of the FDTD (2,2) method, the numerical phase velocity is calculated from (2). In our numerical studies, the frequency is 5 GHz and = = = m, which corresponds to . In all other simulations, the same parameters are used, otherwise stated.
As shown in Fig. 2, changes periodically over for a fixed time step when . However, increases as becomes larger with fixed values, which implies that approaches as time steps grow larger. Therefore, the NDE would become smaller as time steps get larger, which agrees with our analytical analysis in the previous section. Fig. 3 shows with respect to when . Similar statements can be also obtained.
Fig. 4 illustrates with different with respect to and . It is easy to find that each surface does not intersect each other. Therefore, we can conclude that approaches as becomes larger. The numerical dispersion results show that the optimum time step of the FDTD(2,2) method is the largest time step defined by the CFL condition, which also agrees with our theoretical analysis.



IV-B The FDTD(2,4) Method
of the FDTD (2,4) method is also calculated to investigate its numerical dispersion with different . As shown in Fig. 5, changes periodically with respect to when . approaches to at the beginning when becomes large, and then becomes larger than as further increases. Therefore, the NDE of the FDTD (2,4) method firstly decreases and then increases over . The statements obtained in Fig. 6 are similar to those of Fig. 5. They agree with our theoretical analysis.
Here, we provide a numerical method to calculate the optimum time step of the FDTD(2,4) method. The optimum time step is defined as
| (22) |
which can make difference between the numerical wavenumber and its analytical counterpart with and minimum.


V Numerical Results and Discussion
In this section, several numerical examples including wave propagation, resonant frequencies of cavities and a practical engineering problem are carried out to validate our previous analysis. The relative error is defined as
| (23) |
where and denotes the reference and calculated values, respectively.
V-A The One Dimensional Case
A wave propagation example is used to verify the accuracy of the two FDTD methods with different time steps in one dimensional case. A Gaussian function with the waveform is selected as the excitation, and uniform mesh size m, and the simulation time is s. Note that reflected electromagnetic waves do not reach probe in the simulations.
V-A1 The FDTD(2,2) Method
as discussed in the previous two sections, the numerical dispersion of the FDTD(2,2) method reaches its minimum value when and it is called the magic time step [30] in one dimensional case. The phase velocity exactly equals to in the free space. Therefore, the numerical results obtained from the FDTD(2,2) method do not suffer from the NDE. The magic time-step has already been proved by a rigorous mathematical manner in [30]. Interested readers are referred to it for more details.
As shown in Fig. 7, when , the waveform obtained from the FDTD(2,2) method exactly agrees with the analytical solution. However, the other two results with and show large discrepancy even though much smaller time steps are used in our simulations. In addition, it can be found that the error obtained from the FDTD(2,2) method when is much larger than that with . It matches our analytical analysis in the previous two sections.
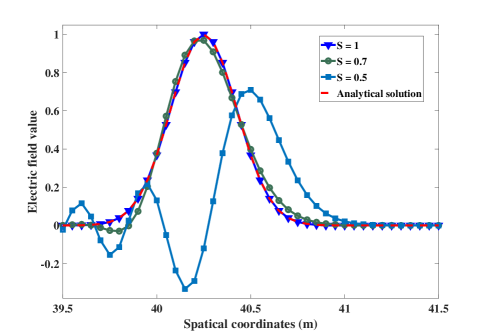
V-A2 The FDTD(2,4) Method

Fig. 8 illustrates the absolute relative error with respect to . It is easy to find that the relative error decreases as becomes larger from zero and reaches zero when . Then, the relative error increases as continues to get larger. Since can be smaller or larger than , the relative error shows different behaviors compared with that of the FDTD(2,2) method.
Fig. 9 shows the waveform obtained from the FDTD(2,4) method. When , the numerical result perfectly matches the analytical solution. However, other results obviously deviate from the analytical solution no matter when or .

V-B The Two Dimensional Case
A two dimensional cavity with dimension of m m and perfectly electric conductor (PEC) boundaries is considered and its resonant frequencies in both transverse magnetic (TM) and transverse electric (TE) modes are calculated through the two FDTD methods. The mesh size is m.
V-B1 The FDTD(2,2) Method
Fig. 10 shows the relative error of resonant frequencies of TM modes obtained from the FDTD(2,2) method. It’s clear that despite of some numerical fluctuations, as increases, the relative error becomes smaller for three modes, which agrees well with our investigations.


Fig. 11 shows relative errors of TE modes. Similar observations can be made as to TM modes. When grows larger, the NDE in the FDTD(2,2) method decreases gradually and more accurate simulation results can be obtained. Therefore, the optimum time step is .
V-B2 The FDTD(2,4) Method
the resonant frequencies of TM and TE modes obtained from the FDTD(2,4) method are shown in Fig. 12 and Fig. 13. It is easy to find that the relative errors of both three TE and TM modes show similar behaviors. The relative error gradually decreases and then slightly becomes larger as become larger. It should be noted that the relative error with small is larger than that with large as shown in Fig. 12 and Fig. 13. It may account for other numerical errors, like low order approximation of boundaries. Note that compared with the results in Fig. 10 and Fig. 11, results obtained from the FDTD(2,4) method are obviously more accurate than those obtained from the FDTD(2,2) method.


V-C The Three Dimensional Case
Case A: a cubic cavity with side length of m in the three dimensional case is considered. The mesh size is m. The resonant frequencies are calculated from the two FDTD methods.

Fig. 14 shows the relative error of resonant frequencies obtained from the FDTD(2,2) method. It is similar to one- and two-dimensional cases. Although there are some numerical fluctuations, the relative error becomes smaller for all the three modes as increases. It agrees well with our investigations.

Fig. 15 shows the resonant frequencies obtained from the FDTD(2,4) method. It is easy to find that relative errors of resonant frequencies show similar behaviors. The relative error gradually decreases and then slightly becomes larger as become larger. The relative error with small is larger than that with large . It may account for other numerical errors.

(a)

(b)

(a)

(b)
Case B: we use the FDTD(2,2) method to further verify our findings for a practical application in this case. A missile is illustrated by a plane wave and the surface current density is calculated from the FDTD(2,2) method with different time steps. The geometry configurations of the missile in our simulations are shown in Fig. 16(a). It is with dimension of 2.31141.46470.5334. The plane wave incidents from the -axis with 700 MHz. Fig. 16(b) shows the reference surface current density calculated from the FEKO. Fig. 17(a) and (b) show the surface current density obtained in the FDTD(2,2) method with and . It can be found that the surface current distribution obtained from the FDTD(2,2) method agree well with the reference solution. The accuracy of results in our simulations seem unchanged with and . There are various factors that can account for those results in this case, like complex geometry, staircase error, possible reflection from the total field/scattered field boundary. It turns out that time steps of the FDTD(2,2) method almost have no significant effects on the accuracy in the practical simulation. Therefore, large time step is preferred in the practical simulations since short simulation time is required and almost the same level of accuracy can also be achieved.
VI Conclusion
In this paper, we comprehensively investigated how time steps affect the accuracy of the FDTD methods in terms of numerical dispersion. Several findings are reported in this paper. Our results show that for the FDTD(2,2) method, smaller time step limited by the CFL condition leads to larger NDE. However, for the FDTD(2,4) method, as time step increase, the NDE first decreases and then increases. However, large time step of the FDTD method is preferred in the practical simulations as shown in our numerical results, which means shorter simulation time.
The findings in this paper not only can further deepen our insights upon the FDTD methods and provide the guidance for selection of optimal time steps in the FDTD simulations, but also correct widespread erroneously thought about effects of time steps on numerical dispersion of different FDTD methods.
References
- [1] R. J. Luebbers, K. S. Kunz, M. Schneider, and F. Hunsberger, “A finite-difference time-domain near zone to far zone transformation (electromagnetic scattering),” IEEE Trans. Antennas Propag., vol. 39, no. 4, pp. 429-433, 1991.
- [2] M. F. Hadi, M. Piket-May, “A modified FDTD (2,4) scheme for modeling electrically large structures with high-phase accuracy,” IEEE Trans. Antennas Propag., vol. 45, no. 2, pp. 254-264, Feb. 1997.
- [3] A. V. Londersele, D. D. Zutter, and D. V. Ginste, “A new hybrid implicit–explicit FDTD method for local subgridding in multiscale 2-D TE scattering problems,” IEEE Trans. Antennas Propag., vol. 64, no. 8, pp. 3509-3520, Aug. 2016.
- [4] Y. Liu, C. D. Sarris, “Efficient modeling of microwave integrated-circuit geometries via a dynamically adaptive mesh refinement (AMR)-FDTD technique,” IEEE Trans. Microw. Theory Tech., vol. 54, no. 2, pp. 689-703, Feb. 2006.
- [5] C. Kuo, B. Houshmand, “Full-wave analysis of packaged microwave circuits with active and nonlinear devices: an FDTD approach,” IEEE Trans. Microw. Theory Tech., vol. 45, no. 5, pp. 819-826, May 1997.
- [6] F. Xu, K. Wu, and W. Hong, “Domain decomposition FDTD algorithm combined with numerical TL calibration technique and its application in parameter extraction of substrate integrated circuits,” IEEE Trans. Microw. Theory Tech., vol. 54, no. 1, pp. 329-338, Jan. 2006.
- [7] X. Cheng. “Computational Electrodynamics and Simulation in High Speed Circuit Using Finite Difference Time Domain (FDTD) Method,” Ph. D. thesis, ST. Cloud State University, USA, 2018.
- [8] J. Mix, G. Haussmann, M. Piket-May and K. Thomas, “EMC/EMI design and analysis using FDTD,” in Proc. IEEE Intl. Symposium on EMC, vol. 1, pp. 177-181, Aug. 1998.
- [9] J. Chen, J. Wang, “A three-dimensional semi-implicit FDTD scheme for calculation of shielding effectiveness of enclosure with thin slots,” IEEE Trans. Electromagn. Compat., vol. 49, no. 2, pp. 354-360, 2007.
- [10] R. Matsubara, K. Inokuchi, “Development of EMC analysis technology using large-scale electromagnetic field analysis,” in 2019 41st IEEE Annual EOS/ESD Symposium (EOS/ESD), pp.1-6, Sep. 2019.
- [11] D. M. Hockanson, X. Ye, J. L. Drewniak, T. H. Hubing, T. P. VanDoren and R. F. DuBoff, “FDTD and experimental investigation of EMI from stacked-card PCB configurations,” IEEE Trans. Electromagn. Compat., vol. 43, pp. 1-10, Feb. 2001.
- [12] A. Yash, R. Chandel, “Crosstalk analysis of current-mode signalling-coupled RLC interconnects using FDTD technique,” IETE Technical Review, vol. 33, no. 2, pp.148-159, 2016.
- [13] B. R. Archambeault, O. R. Ramahi, C. Brench, EMI/EMC computational modeling handbook (Vol. 630) . Springer Science Business Media, 2012.
- [14] W. Yu, R. Mittra, T. Su, Y. Liu, and X. Yang, Parallel finite-difference time-domain method. Artech House, 2006
- [15] W. Yu, X. Yang, Y. Liu, R. Mittra, D. -C. Chang, C. -H. Liao, A. Muto, W.Li, and L. Zhao, “New development of parallel conformal FDTD method in computational electromagnetic engineering,” IEEE Antennas Propag. Mag., vol. 53, no. 3, pp. 15-41, Sep. 2011.
- [16] K. Lan, Y.W. Liu, and W. G. Lin, “A higher order (2,4) scheme for reducing dispersion in FDTD algorithm,” IEEE Trans. Electromagn. Compat., vol. 41, no. 2, pp. 160-165, May 1999.
- [17] W. Fu, E. L. Tan, “Development of split-step FDTD method with higher-order spatial accuracy,” Electron. Lett., vol. 40, no. 20, pp. 1252-1254, Sep. 2004.
- [18] Q. F. Liu, Z. Chen, and W. Y. Yin, “An arbitrary order LOD-FDTD method and its stability and numerical dispersion,” IEEE Trans. Antennas Propag., vol. 57, no. 8, pp. 2409-2417, Aug. 2009.
- [19] T. Namiki, “A new FDTD algorithm based on alternating-direction implicit method,” IEEE Trans. Microw. Theory Tech., vol. 47, no. 10, pp. 2003-2007, Oct. 1999.
- [20] F. Zheng, Z. Chen, and J. Zhang, “Toward the development of a three-dimensional unconditionally stable finite-difference time-domain method,” IEEE Trans. Microw. Theory Tech., vol. 48, no. 9, pp. 1550-1558, Sep. 2000.
- [21] J. Shibayama, M. Muraki, J. Yamauchi, and H. Nakano, “Efficient implicit FDTD algorithm based on locally one-dimensional scheme,” Electron. Lett., vol. 41, no. 19, pp. 1046-1047, Sep. 2005.
- [22] F. Zheng, Z. Chen, “Numerical dispersion analysis of the unconditionally stable 3-D ADI-FDTD method,” IEEE Trans. Microw. Theory Tech., vol. 49, no. 5, pp. 1006-1009, May 2001.
- [23] I. Ahmed, E. K. Chun, and E. P. Li, “Numerical dispersion analysis of the unconditionally stable three-dimensional LOD-FDTD method,” IEEE Trans. Antennas Propag., vol. 58, no. 12, pp. 3983-3989, Dec. 2010.
- [24] E. Li, I. Ahmed, and R. Vahldieck, “Numerical dispersion analysis with an improved LOD-FDTD method,” IEEE Microw. Wireless Compon. Lett., vol. 17, no. 5, pp. 319-321, Apr. 2007.
- [25] J. Pereda, O. Garcia, A. Vegas, and A. Prieto, “Numerical dispersion and stability analysis of the FDTD technique in lossy dielectrics,” IEEE Microwave Guided Wave Lett., vol. 8, no. 7, pp. 245–247, Jul. 1998.
- [26] J. B. Schneider, C. L. Wagner, “FDTD dispersion revisited: Faster-than-light propagation,” IEEE Microwave Guided Wave Lett., vol. 9, no. 2, pp. 54-56, 1999.
- [27] Z. T. Theodoros , T. D. Tsiboukis, “Low-dispersion algorithms based on the higher order (2, 4) FDTD method,” IEEE Trans. Microw. Theory Tech., vol. 52, no. 4, pp.1321-1327, 2004.
- [28] S. C. Yang, Z. Chen, Y. Yu, and W. Y. Yin “An unconditionally stable one-step arbitrary-order leapfrog ADI-FDTD method and its numerical properties,” IEEE Trans. Antennas Propag., vol. 60, no. 4, pp. 1995-2003, Apr. 2012.
- [29] S. J. Cooke, M. Botton, T. M. Antonsen, and B. Levush, “A leapfrog formulation of the 3D ADI-FDTD algorithm,” Intl. Workshop on Computational Electromagnetics in Time-Domain, pp. 1-4, Oct. 15-17, 2007.
- [30] A. Taflove, S. C. Hagness. Computational Electrodynamics: The Finite-Difference Time-Domain Method. Norwood, MA: Artech House, 2005
- [31] S. J. Jaakko, T. D. Tsiboukis, “Reduction of numerical dispersion in FDTD method through artificial anisotropy,” IEEE Trans. Microwave Theory Tech., vol. 48, no. 4, pp. 582-588, Apr. 2000.
- [32] I. Ahmed, Z. Chen, “Dispersion-error optimized ADI FDTD,” Proc. IEEE MTT-S Int. Microw. Symp. Dig., vol. 2006, pp. 173–176, Jun. 2006.
- [33] Q. F. Liu, W. Y. Yin, Z. Chen, and P. G. Liu, “An efficient method to reduce the numerical dispersion in the LODFDTD method based on the (2, 4) stencil,” IEEE Trans. Antennas Propag., vol. 58, no. 7, pp. 2384-2393, Jul. 2010.
- [34] G. Chen, S. Yang, Q. Ren, S. Cui, and D. Su, “Numerical dispersion reduction approach for finite-difference methods,” Electron. Lett., vol. 55, no. 10, pp. 591-593, 2019.
- [35] T. T. Zygiridis, “Optimum time-step size for 2D (2, 4) FDTD method,” Electron. Lett., vol. 47, no. 5, pp. 317–319, Mar. 2011.
- [36] X. H. Wang, J. Y. Gao, Z. Z. Chen, and F. L. Teixeira. “Unconditionally stable one-step leapfrog ADI-FDTD for dispersive media,” IEEE Trans. Antennas Propag., vol. 67, no. 4, pp. 2829-2834, Apr. 2019.
- [37] G. Z. Chen, S. C. Yang, and D. L. Su. “An accurate three-dimensional FDTD (2, 4) method on face-centered cubic grids with low numerical dispersion,” IEEE Antennas Wireless Propa. Lett. vol. 18, no. 9, pp. 1711-1715, Sept. 2019.
- [38] G. Strang. Calculus. MA: Wellesley College, 1991.