Investigating the Production of Leptoquarks by Means of Zeros of Amplitude at Photon Electron Collider
Abstract
Leptoquarks are one of the possible candidates for explaining various anomalies in flavour physics. Nonetheless, their existence is yet to be confirmed from experimental side. In this paper we have shown how zeros of single photon tree-level amplitude can be used to extract information about leptoquarks in case of - colliders. Small number of standard model backgrounds keep the signal clean in this kind of colliders. Unlike other colliders, the zeros of single photon amplitude here depend on as well as the mass of leptoquark along with its electric charge. We perform a PYTHIA based simulation for reconstructing the leptoquark from its decay products of first generation and estimating the background with luminosity of 100 fb-1. Our analysis is done for all the leptoquarks that can be seen at - collider with three different masses (70 GeV, 650 GeV and 1 TeV) and three different centre of momentum energy (200 GeV, 2 TeV and 3 TeV). The effects of non-monochromatic photons on the zeros of amplitude under laser backscattering and equivalent photon approximation have also been addressed.
1 Introduction
Leptoquarks are proposed particles that couple to quarks and leptons simultaneously, and hence carry non-zero baryon number as well as lepton number. They emerge naturally in various extensions of the Standard Model (SM), such as Pati-Salam model pati-salam , GUT based on or GUT1 ; GUT2 ; GUT3 , extended technicolor models technicolor1 ; technicolor2 , etc. These colour-triplet electromagnetically charged bosons (spin zero or one) could be singlet, doublet or triplet under group Rev1a ; Rev2a ; Rev3a ; Rev4a ; Rev5a ; Rev6a . Detection of leptoquark would be a signal for the unification of matter fields. Anomalies observed in the lepton flavour universality ratios , , , related to rare B decays exptRdRk1 ; exptRdRk2 ; exptRdRk3 ; exptRdRk4 ; exptRdRk5 and the deviations in the measurements of angular observables from their theoretical estimates can be addressed using several leptoquark models. Some of these models can explain observed discrepancy in muon g-21 ; g-22 and also accommodate the excess of in a Higgs decay branching fraction to at 8 TeV with 19.7 fb-1 luminosity htomutau . Because of their great importance in elucidating several issues of flavour physics Motiv1a ; Motiv1b ; Motiv1c ; Motiv1d ; Motiv1e ; Motiv1f ; Motiv1g ; Motiv2a ; Motiv3a ; Motiv4a ; Motiv4b ; Motiv4c ; Motiv4d ; Motiv4e ; Motiv4g ; Motiv5a ; Motiv6a ; Motiv7a ; Motiv8a ; Motiv9a ; Motiv10a ; Motive11 ; Motive12a ; Motive12b ; Motive13a ; Motive13b ; Motive13c ; Motive13d ; Motive13e ; Motive13f ; Motive14 ; Motive15 ; Motive16a , leptoquarks have been studied in literature in gory details during last few decades Rev1a ; Rev2a ; Rev3a ; Rev4a ; Rev5a ; Rev6a ; ModS1a ; ModS2a ; ModS2b ; ModS2c ; ModS3a ; ModS4a ; ModS5a ; ModS6a ; ModS6b ; ModS7 ; ModS8a ; ModS8b ; Exp1a ; Exp10a ; Exp13a ; Exp13b . In parallel, numerous searches for leptoquarks have been performed in different colliders Exp2a ; Exp2b ; Exp3a ; Exp5a ; Exp6a ; Exp7a ; Exp8a ; Exp9a ; Exp11a ; Exp12a ; Exp14a ; Exp15a ; LEP1 ; LEP2 .
On the other hand, the phenomenon of RAZ (radiation amplitude zero) was first discussed for process at or collider in order to probe the magnetic property of -boson RAZ1 . This phenomenon has been studied extensively in literature for various BSM models like supersymmetry, leptoquarks, other gauge theories, etc and physics behind its occurrence has also been scrutinized RAZ2 ; RAZ2p ; RAZ3 ; RAZ4 ; RAZ5 ; RAZ7 ; RAZ8 ; RAZ9 ; RAZ10 ; RAZ11 ; RAZ12 ; RAZ13 ; RAZ14 ; RAZ15 ; RAZ16 ; RAZ17 ; RAZ18 ; RAZ19 ; RAZ19a ; RAZ20 ; RAZ21 ; RAZ22 ; RAZ23 ; RAZ24 ; RAZ25 ; RAZ26 ; RAZ27 ; RAZ27p ; RAZ28 ; RAZ29 ; RAZ30 ; RAZ31 ; RAZ32 . In non-Abelian theories the tree-level amplitudes111The word “amplitude” in this context is synonymous to where is the matrix element for a given process. for single photon emission processes, which is the sum generated by attaching photon to the internal and external particles in all possible ways, can be factorized into two parts: a) the first part contains the combination of generators of the gauge group, various kinematic invariants, charges and other internal symmetry indices, whereas b) the second part corresponds to the actual amplitudes of the Abelian fields containing the dependence on the spin or polarization indices RAZ2 ; RAZ2p . The first factor goes to zero in certain kinematical zones depending on the charge and four momenta of external particles and forces the single-photon tree amplitudes to vanish RAZ3 . The general criterion for tree-level single photon amplitude to vanish is that must be same for all the external particles (other than photon) involved in the process RAZ3 where, and are the four momentum and charge of th external particle and is the four momenta of photon. For scattering processes with photon in final state, this condition reduces to:
| (1) |
where, and are the charges for the incoming particles and and is the angle between photon and in the centre of momentum (CM) frame at which RAZ occurs provided that the masses of colliding particles are negligible with respect to total energy of the system, i.e. .
Linear colliders in the range of a few hundred GeV to 1.5 TeV are going to be build in near future. These colliders can provide the possibility for studying electron-photon interactions at very high energy EPhC1a ; EPhC2a ; EPhC2b ; EPhC2c ; EPhC2d ; EPhC2e ; EPhC3a ; EPhC3b ; EPhC3c ; EPhC4a . Using modern laser technology, high energetic photons with large luminosity can be prepared through laser backscattering for this kind of studies. Since very few SM processes contribute to the background for these electron-photon colliders, they can reveal clean signals of leptoquarks through zeros of tree-level single photon amplitude EphLQ1 ; EphLQ2 ; EphLQ3 . In this paper we have studied this possibility in detail. The phenomena of RAZ in various leptoquark models has already been described in literature in context of - colliders where leptoquark is expected to be produced associated with a photon or the it undergoes radiative decays RAZLQ1 ; RAZLQ2 . Though our scenario looks quite similar to it, there arises great difference between these two colliders while considering the position of zero amplitude in the phase space. It is evident from Eq. (1) that RAZ for - colliders occurs at some particular angle between the photon and the quark which depends only on the electric charge of electron and the quark; however, we show that the same angle for zero amplitude at - colliders depends on the mass of the leptoquark as well as along with the electric charge RAZLQ3 . Nevertheless, the general condition for tree-level single photon amplitude being zero RAZ3 still remains valid.
In this paper we have analysed all kinds of leptoquarks that are going to be produced at - colliders for three different masses (70 GeV, 650 GeV and 1 TeV) with three different centre of momentum energy (200 GeV, 2 TeV and 3 TeV). Though leptoquark with light mass seems to be ruled out, most of these analysis assumes coupling of leptoquark to single generation of quark and lepton, whereas, the results from UA2 and CDF collaboration show that there is still room for low mass leptoquark with sufficiently small couplings and appropriate branching fractions to different generations of quarks and leptons. On the other hand, the bounds on couplings and branching fractions of higher mass leptoquarks are more relaxed. The leptoquark will eventually decay to a lepton and a quark, and hence we it will produce a mono-lepton plus di-jet signal at detector. In a PYTHIA based analysis, we reconstruct the leptoquark from the invariant mass of the lepton and one jet. Then we look for the angle between the reconstructed leptoquark and electron and construct the angular distribution which should match with the theoretical estimates. Observation of the zeros of this distribution at the theoretically predicted portion of phase space would indicate the presence of some leptoquarks. Furthermore, we have studied the effects of non-monochromatic photons on the zeros of angular distribution under laser backscattering and equivalent photon approximation schemes considering the current experimental limitations of electron-photon colliders.
The paper is disposed in the following way. In the next section (sec. 2) we describe the theoretical approach to the production of scalar as well as vector leptoquarks at - collider and find the conditions for the zeros of angular distribution. The experimental constrains on the mass, coupling and branching fractions of the leptoquarks have been summarised in sec. 3. In sec. 4, we describe the simulation set up, choice of benchmark points and centre of momentum energies, production cross sections and branching fractions of the leptoquarks and PYTHIA based simulation for different types of leptoquarks produced at the electron-photon collider. Sec. 5 deals with effects of non-monochromatic photons on the zeros of differential distribution. Finally, we conclude in sec. 6.
2 Theoretical formalism
In this section, we develop the theoretical formalism for the production of a leptoquark (more precisely anti-leptoquark) associated with a quark or an anti-quark at the electron-photon collider to get the mathematical expression for the differential distribution of this process. We consider the process where is a quark and is a leptoquark (the sign ‘’ indicates charge conjugate), for which there are three possible tree-level Feynman diagram, as shown in fig. 1.

2.1 Scalar Leptoquark
If the leptoquark is a scalar one, the matrix elements for the respective diagrams are as follows:
| (2) | ||||
| (3) | ||||
| (4) |
where , and are the four momenta of the particles electron, photon and the produced quark respectively, are matrices describing the couplings of leptoquark with left-handed and right-handed leptons and quarks respectively, denotes the charge of positron, signifies the charge of quark in the unit , indicates the mass of leptoquark, is the polarization of the photon and . Here, we have deliberately neglected the masses of electron and the quark since they would have insignificant effects in determining the zero of amplitude involving production of very heavy leptoquark for all practical purposes unless the produced quark is top. Therefore, after taking the spin and polarization sum of initial and final state particles, the modulus squared matrix element for this mode becomes:
| (5) |
where, and is the angle between electron and the leptoquark or equivalently photon and the quark .
2.2 Vector Leptoquark
Now, if the leptoquark be a vector particle, the matrix elements will get modified in the following way:
| (6) | ||||
| (7) | ||||
| (8) |
Here, is polarization vectors for the vector leptoquark. After taking the spin and polarization sum of initial and final state particles222It should be noted that: where is the four-momentum of the leptoquark., the modulus squared matrix element becomes:
| (9) |
The differential cross-section for this process turns out to be:
| (10) |
Here, the one fourth factor comes because of the average over initial state spins and polarizations; on the other hand, the factor three indicates the number of colour combinations available in the final state.
Now, it is evident from the Eqs. (5) and (9) that the differential cross-section vanishes iff:
| (11) |
since all the other terms are positive quantities. This also follows from the general condition for tree-level single photon amplitude to vanish RAZ3 :
| (12) |
where is the charge of leptoquark in unit of and can be expressed as: . However, the striking difference between single photon emission with two body final state and this process is that in the former case does not depend on the mass of fourth particle as well as the centre of momentum energy (as shown in Eq. (1)) after neglecting the masses of fermions, whereas in the later scenario does depend on the mass of leptoquark and (as can be seen from Eq. (11)). The variation of with increasing centre of momentum energy () for different masses of leptoquark has been shown in fig. 2; the left panel depicts the variation for production of a leptoquark associated with a down-type quark, while the right panel describes the same with a up-type anti-quark. It can also be observed from Eq. (11) that approaches amyptotically when . For the vanishing amplitude to be inside the physical region, the condition that must satisfy is:
| (13) |
which in turn would imply that
| (14) |
It should be noted that instead of quark , if the leptoquark is produced with an anti-quark , all the expressions for that process can be achieved by replacing with and with in the equations from Eq. (2) to Eq. (13) where is the charge of in unit of .


All of the leptoquarks Rev1a ; Rev2a ; Rev3a ; Rev4a ; Rev5a ; Rev6a , that can be produced at - collider, have been listed in table 2.2. Here, , are quark and lepton doublets whereas , and are fields for -quark, -quark and electron respectively. The transpose acts on indices only. and denote scalar and vector triplet respectively in the adjoint representation of SU(2); they are defined as:
| \hlineB 5 LQ | Y | Interaction | Process | ||
| \hlineB 5 Scalar Leptoquarks | |||||
| , | |||||
| —— | |||||
| —— | |||||
| —— | —— | ||||
| , | —— | ||||
| — | — | ||||
| \hlineB 5 Vector Leptoquarks | |||||
| —— | |||||
| — | —— | ||||
| —— | |||||
| —— | |||||
| — | — | ||||
| \hlineB 5 |
3 Mass and coupling
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/f12f5864-d3e8-4677-9e19-1ba92f297c19/x3.png)
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/f12f5864-d3e8-4677-9e19-1ba92f297c19/x4.png)
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/f12f5864-d3e8-4677-9e19-1ba92f297c19/x5.png)
The measurement of ratio from PEP and PETRA constrains the scalar leptoquarks to have GeV Exp10a in a model-independent way depending on the charges of them only where they are assumed to be pair-produced in the decay of a virtual photon. Measurement from AMY Exp9a provides GeV for scalar leptoquarks and similar bound for vector ones too. The LEP constrains GeV LEP1 ; LEP2 with the coupling to to be assuming the pair-production of leptoquarks from and further decay of them into jets and two leptons. For decay into first two generations of quarks and leptons, this lower bound is almost independent of branching fraction; however for third generation it depends slightly. UA2 provides the relation between lowest allowed mass and the branching ratio of the leptoquark Exp6a . Assuming branching to first generation, di-electron+ di-jet channel gives GeV, electron++di-jet channel shows GeV and combination of them provides GeV. However, branching to first generation will exclude the mass lower than 74 GeV. DELPHI concludes GeV Exp7a , but their analysis assumes large coupling for leptoquark-lepton-quark . CDF and D0 suggest the mass of leptoquarks to be greater than 113 GeV and 126 GeV Exp8a respectively, on first and second generation of leptoquarks. Several bounds from meson decays, meson-antimeson mixing, lepton flavour violating decays, lepton-quark universality, of muon and electron, neutrino oscillation and other rare processes have been presented in Ref. Rev6a ; Motiv5a ; LQbound1 ; LQbound2 ; pdg . If the leptoquark couples to left handed quarks and leptons of first generation only, then according to pdg pdg for scalar leptoquark and for the vector one where ; however, the constraints change for the second generation as (scalar) and (vector). This analysis is done for leptoquark induced four-fermion interaction. Results from ATLAS and CMS Exp2a ; Exp2b ; Exp3a rule out leptoquarks with mass upto 1500 GeV for first and second generation leptoquarks with 100% branching and 1280 GeV for 50% branching.
In the fig. 2.2, we show the plots for branching fraction against the mass of leptoquark from Tevatron and LHC. In the top left panel, data from D0 has been presented, where the brown (obliquely meshed) region represents the disallowed mass range for leptoquark from LEP experiment and the greenish (horizontally meshed) and bluish (vertically meshed) areas indicate the excluded portions for the mass of first and second generation leptoquarks from two-electron plus two-jet and two-muon plus two-jet channels at D0. The rest three plots are from LHC for three generations of leptoquarks. The continuous black line signify the observed limit whereas the green and yellow areas indicate and regions. The black, blue and red portions with dashed line inside show theoretical predictions with branching to be 100%, 50% and 10% respectively. Nevertheless, all these analyses have been done assuming that one leptoquark couples to quark and lepton from one generation only. The scenario changes drastically if branching for a leptoquark to quarks and leptons of all the generations are kept open.
4 Leptoquark models and simulation
For our purpose, we choose four leptoquarks of different charges from scalar sector and same from the vector sector separately. For every leptoquark scenario, we have studied three different benchmark points (with mass 70 GeV, 650 GeV and 1.5 TeV respectively and different couplings), each of which has been scrutinised at three distinct energy scale (200 GeV, 2 TeV, 3 TeV). The couplings have been picked out in such a way that they lie inside the allowed region, as shown in fig. 2.2. For low mass leptoquark we use the data from D0, which allows around 25% branching to first and second generations of quarks and leptons at GeV. For the heavy leptoquark scenarios, one should look at the graphs from ATLAS and CMS. There is no data for ATLAS beyond the mass range ; similarly CMS probes the mass range for leptoquark to be .
| \hlineB 5 Lepto- | Bench- | |||||||
| quarks | mark | in | ||||||
| points | GeV | |||||||
| , | BP1 | 70 | 0.035 | 0.04 | 0.035 | 0.03 | 0.03 | 0.03 |
| , | BP2 | 650 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 |
| BP3 | 1500 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | |
| , | BP1 | 70 | 0.07 | 0.07 | 0.1 | — | — | — |
| , | BP2 | 650 | 0.07 | 0.07 | 0.1 | — | — | — |
| , | BP3 | 1500 | 0.07 | 0.07 | 0.1 | — | — | — |
| BP1 | 70 | 0.05 | 0.05 | 0.1 | 0.1 | 0.1 | 0.1 | |
| BP2 | 650 | 0.05 | 0.05 | 0.1 | 0.1 | 0.1 | 0.1 | |
| BP3 | 1500 | 0.05 | 0.05 | 0.1 | 0.1 | 0.1 | 0.1 | |
| \hlineB 5 |

[-2mm]![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/f12f5864-d3e8-4677-9e19-1ba92f297c19/x6.png) \belowbaseline[0pt]
\belowbaseline[0pt]![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/f12f5864-d3e8-4677-9e19-1ba92f297c19/x7.png)
[-2mm]![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/f12f5864-d3e8-4677-9e19-1ba92f297c19/x8.png) \belowbaseline[0pt]
\belowbaseline[0pt]![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/f12f5864-d3e8-4677-9e19-1ba92f297c19/x9.png)
[-2mm]![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/f12f5864-d3e8-4677-9e19-1ba92f297c19/x10.png) \belowbaseline[0pt]
\belowbaseline[0pt]![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/f12f5864-d3e8-4677-9e19-1ba92f297c19/x11.png)
[-2mm] \belowbaseline[0pt]
\belowbaseline[0pt]
[-2mm]![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/f12f5864-d3e8-4677-9e19-1ba92f297c19/x13.png) \belowbaseline[0pt]
\belowbaseline[0pt]![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/f12f5864-d3e8-4677-9e19-1ba92f297c19/x14.png)
[-2mm]![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/f12f5864-d3e8-4677-9e19-1ba92f297c19/x15.png) \belowbaseline[0pt]
\belowbaseline[0pt]![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/f12f5864-d3e8-4677-9e19-1ba92f297c19/x16.png)
In the fig. 6, the differential cross-section has been delineated against the cosine of the angle between initial state electron and the leptoquark (or equivalently, the angle between photon and the quark that is produced associated with the leptoquark) at different centre of momentum energies for various benchmark points. The green (ragged) lines portray the simulated data with hundred bins within the range whereas, the brown (smooth) lines represent the theoretical predictions given by Eq. (10). The plots are

arranged in the order of table LABEL:tab:S1_recons. The left and right plots at the top in BP1 row are for 200 GeV and 2 TeV centre of momentum energies respectively while the third one is for 3 TeV. In BP2 row, the first and second plots are done for 2 TeV and 3 TeV centre of momentum energies respectively. Likewise, for BP3 also the plots for valued 2 TeV and 3 TeV are presented in the left and right panel of the third row. As can be seen, the angular distribution in each graph vanishes at some point except the first one in third row which fails to satisfy the condition described by Eq. 13. The positions of zeros can be verified from the left column ( titled “ or ”) of table LABEL:tab:zeros.
4.2.2 Leptoquark
| \hlineB 5 Bench-mark points | in TeV | Cut | Signal | Back-ground | Signi-ficance |
| BP1 | 0.2 | GeV | 5870.1 | 43725.0 | 26.4 |
| cut1+ | 5549.6 | 32989.8 | 28.3 | ||
| 2 | GeV | 80.3 | 319.4 | 4.0 | |
| cut1+ | 50.9 | 114.2 | 4.0 | ||
| 3 | GeV | 33.6 | 219.8 | 2.1 | |
| cut1+ | 19.4 | 44.2 | 2.4 | ||
| BP2 | 2 | GeV | 27.0 | 2003.6 | 0.6 |
| cut1+ | 20.8 | 129.1 | 1.7 | ||
| 3 | GeV | 11.99 | 1660.7 | 0.3 | |
| cut1+ | 10.8 | 167.5 | 0.8 | ||
| BP3 | 2 | GeV | 19.4 | 1061.6 | 0.6 |
| cut1+ | 13.8 | 391.5 | 0.7 | ||
| 3 | GeV | 7.6 | 815.0 | 0.3 | |
| cut1+ | 7.2 | 254.7 | 0.4 | ||
| \hlineB 5 |
The signal-background analysis for with luminosity of 100 fb-1 has been rendered in table 7. For BP1, the cut on invariant mass of lepton-jet pair shows significances of , and respectively, at three different values of centre of momentum energy;

after applying the angular cuts, as described in case of , the significances become , and respectively. In case of BP2, only significances of and are achieved by cut1 at 2 TeV and 3 TeV centre of momentum energies respectively, which increase to and respectively after implementation of the angular cut . For BP3 with 2 TeV energy, the significances reached by the two cuts are and and the same for 3 TeV energy are and respectively. It should be noticed that the significances are quite low in case of compared to especially with BP2 and BP3, and hence escalation in luminosity is essential for amelioration of the statistics.
Angular distributions for this case have been limned in fig. 7 where the brown (even) and green (uneven) lines signify the theoretical estimates and simulated data respectively. The plots are arranged in the same order as of table 7. It can be observed that the distribution in every graph comes to zero at some point of phase space. The positions of zeros can be verified from the right column ( titled “ or ”) of table LABEL:tab:zeros.
4.2.3 Leptoquark
The PYTHIA analysis for leptoquark has been presented in table 8. The cut on provides significances of , and for the signal events at three centre of momentum energies in case of BP1 which change to , and respectively after using suitable angular cuts on . For BP2, signal events are produced with significances and at 2 TeV and 3 TeV centre of momentum energies respectively, any they get increased to and after applying the angular cut as . For BP3 at 2 TeV, the significances become and after implementation of the two cuts and the same become and respectively for 3 TeV.
The fig. 8 describes the differential distribution with respect to the cosine of angle between leptoquark and initial state electron in this scenario. The plots are arranged in the order of table 8. As the earlier cases the green (jagged) and brown (smooth) lines indicate the simulated data with 100 bins and the theoretical expectation for various benchmark points at different centre of momentum energy respectively. Unlike the other two cases, the angular distributions never vanish inside the physical region since this leptoquark does not satisfy Eq. (14).

| \hlineB 5 Bench-mark points | in TeV | Cut | Signal | Back-ground | Signi-ficance |
| BP1 | 0.2 | GeV | 24719.2 | 43725.0 | 94.5 |
| cut1+ | 23448.8 | 32989.8 | 98.7 | ||
| 2 | GeV | 365.7 | 319.4 | 13.9 | |
| cut1+ | 251.7 | 114.2 | 13.2 | ||
| 3 | GeV | 148.9 | 219.8 | 7.8 | |
| cut1+ | 96.2 | 44.2 | 8.1 | ||
| BP2 | 2 | GeV | 757.4 | 2003.6 | 14.4 |
| cut1+ | 585.5 | 129.1 | 21.9 | ||
| 3 | GeV | 362.6 | 1660.7 | 8.1 | |
| cut1+ | 329.5 | 167.5 | 14.8 | ||
| BP3 | 2 | GeV | 440.9 | 1061.6 | 11.4 |
| cut1+ | 311.2 | 391.5 | 11.7 | ||
| 3 | GeV | 187.8 | 815.0 | 5.9 | |
| cut1+ | 180.0 | 254.7 | 8.6 | ||
| \hlineB 5 |
4.2.4 Leptoquarks
The signal-background analysis for with luminosity of has been rendered in table 9. For BP1, the cut on invariant mass of lepton-jet pair shows significances of , and at centre of momentum energies to be 200 GeV, 2 TeV and 3 TeV respectively. The angular cuts modify these significances to become , and respectively. In case of BP2, the significances achieved by cut1 at 2 TeV and 3 TeV centre of momentum energies are and only, which increase to and respectively after implementation of the angular cut . For BP3 with 2 TeV energy, the significances reached by the two cuts are and respectively, which change to and at to be 3 TeV. In this case also the significances are quite low compared to especially with BP2 and BP3. Increase in luminosity is needed for improvement of the statistics.
| \hlineB 5 Bench-mark points | in TeV | Cut | Signal | Back-ground | Signi-ficance |
| BP1 | 0.2 | GeV | 8237.3 | 43725.0 | 36.1 |
| cut1+ | 7812.9 | 32989.8 | 38.7 | ||
| 2 | GeV | 132.7 | 319.4 | 6.2 | |
| cut1+ | 99.3 | 114.2 | 6.8 | ||
| 3 | GeV | 53.6 | 219.8 | 3.2 | |
| cut1+ | 38.0 | 44.2 | 4.2 | ||
| BP2 | 2 | GeV | 40.4 | 2003.6 | 0.9 |
| cut1+ | 31.4 | 129.1 | 2.5 | ||
| 3 | GeV | 21.2 | 1660.7 | 0.5 | |
| cut1+ | 19.6 | 167.5 | 1.4 | ||
| BP3 | 2 | GeV | 20.4 | 1061.6 | 0.6 |
| cut1+ | 14.4 | 391.5 | 0.7 | ||
| 3 | GeV | 9.7 | 815.0 | 0.3 | |
| cut1+ | 9.3 | 254.7 | 0.6 | ||
| \hlineB 5 |
Fig. 9 shows the comparison between theoretical expectation and PYTHIA simulated data for for the production of . The plots are arranged in the order of table 9. As the earlier cases the green (uneven) and brown (even) lines indicate the simulated data with 100 bins and the theoretical expectation for various benchmark points at different centre of momentum energy respectively. In this case also no zero of differential distribution in any of the diagrams is found since its charge is smaller than unit.

4.3 Vector leptoquarks
4.3.1 Leptoquark
| \hlineB 5 Bench-mark points | in TeV | Cut | Signal | Back-ground | Signi-ficance |
| BP1 | 0.2 | GeV | 10399.3 | 43725.0 | 44.7 |
| cut1+ | 9700.3 | 32989.8 | 46.9 | ||
| 2 | GeV | 14666.5 | 319.4 | 119.8 | |
| cut1+ | 9555.0 | 114.2 | 97.17 | ||
| 3 | GeV | 14799.6 | 219.8 | 120.8 | |
| cut1+ | 8736.1 | 44.2 | 93.2 | ||
| BP2 | 2 | GeV | 443.3 | 2003.6 | 9.0 |
| cut1+ | 337.5 | 129.1 | 15.6 | ||
| 3 | GeV | 530.0 | 1660.7 | 11.3 | |
| cut1+ | 483.7 | 167.5 | 19.0 | ||
| BP3 | 2 | GeV | 144.4 | 1061.6 | 4.2 |
| cut1+ | 102.2 | 391.5 | 4.6 | ||
| 3 | GeV | 63.9 | 815.0 | 2.2 | |
| cut1+ | 60.7 | 254.7 | 3.4 | ||
| \hlineB 5 |
In table 10, we summarise the signal background analysis for the vector singlet leptoquark . For BP1 at 200 GeV, the invariant mass cut of 10 GeV gives significance and further application of the angular cut of changes it to . For BP1 at centre of momentum energies to be 2 TeV and 3 TeV, the significances after the first cut are and respectively. In these cases, the signal events after the first cut are so large in number relative to the background events that the angular cut becomes obsolete. In case of BP2, the cut on produce signal events with significances and for the two values of , which get enhanced to and respectively after constraining the angle within the limit . For BP3 at TeV, the angular cut increases the significance to from . Likewise, for BP3 at TeV, the angular cut increases the significance to from .

Angular distribution for this case has been limned in fig. 10 where the brown (smooth) and green (ragged) lines signify the theoretical estimates and simulated data respectively. The plots are arranged in terms of benchmark points and centre of momentum energy according to the table 10. All the curves show zero certainly at some points of phase space which matches with the right column of table LABEL:tab:zeros.
4.3.2 Leptoquark
| \hlineB 5 Bench-mark points | in TeV | Cut | Signal | Back-ground | Signi-ficance |
| BP1 | 0.2 | GeV | 294306.3 | 43725.0 | 506.2 |
| cut1+ | 275902.1 | 32989.8 | 496.4 | ||
| 2 | GeV | 399147.0 | 319.4 | 631.5 | |
| cut1+ | 257096.9 | 114.2 | 506.9 | ||
| 3 | GeV | 404429.7 | 219.8 | 635.8 | |
| cut1+ | 238127.0 | 44.2 | 487.9 | ||
| BP2 | 2 | GeV | 1560.1 | 2003.6 | 26.1 |
| cut1+ | 1215.5 | 129.1 | 33.1 | ||
| 3 | GeV | 1920.1 | 1660.7 | 32.1 | |
| cut1+ | 1754.7 | 167.5 | 40.0 | ||
| BP3 | 2 | GeV | 119.3 | 1061.6 | 3.5 |
| cut1+ | 85.5 | 391.5 | 3.9 | ||
| 3 | GeV | 139.1 | 815.0 | 4.5 | |
| cut1+ | 132.4 | 254.7 | 6.7 | ||
| \hlineB 5 |
The signal background analysis for leptoquark has been shown in table 11. For BP1, the significances of leptoquark production is very high (, and ) at all the three values of and angular cuts become almost obsolete. For BP2, the significances after first cut are and which get enhanced to and respectively after the second cut at the two different values of . For BP3 at 2 TeV centre of momentum energy the significances after the two cuts are and respectively. At 3 TeV centre of momentum energy for the same benchmark point, the significances after the two cuts become and respectively.

In fig. 11, we show the angular distribution for the production of leptoquark associated with an antiquark for all the three benchmark points at different centre of momentum energies as described in table 11. As before, the brown (even) and green (uneven) lines signify the theoretical expectations and the PYTHIA simulated data respectively. In this case also, no zero in any of the plots is found.
4.3.3 Leptoquark
| \hlineB 5 Bench-mark points | in TeV | Cut | Signal | Back-ground | Signi-ficance |
| BP1 | 0.2 | GeV | 102107.7 | 43725.0 | 267.4 |
| cut1+ | 96573.2 | 32989.8 | 268.3 | ||
| 2 | GeV | 17380.0 | 319.4 | 130.6 | |
| cut1+ | 11072.0 | 114.2 | 104.7 | ||
| 3 | GeV | 16809.0 | 219.8 | 128.8 | |
| cut1+ | 9738.8 | 44.2 | 98.5 | ||
| BP2 | 2 | GeV | 236.5 | 2003.6 | 5.0 |
| cut1+ | 179.6 | 129.1 | 10.2 | ||
| 3 | GeV | 117.5 | 1660.7 | 2.8 | |
| cut1+ | 105.7 | 167.5 | 6.4 | ||
| BP3 | 2 | GeV | 154.1 | 1061.6 | 4.4 |
| cut1+ | 109.6 | 391.5 | 4.9 | ||
| 3 | GeV | 62.5 | 815.0 | 2.1 | |
| cut1+ | 60.1 | 254.7 | 3.4 | ||
| \hlineB 5 |
Table 12 summarises the reconstruction of leptoquark at 100 fb-1 luminosity. In this case also the significance for production of the leptoquark is quite high after the first cut for BP1 (, and respectively) and hence the second cuts become unimportant. For BP2, the significances after the invariant mass cut are and which get improved to and respectively after the angular cut for 2 TeV and 3 TeV centre of momentum energies respectively. For BP3 at 2 TeV, the significance goes to from after implementing the angular cut of . For 3 TeV the corresponding change in significance is from to .
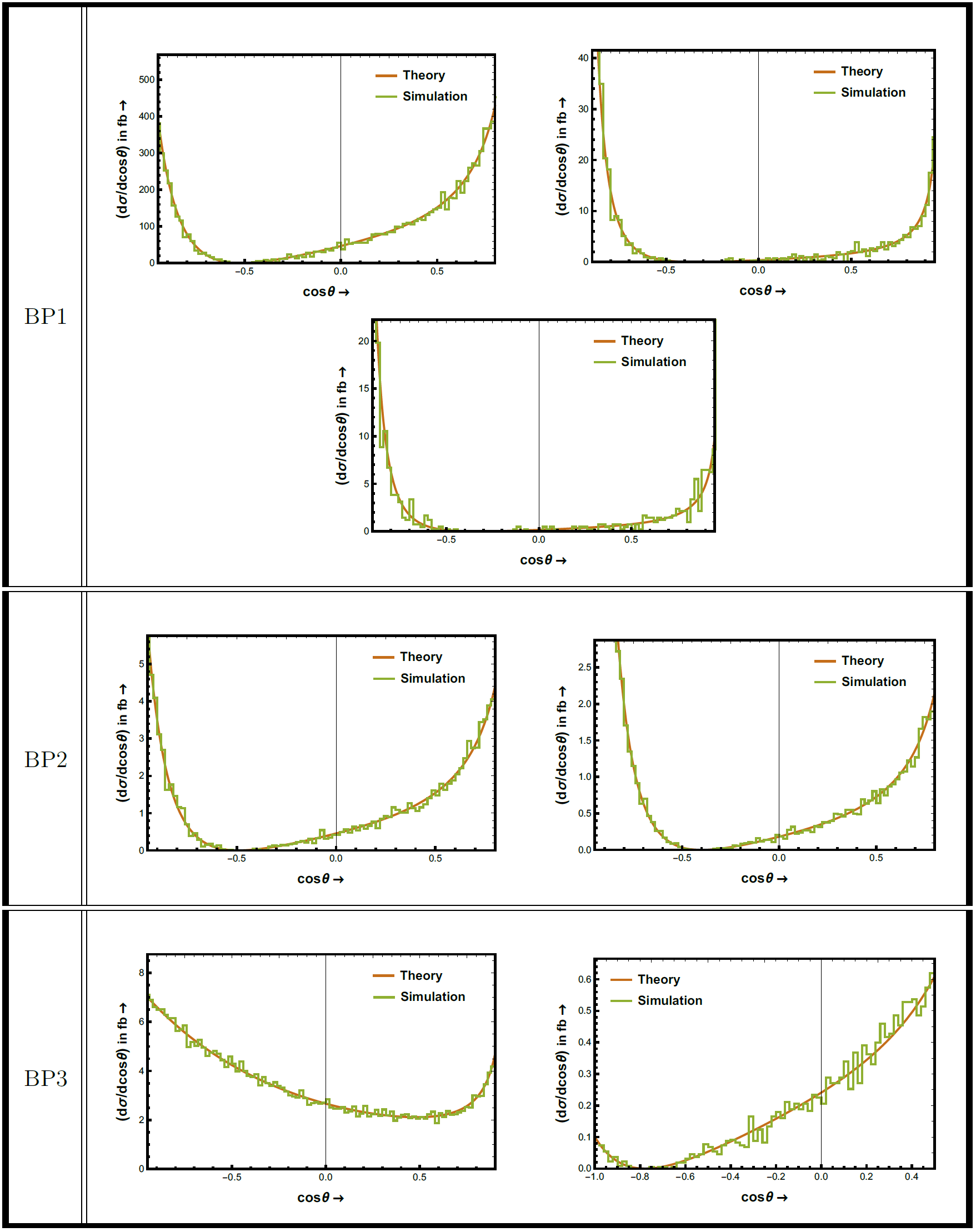
In fig. 12, we show the differential distribution for the production of this leptoquark. We ordered the graphs in the same way as in table 12. The brown (smooth) and green (coarse) lines signify the theoretical estimates and the simulated data respectively. As expected the distributions at different centre of momentum energies for various benchmark points go to zero at different points of phase space except the plot at the left panel in third row. The positions of zeros can be verified from the left column ( titled “ or ”) of table LABEL:tab:zeros.
4.3.4 Leptoquark
| \hlineB 5 Bench-mark points | in TeV | Cut | Signal | Back-ground | Signi-ficance |
| BP1 | 0.2 | GeV | 402140.1 | 43725.0 | 602.2 |
| cut1+ | 376284.9 | 32989.8 | 588.2 | ||
| 2 | GeV | 421151.4 | 319.4 | 648.7 | |
| cut1+ | 268692.3 | 114.2 | 518.2 | ||
| 3 | GeV | 421146.5 | 219.8 | 648.8 | |
| cut1+ | 247085.8 | 44.2 | 497.0 | ||
| BP2 | 2 | GeV | 1038.7 | 2003.6 | 18.8 |
| cut1+ | 814.4 | 129.1 | 26.5 | ||
| 3 | GeV | 1110.4 | 1660.7 | 21.1 | |
| cut1+ | 1014.0 | 167.5 | 29.5 | ||
| BP3 | 2 | GeV | 162.4 | 1061.6 | 4.6 |
| cut1+ | 115.5 | 391.5 | 5.1 | ||
| 3 | GeV | 119.3 | 815.0 | 3.9 | |
| cut1+ | 113.9 | 254.7 | 5.9 | ||
| \hlineB 5 |
We present the PYTHIA analysis for leptoquark in table 13 with a luminosity of 100 fb-1. By putting a cut on the invariant mass of lepton jet pair, we get the signals with very high significances (, and ) in case of BP1 for all the three centre of momentum energies. The angular cut in this case becomes inessential. The leptoquark for

BP2 can be reconstructed with the significances and at to be 2 TeV and 3 TeV respectively. Using the angular cut, the significances can be upgraded to and respectively. For BP3 at 2 TeV, the cut of 10 GeV on around the mass of leptoquark provides significance for the signal events whereas the angular cut of enhances it to . For same benchmark point at 3 TeV, significance for the signal events goes to from after applying the angular cut of .
In fig. 13, we show the angular distribution for the production of leptoquark associated with a -quark for all the three bench mark points at different centre of momentum energies. The brown (even) and green (uneven) lines signify the theoretical expectations and the PYTHIA simulated data respectively. In this case also, no zero in any of the distributions is found.
5 Effects of non-monochromatic photons
All of our simulations until this point were performed with monochromatic photon beams. However, the experimental collider technology developed so far cannot deal with monochromatic photons in the initial state. Rather the photons used in modern colliders have some energy distribution. The two ways for the production of these high energetic photons, we are going to discuss, are: laser backscattering and quasi-real photons emitted by fast charged leptons. For the second process one can use protons instead of leptons too but it would make the environment messier due to presence of strongly interacting particle in initial state and therefore, we would stick to leptons only for our purpose of discussion.
In case of laser backscattering, a laser beam interacts with high energy electrons or positrons and thus highly photons produced in the backward direction due to Compton scattering. This facility will be available in linear colliders like CLIC clic , ILC ilc etc. This option for photon is there in ClacHEP, but not in MadGraph mad . The distribution of photon in this case is given by EPhC3b :
| (15) |
where, is the fraction of energy for backscattered photon relative to the energy of parent charged lepton, the maximum value of is which can also be written as , the constant with and being electric charge and mass of positron respectively and the total cross-section for Compton scattering is given by:
| (16) |
If laser and positron with energies and collide at a small angle for the backscattering, then the quantity is defined as . However, the value of is taken as 4.82 in CalcHEP.
On the other hand, any fast moving charged particle can be considered as an electromagnetic radiation field by equivalent photon approximation (EPA) EPA1 ; EPA2 ; EPA3 . This radiation can be interpreted as a flux of quasi-real photons with some energy distribution. Following Williams-Weizsäcker approximation, this distribution can be taken as:
| (17) |
where, is the fraction of energy for the quasi-real photon with respect to that of the positron, is electromagnetic coupling constant, the minimum value for is which can be expressed as and the maximum value for is that signifies the region for photon virtuality. It should kept in mind that the four momentum of quasi-real photon is denoted by in lab frame. This scheme is available in both MadGraph and ClacHEP.
To visualise the effects of non-monochromatic photons on the zeros of angular distribution for the production of leptoquark associated with a quark (or anti-quark) at - collider, we pick four different scenarios, one from each of the leptoquark models having the zero inside physical region. Two of them are taken from lower energy and mass region and rest two are taken from higher energy and mass region. These four scenarios are as follows: a) BP1 for at TeV, b) BP2 for at TeV c) BP3 for at TeV and d) BP1 for at TeV. The signal background analysis and the cross-section for production of leptoquarks in these four cases with laser backscattering and EPA has been presented in tables 14 and 15 respectively. It can easily be seen from these tables that the production cross-section,signal event and the significance get enhanced to a great extent by laser backscattering compared to monochromatic photon beams whereas EPA scheme diminishes them notably. The increments in significances under laser backscattering for the above four scenarios are 83%, 47%, 11% and 40%, respectively, whereas under EPA, the significances reduce by 27%, 65%, 91% and 51%, respectively, for those cases. The production cross-section and signal event for laser backscattering are slightly lower than that of monochromatic case in only BP3 scenario for at TeV. This occurs because of phase space suppression for low energy photons due to heavy mass of leptoquark in BP3 scenario.
| \hlineB 5 Photon | Cross-section in fb | |||
| , BP1 TeV | , BP2 TeV | , BP3 TeV | , BP1 TeV | |
| Laser back- scattering | 688.20 | 4.87 | 11.11 | 3337.54 |
| EPA | 101.42 | 0.81 | 0.40 | 486.94 |
| Monochromatic | 430.24 | 2.89 | 14.84 | 2127.02 |
| \hlineB 5 | ||||
| \hlineB 5 Model | Bench-mark points | in TeV | Photon | Cut | Signal | Back-ground | Signi- ficance |
| \hlineB 5 | BP1 | 0.2 | Laser Back- | cut1 | 18518.7 | 36417.9 | 79.0 |
| scattering | cut1+cut2 | 17499.5 | 18173.8 | 92.65 | |||
| EPA | cut1 | 2863.6 | 1964.4 | 41.2 | |||
| cut1+cut2 | 2051.6 | 1038.2 | 36.9 | ||||
| mono- | cut1 | 11133.6 | 43725.0 | 47.5 | |||
| chromatic | cut1+cut2 | 10537.8 | 32989.8 | 50.5 | |||
| BP2 | 2 | Laser Back- | cut1 | 62.7 | 2078.4 | 1.4 | |
| scattering | cut1+cut2 | 48.1 | 326.1 | 2.5 | |||
| EPA | cut1 | 11.7 | 390.2 | 0.6 | |||
| cut1+cut2 | 7.0 | 230.8 | 0.5 | ||||
| mono- | cut1 | 27.0 | 2003.6 | 0.6 | |||
| chromatic | cut1+cut2 | 20.8 | 129.1 | 1.7 | |||
| BP3 | 2 | Laser Back- | cut1 | 131.8 | 446.3 | 5.5 | |
| scattering | cut1+cut2 | 93.4 | 246.0 | 5.1 | |||
| EPA | cut1 | 4.5 | 86.1 | 0.5 | |||
| cut1+cut2 | 3.5 | 79.7 | 0.4 | ||||
| mono- | cut1 | 144.4 | 1061.6 | 4.2 | |||
| chromatic | cut1+cut2 | 102.2 | 391.5 | 4.6 | |||
| BP1 | 0.2 | Laser Back- | cut1 | 168135.3 | 36417.9 | 371.8 | |
| scattering | cut1+cut2 | 157708.8 | 18173.8 | 376.0 | |||
| EPA | cut1 | 24697.2 | 1964.4 | 151.3 | |||
| cut1+cut2 | 17881.0 | 1038.2 | 130.0 | ||||
| mono- | cut1 | 102107.7 | 43725.0 | 267.4 | |||
| chromatic | cut1+cut2 | 96573.2 | 32989.8 | 268.3 | |||
| \hlineB 5 |
The weighted differential distributions () for the production of in BP1 scenario at TeV for laser backscattering, EPA and monochromatic photons, which are represented by orange, blue and green line respectively, are shown in the left panel of fig. 14. As expected, the three distributions do not coincide. Still laser backscattering looks optimistic since it preserves the zero of angular distribution (though slightly deviated from the monochromatic case). The slight shift of zero in this case is due to variation in at each collision causing from the distribution of photon energy. But in the EPA scheme, the zero gets smeared off. The reason behind this smearing effect lies in the distribution for transverse momentum of photons which is depicted in right panel of fig. 14. Although most of the photons in EPA have small , there is a non-zero possibility for them to acquire very high too. As can be seen from the right panel of fig. 14, the highest achieved by photons from 100 GeV positron under EPA is around 90 GeV. Due to this non-zero the direction of photons changes in case of each collision and hence and no longer move collinearly in opposite directions.


Another important point to mention is that here we have presented the angular distribution for all the cases in terms of angle between electron and leptoquark; however, one can use the distribution in terms of angle between photon and leptoquark too. In the case of monochromatic photons, the system lies in centre of momentum frame and the two angles mentioned above are supplementary to each other; hence the distributions with respect to them are equivalent apart from a negative sign. For laser backscattering, the system no longer lies in centre of momentum frame due to varying energy of photons; however the above-mentioned two angles still remain supplementary to each other since all the photons are found with zero only and therefore, the two distributions look quite similar discarding the negative sign. But in EPA scenario, neither the system lies in centre of momentum frame nor the angle between photon-leptoquark and electron-leptoquark remain supplementary as well; hence the angular distributions with respect to these two angles disagree conspicuously. Talking in terms of zeros of angular distributions, the situations are worse while considering angle between photon and leptoquark under EPA. Similar kind of things happen for other leptoquark models with different benchmark point and centre of momentum energy also.
6 Conclusion
In conclusion, we have studied zeros of single photon tree-level amplitude at the - collider producing a leptoquark associated with a quark (or antiquark). Unlike other colliders, we find that the position of zeros of single photon tree-level amplitude in this case does depend on the centre of momentum energy as well as the mass and charge of leptoquark. The cosine of angle between leptoquark and initial state electron, at which zero of the angular distribution happens, approaches asymptotically depending on the charge of the produced leptoquark for very high value of with respect to the mass of leptoquark. No zero in the differential distribution can be found for leptoquarks having charges smaller than -1 unit. In a PYTHIA based analysis we look for both light and heavy leptoquarks at both low and high energy scales. Light leptoquarks having small couplings to quarks and leptons of all generation is not completely ruled out by Tevatron. In our simulation, we reconstruct the leptoquark from the lepton-jet pair and then study the differential distribution against the cosine of the angle between it and the initial state electron which matches with the theoretical expectation. We have also studied the consequences of using non-monochromatic photons for the production of leptoquarks at electron-photon colliders. The production cross-section and significance increase notably under laser backscattering and decrease terribly under equivalent photon approximation. It turns out that non-zero transverse momentum of photons smears off the zeros of angular distributions completely in equivalent photon approximation whereas laser backscattering preserves them (though slightly deviated from the monochromatic case) since all the photons here move only in the direction opposite to electron. It seems that laser backscattering is very promising for investigating the production of leptoquarks at - collider by means of zeros of differential distribution.
7 Acknowledgement
The authors thank Abhay Deshpande, Yoshitaka Kuno, Saurabh Sandilya and Vishal Bhardwaj for some useful discussions. The authors also thank Alexander Pukhov and Olivier Mattelaer for private communications. PB and AK also thank SERB India, grant no: CRG/2018/004971 for the financial support.
References
- (1) Jogesh C. Pati and Abdus Salam, Lepton number as the fourth “color”, Phys. Rev. D 10 (1974) 275
- (2) H. Georgi and S.L. Glashow, Unity of all elementary – particle forces, Phys. Rev. Lett. 32 (1974) 438.
- (3) H. Georgi, The state of art – gauge theories, AIP Conf. Proc. 23, (1975) 575;
- (4) H. Fritzsch and P. Minkowski, Unified interactions of leptons and hadrons, Ann. Phys. 93 (1975) 193.
- (5) E. Farhi and L. Susskind, Technicolour, Phys. Reports 74 (1981) 277.
- (6) K. Lane and M. Ramana, Walking technicolor signatures at hadron colliders, Phys. Rev. D44 (1991) 2678.
- (7) W. Buchmüller, R. Rückl, D. Wyler, Leptoquarks in Lepton-Quark Collisions, Phys. Lett. B 191 (1987) 442-448.
- (8) J. Blümlein and R. Rückl, Production of scalar and vector leptoquarks in annihilation, Phys. Lett. B 304 (1993) 337-346.
- (9) I. Doršner, S. Fajfer, A. Greljo, J.F. Kamenik, N. Košnik, Physics of leptoquarks in precision experiments and at particle colliders, Phys. Rept. 641 (2016).
- (10) Alexander Belyaev, Claude Leroy, Rashid Mehdiyev, Alexander Pukhov, Leptoquark Single and Pair production at LHC with CalcHEP/CompHEP in the complete model, JHEP 0509 (2005) 005.
- (11) Miriam Leurer, A Comprehensive Study of Leptoquark Bounds, Phys. Rev. D 49 (1994) 333-342.
- (12) Sacha Davidson, David Bailey, Bruce A. Campbell, Model independent constraints on leptoquarks from rare processes, Z. Phys. C 61, 613-644 (1994).
- (13) J. P. Lees et al. [BaBar Collaboration], Evidence for an excess of , Phys. Rev. Lett. 109 (2012) 101802.
- (14) A. Matyja et al. [Belle Collaboration], Observation of decay at Belle Phys. Rev. Lett. 99 (2007) 191807.
- (15) R. Aaij et al. [LHCb Collaboration], Measurement of the ratio of branching fractions , Phys. Rev. Lett. 115 (2015) 111803.
- (16) R. Aaij et al. [LHCb Collaboration], Test of lepton universality using Phys. Rev. Lett. 113 (2014) 151601.
- (17) R. Aaij et al. [LHCb Collaboration], Angular analysis of the decay using 3 fb-1 of integrated luminosity, JHEP 1602 (2016) 104.
- (18) G. W. Bennett et al. [Muon g-2 Collaboration], Measurement of the negative muon anomalous magnetic moment to 0.7 ppm, Phys. Rev. Lett. 92 (2004) 161802.
- (19) G. W. Bennett et al. [Muon g-2 Collaboration], Final report of the E821 muon anomalous magnetic moment measurement at BNL, Phys. Rev. D 73 (2006) 072003.
- (20) V. Khachatryan et al. [CMS Collaboration], Search for lepton-flavour-violating decays of the Higgs boson, Phys. Lett. B 749 (2015) 337.
- (21) Nejc Košnik, Damir Bečirević, Ilja Doršner, Svjetlana Fajfer, Darius A. Faroughy, Olcyr Sumensari, Ultraviolet Complete Leptoquark Scenario Addressing the B Physics Anomalies, Springer Proc. Phys. 234 (2019) 425-430.
- (22) Ilja Doršner, Svjetlana Fajfer, Olcyr Sumensari, Muon g-2 and scalar leptoquark mixing, arXiv:1910.03877 [hep-ph].
- (23) Damir Bečirević, Ilja Doršner, Svjetlana Fajfer, Nejc Košnik, Darius A. Faroughy, Olcyr Sumensari, Scalar leptoquarks from grand unified theories to accommodate the B-physics anomalies, Phys. Rev. D 98 (2018) no.5, 055003.
- (24) Damir Bečirević, Svjetlana Fajfer, Nejc Košnik, Olcyr Sumensari, Leptoquark model to explain the -physics anomalies, and , Phys. Rev. D 94 (2016) no.11, 115021.
- (25) Svjetlana Fajfer, Nejc Košnik, Vector leptoquark resolution of and puzzles, Phys. Lett. B 755 (2016) 270-274.
- (26) Ilja Doršner, Svjetlana Fajfer, Nejc Košnik, Leptoquark mechanism of neutrino masses within the grand unification framework, Eur. Phys.J. C 77 (2017) no.6, 417.
- (27) S. Fajfer, N. Košnik, L. Vale Silva, Footprints of leptoquarks: from to , Eur. Phys. J. C 78 (2018) no.4, 275.
- (28) Priyotosh Bandyopadhyay and Rusa Mandal, Vacuum stability in an extended standard model with a leptoquark, Phys. Rev. D95 (2017) no.3, 035007.
- (29) Ufuk Aydemir, Tanumoy Mandal and Subhadip Mitra, Addressing the anomalies with an leptoquark from SO(10) grand unification, Phys. Rev. D 101 (2020) no.1, 015011.
- (30) Suchismita Sahoo, Rukmani Mohanta and Anjan K. Giri, Explaining the and anomalies with vector leptoquarks, Phys. Rev. D 95 (2017) no.3, 035027.
- (31) Suchismita Sahoo and Rukmani Mohanta, Impact of vector leptoquark on anomalies, J. Phys. G 45 (2018) no.8, 085003.
- (32) Suchismita Sahoo and Rukmani Mohanta, Study of the rare semileptonic decays in scalar leptoquark model, Phys. Rev. D93 (2016) no.3, 034018.
- (33) Murugeswaran Duraisamy, Suchismita Sahoo and Rukmani Mohanta,Rare semileptonic decay in vector leptoquark model, Phys. Rev. D 95 (2017) no.3, 035022.
- (34) Suchismita Sahoo and Rukmani Mohanta, Effects of scalar leptoquark on semileptonic decays, New J. Phys. 18 (2016) no.9, 093051.
- (35) Rukmani Mohanta, Effects of scalar leptoquarks on the decays of meson, Phys. Rev. D 89 (2014) no.1, 014020.
- (36) Martin Bauer, Matthias Neubert, Minimal Leptoquark Explanation for the , , and Anomalies, Phys. Rev. Lett. 116 (2016) no.14, 141802.
- (37) Riccardo Barbieri, Christopher W. Murphy, Fabrizio Senia, B-decay anomalies in a composite leptoquark model, Eur. Phys. J. C 77 (2017) no.1, 8.
- (38) N.G. Deshpande and B. Dutta, Leptoquark explanation of HERA anomaly in the context of gauge unification, Phys. Lett. B 424 (1998) 313-321.
- (39) Dario Buttazzo, Admir Greljo, Gino Isidoria and David Marzoccaa, B-physics anomalies: a guide to combined explanations, JHEP 11 (2017) 044.
- (40) Kingman Cheung, Muon anomalous magnetic moment and leptoquark solutions, Phys. Rev. D 64, 033001 (2001).
- (41) D. Das, K. Ghosh, M. Mitra, S. Mandal, Probing sterile neutrinos in the framework of inverse seesaw mechanism through leptoquark productions, Phys. Rev. D 97 (2018) 015024.
- (42) Tanumoy Mandal, Subhadip Mitra and Swapnil Raz, motivated leptoquark scenarios: impact of interference on the exclusion limits from LHC data, Phys. Rev. D 99 (2019) no.5, 055028.
- (43) N. Assad, B. Fornal, B. Grinstein, Baryon number and Lepton universality violation in leptoquark and diquark models, Phys. Lett. B 777 (2018) 324-331.
- (44) B. Fornal, S. A. Gadam, B. Grinstein, Left-right SU(4) vector leptoquark model for flavor anomalies, Phys. Rev. D 99 (2019) 055025.
- (45) E. C. Leskow, G. D’Ambrosio, A. Crivellin and D. Müller, , lepton flavor violation, and Z decays with leptoquarks: correlations and future prospects, Phys. Rev. D 95 (2017) 055018.
- (46) A. Crivellin, D. Müller, T. Ota, Simultaneous explanation of and : the last scalar leptoquarks standing, JHEP 1709 (2017) 040.
- (47) A. Crivellin, D. Müller, F. Saturnino, Flavour phenomenology of the leptoquark singlet-triplet model, arXiv: 1912.04224[hep-ph].
- (48) L. Calibbi, A. Crivellin, T. Li, Model of vector leptoquarks in view of B-physics anomalies, Phys. Rev. D 98 (2018) no. 11, 115002.
- (49) A. Crivellin, C. Greub, D. Müller, F. Saturnino, Importance of loop effects in explaining the accumulated evidence for new physics in B decays with a vector leptoquark, Phys. Rev. Lett. 122 (2019) no. 1, 011805.
- (50) J. Aebischer, A. Crivellin, C. Greub, QCD improved matching for semileptonic B decays with leptoquarks, Phys. Rev. D 99 (2019) no. 5, 055002.
- (51) Rusa Mandal, Fermionic dark matter in leptoquark portal, Eur. Phys. J. C 78 (2018) 726.
- (52) Wei-Shu Hou, Tanmoy Modak, Gwo-Guang Wong, Scalar leptoquark effects on decay, Eur. Phys. J C 79 (2019) 964.
- (53) Claudia Cornella, Javier Fuentes-Martin, Gino Isidori,Revisiting the vector leptoquark explanation of the B-physics anomalies, JHEP 07 (2019) 168.
- (54) Priyotosh Bandyopadhyay and Rusa Mandal, Revisiting scalar leptoquark at the LHC, Eur. Phys. J. C 78 (2018) 491.
- (55) Arvind Bhaskar, Debottam Das, Bibhabasu De and Subhadip Mitra, Enhancement of Higgs Production Through Leptoquarks at the LHC, arXiv:2002.12571 [hep-ph].
- (56) Kushagra Chandak, Tanumoy Mandal, Subhadip Mitra, Hunting for scalar leptoquarks with boosted tops and light leptons, Phys. Rev. D 100 (2019) no.7, 075019.
- (57) Tanumoy Mandal, Subhadip Mitra, Satyajit Seth, Single Productions of Colored Particles at the LHC: An Example with Scalar Leptoquarks, JHEP 1507 (2015) 028.
- (58) A. Alves, O. J. P. Éboli, G. G. di Cortona, R. R. Moreira, Indirect and monojet constraints on scalar leptoquarks, Phys. Rev. D 99 (2019) 095005.
- (59) Ilja Doršner, Svjetlana Fajfer, Monalisa Patra, A comparative study of the and leptoquark effects in the light quark regime, Eur. Phys. J. C 80 (2020) no.3, 204.
- (60) Rusa Mandal, Antonio Pich, Constraints on scalar leptoquarks from lepton and kaon physics, JHEP 1912 (2019) 089.
- (61) S. Mandal, M. Mitra, N. Sinha, Probing leptoquark and heavy neutrino at LHeC, Phys. Rev. D 98 (2018) 095004.
- (62) R. Padhan, S. Mandal, M. Mitra, N. Sinha, Signatures of class of leptoquarks at upcoming colliders, arXiv:1912.07236[hep-ph].
- (63) Sacha Davidson, Sebastien Descotes-Genon, Minimal flavour violation for leptoquarks, JHEP 11 (2010) 073.
- (64) Javier Fuentes-Martin, Gino Isidori, Matthias König, Nudzeim Selimović, Vector leptoquarks beyond tree level, Phys. Rev. D 101 (2020) no. 3, 035024.
- (65) Michael J. Baker, Javier Fuentes-Martin, Gino Isidori, Matthias König, High-signatures in vector–leptoquark models, Eur. Phys. J. C 79 (2019) no. 4, 334.
- (66) Gautam Bhattacharyya, John R. Ellis, K. Sridhar, Bounds on the masses and couplings of leptoquarks from leptonic partial widths of the Z, Phys. Lett. B 336 (1994) 100-106.
- (67) J. L. Hewett and T. G. Rizzo, Leptoquark-boson signals at colliders, Phys. Rev. D 36 (1987) 3367.
- (68) T. Plehn, H. Spiesberger, M. Spira, P.M. Zerwas, Formation and Decay of Scalar Leptoquarks/Squarks in ep collisions, Z. Phys. C 74 (1997) 611-614.
- (69) M. Krämer, T. Plehn, M. Spira, and P. M. Zerwas, Pair Production of Scalar Leptoquarks at the Fermilab Tevatron, Phys. Rev. Lett. 79 (1997) 341-344.
- (70) AMY Collaboration (G.N. Kim et al.), A search for leptoquark and colored lepton pair production in annihilations at TRISTAN, Phys. Lett. B 240 (1990) 243-249.
- (71) G. Alexander et al. [OPAL collaboration], A search for scalar leptoquarks in Z0 deacys, Phys. Lett. B 263 (1991) 123-134.
- (72) B. Adeva et al. [L3 collaboration], search for scalar leptoquarks in Z0 deacys, Phys. Lett. B 261 (1991) 169-176.
- (73) UA2 Collaboration, A search for scalar leptoquarks at the CERN collider, Physics Letters B 274 ( 1992 ) 507-512.
- (74) DELPHI Collaboration, Search for single leptoquark production in collisions up to = 208 GeV with the DELPHI detector, DELPHI 2001-080 CONF 508.
- (75) Kaori Maeshima for the CDF Collaboration, Leptoquark Searches at the Tevatron, FERMILAB-Conf-96, 413-E.
- (76) The ATLAS Collaboration, Search for scalar leptoquarks in collisions at = 13 TeV with the ATLAS experiment, New J. Phys. 18 (2016) 093016.
- (77) The ATLAS Collaboration, Searches for third-generation scalar leptoquarks in = 13 TeV collisions with the ATLAS detector, JHEP 06 (2019) 144.
- (78) The CMS Collaboration, Search for third-generation scalar leptoquarks decaying to a top quark and lepton at = 13 TeV, Eur. Phys. J. C 78 (2018) 707.
- (79) Darin E. Acosta, Susan K. Blessing, Leptoquark Searches at HERA and the Tevatron, Ann. Rev. Nucl. Part. Sci. 49 (1999) 389-434.
- (80) ZEUS Collaboration (S. Chekanov et al.), A Search for resonance decays to lepton + jet at HERA and limits on leptoquarks, Phys. Rev. D 68 (2003) 052004.
- (81) H1 Collaboration, Search for Leptoquark Bosons in ep Collisions at HERA, Phys. Lett. B 629 (2005) 9-19.
- (82) Guoliang Wang, Leptoquark searches at the Tevatron, AIP Conference Proceedings 407, 345 (1997).
- (83) Thomas Nunnemann (on behalf of the D0 Collaboration), Searches for Leptoquark Production at D0, arXiv:0710.0255 [hep-ex].
- (84) K. O. Mikaelian, M. A. Samuel and D. Sahdev, Magnetic moment of weak bosons produced in and collisions, Phys. Rev. Lett. 43 (1979) 746.
- (85) C. J. Goebel, F. Halzen, and J. P. Leveille, Angular zeros of Brown, Mikaelian, Sahdev, and Samuel and the factorization of tree amplitudes in gauge theories, Phys. Rev. D 23 (1981) 2682.
- (86) Zhu Dongpei, Zeros in scattering amplitudes and the structure of non-Abelian gauge theories, Phys. Rev. D 22 (1980) 2266.
- (87) Stanley J. Brodsky and Robert W. Brown, Zeros in amplitudes: gauge theory and radiation interference, Phys. Rev. Lett. 49 (1982) 966.
- (88) K. O. Mikelian, Zeros in energy and angular distributions with real or virtual photons, Phys. Rev. D 25 (1982) 66.
- (89) K. O. Mikelian, Angular distribution of W bosons in hadron hadron , Phys. Rev. D 26 (1982) 1085-1089.
- (90) M. L. Laursen, M. A. Samuel, Achin Sen, Amplitude zeros in collisions and the quark magnetic moment, Phys. Rev. D 26 (1982) 2535.
- (91) M. L. Laursen, M. A. Samuel, Achin Sen, G. Tupper, Do amplitude zeros persists in higher order?, Nucl. Phys. B 226 (1983) 429-436.
- (92) R. W. Brown, K. L. Kowalski, Stanley J. Brodsky, Classical radiation zeros in gauge theory amplitudes, Phys. Rev. D 28 (1983) 624.
- (93) R. W. Robinett, The W magnetic moment in electroweak mixing and the composite models and amplitude zeros in , Phys. Rev. D 28 (1983) 1185.
- (94) G. Passarino, Physical null zones and radiation representation, Nucl. Phys. B 224 (1983) 265-288.
- (95) M. A. Samuel, Amplitude zeros, Phys. Rev. D 27 (1983) 2724-2731.
- (96) M. L. Laursen, M. A. Samuel, A. Sen, On the spoiling of amplitude (radiation) zeros at the one loop level and infrared finiteness, Phys. Rev. D 28 (1983) 650.
- (97) M. L. Laursen, M. A. Samuel, A. Sen, Radiation zeros and a test for the values of the lepton, Phys. Rev. D 29 (1984) 2652-2654.
- (98) K. Hagiwara, F. Halzen, F. Herzog, Jets in collisions: radiation zeros and the electric charges of coloured quarks, Phys. Lett. B 135 (1984), 324
- (99) Mark A. Samuel, Achin Sen, Garrett S. Sylvester, M. L. Laursen, General criteria for radiation amplitude zeros, Phys. Rev. D 29 (1984) 994.
- (100) G. Passarino, Radiation zeros and gravity, Nucl. Phys. B 241 (1984) 48-60.
- (101) R. W. Robinett, A class of supersymmetric radiation zeros, Phys. Rev. D 30 (1984) 688.
- (102) R. W. Brown, K. Kowalski, Szeros, Phys. Lett B 144 (1984) 235-239.
- (103) R. W. Brown, Understanding something about nothing: radiation zeros, AIP. Conf. Proc. 350 (1995) 261-272.
- (104) J. D. Stroughair, C. L. Bilachak, The determiantion of the W anomalous magnetic moment in , Z. Phys. C 29 (1984) 415-419.
- (105) J. H. Reid, A. Sen, On the factorization of collinear and infrared singularities in qcd corrections to the Mikaelian zero, Prog. Theor. Phys. 75 (1986) 98.
- (106) J. H. Reid, G. Tupper, M. van Zijl, A study of the amplitude zero in using the Lund Model, Phys. Lett. B 218 (1989) 473.
- (107) Mark A.Samuel, Mariana Frank, C. Hamzaoui, Dominique Pouliot, Kenneth B.Samuel, Guowen Li, On the uniqueness of the radiation amplitude zero in radiative W decay, Phys. Lett. B 243 (1990) 293-295.
- (108) G. Couture, Radiative zeros and extra neutral gauge bosons at Large Hadron Colliders, Phys. Rev. D 39 (1989) 2527-2535.
- (109) M. A. Samuel, G. Li, N. Sinha, R. Sinha, M. K. Sundersan, The magnetic moment of the W boson, Phys. Lett. B 280 (1992) 124-128.
- (110) M. A. Samuel, N. Sinha, R. Sinha, M. K. Sundersan, W radiative decays and the determination of magnetic dipole and electric quadrupole moments of the W, Phys. Rev. D 44 (1991) 2064.
- (111) M. A. Samuel, G. Li, N. Sinha, R. Sinha, M. K. Sundersan, Bounds on the magnetic moment of the W boson, Phys. Rev. Lett. 67 (1991) 9-11.
- (112) X. G. He and H. Lew, Scattering amplitude zero in , Mod. Phys. Lett. A 3 (1988) 1199-1203.
- (113) M. A. Doncheski, F. Halzen, Observable radiation zer in HERA intreactions, Z. Phys. C 52 (1991) 673-676.
- (114) M. Heyssler, W. J. Stirling, Radiation zeros at HERA, more about nothing, Eur. Phys. J. C 4 (1998) 289-299.
- (115) Fizuli Mamedov, Weak Boson Production Amplitude Zeros; Equalities of the Helicity Amplitudes, Phys. Rev. D 66 (2002) 033004.
- (116) D0 Collaboration, First study of the radiation-amplitude zero in production and limits on anomalous couplings at = 1.96 TeV, Phys. Rev. Lett. 100 (2008) 241805.
- (117) K. Hagiwara, T. Yamada, Null radiation zone at LHC, Phys. Rev. D 87 (2013) no. 1, 014021.
- (118) B. Badelek et al, The Photon Collider at TESLA, Int.J.Mod.Phys.A. 2004.19:5097-5186
- (119) Valery Telnov, Photon collider at TESLA: parameters and interaction region issues, arXiv:hep-ex/0101002.
- (120) Valery Telnov, Photon collider Higgs factories, Journal of Instrumentation, 9(09), C09020-C09020.
- (121) Valery Telnov, Photon collider at TESLA, Nucl. Instrum. Meth. A 472 (2001) 43-60.
- (122) Valery Telnov, Status of gamma-gamma, gamma-electron colliders, Nuclear Physics B (Proc. Suppl.) 82 (2000) 359-366.
- (123) Valery Telnov, Prospects of high energy photon colliders, Nuclear and Particle Physics Proceedings Volumes 273-275, (2016), 219-224.
- (124) I. F. Ginzburg et al., Production of high-energy colliding and beams with a high luminosity at VLEPP accelerators, Pis’ma Zh.Eksp.Teor.Fiz. 34, No, 9, 514-518 (1981).
- (125) I. F. Ginzburg et al., Colliding and beams based on the single-pass colliders (VLEPP type), Nuclear Instrumentation and Methods in Physics Research, 205(1-2), 47-68.
- (126) I. F. Ginzburg et al., An Interaction Region for Gamma-Gamma and Gamma-Electron Collisions at TESLA/SBLC, arXiv: 9707017v1 [hep-ex].
- (127) Mayda M. Velasco et al., Photon-Photon and Electron-Photon Colliders with Energies Below a TeV, SLAC ECONF C010630 E3005.
- (128) F. Cuypers, Leptoquark production in electron photon scattering, Nucl. Phys. B 474 (1996) 57-71.
- (129) J. E. C. Montalvo and J. P. Éboli, Composite vector leptoquarks in , and colliders, Phys. Rev. D 47 (1993) 837.
- (130) O. J. P. Eboli, E. M. Gregores, M. B. Margo, P. G. Mercadante, S. F. Novaes, Searching for leptoquarks in electron photon colliders, Phys. Lett. B 311 (1993) 147-152.
- (131) N.G. Deshpande, Xiao-Gang He and Sechul Oh, Amplitude Zeros in Radiative Decays of Scalar Particles, Phys. Rev. D 51 (1995) 2295-2301.
- (132) M. A. Doncheski, Robinett, Radiation zeros and scalar particles beyond the standard model, Phys. Lett. B 435 (1998) 364-372.
- (133) H. Nadeau and D. London, Leptoquarks at colliders, Phys. Rev. D 47 (1993) 3742.
- (134) M. Leurer, Acomprehensive study of leptoquark bounds, Phys. Rev. D 49 (1994) 333-342.
- (135) M. Leurer, Bounds on vector leptoquarks, Phys. Rev. D 50 (1994) 536-541.
- (136) M. Tanabashi et al. (Particle Data Group), Phys. Rev. D 98 (2018) 030001.
- (137) A. Belyaev, N. D. Christensen and A. Pukhov, Comput. Phys. Commun. 184 (2013) 1729 doi:10.1016/j.cpc.2013.01.014 [arXiv:1207.6082 [hep-ph]].
- (138) F. Staub, Comput. Phys. Commun. 185, 1773 (2014) [arXiv:1309.7223 [hep-ph]].
- (139) T. Sjostrand, L. Lonnblad and S. Mrenna, hep-ph/0108264.
- (140) M. Cacciari, G. P. Salam and G. Soyez, Eur. Phys. J. C 72 (2012) 1896 doi:10.1140/epjc/s10052-012-1896-2 [arXiv:1111.6097 [hep-ph]].
- (141) CLIC collaboration, clic-study.web.cern.ch .
- (142) ILC collaboration, ilchome.web.cern.ch .
- (143) J. Alwall, R. Frederix, S. Frixione, V. Hirschi, F. Maltoni, O. Mattelaer, H. S. Shao, T. Stelzer, P. Torrielli and M. Zaro, The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations, JHEP 07 (2014) 079.
- (144) V. M. Budnev, I. F. Ginzburg, G. V. Meledin, V. G. Serbo, The two-photon particle production mechanism. Physical problems. Applications. Equivalent photon approximation, Phys. Rept. 15 (1975) 181-281.
- (145) E. J. Williams, Kgl. Danske Vidensk. Selskab. Mat.-Fiz. Medd. 13 (1935) N4.
- (146) K. F. von Weizsäcker, Z. Physik 88 (1934) 612.