Inversion Diameter and Treewidth
Abstract
In an oriented graph , the inversion of a subset of vertices consists in reversing the orientation of all arcs with both end-vertices in . The inversion graph of a graph , denoted by , is the graph whose vertices are orientations of in which two orientations and are adjacent if and only if there is an inversion transforming into . The inversion diameter of a graph is the diameter of its inversion graph denoted by . Havet, Hörsch, and Rambaud (2024) first proved that for of treewidth , , and there are graphs of treewidth with inversion diameter . In this paper, we construct graphs of treewidth with inversion diameter , which implies that the previous upper bound is tight. Moreover, for graphs with maximum degree , Havet, Hörsch, and Rambaud (2024) proved and conjectured that . We prove the conjecture when with the help of computer calculations.
Keywords: inversion diameter; orientation; treewidth.
1 Introduction
An orientation of an undirected graph is an assignment of a direction to each edge, turning the initial graph into a directed graph. Let be a simple graph and an orientation of . If is a vertex set of , the inversion of on is a orientation by reversing the orientation of all arcs with both ends in .
The concept of inversion was first introduced by Belkhechine et al. [4]. They studied the inversion number of a directed graph , denoted by , which is the minimum number of inversions that transform into an acyclic graph. They proved, for every fixed , given a tournament , determining whether is polynomial-time solvable. In contrast, Bang-Jensen et al. [3] proved that given any directed graph , determining whether is NP-complete.
The maximum inversion numbers of all oriented graphs of order , denoted by , has also been investigated. Aubian et al. [2] and Alon et al. [1] proved . Besides these results, various related questions have also been studied.
Let be a simple graph. The inversion is a transformation between different orientations of . Instead of transforming an orientation into an acyclic orientation, it is also natural to consider the transformation between two orientations. The inversion graph of denoted by , is the graph whose vertices are the orientations of in which two orientations and are adjacent if and only if there is an inversion transforming into . The inversion diameter of is the diameter of , denoted by . It represents the maximum number of required inversions to transform an orientation of into another orientation of it.
Havet et al. [5] first introduced inversion diameter and studied it on various class of graphs. Let be a graph and let be a total ordering on . For every pair of vertices in , let and . We simply write for and for . The ordering is -strong if for every
-
•
, if , and
-
•
otherwise.
A graph is strongly -degenerate if it admits a -strong ordering of its vertices. Havet et al. [5] showed that
Theorem 1.1 (Havet et al. [5])
Let be a graph and let be a positive integer. If is strong -degenerate, then .
With the help of Theorem 1.1, they showed various bounds on depending on the structure of as following:
Theorem 1.2 (Havet et al. [5])
-
1.
For every graph with at least one edge and maximum degree , .
-
2.
for every planar graph .
-
3.
for ever graph of treewidth at most .
Havet et al. [5] also proved that for fixed , given a graph , determining whether is NP-hard. For a graph with maximum degree (sub-cubic graph), Havet et al. [5] showed a better bound . Moreover, they proposed a conjecture on graphs with maximum degree as Conjecture 1.3.
Conjecture 1.3 (Havet et al. [5])
For every graph with at least one edge and maximum degree , .
The conjecture is true for [5]. In this paper, we prove the conjecture when . Computer assistance will be used in the proof of Theorem 1.4. A pure mathematical proof is still worth studying.
Theorem 1.4
If is a graph of maximum degree , then .
For graphs with treewidth at most , Havet et al. [5] showed that there are graphs of treewidth at most with inversion diameter . In this paper, we show that the upper bound for graphs of treewidth at most is tight by proving Theorem 1.5. It answers a question proposed by Havet et al. in [5].
Theorem 1.5
For any positive integer , there are graphs of treewidth with inversion diameter .
2 Preliminary
Let be a graph. The distance between and , denoted by , is the number of edges in a shortest path joining and . For any vertex , denote . Then is the degree of . Let be the maximum degree of . We call -regular if for any . Let be a graph and a vertex subset. Let denote the subgraph of induced by . For a graph and a vertex , denote the graph induced by . For a graph and a induced subgraph , denote the graph induced by .
A label of is a mapping . A -dim vector assignment of with the label is a mapping such that for every edge , where to be the scalar product of and over . Usually, we use bold letter to represent . We use (resp. ) to represent vectors in whose coordinates are all (resp. ). We say a vector is odd (resp. even), if is one (resp. zero), i.e., has odd (resp. even) number of .
The inversion diameter has a close relationship with vector assignment as following.
Proposition 2.1 ([5])
For every graph and every positive integer , the following are equivalent.
-
1.
.
-
2.
For every label , there exists a -dim vector assignment of with the label .
The treewidth of a graph is denoted by . There are many ways to define treewidth. Here we give a definition of treewidth from the perspective of -tree.
Definition 2.2
A graph is a k-tree if
-
1.
either it is a -clique,
-
2.
or there exists a vertex such that is a -clique, and is a k-tree.
We say a graph is a partial -tree if it is a subgraph of a -tree. It is known that a graph is a partial -tree, if and only if the treewidth of is at most [6, 7].
Let denote the linear space spanned by . For two vectors and in , we write if . For a vector and a linear space in , we write if for any . The orthogonal complementary space of is . For any positive integer , write .
Definition 2.3
We say a sequence of vector are orthogonal if for any and . We say they are self-orthogonal if for any , that is, they are orthogonal and every vector is even.
Definition 2.4
A linear space is self-orthogonal if .
Let be a self-orthogonal linear space. Then is orthogonal and every vector in is even. It is easy to verify that is self-orthogonal if and only if it has self-orthogonal base vectors.
For a linear space and a vector , denote by the set and denote the space spanned by and a basis of , that is the summation space of and .
3 Proof of Theorem 1.5
For , we define a sequence of graph with a fixed label . First, let be a -clique with an arbitrarily label . Then, we recursively construct as following:
(i) for each -clique with vertices in and each , we add a new vertex such that and , for all ;
(ii) .
Since , we add new vertices for each -clique in . By Definition 2.2, is a -tree for any , that is, of treewidth at most . Since when , we may use to denote the label of for any . For any vertex with , there exists an unique such that . We say is the level of , denoted by . For a vertex set with , the level of is defined to be the maximum level of vertices in denoted by , that is, . Clearly, if is a vertex in , then . Similarly, if is a vertex set in , then .
Note that if is a subgraph of , then . So is an increasing sequence with upper bound by Theorem 1.2.
Let . Then . We will show that and then is of inversion diameter when is sufficiently large.
Next we suppose . Then for any , has a -dim vector assignment with the label by Proposition 2.1. Thus for each , there is a vector corresponding to it. The following lemmas show the properties of the vectors assigned to -cliques in .
Lemma 3.1
If there is a -clique of level with vertices in , then are linear independent.
Proof. Otherwise, without loss of generality, assume where for all . By the construction, there exists a vertex connecting each with for all and . Therefore,
a contradiction.
Lemma 3.2
If there is a -clique in of level with vertices , and is a vertex of level connecting all , then either are linear independent, or .
Proof. Firstly, by Lemma 3.1, are linear independent. Note that for any , is also a -clique of level in . Then by Lemma 3.1, for any , are linear independent. Assume where for all . If for some , then it contradicts that are linear independent. Therefore, .
Lemma 3.3
Let be vertices of a -clique of level in and . Then for any , has a solution such that either are linear independent, or .
Proof. Let . By the construction, there exists a vertex of level connecting such that for all . Then we have . By Lemma 3.2, either are linear independent, or .
The above lemmas actually work for arbitrary . The following lemmas need the assumption . If , we have a strong conclusion.
Lemma 3.4
Let be vertices of a -clique of level in and . Then has a solution such that are linear independent.
Proof. We prove it by contradiction. By Lemma 3.1, are linear independent. Let be the solution space of . Suppose is a subspace of . Since is a matrix, . By letting in Lemma 3.3, we have .
For each , the solution set of is in . By Lemma 3.3, . Therefore, for any , which contradicts that because are linear independent.
Definition 3.5
Let be a -clique of for some . is called a bad clique if , where and .
Note that a single vertex is always a bad -clique. If , “large” bad clique will finally cause contradictions. The following lemma is the main part of our proof which states that we can find “large” bad clique when is sufficiently large.
Lemma 3.6
If there exists a bad -clique of level in with , then there exists a bad clique in of size at least .
Proof. We prove it by contradiction. Suppose the -clique with vertices of level is the largest bad clique in , where . Then by Lemma 3.1. Let . Then by Definition 3.5. For , we have which means U is self-orthogonal.
We first show that . Suppose . Then . Since , by the construction of , there exists a vertex of level such that and for each . Let . By Lemma 3.1, we have are linear independent. By for each , we have that . Thus which implies . Hence is a bad -clique, a contradiction with the maximality of . So . In fact, we conclude that U is a self-orthogonal -dim subspace of and then each vector in U is even.
Since , there is , say , such that . Then . If is even, then , which contradicts with . Thus we have is odd.
Claim 3.7
If is a vertex in such that and for each , then u is odd.
Proof of Claim 3.7. Suppose u is even. Then . We have and . From Lemma 3.1 and , we know . Then . Thus is a bad -clique, which contradicts with the maximality of .
Fix a vertex of level such that and for each . Then . By the construction of , there exists a set of vertices satisfying the following:
-
1.
is a -clique;
-
2.
, for each ;
-
3.
and , for each .
Claim 3.8
is even for each .
Proof of Claim 3.8. Suppose there is such that is odd. Let . Recall that is odd. Then
On the other hand, for any ,
Hence . We have and . From Lemma 3.1 and , we know . Then which implies is a bad -clique, a contradiction with the maximality of .
| 1 | 0 | 0 | 1 | 1 | 0 | 0 | |
| 0 | 1 | 1 | 1 | 0 | 0 | ||
| 0 | 0 | 0 | |||||
| 1 | 1 | 0 | 0 | 0 | 0 | ||
| 1 | 1 | 0 | 0 | 0 | 0 | ||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Now we complete the proof of Lemma 3.6. For each , let . By Claim 3.7, is odd. By Claim 3.8, is even for each . It is not difficult to show that , and . Check Table 1 for the inner products between the vectors that we are working on. Let and . Then from Lemma 3.1. Since , we have . Let . Since and for each , we have . Note that . We have which implies . If , then which implies . Since , we have , a contradiction with . Hence . By Lemma 3.2, we have .
Since , we have for each which implies . So . If , then is a bad -clique, a contradiction with the maximality of . Hence . Let such that . By the construction of , there exists a vertex connecting to all vertices of such that for each . Then . From Claim 3.7, x is odd. Since U is a self-orthogonal subspace and for any (see Table 1), we have that the vectors in are all even. By and x being odd, we have is odd.
Let (if , then let ). Then there is connecting to all vertices of such that for each . Since , by Lemma 3.1, . Then . Since for each , from Claim 3.7, is odd. Note that . Since all vectors in are even and are odd, we have . From Lemma 3.2, . Since , we derive a contradiction.
With the help of those lemmas, we can derive a contradiction when and hence, .
Theorem 3.9
.
Proof. Suppose . By Lemma 3.6, the largest bad clique in is of size . Then . By Lemma 3.1, and then by . We have by checking the dimensions. Then we can derive a contradiction by Lemma 3.4.
Now we can give the proof of our main Theorem.
Proof of Theorem 1.5. For any , we have by Theorem 3.9. Then there exists a such that for every , . Thus for all , are desired graphs of treewidth at most and inversion diameter .

4 Proof of Theorem 1.4
In this section, we intend to give the proof of Theorem 1.4.
Let be a graph. We say is -critical if and for any proper subgraph , . Clearly, a -critical graph is connected. If is -critical, by Proposition 2.1, there exists a label such that there is no -dim vector assignment of with . We call such a bad label.
Let be a -critical graph with a bad label and an induced subgraph of . Denote . By the definition of -critical graph, admits a -dim vector assignment with . For a vertex , define . Note that .
Let be a subgraph of . We say is an available boundary family if we can assign each vertex a set such that:
-
1.
, and
-
2.
is an independent set in .
When there is no ambiguity, we may ignore the subscript .
The following lemma states that if we already have a vector assignment of , then we can reassign the vectors for from and the result is also a valid vector assignment.
Lemma 4.1
Let be an induced subgraph of a -critical graph with a bad label . Let be a -dim vector assignment on with and an available boundary family. Then for any -dim vector assignment on satisfying
-
1.
, , and
-
2.
, ,
we have is a -dim vector assignment on with .
Proof. We only need to verify that for all . Note that from the definition. Then is an independent set. Since we already have for all and is an independent set, we now only need to verify that for all satisfying and . Since and , we have by the definition of .
We say is reducible if there exists an available boundary family and a -dim vector assignment on with such that for any . The following lemma states that there is no reducible structure in -critical graph.
Lemma 4.2
Let be a -critical graph with a bad label . Then there is no reducible induced subgraph of .
Proof. Suppose is an induced reducible subgraph of . Then admits a -dim vector assignments with , an available boundary family and a -dim vector assignment on such that for any . Define a function by letting for any and for any . By the definition, is a -dim vector assignment with label . By Lemma 4.1, is a -dim vector assignment of with label . Since there is no edge between and , is a -dim vector assignment of with , a contradiction.
In the following, we are going to find certain reducible structures in -critical graph.
Lemma 4.3
Let be a -critical graph with a bad label . For any vertex , at least one edge adjacent to is labeled by .
Proof. Suppose there exists a vertex such that for all . Let . Then admits a -dim vector assignment with . Let . Then it is not difficult to verify that is a -dim vector assignment of with , a contradiction.
Lemma 4.4
Let be a graph with a label . If admits a -dim vector assignment with , then there exists a -dim vector assignment with such that for every vertex of degree at most , .
Proof. Let be the -dim vector assignment of with which minimizes . Suppose . Let and . Then since . Choose and define a function by letting for any and . It is easy to verify that is a -dim vector assignment of with , but , a contradiction.
Lemma 4.5
Let be a -critical graph of maximum degree with a bad label . Then is 3-regular.
Proof. Suppose there exists a vertex such that . Let . Then by Lemma 4.3, . Let . Then . By hypothesis, admits a -dim vector assignment with . Since , . Let . Then is an available boundary family. Let and we can choose such that . Then is reducible, a contradiction with Lemma 4.2.
Suppose there exists a vertex such that . Let . By Lemma 4.3, without loss of generality, assume . Let . Then . By hypothesis and Lemma 4.4, admits a -dim vector assignment with such that . Let and . Then is an available boundary family. Since , we have . Let . If (resp. ), choose (resp. ). It is easy to verify in either case, there exists such that for . So is reducible, a contradiction with Lemma 4.2.


Lemma 4.6
Let be a -critical 3-regular graph with a bad label . There is no induced in , where is the graph obtained by deleting an edge in .
Proof. Suppose there exists a in with vertex set and (See Figure 3).
Let . Then . By hypothesis and Lemma 4.4, admits a -dim vector assignment with such that . Let . Then is an available boundary family. We have the following properties:
With above properties, we claim that is reducible. The claim is proved by computer by enumerating all available boundary families with above properties. The source codes can be found on GitHub. Therefore, we derive a contradiction with Lemma 4.2.
Lemma 4.7
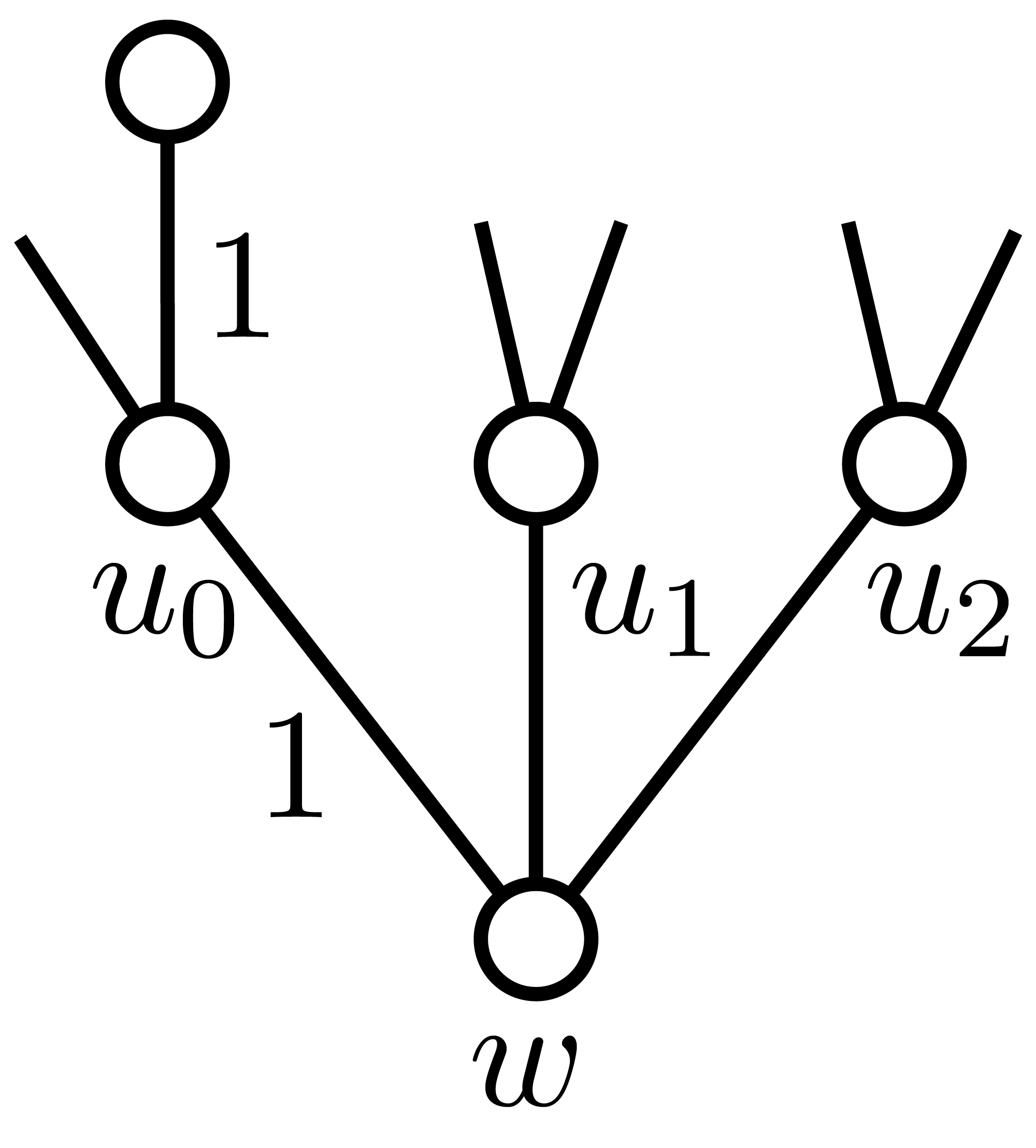
Let be a -critical 3-regular graph with a bad label . Then there is no triangle in .
Proof. Suppose there exists a triangle with vertices and let be the neighbor of , for (See Figure 3). By Lemma 4.6, are either distinct vertices, or . If , then by being 3-regular. However, [5], which contradicts that is -critical. Hence, we conclude that are distinct vertices. Let . Then . By hypothesis and Lemma 4.4, admits a -dim vector assignment with such that . We can assume, without loss of generality, that satisfies the property: if , then . Let and . Now we have the following properties:
With above properties, we claim that is reducible which is proved by computer. The source codes can be found on GitHub. Therefore, we derive a contradiction with Lemma 4.2.

Lemma 4.8
Let be a -critical 3-regular graph with a bad label . Then there is no with two edges labeled one in .
Proof. Suppose there exists a path such that . By Lemma 4.7, . Let be the neighbor of (See Figure 5). By Lemma 4.7, is an independent set. Let . Then . By hypothesis, admits a -dim vector assignment with . Let . Then is an available boundary family. We have the following properties:
-
1.
For each , by .
-
2.
, because .
-
3.
For each , if , then by Lemma 4.3.
With above properties, we claim that is reducible which is proved by computer (GitHub). Therefore, we derive a contradiction with Lemma 4.2.
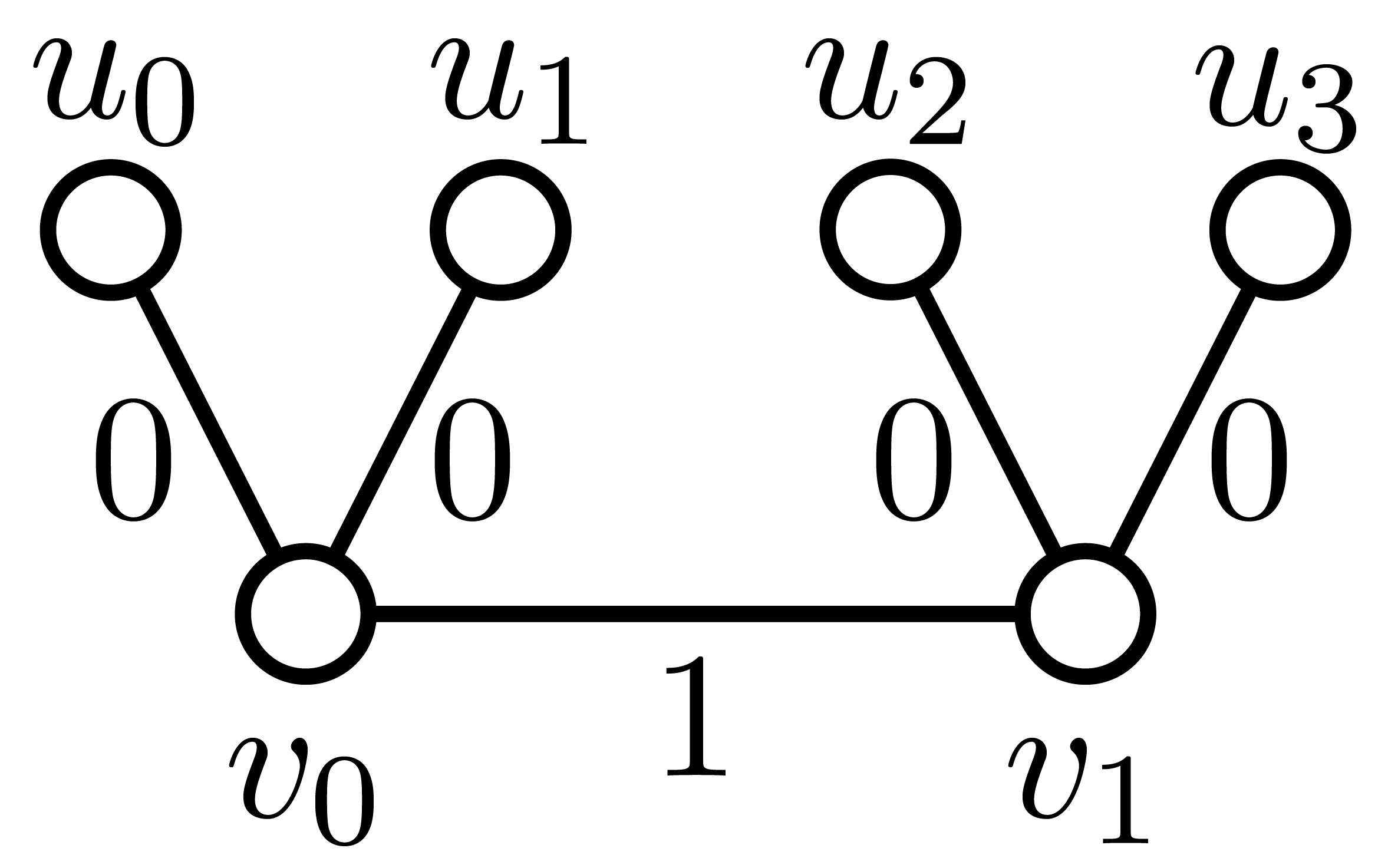
Lemma 4.9
Let be a -critical 3-regular graph with a bad label . Then there is no in .
Proof. Suppose there exists a with vertices and for every and (See Figure 5). By Lemmas 4.3 and 4.8, without loss of generality, we can assume and other edges in are labeled zero. By Lemma 4.7, is an independent set. Let . Then . By hypothesis, admits a -dim vector assignment . Let . Then is an available boundary family. We have the following properties:
-
1.
For each , by .
-
2.
By Lemma 4.3, and for .
With above properties, we claim that is reducible which is proved by computer (GitHub). Therefore, we derive a contradiction with Lemma 4.2.

Lemma 4.10
Let be a -critical 3-regular graph with a bad label . Then there is no with at least on edge is labeled one in .
Proof. Suppose there exists a with vertices and . Let be the neighbor of for (See Figure 7). By Lemmas 4.7 and 4.9, are distinct vertices. By Lemma 4.8, . Let . Then . By hypothesis and Lemma 4.4, admits a -dim vector assignment with such that .
Let us first consider the case . In this case, let . Then is an available boundary family. We claim is reducible with which is proved by computer (GitHub), a contradiction with Lemma 4.2.
Now suppose . Then by Lemma 4.8. Since is 3-regular, there exists such that . Let for and for other . Then is an available boundary family. Since for each , we have by Lemma 4.3. Moreover, for , we have since . We claim that we can choose for any such that and do not occur, where . The claim can be proved by simple discussion. Then define by letting and for all other vertex . By lemma 4.1, is a -dim vector assignment of with .
Let , then is an available boundary family. We claim is reducible with which is proved by computer (GitHub). A contradiction.
Now we have plenty of forbidden structures in , and we can finally prove Theorem 1.4.
Proof of Theorem 1.4. By contradiction. Let be the counter example with minimum number of vertices and then minimum edges. Then is -critical. Since , is 3-regular by Lemma 4.5. Let be a bad label of .
We assume satisfying by Lemma 4.3. Let be the neighbor of and the neighbor of (See Figure 7). By Lemmas 4.7 and 4.10, is an independent set. Let . Then . By hypothesis, admits a -dim vector assignment . Let . Then is an available boundary family. Since , we have . By Lemma 4.4, we have for every . Then we claim that is reducible which is proved by computer (GitHub), a contradiction with Lemma 4.2.
Acknowledgement
Y. Yang is supported by the Fundamental Research Funds for the Central University (Grant 500423306) in China. M. Lu is supported by the National Natural Science Foundation of China (Grant 12171272 & 12161141003).
References
- [1] N. Alon, E. Powierski, M. Savery, A. Scott, and E. Wilmer. Invertibility of digraphs and tournaments. SIAM Journal on Discrete Mathematics, 38(1):327–347, 2024.
- [2] G. Aubian, F. Havet, F. Hörsch, F. Klingelhoefer, N. Nisse, C. Rambaud, and Q. Vermande. Problems, proofs, and disproofs on the inversion number. arXiv preprint arXiv:2212.09188, 2022.
- [3] J. Bang-Jensen, J. C. F. da Silva, and F. Havet. On the inversion number of oriented graphs. Discrete Mathematics & Theoretical Computer Science, 23(Special issues), 2022.
- [4] H. Belkhechine, M. Bouaziz, I. Boudabbous, and M. Pouzet. Inversion dans les tournois. Comptes Rendus. Mathématique, 348(13-14):703–707, 2010.
- [5] F. Havet, F. Hörsch, and C. Rembaud. Diameter of the inversion graph. arXiv preprint arXiv:2405.04119, 2024.
- [6] P. Scheffler. Die Baumweite von Graphen als ein Maß für die Kompliziertheit algorithmischer Probleme, volume 4. Akademie der Wissenschaften der DDR, Karl-Weierstrass-Institut für Mathematik, 1989.
- [7] J. van Leeuwen. Graph algorithms. In Algorithms and complexity, pages 525–631. Elsevier, 1990.