Inverse Source Problem for Acoustically- Modulated Electromagnetic Waves
Abstract.
We propose a method to reconstruct the electrical current density from acoustically-modulated boundary measurements of time-harmonic electromagnetic fields. We show that the current can be uniquely reconstructed with Lipschitz stability. We also report numerical simulations to illustrate the analytical results.
1. Introduction
The inverse source problem for the Maxwell equations is of fundamental interest and considerable practical importance, with applications ranging from geophysics to biomedical imaging [20, 1, 8, 9, 33]. The problem is usually stated in the following form: determine the electric current density from boundary measurements of the electric and magnetic fields. It is well known that this problem is underdetermined and does not admit a unique solution, due to the existence of so-called nonradiating sources [16]. However, if the source is spatially localized or some other a priori information is available, it is often possible to characterize the source to some extent. Such a method is applied to the localization of low-frequency electric and magnetic signals originating from current sources in the brain or heart [30].
In this paper, we propose an alternative approach to the electromagnetic inverse source problem. In this approach, which is an extension of the authors’ previous work on the acousto-electric inverse source problem for static fields [26], a wavefield is used to control the material properties of a medium of interest, which is then probed by a second wavefield. Also see related work on hybrid imaging [2, 3, 4, 5, 6, 7, 10, 12, 13, 14, 15, 19, 22, 23, 24, 25, 26, 28, 31, 32]. Here the electric current density as well as the conductivity, electric permittivity and magnetic permeability are spatially modulated by an acoustic wave. In this manner, we find that it is possible to uniquely recover the current density from boundary measurements of the fields with Lipschitz stability.
The remainder of this paper is organized as follows. In Section 2 we introduce a model for the acoustic modulation of the current density and the material parameters. In Sections 3 and 4 this model is used to formulate the inverse source problem and thereby derive an internal functional from which the source may be recovered. Numerically simulated reconstructions are given in Section 5. Finally, our conclusions are presented in Section 6.
2. Model
We begin by developing a simple model for acoustic modulation of the electrical current density and material parameters, following the approach of [26]. We begin by considering the time-harmonic Maxwell equations in a bounded domain :
| (1) | |||||
We also impose the impedance boundary condition
| (2) |
which arises since is taken to be enclosed by a good conductor. Here the vector functions , and are the current density, the electric field, and the magnetic field, respectively. The scalar functions , , and are the electric permittivity, magnetic permeability, conductivity, and surface impedance, respectively. The vector is the outward unit outward normal to and is a fixed frequency. Note that in the above, we do not write the equations governing the divergence of and which are not needed in what follows.
The inverse source problem is to reconstruct the source from boundary measurements, assuming that the coefficients , , , are known. A typical measurement is the tangential electric field on the boundary:
| (3) |
This problem does not have a unique solution [16]. That is, distinct sources may give rise to the same boundary measurements.
Remark 2.1.
An alternative measurement is . Knowledge of is equivalent to knowledge of when the impedance boundary condition (2) is taken into account, since on .
We now examine the effect of acoustic modulation. Following [26, 6], we consider a system of charge carriers in a fluid, in which a small-amplitude acoustic plane wave propagates. It follows that the current density is modulated according to
| (4) |
where is the conductivity in the absence of the acoustic wave, is a small parameter that is proportional to the acoustic pressure, is the wave vector of the acoustic wave and is its phase. Likewise, the conductivity and permittivity are also modulated:
where and are the unmodulated conductivity and permittivity, and the constants are known as the elasto-electric constants. For simplicity we assume that the impedance is not affected by the acoustic modulation. It follows that the modulated electric and magnetic fields and satisfy the modified Maxwell equations
| (5) | |||||
together with the boundary condition
| (6) |
The corresponding boundary measurement becomes
| (7) |
3. Internal Functional
In this section, we derive the internal functional from boundary measurements of the electric field. We also introduce the necessary function spaces and specify certain technical requirements on the conductivity and permittivity.
3.1. Function Spaces
We will use the following standard spaces to discuss the wellposedness of the Maxwell’s equations [11]. Let be an open bounded set with a boundary, and
The norm on is given by
The two tangential trace maps and have the following definitions
and
where
and
Here is the surface divergence and is the surface curl. The two spaces and are dual to each other. To handle the impedance boundary condition, we define the tangential trace of a vector field
| (8) |
and the space
The norm on is
We denote the -inner product by
and the inner product by
where denotes the complex conjugate. We denote the dual paring of and by .
3.2. Assumptions and Weak Formulation
We will make the following assumptions throughout this paper.
-
A-1.
The domain is an open bounded connected domain in with boundary.
-
A-2.
The medium is nonmagnetic with in , where is the magnetic permeability in vacuum. The coefficients and are real piecewise functions.
-
A-3.
There exists positive constants and , such that
(9) and the conductivity is nonzero.
-
A-4.
The source is an vector field and is compactly supported in .
Remark: We conclude from A-2 that and are piecewise by the Sobolev embedding theorem. We conclude from A-3 that and , so long as is sufficiently small.
3.3. Internal Functional
We now derive the internal functional for both classical and weak solutions. To proceed, we consider the fields and which obey the Maxwell equations without sources:
| (13) | ||||
along with the impedance boundary condition
where . Equivalently,
| (14) | ||||
Note that (13) are explicitly solvable, since the required coefficients are known. Next, we take the inner product of (5) with , the inner product of (14) with , and then subtract to obtain
Integrating the above result over and using the vector identity , we find that
We now integrate by parts the divergence terms, which using the relations and yields
| (15) |
Note that the boundary integral only depends on the tangential components of the fields , , and , which are known from the boundary measurements (7). Therefore, the left-hand side can be determined from experiment. For the right-hand side, we consider the asymptotic expansion in the small quantity . The term is
The ) term is of the form
| (16) |
Varying and in (16), and performing the inverse Fourier transform, we obtain the internal functional
| (17) |
which is known at every point in .
We make the following hypothesis to extract more information from the internal function (17):
Hypothesis 3.1.
There exists a finite open cover of , such that for each , there exist three solutions to (14) in , denoted , and , that are linearly independent on .
The hypothesis means that, in each , we can form the non-singular matrix , where is the th column, . Let be the internal functional defined as in (17), with replaced by . Given the row vector , we have
where we view and as column vectors, and denotes the transpose. Therefore, if we define by specifying its restrictions according to
then is well-defined since both and are global vector fields over , and we have
| (18) |
Note that we view as a vector-valued internal functional.
4. Inverse Problem and Internal Functional
It follows from the above discussion that the inverse problem consists of recovering the source current from the internal functional . In this section we will derive a reconstruction procedure that uniquely recovers with Lipschitz stability. The analysis depends critically on whether the constant vanishes.
4.1. Case I: .
In this situation, the equality (18) does not involve directly.
Proposition 4.1.
Suppose the assumptions A1-A4 and the hypothesis (3.1) hold. If , then we have the following two subcases:
-
(I.1)
If , then the source is uniquely determined with the stability estimate
for some constant independent of .
-
(I.2)
If , then the source cannot be uniquely determined.
Moreover, whenever is uniquely determined, there are explicit reconstruction procedures.
Proof.
If , then (18) implies
This uniquely determines the weak solution everywhere in . Consequently, and are also uniquely determined via the Maxwell’s equations (1). Note that all these procedures are constructive: given , we compute from the above equality, and then from (1).
The stability can be derived as follows. If there is another source with corresponding electric field , and vector internal functional defined as in (18), then is a weak solution of the Maxwell equations. That is,
for all . As the coefficients in this weak formulation are all bounded, there exists a constant such that
We deduce that
If , there exists an open set . For any compactly supported smooth function , if solves (1), then solves (1) with replaced by . Moreover, since , these two pairs both satisfy the boundary condition (2) and produce identical measurement (3). This means that sources of the form are non-radiating. Thus the source cannot be uniquely determined from the boundary measurement (3). ∎
4.1.1. Increased Regularity
The stability estimate for the subcase and is in terms of the norm, which follows because was obtained from using a weak formulation. When the reconstructed and are smooth enough, for example, when , we can utilize the strong formulation to control in in terms of the higher order derivatives of the internal data.
Proposition 4.2.
Suppose the assumptions A1-A4 and the hypothesis (3.1) hold. Suppose, in addition, that . If and , then the following stability estimate holds for any two compactly supported sources :
Here is an open set compactly contained in such that and , and the constant is independent of .
Proof.
Define
Then solves
| (19) |
The following stability estimate is immediate:
It remains to show that the quantity
is finite. To proceed we will employ an interior regularity estimate for elliptic equations. Denote by , , . Then take the divergence of (19) to obtain
| (20) |
Using the identity , we obtain the following elliptic system
For each component of , the left hand side of the above defines a second order elliptic operator with constant coefficients, so we can apply an interior regularity estimate [17, Lemma 6.32]. Since is bounded away from zero and are piecewise , the following quantities are all bounded in :
Thus
Combing this with the fact that , we obtain from [17, Lemma 6.32] that . This increased regularity implies that
Applying [17, Lemma 6.32] again, we obtain that . Next, choose a smooth cutoff function that is compactly supported in and equal to one on . We find that
Thus we obtain that . ∎
4.2. Case II: .
Here (18) implies that
| (21) |
Inserting the above into the Maxwell equations (1), we obtain an equation of the form
| (22) |
where
Note that there are boundary constraints for , including the impedance boundary condition (2) and the measurement (3).
To analyze the stability of the inverse problem, suppose that there is another source with corresponding electric field and vector internal functional , defined by (18). Let be a weak solution of the equation
| (23) |
and obey the impedance boundary condition
| (24) |
where
| (25) |
It remains to establish the solvability of (22) with boundary condition (2) or the solvability of (23) with boundary condition (24). Now (22) and (23) are similar in form to (10). The difference is that in (10), the term has a strictly positive real part and a non-negative imaginary part, which ensures the existence and uniqueness of the weak solution by standard methods [27]. These sign conditions no longer hold for the term in (22) and (23), due to the presence of the elasto-electric constants . Therefore, we divide the discussion into several sub-cases. By Assumption A-3, we see that is either identically zero or bounded away from zero, is either non-positive or non-negative. This observation accounts for the following classification of sub-cases.
Theorem 4.3.
Suppose the assumptions A1-A4 and the hypothesis (3.1) hold. If , we have the following subcases:
-
(II.1)
If , then the source cannot be uniquely determined.
-
(II.2)
If , , and , then the source is uniquely determined. If in addition is strictly bounded away from zero, then we have the following stability estimates. If ,
and if ,
-
(II.3)
If , , and , then the source cannot be uniquely determined.
-
(II.4)
If , then the source is uniquely determined. If , we have the following stability estimate
and if ,
Here is a constant independent of . Moreover, whenever is uniquely determined, there are explicit reconstruction procedures.
The proof is presented in the next few subsections.
Remark 4.4.
It is generally expected that because the former is solely a density effect, and the latter is due to density variation and Brillouin scattering [6]. Thus Case is more likely to occur in practice.
| Case | Subcase | Uniqueness |
|---|---|---|
| (I.1) | Y | |
| (I.2) | N | |
| (II.1) | N | |
| (II.2) , , , | Y | |
| (II.3) , , | N | |
| (II.4) | Y |
4.2.1. Subcase (II.1): .
This subcase corresponds to and . For any , if satisfies the equation (22) and the boundary condition (2), so does . This means, as a result of (18), that sources of the form are non-radiating. Thus the original source cannot be uniquely determined.
4.2.2. Subcase (II.2 and II.3): and .
This subcase corresponds to and . Note that either everywhere or everywhere due to the assumption A-3. In the following discussion, we will keep as a placeholder, for ease of exposition.
We now take the inner product of (23) with and use the vector identity to integrate by parts:
| (26) |
For the boundary integral, we apply the vector triple product identity to obtain
Here is the tangential trace of as defined in (8). From (24), we obtain . Thus the boundary integrand becomes
Therefore, separating the real and imaginary parts of (4.2.2) we obtain
| (27) | ||||
| (28) |
To prove uniqueness, we set . Then and (28) implies . If . We conclude that in . If , there exists an open set . For any compactly supported smooth function , the choice is a non-trivial solution to (23) (24), proving the non-uniqueness.
Now we prove stability assuming that is strictly positive, which implies that is bounded away from zero. When , recall that , so there exists a constant , independent of , such that
| (29) | ||||
where is an arbitrary constant. If we choose so that , then the term can be absorbed into the left hand side, resulting in the following estimate (with a different constant ):
This result, combined with (21), yields the stability estimate
4.2.3. Subcase (II.4): .
This subcase corresponds to . Note that due to the assumption A-3, there exists a constant such that either everywhere or everywhere in .
If , the identities (4.2.2) (27) (28) still hold, hence there exists a constant such that
where the second equality comes from (27). Suppose , then in , proving uniqueness. The above inequality also implies, by the Cauchy-Schwartz inequality, that
Canceling factors of and applying the relation (21) yields the stability estimate
If , we consider equipped with the Dirichlet boundary condition
| (30) |
Since , we conclude that . Thus, there exists a function , such that
Set , then and solves
| (31) |
where is the subspace of with zero tangential trace, and
Note that for , the dual space of , we have
It follows from [27, Theorem 4.17] that there exists a unique solution to (31) with
Remark 4.5.
5. Numerical Experiments
In this section, we present numerical experiments to test the reconstruction of in Case (I.1) and Case (II.4). The code is implemented in Python using the finite element PDE solver NGSolve 111The code is hosted at https://github.com/lowrank/umme . Numerical experiments are performed on the domain consisting of an infinite cylinder of radius , discretized with a uniform triangular mesh of 19276 triangles. The Maxwell equations (1) are solved with a third-order Nédélec element.
We denote by and the electric permittivity and the magnetic permeability in vacuum, respectively. In a medium with electric permittivity and magnetic permeability , we define
We refer to and as the relative electric permittivity and the relative magnetic permeability, respectively. Moreover, let be the light speed in vacuum and define
| (32) |
Using the relation , we can rewrite the Maxwell equations (1) as
together with the impedance boundary condition (2), with impedance .
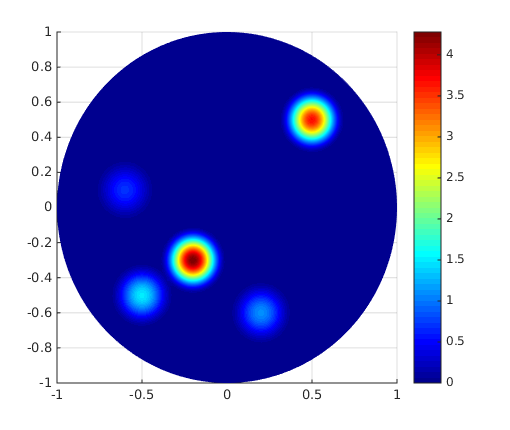
The physical parameters are chosen as follows. According to Assumption A-2, . The frequency is selected such that , which corresponds to a frequency GHz. Density plots of and are displayed in Fig. 1. For , the background value is taken to be 37.2 for blood (see [18]) and there are 3 regions with smaller values of which are 7.79 (top) for fat, 20.2 (left) for nerve and 36.4 (right) for muscle. The source is a real vector, whose components are shown in Fig. 2.



Auxiliary solutions are needed in the reconstruction to compute the vector internal data (18) from the scalar internal data (17). Such solutions are obtained by solving the equation for :
along with the impedance boundary condition
where is defined by
| (33) |
with and . Here the wave number , where are taken from the background values corresponding to blood. The rationale for the choice of is that when the medium is homogeneous, then and are mutually orthogonal plane waves. Clearly, such an orthogonality relation may not hold in practice due to the distortion caused by the inhomogeneity.
5.1. Case (I.1)
In this experiment, the modulation parameters are chosen as , , . The scalar internal data is obtained by solving the forward problem (1). Then multiplicative noise is added to the signal. The vector internal data is calculated from the auxiliary solutions. The reconstruction is carried out using the procedure described in Proposition 4.1. That is, we solve for from (18) and then recover from the Maxwell equations (1) through the following weak formulation by setting in (3.2):
Here is solved under the Galerkin framework by treating the left-hand side as the bilinear form and the right-hand side as the linear form with known . The reconstructed source is shown in Fig. 3.




5.2. Case (II.4)
In this experiment, the modulation parameters are chosen as , , . The scalar internal data is obtained by solving the forward problem (1). Then multiplicative noise is added to the signal. The vector internal data is found using the auxiliary solutions. The reconstruction is performed according to Proposition 4.3. That is, the boundary value problem (22), (3) is solved to obtain . The Maxwell equations (1) are then used to find through the similar approach of Case (I.1). The reconstructed source is shown in Fig. 4.




Remark 5.1.
The reconstructions for Case (II.4) are much better than those for Case (I.1). This can be explained by the corresponding stability estimates. Proposition 4.1 for Case (I.1) requires the norm of to be bounded, which is very sensitive to noise. In contrast, the stability estimate in Proposition 4.3 for Case (II.4) only requires that the norm of be bounded.
6. Acknowledgments
The work of JCS was supported in part by the NSF grant DMS-1912821 and the AFOSR grant FA9550-19-1-0320. The work of YY is supported in part by the NSF grants DMS-1715178 and DMS-2006881.
References
- [1] R. Albanese and P. Monk, The inverse source problem for Maxwell’s equations, Inverse Problems, 22 (2006), p. 1023.
- [2] H. Ammari, E. Bonnetier, Y. Capdeboscq, M. Tanter, and M. Fink, Electrical impedance tomography by elastic deformation, SIAM J. Appl. Math, 68 (2008), p. 1557–1573.
- [3] G. Bal, F. Chung, and J. Schotland, Ultrasound modulated bioluminescence tomography and controllability of the radiative transport equation. SIAM J. Math. Anal., 48 (2016), pp. 1332–1347.
- [4] G. Bal and G. Uhlmann, Inverse diffusion theory of photoacoustics, Inverse Problems, 26 (2010), p. 085010.
- [5] G. Bal, C. Guo, and F. Monard, Imaging of anisotropic conductivities from current densities in two dimensions, SIAM J. Imag. Sci., 7 (2014), pp. 2538–2557.
- [6] G. Bal and J. Schotland, Inverse scattering and acousto-optic tomography, Phys. Rev. Lett., 104 (2010), p. 043902.
- [7] , Ultrasound-modulated bioluminescence tomography, Phys. Rev. E [Rapid Communication], 89 (2014), p. 031201.
- [8] G. Bao, P. Li and Y. Zhao, Stability for the inverse source problems in elastic and electromagnetic waves, J. Math. Pure. Appl., 134 (2020) 122–178.
- [9] N. Bleistein and J. Cohen, Nonuniqueness in the inverse source problem in acoustics and electromagnetics, J. Math. Phys., 18 (1977).
- [10] Y. Capdeboscq, J. Fehrenbach, F. de Gournay, and O. Kavian, Imaging by modification: numerical reconstruction of local conductivities from corresponding power density measurements, SIAM J. Imag. Sci., 2 (2009).
- [11] M. Cessenat, Mathematical Methods in Electromagnetism Linear Theory and Applications, World Scientific, 1996.
- [12] F. Chung, J. Hoskins, and J. Schotland, Coherent acousto-optic tomography with diffuse light, Opt. Lett., 45 (2020), pp. 1623–1626.
- [13] F. Chung, J. Hoskins, and J. Schotland, Radiative transport model for coherent acousto-optic tomography, Inverse Problems, 36 (2020), p. 064004.
- [14] F. Chung and J. Schotland, Inverse transport and acousto-optic imaging, SIAM J. Math. Anal., 49 (2017), pp. 4704–4721.
- [15] F. Chung, T. Yang, and Y. Yang, Ultrasound modulated bioluminescence tomography with a single optical measurement, Inverse Problems, 37 (2021), p. 015004.
- [16] A. Devaney and E. Wolf, Radiating and nonradiating classical current distributions and fields they generate, Phys. Rev. D, 8 (1973), p. 1044.
- [17] G. B. Folland, Introduction to Partial Differential Equations, Princeton University Press, 2 ed., 1995.
- [18] C. Gabriel, Compilation of the dielectric properties of body tissues at RF and microwave frequencies., tech. rep., King’s Coll London (United Kingdom) Dept of Physics, 1996.
- [19] A. Gebauer and O. Scherzer, Impedance-acoustic tomography, SIAM J. Appl. Math, 69 (2008), p. 565.
- [20] V. Isakov, Inverse Source Problems, American Mathematical Society, 1990.
- [21] M. Kempe, M. Larionov, D. Zaslavsky, and A. Genack, Acousto-optic tomography with multiply scattered light, JOSA A, 14 (1997), pp. 1151–1158.
- [22] P. Kuchment and L. Kunyansky, 2d and 3d reconstructions in acousto-electric tomography, Inverse Problems, 27 (2011), p. 055013.
- [23] P. Kuchment and D. Steinhauer, Stabilizing inverse problems by internal data, Inverse Problems, 28 (2012), p. 084007.
- [24] W. Li, Y. Yang, and Y. Zhong, A hybrid inverse problem in the fluorescence ultrasound modulated optical tomography in the diffusive regime, SIAM J. Appl. Math., 79 (2019), pp. 356–376.
- [25] W. Li, Y. Yang, and Y. Zhong, Inverse transport problem in fluorescence ultrasound modulated optical tomography with angularly averaged measurements, Inverse Problems, 36 (2020), p. 025011.
- [26] W. Li, J. C. Schotland, Y. Yang, and Y. Zhong, An Acousto-electric inverse source problem, SIAM J. Imag. Sci., 14, 1601-1616 (2021)
- [27] P. Monk, Finite Element Methods for Maxwell’s Equations, Oxford University Press, 2003.
- [28] A. Nachman, A. Tamasan, and A. Timonov, Conductivity imaging with a single measurement of boundary and interior data., Inverse Problems., 23(6), (2007), p. 2551.
- [29] R. Parmenter, The acousto-electric effect, Phys. Rev, 89 (1953), p. 990.
- [30] R. Plonsey and R. Barr, Bioelectricity: A Quantitative Approach, Springer, 2007.
- [31] J. Schotland, Acousto-optic imaging of random media, Prog. Opt, 65 (2020), pp. 347–380.
- [32] F. Triki, Uniqueness and stability for the inverse medium problem with internal data, Inverse Problems, 26 (2010), p. 095014.
- [33] Y. Zhao, G. Hu, P. Li, and X. Liu, Inverse source problems in electrodynamics, Inverse Problems and Imaging, 12 (2018), pp. 1411–1428.