Inverse magnetic catalysis effect and current quark mass effect on mass spectra and Mott transitions of pions under external magnetic field
Abstract
Mass spectra and Mott transition of pions at finite temperature and magnetic field are investigated in a two-flavor NJL model, and we focus on the inverse magnetic catalysis (IMC) effect and current quark mass (CQM) effect. Due to the dimension reduction of the constituent quarks, the pion masses jump at their Mott transitions, which is independent of the IMC effect and CQM effect. We consider the IMC effect by using a magnetic dependent coupling constant, which is a monotonic decreasing function of magnetic field. With IMC effect, the Mott transition temperature of meson is a monotonic decreasing function of magnetic field. For charged pions , the Mott transition temperature fast increases in weak magnetic field region and then decreases with magnetic field, which are accompanied with some oscillations. Comparing with the case without IMC effect, and are lower when including IMC effect. CQM effect are considered by varying parameter in non-chiral limit. For meson, is not a monotonic function of magnetic field with low , but it is a monotonic decreasing function with larger . In the weak magnetic field region, is higher for larger , but in the strong magnetic field region, it is lower for larger . For meson, is only quantitatively modifies by current quark mass effect, and it becomes higher with larger .
I Introduction
The study of hadron properties in QCD medium is important for our understanding of strong interaction matter, due to its close relation to QCD phase structure and relativistic heavy ion collision. For instance, the chiral symmetry breaking leads to the rich meson spectra, and the mass shift of hadrons will enhance or reduce their thermal production in relativistic heavy ion collisions k1 ; k2 ; k3 .
It is widely believed that the strongest magnetic field in nature may be generated in the initial stage of relativistic heavy ion collisions. The initial magnitude of the field can reach in collisions at the Relativistic Heavy Ion Collider and the Large Hadron Collider b0 ; b1 ; b2 ; b3 ; b4 , where is the electron charge and the pion mass in vacuum. In recent years, the study of magnetic field effects on the hadrons attract much attention. As the Goldstone bosons of the chiral (isospin) symmetry breaking, the properties of neutral (charged) pions at finite magnetic field, temperature and density are widely investigated c1 ; c3 ; hadron1 ; hadron2 ; qm1 ; qm2 ; sigma1 ; sigma2 ; sigma3 ; sigma4 ; l1 ; l2 ; l3 ; l4 ; lqcd5 ; lqcd6 ; ding2008.00493 ; ding2022 ; njl2 ; meson ; mfir ; ritus5 ; ritus6 ; mao1 ; mao11 ; mao2 ; wang ; coppola ; phi ; liuhao3 ; he ; Restrepo ; maocharge ; maopion ; yulang2010.05716 ; q1 ; q2 ; q3 ; q4 ; huangamm1 ; huangamm2 ; q5 ; q6 ; q7 ; q8 ; q9 ; q10 ; su3meson4 ; Scoccola1 ; Scoccola2 ; meijie3 .
The LQCD simulations performed with physical pion mass observe the inverse magnetic catalysis (IMC) phenomenon lattice1 ; lattice11 ; lattice2 ; lattice3 ; lattice4 ; lattice5 ; lattice6 ; lattice7 . Namely, the pseudo-critical temperature of chiral symmetry restoration and the quark mass near drop down with increasing magnetic field. On analytical side, many scenarios are proposed to understand this IMC phenomenon, but the physical mechanism is not clear fukushima ; mao ; hadron2 ; bf1 ; bf12 ; bf13 ; bf2 ; bf3 ; bf4 ; bf5 ; bf51 ; bf52 ; bf8 ; bf9 ; bf11 ; db1 ; db2 ; db3 ; db5 ; db6 ; pnjl1 ; pnjl2 ; pnjl3 ; pnjl4 ; pqm ; ferr1 ; ferr2 ; huangamm2 ; meijie ; imcreview ; ammmao . Besides, how does the IMC effect influence the pion properties under external magnetic field? Previous studies focus on the case with vanishing temperature and density, and report that IMC effect leads to a lower mass for pions under external magnetic field meson ; su3meson4 ; mao11 .
The current quark mass determines the explicit breaking of chiral symmetry. In LQCD simulations, it is considered through different pion mass l4 ; lattice5 ; lattice3 . At vanishing temperature and finite magnetic field, the normalized neutral pion mass increases with current quark mass, but the normalized charged pion mass decreases with current quark mass l4 . In effective models, the current quark mass (CQM) effect on pion properties has not yet been studied.
In this paper, we will investigate the IMC effect and CQM effect on mass spectra and Mott transition of pions at finite temperature and magnetic field. Here we make use of a Pauli-Villars regularized Nambu–Jona-Lasinio (NJL) model, which describes remarkably well the static properties of light mesons njl1 ; njl2 ; njl3 ; njl4 ; njl5 ; zhuang . In our calculations, the IMC effect is introduced by a magnetic field dependent coupling, and the CQM effect is considered by tuning the quark mass parameter.
The rest of paper is organized as follows. Sec.II introduces our theoretical framework for meson spectra and the Mott transition in a Pauli-Villars regularized NJL model. The numerical results and discussions are presented in Sec.III, which focus on inverse magnetic catalysis effect in Sec.IIIA and current quark mass effect in Sec.IIIB. Finally, we give the summary in Sec.IV.
II Framework
The two-flavor NJL model is defined through the Lagrangian density in terms of quark fields njl1 ; njl2 ; njl3 ; njl4 ; njl5 ; zhuang
| (1) |
Here the covariant derivative couples quarks with electric charge to the external magnetic field in -direction through the potential . is the current quark mass, which determines the explicit breaking of chiral symmetry. is the coupling constant in scalar and pseudo-scalar channels, which determines the spontaneously breaking of chiral symmetry and isospin symmetry.
In NJL model, mesons are constructed through quark bubble summations in the frame of random phase approximation njl2 ; njl3 ; njl4 ; njl5 ; zhuang ,
| (2) |
where represents the meson propagator from to in coordinate space, and the corresponding meson polarization function is the quark bubble,
| (3) |
with the meson vertex
the quark propagator matrix in flavor space , and the trace in spin, color and flavor spaces.
According to the Goldstone’s theorem, the pseudo-Goldstone mode of chiral (isospin) symmetry breaking under external magnetic field is the neutral pion (charged pions ) gold1 ; gold2 . The charged pions are no longer the pseudo-Goldstone modes since their direct interaction with magnetic field.
II.0.1 neutral pion
The neutral pion is affected by external magnetic field only through the pair of charged constituent quarks, and its propagator in momentum space can be derived as
| (4) |
with the polarization function and conserved momentum of meson under external magnetic field.
The meson pole mass is defined as the pole of the propagator at zero momentum ,
| (5) |
At nonzero magnetic field, the three-dimensional quark momentum integration in the polarization function becomes a one-dimensional momentum integration and a summation over the discrete Landau levels. The polarization function can be simplified
| (6) |
and
with the summation over all flavors and Landau energy levels, spin factor , quark energy , and Fermi-Dirac distribution function .
The (dynamical) quark mass is determined by the gap equation,
| (7) |
During the chiral symmetry restoration, the quark mass decreases, and the mass increases, as guaranteed by the Goldstone’s theorem gold1 ; gold2 . When the mass is beyond the threshold
| (8) |
the decay channel opens, which defines the Mott transition mott1 ; zhuang ; mott2 ; mott3 .
From the explicit expression of in Eq(6), the factor in the integrated function of becomes at . When we do the integration over , the in the denominator leads to the infrared divergence at the lowest Landau level . Therefore, is not a solution of the pole equation, and there must be a mass jump for meson at the Mott transition. This mass jump is a direct result of the quark dimension reduction mao2 ; maocharge ; q2 ; q3 ; yulang2010.05716 , and independent of the parameters and regularization schemes of NJL model. When the magnetic field disappears, there is no more quark dimension reduction, the integration becomes finite at , and there is no more such a mass jump. It should be mentioned that in chiral limit, no such mass jump happens for meson even under external magnetic field, which has been analytically proved in our previous work mao1 .
II.0.2 charged pions
When constructing charged mesons through quark bubble summations, we should take into account of the interaction between charged mesons and magnetic fields. The charged pions with zero spin are Hermite conjugation to each other, they have the same mass at finite temperature and magnetic field.
The meson propagator can be expressed in terms of the polarization function maocharge ; mao11 ; maopion ,
| (9) |
where is the conserved Ritus momentum of meson under magnetic fields.
The meson pole mass is defined through the pole of the propagator at zero momentum ,
| (10) |
and
| (11) | |||||
| (13) | |||||
with -quark energy , -quark energy , and summations over Landau levels of and quarks in .
The quark dimension reduction also leads to infrared () singularity of the quark bubble at some Landau level and some temperature mao1 ; mao2 , and thus there is no solution of the corresponding pole equation for the meson mass in this case. Because the spins of and quarks at the lowest-Landau-level are always aligned parallel to the external magnetic field, and meson has spin zero. The two constituents at the lowest Landau level () do not satisfy the pole equation (10). Namely, they can not form a charged meson. Considering , the threshold for the singularity of is located at Landau levels and ,
| (14) |
This defines the Mott transition of meson, and a mass jump will happen. There exist other mass jumps located at , see examples in Fig.6 and Fig.12. All these mass jumps are caused by the quark dimension reduction under external magnetic field, and do not depend on the parameters and regularization schemes of NJL model.
III results and discussions
Because of the four-fermion interaction, the NJL model is not a renormalizable theory and needs regularization. In this work, we make use of the gauge invariant Pauli-Villars regularization scheme njl1 ; njl2 ; njl3 ; njl4 ; njl5 ; mao ; maocharge ; mao2 , where the quark momentum runs formally from zero to infinity. The three parameters in the Pauli-Villars regularized NJL model, namely the current quark mass MeV, the coupling constant GeV-2 and the Pauli-Villars mass parameter MeV are fixed by fitting the chiral condensate , pion mass MeV and pion decay constant MeV in vacuum with and . In our current calculations, we consider the situation with finite temperature and magnetic field and vanishing quark chemical potential .
III.1 Inverse magnetic catalysis effect
From LQCD simulations, the inverse magnetic catalysis phenomenon can be characterized either by the chiral condensates or the pseudo-critical temperature of chiral symmetry restoration lattice1 ; lattice11 ; lattice2 ; lattice3 ; lattice4 ; lattice5 ; lattice6 ; lattice7 . Therefore, to include the inverse magnetic catalysis effect in the NJL model, one approach is to fit the LQCD results of chiral condensates geb1 ; meson ; geb3 ; geb4 , and another approach is to fit the LQCD result of pseudo-critical temperature bf8 ; bf9 ; geb1 ; su3meson4 ; mao11 .
In our calculations, following Refs bf8 ; bf9 ; geb1 ; su3meson4 ; mao11 , we use a two-flavor NJL model with a magnetic field dependent coupling , which is determined by fitting the LQCD reported decreasing pseudo-critical temperature of chiral symmetry restoration lattice1 . As plotted in Fig.1, the magnetic field dependent coupling is a monotonic decreasing function of magnetic field, and it reduces at . In this paper, we fix MeV as the scale of magnetic field. As we have checked, with our fitted coupling constant , the magnetic catalysis phenomena of chiral condensates at low temperature and the inverse magnetic catalysis phenomena at high temperature can be reproduced.

III.1.1 neutral pion

With our fitted in Fig.1, we solve the gap equation (7) and pole equation (5) to obtain the meson mass at finite temperature and magnetic field with IMC effect. The results with and without IMC effect are plotted in red and blue, respectively.
Figure 2 depicts the meson mass as a function of magnetic field at vanishing temperature with (red solid line) and without (blue dashed line) inverse magnetic catalysis effect. Because in both cases the magnetic field enhances the breaking of chiral symmetry in vacuum. As the pseudo-Goldstone boson, the meson masses are decreasing functions of magnetic field with and without IMC effect. We observe a lower value for , when including the IMC effect. Similar conclusion is obtained in Refs meson ; su3meson4 , where inverse magnetic catalysis effect is introduced into the two-flavor and three-flavor NJL models.

In Fig.3, we plot the meson mass at finite temperature and fixed magnetic field . With (red lines) and without (blue lines) inverse magnetic catalysis effect, the mass spectra have the similar structure. increases at low temperature region and jumps at the Mott transition . After that, it firstly decreases and then increases with temperature. The inverse magnetic catalysis effect leads to some quantitative modifications. For instance, Mott transition temperature is shifted to a lower value, and becomes lower (higher) at ().

Figure 4 shows the Mott transition temperature of meson as a function of magnetic field, with (red solid line) and without (blue dashed line) inverse magnetic catalysis effect. Without IMC effect, the decreases with the magnetic field in weak magnetic field region , becomes flat in medium magnetic field region and decreases in strong magnetic field region . With IMC effect, the flat structure of Mott transition temperature disappears and monotonically decreases with magnetic field. Furthermore, at fixed magnetic field, has a lower value when including IMC effect.
III.1.2 charged pion
With our fitted in Fig.1, we solve the gap equation (7) and pole equation (10) to obtain meson mass at finite temperature and magnetic field with IMC effect. The results with and without IMC effect are plotted in red and blue, respectively.
As shown in Fig.5, with and without IMC effect, are increasing functions of magnetic field, and no decreasing behavior is observed at vanishing temperature. With IMC effect, has a lower value than without IMC effect, and the deviation becomes larger at stronger magnetic field. Similar results are obtained in three-flavor NJL model including IMC effect su3meson4 .

In Fig.6, we make comparison of as a function of temperature at fixed magnetic field with (red lines) and without (blue lines) inverse magnetic catalysis effect. They show similar structure. decreases in the low temperature region. At the Mott transition , shows the first jump, and two other mass jumps happen at and . With , first decreases and then increases with temperature. With and , decreases with temperature. At high enough temperature, becomes independent of temperature and IMC effect. In the low and high temperature regions, with IMC effect is smaller than without IMC effect. The value of MeV, MeV and MeV are different for the cases with and without IMC effect, which indicates that IMC effect lowers down the temperatures of meson mass jumps.

Figure 7 is the Mott transition temperature of meson as a function of magnetic field, with (red solid line) and without (blue dashed line) inverse magnetic catalysis effect. A fast increase of occurs when turning on external magnetic field, where a peak structure around shows up. Without IMC effect, the decreases with magnetic field and then increases, which are associated with some oscillations. With IMC effect, the decreases as magnetic field goes up, which is also accompanied with some oscillations. At fixed magnetic field, has a lower value, when including IMC effect, .
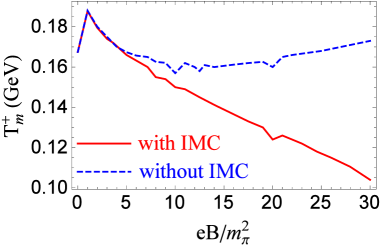
III.2 Current quark mass effect
In this part, we consider the effect of current quark mass on mass spectra and Mott transition of charged pions. The results are plotted with black, blue, red, cyan and magenta lines, respectively, corresponding to MeV. In numerical calculations, we only change the parameter and keep other parameters intact in our NJL model.
III.2.1 neutral pion

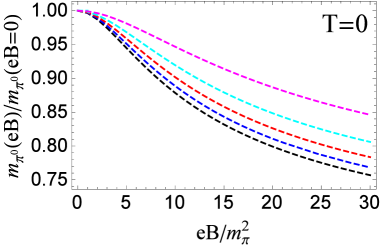
Figure 8 plots the meson mass and normalized meson mass as a function of magnetic field at vanishing temperature with different current quark mass MeV. Because the current quark mass determines the explicit breaking of chiral symmetry. As the pseudo-Goldstone boson, the mass of meson will increase with current quark mass when fixing magnetic field and vanishing temperature. On the other side, magnetic field plays the role of catalysis for spontaneous breaking of chiral symmetry when fixing current quark mass and vanishing temperature, and this will lead to a decreasing . As shown in Fig.8, with fixed magnetic field, becomes larger with larger . Moreover, the deviation between with different looks independent of the magnetic field. With fixed current quark mass, is a decreasing function of magnetic field. Similar as , the normalized meson mass increases with the current quark mass when fixing magnetic field, and decreases with magnetic field when fixing , which are consistent with LQCD results l4 .


In Fig.9, we depict the meson mass and normalized meson mass as a function of temperature with fixed magnetic field and different current quark mass MeV. They show similar structure. slightly increases with temperature, and a mass jump happens at the Mott transition . After Mott transition, first decreases and then increases with temperature. However, there exist some quantitative difference. With larger current quark mass, the is larger in the whole temperature region, and the Mott transition temperature is lower. At high enough temperature, will become degenerate due to the strong thermal motion of constituent quarks. Different from meson mass , the normalized meson mass is larger with smaller current quark mass, and the deviation between different is larger with higher temperature.

The Mott transition temperature of meson is plotted as a function of magnetic field in Fig.10 with different current quark mass MeV. For a lower value of current quark mass MeV, the Mott transition temperature decreases with weak magnetic field , slightly increases in medium magnetic field region and decreases again in strong magnetic field region . For MeV, we obtain a flat curve for the Mott transition temperature in medium magnetic field region , and in weak and strong magnetic field regions, the Mott transition temperature decreases. With the larger value of current quark mass MeV, the Mott transition temperatures are monotonic decreasing functions of magnetic field. In weak magnetic field region, is higher for larger , but in strong magnetic field region, is lower for larger .
In the end of this section, we make some comment on chiral limit with . As discussed in our previous paper mao1 , in chiral limit, the Goldstone boson is massless in chiral breaking phase and its mass continuously increases with temperature in chiral restored phase. The Mott transition temperature is the same as the critical temperature of chiral restoration phase transition, and it increases with magnetic field. Moreover, no mass jump occurs for meson at the Mott transition with or without external magnetic field.
III.2.2 charged pion


Figure 11 shows meson mass and normalized mass as a function of magnetic field with vanishing temperature and different current quark mass MeV. is an increasing function of magnetic field when fixing . With fixed magnetic field, larger value of leads to larger . In weak magnetic field region, the effect is more obvious than in strong magnetic field region, which is indicated by the larger difference of between different cases. However, with fixed magnetic field, the normalized meson mass decreases as goes up, which is consistent with LQCD results l4 .

meson mass is plotted as a function of temperature with fixed magnetic field and different current quark mass MeV in Fig.12. has several mass jumps for all considered current quark mass , which happen at temperature , , , successively. With low temperature , becomes larger with larger . With and , are also larger with larger , but the value of is very close for different . With , changes nonmonotonically with . It is clearly shown that the temperatures with mass jump depend on current quark mass. Within the considered temperature region GeV, we observe three jumps in case of current quark mass MeV, four jumps in case of MeV. For MeV, the first mass jump occurs at GeV, which is beyond the scope of Fig.12.

Figure 13 plots Mott transition temperature of meson as a function of magnetic field with different current quark mass MeV. shows similar behavior when varying current quark mass. Accompanied with some oscillations, increases fast in weak magnetic field region, decreases in medium magnetic field region and slightly increases in strong magnetic field region. With larger current quark mass, Mott transition temperature becomes higher. Note that in case of MeV, the increasing behavior of appears in very strong magnetic field, which is beyond the scope of Fig.13.
IV summary
Mass spectra and Mott transition of pions at finite temperature and magnetic field are investigated in a two-flavor NJL model, and we focus on the inverse magnetic catalysis effect and current quark mass effect.
We consider the inverse magnetic catalysis effect by introducing a magnetic dependent coupling constant into NJL model, which is a monotonic decreasing function of magnetic field. The mass spectra of pions at finite temperature and/or magnetic field are not changed qualitatively by IMC effect. At the Mott transition, the mass jumps of pions happen. Without IMC effect, the Mott transition temperature of meson decreases with magnetic field, but shows a flat structure in medium magnetic field region. With IMC effect, the flat structure of disappears and is a monotonic decreasing function of magnetic field. For charged pions , the Mott transition temperature is not a monotonic function of magnetic field. Without IMC effect, it fast increases in weak magnetic field region, decreases in the medium magnetic field region and slightly increases in strong magnetic field region, which are accompanied with some oscillations. When including IMC effect, the increasing behavior of in strong magnetic field is changed into a decreasing behavior.
The current quark mass effect is studied in non-chiral limit. The masses of pions at vanishing temperature increases as the current quark mass goes up. However, the normalized masses change differently. For meson, increases with . For meson, decreases with . These properties are consistent with LQCD simulations. At the Mott transition, the mass jumps of pions happen. The Mott transition temperature of meson is qualitatively modifies by current quark mass effect. With a low value of current quark mass MeV, decreases with weak magnetic field, slightly increases in the medium magnetic field region, and decreases again in the strong magnetic field region. With MeV, we obtain a flat curve for in the medium magnetic field region, and in the weak and strong magnetic field region, decreases. With a larger value of current quark mass, such as MeV, is a monotonic decreasing functions of magnetic field. In the weak magnetic field region, the Mott transition temperature is higher for larger , but in the strong magnetic field region, the Mott transition temperature is lower for larger . For meson, the Mott transition temperature is only quantitatively modifies by current quark mass effect. Associated with some oscillations, increases fast in the weak magnetic field region, decreases in the medium magnetic field region and slightly increases in the strong magnetic field region. With larger , becomes higher.
Due to the interaction with magnetic field, the charged pions show different behavior from the neutral pion . One common character of pions is the mass jump at their Mott transitions, which is induced by the dimension reduction of the constituent quarks, and independent on the IMC effect and CQM effect. As a consequence of such jumps, it may result in some interesting phenomena in relativistic heavy ion collisions where the strong magnetic field can be created. For instance, when the formed fireball cools down, there might be sudden enhancement/suppression of pions.
Acknowledgement:
Dr. Luyang Li is supported by Natural Science Basic Research Plan in Shaanxi Province of China (Program No.2023-JC-YB-570). Prof. Shijun Mao is supported by the NSFC Grant 12275204 and Fundamental Research Funds for the Central Universities.
References
- (1) C. M. Ko, Z. G. Wu, L. H. Xia and G. E. Brown, Phys. Rev. Lett. 66, 2577 (1991) [Erratum-ibid. 67, 1811 (1991)].
- (2) G. Q. Li and G. E. Brown, Phys. Rev. C 58, 1698 (1998)
- (3) K. Paech, A. Dumitru, J. Schaffner-Bielich, H. Stoecker, G. Zeeb, D. Zschiesche and S. Schramm, Acta Phys. Hung. A 21, 151 (2004).
- (4) J. Rafelski and B. Muller, Phys. Rev. Lett. 36, (1976) 517.
- (5) D. E. Kharzeev, L. D. McLerran and H. J. Warringa, Nucl. Phys. A 803, (2008) 227.
- (6) V. Skokov. A. Y. Illarionov and T. Toneev, Int. J. Mod. Phys. A 24, (2009) 5925.
- (7) W. T. Deng and X. G. Huang, Phys. Rev. C 85, (2012) 044907; Phys. Lett. B 742, (2015) 296.
- (8) K. Tuchin, Adv. High Energy Phys. (2013) 490495.
- (9) N. Agasian and I. Shushpanov, J. High Energy Phys. 10 (2001) 006.
- (10) G. Colucci, E. Fraga and A. Sedrakian, Phys. Lett. B 728, 19 (2014).
- (11) J. Anderson, J. High Energy Phys. 10 (2012) 005, Phys. Rev. D 86, 025020 (2012).
- (12) K. Kamikado and T. Kanazawa, J. High Energy Phys. 03 (2014) 009.
- (13) G. Krein,and C. Miller, Symmetry, 13(4): 551 (2021).
- (14) A. Ayala, J. L. Hernndez, L. A. Hernndez, R. L. S. Farias, R. Zamora, Phys. Rev. D 103, 054038 (2021).
- (15) R. M. Aguirre, Phys. Rev. D 96, 096013 (2017).
- (16) A. Ayala, R. L. S. Farias, S. Hernández-Ortiz, L. A. Hernández, D. M. Paret and R. Zamora, Phys. Rev. D 98, 114008 (2018).
- (17) A. N. Tawfik, A. M. Diab and T. M. Hussein, Chin. Phys. C 43, 034103 (2019).
- (18) A. Das and N. Haque, Phys. Rev. D 101, 074033 (2020).
- (19) G. S. Bali, F. Bruckmann, G. Endrődi, Z. Fodor, S. D. Katz, S. Krieg, A. Schäfer and K. K. Szabó, J. High Energy Phys. 02 (2012) 044.
- (20) Y. Hidaka and A. Yamatomo, Phys. Rev. D 87, 094502 (2013).
- (21) E. Luschevskaya, O. Solovjeva, O. Kochetkov and O. Teryaev, Nucl. Phys. B 898, 627 (2015).
- (22) G. S. Bali, B. Brandt, G. Endrődi and B. Gläßle, PoS LATTICE 2015, 265 (2016).
- (23) E. Luschevskaya, O. Solovjeva and O. Teryaev, Phys. Lett. B 761, 393 (2016).
- (24) G. S. Bali, B. Brandt, G. Endrődi and B. Gläßle, Phys. Rev. D 97, 034505 (2018).
- (25) H. T. Ding, S. T. Li, A. Tomiya, X. D. Wang and Y. Zhang, Phys. Rev. D 104, 014505 (2021).
- (26) H. T. Ding, S. T. Li, J. H. Liu, and X. D. Wang, Phys. Rev. D 105, 034514 (2022).
- (27) S. Klevansky, Rev. Mod. Phys. 64, 649 (1992).
- (28) S. Fayazbakhsh, S. Sadeghian and N. Sadooghi, Phys. Rev. D 86, 085042 (2012).
- (29) S. Fayazbakhsh and N. Sadooghi, Phys. Rev. D 88, 065030 (2013).
- (30) V. D. Orlovsky and Y. A. Simonov, J. High Energy Phys. 09 (2013) 136.
- (31) R. Zhang, W. J. Fu and Y. X. Liu, J. Eur. Phys. C 76, 307 (2016).
- (32) S. Avancini, W. Travres and M. Pinto, Phys. Rev. D 93, 014010 (2016).
- (33) K. Hattori, T. Kojo and N. Su, Nucl. Phys. A 951, 1 (2016).
- (34) Y. A. Simonov, Phys. Atom. Nucl. 79, 455 (2016). [Yad. Fiz. 79, 277 (2016)].
- (35) M. A. Andreichikov, B. O. Kerbikov, E. V. Luschevskaya, Y. A. Simonov and O. E. Solovjeva, J. High Energy Phys. 05 (2017) 007.
- (36) S. Avancini, R. Farias, M. Pinto, W. Travres and V. Timteo, Phys. Lett. B 767, 247 (2017).
- (37) S. J. Mao and Y. X. Wang, Phys. Rev. D 96, 034004 (2017).
- (38) M. A. Andreichikov and Y. A. Simonov, Eur. Phys. J. C 78, 902 (2018).
- (39) C. A. Dominguez, M. Loewe and C. Villavicencio, Phys. Rev. D 98, 034015 (2018).
- (40) Z. Y. Wang and P. F. Zhuang, Phys. Rev. D 97, 034026 (2018).
- (41) M. Coppola, D. Dumm and N. Scoccola, Phys. Lett B 782, 155 (2018).
- (42) H. Liu, X. Wang, L. Yu and M. Huang, Phys. Rev. D 97, 076008 (2018).
- (43) D. G. Dumm, M. I. Villafañe and N. N. Scoccola, Phys. Rev. D 97, 034025 (2018).
- (44) S. S. Avancini, R. L. S. Farias and W. R. Tavares, Phys. Rev. D 99, 056009 (2019).
- (45) N. Chaudhuri, S. Ghosh, S. Sarkar and P. Roy, Phys. Rev. D 99, 116025 (2019).
- (46) M. Coppola, D. G. Dumm, S. Noguera and N. N. Scoccola, Phys. Rev. D 100, 054014 (2019).
- (47) J. Y. Chao, Y. X. Liu and L. Chang, arXiv: 2007.14258.
- (48) S. J. Mao, Phys. Rev. D 99, 056005 (2019).
- (49) J. Moreira, P. Costa, and T. E. Restrepo, Phys. Rev. D 102, 014032 (2020).
- (50) D. N. Li, G. Q. Cao and L. Y. He, Phys. Rev. D 104, 074026 (2021).
- (51) B. K. Sheng, Y. Y. Wang, X. Y. Wang, L. Yu, Phys. Rev. D 103, 094001 (2021).
- (52) S. J. Mao, Chin. Phys. C 45, 021004 (2021).
- (53) K. Xu, J.Y. Chao and M. Huang, Phys. Rev. D 103, 076015 (2021).
- (54) S. S. Avancini, M. Coppola, N. N. Scoccola, and J. C. Sodré, Phys. Rev. D 104, 094040 (2021).
- (55) S. J. Mao and Y. M. Tian, Phys. Rev. D 106, 094017 (2022).
- (56) L. Y. Li and S. J. Mao, Chin. Phys. C 46, 094105 (2022).
- (57) J. P. Carlomagno, D. G. Dumm, M. F. I. Villafae, S. Noguera, and N. N. Scoccola, Phys. Rev. D 106, 094035 (2022).
- (58) J. P. Carlomagno, D. G. Dumm, S. Noguera, and N. N. Scoccola, Phys. Rev. D 106, 074002 (2022).
- (59) J. Mei and S.J. Mao, Phys. Rev. D 107, 074018 (2023).
- (60) G. S. Bali, F. Bruckmann, G. Endrdi, Z. Fodor, S. D. Katz, S. Krieg, A. Schfer and K. K. Szab, Phys. Rev. D 86, 071502 (2012).
- (61) G. S. Bali, F. Bruckmann, G. Endrdi, F. Gruber and A. Schfer, J. High Energy Phys. 04, 130(2013).
- (62) V. Bornyakov, P.V. Buividovich, N. Cundy, O. A. Kochetkov and A. Schfer, Phys. Rev. D 90, 034501 (2014).
- (63) E. M. Ilgenfritz, M. Muller-Preussker, B. Petersson and A. Schreiber, Phys. Rev. D 89, 054512 (2014).
- (64) G. Endrdi, J. High Energy Phys. 07, 173 (2015).
- (65) M. D’Elia, F. Manigrasso, F. Negro and F. Sanfilippo, Phys. Rev. D 98, 054509 (2018).
- (66) G. Endrdi, M. Giordano, S. D. Katz, T. G. Kovacs and F. Pittler, J. High Energy Phys. 07, 009 (2019).
- (67) A. Tomiya, H.T. Ding, X.D. Wang, Y. Zhang, S. Mukherjee and C. Schmidt, PoS Lattice2018, 163 (2019).
- (68) E. S. Fraga and A. J. Mizher, Phys. Rev. D 78, 025016 (2008).
- (69) C. V. Johnson and A. Kundu, J. High Energy Phys. 12, 053 (2008).
- (70) A. J. Mizher, M. N. Chernodub and E. S. Fraga, Phys. Rev. D 82, 105016 (2010).
- (71) K. Fukushima, M. Ruggieri and R. Gatto, Phys. Rev. D 81, 114031 (2010).
- (72) R. Gatto and M. Ruggieri, Phys. Rev. D 82, 054027 (2010); Phys. Rev. D 83, 034016 (2011).
- (73) F. Preis, A. Rebhan and A. Schmitt, J. High Energy Phys. 03, 033 (2011).
- (74) V. Skokov, Phys. Rev. D 85, 034026 (2012).
- (75) E. S. Fraga, J. Noronha and L. F. Palhares, Phys. Rev. D 87, 114014 (2013).
- (76) K. Fukushima and Y. Hidaka, Phys. Rev. Lett 110, 031601 (2013).
- (77) J. Y. Chao, P. C. Chu and M. Huang, Phys. Rev. D 88, 054009 (2013).
- (78) F. Bruckmann, G. Endrdi and T. G. Kovacs, arXiv: 1311.3178.
- (79) T. Kojo and N. Su, Phys. Lett. B 720, 192 (2013).
- (80) F. Bruckmann, G. Endrodi and T. G. Kovacs, J. High Energy Phys. 04, 112 (2013).
- (81) A. Ayala, M. Loewe, A. Jlia Mizher and R. Zamora, Phys. Rev. D 90, 036001 (2014).
- (82) A. Ayala, L. Alberto Hernndez, A. Jlia Mizher, J. Cristbal Rojas and C. Villavicencio, Phys. Rev. D 89, 116017 (2014).
- (83) R. L. S. Farias, K. P. Gomes, G. Krein and M. B. Pinto, Phys. Rev. C 90, 025203 (2014).
- (84) M. Ferreira, P. Costa, O. Lourenco, T. Frederico and C. Providncia, Phys. Rev. D 89, 116011 (2014).
- (85) M. Ferreira, P. Costa and C. Providncia, Phys. Rev. D 89, 036006 (2014).
- (86) M. Ferreira, P. Costa, D. P. Menezes, C. Providncia and N. N. Scoccola, Phys. Rev. D 89, 016002 (2014).
- (87) P. Costa, M. Ferreira, H. Hansen, D. P. Menezes and C. Providncia, Phys. Rev. D 89, 056013 (2014).
- (88) E. J. Ferrer, V.de la Incera, I. Portillo and M. Quiroz, Phys. Rev. D 89, 085034 (2014).
- (89) A. Ayala, C. A. Dominguez, L. A. Hernndez, M. Loewe and R. Zamora, Phys. Rev. D 92, 096011 (2015).
- (90) N. Mueller and J.M. Pawlowski, Phys. Rev. D 91, 116010 (2015).
- (91) E. J. Ferrer, V.de la Incera and X. J. Wen, Phys. Rev. D 91, 054006 (2015).
- (92) J. Braun, W. A. Mian and S. Rechenberger, Phys. Lett. B 755, 265 (2016).
- (93) S. J. Mao, Phys. Lett. B 758, 195 (2016); Phys. Rev. D 94, 036007 (2016); Phys. Rev. D 97, 011501(R) (2018).
- (94) J. Mei and S.J. Mao, Phys. Rev. D 102, 114035 (2020).
- (95) A. Ayala, L. A. Hernndez, M. Loewe and C. Villavicencio, Eur. Phys. J. A 57, 234 (2021).
- (96) S. J. Mao, Phys. Rev. D 106, 034018 (2022).
- (97) Y. Nambu and G. Jona-Lasinio, Phys. Rev. 122, 345 (1961) and 124, 246 (1961).
- (98) M. K. Volkov, Phys. Part. Nucl. 24, 35 (1993).
- (99) T. Hatsuda and T. Kunihiro, Phys. Rep. 247, 221 (1994).
- (100) M. Buballa, Phys. Rep. 407, 205 (2005).
- (101) P. Zhuang, J. Hfner, S. P. Klevansky, Nucl. Phys. A 576, 525 (1994).
- (102) J. Goldstone, Nuovo Cim. 19, 154-164 (1961).
- (103) J. Goldstone, A. Salam and S. Weinberg, Phys. Rev. 127, 965-970 (1962).
- (104) N. F. Mott, Rev. Mod. Phys. 40, 677 (1968).
- (105) J. Huefner, S. Klevansky, and P. Rehberg, Nucl. Phys. A 606, 260 (1996).
- (106) P. Costa, M. Ruivo, and Y. Kalinovsky, Phys. Lett. B 560, 171 (2003).
- (107) H. Liu, L. Yu, M. Chernodub and M. Huang, Phys. Rev. D 94, 113006 (2016).
- (108) A. Ayala, C. A. Dominguez, L. A. Hernndez, M. Loewe, A. Raya, J. C. Rojas and C. Villavicenico, Phys. Rev. D 94, 054019 (2016).
- (109) R. L. S. Farias, V. S. Timoteo, S. S. Avancini, M. B. Pinto and G. Klein, Eur. Phys. J. A 53, 101 (2017).