Intrinsic Superconducting Diode Effect
Abstract
Stimulated by the recent experiment [F. Ando et al., Nature 584, 373 (2020)], we propose an intrinsic mechanism to cause the superconducting diode effect (SDE). SDE refers to the nonreciprocity of the critical current for the metal-superconductor transition. Among various mechanisms for the critical current, the depairing current is known to be intrinsic to each material and has recently been observed in several superconducting systems. We clarify the temperature scaling of the nonreciprocal depairing current near the critical temperature and point out its significant enhancement at low temperatures. It is also found that the nonreciprocal critical current shows sign reversals upon increasing the magnetic field. These behaviors are understood by the nonreciprocity of the Landau critical momentum and the change in the nature of the helical superconductivity. The intrinsic SDE unveils the rich phase diagram and functionalities of noncentrosymmetric superconductors.
Introduction. — Rectification by the semiconductor diode is one of the central building blocks of electronic devices. Apart from the nonreciprocity induced by asymmetric junctions, it has been revealed that nonreciprocal transport can be obtained as a bulk property of materials Tokura and Nagaosa (2018); Ideue and Iwasa (2021). Magnetochiral anisotropy (MCA) Rikken et al. (2001); Krstić et al. (2002); Pop et al. (2014); Rikken and Wyder (2005); Ideue et al. (2017); Wakatsuki and Nagaosa (2018); Hoshino et al. (2018); Wakatsuki et al. (2017); Qin et al. (2017); Yasuda et al. (2019); Itahashi et al. (2020) is an example, described by the equation Here , , and are the resistance, electric current, and the magnetic field, respectively. The coefficient gives rise to different resistance for rightward and leftward electric currents and can be finite in noncentrosymmetric materials. MCA has been observed in (semi)conductors Rikken and Wyder (2005); Ideue et al. (2017); Krstić et al. (2002); Pop et al. (2014) as well as in superconductors Wakatsuki et al. (2017); Qin et al. (2017); Yasuda et al. (2019); Itahashi et al. (2020), and allows us to access various aspects of noncentrosymmetric materials: from spin-orbit splitting in the band structure Ideue et al. (2017) to the spin-singlet and -triplet mixing of Cooper pairs Wakatsuki et al. (2017); Wakatsuki and Nagaosa (2018); Hoshino et al. (2018)
MCA is the inequivalence of and , where both usually take finite values. On the other hand, such a drastic situation is possible in superconductors that either one of vanishes while the other remains finite [Fig. 1]. Such a superconducting diode effect (SDE) has recently been observed in the Nb/V/Ta superlattice without an inversion center and is controlled by the applied inplane magnetic field Ando et al. (2020). This is the first report of the SDE in a bulk material, while similar effects have been recognized in engineered systems Reynoso et al. (2008); Zazunov et al. (2009); Margaris et al. (2010); Yokoyama et al. (2014); Silaev et al. (2014); Campagnano et al. (2015); Dolcini et al. (2015); Chen et al. (2018); Minutillo et al. (2018); Pal and Benjamin (2019); Kopasov et al. (2021) and followed by recent SDE experiments Baumgartner et al. (2021); Lyu et al. (2021). SDE is a promising building block of the dissipationless electric circuits, and is a fascinating phenomenon manifesting the interplay of the inversion breaking and superconductivity. One of the remaining issues is to identify suitable materials providing the best performance; however, the mechanisms to cause SDE in a bulk material Ando et al. (2020) have not been clarified, while the SDE in artificial devices Lyu et al. (2021); Baumgartner et al. (2021) has been well simulated by Bogoliubov-de Gennes (BdG) Baumgartner et al. (2021) and time-dependent Ginzburg-Landau (GL) theories Lyu et al. (2021).
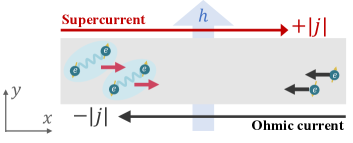
SDE is the nonreciprocity of the critical current for the resistive transition. In usual situations, in particular, under out-of-plane magnetic fields, the resistive transition is caused by the vortex motion. The details of the vortex motion depend on the device setup such as impurity concentrations Blatter et al. (1994), and in turn, has an advantage of tunability by the nanostructure engineering Villegas et al. (2003); Lyu et al. (2021). Apart from the extrinsic mechanisms to cause resistivity, the depairing current is known as the critical current unique to each superconducting material. Here, the metal-superconductor transition is literally caused by the dissociation of the flowing Cooper pairs Tinkham (2004); Dew-Hughes (2001). The depairing current always gives the upper limit of the critical current and is an important material parameter characterizing superconductors Blatter et al. (1994). The depairing limit generally requires a huge current density, but is within the scope of experimental techniques. Indeed, the depairing limit has recently been achieved in the microbridge superconducting devices of YBa2Cu3O7-δ Nawaz et al. (2013), Ba0.5K0.5Fe2As2 Li et al. (2013), and Fe1+yTe1-xSex Sun et al. (2020).
In this Letter, as a first step of the theoretical research on SDE of bulk materials, we propose the intrinsic mechanism of SDE by studying the nonreciprocity in the depairing current. The results can be tested with the microbridge experiments and establish the foundation of the future study on the bulk SDE. Furthermore, it is revealed that the intrinsic SDE is closely related to the Flude-Ferrell-Larkin-Ovchinnikov state Larkin and Ovchinnikov (1964); Fulde and Ferrell (1964). While the Larkin-Ovchinnikov (LO) state with the spatially inhomogeneous pair potential has been discussed for FeSe Kasahara et al. (2014, 2020), CeCoIn5 Matsuda and Shimahara (2007) and organic superconductors Wosnitza (2018), the Flude-Fellel (FF) type order parameter is known to ubiquitously appear in noncentrosymmetric superconductors and is particularly called the helical superconductivity Bauer and Sigrist (2012); Smidman et al. (2017); Agterberg (2003); Barzykin and Gor’kov (2002); Dimitrova and Feigel’man (2003); Kaur et al. (2005); Agterberg and Kaur (2007); Dimitrova and Feigel’man (2007); Samokhin (2008); Yanase and Sigrist (2008); Bauer and Sigrist (2012); Michaeli et al. (2012); Sekihara et al. (2013); Houzet and Meyer (2015). Implications of the helical superconductivity have been obtained in thin films of Pb Sekihara et al. (2013) and doped SrTiO3 Schumann et al. (2020), and a heavy-fermion superlattice Naritsuka et al. (2017, 2021). We show that the intrinsic SDE works as a probe to study the phase diagram of helical superconductivity. Relation to the recent experiments Ando et al. (2020); Ono et al. is also discussed.
Model. — We consider the critical current in two-dimensional (2D) superconductors with a polar axis due to the substrate and/or the crystal structure. The magnetic field is applied along the direction, which makes the critical current nonreciprocal in the direction [Fig. 1]. The system is modeled by the Rashba-Zeeman Hamiltonian with the attractive Hubbard interaction,
| (1) |
Here, and represent the hopping energy and the Rashba spin-orbit coupling, respectively. The magnetic field in the direction is introduced by the Zeeman term . The parameters are given by unless mentioned otherwise. The next-nearest-neighbor hopping is introduced for the latter use. The energy dispersion of the noninteracting part is given by . Here, each band is labeled by the helicity , and the momentum shift under is given by with . The momentum shift is estimated by its Fermi-surface (FS) average, .
We solve the model (1) within the mean-field approximation. The attractive Hubbard interaction is approximated by
| (2) |
The -wave pair potential is considered with a center-of-mass momentum to describe the current-flowing state. For a given , the value of is determined self-consistently by the gap equation with the temperature . To describe the superconducting transitions and the supercurrent, it is convenient to introduce the condensation energy for each , that is, the difference of the free energy per unit area in the normal and superconducting states. The sheet current density is obtained by , which coincides with the expectation value of the current operator Sup .
When an electric current is applied, the superconducting state with satisfying should be realized. However, no superconducting state can sustain when or , with and Thus, the depairing current in the positive and negative directions is given by the maximum and minimum of , respectively. In particular, the nonreciprocal component is given by
| (3) |
The SDE is identified with a finite of the system. We also define the averaged critical current , by which the strength of the nonreciprocal nature can be expressed as .
GL analysis. — First, we discuss the SDE by the GL theory. The GL free energy gives a good approximation of near the transition temperature when the optimized order parameter is substituted. The GL coefficients are assumed to have the following form: , and , which is valid for the description up to . When the higher-order gradient terms are neglected, the broken inversion and time-reversal symmetries are encoded solely into , which shifts the minimum of from to . Thus, the superconducting state with a finite , namely the helical superconductivity is realized Agterberg (2003); Smidman et al. (2017). The helical superconducting state with does not carry a supercurrent Agterberg (2003); Dimitrova and Feigel’man (2003, 2007), as the most stable state generally should be.
It is convenient to rewrite the GL coefficients as and , where the linear term in is erased. Clearly, for is equivalent to the GL free energy of a centrosymmetric superconductor, leading to a reciprocal critical current Smidman et al. (2017). Thus, the SDE is caused by the higher-order terms, and ,
| (4) |
up to first order in and Sup . Note that in contrast to the averaged critical current Tinkham (2004); Sup , since . Thus, a small but finite is predicted by the GL theory, while a larger is expected at low temperatures. The result obtained here is valid for general noncentrosymmetric superconductors without orbital depairing effect, e.g., superconducting thin films under inplane magnetic fields.
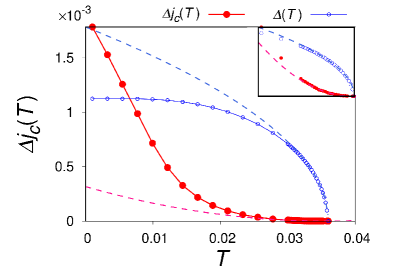
Critical current under low fields. — Equipped with the insight of the GL theory, we discuss the temperature dependence of based on the model (1). The result is shown in Fig. 2 for . As shown in the inset, the temperature scaling is confirmed near the transition temperature . The scaling law becomes inaccurate as gets large, where also deviates from . Importantly, is strongly enhanced at low temperatures.
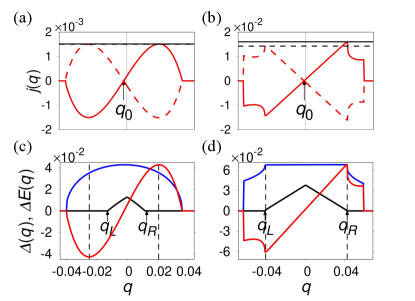
To clarify the origin of the SDE, we show by red lines in Figs. 3. In Fig. 3 (a) for , is a smooth curve and its tiny asymmetry gives rise to , as is illustrated by the difference of the solid and dashed horizontal lines (indicating and ). This is consistent with the GL picture where is caused by the asymmetry factors . Two curves, and , cross at , indicating the helical superconductivity. In Fig. 3 (c), and the minimum excitation energy are shown in addition to , by the blue and black lines, respectively. The superconducting state remains stable even after the spectrum becomes gapless, and reaches the maximum and minimum of in the gapless region.
As shown in Fig. 3 (b), the dispersion of at is significantly different from that at , and a large is realized. The maximum and minimum of are achieved at the ends of the region where is almost linear in . These momenta approximately coincide with the Landau critical momenta, and , i.e. the first ’s satisfying , as is clear from Fig. 3 (d). Actually, the depairing effect takes place after or : The excited quasiparticles reduce and and finally cause a first-order phase transition into the normal state. From these observations, we obtain the formula
| (5) |
by using, e.g., with the superfluid weight . Thus, the nonreciprocal Landau critical momentum measured from gives rise to the SDE at extremely low temperatures. As gets larger, the maximum and minimum of deviate from and , and Eq. (5) becomes no longer valid. The mechanism of the SDE at low temperatures is not captured by the GL theory.
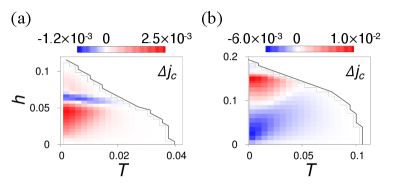
Phase diagram. — In Figs. 4 (a) and (b), we show the temperature and magnetic-field dependence of the nonreciprocal component for and . Let us focus on the low-field region, where positive and negative values of are widely obtained for Fig. 4 (a) and (b), respectively. The sign reversal of by can be understood based on Eq. (5). Indeed, we show in the Supplemental Material Sup that causes a sign reversal as increases, leading to that of as well. It is also shown that for large values of , is dominated by the nonreciprocal Landau critical momentum , while it is dominated by for small values of . A relatively large SDE for is explained by large values of as a result of the anisotropy Sup . The pronounced aspect of Fig. 4 is the sign reversals prevailing under moderate and high magnetic fields. This point will be discussed in the following.
Critical current under high fields. —
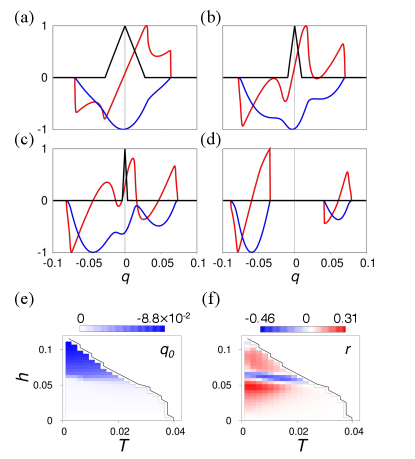
To see the origin of the high-field behavior, we show the condensation energy at for various values of in Fig. 5. To be specific, the case of Fig. 4 (a) is considered. The condensation energy shown by the blue line has a single-well structure under low magnetic fields [panel (a)]. The structure near is developed under higher magnetic fields [panel (b)], to form two local minima [panel (c)], where the left one becomes most stable. These side wells are the precursor of the high-field helical superconducting states [panel (d)], where the central minimum finally disappears. Such a change is most evident in shown in Fig. 5 (e). Under low fields, is determined by the balance of two Fermi surfaces shifted in the opposite directions, resulting in ; on the other hand, under high fields, almost coincides with of the Fermi surface with a larger density of states Dimitrova and Feigel’man (2003); Agterberg and Kaur (2007); Smidman et al. (2017); Yanase and Sigrist (2008). This determines the “crossover line” 111This terminology is named after the crossover generally seen in noncentrosymmetric superconductors, while the line changes to the first-order transition at lower temperature in this model, as in Figs.5(b)-5(d). of helical superconductivity visible at in Fig. 5 (e).
The evolution of by follows that of . Overall, consists of several almost-straight lines and their interpolation, since is approximated by the square function of around each local minimum. Comparing Figs. 5 (a) and (b), the point achieving is changed from to a critical momentum of the left well, which we name . In the panel (c), remains to give , whose value is significantly enhanced owing to the development of the left minimum. This causes the sign reversal of . In the panel (d), is determined by the tiny asymmetry of the left well. It should be noticed that the ratio shown in Fig. 5 (f) is quite large around the crossover line, takes values up to , as is understood from Figs. 5 (a)-(c). Thus, the sign reversals and huge values of under magnetic fields are caused by the change in the helical superconducting states. According to Figs. 5 (e) and (f), the sign reversal also occurs near by the crossover.
Figure 4 (b) can be understood similarly. In this case, the crossover line is identified to be Sup , where changes its sign. The high-field helical superconducting states span only a small fraction in the phase diagram. The difference from Fig. 4 (a) is another sign reversal at . In this region, is determined by the nonreciprocal Landau critical momentum, and turns out to change its sign by increasing . This is because shows nonmonotonic behavior, while grows linearly and finally becomes dominant Sup . The sign reversal survives at higher temperatures and reaches the transition temperature.
Discussion — We have revealed the sign reversals of the SDE, which is closely connected with the change in the helical superconducting states. Thus, the intrinsic SDE is a promising bulk probe directly unveiling the crossover line. This probe is complementary to the junction Kaur et al. (2005) and spectroscopy Smidman et al. (2017) experiments proposed to detect the helical superconductivity.
In the end, we briefly discuss the connection with the experimental results of SDE Ando et al. (2020). The sign reversals of by increasing the magnetic field at low temperatures have recently been observed Ono et al. , which might be explained by our results for the intrinsic SDE. An “inverse effect,” the nonreciprocity of the critical magnetic field under applied electric current, has also been reported Miyasaka et al. (2021), implying the nonreciprocity as a bulk property of the superconductor. Thus, the SDE with sign reversals implies the crossover in the superconducting state of the Nb/V/Ta superlattice. On the other hand, near seems to be at variance with the intrinsic SDE Ando et al. (2020). This point might be overcome by considering the effect of vortices, which is left as an intriguing future issue.
Acknowledgements.
We appreciate helpful discussions with T. Ono, Y. Miyasaka, R. Kawarazaki, H. Narita, and H. Watanabe. This work was supported by JSPS KAKENHI (Grants No. JP18H05227, No. JP18H01178, No. 20H05159, No. 21K13880, and No. 21J14804), JSPS research fellowship, WISE Program MEXT, and SPIRITS 2020 of Kyoto University. Note added.— During finalizing the manuscript, we became aware of independent overlapping works. A recent arXiv post by N. Yuan and L. Fu Yuan and Fu (2021) studies the depairing currrent of the Rashba-Zeeman model mainly using the GL theory. However, sign reversals of the SDE are not obtained. The work by J. He and N. Nagaosa et al. He et al. (2021) studies the related topic independently of ours. We thank J. He for coordinating submission to arXiv.References
- Tokura and Nagaosa (2018) Y. Tokura and N. Nagaosa, Nat. Commun. 9, 3740 (2018).
- Ideue and Iwasa (2021) T. Ideue and Y. Iwasa, Annu. Rev. Condens. Matter Phys. 12, 201 (2021).
- Rikken et al. (2001) G. L. Rikken, J. Fölling, and P. Wyder, Phys. Rev. Lett. 87, 236602 (2001).
- Krstić et al. (2002) V. Krstić, S. Roth, M. Burghard, K. Kern, and G. L. J. A. Rikken, J. Chem. Phys. 117, 11315 (2002).
- Pop et al. (2014) F. Pop, P. Auban-Senzier, E. Canadell, G. L. J. A. Rikken, and N. Avarvari, Nat. Commun. 5, 3757 (2014).
- Rikken and Wyder (2005) G. L. J. A. Rikken and P. Wyder, Phys. Rev. Lett. 94, 016601 (2005).
- Ideue et al. (2017) T. Ideue, K. Hamamoto, S. Koshikawa, M. Ezawa, S. Shimizu, Y. Kaneko, Y. Tokura, N. Nagaosa, and Y. Iwasa, Nat. Phys. 13, 578 (2017).
- Wakatsuki and Nagaosa (2018) R. Wakatsuki and N. Nagaosa, Phys. Rev. Lett. 121, 026601 (2018).
- Hoshino et al. (2018) S. Hoshino, R. Wakatsuki, K. Hamamoto, and N. Nagaosa, Phys. Rev. B Condens. Matter 98, 054510 (2018).
- Wakatsuki et al. (2017) R. Wakatsuki, Y. Saito, S. Hoshino, Y. M. Itahashi, T. Ideue, M. Ezawa, Y. Iwasa, and N. Nagaosa, Science Advances 3, e1602390 (2017).
- Qin et al. (2017) F. Qin, W. Shi, T. Ideue, M. Yoshida, A. Zak, R. Tenne, T. Kikitsu, D. Inoue, D. Hashizume, and Y. Iwasa, Nat. Commun. 8, 14465 (2017).
- Yasuda et al. (2019) K. Yasuda, H. Yasuda, T. Liang, R. Yoshimi, A. Tsukazaki, K. S. Takahashi, N. Nagaosa, M. Kawasaki, and Y. Tokura, Nat. Commun. 10, 2734 (2019).
- Itahashi et al. (2020) Y. M. Itahashi, T. Ideue, Y. Saito, S. Shimizu, T. Ouchi, T. Nojima, and Y. Iwasa, Science advances 6, eaay9120 (2020).
- Ando et al. (2020) F. Ando, Y. Miyasaka, T. Li, J. Ishizuka, T. Arakawa, Y. Shiota, T. Moriyama, Y. Yanase, and T. Ono, Nature 584, 373 (2020).
- Reynoso et al. (2008) A. A. Reynoso, G. Usaj, C. A. Balseiro, D. Feinberg, and M. Avignon, Phys. Rev. Lett. 101, 107001 (2008).
- Zazunov et al. (2009) A. Zazunov, R. Egger, T. Jonckheere, and T. Martin, Phys. Rev. Lett. 103, 147004 (2009).
- Margaris et al. (2010) I. Margaris, V. Paltoglou, and N. Flytzanis, J. Phys. Condens. Matter 22, 445701 (2010).
- Yokoyama et al. (2014) T. Yokoyama, M. Eto, and Y. V. Nazarov, Phys. Rev. B Condens. Matter 89, 195407 (2014).
- Silaev et al. (2014) M. A. Silaev, A. Y. Aladyshkin, M. V. Silaeva, and A. S. Aladyshkina, J. Phys. Condens. Matter 26, 095702 (2014).
- Campagnano et al. (2015) G. Campagnano, P. Lucignano, D. Giuliano, and A. Tagliacozzo, J. Phys. Condens. Matter 27, 205301 (2015).
- Dolcini et al. (2015) F. Dolcini, M. Houzet, and J. S. Meyer, Phys. Rev. B Condens. Matter 92, 035428 (2015).
- Chen et al. (2018) C.-Z. Chen, J. J. He, M. N. Ali, G.-H. Lee, K. C. Fong, and K. T. Law, Phys. Rev. B Condens. Matter 98, 075430 (2018).
- Minutillo et al. (2018) M. Minutillo, D. Giuliano, P. Lucignano, A. Tagliacozzo, and G. Campagnano, Phys. Rev. B Condens. Matter 98, 144510 (2018).
- Pal and Benjamin (2019) S. Pal and C. Benjamin, EPL 126, 57002 (2019).
- Kopasov et al. (2021) A. A. Kopasov, A. G. Kutlin, and A. S. Mel’nikov, Phys. Rev. B Condens. Matter 103, 144520 (2021).
- Baumgartner et al. (2021) C. Baumgartner, L. Fuchs, A. Costa, S. Reinhardt, S. Gronin, G. C. Gardner, T. Lindemann, M. J. Manfra, P. E. Faria Junior, D. Kochan, J. Fabian, N. Paradiso, and C. Strunk, Nat. Nanotechnol. , 10.1038/s41565 (2021).
- Lyu et al. (2021) Y.-Y. Lyu, J. Jiang, Y.-L. Wang, Z.-L. Xiao, S. Dong, Q.-H. Chen, M. V. Milošević, H. Wang, R. Divan, J. E. Pearson, P. Wu, F. M. Peeters, and W.-K. Kwok, Nat. Commun. 12, 2703 (2021).
- Blatter et al. (1994) G. Blatter, M. V. Feigel’man, V. B. Geshkenbein, A. I. Larkin, and V. M. Vinokur, Rev. Mod. Phys. 66, 1125 (1994).
- Villegas et al. (2003) J. E. Villegas, S. Savel’ev, F. Nori, E. M. Gonzalez, J. V. Anguita, R. García, and J. L. Vicent, Science 302, 1188 (2003).
- Tinkham (2004) M. Tinkham, Introduction to Superconductivity (Courier Corporation, 2004).
- Dew-Hughes (2001) D. Dew-Hughes, Low Temp. Phys. 27, 713 (2001).
- Nawaz et al. (2013) S. Nawaz, R. Arpaia, F. Lombardi, and T. Bauch, Phys. Rev. Lett. 110, 167004 (2013).
- Li et al. (2013) J. Li, J. Yuan, Y.-H. Yuan, J.-Y. Ge, M.-Y. Li, H.-L. Feng, P. J. Pereira, A. Ishii, T. Hatano, A. V. Silhanek, L. F. Chibotaru, J. Vanacken, K. Yamaura, H.-B. Wang, E. Takayama-Muromachi, and V. V. Moshchalkov, Appl. Phys. Lett. 103, 062603 (2013).
- Sun et al. (2020) Y. Sun, H. Ohnuma, S.-Y. Ayukawa, T. Noji, Y. Koike, T. Tamegai, and H. Kitano, Phys. Rev. B 101, 134516 (2020).
- Larkin and Ovchinnikov (1964) A. I. Larkin and Y. N. Ovchinnikov, Zh. Eksperim. i Teor. Fiz. 47, 1136 (1964).
- Fulde and Ferrell (1964) P. Fulde and R. A. Ferrell, Phys. Rev. 135, A550 (1964).
- Kasahara et al. (2014) S. Kasahara, T. Watashige, T. Hanaguri, Y. Kohsaka, T. Yamashita, Y. Shimoyama, Y. Mizukami, R. Endo, H. Ikeda, K. Aoyama, T. Terashima, S. Uji, T. Wolf, H. von Löhneysen, T. Shibauchi, and Y. Matsuda, Proc. Natl. Acad. Sci. U. S. A. 111, 16309 (2014).
- Kasahara et al. (2020) S. Kasahara, Y. Sato, S. Licciardello, M. Čulo, S. Arsenijević, T. Ottenbros, T. Tominaga, J. Böker, I. Eremin, T. Shibauchi, J. Wosnitza, N. E. Hussey, and Y. Matsuda, Phys. Rev. Lett. 124, 107001 (2020).
- Matsuda and Shimahara (2007) Y. Matsuda and H. Shimahara, J. Phys. Soc. Jpn. 76, 051005 (2007).
- Wosnitza (2018) J. Wosnitza, Ann. Phys. 530, 1700282 (2018).
- Bauer and Sigrist (2012) E. Bauer and M. Sigrist, Non-Centrosymmetric Superconductors: Introduction and Overview (Springer Science & Business Media, 2012).
- Smidman et al. (2017) M. Smidman, M. B. Salamon, H. Q. Yuan, and D. F. Agterberg, Rep. Prog. Phys. 80, 036501 (2017).
- Agterberg (2003) D. F. Agterberg, Physica C Supercond. 387, 13 (2003).
- Barzykin and Gor’kov (2002) V. Barzykin and L. P. Gor’kov, Phys. Rev. Lett. 89, 227002 (2002).
- Dimitrova and Feigel’man (2003) O. V. Dimitrova and M. V. Feigel’man, JETP Lett. 78, 637 (2003).
- Kaur et al. (2005) R. P. Kaur, D. F. Agterberg, and M. Sigrist, Phys. Rev. Lett. 94, 137002 (2005).
- Agterberg and Kaur (2007) D. F. Agterberg and R. P. Kaur, Phys. Rev. B Condens. Matter 75, 064511 (2007).
- Dimitrova and Feigel’man (2007) O. Dimitrova and M. V. Feigel’man, Phys. Rev. B Condens. Matter 76, 014522 (2007).
- Samokhin (2008) K. V. Samokhin, Phys. Rev. B Condens. Matter 78, 224520 (2008).
- Yanase and Sigrist (2008) Y. Yanase and M. Sigrist, J. Phys. Soc. Jpn. 77, 342 (2008).
- Michaeli et al. (2012) K. Michaeli, A. C. Potter, and P. A. Lee, Phys. Rev. Lett. 108, 117003 (2012).
- Sekihara et al. (2013) T. Sekihara, R. Masutomi, and T. Okamoto, Phys. Rev. Lett. 111, 057005 (2013).
- Houzet and Meyer (2015) M. Houzet and J. S. Meyer, Phys. Rev. B Condens. Matter 92, 014509 (2015).
- Schumann et al. (2020) T. Schumann, L. Galletti, H. Jeong, K. Ahadi, W. M. Strickland, S. Salmani-Rezaie, and S. Stemmer, Phys. Rev. B Condens. Matter 101, 100503 (2020).
- Naritsuka et al. (2017) M. Naritsuka, T. Ishii, S. Miyake, Y. Tokiwa, R. Toda, M. Shimozawa, T. Terashima, T. Shibauchi, Y. Matsuda, and Y. Kasahara, Phys. Rev. B Condens. Matter 96, 174512 (2017).
- Naritsuka et al. (2021) M. Naritsuka, T. Terashima, and Y. Matsuda, J. Phys. Condens. Matter 33, 273001 (2021).
- (57) T. Ono, Y. Miyasaka, and R. Kawarazaki, Private communication.
- (58) See Supplemental Material for more details.
- Note (1) This terminology is named after the crossover generally seen in noncentrosymmetric superconductors, while the line changes to the first-order transition at lower temperature in this model, as in Figs.5(b)-5(d).
- Miyasaka et al. (2021) Y. Miyasaka, R. Kawarazaki, H. Narita, F. Ando, Y. Ikeda, R. Hisatomi, A. Daido, Y. Shiota, T. Moriyama, Y. Yanase, and T. Ono, Appl. Phys. Express 14, 073003 (2021).
- Yuan and Fu (2021) N. F. Q. Yuan and L. Fu, (2021), arXiv:2106.01909 [cond-mat.supr-con] .
- He et al. (2021) J. J. He, Y. Tanaka, and N. Nagaosa, “A phenomenological theory of superconductor diodes in presence of magnetochiral anisotropy,” (2021), arXiv:2106.03575 [cond-mat.supr-con] .
I Formulation to evaluate the electric current
Here, we show the details of the formulation to calculate the current expectation values in the superconducting states. The free energy per unit volume in the superconducting state is given by
| (6) |
Here, represents the trace over the spin degrees of freedom, while represents that over both the spin and the Nambu degrees of freedom. represents the system size with the diameter in the direction. We introduced the Bogoliubov-de Genens (BdG) Hamiltonian by
| (7) | |||
| (8) |
with the momentum and the Nambu spinor . Here, we choose to be compatible with the periodic boundary conditions, . The constant term in Eq. (7) is equivalent to the first term of Eq. (6). The normal-state Bloch Hamiltonian is given by .
The electric current (the sheet current density) is defined by
| (9) |
Here, the current operator is given by
| (10) | ||||
| (11) |
After some calculations, we obtain
| (12) | ||||
| (13) |
with the Fermi distribution function .
The gap equation is given by
| (14) |
which determines the pair potential self-consistently. The solution is written as , and satisfies Eq. (14), or equivalently,
| (15) |
By using , the condensation energy defined in the main text is written as
| (16) |
where holds as is easily confirmed with Eqs. (6) and (8). By using Eqs. (13) and (14), we obtain
| (17) |
The obtained equality goes along with the standard expression with the uniform vector potential since changes by when changes by .
II GL analysis
Here we show the details of the GL analysis of the superconducting diode effect. Let us start from the expression
| (18) |
keeping the order parameter of the form in mind. The coefficients are given by
| (19) |
Here we omit the tilde of in the main text for simplicity, and redefine . The order parameter is optimized by
| (20) |
Assuming for the range of we are interested in, has a nontrivial real solution only when . Thus, the GL free energy is given by
| (21) |
with the Heaviside step function. Since the minimum of is , the transition from the normal to helical superconducting state occurs when the sign of changes from negative to positive as lowering the temperature. Thus, we conclude .
We first consider the case . The supercurrent is given by ,
| (22) |
This is an odd function of , and thus the critical current is reciprocal. Actually, The maximum and minimum of are achieved at satisfying
| (23) |
Accordingly, scales as , as is the inverse of the coherence length. Thus, the reciprocal critical current is given by
| (24) |
Note that this coincides with up to first order in and . Thus, the well-known scaling law is reproduced for .
Let us consider the first-order change caused by and . We obtain
| (25) |
and
| (26) |
When the critical current is realized at , we obtain up to first order in and ,
| (27) |
Here, represents . Thus, we obtain the nonreciprocal component of the critical current,
| (28) |
This scales as .
| (a) | (b) | (c) | (d) |
|---|---|---|---|
 |
 |
 |
 |
III Calculation details and Phase diagrams
Here we explain the details of the numerical calculations and show some additional figures related to the phase diagrams. All the calculations for the figures in the main text and those presented here are done with and . Exceptionally, we adopt for Fig. 5 and in Fig. 2 to reduce the finite-size effect. To obtain , is maximized/minimized among . The normalization of Figs. 5 (a)-(d) is done with , , and for , , and , respectively. Note that we show in Figs. 5 (a)-(d) only the most stable state that minimizes for each . In particular, there is a metastable superconducting state for smaller (larger) ’s of the left (right) peaks in Fig. 5 (d). The supercurrent sustained by these states might be observed when the experimental time scale is small. For Figs. 5 (a)-(d), it is confirmed that the superconducting solution is (if any) unique for each .
In Figs. 6 (a) and (b), we show the temperature and magnetic-filed dependence of the minimum excitation energy for and , respectively. The spectrum becomes gapless in the high-field helical superconducting states, which can be detected by scanning tunneling microscopy. Figures 6 (c) and (d) show and for . In Figs. 6 (c) and (d), the crossover line is seen to be , and a huge nonreciprocal nature is observed. To be precise, becomes positive in a tiny region near and for . However, this is probably due to the peculiarity of the model, where the Lifshitz transition of the outer Fermi surface occurs around .
IV Evolution of Landau critical momenta
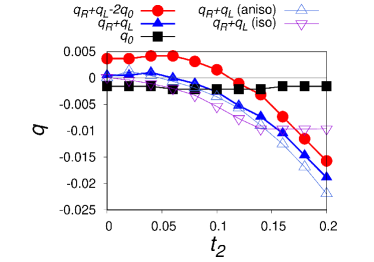
As discussed in the main text, the sign reversal of by can be understood based on the nonreciprocity of the Landau critical momenta. In Fig. 7, we show and obtained from at and , with varying from to . The sign reversal of (red closed circles) naturally explains that of . For large values of , is dominated by the nonreciprocal Landau critical momentum (blue closed triangles), while it is dominated by (black closed squares) for small values of . It should be noted that a large SDE is obtained for , although and contribute destructively.
To understand the behavior of , we discuss the Landau critical momenta with the help of the single-band formula . In our case, should be replaced with for each band, and we obtain,
| (29) |
whose positive and negative solutions for correspond to and , respectively. Here, specifies the points on the Fermi surface with the helicity , while is the unit vector parallel to . Equation (29) well reproduces the result for , as shown by skyblue open triangles in Fig. 7. To go further, let us simplify the expression by replacing in the first line of Eq. (29) with its average on the Fermi surface: . We obtain for [see the next section for the derivation],
| (30) |
whose helicities are interchanged for . Here, we defined , and . Equation (30) qualitatively agrees with for , as shown by the open purple inverted triangles in Fig. 7. In this regime, we have small and the first line of Eq. (30) is applied. Since , the difference of the Fermi velocities plays a key role to obtain a large . It is expected that the anisotropy of the system is advantageous to obtain a large value of . On the other hand, Eq. (30) underestimates around , where the third line of Eq. (30) is applied. This indicates that the isotropic simplification is not valid for strongly anisotropic systems with large . Thus, overall, large anisotropy of the system is expected to be the key to obtain a large SDE.
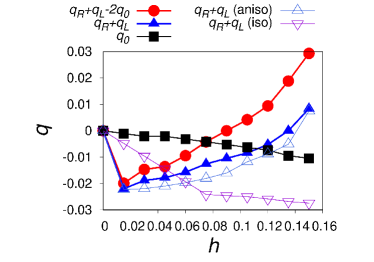
In Fig. 8, we show the magnetic-field dependence of , and their combinations for . The notations are the same as those of Fig. 7. While is nonmonotonic, grows linearly and finally the sign reversal of occurs. “ (aniso)”, i.e. Eq. (29), qualitatively captures the behavior of , whose slight deviation is probably due to the higher-order corrections of . The isotropic simplification does not work for as is clear in Fig. 8. The sign reversal of is the origin of that of in the phase diagram for under moderate magnetic fields.
IV.1 Derivation of Eq. (30)
Here, we derive Eq. (30). By using , we obtain
| (31) | ||||
| (32) |
Let us first consider the positive solution . We also fix . Then, we obtain
| (33) |
When , we obtain
| (34) |
The consistency can be checked as follows. The above inequality reads
| (35) |
Thus, this solution is valid for
| (36) |
Considering only the linear dependence in , we obtain
| (37) |
In the same way, we obtain
| (38) |
for , i.e. . The negative solutions are obtained as follows:
| (39) |
Summing up and , we obtain Eq. (30).