Intrinsic Hall conductivities induced by the orbital magnetic moment

The Hall effect is the generation of a voltage transverse to the applied current, and it can arise from several different mechanisms Hall (1879); Nagaosa et al. (2010); Xiao et al. (2006); Sodemann and Fu (2015); Papaj and Fu (2019); Mandal et al. (2020). The most prominent among them is the classical Hall effect, which arises in the presence of a magnetic field from the Lorentz force on the Bloch electrons Hall (1879, 1880). Another fascinating Hall effect is the anomalous Hall effect Karplus and Luttinger (1954); Sinitsyn (2008); Nagaosa et al. (2010); Zhang (2016) that occurs in the absence of a magnetic field in time reversal symmetry (TRS) broken systems. Its intrinsic part arises from the Berry curvature (BC), a geometrical property of the electronic wave-function Culcer et al. (2003); Haldane (2004), and it is used as a tool to probe the topological properties of material. This scattering-time independent anomalous Hall effect is quite counter-intuitive since transport signatures are mostly dissipative (scattering time dependent). In this letter, we explore another novel intrinsic Hall effect in the presence of a magnetic field, generated by the combination of the BC induced anomalous velocity and the orbital magnetic moment (OMM) Chang and Niu (1996); Cooper et al. (1997); Chang and Niu (2008); THONHAUSER (2011); Ma and Pesin (2015); Zhong et al. (2016); Morimoto et al. (2016); Sekine and MacDonald (2018); Zhou et al. (2019); Knoll et al. (2020); Das and Agarwal (2019); Gao (2019); Aryasetiawan and Karlsson (2019); Xiao and Niu (2020).

A simple way to understand the OMM-induced intrinsic Hall effect [see Fig. 1] is to start with the well known expression for the intrinsic anomalous Hall effect,

$$\sigma_{ij}^{\rm A}=-\dfrac{e^{2}}{\hbar}\epsilon_{ijl}\int[d{\bf k}]\Omega_{l}f~{}.$$

(1)

Here, ‘$-e$’ is the electronic charge, $\epsilon_{ijl}$ is the Levi-Civita tensor, $\Omega_{l}$ denotes the $l$ component of the BC and $[d{\bf k}]=d{\bf k}/(2\pi)^{d_{0}}$ in $d_{0}$ dimensions. We have defined $f=f[\beta(\epsilon-\mu)]$ with $f(x)=1/(1+e^{x})$ as the Fermi-Dirac distribution function for the concerned band with dispersion $\epsilon$ and inverse temperature $\beta=1/(k_{B}T)$. In materials with intrinsic TRS, the BC is an odd function of the crystal momentum and thus the anomalous Hall effect vanishes when summed over the Brillouin zone. However, the OMM (${\bf m}$) modifies the electronic band dispersion in the presence of magnetic field ${\bf B}$, through a Zeeman like coupling $\epsilon\to\tilde{\epsilon}=\epsilon-{\bf m}\cdot{\bf B}$. Thus, to lowest order in the magnetic field, Eq. (1) reduces to

$$\sigma_{ij}^{\rm O}=\dfrac{e^{2}}{\hbar}\epsilon_{ijl}\int[d{\bf k}]\Omega_{l}\epsilon_{m}~{}f^{\prime}~{},$$

(2)

with $\epsilon_{m}={\bf m}\cdot{\bf B}$ and $f^{\prime}=\partial_{\epsilon}f$. This dissipation-less Hall effect also manifests in other thermo-electric and thermal transport phenomena such as the Nernst effect, the Ettinghausen effect and the thermal Hall effect. These contributions are purely quantum mechanical in nature and have no classical analogue.

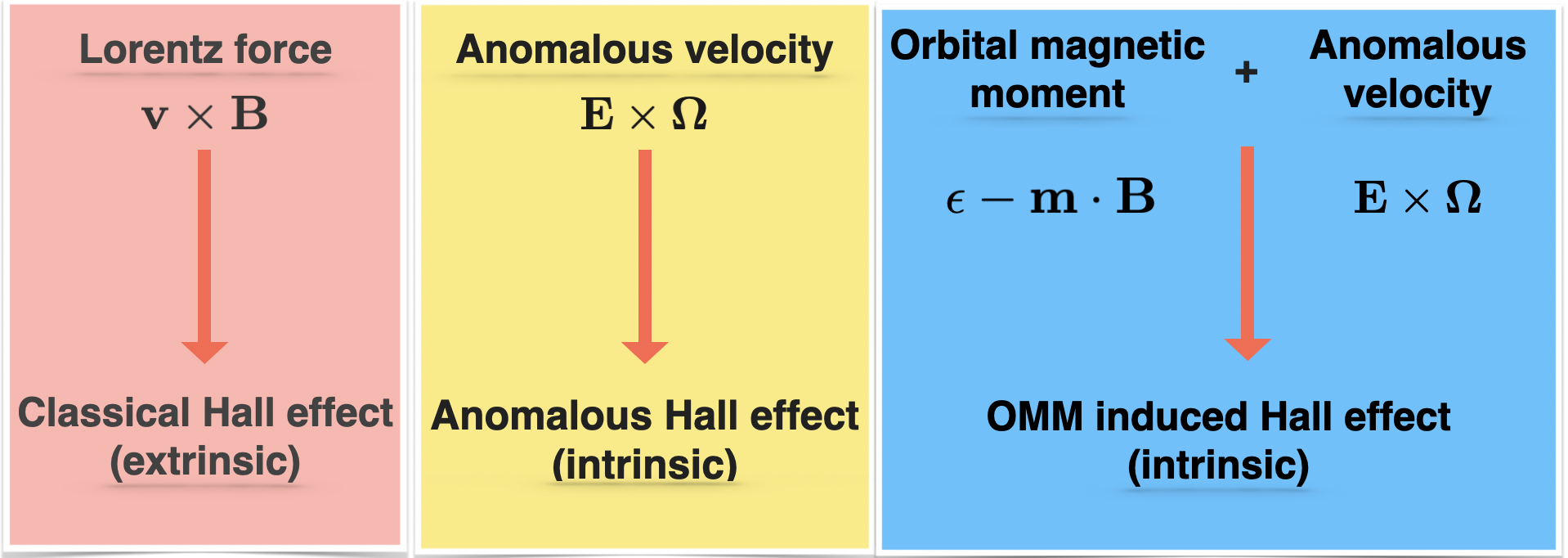
In non-centrosymmetric materials with TRS, the OMM-induced Hall conductivity, specified by Eq. (2), is the only intrinsic Hall response.

In contrast to the classical Hall conductivities, the OM-induced Hall conductivities dominate near the band edges or band crossings, which are also the ‘hotspot’ of the BC and the OMM. Using gapped graphene and Weyl metals as specific examples for 2D and 3D systems, we demonstrate that these OM-induced Hall components have a significant impact on the magneto-resistance (MR) measurements, giving rise to a negative MR Zhou et al. (2019). Most importantly, we show that the additional OMM-induced Hall conductivity contribution leads to a significant under-estimation in the charge carrier density measured in conventional Hall resistivity experiments.

The phenomenological transport equations for the Hall response in charge current (${\bf j}$) and thermal current (${\bf J}$) are given by

$$\begin{pmatrix}j_{x}\\ J_{x}\end{pmatrix}=\begin{pmatrix}\sigma_{xy}&\alpha_{xy}\\ \bar{\alpha}_{xy}&\bar{\kappa}_{xy}\end{pmatrix}\begin{pmatrix}E_{y}\\ -\nabla_{y}T\end{pmatrix}~{}.$$

(3)

Here, ${\bf E}$ denotes the electric field and ${\bf\nabla}T$ is the temperature gradient. The conductivities $\sigma_{xy}$ and $\alpha_{xy}$ ($\bar{\alpha}_{xy}$ and $\bar{\kappa}_{xy}$) capture the charge (heat) flow perpendicular to the applied electrical and thermal bias. We will refer to all these collectively as Hall conductivities. Other experimentally relevant transport quantities such as the Nernst, Seebeck, and thermal conductivity can be expressed in terms of these.

In presence of the BC, the magneto-transport in the semiclassical regime is described by three ingredients: i) the equations of motion of the carriers, ii) the modified momentum space volume for the Brillouin zone (BZ) integration and iii) the non-equilibrium distribution function. In the ‘normal’ Hall configuration Hall (1879) (${\bf E}\perp{\bf B}$), the equation of motion describing the position (r) and momentum ($\hbar{\bf k}$) dynamics of the carrier wave-packet is given by Sundaram and Niu (1999); Xiao et al. (2010)

	$\displaystyle\hbar{\bf\dot{k}}$	$\displaystyle=$	$\displaystyle D\left[-e{\bf E}-e(\tilde{\bf v}\times{\bf B})\right]~{},$		(4)
	$\displaystyle\hbar{\bf\dot{r}}$	$\displaystyle=$	$\displaystyle D\left[\hbar\tilde{\bf v}+e{\bf E}\times{\bf\Omega}+e(\tilde{\bf v}\cdot{\bf\Omega}){\bf B}\right]~{}.$		(5)

Here, $D$ is the phase-space factor Xiao et al. (2005) defined as $1/D=\left[1+\frac{e}{\hbar}({\bf B}\cdot{\bf\Omega})\right]$. The OMM modified band velocity is given by $\hbar\tilde{\bf v}=\nabla_{\bf k}\tilde{\epsilon}$. Consequently, the carrier velocity can be expressed as $\tilde{\bf v}={\bf v}-{\bf v}_{m}$ where the band velocity is $\hbar{\bf v}=\nabla_{\bf k}\epsilon$ and the OMM-induced velocity $\hbar{\bf v}_{m}=\nabla_{\bf k}\epsilon_{m}$. In presence of BC and magnetic field, the phase-space volume is modified by $d{\bf k}\to[D]^{-1}d{\bf k}$. For calculating the non-equilibrium distribution function, $g_{{\bf r},{\bf k}}$, we use the semiclassical Boltzmann equation given by  Ashcroft and Mermin (1976)

$$\dfrac{\partial g_{{\bf r},{\bf k}}}{\partial t}+\dot{\bf k}\cdot\nabla_{\bf k}g_{{\bf r},{\bf k}}+\dot{\bf r}\cdot\nabla_{\bf r}g_{{\bf r},{\bf k}}=-\frac{g_{{\bf r},{\bf k}}-\tilde{f}}{\tau}~{}.$$

(6)

Here, $\tilde{f}=f[\beta(\tilde{\epsilon}-\mu)]$ and $\tau$ is the scattering time. In the steady state regime with bias, we have $g_{{\bf r},{\bf k}}\approx\tilde{f}+\delta g_{{\bf r},{\bf k}}$, where $\delta g_{{\bf r},{\bf k}}$ is the non-equilibrium part. To the lowest order in external biases and magnetic field, in the normal Hall configuration [$({\bf E}~{}\mbox{and}~{}\nabla_{\bf r}T)\cdot{\bf B}=0$], $\delta g_{{\bf r},{\bf k}}$ can be calculated to be

	$\displaystyle\delta g$	$\displaystyle=$	$\displaystyle\tau\Big{[}\tau\frac{e}{\hbar}\{({\bf v}\times{\bf B})\cdot\nabla_{\bf k}\}f^{\prime}{\bf v}-\Omega_{\rm B}f^{\prime}{\bf v}-f^{\prime}{\bf v}_{m}-\epsilon_{m}f^{\prime\prime}{\bf v}\Big{]}$		(7)
			$\displaystyle\cdot\left[e{\bf E}+\beta\left(\epsilon-\mu\right)k_{B}\nabla_{\bf r}T\right]-\tau f^{\prime}\beta\epsilon_{m}{\bf v}\cdot k_{B}\nabla_{\bf r}T.~{}~{}~{}~{}$

Here, we have defined, $\Omega_{\rm B}=e/\hbar\bf{\Omega}\cdot\bf{B}$ and $f^{\prime\prime}=\partial^{2}_{\epsilon}f$. Using these in conjugation with the proper definition of the physically observable current, which excludes the OMM-induced circulating currents (see Supplementary material (SM) ¹¹1 Supplementary material detailing semiclassical calculation for i) intrinsic off-diagonal, ii) extrinsic off-diagonal, and iii) extrinsic diagonal components of the conductivity, iv) Hall coefficients, v) magneto-resistance, and vi) Weyl metals. for details), all the conductivities can be calculated.

If the magnetic field is applied along the $z$-direction then the conductivities defined in Eq. (3) represent the ‘normal’ Hall conductivities Hall (1879). We find that in an intrinsically TRS preserving system there are two distinct contributions of these. The well known Lorentz force contribution is $\propto\tau^{2}$, and are given by  Hurd (1972); Ziman (1972); Auerbach (2018)

	$\displaystyle\begin{pmatrix}\sigma_{xy}^{\rm L}&\alpha_{xy}^{\rm L}\\ \bar{\alpha}_{xy}^{\rm L}&\bar{\kappa}_{xy}^{\rm L}\end{pmatrix}$	$\displaystyle=$	$\displaystyle-\dfrac{e^{3}\tau^{2}}{\hbar}\int[d{\bf k}]\begin{pmatrix}1&-\frac{\epsilon-\mu}{eT}\\ -\frac{\epsilon-\mu}{e}&\frac{\left(\epsilon-\mu\right)^{2}}{e^{2}T}\end{pmatrix}f^{\prime}$		(8)
		$\displaystyle\times$	$\displaystyle[v_{x}({\bf v\times{\bf B}})\cdot{\nabla}_{\bf k}v_{y}]~{}.$

In addition to the Hall conductivity, the Lorentz force also modifies the longitudinal conductivity. This modification can be calculated to be $\delta\sigma_{xx}^{\rm L}=-(e^{4}\tau^{3}/\hbar^{2})\int[d{\bf k}]v_{x}[\{({\bf v}\times{\bf B})\cdot\nabla_{\bf k}\}^{2}v_{x}]f^{\prime}$.

More interestingly, the OMM combines with the anomalous velocity (see Fig. 1) to give rise to an additional intrinsic component of the Hall conductivities. We calculate these OMM-induced conductivities to be (see SMNote (1) for details)

$$\begin{pmatrix}\sigma_{xy}^{\rm O}&\alpha_{xy}^{\rm O}\\ \bar{\alpha}_{xy}^{\rm O}&\bar{\kappa}_{xy}^{\rm O}\end{pmatrix}=\dfrac{e^{2}}{\hbar}\int[d{\bf k}]\epsilon_{m}\Omega_{z}\begin{pmatrix}1&-\frac{\epsilon-\mu}{eT}\\ -\frac{\epsilon-\mu}{e}&\frac{\left(\epsilon-\mu\right)^{2}}{e^{2}T}~{}\end{pmatrix}f^{\prime}~{}.$$

(9)

The prediction of these intrinsic OMM-induced Hall conductivities is one of the main highlights of this paper. These dissipation-less components are of purely quantum mechanical origin and have no classical counterpart. In this letter, we will focus on non-magnetic systems which break inversion symmetry and intrinsically preserve the TRS. The case of magnetic systems which intrinsically break the TRS is discussed in detail in the SM Note (1).

In addition to the Hall components, the BC and the OMM also give rise to modifications in the longitudinal conductivities. The longitudinal component of the charge conductivity is given by Das and Agarwal (2019)

	$\displaystyle\delta\sigma_{xx}^{\rm O}=-e^{2}\tau\int[d{\bf k}]\Big{[}v_{x}^{2}\Omega_{\rm B}^{2}f^{\prime}+v_{x}\left(\epsilon_{m}f^{\prime\prime}+2\Omega_{\rm B}f^{\prime}\right)v_{mx}$
	$\displaystyle+v_{x}^{2}(\epsilon_{m}^{2}f^{\prime\prime\prime}/2+\Omega_{\rm B}\epsilon_{m}f^{\prime\prime})+v_{mx}(f^{\prime}v_{mx}+\epsilon_{m}f^{\prime\prime}v_{x})\Big{]}.~{}~{}~{}~{}$		(10)

The details of the calculation and the longitudinal contributions in the thermo-electric and thermal conductivities are presented in the SM Note (1).

We find that similar to the classical Hall conductivities, the OMM-induced Hall conductivities also satisfy the i) Onsager’s reciprocity relation, ii) the Wiedemann-Franz law, and iii) the Mott relation. This ensures that the other three conductivities can be deduced from the Hall conductivity Xiao et al. (2006); Dong et al. (2020). More explicitly, if the Hall conductivity is known, then for $\mu\gg k_{B}T$, the Wiedemann-Franz law implies $\bar{\kappa}_{xy}^{\rm O}=\pi^{2}k_{B}^{2}T\sigma_{xy}^{\rm O}/(3e^{2})$, the Mott relation ensures $\alpha_{xy}^{\rm O}=-\pi^{2}k_{B}^{2}T\partial_{\mu}\sigma_{xy}^{\rm O}/(3e)$, and the Onsagar’s relation leads to $\bar{\alpha}_{xy}^{\rm O}=T\alpha_{xy}^{\rm O}$.

To explore the quantitative impact of the OMM-induced conductivities, we consider two experimentally interesting systems with broken inversion symmetry. In two dimension, we choose gapped graphene whose low energy physics is described by a massive Dirac Hamiltonian. Gapped graphene can be realized by a heterostructure of graphene on hexagonal boron nitride Zhou et al. (2007); Yankowitz et al. (2012); Song et al. (2015). The valley resolved Hamiltonian of this system is given by Xiao et al. (2007)

$${\mathcal{H}}=\hbar v_{F}(\tau_{z}k_{x}\sigma_{x}+k_{y}\sigma_{y})+\Delta_{g}\sigma_{z}~{}.$$

(11)

Here, $\sigma_{i}$ are the Pauli spin matrices denoting the pseudo-spin, $\tau_{z}=\pm 1$ denotes the $K/K^{\prime}$ valley degree of freedom and $2\Delta_{g}$ is the bandgap at each valley induced by the breaking of the sub-lattice symmetry Zhou et al. (2007). The bands for the two spins are degenerate ($g_{s}=2$) and there are two valleys ($g_{v}=2$) in the Brillouin zone. In three dimension, we choose an inversion symmetry broken Weyl metal (WM). WMs can be realized in the inversion symmetry broken TaAs family Huang et al. (2015); Lv et al. (2015); Armitage et al. (2018). A minimal model of such WM hosts two pairs of Weyl nodes of opposite chirality ($g_{w}=4$). The Hamiltonian for each of the Weyl node is Das and Agarwal (2020); Das et al. (2020)

$${\mathcal{H}}=\chi\hbar v_{F}\left(\sigma_{x}k_{x}+\sigma_{y}k_{y}+\sigma_{z}k_{z}\right)~{}.$$

(12)

Here, $\chi$ denotes the chirality of the given Weyl node.

We calculate the BC, OMM, and the OMM-induced electric and thermo-electric conductivities for both these systems [Eqs. (11) and (12)], and the results are tabulated in Table 1. For the OMM-induced conductivities we have defined a dimensionless parameter $(\gamma_{\rm B}$) related to the OMM coupling energy scale at the Fermi surface, $\gamma_{\rm B}=|{\bf m}(\mu)|B/\mu$. The model specific expressions of $\gamma_{B}$ are also tabulated in Table 1.

The classical Hall conductivity for both these systems can be expressed as $\sigma_{xy}^{\rm L}=-\omega_{c}\tau\sigma_{\rm D}$, where the cyclotron frequency is $\omega_{c}=eB/m^{*}$ and the Drude conductivity is given by $\sigma_{\rm D}=ne^{2}\tau/m^{*}$. The carrier density $n$ is specified in Table 1 as a function of $\mu$ and the inertial or cyclotron mass for both these isotropic systems is given by $m^{*}=\mu/v_{F}^{2}$ Sachdeva et al. (2015).

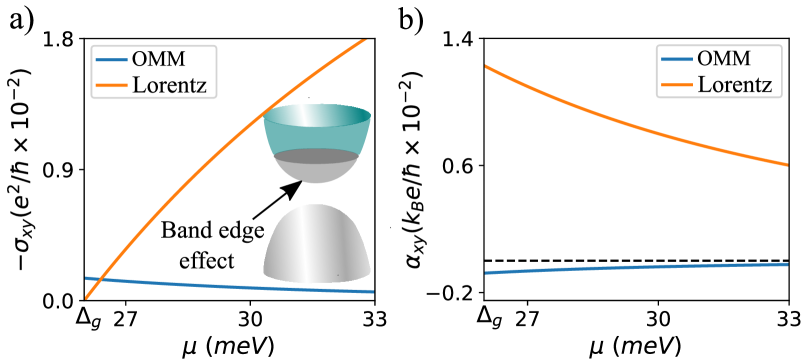
We find that chemical potential dependence of $\sigma_{xy}^{\rm O}$ is opposite to its classical counterpart. $\sigma_{xy}^{\rm O}$ is largest near the band-edge or the band crossing point, the ‘hotspots’ of the BC and the OMM, and it decreases as we move away from the band-edge to regions of larger carrier density. This is highlighted in Fig. 2(a). Depending on the value of the scattering timescale, the OMM contribution can be of the same order as the classical Hall contribution in the low carrier region near the band edge. In the thermoelectric Hall conductivity, the magnitude of both the Lorentz and the OMM contributions are peaked near the band-edge and they decrease as we move away from the band edge. We find that similar to the Lorentz contribution, $\sigma_{xy}^{\rm O}$ retains the sign of the charge carriers, changing from positive to negative as we move from the conduction band (electrons) to the valance band (holes). However, $\alpha_{xy}^{\rm O}$ retains the same sign for both the bands.

These relatively unexplored OMM-induced Hall conductivities have a significant impact on i) the Hall resistivity (or coefficient) which is used to determine the carrier density, and ii) the transverse MR. We discuss both of these below.

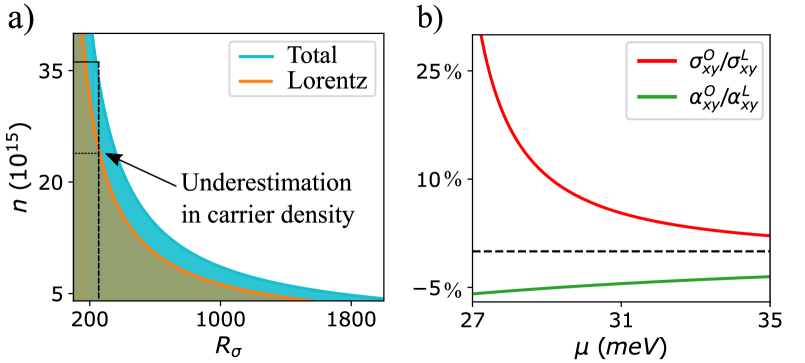
Similar to the electron gas with parabolic dispersion, we find that the classical Hall resistivity [$\rho_{xy}=-\sigma_{xy}/({\sigma_{xx}^{2}+\sigma_{xy}^{2}})$] in gapped graphene and in WM can be expressed as $\rho_{xy}^{\rm L}=B/(ne)$ where $n$ is the carrier density Ashcroft and Mermin (1976). Owing to this very simple carrier density dependence, the Hall resistivity measurement is routinely used to experimentally estimate the carrier density in terms of Hall coefficient ($R_{\sigma}$),

$$n=\frac{1}{e}R_{\sigma}^{\rm L}~{},~{}~{}~{}{\rm where}~{}~{}~{}R_{\sigma}^{\rm L}\equiv\left.\frac{\partial\rho_{xy}^{\rm L}}{\partial B}\right|_{B\to 0}~{}.$$

(13)

However, in presence of the OMM-induced Hall conductivity, the total Hall resistivity is given by $\rho_{xy}^{\rm total}=\rho_{xy}^{\rm L}\left[1+\sigma_{xy}^{\rm O}/\sigma_{xy}^{\rm L}\right]~{}+{\cal O}(B^{3})$. Thus, we have $R_{\sigma}^{\rm L}\to R_{\sigma}^{\rm total}$, where the total ($B$ independent) Hall coefficient is

$$R_{\sigma}^{\rm total}=R_{\sigma}^{\rm L}\left(1+\dfrac{\sigma_{xy}^{\rm O}}{\sigma_{xy}^{\rm L}}\right)~{}.$$

(14)

This additional contribution, $R_{\sigma}^{\rm O}=r_{\sigma}R_{\sigma}^{\rm L}$, with $r_{\sigma}\equiv\sigma_{xy}^{\rm O}/\sigma_{xy}^{\rm L}$ leads to an underestimation of the carrier density that we extract from Hall measurement, particularly near the band edges as shown in Fig. 3.

In gapped graphene, we find the OMM-induced non-universal correction to the the Hall coefficient to be

$$r_{\sigma}^{\rm GG}=\frac{\sigma^{\rm O}_{xy}}{\sigma_{xy}^{\rm L}}=\dfrac{1}{2}\dfrac{\Delta_{g}^{2}}{(\mu^{2}-\Delta_{g}^{2})}\dfrac{\hbar^{2}}{\mu^{2}\tau^{2}}~{}.$$

(15)

This correction explicitly depends on the ratio of scattering energy scale and the chemical potential and represents $35\%$ underestimation of the carrier density, as shown in Fig. 3(a). A similar correction for the WM can be easily obtained to be $r_{\sigma}^{\rm WM}={\hbar^{2}}/{(4\mu^{2}\tau^{2})}$. For the typical choice of $\mu=25$ meV and $\tau=0.1$ ps, this turns out to be $2\%$ which leads to approximately $2\%$ underestimation of the carrier density, without explicitly accounting for the OMM correction ²²2Similar OMM induced corrections can also be obtained for the Nernst number $R_{\nu}\equiv(\sigma_{xx}\bar{\kappa}_{xx})^{-1}\partial_{B}\alpha_{xy}|_{B\to 0}$ and the thermal Hall number Auerbach (2019) $R_{\bar{\kappa}}\equiv(\bar{\kappa}_{xx})^{-2}\partial_{B}\bar{\kappa}_{xy}|_{B\to 0}$. Both of these have the form $R_{i}=R_{i}^{\rm L}(1+r_{i})$ with $r_{\nu}=\nu_{xy}^{\rm O}/\nu_{xy}^{\rm L}$ and $r_{\bar{\kappa}}=\bar{\kappa}_{xy}^{\rm O}/\bar{\kappa}_{xy}^{\rm L}$. More importantly, the OMM contribution in these Hall coefficients are extrinsic in nature making them non-universal, in contrast to the Lorentz contribution which is intrinsic Auerbach (2018, 2019). .

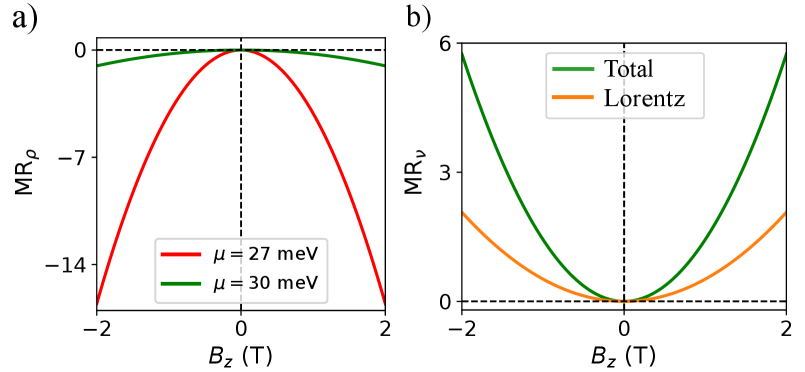
The OMM-induced intrinsic Hall conductivities also manifest in the measured MR of resistivity (MR_ρ for $\rho_{xx}$), MR of the Seebeck conductivity (MR_ν for $\nu_{xx}=\rho_{xx}\alpha_{xx}+\rho_{xy}\alpha_{xy}$) and in other transport measurements.

For the MR${}_{\rho}\equiv\rho_{xx}(B)/\rho_{xx}(0)-1$, the OMM-induced Hall conductivity can give rise to a negative MR Zhou et al. (2019). For an time-reversal symmetric system, to lowest order in the magnetic field, the MR can be calculated to be,

$${\rm MR}_{\rho}=-\left[\frac{\delta\sigma_{xx}^{\rm O}}{\sigma^{\rm D}}+\frac{\sigma^{\rm O}_{xy}(\sigma^{\rm O}_{xy}+2\sigma^{\rm L}_{xy})}{(\sigma^{\rm D})^{2}}\right]~{}.$$

(16)

As expected, we find that the Lorentz force by itself cannot induce any MR. The quadratic negative MR_ρ is maximum near the band edges where the Drude conductivity is minimal, and the OM-induced contributions are maximum. Here the second term is $\propto 1/\tau^{2}$ while the rest are independent of $\tau$. We find that the OMM and BC induced longitudinal conductivity correction $\delta\sigma^{\rm O}_{xx}$, calculated from Eq. (Intrinsic Hall conductivities induced by the orbital magnetic moment) and tabulated in Table 1, decrease the conductance for both gapped graphene and WM. Thus, the first term in Eq. (16) leads to a positive MR_ρ component. However, the OMM-induced Hall conductivity corrections are stronger and it makes the total MR_ρ negative, as shown in Fig. 4(a).

The MR in the Seebeck coefficient is defined as MR${}_{\nu}\equiv\nu_{xx}(B)/\nu_{xx}(0)-1$. For systems which intrinsically preserve TRS, to lowest order in magnetic field, we obtain

$${\rm MR}_{\nu}={\rm MR}_{\rho}+\dfrac{\delta\alpha^{\rm L}_{xx}+\delta\alpha^{\rm O}_{xx}}{\alpha_{\rm D}}+\dfrac{\sigma_{xy}}{\sigma_{\rm D}}\dfrac{\alpha_{xy}}{\alpha_{\rm D}}.$$

(17)

Here $\sigma_{xy}=\sigma_{xy}^{\rm L}+\sigma_{xy}^{\rm O}$ and $\alpha_{xy}=\alpha_{xy}^{\rm L}+\alpha_{xy}^{\rm O}$. In contrast to its resistivity counterpart, the Lorentz force contribution alone ($\delta\alpha_{xx}^{\rm L}$, $\sigma_{xy}^{\rm L}$ and $\alpha_{xy}^{\rm L}$) causes a finite positive MR_ν. We find that the OMM-induced corrections contribute to the MR_ν, thus enhancing the strength of the total MR_ν. This is shown explicitly for the case of gapped graphene in Fig. 4(b). Similar result is also obtained for WM which is shown in the SM Note (1).

Going beyond the inversion symmetric materials discussed in this letter, the OMM-induced Hall effect is also present in materials which intrinsically break TRS. However, in these systems the Hall current has an additional intrinsic $B$- independent anomalous Hall and extrinsic $B$-dependent contributions arising from the BC. We derive the expressions for all these contributions explicitly in the SM Note (1). One simplification used in our work is a constant $\tau$ approximation. However, the energy or momentum dependence of $\tau$ can be easily incorporated in our formulation without changing the results qualitatively.

To summarize, we have predicted novel OMM-induced intrinsic $B$-linear Hall effect in all the conductivities. These are purely quantum mechanical in nature and they have no classical analog. These OMM-induced Hall effects originate from the geometric properties of the electronic wave-functions (the BC and the OMM) and are the only dissipation-less Hall effect in a non-centrosymmetric material. In contrast to the Lorentz force’s contributions, the OMM-induced Hall conductivities dominate near the band edges or band crossings, which are ‘hotspots’ of the BC and the OMM, and these decrease on increasing the carrier concentration. These OMM-induced Hall components significantly impact the transverse MR measurements, giving rise to a negative MR_ρ (quadratic in $B$) and an increase in the strength of positive MR in the Seebeck effect. We also show that the OMM-induced Hall conductivity leads to a significant under-estimation in the charge carrier density measured in the Hall resistivity experiments.