Intrinsic constraint on for unconventional superconductivity
Abstract
Can room temperature superconductivity be achieved in correlated materials under ambient pressure? Our answer to this billion-dollar question is probably no, at least for realistic models within the current theoretical framework. This is shown by our systematic simulations on the pairing instability of some effective models for two-dimensional superconductivity. For a square lattice model with nearest-neighbour pairing, we find a plaquette state formed of weakly-connected blocks for sufficiently large pairing interaction. The superconductivity is suppressed on both sides away from its melting quantum critical point. Thus, the plaquette state constrains the magnitude of for large pairing interactions and may be viewed as a strong-coupling parent state of -wave superconductivity, in resemblance of other competing orders. We then extend our simulations to a variety of effective models covering nearest-neighbour or onsite pairings, single layer or two-layer structures, intralayer or interlayer pairings, and find an intrinsic maximum of the ratio , where is the onsite or nearest-neighbour pairing interaction. Comparison with existing experiments supports this constraint in cuprate, iron-based, nickelate, and heavy fermion superconductors, despite that these compounds are so complicated well beyond our simplified models. As a result, the known families of unconventional superconductivity, possibly except the infinite-layer nickelates, seem to almost exhaust their potentials in reaching the maximal allowed by their spin exchange interaction, while achieving room temperature superconductor would require a much larger beyond 400-700 meV, which seems unrealistic and hence demands novel pairing mechanisms.
Despite the century-long pursuit of high-temperature superconductors, the possible existence of a theoretical upper limit to their transition temperature () under ambient pressure remains unsettled 1; 2; 3; 4; 5. Both mean-field and weak-coupling Eliashberg theories 6 predict an artificial that grows continuously with increasing pairing interaction, while experiments often find superconducting domes with maximum near the phase boundaries of some long- or short-range orders associated with spin, charge, orbital, or structural degrees of freedom 7; 8; 9; 10; 11; 12; 13; 14; 15; 16. The dome implies a dual role of the competing orders, which not only provide the pairing glues but also constrain the magnitude of maximum . However, they are mostly external factors associated with instabilities of other channels. One may wonder if any intrinsic constraint on may exist owing solely to the pairing instability.
Important lessons may be learned from cuprate high-temperature superconductors in the underdoped region, where strong pairing interactions relative to the renormalized effective quasiparticle hopping parameters favor short-range electron pairs 17 that in some literatures are thought to form already at high temperatures but only become superconducting when a (quasi-)long-range phase coherence is developed 18; 19. This raises a few general questions: What is the true strong-coupling limit of the pairing state? How is this strong-coupling state related to the high-temperature superconductivity? Would it put any intrinsic constraint on the maximal value of ? Since the absolute magnitude of is determined by certain basic energy scale, such as the pairing interaction , the question of maximum turns into the question of their maximum dimensionless ratio . To address these important issues and gain insights into possible intrinsic constraints on , we propose here to discard instabilities from all other channels such as magnetic or charge orders and focus only on the pairing instability, since all other instabilities are expected to compete with the superconductivity and further suppress . Their contributions to the pairing can all be included phenomenologically in a pairing interaction term.
Theoretically, one may derive various ratios with respect to other measurable energy scales such as the Fermi energy and the superfluid density. However, it has been shown that these ratios may be violated in artificial models 4, thus preventing a useful bound for constraining . To avoid such complication, instead of deriving a model-independent constraint, we first restrict ourselves to a minimal effective model that is most relevant in real correlated materials and includes only the quasiparticle hopping and nearest-neighbour spin-singlet pairing interaction. For the one band model on a square lattice, we find a plaquette state in the strong-coupling limit that breaks both the translational and time reversal symmetries and exhibits unusual spectral properties with a pseudogap or insulating-like normal state. This plaquette state may be regarded as the strong-coupling parent state of -wave superconductivity, since the latter emerges as the plaquettes melt and short-range electron pairs get mobilized to attain long-distance phase coherence at a reduced pairing interaction. A tentative phase diagram is then constructed where reaches its maximum at the plaquette quantum critical point (QCP), resembling those often observed in experiments with other competing orders. This suggests some intrinsic constraints that prevent from exhausting all kinetic or pairing energies in order to achieve a delicate balance between pairing and phase coherence. We then extend the calculations to more general models with either nearest-neighbour or onsite pairings, single layer or two-layer structures, intralayer or interlayer pairings, and obtain a maximum . A close examination of existing experiments in known unconventional superconductors, including cuprate, iron-based, nickelate, and heavy fermion superconductors, seems to quite universally support the obtained ratio, indicating that these families, possibly except the infinite-layer nickelates, have almost reached their maximum allowed by their respective spin exchange interactions. A room-temperature superconductor would then require a much larger pairing interaction beyond 400-700 meV within the current theoretical framework, which seems unrealistic from a single mechanism in correlated electron systems under ambient pressure. Our work therefore provides a useful criterion that may help to avoid futile efforts in exploring high-temperature superconductors along wrong directions. It also points out the necessity of new pairing mechanisms, possibly combining different pairing interactions, in order to achieve the room-temperature superconductivity.
Results
The theoretical phase diagram
As shown in the Method, we first construct and study a minimal effective model that contains only the quasiparticle hopping and pairing terms on a square lattice and then discuss its extension to several other effective models. The hopping terms include the nearest-neighbour hopping and next-nearest-neighbour hopping , which should be renormalized by a Gutzwiller factor as in the cuprate high-temperature superconductors. The pairing interaction is given primarily by the antiferromagnetic spin exchange between nearest-neighbour sites, but may also arise from other mechanisms such as the attractive charge-density interactions and the spin-fluctuation mediated pairing interactions, as suggested by many experiments in recent years 20; 21; 22. For cuprates, the importance of the nearest-neighbour antiferromagnetic spin interaction has been justified in a number of measurements 23; 24; 25. To promote the maximum , we further include the effect of the associated attractive charge-density interaction generated by the superexchange mechanism. The static auxiliary field Monte Carlo approach 26; 27; 28; 29; 30; 31; 32; 33 is then used to simulate the spin-singlet pairing fields defined on all nearest-neighbour bonds as detailed in the Method. It allows us to simulate the phase correlation of the pairing fields and thus determine based on phase coherence rather than the BCS-type mean-field transition. The validity of our approach in estimating has been verified in the recently-discovered bilayer and trilayer nickelate superconductors 34; 35 and by its consistency with the rigorous Quantum Monte Carlo simulations for the attractive Hubbard model 2.
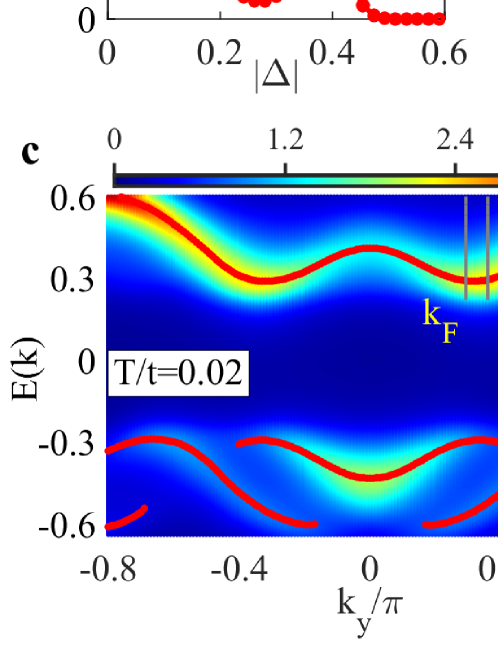
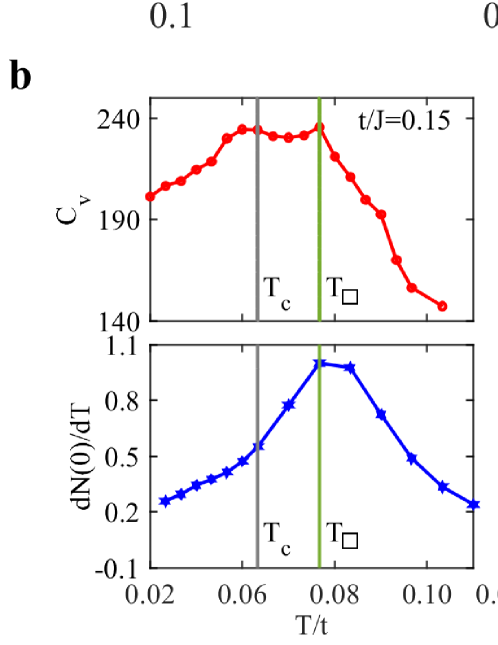
Figure 1(a) shows a typical theoretical phase diagram for the one-band square lattice model, where we have intentionally plot against . A nonuniform plaquette state emerges at sufficiently strong paring interaction formed of blocks induced by high-order pair hopping in the effective action of the pairing fields after integrating out the electron degrees of freedom. A typical pairing configuration of the plaquette state is given in the inset of Fig. 1. The paring amplitudes are relatively stronger on internal bonds of the plaquettes and weaker on their links. The phases show a -wave-like character along the and directions. Thus, the plaquette state breaks the lattice translational symmetry though the electron density remains uniform. Its transition temperature decreases with increasing and diminishes at the QCP (), where the plaquettes melt completely and uniform superconductivity emerges with a maximum for the chosen parameters (see Method). Tuning the next-nearest-neighbour hopping and the chemical potential may slightly change the ratio and the location of the QCP, but does not alter the qualitative physics. Inside the plaquette state, is greatly reduced as the pairing interaction increases. The nonmonotonic evolution of resembles typical phase diagrams observed in many unconventional superconductors with other competing orders such as long-range magnetism, charge density wave, or nematicity 7; 8; 9; 10; 11; 12; 13; 14; 15; 16. However, the plaquette state reflects the internal instability in the pairing channel and may be regarded as the true strong-coupling parent state of -wave superconductivity that constrains the magnitude of . Near the plaquette QCP, the superconductivity also breaks the time reversal symmetry below . At high temperatures, the normal state exhibits pseudogap-like behavior whose onset temperature follows closely the variation of or 36; 37 determined from the specific heat or the temperature derivative of the quasiparticle density of states at the Fermi energy . As shown in Fig. 1(b), we find peaks in the specific heat for all transitions at , , and , while in the feature at is greatly suppressed for . Here and after, is set as the energy unit if not explicitly noted.
The plaquette state at strong coupling
The plaquette state and its phase transition may be seen in the joint distribution of the paring amplitudes along the and directions attached to the same site or the marginal distribution of the pairing field amplitudes on all bonds. As shown in Fig. 2(a), at low temperatures displays a four-point structure due to the nonuniform pairing configurations. As increases, the four points gradually shrink into a single point, where the translational symmetry is recovered and the plaquette state melts into the uniform superconductivity. Correspondingly, the amplitude distribution also contains two peaks in the plaquette state. As shown in Fig. 2(b) for , these peaks get gradually broadened with increasing temperature and merge into a single peak above .
At sufficiently low temperatures, the plaquette state may also develop long-distance phase coherence and exhibits unusual spectral features due to the nonuniform spatial distribution of the pairing amplitudes. As shown in Fig. 2(c) for , its momentum-energy dependent spectral function at negative energies splits into two sets of dispersions. One dispersion resembles that of uniform superconductivity, but its back-bending vector differs consistently from the Fermi vector , which has also been observed experimentally for possible pair density wave (PDW) state 38; 39; 40. At high temperatures, the two dispersions recombine into a single curve pointing upwards even in the normal state. The gap indicates a pseudogap or insulating-like phase due to the large nearest-neighbour pairing interaction. This suggests that the normal state may also undergo a metal-insulator transition as decrease, a phenomenon observed in cuprate superconductors under high pressure but unexplained 41. At intermediate temperature , the superconducting phase coherence is lost and the plaquette state is in a sense similar to the fermionic quadrupling phase with broken time reversal symmetry proposed earlier in experiment 42; 43.
Time reversal symmetry breaking
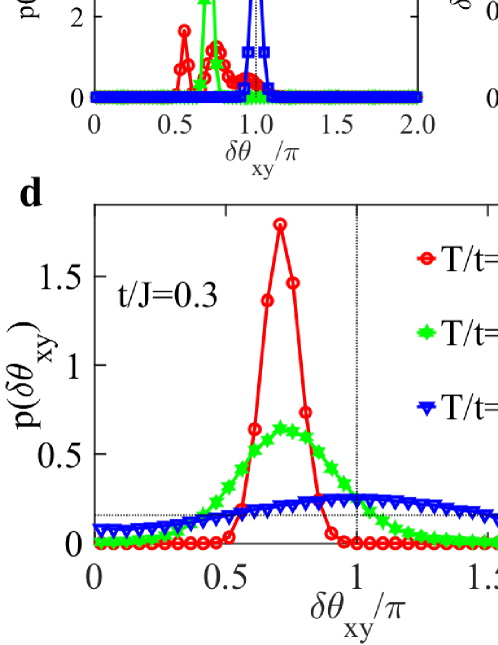
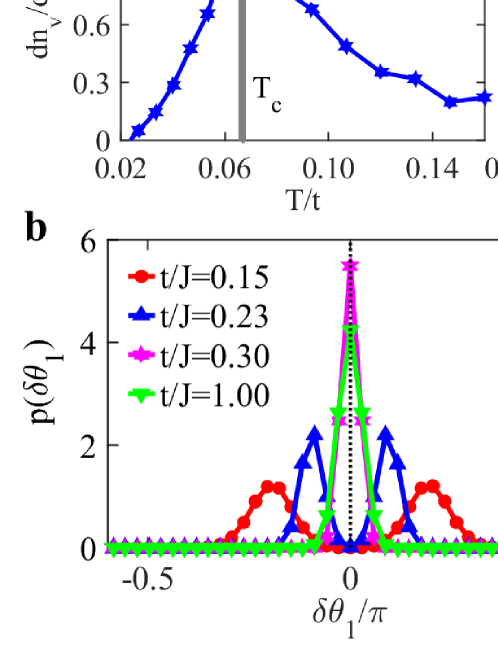
The time reversal symmetry breaking may be seen from the probabilistic distribution of the phase difference of the pairing fields along the and directions. The results are shown in Fig. 3(a) for three different values of . For small in the plaquette state, the existence of multiple peaks mark the phase difference on different bonds. For large , there exists a single maximum around , which signals the uniform -wave superconductivity with opposite sign of the pairing field along the and directions. Quite unexpectedly, for , we still have a single peak but its position deviates from . To see such a variation more clearly, Fig. 3(b) plots the average deviation () and the smallest deviation () of the peak positions. While evovles nonmonotonically and reaches a minimum at the plaquette QCP, keeps increasing with . Interestingly, the two quantities become equal beyond the plaquette QCP but only approach at a much larger .
Under time reversal operation, the phase of the pairing field changes sign so that (mod 2). Thus, the deviation of the peak position from around indicates an intermediate region of uniform superconductivity that breaks the time reversal symmetry, with the gap function , representing pairing with a nodeless gap. Here is the -wave component and denotes an extended -wave component from the nearest-neighbour pairing interaction. The onsite pairing is not excluded due to the strong Coulomb repulsion. We have therefore a two-stage transition from the plaquette to the uniform -wave superconductivity, with an intermediate region that recovers the translational symmetry but still breaks the time reversal symmetry. Similar pairing may have been found under certain conditions in twisted double-layer cuprates 44 and infinite-layer nickelates 46; 45. In the latter case, it arises from the interplay of Kondo and superexchange interactions 47. Here it is associated with the quasiparticle hopping, . Integrating out the electron degrees of freedom leads to a term like , while the second order hopping process such as contributes a term . Their combined free energy may be minimized at away from 0 and 48. Thus, time reversal symmetry breaking represents an intrinsic tendency of the superconductivity with nearest-neighbour pairing at strong coupling, where the normal state is no longer a Fermi liquid.
To further confirm the two-stage transition, Fig. 3(c) plots the gap function with near the nodal and antinodal directions in the momentum space deduced from the spectral function. The gap near the antinode is always finite, but varies nonmonotonically with a maximum at the plaquette QCP , in good correspondence with the maximum . By contrast, the gap near the nodal direction decreases continuously and only diminishes at , confirming a full gap for consistent with the above phase analysis. The transition temperature of the phase may also be extracted from the temperature evolution of . As shown in Fig. 3(d) for , the peak in gets broadened and moves gradually to as the temperature increases across . The angle-dependent gap functions are given in Fig. 3(e), showing a fully gapped pairing state and a nodal -wave pairing state below and above , respectively. Note that the higher-temperature -wave gap contains a finite gapless region on the Fermi surface, which has also been observed previously in some experiments 49.
Superconducting phase coherence
The superconducting transition is determined from the phase mutual information of the pairing fields as well as the vortex number (see Method) 33; 34. Figure 4(a) shows the semilog plot of the phase mutual information between two bonds of the largest distance for , 0.22, 0.30 on the 1010 lattice. We find a slope change at low temperature, marking the establishment of long-distance phase coherence of the pairing fields. The slope change at higher temperature is associated with the onset of the spatial phase correlation, which has a temperature scale in rough agreement with for in Fig. 1 and is therefore responsible for the pseudogap above the superconducting .
The low-temperature transition coincides with the peak position of also plotted in Fig. 4(a). The maximum of implies a rapid development of the vortex number with increasing temperature, which is a characteristic feature of the Berezinskii-Kosterlitz-Thouless (BKT) transition for two-dimensional superconductivity 50; 51; 52. We thus identify this transition as the superconducting transition. The value of is examined for other lattice size and found to vary only slightly, confirming the robustness of our qualitative conclusions.
The final phase diagram is already discussed in Fig. 1(a), showing nonmonotonic variation of with and a maximum at the plaquette QCP. This evolution may also be understood from the phase difference of the pairing fields on neighbouring bonds. Figure 4(b) plots the probabilistic distribution of . We find two symmetric peaks around zero in the plaquette state and a single peak in the uniform superconducting state. Interestingly, as shown in Fig. 4(c), while the peak position decreases gradually and diminishes above , the inverse of its fluctuation, as well as that between next-nearest-neighbour bonds, also varies nonmontonically with and exhibits a maximum near the plaquette QCP, in good correspondence with the evolution of . This coincidence is unexpected at first glance but easy to understand, since a smaller fluctuation of around zero indicates a larger phase stiffness of the pairing fields on neighbouring bonds, thus favoring larger superfluid density and . Theoretically, this is usually described by the free energy 53, , such that the phase fluctuation is inversely related to the superfluid density . This explains our observed correlation between the fluctuation of the phase difference and the magnitude of in Fig. 4(c).
| Nd1-xSrxNiO2 | Pr1-xSrxNiO2 | La1-xSrxNiO2 | CaFe2As2 | BaFe2As2 | SrFe2As2 | |
| (K) | 12 83 | 14 84 | 18.8 85 | 25 89 | 22.5 90 | 21 91 |
| (meV) | 63.6 86 | 66.5, 64 87 | 61.6 88 | 99.8 96 | 118.496 | 56.1 96 |
| 0.016 | 0.019 | 0.026 | 0.022 | 0.016 | 0.032 | |
| Ba1-xKxFe2As2 | BaFe2-xNixAs2 | NaFeAs | bulk FeSe | CeCoIn5 | CeCu2Si2 | |
| (K) | 38.5 92 | 20.5 93 | 25 94 | 895 | 2.3 99 | 0.7 99 |
| (meV) | 106.6 97 | 118.4 97 | 80 96 | 11.0 98 | 4.3 100 | 6.5 100 |
| 0.031 | 0.015 | 0.027 | 0.063 | 0.046 | 0.0093 | |
| URu2Si2 | UBe13 | UPd2Al3 | PuCoGa5 | YbRh2Si2 | YBa2Cu4O8 | |
| (K) | 1.5 99 | 0.95 99 | 2 99 | 18.4 99 | 0.002 99 | 81 20 |
| (meV) | 4.7 100 | 4.7 100 | 5.2 100 | 34.5 101 | 6.0 100 | 105 20 |
| 0.028 | 0.017 | 0.033 | 0.046 | 0.000028 | 0.067 | |
| NdBa2Cu3O6+δ | Tl2Ba2CuO6+δ | HgBaCuO4+δ | HgBa2CaCu2O6+δ | La2-xSrxCuO4 | Nd2-xCexCuO4 | |
| (K) | 95 20 | 93 20 | 97 20 | 127 20 | 39 20 | 24 20 |
| (meV) | 135 20 | 127 20 | 135 20 | 176 20 | 157 20 | 147 20 |
| 0.061 | 0.063 | 0.062 | 0.062 | 0.021 | 0.014 | |
| Ca2-xNaxCuO2Cl2 | Bi2Sr2-xLaxCuO6+δ | Bi2Sr2-xLaxCuO8+δ | Bi2+xSr2-xCa2Cu3O10+δ | |||
| (K) | 28 20 | 38 20 | 95 20 | 111 20 | ||
| (meV) | 166 20 | 153 20 | 161 20 | 165 20 | ||
| 0.015 | 0.021 | 0.051 | 0.058 | |||
| (Ca0.1La0.9)(Ba1.65La0.35)Cu3Oy | (Ca0.4La0.6)(Ba1.35La0.65)Cu3Oy | |||||
| (K) | 58 23 | 80 23 | ||||
| (meV) | 120 76 | 134 76 | ||||
| 0.042 | 0.052 | |||||
Discussion on the plaquette state
The plaquette state may also have other exotic properties detectable in experiment. For example, pairing field modulation may affect local spin susceptibility 54; 55 and cause some spin resonance mode 56. In fact, the plaquette state shares many similarities with the supersolid phase realized in dipolar cold atoms 57; 58; 59; 60; 61. Both break translational symmetry and phase symmetry at zero temperature. Similar to the plaquette state, the microscopic configurations of supersolid consist of weakly connected droplets. Both occupy an intermediate region of their respective phase diagram: the plaquette state occurs between the uniform superconductivity and a disordered phase of coexisting plaquettes and dimers for extremely large pairing interaction, while the supersolid exists between the superfluid phase and an incoherent droplet solid. Given these similarities, one may anticipate that vortices may exist in the supersolid phase, while two modes with different dispersions for some dynamic structure factor observed in supersolid 58 may also emerge in the plaquette state.
Though the Bose-Einstein condensation (BEC) 62 has traditionally been argued to be the strong coupling limit of the superconductivity, our results suggest that it may only hold for local -wave pairing with onsite attractive interaction. For unconventional superconductors with strong onsite Coulomb repulsion, onsite -wave pairing is generally unfavored and the pairs tend to occupy different sites. As a result, short-range pairing emerges for nearest-neighbour spin exchange interaction and, at strong coupling, causes an ordered plaquette state that breaks the translational symmetry. This differs from the local two-particle bound state typical of the BEC. On the other hand, the plaquette state does share some similarities with the BEC, which include the U-shaped density of states near the Fermi energy, the flat dispersion around , and the pseudogap in the normal state at high temperatures.
Our proposed plaquette state is also different from the widely-studied PDW state 38; 66; 39; 67, even though both exhibit real-space modulation of the pairing fields. While the PDW may generally lead to a charge density wave, the plaquette state ideally has a homogeneous charge distribution and breaks the time reversal symmetry. The PDW is by far only found experimentally in superconducting region 64; 63; 65 and might arise theoretically from the interplay of magnetism and superconductivity 68, while the plaquette state proposed here represents an intrinsic pairing instability at strong coupling and might be closely related to the structure recently observed in underdoped cuprates 69; 70.
Constraint on
Another important observation of our calculations is that the superconductivity may intrinsically be suppressed for sufficiently strong pairing interaction even without considering competing orders from other channels. Thus, is constrained from both sides of strong and weak pairing interactions. It is then sensible to study the ratio to have a feeling about the maximum allowed by the pairing interaction 20; 72; 71. For the one band square lattice model discussed so far, we find a maximum ratio . Tuning the next-nearest-neighbour hopping or the chemical potential can only slight improve this ratio. Specifically, at half-filling with and near the van Hove singularity, the maximum is enhanced to 0.045. Motivated by the possible importance of apex oxygen on 73, we have also studied a model with an extra conduction layer, and find the maximum may be at most enhanced to about for certain special (nearest-neighbour) interlayer hopping. On the other hand, local interlayer hopping is found to suppress this maximum ratio. Taking meV from the angle-resolved photoemission spectroscopy (ARPES) and the specific heat analysis 74; 75 and meV from the resonant inelastic X-ray scattering measurement (RIXS) 20; 76, these ratios yield the highest to be 100-130 K, consistent with the reported 97 K for single-layer and K for multi-layer cuprate superconductors under ambient pressure 73.
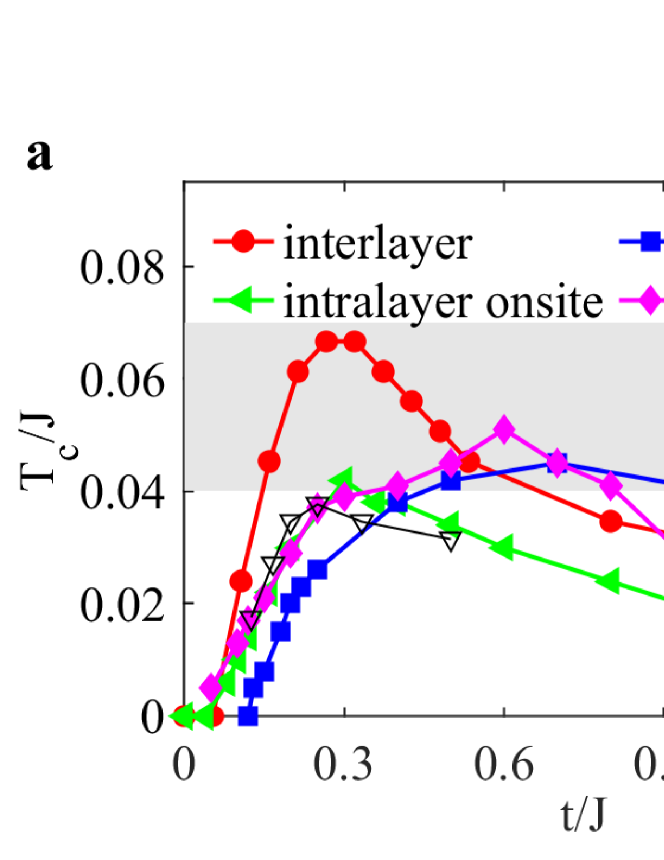
To further explore the above idea, we extend our calculations to other variations of the minimum effective model, covering nearest-neighbour or onsite pairings, single or multi-layer structures, and intralayer or interlayer pairings (see Method). It is important to note that our models do not depend on fine details of the microscopic pairing mechanism, as long as the effective pairing interaction and the low-energy Hamiltonians remain the same. Figure 5(a) shows the variations of versus in these models, where only the nearest-neighbour hopping is considered for simplicity. is the local attractive Hubbard interaction for onsite pairing, and is the interlayer superexchange interaction for interlayer pairing as discussed previously for La3Ni2O7 under high pressure 77; 34. We see all curves behave nonmonotonically with the pairing interaction, although they may have different strong-coupling limit (e.g., BEC for onsite pairing and preformed local interlayer pairing for bilayer nickelates), with the maximum lying within the interval from 0.04 to 0.07. Notably, for the attractive Hubbard model, our simulations yield consistent results compared with previous quantum Monte Carlo simulations (open down-pointing triangles) 2, which reinforces the reliability of our approach, and introducing an additional conduction layer gives the same maximum ratio 78; 79. Note that we have ignored long distance pairing since it is typically weaker than onsite or nearest-neighbour ones for reaching the maximum . We also only focus on quasi-two-dimensional models since three dimensionality usually suppresses in experimental observations 8. Our results are insensitive to the chemical potential or electron fillings in reasonable parameter ranges. This is because we have ignored all other instabilities to maximize the pairing instability, and the superconductivity occurs in a much lower energy scale compared to the Fermi energy. Our phase diagram is therefore not the full phase diagram with all possible ground states of a physical model, but a phase diagram that intentionally exaggerates the superconductivity and other possible instabilities in the pairing channel, so that the derived could be a better estimate of its potential upper limit.
To see if the above constraint may indeed apply in real materials, Fig. 5(b) and Table 1 collect the data for a number of well-known unconventional superconductors 81; 80; 82; 83; 84; 85; 89; 90; 91; 86; 87; 88; 96; 92; 93; 94; 95; 99; 97; 98; 100; 20; 101; 23; 76. The spin energy scale in cuprate, iron-based, and nickelate superconductors have been determined mainly by the spin wave fitting in inelastic neutron scattering (INS) or RIXS experiments 23; 24; 25; 97; 102, where has been found to vary only slightly with doping, which differs from the renormalized one due to the feedback effect observed in low-energy measurements by INS 103 and two-magnon extraction in Raman spectra 104. In iron-based superconductors such as CaFe2As2, SrFe2As2, BaFe2As2, and NaFeAs, the ratios are less than 0.063 96; 89; 94; 97; 98; 90; 91; 92; 93; 95, where the value of is extracted from the reported by taking the effective spin size for SrFe2As2 and for all others except for FeSe following the literatures 81; 80; 82. The large error bar exceeding the shaded area in Fig. 5(b) comes from the bulk FeSe ( K), for which neutron scattering measurements reported the ratio at K 98. Unfortunately, we do not find the data for FeSe films, whose high might involve contributions from the interface. To the best of our knowledge, there is also no exact estimate of for the 1111 systems. It has been reported that SmOFeAs adopts an intermediate spin dispersion between those of NaFeAs and BaFe2As2 105. Assuming that the spin interaction is not sensitive to the doping, as observed in BaFe2-xNixAs2 and NaFe1-xCoxAs 97; 102, we might roughly estimate meV for SmO1-xFxFeAs and thus obtain a maximum ratio given its maximum =55 K 106. While for LaO1-xFxFeAs, experiments only indicate an overall magnitude of meV along different directions 107, which yields with its maximum K using 108. Both fall within our proposed range.
The infinite-layer nickelate superconductors have a small maximum ratio of about 0.026, possibly due to disorder, which indicates the potential to reach a higher 83; 84; 86; 87; 85; 88. RIXS measurements 109 on the high-pressure high-temperature bilayer nickelate superconductor La3Ni2O7 reported an interlayer spin interaction strength () of about 140 meV assuming its spin size , which also seems to be confirmed by inelastic neutron measurements 110. Although these measurements were performed under ambient pressure, it gives a rough estimate of the magnitude of . If we naively apply this value to the high pressure region where the superconductivity was reported with K, we find for the bilayer nickelate superconductors, which agrees well with our previous Monte Carlo simulations 34. Recently, superconductivity has been reported also in the trilayer nickelate superconductor La4Ni3O10 under high pressure, albeit with a much smaller K 111. It has been proposed theoretically that competition and frustration of interlayer pairing between the inner layer and two outer layers may lead to strong superconducting fluctuations and thus reduce the maximum ratio of to 35. This, together with layer imbalance and the possibly smaller interlayer , may explain the much reduced in the trilayer nickelate compared to those in the bilayer ones.
By contrast, the cuprate high-temperature superconductors have the highest in the trilayer structure, and their overall ratios can reach up to 0.067, as observed in HgBa2CaCu2O6+δ, YBa2Cu4O8, YBa2Cu3O6+δ, NdBa2Cu3O6+δ, Tl2Ba2CuO6+δ, and Bi2+xSr2-xCa2Cu3O10+δ 20. This opposite tendency reflects an intrinsic distinction in the pairing mechanisms between multilayer nickelate and cuprate superconductors. In heavy-fermion superconductors such as CeCoIn5 or PuCoGa5, systematic measurements of are lacking. We therefore estimate the spin interaction energy from the coherence temperature scale, namely the Ruderman-Kittle-Kasuya-Yosida (RKKY) scale, and find the highest to be about 100; 99; 101. To the best of our knowledge, a spin wave fitting has only been applied to CePd2Si2 and yields meV under ambient pressure 112. Combining naively this value with its K at 3 GPa gives the ratio , in good alignment with our suggested constraint.
Despite the vast complexities across all these different families of unconventional superconductors far beyond our simplified models, their maximum values all fall within the same range of predicted above, suggesting that our calculations indeed capture some essence of the fundamental physics of unconventional superconductivity. Consequently, our derived maximum ratio represents a practical constraint for some quite generic situations in real materials.
Last, we comment on the ratio widely used in previous literatures. Unlike , we find the maximum depends more sensitively on models and may reach 0.29, 0.15, 0.105 upon tuning the hopping parameters or the chemical potential for interlayer, intralayer onsite, intralayer nearest-neighbour (nn) pairings, respectively. Its maximum typically occurs at different optimal compared to that for the maximum . For the attractive Hubbard model, our derived maximum is close to the quantum Monte Carlo result , which confirms the validity of our estimate 2. While the maximum ratios lie within the proposed narrow range possibly due to their similar local or short-range pairing forms at strong coupling, we ascribe the large variation of the ratio to the fact that the long-range phase coherence determining may rely heavily on the cooperative hopping of paired electrons and hence differ greatly for different orbital degeneracies, pairing configurations, and lattice geometries beyond the simple hopping parameters. The quasiparticle hopping is also more strongly renormalized by correlation effects, which makes it difficult to measure in practice. It is for these reasons that we have chosen to treat as a tuning parameter and focus on the ratio that can be better compared with experiment.
Route to room temperature superconductivity?
It is important to emphasize again that the above agreement by no means implies that all these superconductors, including hole-doped cuprates, are fully described by the specified pairing mechanisms in our simplified models. There is also no rigorous theoretical proof for a maximum in unconventional superconductors 4. Nevertheless, if we take the above constraint seriously, achieving room temperature superconductivity seems unlikely under ambient pressure within the current theoretical framework. For to reach 300 K, we need a pairing interaction of the order meV, which is twice higher than the spin exchange interaction in cuprates and seems unrealistic in most correlated materials. Moreover, the maximum is only realized at an optimal ratio of , thus also requiring a larger quasiparticle hopping , a situation that seems to only occur under pressure. Contrary to the weak-coupling BCS theory which predicts a higher for a larger density of states (smaller ), the maximum is constrained by the magnitude of . Thus a high is not favored in flat-band systems.
It is therefore imperative to explore alternative avenues to enhance the ratio under ambient pressure. It has been noticed that three-layer cuprate superconductors have the highest . One may therefore speculate that multi-layer may promote . Indeed, the maximum increases from 97 K in the single-layer HgBa2CuO4+δ to 127 K in the two-layer HgBa2CaCu2O6+δ and 135 K in the three-layer HgBa2Ca2Cu3O9+δ 73. However, the ratio seems to remain unchanged and the increase of seems to come purely from the increase of 20. On the other hand, the maximum does increase from 0.021 in the single-layer Bi2Sr2-xLaxCuO6+δ to 0.058 in the three-layer Bi2+xSr2-xCa2Cu3O10+δ in Bi-systems 20, but the latter still lies within our proposed range, implying that increasing the number of layers from Bi2201 to Bi2223 only helps to tune the optimal conditions for maximizing , while the constraint itself is not touched. We have also examined the effect of additional local interlayer hopping and find that it actually reduces the maximum . Additionally, one may follow the studies of FeSe films 113; 114 and consider to improve by introducing phonons, but this seems empirically at most to provide an increase of around 40 K, given the limited characteristic phonon frequencies under ambient pressure 115; 116. A larger spin interaction occurs for the Hund’s rule coupling inside an atom. However, it is not clear if intra-atomic inter-orbital pairing may support a high due to their very different orbital characters of the paired electrons.
Putting together, the known unconventional superconductor families, possibly except the infinite-layer nickelates, seem to have almost exhausted their potentials in reaching the highest allowed by their respective spin exchange interactions. As a result, room-temperature superconductivity at ambient pressure is unlikely to occur based on a single pairing mechanism within the current theoretical framework. This not only helps rule out some evidently wrong directions 117; 118, but also points out the necessity of exploring alternative approaches to achieve room-temperature superconductors at ambient pressure 119; 79; 121; 122; 123; 77; 101; 1; 124; 125; 120; 126. It encourages the possibility of incorporating different pairing mechanisms 130; 128; 127; 8; 129; 131, including but not limited to magnetic, charge, orbital, or nematic fluctuations, excitons, bipolarons, etc, to improve the overall effective pairing interaction, for which FeSe films may be a good example 132; 133; 134. Our derived ratios provide a tentative guide in future material exploration of novel high-temperature superconductors. Theoretically, by utilizing from newly developed methods 135 and effective hopping from strongly correlated calculations 136, an approximate estimate of the upper limit of may be predicted for the selection of promising candidates. Experimentally, estimating from RIXS, INS, or other state-of-the-art techniques in newly discovered materials may also help identify their potential in reaching the desired . Last but not least, understanding unconventional superconductivity from a real-space, strong-coupling perspective may already provide an operational and more practical avenue for material design compared to the momentum-space, weak-coupling approach.
Method
Models
We first consider a minimal effective model on the square lattice:
| (1) |
where is the renormalized quasiparticle hopping parameters, is the chemical potential, and the pairing interaction is written in terms of the spin-singlet operator on nearest-neighbour bonds and is the annhilation (creation) operator of the quasiparticles to be paired. For the superexchange mechanism, is given by the nearest-neighbour antiferromagnetic interaction as well as the attractive charge density interaction. A complex auxiliary field is introduced to decouple the pairing interaction and solve the model 53:
| (2) |
To avoid the negative sign problem, we assume a static approximation, , and employ the auxiliary field Monte Carlo approach 26; 27; 28; 29; 30; 31; 32; 33. We follow the standard procedure by integrating out the fermionic degrees of freedom and simulate the final effective action only of the pairing fields by the Metropolis algorithm 33. This method ignores the dynamic fluctuations of the pairing fields but takes full consideration of their spatial and thermal fluctuations, and is therefore particularly suitable for studying the phase transition at finite temperature 137. For numerical calculations, we consider a square lattice with periodic boundary conditions and include only the nearest-neighbour hopping and the next-nearest-neighbour hopping as in the cuprate high-temperature superconductors 138; 139. The chemical potential is fixed to . The presented results have been examined and found qualitatively unchanged for other values of the parameters or on a larger lattice. A twisted boundary condition is used for spectral calculations 140.
To derive the constraint, we extend the above model to the following variations:
(1) A two-layer model with intralayer nearest-neighbour pairing and interlayer hopping:
where the subscript represents the layer index, , and denotes the local interlayer hopping.
(2) A two-layer model with an extra conduction layer motivated by the possible importance of apex oxygens in cuprates:
| (4) | |||||
where denotes local () or nearest-neighbour ( or ) interlayer hopping.
(3) A single-layer model with onsite pairing interaction as in the attractive Hubbard model:
| (5) |
where and is given by the local attractive Hubbard interaction.
(4) A two-layer model with onsite pairing in one layer and an extra conduction layer:
| (6) | |||||
where and denotes local () or nearest-neighbour ( or ) interlayer hopping.
(5) A two-layer model with interlayer pairing:
| (7) |
where .
Models (1) and (2) are constructed to reflect the effects of interlayer hopping and apex oxygen in cuprate superconductors, models (3) and (4) apply for onsite pairing with local attractive interaction, and model (5) is motivated by the bilayer nickelate superconductor.
Mutual information and vortex number
The phase mutual information of the pairing fields is defined as 33; 34:
| (8) |
where is the marginal distribution of the pairing field phase on two bonds with a distance , and is their joint probabilistic distribution. For onsite or interlayer pairing, simplifies to . The vortex number is calculated using
| (9) |
where is the winding number for with the phase of for nearest-neighbour pairing and denotes the statistic average over all pairing configurations. For onsite or interlayer pairing, is the phase of the pairing field at site .
Acknowledgements
This work was supported by the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDB33010100), the National Natural Science Foundation of China (Grants No. 12474136 and No. 12174429), and the National Key Research and Development Program of China (Grant No. 2022YFA1402203).
References
- 1 Zhang, C. et al. Bipolaronic high-temperature superconductivity. Phys. Rev. X 13, 011010 (2023).
- 2 Paiva, T., Scalettar, R., Randeria, M. & Trivedi, N. Fermions in 2D optical lattices: temperature and entropy scales for observing antiferromagnetism and superfluidity. Phys. Rev. Lett. 104, 066406 (2010).
- 3 Hazra, T., Verma, N. & Randeria, M. Bounds on the superconducting transition temperature: applications to twisted bilayer graphene and cold atoms. Phys. Rev. X 9, 031049 (2019).
- 4 Hofmann, J. S., Chowdhury, D., Kivelson, S. A. & Berg, E. Heuristic bounds on superconductivity and how to exceed them. npj Quantum Mater. 7, 83 (2022).
- 5 Esterlis, I., Kivelson, S. A. & Scalapino, D. J. A bound on the superconducting transition temperature. npj Quant. Mater. 3, 59 (2018).
- 6 Monthoux, P., Balatsky, A. V. & Pines, D. Weak-coupling theory of high-temperature superconductivity in the antiferromagnetically correlated copper oxides. Phys. Rev. B 46, 14803–14817 (1992).
- 7 Mathur, N. D. et al. Magnetically mediated superconductivity in heavy fermion compounds. Nature 394, 39–43 (1998).
- 8 Monthoux, P., Pines, D. & Lonzarich, G. G. Superconductivity without phonons. Nature 450, 1177–1183 (2007).
- 9 Norman, M. R. The challenge of unconventional superconductivity, Science 332, 196–200 (2011).
- 10 Kivelson, S. A. Superconducting materials: Superconductivity on the verge of catastrophe. Nat. Mater. 5, 343–344 (2006).
- 11 Ganin, A. Y. et al. Bulk superconductivity at 38 K in a molecular system. Nat. Mater. 7, 367–371 (2008).
- 12 Wu, W. et al. Superconductivity in the vicinity of antiferromagnetic order in CrAs. Nat. Commun. 5, 5508 (2014).
- 13 Seo, S. et al. Controlling superconductivity by tunable quantum critical points. Nat. Commun. 6, 6433 (2015).
- 14 Chen, K. Y. et al. Double superconducting dome and triple enhancement of in the Kagome superconductor under high Pressure. Phys. Rev. Lett. 126, 247001 (2021).
- 15 Gruner, T. et al. Charge density wave quantum critical point with strong enhancement of superconductivity. Nat. Phys. 13, 967–972 (2017).
- 16 Yu, F. H. et al. Unusual competition of superconductivity and charge-density-wave state in a compressed topological kagome metal. Nat. Commun. 12, 3645 (2021).
- 17 Sobirey, L. et al. Observing the influence of reduced dimensionality on fermionic superfluids. Phys. Rev. Lett. 129, 83601 (2022).
- 18 Keimer, B., Kivelson, S. A., Norman, M. R., Uchida, S. & Zaanen, J. From quantum matter to high-temperature superconductivity in copper oxides. Nature 518, 179–186 (2015).
- 19 Emery, V. J. & Kivelson, S. A. Importance of phase fluctuations in superconductors with small superfluid density. Nature 374, 434–437 (1995).
- 20 Wang, L. et al. Paramagnons and high-temperature superconductivity in a model family of cuprates. Nat. Commun. 13, 3163 (2022).
- 21 Chen, Z. et al. Anomalously strong near-neighbor attraction in doped 1D cuprate chains. Science 373, 1235-1239 (2021).
- 22 O’Mahony, S. M. et al. On the electron pairing mechanism of copper-oxide high temperature superconductivity. Proc. Natl. Acad. Sci. USA 119, e2207449119 (2022).
- 23 Ofer, R. et al. Magnetic analog of the isotope effect in cuprates. Phys. Rev. B 74, 220508(R) (2006).
- 24 Tacon, M. Le et al. Intense paramagnon excitations in a large family of high-temperature superconductors. Nat. Phys. 7, 725–730 (2011).
- 25 Dean, M. P. M. et al. Persistence of magnetic excitations in La2-xSrxCuO4 from the undoped insulator to the heavily overdoped non-superconducting metal. Nat. Mater. 12, 1019–1023 (2013).
- 26 Mayr, M., Alvarez, G., Şen, C. & Dagotto, E. Phase fluctuations in strongly coupled -wave superconductors, Phys. Rev. Lett. 94, 217001 (2005).
- 27 Dubi, Y., Meir, Y. & Avishai, Y. Nature of the superconductor-insulator transition in disordered superconductors. Nature 449, 876–880 (2007).
- 28 Pasrija, K., Chakraborty, P. B. & Kumar, S. Effective Hamiltonian based Monte Carlo for the BCS to BEC crossover in the attractive Hubbard model. Phys. Rev. B 94, 165150 (2016).
- 29 Dong, J. J., Huang, D. & Yang, Y.-F. Mutual information, quantum phase transition and phase coherence in Kondo systems. Phys. Rev. B 104, L081115 (2021).
- 30 Mukherjee, A. et al. Testing the Monte Carlo-mean field approximation in the one-band Hubbard model. Phys. Rev. B 90, 205113 (2014).
- 31 Atkinson, W. A., Bazak, J. D. & Andersen, B. M. Robust nodal -wave spectrum in simulations of a strongly fluctuating competing order in underdoped cuprate superconductors. Phys. Rev. Lett. 109, 267004 (2012).
- 32 Zhong, Y. W., Li, T. & Han, Q. Monte Carlo study of thermal fluctuations and Fermi-arc formation in -wave superconductors. Phys. Rev. B 84, 024522 (2011).
- 33 Qin, Q., Dong, J.-J., Sheng, Y., Huang, D. & Yang, Y.-F. Superconducting fluctuations and charge-4 plaquette state at strong coupling. Phys. Rev. B 108, 054506 (2023).
- 34 Qin, Q. & Yang, Y.-F. High- superconductivity by mobilizing local spin singlets and possible route to higher in pressurized La3Ni2O7. Phys. Rev. B 108, L140504 (2023).
- 35 Qin, Q., Wang, J. & Yang, Y. Frustrated superconductivity in the trilayer nickelate La4Ni3O10. Preprint at https://arxiv.org/abs/2405.04340 (2024).
- 36 Armitage, N. P., Fournier, P. & Greene, R. L. Progress and perspectives on electron-doped cuprates. Rev. Mod. Phys. 82, 2421–2487 (2010).
- 37 Jang, H. et al. Hybridization-controlled pseudogap state in the quantum critical superconductor CeCoIn5. Phys. Rev. Lett. 130, 076301 (2023).
- 38 Agterberg, D. F. & Tsunetsugu, H. Dislocations and vortices in pair-density-wave superconductors. Nat. Phys. 4, 639–642 (2008).
- 39 Lee, P. A. Amperean pairing and the pseudogap phase of cuprate superconductors. Phys. Rev. X 4, 031017 (2014).
- 40 He, R. H. et al. From a single-band metal to a high-temperature superconductor via two thermal phase transitions. Science 331, 1579–1583 (2011).
- 41 Zhou, Y. et al. Quantum phase transition from superconducting to insulating-like state in a pressurized cuprate superconductor. Nat. Phys. 18, 406–410 (2022).
- 42 Grinenko, V. et al. State with spontaneously broken time-reversal symmetry above the superconducting phase transition. Nat. Phys. 17, 1254–1259 (2021).
- 43 Shipulin, I. et al. Calorimetric evidence for two phase transitions in Ba1-xKxFe2As2 with fermion pairing and quadrupling states. Nat. Commun. 14, 6734 (2023).
- 44 Can, O. et al. High-temperature topological superconductivity in twisted double-layer copper oxides. Nat. Phys. 17, 519–524 (2021).
- 45 Ji, H. et al. Rotational symmetry breaking in superconducting nickelate NdSrNiO2 films. Nat. Commun. 14, 7155 (2023).
- 46 Wang, Z., Zhang, G. M., Yang, Y. F. & Zhang, F. C. Distinct pairing symmetries of superconductivity in infinite-layer nickelates. Phys. Rev. B 102, 220501(R) (2020).
- 47 Zhang, G. M., Yang, Y. F. & Zhang, F. C. Self-doped Mott insulator for parent compounds of nickelate superconductors. Phys. Rev. B 101, 020501(R) (2020).
- 48 Tešanović, Z. D-wave duality and its reflections in high-temperature superconductors. Nat. Phys. 4, 408–414 (2008).
- 49 Vishik, I. M. et al., Phase competition in trisected superconducting dome. Proc. Natl. Acad. Sci. USA 109, 18332-18337 (2012).
- 50 Berezinskii, V. L. Destruction of long-range order in one-dimensional and two-dimensional systems possessing a continuous symmetry group. II. Quantum systems. Zh. Eksp. Teor. Fiz. 61, 1144 (1971) [Sov. Phys. JETP 34, 610–616 (1972)].
- 51 Kosterlitz, J. M. & Thouless, D. J. Ordering, metastability and phase transitions in two-dimensional systems. J. Phys. C 6, 1181 (1973).
- 52 Kosterlitz, J. M. The critical properties of the two-dimensional XY Model. J. Phys. C 7, 1046–1060 (1974).
- 53 P. Coleman, Introduction to Many-body Physics, (Cambridge University Press, Cambridge, England, 2015).
- 54 Choubey, P. et al. Atomic-scale electronic structure of the cuprate pair density wave state coexisting with superconductivity. Proc. Natl. Acad. Sci. USA 117, 14805–14811 (2020).
- 55 Kinjo, K. et al. Superconducting spin smecticity evidencing the Fulde-Ferrell-Larkin-Ovchinnikov state in Sr2RuO4. Science 376, 397–400 (2022).
- 56 Stock, C., Broholm, C., Hudis, J., Kang, H. J. & Petrovic, C. Spin resonance in the -wave superconductor CeCoIn5. Phys. Rev. Lett. 100, 087001 (2008).
- 57 Saccani, S., Moroni, S. & Boninsegni, M. Excitation spectrum of a supersolid. Phys. Rev. Lett. 108, 175301 (2012).
- 58 Natale, G. et al. Excitation spectrum of a trapped dipolar supersolid and its experimental evidence. Phys. Rev. Lett. 123, 050402 (2019).
- 59 Guo, M. et al. The low-energy goldstone mode in a trapped dipolar supersolid. Nature 574, 386–389 (2019).
- 60 Ilzhöfer, P. et al. Phase coherence in out-of-equilibrium supersolid states of ultracold dipolar atoms. Nat. Phys. 17, 356–361 (2021).
- 61 Tanzi, L. et al. Supersolid symmetry breaking from compressional oscillations in a dipolar quantum gas. Nature 574, 382–385 (2019).
- 62 Chen, Q., Wang, Z., Boyack, R., Yang, S. & Levin, K. When superconductivity crosses over: from BCS to BEC. Preprint at https://arxiv.org/abs/2208.01774 (2022).
- 63 Zhao, H. et al. Smectic pair-density-wave order in EuRbFe4As4. Nature 618, 940-945 (2023).
- 64 Chen, H. et al. Roton pair density wave in a strong-coupling Kagome superconductor. Nature 599, 222–228 (2021).
- 65 Du, Z. et al. Imaging the energy gap modulations of the cuprate pair-density-wave state. Nature 580, 65–70 (2020).
- 66 Agterberg, D. F. et al. The Physics of pair-density waves: cuprate superconductors and beyond. Annu. Rev. Condens. Matter Phys. 11, 231–270 (2020).
- 67 Berg, E., Fradkin, E. & Kivelson, S. A. Charge-4e superconductivity from pair-density-wave order in certain high-temperature superconductors. Nat. Phys. 5, 830–833 (2009).
- 68 Chen, J., Wang, J. & Yang, Y.-F. Pair density wave, unconventional superconductivity, and non-Fermi liquid quantum critical phase in frustrated Kondo lattice. Phys. Rev. B 109, 014103 (2024).
- 69 Ye, S. et al. The emergence of global phase coherence from local pairing in underdoped cuprates. Nat. Phys. 19, 1301–1307 (2023).
- 70 Li, H. et al. Low-energy gap emerging from confined nematic states in extremely underdoped cuprate superconductors. npj Quantum Mater. 8, 18 (2023).
- 71 Ruan, W. et al. Relationship between the parent charge transfer gap and maximum transition temperature in cuprates. Sci. Bull. 61, 1826–1832 (2016).
- 72 Wang, Z. et al. Correlating the charge-transfer gap to the maximum transition temperature in Bi2Sr2Can-1CunO2n+4+δ. Science 381, 227–231 (2023).
- 73 Scalapino, D. J. A common thread: The pairing interaction for unconventional superconductors. Rev. Mod. Phys. 84, 1383–1417 (2012).
- 74 Chen, S. Di et al. Unconventional spectral signature of in a pure -wave superconductor. Nature 601, 562–567 (2022).
- 75 Harrison, N. & Chan, M. K. Thermodynamic evidence for electron correlation-driven flattening of the quasiparticle bands in the high- cuprates. Preprint at https://arxiv.org/abs/2303.12956 (2023).
- 76 Ellis, D. S. et al. Correlation of the superconducting critical temperature with spin and orbital excitations in (Cax La1-x)(Ba1.75-xLa0.25+x)Cu3Oy as measured by resonant inelastic X-ray scattering. Phys. Rev. B 92, 104507 (2015).
- 77 Yang, Y.-F., Zhang, G.-M. & Zhang, F.-C. Interlayer valence bonds and two-component theory for high- superconductivity of La3Ni2O7 under pressure. Phys. Rev. B 108, L201108 (2023).
- 78 Wachtel, G., Bar-Yaacov, A. & Orgad, D. Superfluid stiffness renormalization and critical temperature enhancement in a composite superconductor. Phys. Rev. B 86, 134531 (2012).
- 79 Berg, E., Orgad, D., & Kivelson, S. A. Route to high-temperature superconductivity in composite systems. Phys. Rev. B 78, 094509 (2008).
- 80 Zhang, C. et al. Effect of pnictogen height on spin waves in iron pnictides. Phys. Rev. Lett. 112, 217202 (2014).
- 81 Zhao, J. et al. Spin waves and magnetic exchange interactions in CaFe2As2. Nat. Phys. 5, 555–560 (2009).
- 82 Ewings, R. A. et al. Itinerant spin excitations in SrFe2As2 measured by inelastic neutron scattering. Phys. Rev. B 83, 214519 (2011).
- 83 Zeng, S. et al. Phase diagram and superconducting dome of infinite-layer thin films. Phys. Rev. Lett. 125, 147003 (2020).
- 84 Osada, M., Wang, B. Y., Lee, K., Li, D. & Hwang, H. Y. Phase diagram of infinite layer praseodymium nickelate thin films. Phys. Rev. Mater. 4, 121801 (2020).
- 85 Sun, W. et al. Evidence for anisotropic superconductivity beyond Pauli limit in infinite-layer lanthanum nickelates. Adv. Mater. 35, 2303400 (2023).
- 86 Lu, H. et al. Magnetic excitations in infinite-layer nickelates. Science 373, 213–216 (2021).
- 87 Gao, Q. et al. Magnetic excitations in strained infinite-layer nickelate PrNiO2. Preprint at https://arxiv.org/abs/2208.05614 (2022).
- 88 Rossi, M. et al. Universal orbital and magnetic structures in infinite-layer nickelates. Preprint at https://arxiv.org/abs/2312.16444 (2023).
- 89 Chen, D. Y. et al. Superconductivity in undoped CaFe2As2 single crystals. Chin. Phys. Lett. 33, 067402 (2016).
- 90 Kim, J. S., Blasius, T. D., Kim, E. G. & Stewart, G. R. Superconductivity in undoped single crystals of BaFe2As2: field and current dependence. J. Phys. Condens. Matter 21, 342201 (2009).
- 91 Saha, S. R., Butch, N. P., Kirshenbaum, K., Paglione, J. & Zavalij, P. Y. Superconducting and ferromagnetic phases induced by lattice distortions in stoichiometric single crystals. Phys. Rev. Lett. 103, 37005 (2009).
- 92 Rotter, M., Tegel, M. & Johrendt, D. Superconductivity at 38 K in the Iron Arsenide . Phys. Rev. Lett. 101, 107006 (2008).
- 93 Li, L. J. et al. Superconductivity induced by Ni doping in BaFe2As2 single crystals. New J. Phys. 11, 25008 (2009).
- 94 Chu, C. W. et al. The synthesis and characterization of LiFeAs and NaFeAs. Phys. C: Supercond. its Appl. 469, 326–331 (2009).
- 95 Hsu, F.-C. et al. Superconductivity in the PbO-type structure -FeSe. Proc. Natl. Acad. Sci. 105, 14262–14264 (2008).
- 96 Dai, P. Antiferromagnetic order and spin dynamics in iron-based superconductors. Rev. Mod. Phys. 87, 855–896 (2015).
- 97 Wang, M. et al. Doping dependence of spin excitations and its correlations with high-temperature superconductivity in iron pnictides. Nat. Commun. 4, 2874 (2013).
- 98 Gu, Y. et al. Frustrated magnetic interactions in FeSe. Phys. Rev. B 106, L060504 (2022).
- 99 Li, Y., Sheng, Y. T. & Yang, Y.-F. Theoretical progress and material studies of heavy fermion superconductors. Acta Phys. Sin. 70, 017402 (2021).
- 100 Yang, Y.-F., Fisk, Z., Lee, H. O., Thompson, J. D. & Pines, D. Scaling the Kondo lattice. Nature 454, 611–613 (2008).
- 101 Pines, D. Finding new superconductors: The spin-fluctuation gateway to high and possible room temperature superconductivity. J. Phys. Chem. B 117, 13145–13153 (2013).
- 102 Pelliciari, J. et al. Intralayer doping effects on the high-energy magnetic correlations in NaFeAs. Phys. Rev. B 93, 134515 (2016).
- 103 Wakimoto, S. et al. Direct relation between the low-energy spin excitations and superconductivity of overdoped high- superconductors. Phys. Rev. Lett. 92, 217004 (2004).
- 104 Li, Y. et al. Feedback effect on high-energy magnetic fluctuations in the model high-temperature superconductor HgBa2CuO4+δ observed by electronic Raman scattering. Phys. Rev. Lett. 108, 227003 (2012).
- 105 Pelliciari, J. et al. Presence of magnetic excitations in SmFeAsO. Appl. Phys. Lett. 109, 122601 (2016).
- 106 Ren, Z. et al. Superconductivity at 55 K in iron-based F-doped layered quaternary compound Sm[O1-xFx] FeAs. Chin. Phys. Lett. 25, 2215 (2008).
- 107 Ramazanoglu, M. et al. Two-dimensional magnetic interactions in LaFeAsO. Phys. Rev. B 87, 140509 (2013).
- 108 de la Cruz, C. et al. Magnetic order close to superconductivity in the iron-based layered LaO1-xFxFeAs systems. Nature 453, 899–902 (2008).
- 109 Chen, X. et al. Electronic and magnetic excitations in La3Ni2O7. Preprint at https://arxiv.org/abs/2401.12657 (2024).
- 110 Xie, T., et al. Neutron scattering studies on the high- superconductor La3Ni2O7-δ at ambient pressure. Preprint at https://doi.org/10.48550/arXiv.2401.12635 (2024).
- 111 Zhu, Y. et al. Superconductivity in pressurized trilayer La4Ni3O10-δ single crystals. Nature 631, 531–536 (2024).
- 112 Dijk, N. H. Van. et al. Magnetic excitations in heavy-fermion CePd2Si2. Phys. Rev. B 61, 8922–8931 (2000).
- 113 Song, Q. et al. Evidence of cooperative effect on the enhanced superconducting transition temperature at the FeSe/SrTiO3 interface. Nat. Commun. 10, 758 (2019).
- 114 Lee, J. J. et al. Interfacial mode coupling as the origin of the enhancement of in FeSe films on SrTiO3. Nature 515, 245–248 (2014).
- 115 Cai, X., Li, Z.-X. & Yao, H. High-temperature superconductivity induced by the Su-Schrieffer-Heeger electron-phonon coupling. Preprint at https://arxiv.org/abs/2308.06222 (2023).
- 116 McMillan, W. L. Transition temperature of strong-coupled superconductors. Phys. Rev. 167, 331–344 (1968).
- 117 Lee, S., Kim, J. H. & Kwon, Y. W. The first room-temperature ambient-pressure superconductor. Preprint at https://arxiv.org/abs/2307.12008.
- 118 Lee, S. et al. Superconductor Pb10-xCux(PO4)6O showing levitation at room temperature and atmospheric pressure and mechanism. Preprint at https://arxiv.org/abs/2307.12037 (2023).
- 119 Towards a complete theory of high . Nat. Phys. 2, 138 (2006).
- 120 Dahm, T. et al. Strength of the spin-fluctuation-mediated pairing interaction in a high-temperature superconductor. Nat. Phys. 5, 217–221 (2009).
- 121 Gao, M., Lu, Z.-Y., & Xiang, T. Finding high-temperature superconductors by metallizing the -bonding electrons. Physics 44, 421 (2015), https://wuli.iphy.ac.cn/article/doi/10.7693/wl20150701
- 122 Hu, J. P. Identifying the genes of unconventional high temperature superconductors. Sci. Bull. 61, 561 (2016).
- 123 Pines, D. Emergent behavior in strongly correlated electron systems. Rep. Prog. Phys. 79, 092501 (2016).
- 124 Lee, D. & Carlo, M. Routes to high-temperature superconductivity : A lesson from FeSe/SrTiO3. Annu. Rev. Condens. Matter Phys. 9,261-282 (2018).
- 125 Kivelson, S. A. Physics of superconducting transition temperatures. J. Supercond. Nov. Magn. 33,5-10 (2020).
- 126 Basov, D. N. & Chubukov, A. V. Manifesto for a higher Tc. Nat. Phys. 7, 272–276 (2011).
- 127 Barantani, F. et al. Resonant inelastic X-ray scattering study of electron-exciton coupling in high- cuprates. Phys. Rev. X 12, 21068 (2022).
- 128 Dzhumanov, S., Baratov, A. A. & Abboudy, S. Pairing theory of polarons in real and momentum space. Phys. Rev. B 54, 13121–13128 (1996).
- 129 Sous, J., Chakraborty, M., Krems, R. V & Berciu, M. Light bipolarons stabilized by Peierls electron-phonon coupling. Phys. Rev. Lett. 121, 247001 (2018).
- 130 Lederer, S., Schattner, Y., Berg, E. & Kivelson, S. A. Enhancement of superconductivity near a nematic quantum critical point. Phys. Rev. Lett. 114, 097001 (2015).
- 131 Aji, V., Shekhter, A. & Varma, C. M. Theory of the coupling of quantum-critical fluctuations to fermions and -Wave superconductivity in cuprates. Phys. Rev. B 81, 64515 (2010).
- 132 Wang, Q.-Y. et al. Interface-Induced high-temperature superconductivity in single unit-cell FeSe films on SrTiO3. Chin. Phys. Lett. 29, 37402 (2012).
- 133 Liu, D. et al. Electronic origin of high-temperature superconductivity in single-layer FeSe superconductor. Nat. Commun. 3, 931 (2012).
- 134 Tan, S. et al. Interface-induced superconductivity and strain-dependent spin density waves in FeSe/SrTiO3 thin films. Nat. Mater, 12, 634–640 (2013).
- 135 Cui, Z.-H., Zhai, H., Zhang X., & Chan, G. K.-L. Systematic electronic structure in the cuprate parent state from quantum many-body simulations. Science 377, 1192 (2022).
- 136 Cataldo, S. Di, Worm, P. , Tomczak, J. M., Si, L. & Held, K. Unconventional superconductivity without doping in infinite-layer nickelates under pressure. Nat. Commun. 15, 3952 (2024).
- 137 Dong, J. J. & Yang, Y.-F. Development of long-range phase coherence on the Kondo lattice. Phys. Rev. B 106, L161114 (2022).
- 138 Carbotte, J. P. Properties of a two-dimensional D-wave superconductor from phenomenological susceptibility. Phys. Rev. B 49, 4176 (1994).
- 139 Monthoux, P. & Lonzarich, G. G. Magnetically mediated superconductivity in quasi-two and three Dimensions. Phys. Rev. B 63, 054529 (2001).
- 140 Li, J., Cheng, C., Paiva, T., Lin, H. Q. & Mondaini, R. Giant magnetoresistance in Hubbard chains. Phys. Rev. Lett. 121, 020403 (2018).