Intrinsic and extrinsic thermodynamics for stochastic population processes with multi-level large-deviation structure
Abstract
A set of core features is set forth as the essence of a thermodynamic description, which derive from large-deviation properties in systems with hierarchies of timescales, but which are not dependent upon conservation laws or microscopic reversibility in the substrate hosting the process. The most fundamental elements are the concept of a macrostate in relation to the large-deviation entropy, and the decomposition of contributions to irreversibility among interacting subsystems, which is the origin of the dependence on a concept of heat in both classical and stochastic thermodynamics. A natural decomposition is shown to exist, into a relative entropy and a housekeeping entropy rate, which define respectively the intensive thermodynamics of a system and an extensive thermodynamic vector embedding the system in its context. Both intensive and extensive components are functions of Hartley information of the momentary system stationary state, which is information about the joint effect of system processes on its contribution to irreversibility. Results are derived for stochastic Chemical Reaction Networks, including a Legendre duality for the housekeeping entropy rate to thermodynamically characterize fully-irreversible processes on an equal footing with those at the opposite limit of detailed-balance. The work is meant to encourage development of inherent thermodynamic descriptions for rule-based systems and the living state, which are not conceived as reductive explanations to heat flows.
I Introduction
The statistical derivations underlying most thermodynamic phenomena
are understood to be widely applicable, and are mostly developed in
general terms. Yet where thermodynamics is offered as an ontology to
understand new patterns and causes in nature – the
thermodynamics of
computation Szilard:MD:29 ; Landauer:IHGCP:61 ; Bennett:TC:82 ; Wolpert:stoch_thermo_comp:19
or stochastic
thermodynamics Seifert:stoch_thermo_rev:12 ,111
Stochastic thermodynamics is the modern realization of a program to
create a non-equilibrium thermodynamics that began with
Onsager Onsager:RRIP1:31 ; Onsager:RRIP2:31 and took much of its
modern form under Prigogine and
coworkers Glansdorff:structure:71 ; Prigogine:MT:98 . Since the
beginning its core method has been to derive rules or constraints for
non-stationary thermal dynamics from dissipation of free energies
defined by Gibbs equilibria, from any combination of thermal baths or
asymptotic reservoirs.
The parallel and contemporaneous development of thermodynamics of
computation can be viewed as a quasistatic analysis with discrete
changes in the boundary conditions on a thermal bath corresponding to
logical events in algorithms. Early stochastic thermodynamics
combined elements of both traditions, with the quantities termed
“non-equilibrium entropies” corresponding to the information
entropies over computer states, distinct from quasistatic entropies
associated with heat in a locally-equilibrium environment, with
boundary conditions altered by the explicitly-modeled stochastic state
transitions.
More recently stochastic thermodynamics incorporated time-reversal
methods originally developed for measures in dynamical
systems Searles:fluct_thm:99 ; Evans:fluct_thm:02 ; Gallavotti:dyn_ens_NESM:95 ; Gallavotti:dyn_ens_SS:95
leading to a variety of fluctuation
theorems Jarzynski:fluctuations:08 ; Chetrite:fluct_diff:08 ; Esposito:fluct_theorems:10
and nonequilibrium work
relations Crooks:NE_work_relns:99 ; Crooks:path_ens_aves:00 ; Kurchan:NEWRs:07 ,
still however relating path probability ratios either to dissipation
of heat or to differences in equilibrium free energies.
or where these methods are taken to define a foundation for the
statistical physics of reproduction or
adaptation England:statphys_selfrepl:13 ; Perunov:adaptation:15
– these problems are framed in terms of two
properties particular to the domain of mechanics: the conservation of
energy and microscopic reversibility. Other applications of the same
mathematics, with designations such as
intensity of
choice Luce:choice:59 ; McFadden:quantal_choice:76
tipping points, or
early warning signs Lenton:climate_tip_ew:12 , are
recognized as analogies to thermodynamics, on the understanding that
they only become the “thermodynamics of” something when they derive
its causes from energy conservation connected to the entropies of
heat.
This accepted detachment of mathematics from phenomenology, with thermodynamic phenomena interpreted in their historical terms and mathematics kept interpretation-free, contrasts with the way statistical mechanics was allowed to expand the ontological categories of physics at the end of the last century. The kinetic theory of heat Joule:sci_papers:44 ; Clausius:mech_the_heat:65 ; Boltzmann:second_law:86 was not established as an analogy to gambling222The large-deviation rate function underlies the solution of the gambler’s ruin problem of Pascal, Fermat, and Bernoulli Hald:prob_pre_1750:90 . used to describe patterns in the fluid caloric.333However, as late as 1957 Jaynes Jaynes:ITSM_I:57 ; Jaynes:ITSM_II:57 needed to assert that the information entropy of Shannon referred to the same quantity as the physical entropy of Boltzmann, and was not merely the identical mathematical function. Even the adoption of “entropy production” to refer to changes in the state-variable entropy by irreversible transformations – along the course of which the state-variable entropy is not even defined – is a retreat to a substance syntax; I would prefer the less euphonious but categorically better expression “loss of large-deviation accessibility”. Thermodynamics instead took the experienced phenomena involving heat, and where there had formerly been only names and metaphors to refer to them, it brought into existence concepts capturing their essential nature, not dissolving their reality as phenomena Rota:lect_notes:08 , but endowing it with a semantics. The distinction is between formalization in the service of reduction to remain within an existing ontology, and formalization as the foundation for discovery of new conceptual primitives. Through generalizations and extensions that could not have been imagined in the late 19th century GellMann:RG:54 ; Wilson:RG:74 ; Weinberg:phenom_Lagr:79 ; Polchinski:RGEL:84 (revisited in Sec. VII), essentially thermodynamic insights went on to do the same for our fundamental theory of objects and interactions, the nature of the vacuum and the hierarchy of matter, and the presence of stable macro-worlds at all.
This paper is written with the view that the essence of a thermodynamic description is not found in its connection to conservation laws, microscopic reversibility, or the equilibrium state relations they entail, despite the central role those play in the fields mentioned Landauer:IHGCP:61 ; England:statphys_selfrepl:13 ; Perunov:adaptation:15 ; Seifert:stoch_thermo_rev:12 . At the same time, it grants an argument that has been maintained across a half-century of enormous growth in both statistical methods and applications Fermi:TD:56 ; Bertini:macro_NEThermo:09 : that thermodynamics should not be conflated with its statistical methods. The focus will therefore be on the patterns and relations that make a phenomenon essentially thermodynamic, which statistical mechanics made it possible to articulate as concepts. The paper proposes a sequence of these and exhibits constructions of them unconnected to energy conservation or microscopic reversibility.
Essential concepts are of three kinds: 1) the nature and origin of macrostates; 2) the roles of entropy in relation to irreversibility and fluctuation; and 3) the natural apportionment of irreversibility between a system and its environment, which defines an intrinsic thermodynamics for the system and an extrinsic thermodynamics that embeds the system in its context, in analogy to the way differential geometry defines an intrinsic curvature for a manifold distinct from extrinsic curvatures that may embed the manifold in another manifold of higher dimension.444This analogy is not a reference to natural information geometries Amari:inf_geom:01 ; Ay:info_geom:17 that can also be constructed, though perhaps those geometries would provide an additional layer of semantics to the constructions here.
All of these concepts originate in the large-deviation properties of stochastic processes with multi-level timescale structure. They will be demonstrated here using a simple class of stochastic population processes, further specified as Chemical Reaction Network models as more complex relations need to be presented.
Emphasis will be laid on the different roles of entropy as a functional on general distributions versus entropy as a state function on macrostates, and on the Lyapunov role of entropy in the 2nd law Boltzmann:second_law:86 ; Fermi:TD:56 versus its large-deviation role in fluctuations Ellis:ELDSM:85 , through which the state-function entropy is most generally definable Touchette:large_dev:09 . Both Shannon’s information entropy Shannon:MTC:49 and the older Hartley function Hartley:information:28 , will appear here as they do in stochastic thermodynamics generally Seifert:stoch_thermo_rev:12 . The different meanings these functions carry, which sound contradictory when described and can be difficult to compare in derivations with different aims, become clear as each appears in the course of a single calculation. Most important, they have unambiguous roles in relation to either large deviations or system decomposition without need of a reference to heat.
Main results and order of the derivation
Sec. II explains what is meant by multi-level systems with respect to a robust separation of timescales, and introduces a family of models constructed recursively from nested population processes. Macrostates are related to microstates within levels, and if timescale separations arise that create new levels, they come from properties of a subset of long-lived, metastable macrostates. Such states within a level, and transitions between them that are much shorter than their characteristic lifetimes, map by coarse-graining to the elementary states and events at the next level.
The environment of a system that arises in some level of a hierarchical model is understood to include both the thermalized substrate at the level below, and other subsystems with explicit dynamics within the same level. Sec. II.3 introduces the problem of system/environment partitioning of changes in entropy, and states555The technical requirements are either evident or known from fluctuation theorems Speck:HS_heat_FT:05 ; Harris:fluct_thms:07 ; variant proofs are given in later sections. Their significance for system decomposition is the result of interest here. the first main claim: the natural partition employs a relative entropy Cover:EIT:91 within the system and a housekeeping entropy rate Hatano:NESS_Langevin:01 to embed the system in the environment. It results in two independently non-negative entropy changes (plus a third entirely within the environment that is usually ignored), which define the intensive thermodynamic of the focal system and the extensive, or embedding thermodynamics of the system into the whole.
Sec. III expresses the relation of macrostates to microstates in terms of the large-deviations concept of separation of scale from structure Touchette:large_dev:09 . Large-deviations scaling, defined as the convergence of distributions for aggregate statistics toward exponential families, creates a formal concept of a macroworld having definite structure, yet separated by an indefinite or even infinite range of scale from the specifications of micro-worlds.
Large-deviations for population processes are handled with the Hamilton-Jacobi theory Bertini:macro_NEThermo:09 following from the time dependence of the cumulant-generating function (CGF), and its Legendre duality Amari:inf_geom:01 to a large-deviation function called the effective action Smith:LDP_SEA:11 . Macrostates are identified with the distributions that can be assigned large-deviation probabilities from a system’s stationary distribution. Freedom to study any CGF makes this definition, although concrete, flexible enough to require choosing what Gell-Mann and Lloyd GellMann:EC:96 ; GellMann:eff_complx:04 term “a judge”. The resulting definition, however, does not depend on whether the system has any underlying mechanics or conservation laws, explicit or implicit.
To make contact with multi-level dynamics and problems of interest in stochastic thermodynamics Seifert:stoch_thermo_rev:12 ; Polettini:open_CNs_I:14 ; Polettini:stoch_macro_thermo:16 , while retaining a definite notation, Sec. IV assumes generators of the form used for Chemical Reaction Networks (CRNs) Horn:mass_action:72 ; Feinberg:notes:79 ; Krishnamurthy:CRN_moments:17 ; Smith:CRN_moments:17 . The finite-to-infinite mapping that relates macrostates to microstates has counterparts for CRNs in maps from the generator matrix to the transition matrix, and from mass-action macroscopic currents to probability currents between microstates.
This section formally distinguishes the Lyapunov Fermi:TD:56 and large-deviation Ellis:ELDSM:85 roles of entropy, and shows how the definition of macrostates from Sec. III first introduces scale-dependence in the state function entropy that was not present in the Lyapunov function for arbitrary multi-scale models of Sec. II. In the Hamilton-Jacobi representation, Lyapunov and large-deviation entropy changes occur within different manifolds and have different interpretations. These differences are subordinate to the more fundamental difference between the entropy state function and entropy as a functional on arbitrary distributions over microstates. A properly formulated 2nd law, which is never violated, is computed from both deterministic and fluctuation macrostate-entropies. The roles of Hartley informations Hartley:information:28 for stationary states in stochastic thermodynamics Speck:HS_heat_FT:05 ; Seifert:FDT:10 ; Seifert:stoch_thermo_rev:12 enter naturally as macrostate relative entropies.
Sec. V derives the proofs of monotonicity of the intrinsic and extrinsic entropy changes from Sec. II, using a cycle decomposition of currents in the stationary distribution.666The decomposition is related to that used by Schnakenberg Schnakenberg:ME_graphs:76 to compute dissipation in the stationary state, but more cycles are required in order to compute dynamical quantities. Whether only cycles or more complex hyperflows Andersen:generic_strat:14 are required in a basis for macroscopic currents distinguishes complexity classes for CRNs. Because cycles are always a sufficient basis in the microstate space, the breakdown of a structural equivalence between micro- and macro-states for complex CRNs occurs in just the terms responsible for the complex relations between state-function and global entropies derived in Sec. IV.
Sec. VI illustrates two uses of the intensive/extensive decomposition of entropy changes. It studies a simple model of polymerization and hydrolysis under competing spontaneous and driven reactions in an environment that can be in various states of disequilibrium. First a simple linear model of the kind treated by Schnakenberg Schnakenberg:ME_graphs:76 is considered, in a limit where one elementary reaction becomes strictly irreversible. Although the housekeeping entropy rate becomes uninformative because it is referenced to a diverging chemical potential, this is a harmless divergence analogous to a scale divergence of an extensive potential. A Legendre dual to the entropy rate remains regular, reflecting the existence of a thermodynamics-of-events about which energy conservation, although present on the path to the limit, asymptotically is not a source of any relevant constraints.
A second example introduces autocatalysis into the coupling to the disequilibrium environment, so that the system can become bistable. The components of entropy rate usually attributed to the “environment” omit information about the interaction of reactions responsible for the bistability, and attribute too much of the loss of large-deviation accessibility to the environment. Housekeeping entropy rate gives the correct accounting, recognizing that part of the system’s irreversibility depends on the measure for system relative entropy created by the interaction.
Sec.VII offers an alternative characterization of thermodynamic descriptions when conservation and reversibility are not central. In 20th century physics the problem of the nature and source of macroworlds has taken on a clear formulation, and provides an alternative conceptual center for thermodynamics to relations between work and heat. System decomposition and the conditional independence structures within the loss of large-deviation accessibility replace adiabatic transformation and heat flow as the central abstractions to describe irreversibility, and define the entropy interpretation of the Hartley information. Such a shift in view will be needed if path ensembles are to be put on an equal footing with state ensembles to create a fully non-equilibrium thermodynamics. The alternative formulation is meant to support the development of a native thermodynamics of stochastic rule-based systems and a richer phenomenology of living states.
II Multi-level systems
To provide a concrete class of examples for the large-deviation relations that can arise in multi-scale systems, we consider systems with natural levels, such that within each level a given system may be represented by a discrete population process. The population process in turn admits leading-exponential approximations of its large-deviation behavior in the form of a continuous dynamical system. These dynamical systems are variously termed momentum-space WKB approximations Assaf:mom_WKB:17 , Hamilton-Jacobi representations Bertini:macro_NEThermo:09 , or eikonal expansions Freidlin:RPDS:98 . They exist for many other classes of stochastic process besides the one assumed here Martin:MSR:73 ; Kamenev:DP:02 , and may be obtained either directly from the Gärtner-Ellis theorem Ellis:ELDSM:85 for cumulant-generating functions (the approach taken here), by direct WKB asymptotics, or through saddle-point methods in 2-field functional integrals.
A connection between levels is made by supposing that the large-deviation behavior possesses one or more fixed points of the dynamical system. These are coarse-grained to become the elementary states in a similar discrete population process one level up in the scaling hierarchy. Nonlinearities in the dynamical system that produce multiple isolated, metastable fixed points are of particular interest, as transitions between these occur on timescales that are exponentially stretched, in the large-deviation scale factor, relative to the relaxation times. The resulting robust criterion for separation of timescales will be the basis for the thermodynamic limits that distinguish levels and justify the coarse-graining.
II.0.1 Micro to macro, within and between levels
Models of this kind may be embedded recursively in scale through any number of levels. Here we will focus on three adjacent levels, diagrammed in Fig. 1, and on the separation of timescales within a level, and the coarse-grainings that define the maps between levels. The middle level, termed the mesoscale, will be represented explicitly as a stochastic process, and all results that come from large-deviations scaling will be derived within this level. The microscale one level below, and the macroscale one level above, are described only as needed to define the coarse-graining maps of variables between adjacent levels. Important properties such as bidirectionality of escapes from metastable fixed point in the stationary distribution, which the large-deviation analysis in the mesoscale supplies as properties of elementary transitions in the macroscale, will be assumed self-consistently as inputs from the microscale to the mesoscale.

Within the description at a single level, the discrete population states will be termed microstates, as is standard in (both classical and stochastic) thermodynamics. Microstates are different in kind from macrostates, which correspond to a sub-class of distributions (defined below), and from fixed points of the dynamical system. There is no unique recipe for coarse-graining descriptions to reduce dimensionality in a multi-scale system, because the diversity of stochastic processes is vast. Here, to obtain a manageable terminology and class of models, we limit to cases in which the dynamical-system fixed points at one level can be put in correspondence with the microstates at the next higher level. Table 1 shows the terms that arise within, and correspondences between, levels.
| macroscale | mesoscale | microscale |
|---|---|---|
| microstate | H-J fixed point | |
| thermalization of the microscale | H-J relaxation trajectories | |
| elementary transitions between microstates | H-J first-passages | |
| arbitrary distribution on microstates | coarse-grained distribution on fixed points | |
| macrostate (distribution) H-J variables | ||
| microstate | H-J fixed point | |
| … | … |
II.1 Models based on population processes
The following elements furnish a description of a system:
The multiscale distribution:
The central object of study is any probability distribution , defined down to the smallest scale in the model, and the natural coarse-grainings of produced by the dynamics. To simplify notation, we will write for the general distribution, across all levels, and let the indexing of indicate which level is being used in a given computation.
Fast relaxation to fixed points at the microscale:
The counterpart, in our analysis of the mesoscale, to Prigogine’s Glansdorff:structure:71 ; Prigogine:MT:98 assumption of local equilibrium in a bath, is fast relaxation of the distribution on the microscale, to a distribution with modes around the fixed points. In the mesoscale these fixed points become the elementary population states indexed , and the coarse-grained probability distribution is denoted . If a population consists of individuals of types indexed , then is a vector in which the non-negative integer coefficient counts the number of individuals of type .
Elementary transitions in the mesoscale:
First-passages occurring in the (implicit) large-deviations theory, between fixed points and at the microscale, appear in the mesoscale as elementary transitions . In Fig. 1, the elementary states are grid points and elementary transitions occur along lines in the grid in the middle layer. We assume as input to the mesoscale the usual condition of weak reversibility Polettini:open_CNs_I:14 , meaning that if an elementary transition occurs with nonzero rate, then the transition also occurs with nonzero rate. Weak reversibility is a property we will derive for first passages within the mesoscale, motivating its adoption at the lower level.
Thermalization in the microscale:
The elementary transitions are separated by typical intervals exponentially longer in some scale factor than the typical time in which a single transition completes. (In the large-deviation theory, they are instantons.) That timescale separation defines thermalization at the microscale, and makes microscale fluctuations conditionally independent of each other, given the index of the basin in which they occur. Thermalization also decouples components in the mesoscale at different except through the allowed elementary state transitions.
A System/Environment partition within the mesoscale:
Generally, in addition to considering the thermalized microscale a part of the “environment” in which mesoscale stochastic events take place, we will choose some partition of the type-indices to distinguish one subset, called the system (), from one or more other subsets that also form part of the environment (). Unlike the thermalized microscale, the environment-part in the mesoscale is slow and explicitly stochastic, like the system. The vector indexes a tensor product space , so we write .
Marginal and conditional distributions in system and environment:
On , is a joint distribution. A marginal distribution for the system is defined by , where fixes the component of in the sum. From the joint and the marginal a conditional distribution at each is given by . The components of can fill the role often given to chemostats in open-system models of CRNs. Here we keep them as explicit distributions, potentially having dynamics that can respond to changes in .
Notations involving pairs of indices:
Several different sums over the pairs of indices associated with state transitions appear in the following derivations. To make equations easier to read, the following notations are used throughout:
is an unordered pair of indices.
counts every pair
in both orders.
counts every unordered pair once.
Therefore for any function , .
is a sum on the component of .
counts all unordered pairs with common -component .
II.2 Stochastic description within the mesoscale
The coarse-grained distribution at the mesoscale evolves in time under a master equation
| (1) |
Here and below, indicates the time derivative. The generator is a stochastic matrix on the left, which we write , where is the row-vector on index corresponding to the uniform (unnormalized) measure. (following a standard notation Polettini:open_CNs_I:14 ) is the component of giving the transition rate from state to state .
For all of what follows, it will be necessary to restrict to systems that possess a stationary, normalizable distribution denoted , satisfying . The stationary distribution will take the place of conservation laws as the basis for the definition of macrostates. Moreover, if is everywhere continuous, and the number of distinct events generating transitions in the mesoscale (in a sense made precise below) is finite, first passages between fixed points corresponding to modes of will occur at rates satisfying a condition of detailed balance. The joint, marginal, and conditional stationary distributions are denoted .
The marginal stochastic process on :
The system-marginal distribution evolves under a master equation , for which the transition matrix has components that are functions of the instantaneous environmental distribution, given by
| (2) |
Time-independent overall stationary distribution as a reference:
Now we make an assumption that is crucial to being able to define a Lyapunov function for the whole multi-level system distribution : namely, that the parameters in the mesoscale transition matrix and hence the stationary distribution are time-independent. All dynamics is made explicit as dynamics of distributions and , but the explicitly-written distributions are the only source of dynamics: once the microscale has thermalized, there are no further un-written sources of time-dependence in the system.
Detailed balance propagating up from the microscale:
Finally we assume, propagating up from the microscale, a condition of detailed balance that we will prove as a property of first-passages in the mesoscale, and then apply recursively:
| (3) |
Note that condition (3) is not an assumption of microscopic reversibility in whatever faster stochastic process is operating below in the microscale. To understand why, using constructions that will be carried out explicitly within the mesoscale, see that even with rate constants satisfying Eq. (3), the system-marginal transition rates (2) need not satisfy a condition of detailed balance. Indeed we will want to be able to work in limits for the environment’s conditional distributions in which some transitions can be made completely irreversible: that is but . Even from such irreversible dynamics among microstates, first-passage rates with detailed balance in the stationary distribution will result, and it is that property that is assumed in Eq. (3).
From these assumptions on and , it follows that the relative entropy of any distribution from the stationary distribution is non-decreasing,
| (4) |
The result is elementary for systems with detailed balance, because each term in the third line of Eq. (4) is individually non-negative. We use relative entropy to refer to minus the Kullback-Leibler divergence of from Cover:EIT:91 , to follow the usual sign convention for a non-decreasing entropy.
II.3 System-environment decompositions of the entropy change
The exchange of heat for work is central to classical thermodynamics because energy conservation is a constraint on joint configurations across sub-systems, either multiple thermal systems in contact or a mechanical subsystem having only deterministic variables, some of which set the boundary conditions on thermal subsystems that also host fluctuations. Only the state-function entropy, however, is a “function” of energy in any sense, so the only notion of a limiting partition of irreversible effects between subsystems derivable from energy conservation is the one defined by adiabatic transformations passing through sequences of macrostates.
In more general cases, with or without conservation laws, the boundary conditions on a system are imposed only through the elements of the marginal transition matrix . The problem remains, of understanding how one subsystem can limit entropy change in another through a boundary, but it is no longer organized with reference to adiabatic transformations.
We wish to understand what constitutes a thermodynamically natural decomposition of the mesoscale process into a system and an environment. A widely-adopted decomposition Seifert:stoch_thermo_rev:12 ; Polettini:open_CNs_I:14 ; Polettini:stoch_macro_thermo:16 for systems with energy conservation777The decomposition is the same one used to define an energy cost of computation Landauer:IHGCP:61 ; Bennett:TC:82 by constructing logical states through the analogues to heat engines Szilard:MD:29 ; Smith:NS_thermo_II:08 . separates a Shannon entropy of from heat generation associated with terms by the local equilibrium assumption for the bath. We begin by writing down this information/heat decomposition, and arguing that it is not the natural partition with respect to irreversibility.
Entropy relative to the stationary state rather than Shannon entropy:
The following will differ from the usual construction in replacing Shannon entropy with a suitable relative entropy, without changing the essence of the decomposition. Two arguments can be given for preferring the relative entropy: It would be clear, for a system with a continuous state space in which would become a density, that the logarithm of a dimensional quantity is undefined. Hence some reference measure is always implicitly assumed. A uniform measure is not a coordinate-invariant concept, and a measure that is uniform in one coordinate system makes those coordinates part of the system specification. Since discrete processes are often used as approximations to continuum limits, the same concerns apply. The more general lesson is that a logarithmic entropy unit is always given meaning with respect to some measure. Only for systems such as symbol strings, for which a combinatorial measure on integers is the natural measure, is Shannon entropy the corresponding natural entropy. For other cases, such as CRNs, the natural entropy is relative entropy referenced to the Gibbs equilibrium Smith:NS_thermo_I:08 , and its change gives the dissipation of chemical work. For the processes described here, the counterpart to Shannon entropy that solves these consistency requirements, but does not yet address the question of naturalness, is the relative entropy referenced to the steady state marginal . Its time derivative is given by
| (5) |
The quantity (5) need not be either positive or negative in general.
A second term that separates out of the change in total relative entropy (4) comes from changes in environmental states through events that do not result in net change of the system state.888Note may depend on the system index-component shared by both and , so these rates can depend on system state. Catalysis acts through such dependencies. The relative entropy of the conditional distribution at a particular index from its stationary reference has time derivative
| (6) | ||||
Unlike the change of system relative entropy (5), Eq. (6) is non-negative term-by-term, in the same way as Eq. (4).
The remaining terms to complete the entropy change (4) come from joint transformations in system and environment indices and , and in usual treatments have the interpretation of dissipated heats.999When more than one environment transition couples to the same system transition, there can be reasons to further partition these terms; an example is given in Sec. VI.1. They are functions of the pair of indices . An average change in relative entropy of the environment, over all processes that couple to a given system state-change, is
| (7) |
(Note that if we had wished to use the un-referenced Shannon entropy in place of the relative entropy (5) – for instance, in an application to digital computing – we could shift the measures to the dissipation term to produce what is normally considered the “environmental” heat dissipation, given by
| (8) |
The quantity (8) is regarded as a property of the environment (both slow variables and the thermal bath) because it is a function only of the transition rates and of the marginal distributions .)
II.3.1 The information/heat decomposition of total relative-entropy change
Eq. (4) is decomposed in terms of the quantities in equations (5–7) as
| (9) |
The total is non-negative and the third line is independently non-negative, as already mentioned. The sum of the first two lines is also non-negative, a result that can be proved as a fluctuation theorem for what is normally called “total entropy change” Esposito:fluct_theorems:10 .101010More detailed proofs for a decomposition of the same sum will be given below.
Here we encounter the first property that makes a decomposition of a thermal system “natural”. The term in is not generally considered, and it does not need to be considered, because thermal relaxation at the microscale makes transitions in at fixed conditionally independent of transitions that change . Total relative entropy changes as a sum of two independently non-decreasing contributions.
The first and second lines in Eq. (9) are not likewise independently non-negative. Negative values of the second or first line, respectively, describe phenomena such as randomization-driven endothermic reactions, or heat-driven information generators. To the extent that they do not use thermalization in the microscale to make the system and environment conditionally independent, as the third term in Eq. (9) is independent, we say they do not provide a natural system/environment decomposition.
II.3.2 Relative entropy referencing the system steady state at instantaneous parameters
Remarkably, a natural division does exist, based on the housekeeping heat introduced by Hatano and Sasa Hatano:NESS_Langevin:01 . The decomposition uses the solution to , which would be the stationary marginal distribution for the system at the instantaneous value of . As for the whole-system stationary distribution , we restrict to cases in which exists and is normalizable.111111This can be a significant further restriction when we wish to study limits of sequences of environments to model chemostats. For systems with unbounded state spaces, such as arise in polymerization models, it is quite natural for a chemostat-driven system to possess no normalizable steady-state distributions. In such cases other methods of analysis must be used Esposito:copol_eff:10 .
Treating as fixed and considering only the dynamics of with as a reference, we may consider a time derivative in place of Eq. (5). Note that the rates in the transition matrix no longer need satisfy any simplified balance condition in relation to , such as detailed balance. Non-negativity of was proved by Schnakenberg Schnakenberg:ME_graphs:76 by an argument that applies to discrete population processes with normalized stationary distributions of the kind assumed here. We will derive a slightly more detailed decomposition proving this result for the case of CRNs, in a later section.
The dissipation term that complements the change in is obtained by shifting the “environmental” entropy change (8) by to obtain the housekeeping heat121212These terms are used because this is how they are known. No energy interpretation is assumed here, so a better term would be “housekeeping entropy change”.
| (10) |
Non-negativity of Eq. (10) is implied by a fluctuation theorem Speck:HS_heat_FT:05 , and a time-local proof with interesting further structure for CRNs will be given below.
The total change in relative entropy (4) is then the sum
| (11) |
Each line in Eq. (11) is now independently non-negative. The first measures a gain of entropy within the system , conditionally independent of changes in the environment given the marginal transition matrix . The third measures a gain of entropy in the environment independent of any changes in the system at all. The second, housekeeping entropy rate, measures a change of entropy in the environment that is conditionally independent of changes of entropy within the system, given as represented in . Any of the terms may be changed, holding the conditioning data or , or omitted, without changing the limits for the others. They respect the conditional independence created by thermalization in the microscale, and by that criterion constitute a natural decomposition of the system.
II.3.3 Intrinsic and extrinsic thermodynamics
We take and as a specification of the intrinsic thermodynamics of the system , analogous to the role of intrinsic curvature of a manifold in differential geometry. The vector (indexed by pairs of system indices) of housekeeping entropy differentials, , correspondingly defines the way is thermodynamically embedded in the mesoscale system, analogous to the role of components of an embedding curvature for a submanifold within larger manifold.
II.3.4 System Hartley information as a temporal connection
The natural decomposition (11) differs from the information/heat decomposition (9) in what is regarded as inherent to the system versus the environment. The attribution of Shannon entropy as a “system” property follows from the fact that it involves only , and its change counts only actual transitions with rate . Likewise, the “environment” heat (8) is a function only of the actual distribution and the realized currents.
Those events that occur within or , however, fail to capture the additional features of : that specific transitions are coupled as a system, and that they have the dependence on of Eq. (2). The stationary distribution is the function of reflecting its status as a system.
The differences between the three entropy-change terms (7,8,10) are differences of the Hartley informations Hartley:information:28 , respectively for or . In the natural decomposition (11), they are not acted upon by the time derivative, but rather define the tangent plane of zero change for terms that are acted upon by the transition matrix, and resemble connection coefficients specifying parallel transport in differential geometry.
III Hamilton-Jacobi theory for large deviations
The central concepts in thermodynamics are that of the macrostate, and of the entropy as a state function from which properties of macrostates and constraints on their transformations are derived. In classical thermodynamics Fermi:TD:56 ; Kittel:TP:80 , macrostates are introduced in association with average values of conserved quantities (e.g. energy, particle numbers), because conservation laws naturally generate conditional independence between subsystems in contact, given a simple boundary condition (the partition of the conserved quantity between them).
Here we wish to separate the construction that defines a macrostate from the properties that make one or another class of macrostates dynamically robust in a given system (conservation laws are important for the latter). The defining construction can be quite general, but it must in all cases create a dimensional reduction by an indefinite (or in the limit infinite) factor, from the dimensionality of the microstate space that is definite but arbitrarily large, to the dimensionality of a space of macrostate variables that is fixed and independent of the dimensionality of microstates. Only dimensional reductions of this kind are compatible with the large-deviation definition of macroworlds as worlds in which structure can be characterized asymptotically separate from scale Touchette:large_dev:09 . Robustness can then be characterized separately within the large-deviation analysis in terms of closure approximations or spectra of relaxation times for various classes of macrostates.
Dimensional reduction by an indefinite degree is achieved by associating macrostates with particular classes of distributions over microstates: namely, those distributions produced in exponential families to define generating functions. The coordinates in the tilting weights that define the family are independent of the dimension of the microstate space for a given family and become the intensive state variables (see Amari:inf_geom:01 ). They are related by Legendre transform to deviations that are the dual extensive state variables. Relative entropies such as , defined as functionals on arbitrary distributions, and dual under Legendre transform to suitable cumulant-generating functions, become state functions when restricted to the distributions for macrostates. The extensive state variables are their arguments and the intensive state variables their gradients. Legendre duality leads to a system of Hamiltonian equations Bertini:macro_NEThermo:09 for time evolution of macrostate variables, and from these the large-deviation scaling behavior, timescale structure, and moment closure or other properties of the chosen system of macrostates are derived.
In the treatment of Sec. II, the relative entropy increased deterministically without reference to any particular level of system timescales, or the size-scale factors associated with various levels. As such it fulfilled the Lyapunov role of (minus) the entropy, but not the large-deviation role that is the other defining characteristic of entropy Ellis:ELDSM:85 ; Touchette:large_dev:09 . The selection of a subclass of distributions as macrostates introduces level-dependence, scale-dependence, and the large-deviation role of entropy, and lets us construct the relation between the Lyapunov and large-deviation roles of entropy for macroworlds, which are generally distinct. As a quantity capable of fluctuations, the macrostate entropy can decrease along subsets of classical trajectories; these fluctuations are the objects of study in stochastic thermodynamics. The Hamiltonian dynamical system is a particularly clarifying representation for the way it separates relaxation and fluctuation trajectories for macrostates into distinct sub-manifolds. In distinguishing the unconditional versus conditional nature of the two kinds of histories, it shows how these macro-fluctuations are not “violations” of the 2nd law, but rather a partitioning of the elementary events through which the only properly formulated 2nd law is realized.131313See a brief discussion making essentially this point in Sec. 1.2 of Seifert:stoch_thermo_rev:12 . Seifert refers to the 2nd law as characterizing “mean entropy production”, in keeping with other interpretations of entropies such as the Hartley information in terms of heat. The characterization adopted here is more categorical: the Hartley function and its mean, Shannon information, are not quantities with the same interpretation; likewise, the entropy change (11) is the only entropy relative to the boundary conditions in that is the object of a well-formulated 2nd law. The “entropy productions” resulting from the Prigogine local-equilibrium assumption are conditional entropies for macrostates defined through various large-deviation functions, shown explicitly below.
III.1 Generating functions, Liouville equation, and the Hamilton-Jacobi construction for saddle points
III.1.1 Relation of the Liouville operator to the cumulant-generating function
The -dimensional Laplace transform of a distribution on discrete population states gives the moment-generating function (MGF) for the species-number counts . For time-dependent problems, it is convenient to work in the formal Doi operator algebra for generating functions, in which a vector of raising operators are the arguments of the MGF, and a conjugate vector of lowering operators are the formal counterparts to . MGFs are written as vectors in a Hilbert space built upon a ground state , and the commutation relations of the raising and lowering operators acting in the Hilbert space are .
The basis vectors corresponding to specific population states are denoted . They are eigenvectors of the number operators with eigenvalues :
| (12) |
Through by-now-standard constructions Smith:LDP_SEA:11 , the master equation is converted to a Liouville equation for time evolution of the MGF,
| (13) |
in which the Liouville operator is derived from the elements of the matrix .
To define exponential families and a cumulant-generating function (CGF), it is convenient to work with the Laplace transform with an argument that is a vector of complex coefficients. The corresponding CGF, ,141414We adopt the sign for corresponding to the free energy in thermodynamics. Other standard notations, such as for the CGF Amari:inf_geom:01 , are unavailable because they collide with notations used in the representation of CRNs below. for which the natural argument is , is constructed in the Doi Hilbert space as the inner product with a variant on the Glauber norm,
| (14) |
will be called the tilt of the exponential family, corresponding to its usage in importance sampling Siegmund:IS_seq_tests:76 .
An important quantity will be the vector of expectations of the number operators in the tilted distribution
| (15) |
Time evolution of the CGF follows from Eq. (13), as
| (16) |
Under the saddle-point or leading-exponential approximation that defines the large-deviation limit (developed further below), the expectation of in Eq. (16) is replaced by the same function at classical arguments
| (17) |
From coherent-state to number-potential coordinates:
With a suitable ordering of operators in (with all lowering operators to the right of any raising operator), is the exact value assigned to in the expectation (16), and only the value for depends on saddle-point approximations. In special cases, where are eigenstates of known as coherent states, the assignment to is also exact. Therefore the arguments of in Eq. (17) are called coherent-state coordinates.
However, , which we henceforth denote by , is the affine coordinate system in which the CGF is locally convex,151515 also provides the affine coordinate system in the exponential family, which defines contravariant coordinates in information geometry Amari:inf_geom:01 . and it will be preferable to work in coordinates , which we term number-potential coordinates, because for applications in chemistry has the dimensions of a chemical potential. We abbreviate exponentials and other functions acting component-wise on vectors as , and simply assign . Likewise, is defined in either coordinate system by mapping its arguments: .
III.1.2 Legendre transform of the CGF
To establish notation and methods, consider first distributions that are convex with an interior maximum in . Then the gradient of the CGF
| (18) |
gives the mean (15) in the tilted distribution.
The stochastic effective action is the Legendre transform of , defined as
| (19) |
For distributions over discrete states, to leading exponential order, is a continuously-indexed approximation to minus the log-probability: . Its gradient recovers the tilt coordinate ,
| (20) |
and the CGF is obtained by inverse Legendre transform.
| (21) |
The time evolution of can be obtained by taking a total time derivative of Eq. (19) along any trajectory, and using Eq. (18) to cancel the term in . The partial derivative that remains, evaluated using Eq. (17), gives
| (22) |
Eq. (22) is of Hamilton-Jacobi form, with filling the role of the Hamiltonian. (The reason for this sign correspondence, which affects nothing in the derivation, will become clear below.)
Multiple modes, Legendre-Fenchel transform, and locally-defined extrema
Systems with interesting multi-level structure do not have or globally convex, but rather only locally convex. For these the Legendre-Fenchel transform takes the place of the Legendre transform in Eq. (19), and if constructed with a single coordinate , may have discontinuous derivative.
For these one begins, rather than with the CGF, with , evaluated as a line integral of Eq. (20) in basins around the stationary points at . Each such basin defines invertible pair of functions and . We will not be concerned with the large-deviation construction for general distributions in this paper, which is better carried out using a path integral. We return in a later section to the special case of multiple metastable fixed points in the stationary distribution, and the modes associated with the stationary distribution , and provide a more complete treatment.
III.1.3 Hamiltonian equations of motion and the action
Partial derivatives with respect to and commute, so the relation (20), used to evaluate of Eq. (22), gives the relation
| (23) |
The dual construction for the time dependence of from Eq. (18) gives
| (24) |
The evolution equations (23,24) describe stationary trajectories of an extended-time Lagrange-Hamilton action functional which may be written in either coherent-state or number-potential coordinates, as161616The same action functionals are arrived at somewhat more indirectly via 2-field functional integral constructions such as the Doi-Peliti method.
| (25) |
From the form of the first term in either line, it is clear that the two sets of coordinates relate to each other through a canonical transformation Goldstein:ClassMech:01 .
Circulation-free vector field of for the stationary distribution
In order for to be a continuum approximation to , if exists and is smooth everywhere, the vector field obtained from stationary trajectories of the action (25) must have zero circulation in order to be a well-defined gradient through Eq. (20). To check that this is the case, consider the increment of under a small interval under Eq. (23):
| (26) |
The gradient in of therefore increments in time as
| (27) |
Contraction of Eq. (27) with the antisymmetric symbol in and vanishes
| (28) |
so the circulation of is the same everywhere as at the fixed points.
From Eq. (20), it is required to be the case that , the inverse of the Fisher metric Amari:inf_geom:01 , symmetric by construction and thus giving . The only difference between the fixed point and any other point is that for distant points we are relying on Hamiltonian trajectories to evaluate , whereas the the fixed point the Fisher metric may be calculated by means not relying on the large-deviation saddle-point approximation. Therefore Eq. (28) may be read as a check that symmetry of the Fisher metric is preserved by Hamiltonian trajectories directly from the symmetric partial derivative of in Eq. (27).
III.2 The stationary distribution and macrostates
Up to this point only the Lyapunov role (4) of the relative entropy has been developed. While the increase of has the appearance of the classical 2nd law, we can understand from three observations that this relative entropy is not the desired generalization of the entropy state function of classical thermodynamics to express the phenomenology of multi-level systems:
-
1.
The relative entropy is a functional on arbitrary distributions, like the Shannon entropy that is a special case. It identifies no concept of macrostate, and has no dependence on state variables.
-
2.
In a multilevel system that may have arbitrarily fine-grained descriptions, there is no upper limit to , and no appearance of the system scale at any particular level, which characterizes state-function entropies.
-
3.
Eq. (4) describes a deterministic increase of relative entropy; the large-deviation role of entropy as a log-probability for macrostate fluctuations Ellis:ELDSM:85 does not appear.
The step that has not yet been taken in our construction is, of course, the identification of a macrostate concept. Here we depart from the usual development based on conservation laws, and follow Gell-Mann and Lloyd GellMann:EC:96 ; GellMann:eff_complx:04 in claiming that the concept of macrostate is not inherent in features of a system’s dynamics, but requires one to explicitly choose a procedure for aggregation or coarse-graining – what they call a “judge” – as part of the commitment to which phenomenology is being described.
We will put forth the definition of macrostates as the tilted distributions arising in generating functions for the stationary distribution . In the case of generating functions for number, these are the distributions appearing in Eq. (14), which we will denote by . They are the least-improbable distributions with a given non-stationary mean to arise through aggregate microscopic fluctuations, and therefore dominate the construction of the large-deviation probability.
The extensive state variable associated with this definition of macrostate is the tilted mean from Eq. (18), which we will denote . If and are sharply peaked – the limit in which the large-deviation approximation is informative – the relative entropy of the macrostate is dominated at the saddle point of , where , and thus
| (29) |
The general relative entropy functional, applied to the macrostate, becomes the entropy state function , which takes as its argument the extensive state variable . Moreover, because probability under is concentrated on configurations with the scale that characterizes the system, tilted means that are not suppressed by very large exponential probabilities will have comparable scale. If is also the scale factor in the large-deviations function (a property that may or may not hold, depending on the system studied), then in scale, and the entropy state function now has the characteristic scale of the mesoscale level of the process description.
The three classes of distributions that enter a thermodynamic description are summarized in Table 2.
| notation | definition | comment |
|---|---|---|
| , , | whole-system, -marginal, -conditional distributions in the global stationary state | |
| marginal system steady-state distribution | function of instantaneous environment conditional distribution | |
| macrostate tilted to saddle-point value | defined relative to global stationary distributions ; may be defined for whole-system, , or |
III.2.1 Coherent states, dimensional reduction, and the -divergence
A special case, which is illustrative for its simplicity and which arises for an important sub-class of stochastic CRNs, is the case when is a coherent state, an eigenvector of the lowering operator . Coherent states are the generating functions of product-form Poisson distributions, or cross-sections through such products if the transitions in the population process satisfy conservation laws. They are known Anderson:product_dist:10 to be general solutions for CRN steady states satisfying a condition termed complex balance, and the fixed points associated with such stationary distributions are also known to be unique and interior (no zero-expectations for any ) Feinberg:notes:79 .
Let be the eigenvalue of the stationary coherent state: . Then the mean in the tilted distribution lies in a simple exponential family, (component-wise), and the tilted macrostate is also a coherent state: .
The logarithm of a product-form Poisson distribution in Stirling’s approximation is given by
| (30) |
, known as the -divergence, is a generalization of the Kullback-Leibler divergence to measures such as which need not have a conserved sum. The Lyapunov function from Eq. (4) reduces in the same Stirling approximation to
| (31) |
giving in Eq. (29). On coherent states, the Kullback-Leibler divergence on distributions, which may be of arbitrarily large dimension, reduces to the -divergence on their extensive state variables which have dimension .
The coherent states play a much more general role than their role as exact solutions for the restricted case of complex-balanced CRNs. In the Doi-Peliti 2-field functional integral formalism Doi:SecQuant:76 ; Doi:RDQFT:76 ; Peliti:PIBD:85 ; Peliti:AAZero:86 for generating functionals over discrete-state stochastic processes, the coherent states form an over-complete basis in the Peliti representation of unity. The saddle-point approximation on trajectories, which yields the classical actions (25) and the resulting Hamilton-Jacobi equations, approximates expectations in the exact distribution by those in the nearest coherent-state basis element. Observables in macrostates are thus mapped to observables in coherent states, although in cases when the coherent state is not an exact solution, the saddle-point condition may be sensitive to which observable is being evaluated.
III.2.2 Multiple fixed points and instantons
Systems with multiple metastable fixed points correspond to non-convex and thus multiple modes. For these, monotone decrease of in Eq. (4) does not entail monotonicity of the -divergence in Eq. (31). In such systems, first passages between basins of attraction are solutions to the Hamiltonian equations (23,24) with momentum coordinate . Along these increases, and that increase is what is sometimes termed the “violation of the 2nd law”.
For unimodal , the large-deviation trajectories have a separate use and interpretation from the relaxation trajectories at that give the classical 2nd law in Eq. (49). For multi-modal a special sub-class of trajectories, those known as instantons and responsible for first-passages between fixed-points Cardy:Instantons:78 ; Coleman:AoS:85 , must be used to refine the interpretation of classical relaxation trajectories. That refinement relates the transient increases in the large-deviation function to the deterministic 2nd law (4) that continues to apply.
This section briefly introduces the Legendre duality that defines first-passage probabilities in metastable systems, arriving at the chain rule for entropy that separates the roles of classical and instanton trajectories. Let be a fixed point of the Hamiltonian equations for , and denote by the values of classical state variables obtained along trajectories from . Call these escape trajectories. The set of all is partitioned among basins of repulsion from fixed points. Saddle points and escape separatrices are limit points of escapes from two or more basins.
Within one such basin, we may construct as a Legendre transform of a summand in the overall CGF, as
| (32) |
ranges only over the values that arise on escape trajectories from , which generally are bounded Smith:CRN_CTM:20 , and within that range
| (33) |
Next, let the function 171717Note that the maps and need not be reflexive. That is, we may have for any , because escape and relaxation separatrices may differ. denote the fixed point to which a trajectory with relaxes, starting from . From the large-deviation identification of , recognize that the large-deviation function for the stationary distribution is given by , where denotes the special macrostate for which the stationary value is a fixed-point value .
Then the expression (29) for the Kullback-Leibler divergence appearing in Eq. (4) may be approximated to leading exponential order as
| (34) |
Eq. (34) is the chain rule for relative entropy. is the conditional entropy of the macrostate relative to the macrostate to which it is connected by a Hamiltonian trajectory. is the unconditioned entropy of relative to .
Relaxation along trajectories describes a classical 2nd law only for the conditional part of the relative entropy. Deterministic relaxation of the unconditioned entropy is derived from the refinement of the (as it turns out, only apparent) classical trajectory with an instanton sum. The general method is described in depth in Cardy:Instantons:78 and Coleman:AoS:85 Ch.7, using path integrals that require too much digression to fit within the scope of this paper. The structure of the instanton sum, and in particular the way it creates a new elementary stochastic process at the macroscale for which is the Lyapunov function, will be explained in Sec. IV.2.2 following Smith:LDP_SEA:11 , after the behavior of along and trajectories has been characterized.
IV Population processes with CRN-form generators
The results up to this point apply to general processes with discrete state spaces, normalizable stationary distributions, and some kind of tensor-product structure on states. For the next steps we restrict to stochastic population processes that can be written in a form equivalent to Chemical Reaction Networks Horn:mass_action:72 ; Feinberg:notes:79 ; Gunawardena:CRN_for_bio:03 . CRNs are an expressive enough class to include many non-mechanical systems such as evolving Darwinian populations Smith:evo_games:15 , and to implement algorithmically complex processes Andersen:NP_autocat:12 . Yet they possess generators with a compact and simple structure Krishnamurthy:CRN_moments:17 ; Smith:CRN_moments:17 , in which similarities of microstate and macrostate phenomena are simply reflected in the formalism.
IV.1 Hypergraph generator of state-space transitions
Population states give counts of individuals, grouped according to their types which are termed species. Stochastic Chemical Reaction Networks assume independent elementary events grouped into types termed reactions. Each reaction event removes a multiset181818A multiset is a collection of distinct individuals, which may contain more than one individual from the same species. of individuals termed a complex from the population, and places some (generally different) multiset of individuals back into it. The map from species to complexes is called the stoichiometry of the CRN. Reactions occur with probabilities proportional per unit time to rates. The simplest rate model, used here, multiplies a half-reaction rate constant by a combinatorial factor for proportional sampling without replacement from the population to form the complex, which in the mean-field limit leads to mass-action kinetics.
Complexes will be indexed with subscripts , and an ordered pair such as labels the reaction removing and creating . With these conventions the Liouville-operator representation of the generator from Eq. (13) takes the form Krishnamurthy:CRN_moments:17 ; Smith:CRN_moments:17
| (35) |
are half-reaction rate constants, organized in the second line into an adjacency matrix on complexes. is a column vector with components that, in the Doi algebra, produce the combinatorial factors and state shifts reflecting proportional sampling without replacement. Here is the matrix of stoichiometric coefficients, with entry giving the number of individuals of species that make up complex . Further condensing notation, are column vectors in index , and are row vectors on index . is understood as the component-wise product of powers over the species index . is a transpose (row) vector, and vector and matrix products are used in the second line of Eq. (35).
The generator (35) defines a hypergraph Berge:hypergraphs:73 in which is the adjacency matrix on an ordinary graph over complexes known as the complex graph Gunawardena:CRN_for_bio:03 ; Baez:QTRN_eq:14 . The stoichiometric vectors , defining complexes as multisets, make the edges in directed hyper-edges relative to the population states that are the Markov states for the process.191919Properly, the generator should be called a “directed multi-hypergraph” because the complexes are multisets rather than sets. The concurrent removal or addition of complexes is the source of both expressive power and analytic difficulty provided by hypergraph-generators.
A master equation (1) acting in the state space rather than on the generating function may be written in terms of the same operators, as
| (36) |
Here a formal shift operator is used in place of an explicit sum over shifted indices, and creates shifts by the stoichiometric vector . refers to the matrix with diagonal entries given by the components .
In the master equation the combinatorial factors must be given explicitly. These are written as a vector with components that are falling factorials from , denoted with the underscore as .
The matrix elements of Eq. (1) may be read off from Eq. (36) in terms of elements in the hypergraph, as
| (37) |
between all pairs separated by the stoichiometric difference vector . If multiple reactions produce transitions between the same pairs of states, the aggregate rates become
| (38) |
In this way a finite adjacency matrix on complexes may generate an infinite-rank transition matrix , which is the adjacency matrix for an ordinary graph over states. We will see that for CRNs, the hypergraph furnishes a representation for macrostates similar to the representation given by the simple graph for microstates.
From Eq. (38), marginal transition rates for the system may be defined using the average (2) over . Note that the dependence of the activity products on species within the system remains that of a falling factorial, even if the average over activities of species in the environment is complicated. Denote by and the restrictions of the activity and shift functions to the species in the system , and by the rate constants after computing the sum in Eq. (2) over the index for species in the environment.
IV.1.1 Descaling of transition matrices for microstates
Proofs of monotonic change, whether of total relative entropy (1) or for the components of entropy change partitioned out in Sec. II.3, take a particularly simple form for CRNs generated by finitely many reactions. They make use of finite cycle decompositions of the current through any microstate or complex, which are derived from descaled adjacency matrices.
The descaling that produces a transition matrix that annihilates the uniform measure on both the left and the right is
| (39) |
for the whole mesoscale, or
| (40) |
for the subsystem , by definition of the stationary states. in Eq. (40) is the adjacency matrix on complexes that gives rate constants from Eq. (2). These descalings are familiar as the ones leading to the dual time-reversed generators in the fluctuation theorem for housekeeping heat Speck:HS_heat_FT:05 .
We return to use the descaled microstate transition matrices (39,40) in monotonicity proofs for general CRNs in Sec. V, but before doing that, we use the descaling in the state space to motivate an analogous and simpler descaling for macrostates at the level of the hypergraph. That descaling illustrates the cycle decomposition on finitely many states, though it only yields the -Divergence of Eq. (31) as a Lyapunov function for the complex-balanced CRNs.
IV.1.2 Descaling of transition matrices for macrostates
The coherent states, which are the moment-generating functions of Poisson distributions and their duals in the Doi Hilbert space, are defined as
| (41) |
where is a vector of (generally complex) numbers and is its Hermitian conjugate. They are eigenstates respectively of the raising and lowering operators with eigenvalues and .
On the constant trajectories corresponding to a fixed point of the Hamiltonian equations (23, 24), and , the fixed-point number. We may descale the coherent-state parameters and , which correspond to classical state variables, by defining
| (42) |
In vector notation, , . The scaling (42) was introduced by Baish Baish:DP_duality:15 to study dualities of correlation functions in Doi-Peliti functional integrals.
The compensating descaling of the adjacency matrix
| (43) |
may be compared with Eq. (39) for . A similar descaling may be done for using . Henceforth we omit the duplicate notation, and carry out proofs with respect to whatever is the stationary distribution for a given adjacency matrix and hypergraph.
IV.1.3 Equations of motion and the manifold
The Hamiltonian equations derived by variation of the action (44) can be written
| (45) |
The general solution is shown first in each line and then particular limiting forms are shown.
The sub-manifold contains all relaxation trajectories for any CRN. It is dynamically stable because is a stochastic matrix on the left, and thus in the second line of Eq. (45). The image of is called the stoichiometric subspace, and its dimension is denoted .
An important simplifying property of some CRNs is known as complex balance of the stationary distributions.202020Complex balance can be ensured at all parameters if a topological character of the CRN known as deficiency equals zero, but may also be true for nonzero-deficiency networks for suitably tuned parameters. In this work nothing requires us to distinguish these reasons for complex balance. It is the condition that the fixed point and not only . Since corresponds to and thus , and in the first line of Eq. (45) at any . Complex-balanced CRNs (with suitable conditions on to ensure ergodicity on the complex network Gunawardena:CRN_for_bio:03 ) always possess unique interior fixed points Feinberg:notes:79 ; Feinberg:def_01:87 and simple product-form stationary distributions at these fixed points Anderson:product_dist:10 .
For non-complex-balanced stationary solutions, although escapes may have as initial conditions, that value is not dynamically maintained. Recalling the definition (12) of the number operator, the field , so non-constant is required for instantons to escape from stable fixed points and terminate in saddle fixed points, in both of which limits .
All relaxations and also the escape trajectories from fixed points (the instantons) share the property that for a CRN with time-independent parameters.212121We can see that this must be true because is a Hamiltonian conserved under the equations of motion, and because instantons trace the values of and in the stationary distribution , which must then have to satisfy the Hamilton-Jacobi equation (22). This submanifold separates into two branches, with for relaxations and for escapes.
IV.1.4 The Schlögl cubic model to illustrate
The features of CRNs with multiple metastable fixed points are exhibited in a cubic 1-species model introduced by Schlögl Schlogl:near_SS_thermo:71 , which has been extensively studied Dykman:chem_paths:94 ; Krishnamurthy:CRN_moments:17 ; Smith:CRN_moments:17 as an example of dynamical bistability.
The reaction schema in simplified form is
| (46) |
We choose rate constants so that the mass-action equation for the number of particles, given by , is
| (47) |
The three fixed points are , of which and are stable, and is a saddle.
The relaxation and escape branches of the manifold are shown in Fig. 2. Because the Schlögl model is 1-dimensional, the condition fixes along escape trajectories. Because the stochastic model is a birth-death process, it is also exactly solvable vanKampen:Stoch_Proc:07 . We will return to the example in Sec. VI.2 to study properties of the intensive and extensive thermodynamic potentials for it.

IV.2 Large-deviation and Lyapunov roles of the effective action
The role of entropy in the understanding of Boltzmann and Gibbs was that of a Lyapunov function Fermi:TD:56 ; Kittel:TP:80 , accounting for unidirectionality from microscopically reversible mechanics. The much later understanding of entropy in relation to fluctuations Ellis:ELDSM:85 ; Touchette:large_dev:09 – precisely the opposite of deterministic evolution – is that of a large-deviation function.
The chain rule in Eq. (34) of Sec. III.2.2 relates the conditional relative entropy associated with quasi-deterministic relaxation to an additional unconditioned entropy of metastable states that are stable fixed points of the Hamiltonian dynamical system. Here we complete the description of the relation between the Lyapunov and large-deviation roles of the macrostate entropy (29), and show how the sum over instantons rather than a single Hamiltonian trajectory results in deterministic increase of the unconditioned relative entropy . In the Hamilton-Jacobi representation this means constructing relations between the and the branches of the manifold. For special cases, such as CRNs with detailed balance or one-dimensional systems, the mapping is one of simple time reversal of the fields in trajectories. More generally, even for complex-balanced CRNs where the Lyapunov and large-deviation functions are the same, the relations between relaxation and escape trajectories become more variable.
IV.2.1 Convexity proof of the Lyapunov property of macrostate entropy in Hamilton-Jacobi variables
Begin with the dynamics of the relative entropy from Eq. (29), as the state variable evolves along a relaxation solution to the Hamiltonian equations of motion. The properties of follow from its construction as a large-deviation function along escape trajectories. From Eq. (20), the time derivative of along an escape trajectories is given by
| (48) |
Hamiltonian trajectories are least-improbable paths of fluctuation, so escapes are conditionally dependent along trajectories. The conditional probability to extend a path, having reached any position along the path, is always positive, giving in Eq. (48).
Next compute along a relaxation trajectory, for simplicity considering (an equivalent construction exists for in terms of ). The continuum limit of the relative entropy from Eq. (4) replaces , and continuously-indexed and are defined through the large-deviation functions.
Writing the CRN Liouville operator (35) in coherent-state arguments, the time dependence is evaluated as
| (49) |
In Eq. (49) abbreviates from Eq. (22), for the that is the continuum approximation of . The third through fifth lines expand explicitly in terms of rate constants following Eq. (35), to collocate all terms in in the Liouville operator. The fourth line expands and to linear order in in neighborhoods of the saddle point of . The matrix is the inverse of the Fisher metric that is the variance Amari:inf_geom:01 , so the product of the two is just the identity .
In the penultimate line of Eq. (49), is the value of for the escape trajectory passing through , and now is the velocity along the relaxation trajectory rather than the Hamilton-Jacobi escape solution at . So the net effect of the large-deviation approximation on relative entropy has been to replace escape with relaxation velocity vectors at a fixed value of Legendre dual to .
Lemma: .
Proof: The proof follows from four observations:
-
1.
: As noted, for both escapes and relaxations, .
-
2.
Convexity: Both the potential value for the escape trajectory, and the velocity of the relaxation trajectory, are evaluated at the same location . The Liouville function , with all , is convex on the -dimensional sub-manifold of fixed . is bounded above at fixed , and in order for cycles to be possible, shift vectors giving positive exponentials must exist for all directions of in the stoichiometric subspace. Therefore at large in every direction, and the region at fixed is bounded. The boundary at fixed is likewise convex with respect to as affine coordinates, and is its interior.
-
3.
Chord: The vector is thus a chord spanning the submanifold of co-dimension 1 within the -dimensional manifold of fixed .
-
4.
Outward-directedness: The equation of motion gives as the outward normal function to the surface . The outward normal at is the classical relaxation trajectory. Every chord of the surface lies in its interior, implying that for any , and thus .
The conditional part of the relative entropy, , is thus shown to be monotone increasing along relaxation trajectories, which is the Lyapunov role for the entropy state function familiar from classical thermodynamics. That increase ends when terminates in the trajectory fixed point .
IV.2.2 Instantons and the loss of Large-deviation accessibility from first passages
The deterministic analysis of Eq. (49) is refined by the inclusion of instanton trajectories through the following sequence of observations, completing the discussion begun in Sec. III.2.2. Relevant trajectories are shown in Fig. 1.
-
1.
The 2nd law as formulated in Eq. (4) is approximated in the large-deviation limit not by a single Hamiltonian trajectory, but by the sum of all Hamiltonian trajectories, from an initial condition. Along a single trajectory, could increase or decrease.
-
2.
increases everywhere in the submanifold of the manifold , by Eq. (49). This is the classical increase of (relative) entropy of Boltzmann and Gibbs. decreases everywhere in the submanifold of the manifold , by Eq. (48). This is the construction of the log-probability for large deviations. These escape paths, however, simply lead to the evaluations of , the stationary distribution.
- 3.
-
4.
If a CRN has multiple fixed points and instantons, all trajectories are exponentially close to the exact trajectory before they enter a small neighborhood around the terminus of the exact trajectory; that is: they give the appearance of being the black deterministic trajectory in Fig. 1. The trajectory sum is correspondingly close to the deterministic relaxation that increases the conditional entropy in Eq. (34).
-
5.
On longer times, however, the infinite sum of formally distinct Hamiltonian trajectories disperses into a sum over series of instantons making a random walk among fixed points, with an integral for each passage over the possible times at which the escape occurs. (See Coleman:AoS:85 Ch.7.) Such a sum is shown as a tree of colored first-passage trajectories in Fig. 1. The “cross-sectional” sum at a single observation time over instantons distinguished by their escaping times gives the same result as a longitudinal line integral along a single instanton between the start time and the observation. That integral of through a full passage (escape instanton + succeeding relaxation) gives . The escape from fixed point to a saddle between and a fixed point in an adjacent basin, which we denote , is an integral over Eq. (48), while the relaxation from the saddle to the fixed point is an integral over Eq. (49). These are the classical “entropy fluctuations” of stochastic thermodynamics.
-
6.
The contribution to the probability of a trajectory from each instanton comes only from the sub-manifold, and is given by , just the leaving rate from the macrostate . The result, upon coarse-graining to the macroscale (see Table 1 and the top diagram in Fig. 1) where first-passages become instantaneous elementary events, is a new stochastic process on discrete states corresponding to the mesoscale Hamiltonian fixed points . The coarse-grained counterpart to from Eq. (34) is the Lyapunov function reduced by a transition matrix with matrix elements . The coarse-graining and the reduction of are described in detail for a 2-basin example in Smith:LDP_SEA:11 .
-
7.
The properties of are exactly those we have assumed for as inputs to the mesoscale, completing the self-consistency of our recursively-defined multi-level model universe.
V Cycle decompositions and non-decrease of intrinsic and extrinsic relative entropies
Schnakenberg Schnakenberg:ME_graphs:76 introduced a method to solve for the dissipation of a driven CRN in terms of steady cyclic currents within the network, coupled to flows into or out of environmental buffers modeled as chemostats Polettini:open_CNs_I:14 . A similar decomposition can be used here to derive the positive-semidefiniteness of the relative entropy and housekeeping terms in Eq. (11). The form of the CRN generator leads to a decomposition of entropy changes into sums of densities convected around a basis of cycles by the stationary-state currents. Positivity is proved by convexity arguments similar to those for the standard fluctuation theorems Speck:HS_heat_FT:05 ; Harris:fluct_thms:07 ; Esposito:fluct_theorems:10 , and the cycle decomposition expresses the duality relations of those theorems in terms of shifts forward or backward around cycles.
Sec. IV constructed the relation between the hypergraph adjacency matrix and stoichiometry , and the microstate transition matrix . Each reaction in the hypergraph acts regularly as a rule on indefinitely many microstates, making CRNs an example of rule-based systems Danos:rule_based_modeling:08 . This section extends that mapping to cycle decompositions. For finitely-generated CRNs, there is a finite basis of either cyclic flows through complexes or stoichiometrically coupled cycles called hyperflows Andersen:generic_strat:14 , with the interpretation of mass-action currents. From these, a (generally infinite) basis of finite-length cycles can be constructed for flows in the microstate space, which projects onto the basis in the hypergraph. We first use the finite basis of macrostate currents to prove monotonicity results for -divergences where those exist, showing how the projection of cycles can result in a projection of the Lyapunov property between levels.
The parallelism between microstates and macrostates only holds, however, when the bases for currents at both levels contain only cycles. More generally, when macrostate currents include non-cyclic hyperflows, the analogy between the two levels is broken, leading to loss of the -divergence as a Lyapunov function on macrostate variables and generally to much greater difficulty of solving for the stationary distribution on microstates. The conditions for different classes of flows on the hypergraph are the basis for a complexity classification of CRNs, and both the form of the large-deviation function and the symmetry between its Lyapunov and large-deviation roles differ across classes.
V.1 Complexity classes and cycle decompositions of stationary currents on the hypergraph
Remarkably, the properties of classical fixed points in the Hamilton-Jacobi representation are sufficient to classify CRNs in a hierarchy with three nested levels of complexity, according to the mass-action currents at the fixed points. Let again denote the fixed point.
-
1.
The CRNs with detailed balance are those in which , for all pairs of complexes connected by a reaction. Under the descaling (43), this condition is that .
-
2.
The CRNs with complex balance only require , for each complex , or under descaling, .
-
3.
The general case requires only , the condition of current balance at each species , or under descaling, only .
The classes are summarized in Table. 3,
| case | complexity class |
|---|---|
| general case | |
| complex-balanced | |
| detailed-balanced |
V.1.1 Complex balance and relations of the Lyapunov and large-deviation roles of
It is known that complex-balanced CRNs (with technical conditions to ensure ergodicity on the complex network under Gunawardena:CRN_for_bio:03 ; Baez:QTRN:13 ) possess unique interior fixed points Feinberg:notes:79 , and moreover that their exact steady states are products of Poisson distributions or sections through such products Anderson:product_dist:10 defined by conserved quantities under the stoichiometry. Their generating functions are the coherent states from Sec. III.2.1. It is immediate that all classical states obtained by exponential tilts with parameter are likewise coherent states with state variables
| (50) |
and that the -divergence of Eq. (30) is the macrostate relative entropy function.
From the equations of motion (45), within either the or sub-manifolds, the time derivatives of along escape and relaxation trajectories, Eq. (49) and Eq. (48) respectively, take the forms
| (51) |
By Eq. (50), appearing in Eq. (51) evaluate to
| (52) |
Finite cycle decomposition of the steady state current:
By definition of complex balance, , in addition to the general condition that . Any such matrix acting over finitely many complexes may be written as a sum of adjacency matrices for cyclic flows, which we index , with positive coefficients equal to the currents around those cycles in the stationary state. For the subclass with detailed balance, a decomposition in cycles of length 2 is always possible.
Letting denote the sum over directed links in order around the cycle , the trajectory derivatives (51) may be decomposed as
| (53) |
( indicates the vector inner product over the species index .)
Letting denote the sum over all complexes in the cycle , the complex activities (52) may be normalized to vectors with unit measure, as
| (54) |
Then the trajectory derivatives (53), themselves the time derivatives of the -divergence (34), may be written in terms of positive semidefinite KL divergences of the measures from their own images advanced or retarded by one complex around each cycle:
| (55) |
Non-negativity of the KL divergences in every term of Eq. (55) recovers the monotonicities of along relaxation and escape trajectories from Sec. IV.2.1. The total time derivatives are decomposed into terms over finitely many cycles, each independently having the same sign, a stronger decomposition than can be obtained from the convexity proofs for increase of relative entropy Schnakenberg:ME_graphs:76 for general CRNs.
Locally linear coordinates for classical entropy change in complex-balanced CRNs
Note that the cycle-KL divergences, multiplied by the density factors , define a coordinate system that is locally invertible for the coordinates except at isolated points:
| (56) |
The time derivatives of from Eq. (53) may be written in these coordinates as a linear system,
| (57) |
Fig. 3 shows examples of the coordinates (56) for a 2-cycle and a 3-cycle in the simplex of normalized activities for three species .
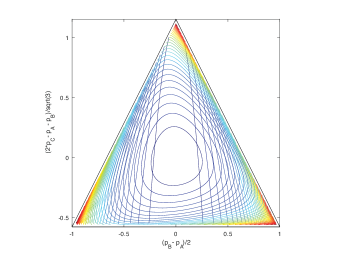
V.1.2 Vorticity in the flowfield of stationary trajectories
Recall (Table 3) that detailed balance means . In this case Eq. (51) implies equal and opposite change of along relaxations and escapes, because the two trajectories are time-reverses of each other. Detailed balance thus generalizes the time-reversal symmetry of 1-dimensional systems to any number of dimensions, and is a correspondingly restrictive condition. This is the assumption in classical thermodynamics that identifies the Lyapunov and large-deviation roles of the entropy state function.
Already for complex-balanced CRNs, exact time reversal is generally broken. The gradients of the tangent vectors to relaxation and escape trajectories, with respect to the exponential-family coordinates in Eq. (50), evaluate to
| (58) |
A measure of the time-asymmetry of the CRN is the vorticity, defined as the antisymmetric part of the matrices (58). This vorticity equals the gradient of the sum of tangent vectors to relaxations and escapes at the same point,
| (59) |
At the fixed point where , the vorticity is the antisymmetric part of the matrix .
V.1.3 Hyperflow decomposition for non-complex-balanced CRNs
For complex-balanced CRNs, describes flows on the complex network, which is an ordinary directed graph. For non-complex balanced flows, but . therefore cannot be written as a sum of adjacency matrices for currents on cycles in the complex graph. However, because net current still equals zero for every species, a basis for the currents at any fixed point still exists in balanced hyperflows. If the elements of are all integer values (as they are for chemistry or for biological population processes), the basis elements are balanced integer hyperflows Andersen:generic_strat:14 . Each such flow is an assignment of a set of non-negative integers to every current with nonzero , such that the net currents at each species vanish.
We may continue to refer to basis hyperflows with index by extension of the complex-balanced case, and for each basis element there is a non-negative current which is the coefficient of that flow in the stationary-state current solution. Integer hyperflows cannot be used to express as sums of KL divergences with uniform sign, in keeping with the variety of complications that arise for in for non-complex-balanced CRNs.
V.2 Cycle decomposition in the microstate space, and non-decrease of relative entropy components
Next we apply a cycle decomposition similar to the one in the previous section, but in the microstate space rather than on the hypergraph, to prove non-negativity of the first two terms in Eq. (11). The crucial distinction between the two levels is that balanced integer flows can always be mapped to cycles in the state space. For cycles in the hypergraph a natural map is unique; for more general flows many mappings may be possible. Relative entropies thus give Lyapunov functions more generally for distributions over microstates than for macrostate variables. However, unlike the hypergraph where basis decompositions are finite, in the state space they generally require solution for infinitely many cycle currents and are difficult except in special cases.
V.2.1 The system-marginal relative entropy from
The system and environment must now be considered explicitly because housekeeping heat is an embedding of in . We therefore work in system indices and descale with the steady state at the instantaneous . In the following derivations and can be any normalizable distributions; macrostates are no longer singled out. The time-change of , fixing as before, follows from Eq. (1) and the form (40), as
| (60) | ||||
From the definition (40), and , as was the case for complex-balanced . Therefore can be written as a sum of adjacency matrices for cycles, weighted by the currents around those cycles in the steady state. For a general CRN, it would not be assured that these cycles were all of finite length or that there were only finitely many of them passing through any given state . However, for a CRN in which both the dimensions of and and their matrix elements are finite, the integer hyperflow decomposition under and is in turn finite, and the basis flows can be embedded in the microstate space to give a decomposition of .
Let index any basis of integer hyperflows spanning . The cyclic flows spanning embed without ambiguity in the state space, as images the cycles on the complex network. Each cycle defines a sequence of state shifts when the transitions in the cycle are activated in order.
Non-complex-balanced integer flows also create cycles through states, because by construction the sum of stoichiometric shifts in a balanced flow is zero. However, there may be a choice in the way a given flow projects into the state space, depending on the realization, defined as the order in which the reaction events in the flow are activated. Any order is acceptable, as long as each state in the cycle can be reached by a reaction that can execute.222222This condition is called reachability. It can be violated if there are boundary states with too few individuals to permit the input complex to some reaction to be formed. States may be grouped into equivalence classes under reachability, as a means to study network features such as autocatalysis. Reachability is beyond the scope of this paper. For the large-population limits to which large-deviation scaling applies, under finitely generated reactions, all states will have arbitrarily many members and will be equivalent under reachability, so all embeddings of a finite integer hyperflow will always complete. We then extend the indexing from the images of the complex-balanced cycles to include all the integer flows.
Once a cycle realization has been chosen for each integer hyperflow, an embedding of these flows in the state space is defined as follows. Pick an arbitrary starting complex in the cycle, and for each , embed an image of the cycle with the starting complex sampled at . Then every state is passed through by every cycle with each complex in the cycle sampling from that state exactly once. Every link has a finite number of cycles passing through it, because the number of integer flows spanning and the length of each flow are both finite.
A set of currents that sum to the steady-state currents over each transition is then assigned to the cycles, indexed by the state where which cycle samples at its starting complex. Solving for the values of the is of course equivalent to solving for , and is not generally a finite problem.
With these notations in place, Eq. (60) becomes
| (61) |
Eq. (61) is a non-positive sum of KL divergences of probability ratios referenced to their own values advanced around cycles, of the same form as Eq. (53) for complex activities for macrostates on the hypergraph. The state space divergence involves an additional sum over the reference state . Because the sum over is finite, the contribution at each is finite and proportional by finite factors to within a finite neighborhood of . Therefore the sum (61) is finite. This proves that the first line of Eq. (11) is non-decreasing.
V.2.2 Non-negativity of the housekeeping entropy rate
The cycle decomposition on the state space may also be used to prove non-negativity of the housekeeping entropy rate (10) introduced by Hatano and Sasa Hatano:NESS_Langevin:01 . Here rather than work with entropy changes over extended-time paths, we prove positivity moment by moment from the master equation.
Unlike the relative entropy within the system, the housekeeping entropy rate is not only a function of aggregated within-system transition rates , but must be disaggregated to all distinct system-environment interactions. Begin by expressing the sum of all transition currents both in terms of elementary events and in the previous cycle decomposition:
| (62) |
where is labeled by the particular reaction connecting and .232323For notational simplicity, we suppose that each ordered pair of complexes is connected by at most one reaction – this still allows a common difference vector to be mediated by several distinct pairs – the generalization to more complex cases is straightforward.
We follow the construction of correlation functions for a counting process from Harris:fluct_thms:07 , for a quantity with event-dependent values defined as
| (63) |
A total housekeeping entropy rate denoted is a sum over pairs of system states, of the quantity in Eq. (10). Written as an expectation of , it is
| (64) |
The sign of Eq. (64) can be deduced from convexity of the observable , as in the usual fluctuation theorems. is nonzero only on transitions, the terms in the sum in Eq. (62). Let be a short time interval. Then the expectation of any function of on the interval will be times its value in an unchanging state, plus a term from transitions. Extracting the contribution for expectations of and over the interval, denoted , gives
| (65) |
Between the third and fourth lines in the evaluation of , index labels and are switched. Because the steady state currents decompose into cycles, whether is summed over the first index or over the second index along a cycle, the sum is the same. Hence the two expressions in Eq. (65) are the same. By Jensen’s inequality, , proving that Eq. (64), which is the second line of Eq. (11), is non-decreasing.
Remark: The Hatano-Sasa generating function is constructed to replace the transition matrix with its adjoint Harris:fluct_thms:07 . In Eq. (65), this relation is reflected in the way switches to the tail position of links, whereas in it is in the head position. Exactly the same sum arises if positivity of is proved by a similar convexity argument, from the expectation of over an interval , which is the inverse exponential of the log-ratio of Hartley information appearing in Eq. (61). Thus the two fluctuation theorems are for generating functions spanning the same chord between two probability measures, though the counting observables in the two generating functions are distinct.
VI Examples
VI.1 Dualizing the housekeeping embedding thermodynamics
In the first example the system is elementary: a 2-state model of polymerization and hydrolysis. Our interest is in how the embedding of such a model in a 1-parameter family of environments is captured in the intensive and extensive thermodynamic parameters, when these produce identical distributions , but with differing housekeeping entropy rate.
The motivation for the model is a question from astrobiology: in how far can two environments be considered analogues simply because they produce similar distributions for a material considered to be of biological interest. For instance, is Titan an analogue to early Earth if both are believed to support significant polymerization of small organic molecules Yung:org_Titan:84 ; Hebrard:Titan_atmos:12 ; Turse:org_Titan:13 , even if polymers on Titan are stable and near equilibrium at low water activity, whereas Earth produced them (putatively) through a competition between ligation driven by disequilibrium leaving groups such as phosphates Westheimer:phosphates:87 ; Pasek:why_P:11 or thioesters Goldford:P_free_metab:17 ; Goldford:bdry_expn:19 and disequilibrium hydrolysis?
The polymerization/hydrolysis mechanism, though elementary, can be a foundation for more complex heterogeneous polymerization models Esposito:copol_eff:10 , in which polymers once formed may be sensitive to other consequences of water activity, such as propensity to fold or to aggregate. We ask, to what extent can the rate balance that governs polymerization, and water activity per se, be decoupled as measures of environmental similarity. The example will show that in the limit where one driving buffer goes to zero concentration and a subset of reactions become strictly irreversible, the two parameters can be made independent.
In this example all influences on what we should call thermodynamic order come from kinetics in buffered non-equilibrium settings. Total entropy production is uninformative because the entropy associated with the polymer distribution sits atop a housekeeping heat that can be varied freely. Even knowing that housekeeping heat depends on a difference of chemical potentials gives no information when that difference is taken to infinity in an irreversible limit. Thus none of the conservation laws linking the model to microscopically reversible mechanics provide information beyond what is in the transition matrix. Yet the thermodynamics of the process retains a regular representation: dualization of the housekeeping heat introduces an intensive state variable that is just the regular current through the polymerization/hydrolysis cycle, even in the strictly irreversible limit.
VI.1.1 One system, families of environments
Elementary reactions:
For simplicity we let environmental distributions be Poisson with large capacity as a model of chemostats, and omit them from the explicit notation. Half-reaction rate constants are denoted and where is a label.
The first reaction type in the model is reversible dehydrating polymerization and hydrolysis, with schema
| (66) |
are monomers in solution, buffered at unit activity, and are monomers attached to the end of a polymer by dehydrating condensation. denotes the number of , which we will interpret as polymer lengths, and is the index for the system state. Water is also buffered, at activity , which is varied as a control parameter across a family of environments.
A second process, involving only environment species to define a reference scale for chemical potentials, is hydrolysis of a phosphoanhydride bond, with schema
| (67) |
is a bound form with activity , and a hydrolyzed form, with activity .242424Eq. (67) is a stand-in for a variety of phosphoryl group-transfer processes, some linear as shown and some higher-order in the hydrolyzed species Pasek:why_P:11 . For higher-order reactions, appropriate powers of the activity would replace in the expressions below, without otherwise changing the results.
Monomer ligation driven by phosphate hydrolysis is the stoichiometrically coupled reaction
| (68) |
Equilibrium constants for the three reactions (66–68) are denoted . In actual chemistry, detailed balance implies the relation . To simplify notation we will choose activity units to set . Reaction 2 contributes only to dissipation internal to the environment (the third line in Eq. (11)), and we omit it, so the scale of never enters.
Poisson stationary distribution over polymer lengths:
The varieties of chemical disequilibrium:
We are interested in families of environments that share the same value of and so are indistinguishable from within the system. Chemical-potential coordinates within such a family are
| (70) |
is the chemical potential for hydrolysis in the stationary polymer distribution. is the chemical potential of the phosphate system for hydrolysis.
Within surfaces of constant we consider variation of phosphate and water activities along contours of fixed ,252525 is a nonlinear function of the value of along this contour. and vary this ratio later to define routes to irreversibility. The thermodynamic equilibrium corresponds to , or
| (71) |
At equilibrium the sub-system stationary distribution is also the marginal of the whole-system equilibrium; to emphasize that it is fixed as and are varied across a family of environments, we reference distributions to .
The activities governing reaction fluxes then depend on the coordinates (70) as
| (72) |
Fixed contours near and far from equilibrium satisfy
| (73) |
Cycle decomposition of steady-state currents:
If environmental marginals are chemostats at the indicated chemical potentials, then currents in the stationary system distribution at a state are proportional to by factors that do not depend on , and can be decomposed into three “specific currents” around cycles, which are functions of the chemostat activities
| (74) |
is the average of forward and reverse currents in reaction (66), and the average of forward and reverse currents in reaction (68), divided by . is the difference of forward and reverse currents, which must be equal and opposite in reactions (66) and (68) in stationary state, also divided by ; it is the only current in Schnakenberg’s fundamental graph Schnakenberg:ME_graphs:76 for this CRN.262626 is so named because we have called it a “-flow” in Krishnamurthy:CRN_moments:17 ; Smith:CRN_moments:17 . The number of possible independent net flows in the stationary state of a CRN equals Feinberg’s Feinberg:notes:79 topological characteristic termed deficiency and denoted . The CRN of this example has . The fundamental graph omits currents and because they do not lead to dissipation in the stationary state, but they do for more general states.
VI.1.2 The housekeeping entropy rate
The housekeeping entropy rate (64), for an arbitrary system distribution , evaluates in terms of the specific currents (74) and the density , to
| (75) | ||||
The second expression is a continuum approximation to first order in derivatives, with understood as usual to be approximated by the appropriate large-deviation function .
To check that the exact (discrete) form of Eq. (75) is positive semidefinite for arbitrary , define measures
| (76) |
From the formulae (74) it follows that
| (77) |
and thus Eq. (75) can be written
| (78) |
with a Kullback-Leibler divergence as elsewhere.
Housekeeping entropy rate as an embedding vector:
Eq. (78) can be put in the form
| (79) |
is a vector with positive-semidefinite components, which by Eq. (77) equals zero only at .
As noted, is an extremal vector for the intensive relative entropy in the simplex of distributions . By Eq. (75), at this extremal point of , .
VI.1.3 Legendre duality for housekeeping entropy rate
The chemical potential if the activity at fixed and . In this limit schema (68) becomes an irreversible reaction. Phenomenologically, all “thermodynamic” characteristics of the system remain regular, only the energetic accounting breaks down because it is referenced to the equilibrium state variable , in a system that nowhere couples to an equilibrium environment.
The divergence of in this limit is like the divergence of any extensive thermodynamic potential in the limit that one of the extensive state variables diverges, except that is an inherently non-equilibrium potential, and only behaves like an extensive variable with respect to dissipation.272727Note that has no status with respect to equilibrium; while entropies are extensive, depends inherently on a rate.
From the view that thermodynamics is about statistical organization and not fundamentally about energy, it is natural to Legendre transform to expose the dynamically intensive current that is dual to . For dualization, we work within the tangent space to the family of constant , but now vary independently of , rather than varying within the non-linear contours (71) at fixed .
The gradient of with respect to at fixed is
| (80) | ||||
By Eq. (74), is convex in , so its derivative, the term in square brackets in the final line of Eq. (80), is invertible to a value for . The Legendre dual potential to on , which we denote , is then given by
| (81) | ||||
Independent variation of control parameters in the irreversible limit:
We may now consider the effects of varying , which remains finite, across the one-parameter family of contours of different as . approaches a constant independent of , and the only term in Eq. (81) including multiples of diverging evaluates to
| (82) | |||||
It approaches within a range around that becomes vanishingly small as , and converges exponentially to zero outside that range.
Thus the susceptibility that is the Legendre dual to , , a function only of , almost everywhere. The potential retains only the -independent terms in Eq. (81). If, for example, we choose a macrostate with mean , then and .
In the irreversible limit the problem is seen to separate. dictates the intensive thermodynamics of the polymer system, while along a contour that fixes , the dual potential describes the non-trivial dependence of entropy change in the environment on . diverges harmlessly as an extensively-scaling potential independent of with a regular susceptibility .
VI.2 Metastability and as the reference measure for relative entropy
The second example uses the same buffered driving environment as the first, but separates phosphate-driven ligation into a distinct, self-catalyzed channel while leaving the reaction (66) with water uncatalyzed. The model for system catalysis is a variant on the cubic Schlögl model of Fig. 2. It is chosen to highlight the difference between the entropy rate (8) typically assigned as “environmental” and the housekeeping entropy rates (10). A quantity is a function only of the realized distributions and . Nowhere does it reflect the joint participation of uncatalyzed and catalyzed reactions within the same system.
The difference may have either sign. We illustrate the case where phosphate activities are chosen to put the system in its bistable regime, and is chosen to make the unstable root of the rate equation (47) a fixed point. For equivalent rate constants a Poisson distribution at mean would be the driven stationary distribution in the previous example, and the is the same in the two models. However, because the loss of large-deviation accessibility in the system results not only from it Shannon entropy change, but from the measure of that entropy relative to the true, bistable stationary distribution .
The autocatalytic model replaces the schema (68) with
| (83) |
Catalysis does not change energetics, so the rate constants must satisfy .
In the mass-action rate law (47), the roots and is unstable. We set a characteristic scale for transitions between water and phosphate control by choosing relative rate constants .
The Schlögl model is a birth-death process, so is exactly solvable. In place of from Eq. (69) adjacent indices are related by a position-dependent effective equilibrium constant
| (84) |
Note that to integer rounding error, at all activity levels.
In terms of the same roots, choose water activity to set the lower limit of Eq. (84) at to
| (85) |
We will vary the activities in the phosphorus system so that moves from a lower stable mode near equilibrium, through a bistable phase, to an upper stable mode driven by phosphorylation farther from equilibrium.
Equilibrium is again defined as in Eq. (71), and there . The marginal distribution for in the whole-system equilibrium, , is then Poisson with parameter . Recall that, as a solution in detailed balance, it does not and cannot reflect the fact that is a CRN capable of bistability. To match rate constants to the roots of the Schlögl model, we define a reference equilibrium for the phosphorus system with activity levels at
| (86) |
We now consider a family of driving environments in which the chemical potential is partitioned between the activities and in the proportions
| (87) |
The two potentials (87) are coordinates in an exponential family for the phosphorus system. Where , the three roots of the mass action law pass through the values from Fig. 2.
The difference in relative dissipations between the driven steady state and , at adjacent indices, is given by the ratio of effective rate constants
| (88) |
Eq. (88) is a sigmoidal function of in the range , graphed versus in Fig. 4. The hydrolysis potential from Eq. (70 for the linear system is replaced in the autocatalytic case by a position-dependent chemical potential
| (89) |
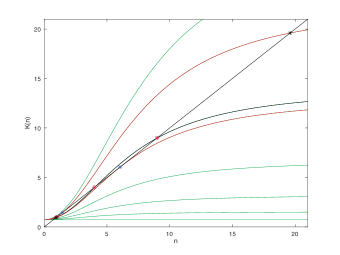
In the cycle decomposition, the specific currents exiting and entering a site , now functions of , depend on activities as
| (90) |
In the chemical-potential coordinates, these become
| (91) |
Positive-semidefiniteness of again follows by using the ratios (76) to produce the form (78), where now instead of Eq. (77), we have
| (92) |
For this example we separate out a term , which is the sum over transitions of Eq. (8), from , to give
| (93) |
does not depend on , and differs from the sum of terms multiplying in Eq. (75) only by the -dependence now multiplying in Eq. (93).
All dependence of on comes from the second term involving . The shape of is shown as a function of in Fig. 5, and the lumped coefficient multiplying the difference term in in Eq. (93) is shown in Fig. 6.


As an example, consider the value that makes the three fixed points, and evaluate the embedding entropies for a Poisson distribution with mean , the unstable fixed point. The “environmental” component
| (94) |
is the same as the value following from Eq. (75) for the non-catalytic CRN, if we set in Eq. (70), where and this is a driven steady state. It is also the value of in Eq. (79) at the extremal distribution for the linear model.
For the same , recognizing that , the gradient relative to the bistable reference distribution in Eq. (93) expands to . The difference of environment from housekeeping entropy changes then evaluates to
| (95) |
The combination is increasing through (See Fig. 6), and is antisymmetric, so Eq. (95) is negative.
Hence not all of the entropy change by reflects a loss of large-deviation accessibility attributable to the environment. A quantity equal to is assigned in the natural decomposition (11) to the system, because a Poisson distribution around is unstable and has excess net probability to relax toward the bistable distribution .
VII Discussion
The problem of macroworlds as an alternative central contribution
A suggestion that thermodynamics should not be mainly about the relation between work and heat flows would have been non-sequitur at the turn of the 20th century. Not only were applications centered around interactions with a thermal system through mechanical boundaries Carnot:essays:60 ; the nature of irreversibility and dissipation as scientific problems was framed in their relation to mechanical principles of time-reversibility Laplace:probs:51 and conservation of energy Clausius:equivalence:62 ; Joule:sci_papers:44 .
Innovations in scaling methods, however, in context of the unification of statistical and quantum theories in the second half of the 20th century, have exposed understanding the existence of macroworlds as one of the central problems in science. Sec. III explained how large-deviations scaling formalizes a concept of macrostate in terms of selected distributions over microstates. When methods derived for phase transitions and critical phenomena in condensed matter Wilson:RG:74 were merged with the renormalization-group approach GellMann:RG:54 to vacuum quantum field theory Polchinski:RGEL:84 , it became clear that renormalization-group flow, a closely related operation282828Through the correspondence of Keldysh to 2-field statistical field methods, the algebras of the two can often be interconverted Kamenev:DP:02 ; Smith:DP:08 . of dimensional reduction to large-deviations scaling, provides a concept of effective fields describing the robust properties of macroworlds through phenomenological Lagrangians Weinberg:phenom_Lagr:79 . Effective fields are the counterparts under renormalization to classical states under large-deviations scaling.
In effective field theories nested through phase transitions (as in the models of this paper) microstates are assimilated back to macrostates. The result has been a theory of the vacuum and the hierarchy of matter in which all earlier, partly phenomenological concepts of elementary and composite objects and interactions has been subsumed within a semantics of distributions. While these physics examples continue to be organized by symmetries and conservation laws, similar scaling methods developed independently for reliable coding Shannon:MTC:49 ; Cover:EIT:91 offer non-mechanical counterparts (see Smith:geo13:16 , Ch. 7).
The alternative characterization offered, then, is that thermodynamics is not fundamentally the theory of the movements of heat, but rather the theory of the emergence of macroworlds from microworlds.
The end of entropy flow, the natural partition, and Hartley information
In the absence of an energy-mediated constraint on the states jointly realizable by a system and its environment, the notion of “entropy flow” between subsystems may never arise.292929Even in classical thermodynamics, it is only well-defined for adiabatic transformations, in which both subsystems remain in classical states constrained by energy at every moment. The default description of entropy change ceases to be the metaphor of a fluid and becomes the literal one: it is the loss of large-deviation accessibility of classical states due to relaxation of the whole-system distribution. The concept of a tangent surface delimiting the amount of entropy gain in one component that can be influenced by the state of another, instead of the adiabatic transformation, is filled by the the vector of Hartley informations of the stationary state for the at that moment. The natural system-environment partition (11) encodes the conditional independence of components of the loss of states accessible by fluctuations.
Hartley information appears as a random variable along trajectories in the construction of the generating functional for housekeeping heat Speck:HS_heat_FT:05 ; Seifert:stoch_thermo_rev:12 . In standard treatments, its interpretation as an entropy is taken to depend on its association with a dissipated heat.303030The exact statement, referring to Eq. (123) in Seifert:stoch_thermo_rev:12 , is: “In the absence of a first law for the master equation dynamics, which would require further physical input not available at this general stage, this identification is by analogy only.” Here, gains its interpretation as an entropy through its role as a carrier of information about the interaction of processes within a system on its own limiting large-deviation function and on its capacity to limit large-deviations in the environment.
Making trajectories first-class citizens
The persistence over 90 years of Onsager’s program Onsager:RRIP1:31 ; Onsager:RRIP2:31 of making equilibrium Gibbs entropies the foundation of non-equilibrium thermodynamics has built an asymmetry into this concept even within physics, at the same time as growth in statistical methods for path ensembles has reduced the reason for an asymmetry to exist, by defining the same tools for paths as for states. The equilibrium Gibbs entropy is defined from the large-deviation function on ensembles of states. The stochastic effective action (25) Smith:LDP_SEA:11 is the corresponding functional for trajectories. However, the role that energy conservation plays in stochastic thermodynamics, as a constraint on which states can be jointly occupied by components within a system and within its environment, will not generally have a counterpart for the jointly realizable trajectories involving these components.313131Consider, as examples, non-Markovian noise sources and error-correcting codes exploiting time correlations to optimize against those environments Verdu:Shannon:98 .
Borrowing a term from computer science, the privileged roles of equilibrium entropy and energy conservation in current non-equilibrium thermodynamics makes spaces of states “first-class citizens” Abelson:SICP:96 , and admits thermodynamic interpretations for ensembles only in so far as those derive from equilibrium heat. Jaynes anticipated Jaynes:caliber:80 ; Jaynes:LOS:03 a self-contained thermodynamic interpretation for path ensembles, though still only in a limited form referenced to the calibers of cross-sections of states. If there is to be a thermodynamics in which trajectories become first-class citizens on par with states, it will need a foundation in more general primitives such as large-deviation accessibility and separation of scales, as in the domain-agnostic framework presented here.
Rule-based systems and life
This paper’s formula for a self-contained and substrate-agnostic thermodynamics is meant to support concept discovery in two domains that should clearly have such a thermodynamics, and for which energy conservation should play a limited role or no role at all for many interesting questions.323232A well-known examples of a constraint that is proved by a fluctuation theorem, but not binding because a more proximal constraint exists, is that of total entropy production versus the “excess heat” in a driven system. Speck:FDT_NESS:06 The former bounds the non-equilibrium entropy change within a distribution, but is uninformative because it diverges on long timescales. The tight bound, under some conditions, is the finite excess heat.
The first domain is rule-based modeling Danos:rule_based_modeling:08 which recognizes the finitary-to-infinitary mappings exhibited here between CRN generators and state spaces as a widely generalizable organizing principle. The algebra and combinatorics of non-commutative rule systems is a very active area of study Harmer:info_carriers:10 ; Andersen:generic_strat:14 ; Behr:alg_graph_rewrt:16 which connects to chemistry, systems biology, theories of algorithms, process calculus, and much more. A thermodynamics of rule-based systems that expands the conceptual scope of science will not be a reduction to their consequences for heat generation.
The second domain is the thermodynamic nature of life Smith:geo13:16 , encompassing rule-based order in its chemical substrate, the multi-level control systems and error correction required to maintain complex dynamical phases, and the nested population dynamics and historical contingency of evolution. There will be order in such systems that derives, sometimes cryptically, from microscopic time-reversibility. But it is inconceivable that there will not be much more order, of novel kinds, that originates from the abundance of architectures – most of them irreversible – standing between the microscopic substrate and robust macrophenomena.
VIII Concluding remarks
The presentation above is not a review of recent technical innovations, but an attempt to select core concepts that depend on formalization to be adequately expressed, and to exhibit them in relation to each other and in a context that does not presume mechanics. The Hamilton-Jacobi and CRN formalisms are of course not new, but needed to be reviewed within a coherent framework to make points about them that are not made elsewhere. Likewise most monotonicity results are known from fluctuation theorems, though alternative proofs for a few are given here. It may therefore be useful to summarize the novel contributions of the paper that are interleaved with standard results above:
Monotonic change of Kullback-Leibler divergence is obvious and positivity of housekeeping heat was known Speck:HS_heat_FT:05 ; Harris:fluct_thms:07 . An emphasis here on entropy increase as loss of accessibility by large deviations, together with the observation that thermalization in a multi-scale system produces separation in the conditional dependence between system and environment degrees of freedom, leads to the decomposition of in Eq. (11) as the natural partition of irreversibility between system and environment changes, irrespective within each of the degree of irreversibility in the other.
The “non-equilibrium entropy production” of stochastic thermodynamics is a complicated sum, of an entropy functional of arbitrary distributions (over stochastic microstates) and a Gibbs entropy state-function (for bath macrostates). The designation “violations of the 2nd law” by stochastic events uses that summation to conflate these two entropy summands which have different relations to constraints by boundary conditions. The decomposition in Eq. (34) of in terms of the Lyapunov entropy state function and a remainder that must be relaxed by instantons, retains an un-violated 2nd law for relative entropy, and also the Lyapunov and large-deviation roles of the classical state-function entropy, in the proper relation.
The dualization by Baish Baish:DP_duality:15 of observable and response fields in Doi-Peliti theory stands in obvious analogy to the construction of the adjoint transition matrix in the fluctuation theorem for housekeeping heat Speck:HS_heat_FT:05 ; Harris:fluct_thms:07 . The standardization of the CRN generator (35) makes the analogy explicit in the descaling (39) of and the descaling (43) of . Moreover, it shows the analogy as an expression of the general relation of microstates to macrostates, and relates the preservation or loss of information in the classical limit to CRN complexity classes.
The distinction between relaxation and escape trajectories in terms of formal momenta is widely developed in momentum-space WKB theory Assaf:mom_WKB:17 , as Hamilton-Jacobi theory Bertini:macro_NEThermo:09 , and in relation to information geometry Smith:IGDP:19 . The convexity proof in Eq. (49) relating the Lyapunov to the large-deviation role of the classical-state entropy, and to the structure of the manifold, is novel.
The use of cycle decompositions in CRNs to compute heat dissipation in the stationary state is standard since Schnakenberg Schnakenberg:ME_graphs:76 . Here a more complete cycle decomposition (keeping detailed-balanced currents) unifies all proofs of monotonicity of entropies for non-stationary distributions, relating the Lyapunov and large-deviation changes in macrostate entropy on complex-balanced CRNs in Eq. (53), and its counterpart (61) in the state space for all CRNs. It also provides an interesting view of the (known) equivalence of the adjoints constructed in the generating function (64) for housekeeping heat in the environment, and an equivalent function for the relative entropy (61) in the system.
The Legendre duality of to the potential in Eq. (81) defines extensivity and intensivity with respect to a different scaling than that for entropy, but a natural one if time-reversal and energy conservation are not the only basis for taking macroscopic limits.
References
- (1) Leo Szilard. Uber die entropieverminderung in einem thermodynamischen system bei eingriffen intelligenter wesen. Zeitschrift für Physik, 53:840–856, 1929.
- (2) R. Landauer. Irreversibility and heat generation in the computing process. IBM J. Res. Development, 3:183–191, 1961.
- (3) Charles H. Bennett. The thermodynamics of computation – a review. Int. J. Theor. Phys., 21:905–940, 1982.
- (4) David H. Wolpert. The stochastic thermodynamics of computation. J. Phys. A: Math. Theor., 52:193001, 2019.
- (5) Udo Seifert. Stochastic thermodynamics, fluctuation theorems, and molecular machines. Rep. Prog. Phys., 75:126001, 2012. arXiv:1205.4176v1.
- (6) Lars Onsager. Reciprocal Relations in Irreversible Processes. I. Phys. Rev., 37:405–426, 1931.
- (7) Lars Onsager. Reciprocal Relations in Irreversible Processes. II. Phys. Rev., 38:2265–2279, 1931.
- (8) P. Glansdorff and I. Prigogine. Thermodynamic Theory of Structure, Stability, and Fluctuations. Wiley, New York, 1971.
- (9) Dilip Kondepudi and Ilya Prigogine. Modern Thermodynamics: From Heat Engines to Dissipative Structures. Wiley, New York, 1998.
- (10) Denis J. Evans and Debra J. Searles. Fluctuation theorem for stochastic systems. Phys. Rev. E, 60:159–164, 1999.
- (11) Denis J. Evans and Debra J. Searles. The fluctuation theorem. Adv. Phys., 51:1529–1585, 2002.
- (12) G. Gallavotti and E. D. G. Cohen. Dynamical ensembles in non-equilibrium statistical mechanics. Phys. Rev. Lett., 74:2694–2697, 1995.
- (13) G. Gallavotti and E. D. G. Cohen. Dynamical ensembles in stationary states. J. Stat. Phys., 80:931–970, 1995.
- (14) C. Jarzynski. Nonequilibrium work relations: foundations and applications. Eur. Phys. J. B, 64:331–340, 2008.
- (15) Raphaël Chetrite and Krzysztof Gawedzki. Fluctuation relations for diffusion processes. Commun. Math. Phys., 282:469–518, 2008.
- (16) Massimiliano Esposito and Christian Van den Broeck. Three detailed fluctuation theorems. Phys. Rev. Lett., 104:090601, 2010.
- (17) Gavin E. Crooks. Entropy production fluctuation theorem and the nonequilibrium work relation for free energy differences. Phys. Rev. E, 6:2721–2726, 1999.
- (18) Gavin E. Crooks. Path-ensemble averages in systems driven far from equilibrium. Phys. Rev. E, 61:2361–2366, 2000.
- (19) Jorge Kurchan. Non-equilibrium work relations. J. Stat. Mech., 2007:P07005, 2007.
- (20) Jeremy L. England. Statistical physics of self-replication. J. Chem. Phys., 139:121923, 2013.
- (21) Nikolai Perunov, Robert Marsland, and Jeremy England. Statistical physics of adaptation. 2015. arXiv:1412.1875v1 [physics.bio-ph].
- (22) R. Duncan Luce. Individual Choice Behavior. Wiley, New York, 1959.
- (23) Daniel McFadden. Quantal choice analysis: a survey. Ann. Econ. Soc. Measurement, 5:363–390, 1976.
- (24) T. M. Lenton, V. N. Livina, V. Dakos, E. H. van Nes, and M. Scheffer. Early warning of climate tipping points from critical slowing down: comparing methods to improve robustness. Phil. Trans. R. Soc. A, 370:1185–1204, 2011.
- (25) J. P. Joule. The Scientific Papers of James Prescott Joule. London: Physical Society, Open Library, 1844. https://openlibrary.org/books/OL239730M/The_scientific_papers_of_James_Prescott_Joule.
- (26) T. Archer Hirst, editor. The Mechanical Theory of Heat, London, 1865. John van Voorst.
- (27) Ludwig Boltzmann. The second law of thermodynamics. In Populäre Schriften, pages 25–50. J. A. Barth, Leipzig, 1905. re-issued Braunschweig: F. Vieweg, 1979.
- (28) Anders Hald. A history of probability and statistics and their applications before 1750. Wiley, New York, 1990.
- (29) E. T. Jaynes. Information theory and statistical mechanics. Phys. Rev., 106:620–630, 1957. reprinted in Jaynes:Papers:83 .
- (30) E. T. Jaynes. Information theory and statistical mechanics. II. Phys. Rev., 108:171–190, 1957. reprinted in Jaynes:Papers:83 .
- (31) Gian-Carlo Rota. Lectures on Being and Time (1998). New Yearbook for Phenomenology and Phenomenological Philosophy, 8:225–319, 2008.
- (32) Murray Gell-Mann and Francis Low. Quantum electrodynamics at small distances. Phys. Rev., 95:1300–1312, 1954.
- (33) K. G. Wilson and J. Kogut. The renormalization group and the expansion. Phys. Rep., Phys. Lett., 12C:75–200, 1974.
- (34) Steven Weinberg. Phenomenological Lagrangians. Physica A, 96:327–340, 1979.
- (35) Joseph G. Polchinski. Renormalization group and effective lagrangians. Nuclear Physics B, 231:269–295, 1984.
- (36) Enrico Fermi. Thermodynamics. Dover, New York, 1956.
- (37) L. Bertini, A. De Sole, D. Gabrielli, G. Jona-Lasinio, and C. Landim. Towards a nonequilibrium thermodynamics: a self-contained macroscopic description of driven diffusive systems. J. Stat. Phys., 135:857–872, 2009.
- (38) Shun-Ichi Amari. Methods of Information Geometry. Amer. Math. Soc., 2001.
- (39) Nihat Ay, Jürgen Jost, Hông Vân Lê, and Lorentz Schwachhöfer. Information Geometry. Schwinger International, Cham, Switzerland, 2017.
- (40) Richard S. Ellis. Entropy, Large Deviations, and Statistical Mechanics. Springer-Verlag, New York, 1985.
- (41) Hugo Touchette. The large deviation approach to statistical mechanics. Phys. Rep., 478:1–69, 2009. arxiv:0804.0327.
- (42) Claude Elwood Shannon and Warren Weaver. The Mathematical Theory of Communication. U. Illinois Press, Urbana, Ill., 1949.
- (43) R. V. L. Hartley. Transmission of information. Bell system technical journal, July:535–563, 1928.
- (44) T. Speck and U. Seifert. Integral fluctuation theorem for the housekeeping heat. J. Phys. A Math. Gen., 38:L581–L588, 2005.
- (45) R. J. Harris and G. M. Schütz. Fluctuation theorems for stochastic dynamics. J. Stat. Mech., page P07020, 2007. doi:10.1088/1742-5468/2007/07/P07020.
- (46) Thomas M. Cover and Joy A. Thomas. Elements of Information Theory. Wiley, New York, 1991.
- (47) Takahiro Hatano and Shin-ichi Sasa. Steady state thermodynamics of Langevin systems. Phys. Rev. Lett., 86:3463–3466, 2001.
- (48) Eric Smith. Large-deviation principles, stochastic effective actions, path entropies, and the structure and meaning of thermodynamic descriptions. Rep. Prog. Phys., 74:046601, 2011. http://arxiv.org/submit/199903.
- (49) Murray Gell-Mann and Seth Lloyd. Information measures, effective complexity, and total information. Complexity, 2:44–52, 1996.
- (50) Murray Gell-Mann and Seth Lloyd. Effective complexity. In Murray Gell-Mann and Constantino Tsallis, editors, Nonextensive Entropy – Interdisciplinary Applications, pages 387–398. Oxford U. Press, New York, 2004.
- (51) Matteo Polettini and Massimiliano Esposito. Irreversible thermodynamics of open chemical networks. I. Emergent cycles and broken conservation laws. J. Chem. Phys., 141:024117, 2014.
- (52) Matteo Polettini, Gregory Bulnes-Cuetara, and Massimiliano Esposito. Bridging stochastic and macroscopic thermodynamics. 2016. arXiv:1602.06555v1.
- (53) F. Horn and R. Jackson. General mass action kinetics. Arch. Rat. Mech. Anal, 47:81–116, 1972.
- (54) Martin Feinberg. Lectures on chemical reaction networks. lecture notes, 1979. https://crnt.osu.edu/LecturesOnReactionNetworks.
- (55) Supriya Krishnamurthy and Eric Smith. Solving moment hierarchies for chemical reaction networks. J. Phys. A: Math. Theor., 50:425002, 2017.
- (56) Eric Smith and Supriya Krishnamurthy. Flows, scaling, and the control of moment hierarchies for stochastic chemical reaction networks. Phys. Rev. E, 96:062102, 2017.
- (57) Udo Seifert and Thomas Speck. Fluctuation-dissipation theorem in nonequilibrium steady states. Europhysics Lett., 89:10007, 2010.
- (58) J. Schnakenberg. Network theory of microscopic and macroscopic behavior of master equation systems. Rev. Mod. Phys, 48:571–585, 1976.
- (59) Jakob L. Andersen, Christoph Flamm, Daniel Merkle, and Peter F. Stadler. Generic strategies for chemical space exploration. Int. J. Comput. Biol. Drug Des., 7:225–258, 2014.
- (60) Michael Assaf and Baruch Meerson. Wkb theory of large deviations in stochastic populations. J. Phys. A, 50:263001, 2017.
- (61) M. I. Freidlin and A. D. Wentzell. Random Perturbations in Dynamical Systems. Springer, New York, second edition, 1998.
- (62) P. C. Martin, E. D. Siggia, and H. A. Rose. Statistical dynamics of classical systems. Phys. Rev. A, 8:423–437, 1973.
- (63) Alex Kamenev. Keldysh and doi-peliti techniques for out-of-equilibrium systems. In I. V. Lerner, B. L. Althsuler, V. I. Fal′ko, and T. Giamarchi, editors, Strongly Correlated Fermions and Bosons in Low-Dimensional Disordered Systems, pages 313–340, Heidelberg, 2002. Springer-Verlag.
- (64) Eric Smith. Thermodynamics of natural selection II: Chemical Carnot cycles. J. Theor. Biol., 252:198–212, 2008. PMID: 18367209.
- (65) Eric Smith. Thermodynamics of natural selection I: Energy and entropy flows through non-equilibrium ensembles. J. Theor. Biol., 252:185–197, 2008. PMID: 18367210.
- (66) Massimiliano Esposito, Katja Lindenberg, and Christian Van den Broeck. Extracting chemical energy by growing disorder: efficiency at maximum power. J. Stat. Mech., doi:10.1088/1742-5468/2010/01/P01008:1–11, 2010.
- (67) Charles Kittel and Herbert Kroemer. Thermal Physics. Freeman, New York, second edition, 1980.
- (68) D. Siegmund. Importance sampling in the Monte Carlo study of sequential tests. Ann. Statist., 4:673–684, 1976.
- (69) Herbert Goldstein, Charles P. Poole, and John L. Safko. Classical Mechanics. Addison Wesley, New York, third edition, 2001.
- (70) David F. Anderson, George Craciun, and Thomas G. Kurtz. Product-form stationary distributions for deficiency zero chemical reaction networks. Bull. Math. Bio., 72:1947–1970, 2010.
- (71) M. Doi. Second quantization representation for classical many-particle system. J. Phys. A, 9:1465–1478, 1976.
- (72) M. Doi. Stochastic theory of diffusion-controlled reaction. J. Phys. A, 9:1479–, 1976.
- (73) L. Peliti. Path-integral approach to birth-death processes on a lattice. J. Physique, 46:1469, 1985.
- (74) L. Peliti. Renormalization of fluctuation effects in reaction. J. Phys. A, 19:L365, 1986.
- (75) J. L. Cardy. Electron localisation in disordered systems and classical solutions in ginzburg-landau field theory. J. Phys. C, 11:L321 – L328, 1987.
- (76) Sidney Coleman. Aspects of Symmetry. Cambridge, New York, 1985.
- (77) Eric Smith and Supriya Krishnamurthy. Eikonal solutions for moment hierarchies of chemical reaction networks in the limits of large particle number. J. Phys. A Math. Theor., submitted, 2020.
- (78) Jeremy Gunawardena. Chemical reaction network theory for in-silico biologists. lecture notes, June 2003. vcp.med.harvard.edu/papers/crnt.pdf.
- (79) Eric Smith and Supriya Krishnamurthy. Symmetry and Collective Fluctuations in Evolutionary Games. IOP Press, Bristol, 2015.
- (80) Jakob L. Andersen, Christoph Flamm, Daniel Merkle, and Peter F. Stadler. Maximizing output and recognizing autocatalysis in chemical reaction networks is NP-complete. J. Sys. Chem., 3:1, 2012.
- (81) Claude Berge. Graphs and Hypergraphs. North-Holland, Amsterdam, rev. ed. edition, 1973.
- (82) John C. Baez and Brendan Fong. Quantum techniques for studying equilibrium in reaction networks. J. Compl. Netw., 3:22–34, 2014. https://academic.oup.com/comnet/article-abstract/3/1/22/490572/Quantum-techniques-for-studying-equilibrium-in?redirectedFrom=fulltext.
- (83) Andrew James Baish. Deriving the jarzynski relation from doi-peliti field theory. Bucknell University Honors Thesis, 2015.
- (84) Martin Feinberg. Chemical reaction network structure and the stability of complex isothermal reactors – I. The deficiency zero and deficiency one theorems. Chem. Enc. Sci., 42:2229–2268, 1987.
- (85) F. Schlögl. On thermodynamics near a steady state. Z. Phys., 248:446–458, 1971.
- (86) M. I. Dykman, Eugenia Mori, John Ross, and P. M. Hunt. Large fluctuations and optimal paths in chemical kinetics. J. Chem. Phys., 100:5735–5750, 1994.
- (87) N. G. van Kampen. Stochastic Processes in Physics and Chemistry. Elsevier, Amsterdam, third edition, 2007.
- (88) Vincent Danos, Jérôme Feret, Walter Fontana, Russell Harmer, and Jean Krivine. Rule-based modelling, symmetries, refinements. Formal methods in systems biology: lecture notes in computer science, 5054:103–122, 2008.
- (89) John C. Baez. Quantum techniques for reaction networks. 2013. https://arxiv.org/abs/1306.3451.
- (90) Yuk Yung, M. Allen, and J. P. Pinto. Photochemistry of the atmosphere of Titan: comparison between model and observations. Astrophys. J. Suppl. Ser., 55:465–506, 1984.
- (91) E. Hébrard, M. Dobrijevic, J. C. Loison, A. Bergeat, and K. M. Hickson. Neutral production of hydrogen isocyanide (HNC) and hydrogen cyanide (HCN) in Titan’s upper atmosphere. Astron. Astrophys., 541:A21, 2012.
- (92) Carol Turse, Johannes Leitner, Maria Firneis, and Dirk Schulze-Makuch. Simulations of prebiotic chemistry under post-imact conditions on Titan. Life (Basel), 3:538–549, 2013.
- (93) Frank H. Westheimer. Why nature chose phosphates. Science, 235:1173–1178, 1987.
- (94) Matthew A. Pasek and Terence P. Kee. On the origin of phosphorylated biomolecules. In Richard Egel, Dirk-Henner Lankenau, and Armen Y. Mulkidjanian, editors, Origins of Life: The Primal Self-Organization, pages 57–84. Springer-Verlag, Berlin, 2011.
- (95) Joshua E. Goldford, Hyman Hartman, Temple F. Smith, and Daniel Segrè. Remnants of an ancient metabolism without phosphate. Cell, 168:1126–1134, 2017.
- (96) Joshua E. Goldford, Hyman Hartman, Robert Marsland III, and Daniel Segrè. Environmental boundary conditions for early life converge to an organo-sulfur metabolism. Nat. Ecol. Evol., 2019. doi:10.1038/s41559-019-1018-8.
- (97) Sadi Carnot. Reflections on the Motive Power of Fire. Dover, New York, e. mendoza (ed.) edition, 1960.
- (98) Pierre Simon Laplace. A Philosophical Essay on Probabilities. Dover, New York, original french 6th ed. by truscott, f. w. and emory, f. l. edition, 1951.
- (99) R. Clausius. On the application of the theorem of the equivalence of transformations to interior work. In Hirst Clausius:mech_the_heat:65 , pages 215–250. Fourth Memoir.
- (100) Eric Smith. Quantum-classical correspondence principles for locally non-equilibrium driven systems. Phys. Rev. E, 77:021109, 2008. originally as SFI preprint # 06-11-040.
- (101) Eric Smith and Harold J. Morowitz. The origin and nature of life on Earth: the emergence of the fourth geosphere. Cambridge U. Press, London, 2016. ISBN: 9781316348772.
- (102) Sergio Verdú. Fifty years of Shannon theory. IEEE Trans. Information Theory, 44:2057–2078, 1998.
- (103) Harold Abelson, Gerald Jay Sussman, and Julie Sussman. Structure and Interpretation of Computer Programs. MIT Press, Cambridge, MA, second edition, 1996.
- (104) E. T. Jaynes. The minimum entropy production principle. Annu. Rev. Phys. Chem., 31:579–601, 1980.
- (105) E. T. Jaynes. Probability Theory: The Logic of Science. Cambridge U. Press, New York, 2003.
- (106) T. Speck and U. Seifert. Restoring a fluctuation-dissipation theorem in a nonequilibrium steady state. Europhys. Lett., 74:391–396, 2006.
- (107) Russ Harmer, Vincent Danos, Jérôme Feret, Jean Krivine, and Walter Fontana. Intrinsic information carriers in combinatorial dynamical systems. Chaos, 20:037108, 2010.
- (108) Nicolas Behr, Vincent Danos, Ilias Garnier, and Tobias Heindel. The algebras of graph rewriting. 2016. arXiv:1612.06240v1 [math-ph] 19 Dec 2016.
- (109) Eric Smith. The information geometry of 2-field functional integrals. submitted, 2019. http://arxiv.org/abs/1906.09312.
- (110) R. D. Rosenkrantz, editor. Jaynes, E. T.: Papers on Probability, Statistics and Statistical Physics. D. Reidel, Dordrecht, Holland, 1983.