Inter-Region Affinity Distillation for Road Marking Segmentation
Abstract
We study the problem of distilling knowledge from a large deep teacher network to a much smaller student network for the task of road marking segmentation. In this work, we explore a novel knowledge distillation (KD) approach that can transfer ‘knowledge’ on scene structure more effectively from a teacher to a student model. Our method is known as Inter-Region Affinity KD (IntRA-KD). It decomposes a given road scene image into different regions and represents each region as a node in a graph. An inter-region affinity graph is then formed by establishing pairwise relationships between nodes based on their similarity in feature distribution. To learn structural knowledge from the teacher network, the student is required to match the graph generated by the teacher. The proposed method shows promising results on three large-scale road marking segmentation benchmarks, i.e., ApolloScape, CULane and LLAMAS, by taking various lightweight models as students and ResNet-101 as the teacher. IntRA-KD consistently brings higher performance gains on all lightweight models, compared to previous distillation methods. Our code is available at https://github.com/cardwing/Codes-for-IntRA-KD.
1 Introduction
††: Corresponding author.Road marking segmentation serves various purposes in autonomous driving, e.g., providing cues for vehicle navigation or extracting basic road elements and lanes for constructing high-definition maps [7]. Training a deep network for road marking segmentation is known to be challenging due to various reasons [8], including tiny road elements, poor lighting conditions and occlusions caused by vehicles. The training difficulty is further compounded by the nature of segmentation labels available for training, which are usually sparse (e.g., very thin and long lane marking against a large background), hence affecting the capability of a network in learning the spatial structure of a road scene [8, 14].
The aforementioned challenges become especially crippling when one is required to train a small model for road marking segmentation. This requirement is not uncommon considering that small models are usually deployed on vehicles with limited computational resources. Knowledge distillation (KD) [6] offers an appealing way to facilitate the training of a small student model by transferring knowledge from a trained teacher model of larger capacity. Various KD methods have been proposed in the past, e.g., with knowledge transferred through softened class scores [6], feature maps matching [9, 13] or spatial attention maps matching [27].
While existing KD methods are shown effective in many classification tasks, we found that they still fall short in transferring knowledge of scene structure for the task of road marking segmentation. Specifically, a road scene typically exhibits consistent configuration, i.e., road elements are orderly distributed in a scene. The structural relationship is crucial to providing the necessary constraint or regularization, especially for small networks, to combat against the sparsity of supervision. However, such structural relationship is rarely exploited in previous distillation methods. The lack of structural awareness makes small models struggle in differentiating visually similar but functionally different road markings.
In this paper, we wish to enhance the structural awareness of a student model by exploring a more effective way to transfer the scene structure prior encoded in a teacher to a student. Our investigation is based on the premise that a teacher model should have a better capability in learning discriminative features and capturing contextual information due to its larger capacity in comparison to the student model. Feature distribution relationships encoded by the teacher on different parts of a deep feature map could reveal rich structural connections between different scene regions, e.g., the lane region should look different from the zebra crossing. Such priors can offer a strong constraint to regularize the learning of the student network.

Our method is known as Inter-Region Affinity Knowledge Distillation (IntRA-KD). As the name implies, knowledge on scene structure is represented as inter-region affinity graphs, as shown as Fig. 1. Each region is a part of a deep feature map, while each node in the graph denotes the feature distribution statistics of each region. Each pair of nodes are connected by an edge representing their similarity in terms of feature distribution. Given the same input image, the student network and the teacher network will both produce their corresponding affinity graph. Through graph matching, a distillation loss on graph consistency is generated to update the student network.
This novel notion of inter-region affinity knowledge distillation is appealing in its simplicity and generality. The method is applicable to various road marking scenarios with an arbitrary number of road element classes. It can also work together with other knowledge distillation methods. It can even be applied on more general segmentation tasks (e.g., Cityscapes [3]). We present an effective and efficient way of building inter-region affinity graphs, including a method to obtain regions from deep feature maps and a new moment pooling operator to derive feature distribution statistics from these regions. Extensive experiments on three popular datasets (ApolloScape [11], CULane [14] and LLAMAS [1]) show that IntRA-KD consistently outperforms other KD methods, e.g., probability map distillation [6] and attention map distillation [27]. It generalizes well to various student architectures, e.g., ERFNet [20], ENet [16] and ResNet-18 [5]. Notably, with IntRA-KD, ERFNet achieves compelling performance in all benchmarks with 21 fewer parameters (2.49 M v.s. 52.53 M) and runs 16 faster (10.2 ms v.s. 171.2 ms) compared to ResNet-101 model. Encouraging results are also observed on Cityscapes [3]. Due to space limit, we include the results in the supplementary material.
2 Related Work
Road marking segmentation. Road marking segmentation is conventionally handled using hand-crafted features to obtain road marking segments. Then, a classification network is employed to classify the category of each segment [10, 19]. These approaches have many drawbacks, e.g., require sophisticated feature engineering process and only work well in simple highway scenarios.
The emergence of deep learning has avoided manual feature design through learning features in an end-to-end manner. These approaches usually adopt the dense prediction formulation, i.e., assign each pixel a category label [8, 14, 24]. For example, Wang et al. [24] exploit deep neural networks to map an input image to a segmentation map. Since large models usually demand huge memory storage and have slow inference speed, many lightweight models, e.g., ERFNet [20], are leveraged to fulfil the requirement of fast inference and small storage [8]. However, due to the limited model size, these small networks perform poorly in road marking segmentation. A common observation is that such small models do not have enough capacity to capture sufficient contextual knowledge given the sparse supervision signals [8, 14, 29]. Several schemes have been proposed to relieve the sparsity problem. For instance, Hou et al. [8] reinforce the learning of contextual knowledge through self knowledge distillation, i.e., using deep-layer attention maps to guide the learning of shallower layers. SCNN [14] resolves this problem through message passing between deep feature layers. Zhang et al. [29] propose a framework to perform lane area segmentation and lane boundary detection simultaneously. The aforementioned methods do not take structural relationship between different areas into account and they do not consider knowledge distillation from teacher networks.
Knowledge distillation. Knowledge distillation was originally introduced by [6] to transfer knowledge from a teacher model to a compact student model. The distilled knowledge can be in diverse forms, e.g., softened output logits [6], intermediate feature maps [4, 9, 13, 31] or pairwise similarity maps between neighbouring layers [26]. There is another line of work [8, 22] that uses self-derived knowledge to reinforce the representation learning of the network itself, without the supervision of a large teacher model. Recent studies have expanded knowledge distillation from one sample to several samples [12, 15, 17, 23]. For instance, Park et al. [15] transfer mutual relations between a batch of data samples in the distillation process. Tung et al. [23] take the similarity scores of features of different samples as distillation targets. The aforementioned approaches [12, 15, 17, 23] do not consider the structural relationship between different areas in one sample. On the contrary, the proposed IntRA-KD takes inter-region relationship into account, which is new in knowledge distillation.
3 Methodology

Road marking segmentation is commonly formulated as a semantic segmentation task [24]. More specifically, given an input image , the objective is to assign a label to each pixel of X, comprising the segmentation map O. Here, and are the height and width of the input image, is the number of classes and class 0 denotes the background. The objective is to learn a mapping : . Contemporary algorithms use CNN as for end-to-end prediction.
Since autonomous vehicles have limited computational resources and demand real-time performance, lightweight models are adopted to fulfil the aforementioned requirements. On account of limited parameter size as well as insufficient guidance due to sparse supervision signals, these small models usually fail in the challenging road marking segmentation task. Knowledge distillation [6, 8, 13] is a common approach to improving the performance of small models by means of distilling knowledge from large models. There are two networks in knowledge distillation, one is called the student and the other is called the teacher. The purpose of knowledge distillation is to transfer dark knowledge from the large, cumbersome teacher model to the small, compact student model. The dark knowledge can take on many forms, e.g., output logits and intermediate layer activations. There exist previous distillation methods [15, 17, 23] that exploit the relationship between a batch of samples. These approaches, however, do not take into account the structural relationship between different areas within a sample.
3.1 Problem Formulation
Unlike existing KD approaches, IntRA-KD considers intrinsic structural knowledge within each sample as a form of knowledge for distillation. Specifically, we consider each input sample to have road marking classes including the background class. We treat each class map as a region. In practice, the number of classes/regions co-existing in a sample can be fewer than . Given the same input, an inter-region affinity graph for the student network and an inter-region affinity graph for the teacher are constructed. Here, an affinity graph is defined as
| (1) |
where is a set of nodes, each of which represents feature distribution statistics of each region. Each pair of nodes are connected by an edge that denotes the similarity between two nodes in terms of feature distribution.
The overall pipeline of our IntRA-KD is shown in Fig. 2. The framework is composed of three main components:
1) Generation of areas of interest (AOI) – to extract regions representing the spatial extent for each node in the graphs.
2) AOI-grounded moment pooling – to quantify the statistics of feature distribution of each region.
3) Inter-region affinity distillation – to construct the inter-region affinity graph and distill structural knowledge from the teacher to the student.
3.2 Inter-Region Affinity Knowledge Distillation

Generation of AOI. The first step of IntRA-KD is to extract regions from a given image to represent the spatial extent of each class. The output of this step is AOI maps constituting a set , where is the height, is the width, and is the number of classes. Each mask map is binary – ‘1’ represents the spatial extent of a particular class, e.g., left lane, while ‘0’ represents other classes and background.
A straightforward solution is to use the ground-truth labels as AOI. However, ground-truth labels only consider the road markings but neglect the surrounding areas around the road markings. We empirically found that naïve distillation in ground-truth areas is ineffective for the transfer of contextual information from a teacher to a student model.
To include a larger area, we use a transformation operation to generate AOI from the ground-truth labels. Unlike labels that only contain road markings, areas obtained after the operation also take into account the surrounding areas of road markings. An illustration of AOI generation is shown in Fig. 3. Suppose we have binary ground-truth label maps comprising a set . For each class label map , we smooth the label map with an average kernel and obtain an AOI map for the corresponding class as , where is an indicator function and has the same size as . Repeating these steps for all ground-truth label maps provides us AOI maps. Note that AOI maps can also be obtained by image morphological operations.
AOI-grounded moment pooling. Suppose the feature maps of a network are represented as , where , and denote the height, width and channel of the feature map, respectively. Once we obtain the AOI maps , we can use them as masks to extract AOI features from for each class region. The obtained AOI features can then be used to compute the inter-region affinity. For effective affinity computation, we regard AOI features of each region as a distribution. Affinity can then be defined as the similarity between two feature distributions.
Moments have been widely-used in many studies [18, 28]. Inspired by these prior studies, we calculate moment statistics of a distribution and use them for affinity computation. In particular, we extract the first moment , second moment and third moment as the high-level statistics of a distribution. The moments of features have explicit meanings, i.e., the first moment represents the mean of the distribution, the second moment (variance) and the third moment (skewness) describe the shape of that distribution. We empirically found that using higher-order moments brings marginal performance gains while requiring heavier computation cost.
To compute , and of class , we introduce the moment pooling operation to process the AOI features.
| (2) | ||||
where computes the number of non-zero elements in and .

An illustration of the process of moment pooling is depicted in Fig. 4. The moment pooling operation has the following properties. First, it can process areas with arbitrary shapes and sizes, which can be seen as an extension of the conventional average pooling. Second, the moment vectors obtained by the moment pooling operation can faithfully reflect the feature distribution of a particular region, and yet, the vectors are in a very low-dimension, thus facilitating efficient affinity computation in the subsequent step.
Inter-region affinity distillation. Since output feature maps of the teacher model and those of the student model may have different dimensions, performing matching of each pair of moment vectors would require extra parameters or operations to guarantee dimension consistency. Instead, we compute the cosine similarity of the moment vectors of class and class , i.e.,
| (3) |
The similarity score captures the similarity of each pair of classes and it is taken as the high-level knowledge to be learned by the student model. The moment vectors and the similarity scores constitute the nodes and the edges of the affinity graph , respectively (see Fig. 2). The inter-region affinity distillation loss is given as follows:
| (4) |
The introduced affinity distillation is robust to the network differences between the teacher and student models since the distillation is only related to the number of classes and is irrelevant to the specific dimension of feature maps. In addition, the affinity knowledge is comprehensive since it gathers information from AOI features from both the foreground and background areas. Finally, in comparison to previous distillation methods [6] that use probability maps as distillation targets, the affinity graph is more memory-efficient since it reduces the size of the distillation targets from to where is usually thousands of times smaller than .

From Fig. 5, we can see that IntRA-KD not only improves the predictions of ERFNet, but also causes a closer feature structure between the student model and the ResNet-101 teacher model. This is reflected by the very similar structure between the affinity graphs of ERFNet and ResNet-101. It is interesting to see that those spatially close and visually similar road markings are pulled closer and those spatially distant and visually different markings are pulled apart in the feature space using IntRA-KD . An example is shown in Fig. 5, illustrating the effectiveness of IntRA-KD in transferring structural knowledge from the teacher model to the student model. We show in the experiment section that such transfers are essential to improve the performance of student models.
Adding IntRA-KD to training. The final loss is composed of three terms, i.e., the cross entropy loss, the inter-region affinity distillation loss and the attention map distillation loss. The attention map distillation loss is optional in our framework but it is useful to complement the region-level knowledge. The final loss is written as
| (5) |
Here, and are used to balance the effect of different distillation losses on the main task loss . Different from the mimicking of feature maps , which demand huge memory resources and are hard to learn, attention maps are more memory-friendly and easier to mimic since only several important areas are needed to learn. The attention map distillation loss is given as follows:
| (6) |
We follow [27] to derive attention maps from feature maps.
4 Experiments
| Name | # Frame | Train | Validation | Test | Resolution | # Class | Temporally continuous ? |
| ApolloScape [11] | 114, 538 | 103, 653 | 10, 000 | 885 | 3384 2710 | 36 | |
| CULane [14] | 133, 235 | 88, 880 | 9, 675 | 34, 680 | 1640 590 | 5 | |
| LLAMAS [1] | 79, 113 | 58, 269 | 10, 029 | 10, 815 | 1276 717 | 5 |

Datasets. We conduct experiments on three datasets, namely ApolloScape [11], CULane [14] and LLAMAS [1]. Figure 6 shows a selected video frame from each of the three datasets. These three datasets are challenging due to poor light conditions, occlusions and the presence of many tiny road markings. Note that CULane and LLAMAS only label lanes according to their relative positions to the ego vehicle while ApolloScape labels every road marking on the road according to their functions. Hence, ApolloScape has much more classes and it is more challenging compared with the other two datasets. Apart from the public result [11], we also reproduce the most related and state-of-the-art methods (e.g., ResNet-50 and UNet-ResNet-34) on ApolloScape for comparison. As to LLAMAS dataset, since the official submission server is not established, the evaluation on the original testing set is impossible. Hence, we split the original validation set into two parts, i.e., one is used for validation and the other is used for testing. Table 1 summarizes the details and train/val/test partitions of the datasets.
Evaluation metrics. We use different metrics on each dataset following the guidelines of the benchmark and practices of existing studies.
1) ApolloScape. We use the official metric, i.e., mean intersection-over-union (mIoU) as evaluation criterion [11].
2) CULane. Following [14], we use -measure as the evaluation metric, which is defined as: , where and .
3) LLAMAS. We use mean average precision (mAP) to evaluate the performance of different algorithms [1].
Implementation details. Since there is no road marking in the upper areas of the input image, we remove the upper part of the original image during both training and testing phases. The size of the processed image is 3384 1010 for ApolloScape, 1640 350 for CULane, and 1276 384 for LLAMAS. To save memory usage, we further resize the processed image to 1692 505, 976 208 and 960 288, respectively. We use SGD [2] to train our models and the learning rate is set as 0.01. Batch size is set as 12 for CULane and LLAMAS, and 8 for ApolloScape. The total number of training episodes is set as 80K for CULane and LLAMAS, and 180K for ApolloScape since ApolloScape is more challenging. The cross entropy loss of background pixels is multiplied by 0.4 for CULane and LLAMAS, and 0.05 for ApolloScape since class imbalance is more severe in ApolloScape. For the teacher model, i.e., ResNet-101, we add the pyramid pooling module [30] to obtain both local and global context information. and are both set as 0.1 and the size of the averaging kernel for obtaining AOI maps is set as 5 5. Our results are not sensitive to the kernel size.
In our experiments, we use either ERFNet [20], ENet [16] or ResNet-18 [5] as the student and ResNet-101 as the teacher. While we choose ERFNet to report most of our ablation studies in this paper, we also report overall results of ENet [16] and ResNet-18 [5]. Detailed results are provided in the supplementary material. We extract both high-level features and middle-level features from ResNet-101 as distillation targets. Specifically, we let the features of block 2 and block 3 of ERFNet to mimic those of block 3 and block 5 of ResNet-101, respectively.
Baseline distillation algorithms. In addition to the state-of-the-art algorithms in each benchmark, we also compare the proposed IntRA-KD with contemporary knowledge distillation algorithms, i.e., KD [6], SKD [13], PS-N [26], IRG [12] and BiFPN [31]. Here, KD denotes probability map distillation; SKD employs both probability map distillation and pairwise similarity map distillation; PS-N takes the pairwise similarity map of neighbouring layers as knowledge; IRG uses the instance features, instance relationship and inter-layer transformation of three consecutive frames for distillation, and BiFPN uses attention maps of neighbouring layers as distillation targets.
| Type | Algorithm | mIoU |
| Baseline | Wide ResNet-38 [25] | 42.2 |
| ENet [16] | 39.8 | |
| ResNet-50 [5] | 41.3 | |
| UNet-ResNet-34 [21] | 42.4 | |
| Teacher | ResNet-101 [5] | 46.6 |
| Student | ERFNet [20] | 40.4 |
| Self distillation | ERFNet-DKS [22] | 40.8 |
| ERFNet-SAD [8] | 40.9 | |
| Teacher-student distillation | ERFNet-KD [6] | 40.7 |
|---|---|---|
| ERFNet-SKD [13] | 40.9 | |
| ERFNet-PS-N [26] | 40.6 | |
| ERFNet-IRG [12] | 41.0 | |
| ERFNet-BiFPN [31] | 41.6 | |
| ERFNet-IntRA-KD (ours) | 43.2 |
| Type | Algorithm | Runtime (ms) | # Param (M) | |
|---|---|---|---|---|
| B | SCNN [14] | 71.6 | 133.5 | 20.72 |
| ResNet-18-SAD [8] | 70.5 | 25.3 | 12.41 | |
| ResNet-34-SAD [8] | 70.7 | 50.5 | 22.72 | |
| T | ResNet-101 [5] | 72.8 | 171.2 | 52.53 |
| S | ERFNet [20] | 70.2 | 10.2 | 2.49 |
| SD | ERFNet-DKS [22] | 70.6 | ||
| ERFNet-SAD [8] | 71.0 | |||
| TSD | ERFNet-KD [6] | 70.5 | ||
| ERFNet-SKD [13] | 70.7 | |||
| ERFNet-PS-N [26] | 70.6 | |||
| ERFNet-IRG [12] | 70.7 | |||
| ERFNet-BiFPN [31] | 71.4 | |||
| ERFNet-IntRA-KD (ours) | 72.4 |
| Type | Algorithm | mAP |
| Baseline | SCNN [14] | 0.597 |
| ResNet-50 [5] | 0.578 | |
| UNet-ResNet-34 [21] | 0.592 | |
| Teacher | ResNet-101 [5] | 0.607 |
| Student | ERFNet [20] | 0.570 |
| Self distillation | ERFNet-DKS [22] | 0.573 |
| ERFNet-SAD [8] | 0.575 | |
| Teacher-student distillation | ERFNet-KD [6] | 0.572 |
|---|---|---|
| ERFNet-SKD [13] | 0.576 | |
| ERFNet-PS-N [26] | 0.575 | |
| ERFNet-IRG [12] | 0.576 | |
| ERFNet-BiFPN [31] | 0.583 | |
| ERFNet-IntRA-KD (ours) | 0.598 |
4.1 Results
Tables 2- 4 summarize the performance of our method, i.e., ERFNet-IntRA-KD , against state-of-the-art algorithms on the testing set of ApolloScape [11], CULane [14] and LLAMAS [1]. We also report the runtime and parameter size of different models in Table 3. The runtime is recorded using a single GPU (GeForce GTX TITAN X Maxwell) and averages across 100 samples. ERFNet-IntRA-KD outperforms all baselines and previous distillation methods in all three benchmarks. Note that ERFNet-IntRA-KD has 21 fewer parameters and runs 16 faster compared with ResNet-101 on CULane testing set; the appealing performance strongly suggests the effectiveness of IntRA-KD.
We also apply IntRA-KD to ENet and ResNet-18, and find that IntRA-KD can equivalently bring more performance gains to the backbone models than the state-of-the-art BiFPN [31] on ApolloScape dataset (Fig. 7). Note that BiFPN is a competitive algorithm in all benchmarks. Encouraging results are also observed on CULane and LLAMAS when applying IntRA-KD to ENet and ResNet-18. Due to space limit, we report detailed performance of applying different distillation algorithms to ENet and ResNet-18 in the supplementary material. The effectiveness of our IntRA-KD on different backbone models validates the good generalization ability of our method.

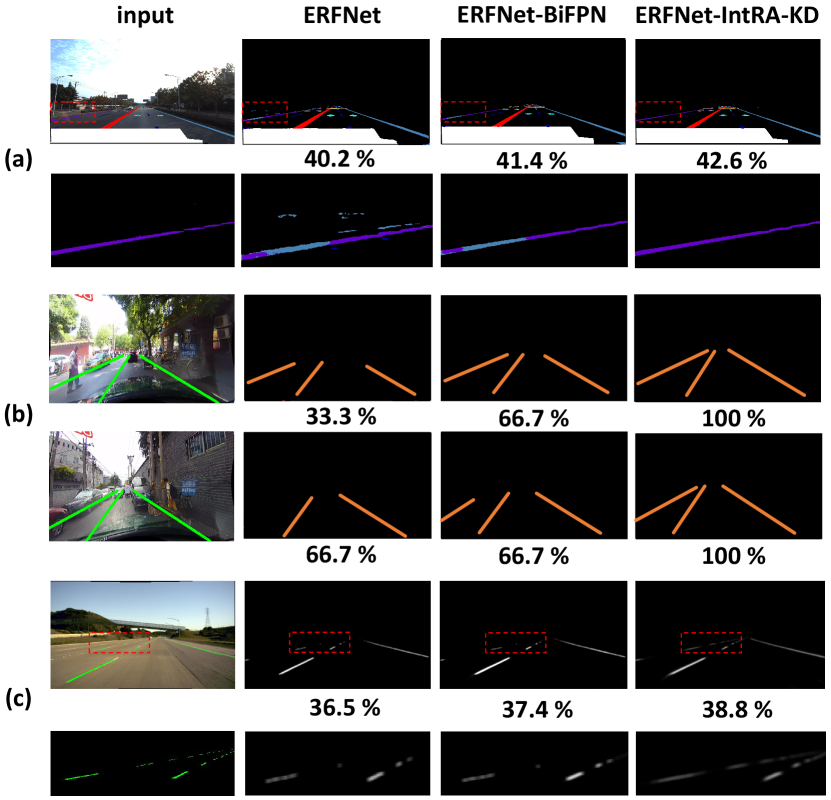

We also show some qualitative results of our IntRA-KD and BiFPN [31] (the most competitive baseline) on three benchmarks. As shown in (a) and (c) of Fig. 8, IntRA-KD helps ERFNet predict more accurately on both long and thin road markings. As to other challenging scenarios of crowded roads and poor light conditions, ERFNet and ERFNet-BiFPN either predict lanes inaccurately or miss the predictions. By contrast, predictions yielded by ERFNet-IntRA-KD are more complete and accurate.
Apart from model predictions, we also show the deep feature embeddings of different methods. As can be seen from Fig. 9, the embedding of ERFNet-IntRA-KD is more structured compared with that of ERFNet and ERFNet-BiFPN. In particular, the features of ERFNet-IntRA-KD are more distinctly clustered according to their classes in the embedding, with similar distribution to the embedding of the ResNet-101 teacher. The results suggest the importance of structural information in knowledge distillation.
4.2 Ablation Study
In this section, we investigate the effect of each component, i.e., different loss terms and the associated coefficients, on the final performance.
Effect of different loss terms. From Fig. 10, we have the following observations: (1) Considering all moments from both middle- and high-level features, i.e., the blue bar with , brings the most performance gains. (2) Attention map distillation, also brings considerable gains compared with the baseline without distillation. (3) Distillation of high-level features brings more performance gains than that of middle-level features. This may be caused by the fact that high-level features contain more semantic-related information, which is beneficial to the segmentation task. (4) Inter-region affinity distillation and attention map distillation are complementary, leading to best performance (i.e., 43.2 mIoU as shown by the red vertical dash line).

Effect of loss coefficients. The coefficients of the attention map loss and affinity distillation loss are all set as 0.1 to normalize the loss values. Here, we test different selections of the loss coefficients, i.e., selecting coefficient value from . ERFNet-IntRA-KD achieves similar performance in all benchmarks, i.e., mIoU in ApolloScape, -measure in CULane and mAP in LLAMAS. Hence, IntRA-KD is robust to the loss coefficients.
5 Conclusion
We have proposed a simple yet effective distillation approach, i.e., IntRA-KD , to effectively transfer scene structural knowledge from a teacher model to a student model. The structural knowledge is represented as an inter-region affinity graph to capture similarity of feature distribution of different scene regions. We applied IntRA-KD to various lightweight models and observed consistent performance gains to these models over other contemporary distillation methods. Promising results on three large-scale road marking segmentation benchmarks strongly suggest the effectiveness of IntRA-KD. Results on Cityscapes are provided in the supplementary material.
Acknowledgement: This work is supported by the SenseTime-NTU Collaboration Project, Collaborative Research grant from SenseTime Group (CUHK Agreement No. TS1610626 No. TS1712093), Singapore MOE AcRF Tier 1 (2018-T1-002-056), NTU SUG, and NTU NAP.
References
- [1] Karsten Behrendt and Ryan Soussan. Unsupervised labeled lane markers using maps. In IEEE International Conference on Computer Vision Workshops, 2019.
- [2] Léon Bottou. Large-scale machine learning with stochastic gradient descent. In International Conference on Computational Statistics, pages 177–186. Springer, 2010.
- [3] Marius Cordts, Mohamed Omran, Sebastian Ramos, Timo Rehfeld, Markus Enzweiler, Rodrigo Benenson, Uwe Franke, Stefan Roth, and Bernt Schiele. The Cityscapes dataset for semantic urban scene understanding. In IEEE Conference on Computer Vision and Pattern Recognition, pages 3213–3223, 2016.
- [4] Mengya Gao, Yujun Shen, Quanquan Li, Junjie Yan, Liang Wan, Dahua Lin, Chen Change Loy, and Xiaoou Tang. An embarrassingly simple approach for knowledge distillation. arXiv preprint arXiv:1812.01819, 2018.
- [5] Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Deep residual learning for image recognition. In IEEE Conference on Computer Vision and Pattern Recognition, pages 770–778, 2016.
- [6] Geoffrey Hinton, Oriol Vinyals, and Jeff Dean. Distilling the knowledge in a neural network. Statistics, 1050:9, 2015.
- [7] Namdar Homayounfar, Wei-Chiu Ma, Justin Liang, Xinyu Wu, Jack Fan, and Raquel Urtasun. Dagmapper: Learning to map by discovering lane topology. In IEEE International Conference on Computer Vision, pages 2911–2920, 2019.
- [8] Yuenan Hou, Zheng Ma, Chunxiao Liu, and Chen Change Loy. Learning lightweight lane detection CNNs by self attention distillation. In IEEE International Conference on Computer Vision, pages 1013–1021, 2019.
- [9] Yuenan Hou, Zheng Ma, Chunxiao Liu, and Chen Change Loy. Learning to steer by mimicking features from heterogeneous auxiliary networks. In Association for the Advancement of Artificial Intelligence, volume 33, pages 8433–8440, 2019.
- [10] Junjie Huang, Huawei Liang, Zhiling Wang, Yan Song, and Yao Deng. Lane marking detection based on adaptive threshold segmentation and road classification. In IEEE International Conference on Robotics and Biomimetics, pages 291–296. IEEE, 2014.
- [11] Xinyu Huang, Xinjing Cheng, Qichuan Geng, Binbin Cao, Dingfu Zhou, Peng Wang, Yuanqing Lin, and Ruigang Yang. The Apolloscape dataset for autonomous driving. In IEEE Conference on Computer Vision and Pattern Recognition Workshops, pages 954–960, 2018.
- [12] Yufan Liu, Jiajiong Cao, Bing Li, Chunfeng Yuan, Weiming Hu, Yangxi Li, and Yunqiang Duan. Knowledge distillation via instance relationship graph. In IEEE Conference on Computer Vision and Pattern Recognition, pages 7096–7104, 2019.
- [13] Yifan Liu, Ke Chen, Chris Liu, Zengchang Qin, Zhenbo Luo, and Jingdong Wang. Structured knowledge distillation for semantic segmentation. In IEEE Conference on Computer Vision and Pattern Recognition, pages 2604–2613, 2019.
- [14] Xingang Pan, Jianping Shi, Ping Luo, Xiaogang Wang, and Xiaoou Tang. Spatial as deep: Spatial CNN for traffic scene understanding. In Association for the Advancement of Artificial Intelligence, 2018.
- [15] Wonpyo Park, Dongju Kim, Yan Lu, and Minsu Cho. Relational knowledge distillation. In IEEE Conference on Computer Vision and Pattern Recognition, pages 3967–3976, 2019.
- [16] Adam Paszke, Abhishek Chaurasia, Sangpil Kim, and Eugenio Culurciello. ENet: A deep neural network architecture for real-time semantic segmentation. arXiv preprint arXiv:1606.02147, 2016.
- [17] Baoyun Peng, Xiao Jin, Jiaheng Liu, Dongsheng Li, Yichao Wu, Yu Liu, Shunfeng Zhou, and Zhaoning Zhang. Correlation congruence for knowledge distillation. In IEEE International Conference on Computer Vision, pages 5007–5016, 2019.
- [18] Xingchao Peng, Qinxun Bai, Xide Xia, Zijun Huang, Kate Saenko, and Bo Wang. Moment matching for multi-source domain adaptation. In IEEE International Conference on Computer Vision, pages 1406–1415, 2019.
- [19] Baoxing Qin, Wei Liu, Xiaotong Shen, Zhuang Jie Chong, Tirthankar Bandyopadhyay, MH Ang, Emilio Frazzoli, and Daniela Rus. A general framework for road marking detection and analysis. In International IEEE Conference on Intelligent Transportation Systems, pages 619–625. IEEE, 2013.
- [20] Eduardo Romera, José M Alvarez, Luis M Bergasa, and Roberto Arroyo. ERFNet: Efficient residual factorized convnet for real-time semantic segmentation. IEEE Transactions on Intelligent Transportation Systems, 19(1):263–272, 2017.
- [21] Olaf Ronneberger, Philipp Fischer, and Thomas Brox. U-net: Convolutional networks for biomedical image segmentation. In International Conference on Medical image computing and computer-assisted intervention, pages 234–241. Springer, 2015.
- [22] Dawei Sun, Anbang Yao, Aojun Zhou, and Hao Zhao. Deeply-supervised knowledge synergy. In IEEE Conference on Computer Vision and Pattern Recognition, pages 6997–7006, 2019.
- [23] Frederick Tung and Greg Mori. Similarity-preserving knowledge distillation. In IEEE International Conference on Computer Vision, pages 1365–1374, 2019.
- [24] Peng Wang, Xinyu Huang, Xinjing Cheng, Dingfu Zhou, Qichuan Geng, and Ruigang Yang. The Apolloscape open dataset for autonomous driving and its application. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2019.
- [25] Zifeng Wu, Chunhua Shen, and Anton Van Den Hengel. Wider or deeper: Revisiting the ResNet model for visual recognition. Pattern Recognition, 90:119–133, 2019.
- [26] Junho Yim, Donggyu Joo, Jihoon Bae, and Junmo Kim. A gift from knowledge distillation: Fast optimization, network minimization and transfer learning. In IEEE Conference on Computer Vision and Pattern Recognition, pages 4133–4141, 2017.
- [27] Sergey Zagoruyko and Nikos Komodakis. Paying more attention to attention: improving the performance of convolutional neural networks via attention transfer. In International Conference on Learning Representations, 2017.
- [28] Werner Zellinger, Thomas Grubinger, Edwin Lughofer, Thomas Natschläger, and Susanne Saminger-Platz. Central moment discrepancy for domain-invariant representation learning. arXiv preprint arXiv:1702.08811, 2017.
- [29] Jie Zhang, Yi Xu, Bingbing Ni, and Zhenyu Duan. Geometric constrained joint lane segmentation and lane boundary detection. In European Conference on Computer Vision, pages 486–502, 2018.
- [30] Hengshuang Zhao, Jianping Shi, Xiaojuan Qi, Xiaogang Wang, and Jiaya Jia. Pyramid scene parsing network. In IEEE Conference on Computer Vision and Pattern Recognition, pages 2881–2890, 2017.
- [31] Lei Zhu, Zijun Deng, Xiaowei Hu, Chi-Wing Fu, Xuemiao Xu, Jing Qin, and Pheng-Ann Heng. Bidirectional feature pyramid network with recurrent attention residual modules for shadow detection. In European Conference on Computer Vision, pages 121–136, 2018.