Intelligent Electric Vehicle Charging Recommendation
Based on Multi-Agent Reinforcement Learning
Abstract.
Electric Vehicle (EV) has become a preferable choice in the modern transportation system due to its environmental and energy sustainability. However, in many large cities, EV drivers often fail to find the proper spots for charging, because of the limited charging infrastructures and the spatiotemporally unbalanced charging demands. Indeed, the recent emergence of deep reinforcement learning provides great potential to improve the charging experience from various aspects over a long-term horizon. In this paper, we propose a framework, named Multi-Agent Spatio-Temporal Reinforcement Learning (Master), for intelligently recommending public accessible charging stations by jointly considering various long-term spatiotemporal factors. Specifically, by regarding each charging station as an individual agent, we formulate this problem as a multi-objective multi-agent reinforcement learning task. We first develop a multi-agent actor-critic framework with the centralized attentive critic to coordinate the recommendation between geo-distributed agents. Moreover, to quantify the influence of future potential charging competition, we introduce a delayed access strategy to exploit the knowledge of future charging competition during training. After that, to effectively optimize multiple learning objectives, we extend the centralized attentive critic to multi-critics and develop a dynamic gradient re-weighting strategy to adaptively guide the optimization direction. Finally, extensive experiments on two real-world datasets demonstrate that Master achieves the best comprehensive performance compared with nine baseline approaches.
† The research was done when the first author was an intern in Baidu Research under the supervision of the second author.
1. Introduction
Due to the low-carbon emission and energy efficiency, Electric vehicles (EVs) are emerging as a favorable choice in the modern transportation system to meet the increasing environmental concerns (Han et al., 2021) and energy insufficiency (Savari et al., 2020). In 2018, there are over 2.61 million EVs on the road in China, and this number will reach 80 million in 2030 (Zheng et al., 2020). Although the government is expanding the publicly accessible charging network to fulfill the explosively growing on-demand charging requirement, it is still difficult for EV drivers to charge their vehicles due to the fully-occupied stations and long waiting time (Wang et al., 2020c; Tian et al., 2016; Li et al., 2015; Du et al., 2018). Undoubtedly, such an unsatisfactory charging experience raises undesirable charging cost and inefficiency, and may even increase the EV driver’s ”range anxiety”, which prevents the further prevalence of EVs. Therefore, it is appealing to provide intelligent charging recommendations to improve the EV drivers’ charging experience from various aspects, such as minimize the charging wait time (CWT), reduce the charging price (CP), as well as optimize the charging failure rate (CFR) to improve the efficiency of the global charging network.
The charging recommendation problem distinguishes itself from traditional recommendation tasks (Guo et al., 2020; Xin et al., 2021) from two perspectives. First, the number of charging spots in a target geographical area may be limited, which may induce potential resource competition between EVs. Second, depending on the battery capacity and charging power, the battery recharging process may block the charging spot for several hours. As a result, the current recommendation may influence future EV charging recommendations and produce a long-term effect on the global charging network. Previously, some efforts (Wang et al., 2020c; Guo et al., 2017; Tian et al., 2016; Wang et al., 2019; Cao et al., 2019; Yang et al., 2014) have been made for charging recommendations via greedy-based strategies by suggesting the most proper station for the current EV driver in each step concerning a single objective (e.g., minimizing the overall CWT). However, such an approach overlooks the long-term contradiction between the space-constrained charging capacity and the spatiotemporally unbalanced charging demands, which leads to sub-optimal recommendations from a global perspective (e.g., longer overall CWT and higher CFR).
Recently, Reinforcement Learning (RL) has shown great advantages in optimizing sequential decision problems in the dynamic environment, such as order dispatching for ride-hailing and shared-bike rebalancing (Li et al., 2019a, 2018). By interacting with the environment, the agent in RL learns the policy to achieve the global optimal long-term reward (Fan et al., 2020). Therefore, it is intuitive for us to improve charging recommendations based on RL, with long-term goals such as minimizing the overall CWT, the average CP, and the CFR. However, there exist several technical challenges in achieving this goal.
The first challenge comes from the large state and action space. There are millions of EVs and thousands of publicly accessible charging stations in a metropolis such as Beijing. Directly learning a centralized agent system across the city requires handling large state and action space and high-dimensional environment, which will induce severe scalability and efficiency issues (Papoudakis et al., 2019; Chu et al., 2019). Moreover, the ”single point of failure” (Lynch, 2009) in the centralized approach may fail the whole system (Li et al., 2019a). As an alternative, an existing approach Wang et al. (2020a) tried to model a small set of vehicles as multiple agents and maximize the cumulative reward in terms of the number of served orders. However, in our charging recommendation task, most charging requests are ad-hoc and from non-repetitive drivers, which renders it impossible to learn a dedicated policy for each individual EV. To address the first challenge, we regard each charging station as an individual agent and formulate EV charging recommendation as a multi-agent reinforcement learning (MARL) task, and we propose a multi-agent actor-critic framework. In this way, each individual agent has a quantity-independent state action space, which can be scaled to more complicated environments and is more robust to other agents’ potential failure.
The second challenge is the coordination and cooperation in the large-scale agent system. For a charging request, only one station will finally serve for charging. Different agents should be coordinated to achieve better recommendations. Moreover, the cooperation between agents is the key for long-term recommendation optimization. For example, consider a heavily occupied charging station with a large number of incoming charging requests. Other stations with sufficient available charging spots can help balance the charging demands via cross-agent cooperation. To tackle this challenge, we analogy the process of agents taking actions to a bidding game (Zhao et al., 2018), and propose a tailor designed centralized attentive critic module to stimulate multiple agents to learn globally coordinated and cooperative policies.
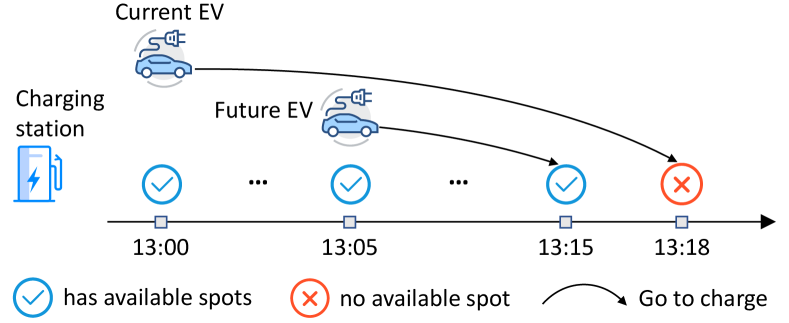
The third challenge is the potential competition of future charging requests. As illustrated in Figure 1, the competition comes from the temporally distributed charging requests for the limited charging resource. In the real world, the potential competition of future charging requests may happen in arbitrary charging stations, leading to problems such as extra CWT and charging failure. However, it is hard to quantify the influence of such future charging requests in advance. To this end, we integrate the future charging competition information into centralized attentive critic module through a delayed access strategy and transform our framework to a centralized training with decentralized execution architecture to enable online recommendation. In this way, the agents can fully harness future knowledge in training phase and take actions immediately without requiring future information during execution.
Finally, it is challenging to jointly optimize multiple optimization objectives. As aforementioned, it is desirable to simultaneously consider various long-term goals, such as the overall CWT, average CP, and the CFR. However, these objectives may in different scales and lie on different manifold structures. Seamlessly optimizing multiple objectives may lead to poor convergence and induce sub-optimal recommendations for certain objectives. Therefore, we extend the centralized attentive critic module to multi-critics for multiple objectives and develop a dynamic gradient re-weighting strategy to adaptively guide the optimization direction by forcing the agents to pay more attention to these poorly optimized objectives.
Along these lines, in this paper, we propose the Multi-Agent Spatio-Temporal Reinforcement Learning (Master) framework for intelligent charging recommendation. Our major contributions are summarized as follows: (1) We formulate the EV charging recommendation problem as a MARL task. To the best of our knowledge, this is the first attempt to apply MARL for multi-objective intelligent charging station recommendations. (2) We develop the multi-agent actor-critic framework with centralized training decentralized execution. In particular, the centralized attentive critic achieves coordination and cooperation between multiple agents globally and exploits future charging competition information through a delayed access strategy during model training. Simultaneously, the decentralized execution of multiple agents avoids the large state action space problem and enables immediate online recommendations without requiring future competition information. (3) We extend the centralized attentive critic to multi-critics to support multiple optimization objectives. By adaptively guiding the optimization direction via a dynamic gradient re-weighting strategy, we improve the learned policy from potential local optima induced by dominating objectives. (4) We conduct extensive experiments on two real-world datasets collected from Beijing and Shanghai. The results demonstrate our model achieves the best comprehensive performance against nine baselines.
2. Problem definition
In this section, we introduce some important definitions and formalize the EV charging recommendation problem.
Consider a set of charging stations , by regarding each day as an episode, we first define the charging request as below.
Definition 1.
Charging request. A charging request is defined as the -th request (i.e., step ) of a day. Specifically, is the location of , is the real-world time of the step , and is the real-world time finishes the charging request.
We say a charging request is finished if it successfully takes the charging action or finally gives up (i.e., charging failure). We further denote as the cardinality of . In the following, we interchangeably use to denote the corresponding EV of .
Definition 2.
Charging wait time (CWT). The charging wait time is defined as the summation of travel time from the location of charging request to the target charging station and the queuing time at until is finished.
Definition 3.
Charging price (CP). The charging price is defined as the unit price per kilowatt hour (kWh). In general, the charging price is a combination of electricity cost and service fee.
Definition 4.
Charging failure rate (CFR). The charging failure rate is defined as the ratio of the number of charging requests who accept our recommendation but fail to charge over the total number of charging requests who accept our recommendation.
Problem 1.
EV Charging Recommendation. Consider a set of charging requests in a day, our problem is to recommend each to the most proper charging station , with the long-term goals of simultaneously minimizing the overall CWT, average CP, and the CFR for the who accept our recommendation.
3. Methodology
In this section, we present the MARL formulation for the EV charging recommendation task and detail our Master framework with centralized training decentralized execution (CTDE). Moreover, we elaborate on the generalized multi-critic architecture for multiple objectives optimization.
3.1. MARL Formulation
We first present our MARL formulation for the EV Charging Recommendation task.
-
•
Agent . In this paper, we regard each charging station as an individual agent. Each agent will make timely recommendation decisions for a sequence of charging requests that keep coming throughout a day with multiple long-term optimization goals.
-
•
Observation . Given a charging request , we define the observation of agent as a combination of the index of , the real-world time , the number of current available charging spots of (supply), the number of charging requests around in the near future (future demand), the charging power of , the estimated time of arrival (ETA) from location to , and the CP of at the next ETA. We further define as the state of all agents at step .
-
•
Action . Given an observation , an intuitional design for the action of agent is a binary decision, i.e., recommending to itself for charging or not. However, because one can only choose one station for charging, multiple agents’ actions may be tied together and are difficult to coordinate. Inspired by the bidding mechanism (Zhao et al., 2018), we design each agent offers a scalar value to ”bid” for as its action . By defining as the joint action, will be recommended to the agent with the highest ”bid” value, i.e., , where .
-
•
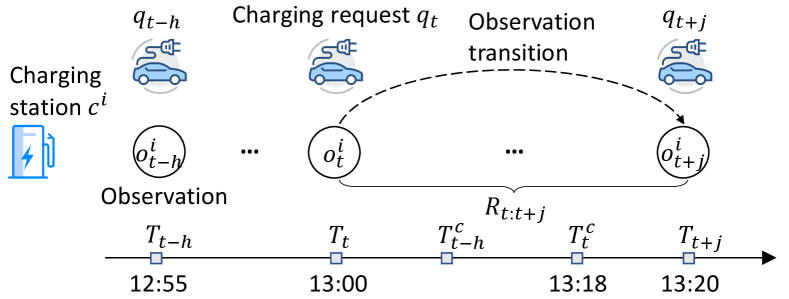
Transition. For each agent , its observation transition is defined as the transition from the current charging request to the next charging request after is finished. Let’s elaborate on this via an illustrative example as shown in Figure 2. Consider a charging request arises at (13:00). At this moment, each agent takes action based on its observation and jointly decide the recommended station . After the request finish time (13:18), the subsequent charging request will arise at (13:20). In this case, the observation transition of agent is defined as , where is the current observation, is the observation corresponding to .
-
•
Reward. In our MARL formulation, we propose a lazy reward settlement scheme (i.e., return rewards when a charging request is finished), and integrate three goals into two natural reward functions. Specifically, if a charging request succeeds in charging, then the environment will return the negative of CWT and negative of CP as the part of reward and reward respectively. For the case that the CWT of exceeds a threshold, the recommendation will be regarded as failure and environment will return much smaller rewards as penalty to stimulate agents reducing the CFR. Overall, we define two immediate rewards function for three goals as
(1) (2) where and are penalty rewards. All agents in our model share the unified rewards, means agents make the recommendation decisions cooperatively. Since the observation transition from to may cross multiple lazy rewards (e.g., and as illustrated in Figure 2), we calculate the cumulative discounted reward by summing the rewards of all recommended charging requests (e.g., and ) whose is between and , denoted by
(3) where is the discount factor, and can be one of the two reward functions or the average of them depending on the learning objectives.
3.2. Centralized Training Decentralized Execution
Centralized training decentralized execution is a class of methods in MARL to stimulate agents to learn coordinated policies and address the non-stationary environment problem (Lowe et al., 2017; Foerster et al., 2018; Iqbal and Sha, 2019). In Master, the CTDE consists of three modules, the centralized attentive critic, the delayed access information strategy to integrate future charging competition, and the decentralized execution process. The advantages of CTDE for EV charging recommendation are two folds. On one hand, the centralized training process can motivate multiple agents to learn cooperation and other specific policies by perceiving a more comprehensive landscape and exploiting future information in hindsight. On the other hand, the execution process is fully decentralized without requiring complete information in the training phase, which guarantees efficiency and flexibility in online recommendation.
3.2.1. Centralized Attentive Critic
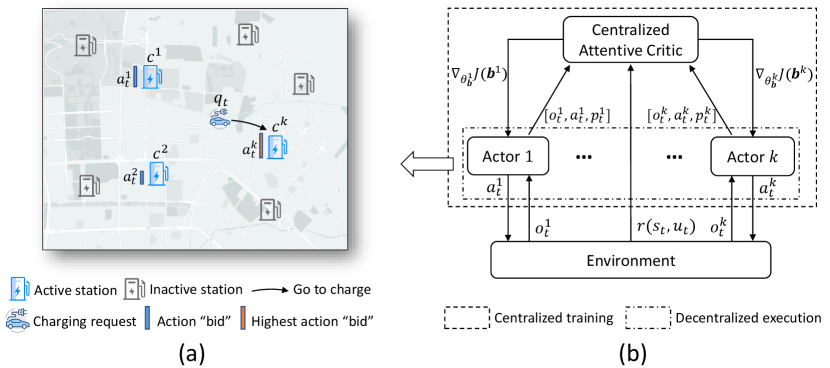
To motivate the agents to make recommendations cooperatively, we devise the multi-agent actor-critic framework with a centralized attentive critic for deterministic policies learning. A similar MARL algorithm with CTDE architecture is proposed in (Lowe et al., 2017), which incorporates the full state and joint action of all agents into the critic to motivate agents to learn coordinated and cooperative policies. However, such an approach suffers from the large state and action space problem in our task.
In practice, the EVs tend to go to nearby stations for charging. Based on this fact, given a charging request , we only activate the agents nearby (e.g., top- nearest ) to take actions, denoted as . We set other agents who are far away from inactive and don’t participate in the recommendation for , as illustrated in Figure 3(a). In this way, only a small number of active agents are involved to learn cooperation for better recommendations. However, one intermediate problem is that the active agents of different are usually different. To this end, we propose to use the attention mechanism which is permutation-invariant to integrate information of the active agents. Specifically, the attention mechanism automatically quantifies the influence of each active agents by
| (4) |
| (5) |
where and are learnable parameters, is the concatenation operation, and are future information that will be detailed in Section 3.2.2. Once the influence weight of each active agent is obtained, we can derive the attentive representation of all active agents by
| (6) |
where are learnable parameters.
Given the state , joint action , and future information of active agents, the actor policy of each agent can be updated by the gradient of the expected return following the chain rule, which can be written by
| (7) |
where are learnable parameters of actor policy of agent , is the experience replay buffer containing the transition tuples . Then, each agent updates its policy by the gradients propagated back from the centralized attentive critic. The entire process is shown in Figure 3(b). As the centralized attentive critic perceived more complete information of all active agents, it can motivate the agents to learn policies in a coordinated and cooperative way. The centralized attentive critic is updated by minimizing the following loss:
| (8) |
| (9) |
where are the learnable parameters of critic , and are the target actor policy of and target critic function with delayed parameters and .
3.2.2. Integrate Future Charging Competition
The public accessible charging stations are usually first-come-first-served, which induces future potential charging competition between the continuously arriving EVs. Recommending charging requests without considering future potential competition will lead to extra CWT or even charging failure. However, it is a non-trivial task to incorporate the future competition since we can not know the precise amount of forthcoming EVs and available charging spots at a future step in advance.
In this work, we further extend the centralized attentive critic with a delayed access strategy to harness the future charging competition information, so as to enable the agents learning policies with future knowledge in hindsight. Specifically, consider a charging request , without changing the execution process, we postpone the access of transition tuples until the future charging competition information in transition with respect to is fully available. Concretely, we extract the accurate number of available charging spots of at every next minutes after to reflect the future potential charging competition for , denoted as . Note that we erase the influence of for , and the number of available charging spots can be negative, means the number of EVs queuing at the station. Overall, we obtain the future charging competition information of each for via a fully-connected layer
| (10) |
where are the learnable parameters. The is integrated into the centralized attentive critic (Eq. (4)Eq. (6)) as the enhanced information to facilitate the agents’ cooperative policy learning.
3.2.3. Decentralized Execution
The execution process is fully decentralized, by only invoking the learned actor policy with its own observation. Specifically, for a charging request , the agent takes action based on its by
| (11) |
And will be recommended to the active agent with the highest among all the actions of . The execution of each agent is lightweight and does not require future charging competition information. More importantly, the large-scale agent system is fault-tolerant even part of the agents are failing.
3.3. Multiple Objectives Optimization
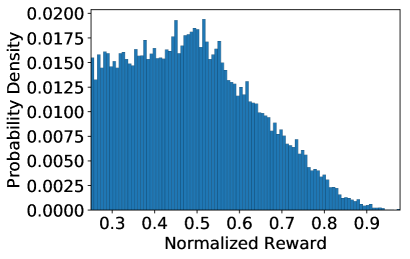
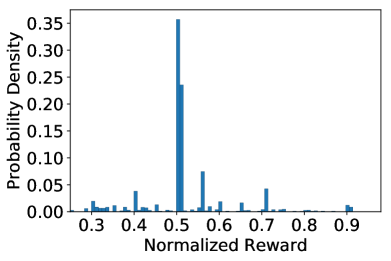
The goal of Electric Vehicle Charging Recommendation task is to simultaneously minimize the overall CWT, average CP and the CFR. We integrate these goals into two objectives corresponding to two reward functions, i.e., and as defined in Eq. (1) and Eq. (2). Figure 4 depicts the normalized reward distributions of and by a random policy executing on a set of charging requests that charging success. As can be seen, the distribution of different objectives can be very different. More importantly, the optimal solution of different objectives may be divergent, e.g., a cheaper charging station may be very popular and need a longer CWT. The above facts imply one policy that performs well on one objective may get stuck on another objective. A recommender that is biased to a particular objective is risky to induce unsatisfactory experience to most users.
A simple way to optimize multiple objectives is to average the reward of multiple objectives with a set of prior weights and maximize the combined reward as a single objective. However, such a static approach is inefficient for convergence and may induce a biased solution to a particular objective. To this end, we develop a dynamic gradient re-weighting strategy to self-adjust the optimization direction to adapt different training stages and enforce the policy to perform well on multiple objectives. Specifically, we extend the centralized attentive critic to multi-critics, where each critic is corresponding to a particular objective. Particularly, in our task, we learn two centralized attentive critics, and , which correspond to the expected returns of reward and , respectively. Since the structure of two critics are identical, we only present for explanation, which is formulated as
| (12) | ||||
where denotes the environment, and is the cumulative discounted reward (defined in Eq. (3)) with respect to .
To quantify the convergence degree of different objectives, we further define two centralized attentive critics associated with two objective-specific optimal policies with respect to reward and , denoted as and . The corresponding optimal policies of each are denoted as and , respectively. Above objective-specific optimal policies and critics can be obtained by pre-training Master on a single reward. Then, we quantify the gap ratio between multi-objective policy and objective-specific optimal policy by
| (13) |
The gap ratio can be derived in the same way. Intuitively, a larger gap ratio indicates a poorly-optimized objective and should be reinforced with a larger update weight, while a small gap ratio indicates a well-optimized objective can be fine-tuned with a smaller step size. Thus, we derive dynamic update weights to adaptively adjust the step size of the two objectives, which is learned by the Boltzmann softmax function,
| (14) |
where is the temperature controls the adjustment sensitivity.
With the above two critics and adaptive update weights, the goal of each agent is to learn an actor policy to maximize the following return,
| (15) |
The complete learning procedure of Master is detailed in Algorithm 1. Note that for the consideration of scalability, we share the parameters of actor and critic networks by all agents.
4. Experiments
4.1. Experimental setup
4.1.1. Data description.
| Description | Beijing | Shanghai |
|---|---|---|
| # of charging stations | 596 | 367 |
| # of supplies records | 38,620,800 | 23,781,600 |
| # of charging requests | 152,889 | 87,142 |
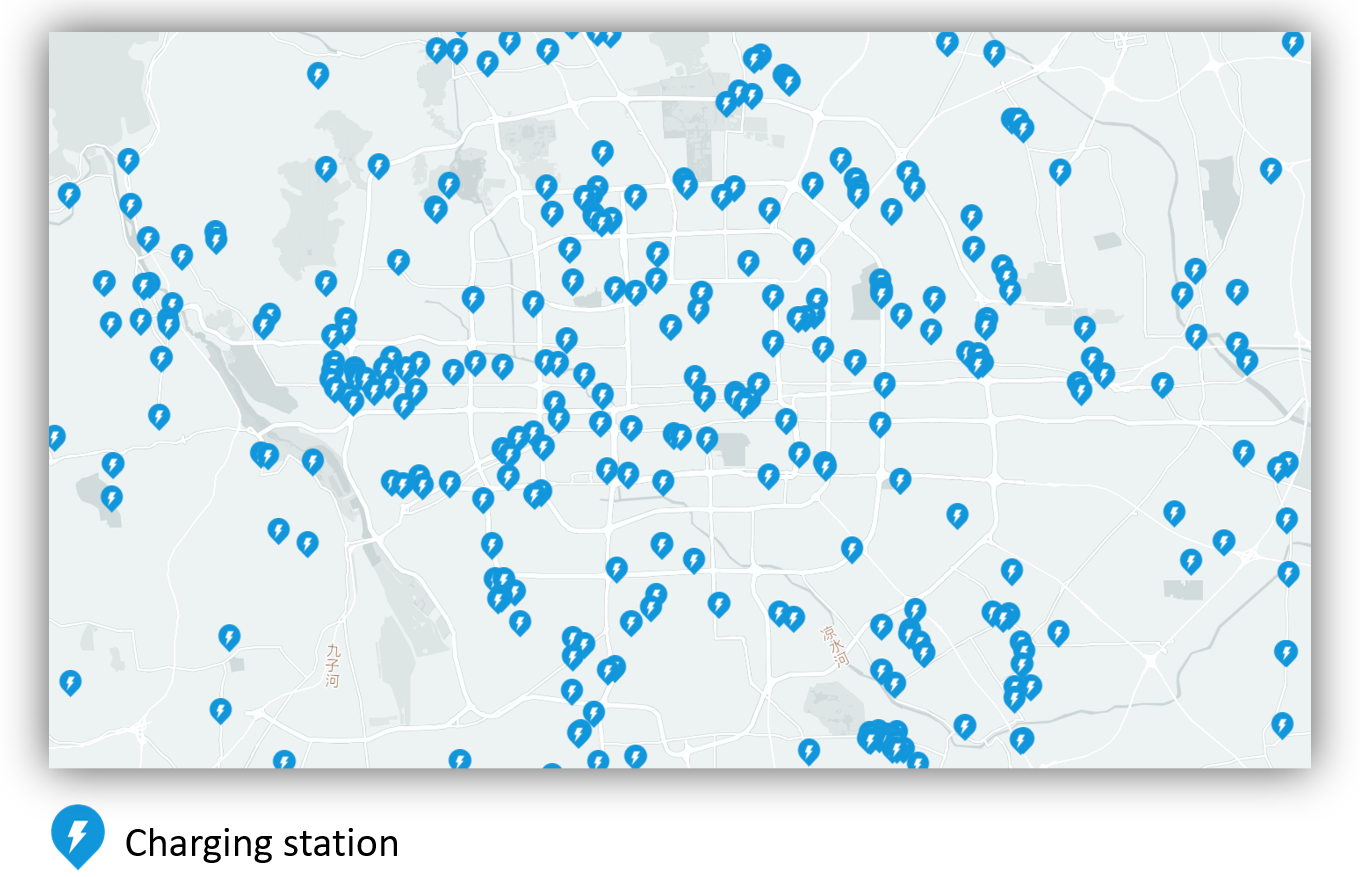
We evaluate Master on two real-world datasets, Beijing and Shanghai, which represent two metropolises in China. Both datasets are ranged from May 18, 2019, to July 01, 2019. All real-time availability (supplies) records, charging prices and charging powers of charging stations are crawled from a publicly accessible app (Zhang et al., 2020), in which all charging spot occupancy information is collected by real-time sensors. The charging request data is collected through Baidu Maps API (Liu et al., 2019; Yuan et al., 2020). We split each city as grids, and aggregate the number of future minutes charging requests in the surrounding area (i.e., the grid the station locates in and eight neighboring grids) as the future demands of the corresponding charging stations. We take the first consecutive days data as the training set, the following three days data as validation set, and the rest days data for testing. All real-world data are loaded into an EV Charging Recommendation simulator (refer to Appendix A and source code for details) for simulation. The spatial distribution of charging stations on Beijing is shown in Figure 5. The statistics of two datasets are summarized in Table 1. More statistical analysis results of the dataset can be found in Appendix B.
4.1.2. Implementation details.
All experiments are performed on a Linux server with 26-core Intel(R) Xeon(R) Gold 5117 CPU @ 2:00 GHz and NVIDIA Tesla P40 GPU. We set minutes for charging competition modeling, set temperature for updated weights adjustment, and select discount factor for learning all RL algorithms. The actor networks and critic networks both consist of three linear network layers with dimension and ReLU activation function for hidden layers. The replay buffer size is , batch size is , and we set for target networks soft update. We employ Adam optimizer for all learnable algorithms and set learning rate as to train our model. We carefully tuned major hyper-parameters of each baseline via a grid search strategy. All RL algorithms are trained to recommend the top- nearest charging stations for iterations and chosen the best iteration by validation set for testing. Detailed settings of the simulator can be found in Appendix A.
4.1.3. Evaluation metrics.
We define four metrics to evaluate the performance of our approach and baseline recommendation algorithms. Define as the set of charging requests who accept our recommendations. We further define as the set of charging requests who accept our recommendations and finally succeed in charging. and are the cardinalities of and , respectively.
To evaluate the overall charging wait time of our recommendations, we define Mean Charging Wait Time (MCWT) over all charging requests :
where is the charging wait time (in minute) of charging request .
To evaluate the average charging price, we define Mean Charging Price (MCP) over all charging requests :
where is the charging price (in CNY) of .
We further define the Total Saving Fee (TSF) to evaluate the average total saving fees per day by comparing our recommendation algorithm with the ground truth charging actions:
where is the charging price of ground truth charging action and is the electric charging quantity of , and is the number of evaluation days. Note the TSF can be a negative number which indicates how many fees overspend comparing with the ground truth charging actions.
We finally define the Charging Failure Rate (CFR) to evaluate the ratio of charging failures in our recommendations:
4.1.4. Baselines.
We compare our approach with the following nine baselines and one basic variant of Master:
-
•
Real is the ground truth charging actions of charging requests.
-
•
Random randomly recommends charging stations for charging.
-
•
Greedy-N recommends the nearest charging station.
-
•
Greedy-P-5 recommends the least expensive charging station among the top- nearest stations.
-
•
Greedy-P-10 recommends the least expensive charging station among the top- nearest stations.
-
•
CDQN (Mnih et al., 2015) is a centralized deep q-network approach, all charging stations are controlled by a centralized agent. CDQN makes recommendation based on the state of all charging stations. The action-value function is a layers MLP with dimension and ReLU activation for hidden layers. The replay buffer size is and batch size is . The learning rate is set to and we use the decayed -greedy strategy for exploration.
-
•
CPPO (Schulman et al., 2017) is a centralized policy gradient approach, the recommendation mode is the same as CDQN. The policy network and value function network both consist of layers MLP with dimension and ReLU activation for hidden layers. The learning rate for policy and value networks are both set to , the for clipping probability ratio is .
-
•
IDDPG (Lillicrap et al., 2015) is a straight-forward approach to achieve MARL using DDPG, where all agents are completely independent. The critic network approximates the expected return only bases on agent-specific observation and action. Other hyper-parameter settings are the same as Master.
-
•
MADDPG (Lowe et al., 2017) is a state-of-the-art algorithm for cooperative MARL. The actor takes action based on agent-specific observation, but the critic can access full state and joint action in training. The critic consists of layers MLP with dimension and ReLU activation for hidden layers. Other hyper-parameter settings are the same as Master. For scaling MADDPG to the large-scale agent system, we share actor and critic networks among all agents.
-
•
MASTER-ATT is a basic variant of Master without charging competition information and multi-critic architecture.
| Algorithm | Beijing | |||
| MCWT | MCP | TSF | CFR | |
| Real | 21.51 | 1.749 | - | 25.9% |
| Random | 38.77 | 1.756 | -447 | 52.9% |
| Greedy-N | 20.27 | 1.791 | -2527 | 31.3% |
| Greedy-P-5 | 23.40 | 1.541 | 9701 | 35.4% |
| Greedy-P-10 | 26.03 | 1.424 | 14059 | 39.9% |
| CDQN | 19.24 | 1.598 | 9683 | 7.4% |
| CPPO | 17.67 | 1.639 | 6707 | 5.3% |
| IDDPG | 13.26 | 1.583 | 11349 | 2.2% |
| MADDPG | 14.01 | 1.570 | 12033 | 4.7% |
| Master-ATT | 11.30 | 1.562 | 12661 | 1.8% |
| Master | 10.46 | 1.512 | 16219 | 0.9% |
| Algorithm | Shanghai | |||
| MCWT | MCP | TSF | CFR | |
| Real | 19.31 | 1.787 | - | 16.7% |
| Random | 38.62 | 1.826 | -698 | 46.1% |
| Greedy-N | 14.44 | 1.838 | -1252 | 16.9% |
| Greedy-P-5 | 16.65 | 1.502 | 10842 | 13.8% |
| Greedy-P-10 | 19.60 | 1.357 | 15649 | 16.5% |
| CDQN | 20.74 | 1.686 | 4650 | 6.5% |
| CPPO | 18.84 | 1.750 | 1918 | 4.6% |
| IDDPG | 14.02 | 1.562 | 9720 | 2.6% |
| MADDPG | 13.63 | 1.553 | 10209 | 2.8% |
| Master-ATT | 12.24 | 1.548 | 10630 | 2.2% |
| Master | 11.80 | 1.497 | 12497 | 1.5% |
4.2. Overall Performance
Table 2 and Table 3 report the overall results of our methods and all the compared baselines on two datasets with respect to our four metrics. As can be seen, overall, Master achieves the most well-rounded performance among all the baselines. Specifically, Master reduces and for (MCWT, MCP, CFR) compared with the ground truth charging actions on Beijing and Shanghai, respectively. And through our recommendation algorithm, we totally help users saving and charging fees per day on Beijing and Shanghai. Besides, Master achieves and improvements for (MCWT, MCP, TSF, CFR) compared with two multi-agent baselines IDDPG and MADDPG on Beijing, and the improvements are and on Shanghai. All the above results demonstrate the effectiveness of Master. Look into Master-ATT and MADDPG, two MARL algorithms with centralized training decentralized execution. We can observe the Master-ATT with centralized attentive critic have all-sided improvements comparing with MADDPG, especially in the MCWT and CFR. This is because the critic in MADDPG integrates full state and joint action suffering from the large state and action space problem, while our centralized attentive critic can effectively avoid this problem in our task.
Looking further into the results, we observe centralized RL algorithms (i.e., CDQN and CPPO) consistently perform worse than multi-agent approaches (i.e., IDDPG, MADDPG, Master-ATT and Master), which validates our intuition that the centralized algorithms suffer from the high dimensional state and action space problem and hard to learn satisfying policies, while multi-agent approaches perform better because of their quantity-independent state action space in large-scale agents environment. We also observe that Greedy-P-10 has the best performance in MCP among all compared algorithms. This is no surprise, because it always recommends the least expensive charging stations without considering other goals, which causes that the Greedy-P-10 performs badly in MCWT and CFR. It is worth mentioning that Master unexpectedly exceeds Greedy-P-10 in TSF on Beijing for the reason that Master has a much lower CFR comparing with Greedy-P-10, more users are benefited from our recommendation.
4.3. Ablation Study
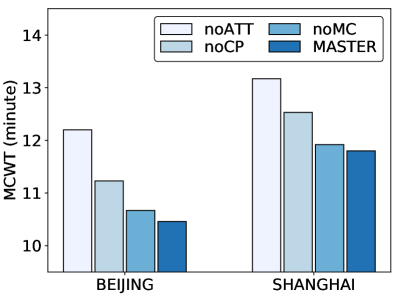
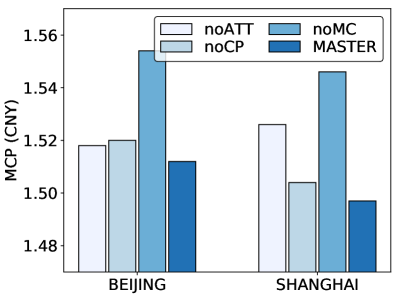
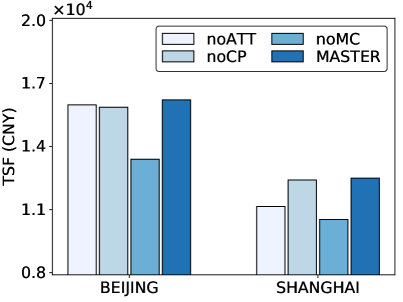
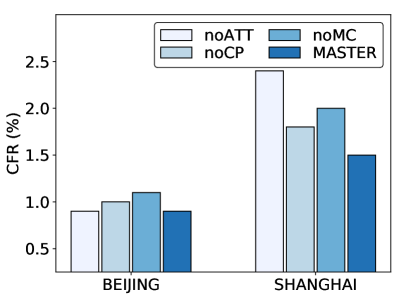
In this section, we conduct ablation studies on Master to further verify the effectiveness of each component. We evaluate the performance of Master and it’s three variants for the four metrics on Beijing and Shanghai. Specifically, the three variants are (1) noATT removes centralized attentive critic, learning agents independently; (2) noCP removes the future potential charging competition information from centralized attentive critic; (3) noMC removes multi-critic architecture, learning policies by a single centralized attentive critic with the average combined reward. The ablation results are reported in Figure 6. As can be seen, removing centralized attentive critic (noATT) or charging competition information (noCP) have a greater impact on MCWT. This is because MCWT is highly related to the cooperation of agents and charging competition of EVs, whereas the removed modules exactly work on these two aspects. Removing multi-critic architecture (noMC) has a large performance degradation on MCP and TSF. This is because noMC suffers from the convergence problem and finally leads to performance variance on multiple objectives. All the above experimental results demonstrate the effectiveness of each component in Master.
4.4. Effect of Recommendation Candidates
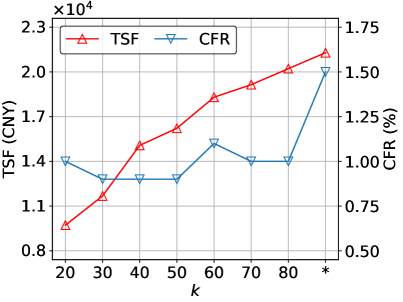
In this section, we study the effect of the number of top- active agents for recommendations on Beijing. We vary from to the number of all the agents. The results are reported in Figure 7, where ”” denotes all the agents are activated for recommendation decision. As can be seen, with relaxing the recommendation constraint , the MCWT increases while the MCP and TSF decrease, further validating the divergence of the optimal solutions for different objectives. This is possible because a more relaxed candidate number will expose more alternative economic but distant charging stations for recommendations. Even so, we should notice that the performance under the most strict constraint (i.e., ) or without constraint (i.e., ) are varying in a small range, i.e., the (MCWT, MCP) are () and (), respectively, are not extreme and still acceptable for the online recommendation. The above results demonstrate that our model are well-rounded with different candidate numbers. It also inspires us that we can explore to make diversified recommendations that are biased to different objectives to satisfy personalized preferences in the future.
4.5. Convergence Analysis
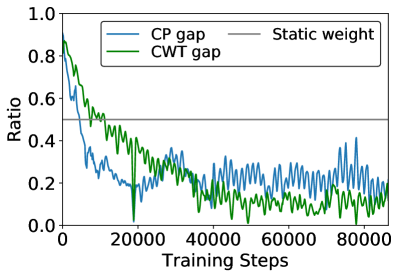
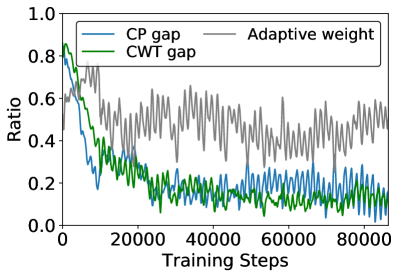
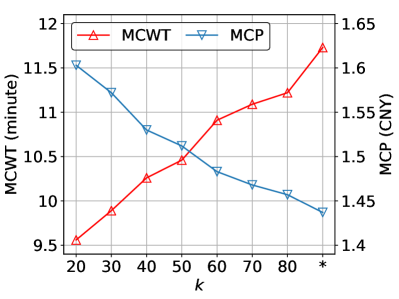
In this section, we study the effect of our multi-objective optimization method by comparing the convergence of Master between the static and our adaptive strategy. Note the Master with static average updated weight is equivalent to Master-noMC (i.e., average two rewards as a single reward for training). More details can be found in proposition C.1 in the Appendix C. The gap ratios (Eq. (13)) and dynamic weights (Eq. (14)) are reported in Figure 8. As can be seen in Figure 8(a), at the beginning of training, the gap ratio of the CP critic is decreasing faster than the CWT one. This is because the distribution of CP reward is more concentrated (as illustrated in Figure 4), it’s easier to accumulate rewards comparing with CWT when agents with poor policies. In such a case, the static method keeps invariant update weights and results in slow convergence for CWT. In contrast, as shown in Figure 8(b), the dynamic re-weighting method in Master assigns a higher weight to the CWT objective when it falls behind the optimization of CP, and adjust them to a synchronous convergence pace. As the training step increase, the convergence of CWT overtakes the CP. This is because the distribution of CWT reward is more even, having larger room for improvement. And the optimization of CWT drags the CP objective to a sub-optimal point since the divergences between two objectives. However, the static method is helpless for such asynchronous convergence, but Master with the dynamic gradient re-weighting strategy weakens such asynchronism, and finally adjust them to be synchronous (i.e., weight approaches 0.5) to learn well-rounded policies.
4.6. Case Study
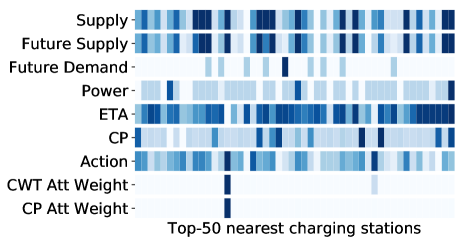
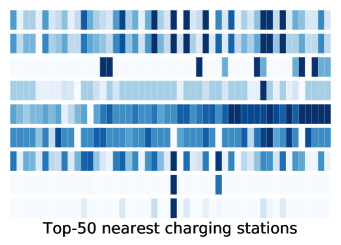
In this section, we visualize the correlation among the attention weights and some input features of two centralized attentive critics (i.e., and ), to qualitatively analysis the effectiveness of Master. Two cases are depicted in Figure 9. We can observe these two critics pay more attention to the charging stations with high action values. This makes sense, since these charging stations are highly competitive bidding participants. The charging request will be recommended to the charging station with the highest action, then environment returns rewards depending on this recommended station. Furthermore, we observe the action is highly correlated with factors such as supply, future supply, future demand, ETA and CP. A charging station with low ETA, CP and sufficient available charging spots (supplies) always has a high action value. Conversely, the charging stations with few available charging spots but high future demands usually derive a low action value for avoiding future charging competitions. The above observations validate the effectiveness of our model to mediate the contradiction between the space-constrained charging capacity and spatiotemporally unbalanced charging demands.
5. Related work
Charging Station Recommendation. In recent years, EVs have become an emerging choice in the modern transportation system due to their low-carbon emission and energy efficiency. Some efforts (Cao et al., 2019; Guo et al., 2017; Kong et al., 2016; Tian et al., 2016; Wang et al., 2018, 2019; Wang et al., 2020c, a; Yuan et al., 2019) have been made for charging station recommendation for EVs. In particular, most studies (Wang et al., 2020c; Guo et al., 2017; Tian et al., 2016; Wang et al., 2019; Cao et al., 2019) focus on recommending charging station locations for EV drivers with the goal of time. For example, Guo et al. (2017) propose to make recommendations of charging stations to minimize the time of traveling and queuing with a game-theoretical approach. Wang et al. (2020c) devise a fairness-aware recommender system to reduce the idle time based on the fairness constraints. Cao et al. (2019) introduce the charging reservation information into the vehicle-to-vehicle system to facilitate the location recommendation. Different from charging location recommendation problem, another line of works (Yuan et al., 2019; Kong et al., 2016; Wang et al., 2018; Wang et al., 2020a) investigate to handle more complicated scenarios, especially considering commercial benefits. Yuan et al. (2019) propose a charging strategy that allows an electric taxi to get partially charged to meet the dynamic passenger demand. In particular, with the help of deep reinforcement learning which has been widely adopted for solving sequential decision-making problems, Wang et al. (2020a) design a multi-agent mean field hierarchical reinforcement learning framework by regarding each electric taxi as an individual agent to provide charging and relocation recommendations for electric taxi drivers, so as to maximize the cumulative rewards of the number of served orders. However, formulating each EV driver as an agent is not suitable for our problem, since most charging requests of a day in our task are ad-hoc and from non-repetitive drivers. Besides, the above works mainly focus on a single recommendation objective, which can not handle multiple divergent recommendation objectives simultaneously.
Multi-Agent Reinforcement Learning. Multi-agent Reinforcement Learning (MARL) is an emerging sub-field of reinforcement learning. Compared with traditional reinforcement learning, MARL expects the agents to learn to cooperate and compete with others. The simplest approach to realize a multi-agent system is learning agents independently (Tan, 1993; Tampuu et al., 2017; Gupta et al., 2017). However, the independent agents are not able to coordinate their actions, failing to achieve complicated cooperation(Sukhbaatar et al., 2016; Matignon et al., 2012; Lowe et al., 2017). A kind of natural approaches to achieve agents’ cooperation is to learn communication among multiple agents (Foerster et al., 2016; Sukhbaatar et al., 2016; Peng et al., 2017; Jiang and Lu, 2018). However, such approaches always lead to high communication overhead because of the large amount of information transfer. Alternatively, there are some works that employ the centralized training decentralized execution architecture to achieve agents’ coordination and cooperation (Lowe et al., 2017; Foerster et al., 2018; Iqbal and Sha, 2019). The advantage of such methods is that the agents can make decentralized execution without involving any other agents’ information, which is lightweight and fault-tolerant in a large-scale agent system.
Multi-Agent Transportation Systems. In the past years, a few studies have successfully applied MARL for several intelligent transportation tasks. For example, (Wei et al., 2019; Wang et al., 2020b) use MARL algorithm for cooperative traffic signal control. (Li et al., 2019a; Lin et al., 2018; Jin et al., 2019; Zhou et al., 2019) apply MARL into the large-scale ride-hailing system to maximize the long-term benefits. Besides, MARL also has been adopted for shared-bike repositioning (Li et al., 2018), express delivery-service scheduling (Li et al., 2019b). However, we argue that our problem is inherently different from the above applications as a recommendation task, and the above approaches cannot be directly adopted for our problem.
6. Conclusion
In this paper, we investigated the intelligent EV charging recommendation task with the long-term goals of simultaneously minimizing the overall CWT, average CP and the CFR. We formulated this problem as a multi-objective MARL task and proposed a spatiotemporal MARL framework, Master. Specifically, by regarding each charging station as an individual agent, we developed the multi-agent actor-critic framework with centralized attentive critic to stimulate the agents to learn coordinated and cooperative policies. Besides, to enhance the recommendation effectiveness, we proposed a delayed access strategy to integrate the future charging competition information during model training. Moreover, we extend the centralized attentive critic to multi-critics with a dynamic gradient re-weighting strategy to adaptively guide the optimization direction of multiple divergent recommendation objectives. Extensive experiments on two real-world datasets demonstrated the effectiveness of Master compared with nine baselines.
Acknowledgements.
This research is supported in part by grants from the National Natural Science Foundation of China (Grant No.91746301, 71531001, 62072423).References
- (1)
- Cao et al. (2019) Yue Cao, Tao Jiang, Omprakash Kaiwartya, Hongjian Sun, Huan Zhou, and Ran Wang. 2019. Toward pre-empted EV charging recommendation through V2V-based reservation system. IEEE Transactions on Systems, Man, and Cybernetics: Systems (2019).
- Chu et al. (2019) Tianshu Chu, Jie Wang, Lara Codecà, and Zhaojian Li. 2019. Multi-agent deep reinforcement learning for large-scale traffic signal control. IEEE Transactions on Intelligent Transportation Systems 21, 3 (2019), 1086–1095.
- Du et al. (2018) Bowen Du, Yongxin Tong, Zimu Zhou, Qian Tao, and Wenjun Zhou. 2018. Demand-aware charger planning for electric vehicle sharing. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. 1330–1338.
- Fan et al. (2020) Wei Fan, Kunpeng Liu, Hao Liu, Pengyang Wang, Yong Ge, and Yanjie Fu. 2020. AutoFS: Automated Feature Selection via Diversity-aware Interactive Reinforcement Learning. In IEEE 20th International Conference on Data Mining.
- Foerster et al. (2016) Jakob Foerster, Ioannis Alexandros Assael, Nando De Freitas, and Shimon Whiteson. 2016. Learning to communicate with deep multi-agent reinforcement learning. In Advances in neural information processing systems. 2137–2145.
- Foerster et al. (2018) Jakob N. Foerster, Gregory Farquhar, Triantafyllos Afouras, Nantas Nardelli, and Shimon Whiteson. 2018. Counterfactual Multi-Agent Policy Gradients. In Proceedings of the 32nd AAAI Conference on Artificial Intelligence. 2974–2982.
- Guo et al. (2020) Qingyu Guo, Fuzhen Zhuang, Chuan Qin, Hengshu Zhu, Xing Xie, Hui Xiong, and Qing He. 2020. A survey on knowledge graph-based recommender systems. IEEE Transactions on Knowledge and Data Engineering (2020).
- Guo et al. (2017) Tianci Guo, Pengcheng You, and Zaiyue Yang. 2017. Recommendation of geographic distributed charging stations for electric vehicles: A game theoretical approach. In IEEE Power & Energy Society General Meeting. 1–5.
- Gupta et al. (2017) Jayesh K Gupta, Maxim Egorov, and Mykel Kochenderfer. 2017. Cooperative multi-agent control using deep reinforcement learning. In International Conference on Autonomous Agents and Multiagent Systems. 66–83.
- Han et al. (2021) Jindong Han, Hao Liu, Hengshu Zhu, Hui Xiong, and Dejing Dou. 2021. Joint Air Quality and Weather Prediction Based on Multi-Adversarial Spatiotemporal Networks. In Proceedings of the 35th AAAI Conference on Artificial Intelligence.
- Iqbal and Sha (2019) Shariq Iqbal and Fei Sha. 2019. Actor-attention-critic for multi-agent reinforcement learning. In International Conference on Machine Learning. 2961–2970.
- Jiang and Lu (2018) Jiechuan Jiang and Zongqing Lu. 2018. Learning attentional communication for multi-agent cooperation. In Advances in neural information processing systems. 7254–7264.
- Jin et al. (2019) Jiarui Jin, Ming Zhou, Weinan Zhang, Minne Li, Zilong Guo, Zhiwei Qin, Yan Jiao, Xiaocheng Tang, Chenxi Wang, Jun Wang, et al. 2019. Coride: joint order dispatching and fleet management for multi-scale ride-hailing platforms. In Proceedings of the 28th ACM International Conference on Information and Knowledge Management. 1983–1992.
- Kong et al. (2016) Fanxin Kong, Qiao Xiang, Linghe Kong, and Xue Liu. 2016. On-line event-driven scheduling for electric vehicle charging via park-and-charge. In IEEE Real-Time Systems Symposium. 69–78.
- Li et al. (2019a) Minne Li, Zhiwei Qin, Yan Jiao, Yaodong Yang, Jun Wang, Chenxi Wang, Guobin Wu, and Jieping Ye. 2019a. Efficient ridesharing order dispatching with mean field multi-agent reinforcement learning. In The World Wide Web Conference. 983–994.
- Li et al. (2015) Yanhua Li, Jun Luo, Chi-Yin Chow, Kam-Lam Chan, Ye Ding, and Fan Zhang. 2015. Growing the charging station network for electric vehicles with trajectory data analytics. In IEEE 31st International Conference on Data Engineering. 1376–1387.
- Li et al. (2018) Yexin Li, Yu Zheng, and Qiang Yang. 2018. Dynamic bike reposition: A spatio-temporal reinforcement learning approach. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. 1724–1733.
- Li et al. (2019b) Yexin Li, Yu Zheng, and Qiang Yang. 2019b. Efficient and Effective Express via Contextual Cooperative Reinforcement Learning. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. 510–519.
- Lillicrap et al. (2015) Timothy P Lillicrap, Jonathan J Hunt, Alexander Pritzel, Nicolas Heess, Tom Erez, Yuval Tassa, David Silver, and Daan Wierstra. 2015. Continuous control with deep reinforcement learning. arXiv preprint arXiv:1509.02971 (2015).
- Lin et al. (2018) Kaixiang Lin, Renyu Zhao, Zhe Xu, and Jiayu Zhou. 2018. Efficient large-scale fleet management via multi-agent deep reinforcement learning. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. 1774–1783.
- Liu et al. (2020a) Hao Liu, Jindong Han, Yanjie Fu, Jingbo Zhou, Xinjiang Lu, and Hui Xiong. 2020a. Multi-modal transportation recommendation with unified route representation learning. Proceedings of the VLDB Endowment (2020), 342–350.
- Liu et al. (2019) Hao Liu, Ting Li, Renjun Hu, Yanjie Fu, Jingjing Gu, and Hui Xiong. 2019. Joint Representation Learning for Multi-Modal Transportation Recommendation. In Proceedings of the 33rd AAAI Conference on Artificial Intelligence. 1036–1043.
- Liu et al. (2020b) Hao Liu, Yongxin Tong, Jindong Han, Panpan Zhang, Xinjiang Lu, and Hui Xiong. 2020b. Incorporating Multi-Source Urban Data for Personalized and Context-Aware Multi-Modal Transportation Recommendation. IEEE Transactions on Knowledge and Data Engineering (2020).
- Lowe et al. (2017) Ryan Lowe, Yi I Wu, Aviv Tamar, Jean Harb, OpenAI Pieter Abbeel, and Igor Mordatch. 2017. Multi-agent actor-critic for mixed cooperative-competitive environments. In Advances in neural information processing systems. 6379–6390.
- Lynch (2009) Gary S Lynch. 2009. Single point of failure. Wiley Online Library.
- Matignon et al. (2012) Laetitia Matignon, Guillaume J Laurent, and Nadine Le Fort-Piat. 2012. Independent reinforcement learners in cooperative Markov games: a survey regarding coordination problems. Knowledge Engineering Review (2012), 1–31.
- Mnih et al. (2015) Volodymyr Mnih, Koray Kavukcuoglu, David Silver, Andrei A Rusu, Joel Veness, Marc G Bellemare, Alex Graves, Martin Riedmiller, Andreas K Fidjeland, Georg Ostrovski, et al. 2015. Human-level control through deep reinforcement learning. Nature (2015), 529–533.
- Papoudakis et al. (2019) Georgios Papoudakis, Filippos Christianos, Arrasy Rahman, and Stefano V Albrecht. 2019. Dealing with non-stationarity in multi-agent deep reinforcement learning. arXiv preprint arXiv:1906.04737 (2019).
- Peng et al. (2017) Peng Peng, Quan Yuan, Ying Wen, Yaodong Yang, Zhenkun Tang, Haitao Long, and Jun Wang. 2017. Multiagent bidirectionally-coordinated nets for learning to play starcraft combat games. arXiv preprint arXiv:1703.10069 (2017).
- Savari et al. (2020) George F Savari, Vijayakumar Krishnasamy, Jagabar Sathik, Ziad M Ali, and Shady HE Abdel Aleem. 2020. Internet of Things based real-time electric vehicle load forecasting and charging station recommendation. ISA transactions (2020), 431–447.
- Schulman et al. (2017) John Schulman, Filip Wolski, Prafulla Dhariwal, Alec Radford, and Oleg Klimov. 2017. Proximal policy optimization algorithms. arXiv preprint arXiv:1707.06347 (2017).
- Sukhbaatar et al. (2016) Sainbayar Sukhbaatar, Arthur Szlam, and Rob Fergus. 2016. Learning multiagent communication with backpropagation. In Advances in neural information processing systems. 2244–2252.
- Tampuu et al. (2017) Ardi Tampuu, Tambet Matiisen, Dorian Kodelja, Ilya Kuzovkin, Kristjan Korjus, Juhan Aru, Jaan Aru, and Raul Vicente. 2017. Multiagent cooperation and competition with deep reinforcement learning. PloS one (2017).
- Tan (1993) Ming Tan. 1993. Multi-agent reinforcement learning: Independent vs. cooperative agents. In Proceedings of the 10th International Conference on Machine Learning. 330–337.
- Tian et al. (2016) Zhiyong Tian, Taeho Jung, Yi Wang, Fan Zhang, Lai Tu, Chengzhong Xu, Chen Tian, and Xiang-Yang Li. 2016. Real-time charging station recommendation system for electric-vehicle taxis. IEEE Transactions on Intelligent Transportation Systems (2016), 3098–3109.
- Wang et al. (2020a) Enshu Wang, Rong Ding, Zhaoxing Yang, Haiming Jin, Chenglin Miao, Lu Su, Fan Zhang, Chunming Qiao, and Xinbing Wang. 2020a. Joint Charging and Relocation Recommendation for E-Taxi Drivers via Multi-Agent Mean Field Hierarchical Reinforcement Learning. IEEE Transactions on Mobile Computing (2020).
- Wang et al. (2018) Guang Wang, Xiaoyang Xie, Fan Zhang, Yunhuai Liu, and Desheng Zhang. 2018. bCharge: Data-driven real-time charging scheduling for large-scale electric bus fleets. In IEEE Real-Time Systems Symposium. 45–55.
- Wang et al. (2019) Guang Wang, Fan Zhang, and Desheng Zhang. 2019. tCharge-A fleet-oriented real-time charging scheduling system for electric taxi fleets. In Proceedings of the 17th Conference on Embedded Networked Sensor Systems. 440–441.
- Wang et al. (2020c) Guang Wang, Yongfeng Zhang, Zhihan Fang, Shuai Wang, Fan Zhang, and Desheng Zhang. 2020c. FairCharge: A data-driven fairness-aware charging recommendation system for large-scale electric taxi fleets. Proceedings of the ACM on Interactive, Mobile, Wearable and Ubiquitous Technologies (2020), 1–25.
- Wang et al. (2020b) Yanan Wang, Tong Xu, Xin Niu, Chang Tan, Enhong Chen, and Hui Xiong. 2020b. STMARL: A Spatio-Temporal Multi-Agent Reinforcement Learning Approach for Cooperative Traffic Light Control. IEEE Transactions on Mobile Computing (2020).
- Wei et al. (2019) Hua Wei, Nan Xu, Huichu Zhang, Guanjie Zheng, Xinshi Zang, Chacha Chen, Weinan Zhang, Yanmin Zhu, Kai Xu, and Zhenhui Li. 2019. Colight: Learning network-level cooperation for traffic signal control. In Proceedings of the 28th ACM International Conference on Information and Knowledge Management. 1913–1922.
- Xin et al. (2021) Haoran Xin, Xinjiang Lu, Tong Xu, Hao Liu, Jingjing Gu, Dejing Dou, and Hui Xiong. 2021. Out-of-Town Recommendation with Travel Intention Modeling. In Proceedings of the 35th AAAI Conference on Artificial Intelligence.
- Yang et al. (2014) Zaiyue Yang, Lihao Sun, Min Ke, Zhiguo Shi, and Jiming Chen. 2014. Optimal charging strategy for plug-in electric taxi with time-varying profits. IEEE Transactions on Smart Grid (2014), 2787–2797.
- Yuan et al. (2019) Yukun Yuan, Desheng Zhang, Fei Miao, Jimin Chen, Tian He, and Shan Lin. 2019. p^ 2Charging: Proactive Partial Charging for Electric Taxi Systems. In IEEE 39th International Conference on Distributed Computing Systems. IEEE, 688–699.
- Yuan et al. (2020) Zixuan Yuan, Hao Liu, Yanchi Liu, Denghui Zhang, Fei Yi, Nengjun Zhu, and Hui Xiong. 2020. Spatio-temporal dual graph attention network for query-poi matching. In Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval. 629–638.
- Zhang et al. (2020) Weijia Zhang, Hao Liu, Yanchi Liu, Jingbo Zhou, and Hui Xiong. 2020. Semi-Supervised Hierarchical Recurrent Graph Neural Network for City-Wide Parking Availability Prediction. In Proceedings of the 34th AAAI Conference on Artificial Intelligence. 1186–1193.
- Zhao et al. (2018) Jun Zhao, Guang Qiu, Ziyu Guan, Wei Zhao, and Xiaofei He. 2018. Deep reinforcement learning for sponsored search real-time bidding. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. 1021–1030.
- Zheng et al. (2020) Yanchong Zheng, Ziyun Shao, Yumeng Zhang, and Linni Jian. 2020. A systematic methodology for mid-and-long term electric vehicle charging load forecasting: The case study of Shenzhen, China. Sustainable Cities and Society (2020), 102084.
- Zhou et al. (2019) Ming Zhou, Jiarui Jin, Weinan Zhang, Zhiwei Qin, Yan Jiao, Chenxi Wang, Guobin Wu, Yong Yu, and Jieping Ye. 2019. Multi-agent reinforcement learning for order-dispatching via order-vehicle distribution matching. In Proceedings of the 28th ACM International Conference on Information and Knowledge Management. 2645–2653.
Appendix A Simulator design
We develop a simulator111https://github.com/Vvrep/MASTER-electric_vehicle_charging_recommendation based on historical real-time availability (supplies) records data, historical real-time charging prices data, and charging powers data of charging stations, along with historical electric vehicles (EVs) charging data, and road network data (Liu et al., 2020a), to simulate how the system runs for a day. We take Baidu API222http://lbsyun.baidu.com/index.php?title=webapi to compute ETA (Liu et al., 2020b) between the location of charging request and charging station. Besides, we train a MLP model to predict the future demands based on the historical charging requests data, and leverage the learned MLP model to predict the future demands in evaluation phase.
Simulation step. Initially, our simulator loads basic supplies, charging prices and charging powers data of charging stations and charging requests by minutes of a day from the real-world dataset. For each minute in simulator, there are three events to be disposed:
-
•
Electric vehicles’ departure and arrival: In this event, we dispose EVs’ departure and arrival at . For EV leaving station, the charging stations will free corresponding number of charging spots. For an arrived EV, the vehicle successfully charges if there still have available spots in the charging station, and the environment will return a negative charging wait time (CWT) and negative charging price (CP) as the rewards if the arrived EV accepted our recommendation. For each successful charging request, the vehicle will block one charging spot in a duration which obeys a Gaussian distribution associated to the charging power of each charging station. If the charging station is full, this EV has to queue until there have an available charging spot, or fail to charge when the CWT exceeds a predefined threshold ( minutes). The penal rewards and of failed request are and , respectively. In the implementation, the number of available charging spots can be a negative number, indicating how many EVs are queuing at station for charging.
-
•
Charging requests recommendation: The policy will make recommendations for each charging request at . The EV of the charging request will drive to the recommended charging station based on the real recommendation acceptance probability, and otherwise will go to the ground truth charging station.
-
•
Transition collection: If there have charging requests at , the transitions for charging stations will be collected and stored into replay memory (Mnih et al., 2015) for learning RL algorithms.
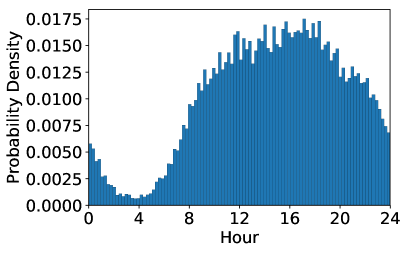
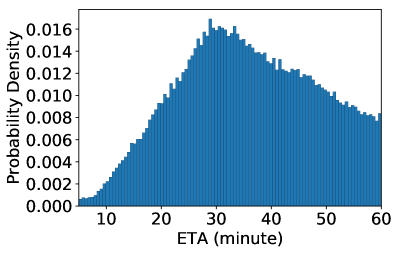
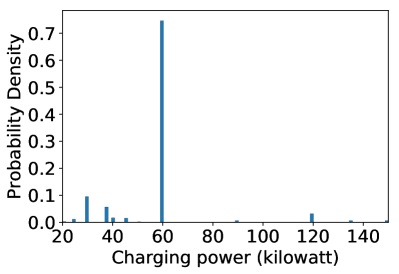
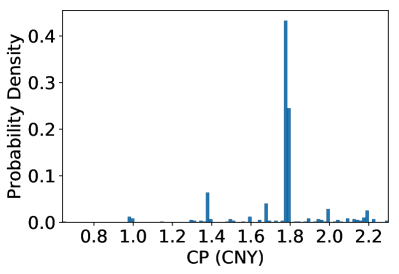
Appendix B Dataset Statistical Analysis
We take Beijing as an example for more statistical analysis. Figure 10 shows the distribution of the quantities of charging requests in different time, and the distributions of ETA, charging powers, and CP. We can observe the charging requests quantity changes notably along with time in a day, which indicates unbalanced charging demands. Besides, we observe it is significantly different by comparing the distributions of ETA with CP, where the latter is much more concentrated. This observation indicates the large differences between the two objectives.
Appendix C Proposition
Proposition C.1.
Define (e.g., ) and (e.g., ) as two different reward functions, then the following two policy gradients to update the policy are equivalent:
| (16) |
| (17) | ||||