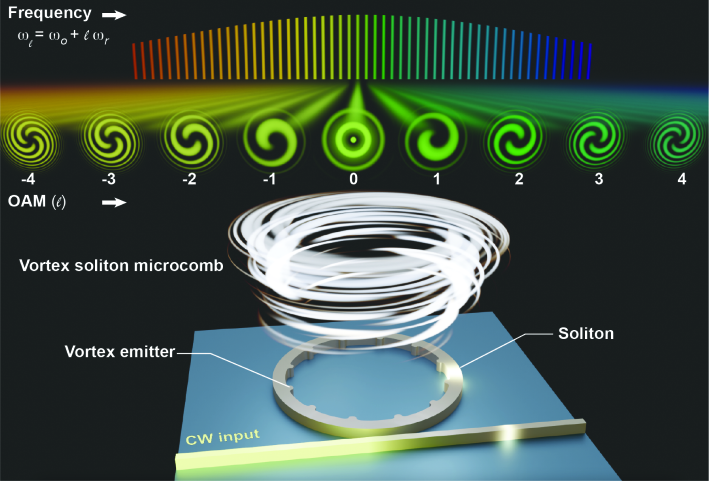
Integrated vortex soliton microcombs

An optical frequency comb (OFC) comprises a myriad of mutually-coherent lasers that are spaced evenly in the frequency domain ⁴. They enable massively parallel data transmission and processing, such as simultaneously interrogating chemical absorption features across a broad frequency range ⁷. An important advance of OFC technology is the demonstration of pulsed mode-locking in optical microresonators ^{8, 9, 10, 11, 12, 13, 14}, which extends their reach to scenarios favoring compact form factors and low power consumption ^{5, 15}. These soliton microcombs are being produced in foundries ^{16, 17} to satisfy the growing demand of high-speed communications ^{18, 19}, portable spectroscopy ^{20, 21, 22}, and photonic deep learning ^{23, 24}.

Akin to the discrete frequencies of an OFC, the orbital angular momentum (OAM) of light offers another theoretically infinite dimension quantized by the spatial topological charges ^{1, 2}. The signature helical wavefronts and phase singularities of OAM beams ²⁵ create new quantum and classical states of light ^{26, 27, 28, 29} for optical tweezing ³⁰, remote sensing ³¹, communications ³², and resolution-enhanced imaging ^{33, 34}. In place of bulk optical elements, microphotonics have been recently introduced to create ^{35, 36, 37} and detect ³⁸ OAM beams on a small footprint. However, spatial separation of the beams into individual OAM orders has remained a prerequisite for processing and detecting multiplexed OAM states, which technically necessitates designated phase patterns and detector arrays ³. Applications involving high-dimensional OAM states are thus being handicapped in acquisition speed and channel capacity by the associated system complexity ³. Mapping the OAM to the frequency domain, e.g., by encoding the OAM information to the comb lines of OFCs, would harness the powerful frequency-domain metrology techniques to realize fast OAM tomography free from massive imaging elements. In this work, we demonstrate a highly-multiplexed coherent OAM source named the vortex soliton microcomb. A standalone microresonator functions as both the comb generator and the vortex beam emitter. The comb lines natively carry distinct OAM with orders correlated to their frequencies, and are verified over a broad wavelength range. It allows one-shot diagnosis of high-dimensional OAM states via conventional spectroscopy techniques.

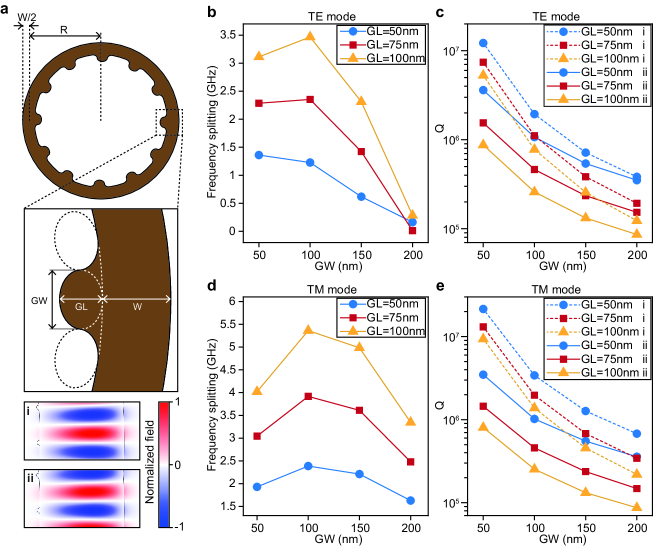
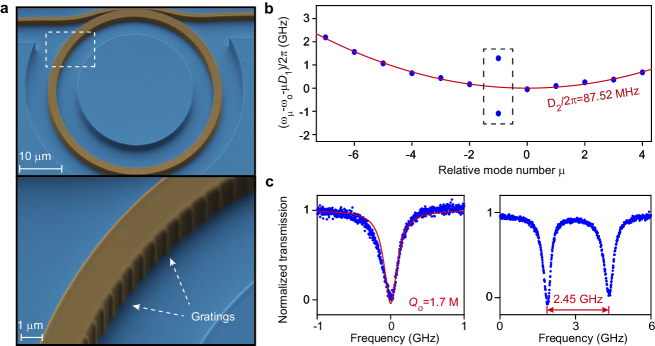
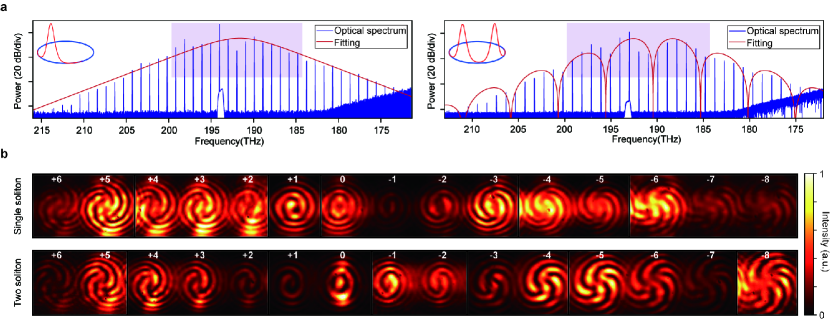
We fabricate the microresonators using 800-nm-thick stoichiometric Si₃N₄ films on 4 µm silica substrate (see Methods). The mean radius and width of the microresonator is set as 22 µm and 2 µm, respectively (Fig. 2a), resulting in the free-spectral-range ($FSR$) around 1 THz. The grating elements are designed oval-shaped, and are smoothly connected to the microresonator to mitigate scattering losses (Extended Data Fig. 1). Setting the size of each element to 50 nm gives vertical emission efficiency of 7%. The mode family dispersion of the microresonator is acquired using a tunable laser near the telecommunication C band. They are expressed as $\omega_{\mu}-\omega_{o}-\mu D_{1}$, in which $\omega_{\mu}$ is the resonant frequency of the $\mu_{\mathrm{th}}$ mode and $D_{1}$ is the $FSR$ (Fig. 2b). For fundamental Transverse Magnetic (TM) modes, parabolic fitting of the mode family dispersion shows anomalous group velocity dispersion. Note that a pair of modes at $\mu=-1$ are symmetrically located at the two sides of the parabola. This is due to the enhanced coupling between the otherwise degenerate clockwise and counterclockwise modes when their azimuthal number equals the number of grating elements. We thus identify the azimuthal number of $\mu=-1$ modes as 160. Further measurement of the transmission spectra of the non-split modes show intrinsic quality factor of 1.7 million (Fig. 1c). Meanwhile, the 2.45 GHz frequency splitting of the doublet is close to our designed value (2.39 GHz), indicating that the geometry of the gratings is precisely controlled in the fabrication process (Extended Data Fig. 2d).

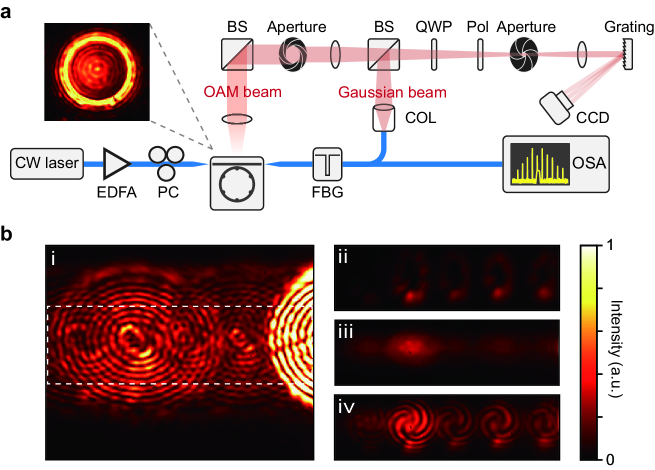
The microresonator is pumped by an amplified continuous-wave laser to initiate parametric oscillations, which then lead to Turing patterns, chaotic modulational instabilities, and solitons at different laser-resonator detunings ^{8, 9, 10}. For the single-soliton state, the optical spectrum features a signature $\mathrm{sech}^{2}$ envelope and spans over 40 THz (Fig. 3a). Two-soliton states are also observed, whose optical spectra are modulated with the period determined by the relative positions of the solitons ^{8, 10}. The experimental setup to identify the OAM state of each emitted comb line is depicted in Extended Data Fig. 2a. Specifically, the vertically emitted beam is collected by an objective lens, and combined with the transmitted light from the bus waveguide that is converted to a Gaussian beam by a collimator ⁶. The polarization of the two beams are both aligned to left-hand circular polarization (LHCP) using a quarter-wave plate and a polarizer to maximize the visibility of the interference patterns. We then direct the combined beams to a blaze grating to separate the comb lines with respect to their frequencies. The interference patterns captured by a CCD camera appear as an array of spirals corresponding to the sequentially arranged OAM orders. The number and winding direction of the spiral arms determine the sign and absolute value of the topological charge $|l|$ (Fig. 3b), respectively. The counterclockwise-winding spirals are identified as positive topological charges, and thus the patterns are assigned to 14 distinct optical vortices with topological charges ranging from -8 to +6. Note that comb lines carrying higher-order OAM are also emitted, but their powers are below the sensitivity of the CCD camera. In addition, mode-unlocked microcombs does not provide stable interference patterns in our setup due to the limited coherence length of the comb lines ⁴⁰.

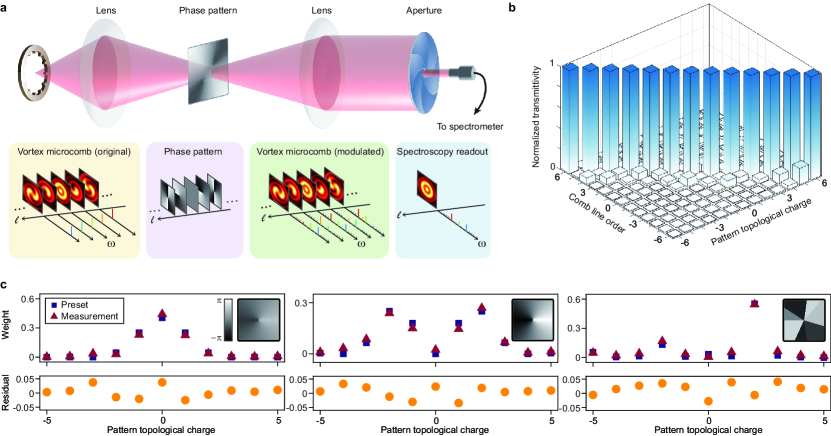
We apply the vortex soliton microcomb to measure the distribution of topological charges in an optical path as a proof-of-concept test (Fig. 4a). The beam is focused on a holographic pattern encoded on a reflective spatial light modulator (SLM), which could emulate the turbulent air vortices in a free-space communication channel ⁴¹. Near the focal point, the phase pattern could be expressed as the summation of different topological charges given by $\sum_{l}b_{l}\exp{(il\theta)}$, and modulates the cross-sectional profiles of the vortex soliton microcomb to

The beam is then projected to the far-field by a convex lens (incorporated on the SLM in our experiment), and the exterior part is blocked by an aperture such that components with nonzero-OAM are prohibited to transmit. Therefore, the transmitted optical spectrum should only contain components with zero-OAM. The power readings of comb lines on a spectrometer are indeed indicators of the weight of pattern topological charges ⁴⁰.

We first encode helical phase patterns with single topological charges onto the SLM to benchmark the performance of the vortex soliton microcomb. The transmitted powers of the comb lines is normalized to their maximum values when the pattern topological charge is varied (Fig. 4b). As expected, each comb line only responds to a specific topological charge, and the channel-to-channel cross-talk of the system has a mean value of -18.5 dB. With proper calibration ⁴⁰, this level of extinction ratio allows measurement of more complicated phase patterns. To exemplify, the weight of topological charges of three different patterns are shown in Fig. 4c. Remarkable agreement between the measured results and the preset values is reached with negligible residual errors. The limiting factors of the accuracy could arise from the pixel sizes and the wavelength-dependent reflectivity of the SLM.