\ul
Instruction-based Hypergraph Pretraining
Abstract.
Pretraining has been widely explored to augment the adaptability of graph learning models to transfer knowledge from large datasets to a downstream task, such as link prediction or classification. However, the gap between training objectives and the discrepancy between data distributions in pretraining and downstream tasks hinders the transfer of the pretrained knowledge. Inspired by instruction-based prompts widely used in pretrained language models, we introduce instructions into graph pretraining. In this paper, we propose a novel pretraining framework named Instruction-based Hypergraph Pretraining. To overcome the discrepancy between pretraining and downstream tasks, text-based instructions are applied to provide explicit guidance on specific tasks for representation learning. Compared to learnable prompts, whose effectiveness depends on the quality and the diversity of training data, text-based instructions intrinsically encapsulate task information and support the model to generalize beyond the structure seen during pretraining. To capture high-order relations with task information in a context-aware manner, a novel prompting hypergraph convolution layer is devised to integrate instructions into information propagation in hypergraphs. Extensive experiments conducted on three public datasets verify the superiority of IHP in various scenarios.
1. Introduction
The burgeoning field of graph-based deep learning has witnessed remarkable advancements, with applications spanning diverse domains such as social networks, bioinformatics, and recommender systems. Graph Neural Networks (GNNs) have emerged as powerful tools for capturing intricate relationships and dependencies within graph-structured datasets. To transfer knowledge from large and diverse datasets to a downstream task with limited data, pretraining has been widely explored to augment the adaptability of GNNs (Hu et al., 2020a; Qiu et al., 2020). However, pretraining also presents several critical issues. Self-supervised learning for pretraining graph models (Qiu et al., 2020; Hu et al., 2020b) addresses the lack of labeled data in the pretext stage, but the training objective gap between the constructed pretext and dedicated downstream tasks hinders the efficient transfer of pretrained knowledge (Sun et al., 2022). Moreover, when labeled data is available during the pretraining stage, the data distribution discrepancy between pretraining and downstream datasets degrades the performance (Wang et al., 2021). In addition, pretrained can suffer from catastrophic forgetting (Zhou and Cao, 2021), resulting in poor generalization ability, especially within small-scale downstream datasets.
Prompt learning, which has been prevalently engaged in Pretrained Language Models (PLMs) (Liu et al., 2023b; Brown et al., 2020), has shown remarkable success in dealing with the aforementioned issues of pretraining. Nonetheless, it is far from straightforward to apply prompts in graphs. In contrast with PLMs, the format of instructions as plain text does not naturally align with the graph-structure data. On the one hand, from a static perspective, graph prompts are supposed to be applied for a certain part of the graph to guide the model depending on specific graph queries. Some specific tasks, such as group identification, can correspond to a relationship among multiple entities. However, traditional graphs are limited in their ability to represent complex relationships, as each edge can only connect two nodes. On the other hand, from a dynamic perspective, prompts need to participate in the context- aware information propagation of the graph model to help capture contextual dependencies among relationships and entities. Nevertheless, dyadic edges in traditional graphs can only propagate information through simple pairwise relationships, which is neither flexible nor efficient. Therefore, we believe that the hypergraph, where each hyperedge is able to simultaneously connect multiple nodes (Feng et al., 2019; Zhou et al., 2006), is a better structure for prompt-based pretraining in graph-based tasks.
However, it is challenging to design the prompt for hypergraph pretraining. Most pioneering works in prompt-based graph pretraining design prompt functions with learnable prompt vectors, which are initialized randomly (Sun et al., 2023; Liu et al., 2023a) or based on pretrained node representations (Sun et al., 2022). Such prompts are not related to semantic instructions for specific tasks, and the effectiveness heavily depends on the quality and diversity of the finetuning data in downstream tasks. The learnable prompt vectors can bring uncertainty in outcomes and the risk of poor generalization, particularly when finetuning data is biased or scarce. In addition, most previous works freeze all parameters except learnable prompts during downstream tasks (Sun et al., 2023; Liu et al., 2023a; Sun et al., 2022). However, this paradigm is suboptimal if abundant unseen nodes appear in the downstream task. The frozen nodes pretrained by pretext tasks cannot offer a direct reference to represent unseen nodes in the downstream task, and the uncertainty from learnable prompts can be exacerbated with those unseen data. These limitations hinder the implementation of these pretraining frameworks in graph-based applications, given that new nodes frequently appear in dynamically evolving graph structures such as social networks, biological networks, and recommender systems.
In light of the above limitations in the existing prompt learning methods for graph-based tasks, it is necessary to design prompts that can provide explicit guidance to the model, helping it focus on specific aspects of the task. To this end, instruction-based prompts represent a more advantageous solution (Su et al., 2023; Brown et al., 2020; Tang et al., 2023). Such prompts guide the model through explicit instructions, which are able to accurately describe specific task requirements related to graph data. By training the model with a variety of instructions, it can adapt to different graph-related queries, improving its generalization across a range of scenarios. In the situation with biased or scarce data, compared to learnable prompts which may overfit the limited examples, instructions allow for the incorporation of domain-specific knowledge that might not be present in the data itself. Instruction-based prompts are also beneficial for addressing unseen nodes in downstream tasks. Rather than relying solely on previously seen examples, text-based instructions provide side information on the new nodes appearing in the graph. Meanwhile, this adaptation to the unseen graph structure requires no extensive computational resources for re-training prompts.

In this paper, we propose a novel framework called Instruction-based Hypergraph Pretraining (IHP). In this framework, high-order relations are represented as hyperedges, and the dependencies among nodes are captured under the guidance of instructions. We show an example of how to integrate instructions into hypergraph pretraining in Fig. 1. If three history enthusiasts read a history book about the French Revolution, we can use one hyperedge to connect them and prompt the hyperedge with instruction through pretraining. In the following downstream task of promoting poetry from the Renaissance period to readers, the model can accordingly locate the readers similar to these three history enthusiasts as the target audiences according to the instruction. To learn node representations under the guidance of instructions, we design a Prompt Hypergraph Convolution (PHC) layer. This PHC layer endows the framework with the ability to be prompted by text-based instructions through hyperedges. Within the hypergraph learning framework, each task-related instruction transformed into prompts is precisely directed to the respective nodes interconnected by the hyperedge. Participating in hypergraph learning, instructions enable the framework to capture high-order relations with task information in a context-aware manner. Furthermore, we design an instruction-based finetuning paradigm. In the downstream task, we freeze the prompt transformation process and update the representations of seen and unseen nodes according to the instructions, ensuring that relationships among nodes are captured in the context of the overall graph. Node representations are updated with different adaptation intensities to achieve a balance between retraining prior knowledge and adapting efficiently for downstream tasks.
The main contributions of this paper are summarized as follows:
-
•
We design a novel framework IHP, an instruction-based pretraining framework based on hypergraphs. To the best of our knowledge, this is the first pretraining framework to leverage instructions to capture high-order relations for graph tasks.
-
•
We proposed a novel PHC layer to prompt text-based instructions into hyperedges. This PHC layer allows instruction information to participate in information propagation during hypergraph convolution, enhancing the flexibility of the hypergraph learning and the generalization of the pretrained model.
-
•
We conduct extensive experiments on three real-world datasets. The marked enhancement observed in the performance of IHP in various scenarios underscores its preeminence as an instruction-based pretraining framework.
2. Related works
2.1. Hypergraph Learning
Interactions in most real-work networks are more complex than dyadic edges used in traditional graphs, in which cases a hypergraph provides a more expressive structure to represent such relations (Lung et al., 2018; Jia et al., 2021; Feige et al., 2015). Beyond the basic hypergraph convolution and attention neural networks(Feng et al., 2019; Bai et al., 2021), hypergraph learning demonstrates adaptability for customization across a variety of graph-based tasks. DHCF (Ji et al., 2020) employs residual connections to effectively capture hybrid multi-order correlations in the user-item graph, simultaneously considering aggregated representations from the original graph and the hypergraph. MHCN (Yu et al., 2021) introduces a multi-channel hypergraph convolutional network that leverages different types of high-order relations among users to predict social links. Seq-HyGAN (Saifuddin et al., 2023) proposes sequential hypergraph attention to capture dependencies between extracted subsequences for sequence classification. To the best of our knowledge, no previous method has applied hypergraph learning for instruction-based pretraining.
2.2. Graph Pretraining and Prompting
Graph learning has attracted interest owing to the prevalence of graph-structured data in various fields. To improve the learning efficacy of such graphs, researchers have been investigating graph pretraining utilizing unlabeled graph data (Jiang et al., 2021; Lu et al., 2021; Hu et al., 2020b). GCC (Qiu et al., 2020) applies contrastive learning to capture the universal topological properties across multiple networks. GPT-GNN (Hu et al., 2020a) introduces a graph generation task during pretraining to capture the characteristics of the graph through the utilization of node features.
With the prevalence of prompt learning, prompting frameworks are applied to mitigate the training objective gap and catastrophic forgetting. A pioneering work GPPT (Sun et al., 2022) designs a pairwise prompting function generating learnable token pairs from standalone nodes for downstream tasks. GraphPrompt (Liu et al., 2023a) multiplies each node embedding by a prompt vector into graph aggregation functions for different tasks. Sun et al. (Sun et al., 2023) introduce a prompting framework that reformulates nodes and edges to induced subgraphs to narrow the gap between different tasks during pretraining and finetuning. However, these works are limited to homogeneous graphs, and learnable prompts provide no explicit semantic clues on graph structures and tasks. On the contrary, our method leverages instruction-based prompts based on plain text instead of learnable prompts. With the guidance of instructions delivered by hyperedges, IHP is able to capture the high-order relations among different nodes.
2.3. Graph Learning with Text Information
Instructions can be regarded as additional text information to the graph structure. Incorporating text into graph learning offers extra contextual understanding and semantic insights, especially when the downstream graph structure is sparse. With the breakthroughs in PLMs, it is straightforward to leverage PLMs and GNNs for textual graph representation following a cascaded architecture (Hamilton et al., 2017). In the cascaded architecture, text information is first encoded by text encoders and then aggregated by graph models to obtain the final representation (Zhu et al., 2021; Li et al., 2021; Jin et al., 2021). In contrast with cascaded architectures, GraphFormers (Yang et al., 2021) and EdgeFormers (Jin et al., 2023a) propose GNN-nested Transformers to jointly encode text and node features in textual graphs. Different from previous works straightforwardly incorporating text encoding in heterogeneous graph learning (Zhang et al., 2019; Jin et al., 2023b), IHP focuses on leveraging instructions to transfer learning capabilities from pretext tasks to downstream tasks. By pretraining with instruction-based prompts, IHP enables the model to develop a generalized understanding of graph properties, which is beneficial when dealing with unseen graph data.
3. Preliminaries
3.1. Problem Formulation
Let the graph for the pretraining task be where and are sets of nodes and edges, respectively. Similarly, let the graph for the downstream task be , and the two instruction sets be and for the pretraining task and the downstream task. Our target is to pretrain the representations of the overlapping nodes, which are defined as target nodes . For example, the target nodes can be the overlapping molecules of different proteins in protein classification, or the overlapping users purchasing items of different domains in cross-domain recommendation. Given the target node set , we define the nodes other than target nodes in the pretraining task as pretraining context nodes in the pretraining task, and the unseen nodes in the downstream task as downstream context nodes . Besides, we define the descriptions of pretraining nodes as and the descriptions of downstream nodes as . The descriptions of different tasks are denoted as , with each task related to arbitrary nodes in graphs. These descriptions are used to construct instructions if available.
3.2. Hypergraph
Definition 1.
(Hypergraph). A hypergraph is defined as , where denotes the node set and represents the edge set. An incidence matrix is used to represent connections among nodes and hyperedges in the hypergraph.
Compared with an edge connecting only two nodes in a traditional graph, a hyperedge connects multiple nodes simultaneously in a hypergraph. Hence, hypergraph naturally possesses the ability to model higher-order connections.
4. Method
In this section, we present the proposed IHP framework with The illustration demonstrated in Figure 2. We start by introducing all the embeddings to be pretrained in this framework. Thereafter, we define two types of hypergraphs and explain how to construct corresponding hyperedges in these hypergraphs. Specifically, we adopt a PHC layer to prompt instructions into hyperedges during hypergraph learning in both pretraining and finetuning stages. We apply an instruction-based finetuning paradigm to update both seen and unseen nodes in the downstream task.

4.1. Embedding Layer
We maintain an embedding layer during pretraining, where is the feature dimension and columns represent all trainable node embeddings. The initial target node embeddings are denoted as and the initial context node embeddings are denoted as . Since target nodes exist in pretraining and downstream tasks, prior knowledge learned from the pretraining tasks can be preserved in and then leveraged in the downstream tasks.
4.2. Hypergraph Construction
We construct the target hypergraph and the context hypergraph based on the original graph. Compared to a graph where edges only connect two nodes, the advantage of a hypergraph is that hyperedges can simultaneously connect multiple nodes as the objectives of an instruction. According to the type of nodes in the graph, we construct two hypergraphs based on four basic types of hyperedges as below:
-
•
Target Hypergraph. The target hypergraph consists of target nodes and hyperedges . Each target-target hyperedge is used to connect a target node with its one-hop target node neighbors. For each group of target nodes connected to one context node, a target-context hyperedge is used to connect them in the hypergraph. Its incidence matrix is denoted as .
-
•
Context Hypergraph. Similar to the target hypergraph, the context hypergraph consists of context nodes and hyperedges . Each context-context hyperedge is used to connect a context node with its one-hop context node neighbors. For each group of context nodes connected to one target node, a context-target hyperedge is used to connect them simultaneously in the hypergraph. Its incidence matrix is denoted as .
In other words, we use the two hypergraphs to ensure the distinction between the target nodes and the context nodes. In this way, the framework can learn from the homogeneity of target nodes and context nodes in a discriminative manner during the following hypergraph pretraining. On the one hand, the information from pretraining is preserved in the target node embeddings and directly transferred to the downstream task. On the other hand, although context nodes are not in the downstream task, they provide the necessary information for the model to capture broader contextual patterns that are not limited to the nodes seen during the downstream task. The relation between target nodes can depend on the similarity among context nodes in pretraining, which is reflected by the context hypergraph. For example, two target nodes related to two context nodes are similar if the two context nodes are similar.
Similarly, a target hypergraph and a context hypergraph are defined for the downstream task with their corresponding incidence matrices and . For both pretraining and downstream tasks, the isolation between the two hypergraphs separates the information propagation paths. In this way, the information of context nodes will not be directly aggregated to the target nodes through hyperedges in hypergraph learning, and vice versa. This design prevents the over-smoothing issue (Bodnar et al., 2022; Keriven, 2022) among target and context nodes, preventing the representations of target nodes from converging to the same values, especially within dense graph data.
4.3. Prompt Hypergraph Convolution
In hypergraph learning, hypergraph convolution is prevalently used for information propagation across nodes in hypergraphs. Nonetheless, current hypergraph convolution methods focus on the direct aggregation of structural information from neighbors connected by hyperedge. To integrate the information from instructions into the hypergraph convolution process, we devise a novel Prompt Hypergraph Convolution layer. First, we construct the hyperedge information based on connected nodes. This step is denoted as hyperedge initialization of the PHC layer. Then, a information prompting step is proposed to endow the fusion of hyperedge information from resources other than the hypergraph structure, such as instructions. Finally, fused information is aggregated back to update the node embeddings in the node update step. To be more concrete, we present the calculation details of a PHC layer in the target hypergraph. The illustration is in Figure 2(c).
4.3.1. Hyperedge Initialization
In the target hypergraph , target nodes are connected by target-target and target-context hyperedges. Therefore, we initialize the representation of a hyperedge by aggregating embeddings of all nodes connected by this hyperedge. The initialized representation of a hyperedge is formulated as follows:
| (1) |
where represents initialized embedding of the hyperedge , is the set of target nodes connected by this hyperedge, and is the embedding of those target nodes as input of the -th PHC layer. We use mean-pooling as the information aggregation method to aggregate structural information from nodes to hyperedges.
4.3.2. Information Prompting
To enable the framework to capture high-order relations under the guidance of instructions during hypergraph convolution, we fuse the initialized representation of a hyperedge with prompted information. With the prompt embedding of a hyperedge denoted as , we fuse with by addition:
| (2) |
where is the fused hyperedge embedding, and is a scalar hyperparameter to control the prompting intensity.
With instructions accessible, the prompt embedding can be obtained based on text information from instructions, as shown in Figure 2(b) and 2(c). If the instruction information is not available, the flexibility of this PHC layer allows other information to be prompted to the hyperedge. For example, a context-target hyperedge in the context hypergraph is converted from a target node. Hence, we can adopt prompt embeddings from the target node embeddings for a context hypergraph without instructions, i.e., , as shown in Figure 2(a). The target node embeddings are output by the -th PHC layer applied on the target hypergraph, after node update in Eq. (3).
4.3.3. Node update
We update the target node embedding by aggregating the fused embeddings from all its connected hyperedges. For a target node , the aggregation step is formulated as follows:
| (3) |
where denotes the output target node embedding, is the set of hyperedges connected to this target node, and is the fused embedding of its connected hyperedges from Eq. (2).
4.3.4. PHC in Matrix Form
To offer a holistic view of convolution, we formulate the matrix form of prompt hypergraph convolution (equivalent to Eq. (1)-(3)) as:
| (4) | ||||
where is the input embedding from -th layer, is the incidence matrix, denotes prompt embeddings for the hyperedges in the hypergraph, and is the output. is the degree matrix of nodes and is degree matrix of hyperedges for normalization. PHC layer is a more general version of hypergraph convolution, which degrades to existing hypergraph convolution (Yu et al., 2021) with prompting intensity .
4.4. Instruction-based Prompt Embedding
To provide explicit guidance for hypergraph learning, instruction-based prompt embeddings are constructed based on available task-related information and fed into the PHC layer for further information propagation. Each instruction is expected to assist in capturing the relationship between the nodes connected by one hyperedge. Hence, the instructions and the formulated hyperedges are designed in one-to-one correspondence. Instructions can be formulated from task descriptions, node descriptions, or a concatenation of both.
We show an example of leveraging the concatenation of task and node descriptions as instructions in Figure 2. Given that target-context hyperedges are context nodes in the original graph, we concatenate the node descriptions and the descriptions of tasks related to these nodes as instructions , where . In this paper, descriptions of context nodes are obtained from the dataset, and the task descriptions are manually created for different tasks. For instance, if target nodes are readers and context nodes are history books in pretraining, the task description can be formulated as ’promote history books to readers.’ In other words, the task description consists of node information (e.g., readers) and/or other task information (e.g., promote or classify).
After the construction of instructions, a pretrained sentence transformer (Wang et al., 2020) is deployed to encode the instructions as text embeddings , which are frozen in both pretraining and downstream tasks. A linear layer is applied to adaptively learn the transformation from text embeddings to prompt embeddings:
| (5) |
where and are the learnable weight matrix and bias for prompt transformation. And is the output prompt embedding, which prompts the target-context hyperedges with instruction information in every PHC layer for the target hypergraph.
4.5. Pretraining and Optimization
4.5.1. Prediction and optimization
The link prediction task is employed in our pretraining stage for optimization. Link prediction is widely recognized as an effective pretraining task, given the abundance of links present in large-scale graph data (Liu et al., 2023a; Sun et al., 2022; Hu et al., 2020a). We use the inner product of two nodes as the link prediction score. For example, in Figure 2(a), the link prediction score between a target node and a context node in pretraining is formulated as:
| (6) |
where and are the final embeddings of the target node and the context node after PHC layers. We remove the superscripts for simplicity. Then, we adopt the pairwise BPR loss (Rendle et al., 2009) to optimize the prediction:
| (7) |
where is the training data, and positive set contains all nodes connected to node . All parameters in the pretraining is regularized by . Adam (Kingma and Ba, 2015) is used as the optimizer.
4.5.2. Instruction-based finetuning
The output of the pretraining stage is the optimal target node embeddings and all parameters in the prompt layer. This pretrained parameter is used to initialize the target nodes and prompt layer in the downstream task. In the downstream task, we freeze in the prompt transformation and further finetune the embeddings of pretrained target nodes and unseen context nodes with downstream instructions. The reasons are twofold. Firstly, freezing this transformation ensures that the model responds to instructions consistently in both pretext and downstream tasks. Since the task-related information is inherently encapsulated in instructions, it is unnecessary to finetune the transformation for learning the task-related information. Second, updating the unseen context nodes with the pretrained target nodes ensures that their features and relationships are captured in the context of the overall graph. This allows for dynamic adaptation of node representations to the specific context of the downstream task, guaranteeing that all nodes are represented according to the downstream instructions.
To address the catastrophic forgetting issue in finetuning, we deploy an adaptation intensity coefficient for the learning rate of target node embeddings. We denote the learning rate of context node embeddings denoted as and set . A lower learning rate for target nodes prevents the framework from forgetting the prior knowledge preserved in the target node embeddings. In this way, the pretrained model achieves a balance between retraining prior knowledge and adapting effectively for downstream tasks.
4.5.3. Efficiency
Our framework is efficient in both space and time complexity. Node embeddings , prompt transformation matrix and prompt transformation bias are the only learnable parameters in IHP. Given the size of pretrained text embeddings as for pretraining and for finetuning, the total space complexity is for pretraining and for finetuning, where . The time complexity depends on the interaction between hyperedges and nodes, and the number of PHC layers . For the four types of hyperedges constructed in IHP, the number of interactions is for pretraining and for finetuning. Therefore, the time complexity is only for pretraining and for finetuning, where . In contrast, a typical graph model GCN (Kipf and Welling, 2017) needs time with nodes and edges.
| Dataset | Goodreads-P | Goodreads-H | Amazon |
|---|---|---|---|
| # nodes | 69,511 | 220,704 | 362,900 |
| # edges | 370,326 | 1,673,926 | 726,531 |
| # target nodes | 10,000 | 10,000 | 22,899 |
| # pretrained nodes | 52,698 | 163,752 | 342,738 |
| # pretrained edges | 271,344 | 1,407,108 | 665,695 |
| # node descriptions | 59,511 | 210,704 | 340,001 |
| Dataset | Goodreads-P | Goodreads-H | Amazon | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Metric | R@10 | R@20 | N@10 | N@20 | R@10 | R@20 | N@10 | N@20 | R@10 | R@20 | N@10 | N@20 |
| LightGCN | 0.2427 | 0.2958 | 0.1684 | 0.1846 | 0.0956 | 0.1111 | \ul0.0818 | \ul0.0869 | 0.0661 | 0.0828 | 0.0497 | 0.0545 |
| SGL | 0.2365 | 0.2935 | 0.1637 | 0.1808 | \ul0.0960 | 0.1108 | 0.0810 | 0.0856 | 0.0683 | 0.0812 | 0.0494 | 0.0530 |
| DirectAU | 0.2106 | 0.3152 | 0.1721 | 0.2011 | 0.0933 | 0.1084 | 0.0807 | 0.0861 | 0.0689 | 0.0808 | 0.0599 | 0.0630 |
| HCCF | 0.2427 | 0.3175 | 0.1884 | 0.2092 | 0.0721 | 0.1062 | 0.0603 | 0.0735 | 0.0682 | 0.0809 | 0.0605 | 0.0639 |
| DHCF | 0.2440 | 0.2995 | 0.1702 | 0.1846 | 0.0735 | 0.0919 | 0.0569 | 0.0636 | 0.0299 | 0.0399 | 0.0177 | 0.0207 |
| GraphFormers | 0.2147 | 0.2770 | 0.1388 | 0.1583 | 0.0889 | \ul0.1187 | 0.0757 | 0.0854 | 0.0401 | 0.0496 | 0.0285 | 0.0313 |
| AttriMask | - | - | - | - | 0.0640 | 0.0960 | 0.0489 | 0.0600 | 0.0741 | 0.0871 | \ul0.0633 | \ul0.0670 |
| GCC | \ul0.2585 | 0.3185 | 0.1933 | 0.2117 | 0.0623 | 0.0947 | 0.0465 | 0.0584 | 0.0749 | 0.0905 | 0.0611 | 0.0656 |
| GraphMAE | 0.2574 | \ul0.3220 | \ul0.1984 | \ul0.2178 | 0.0678 | 0.1020 | 0.0557 | 0.0678 | \ul0.0768 | \ul0.0920 | 0.0585 | 0.0627 |
| IHP | 0.2782 | 0.3380 | 0.2189 | 0.2351 | 0.1032 | 0.1319 | 0.0915 | 0.1005 | 0.0814 | 0.0980 | 0.0692 | 0.0738 |
| Improv. | 7.63% | 4.99% | 10.31% | 7.93% | 7.49% | 11.07% | 11.77% | 15.71% | 5.97% | 6.59% | 9.29% | 10.17% |
5. Experiment
5.1. Experimental Setup
5.1.1. Datasets
We conduct experiments on three real-world datasets: Goodreads-P, Goodreads-H, and Amazon. Goodreads is a publicly available large-scale dataset including information about online readers and books on their shelves (Wan et al., 2019). We regard online readers as the target nodes for the two Goodreads datasets. For Goodreads-P, poetry books are used as context nodes for pretraining, and comics are used as downstream context nodes. For Goodreads-H, history books and biographies are downstream context nodes, while pretraining context nodes contain books in the categories of children, young adults, mystery, thriller, and crime. For these two Goodreads datasets, we predict the link between readers and books. Amazon includes users and items purchased by them (Ni et al., 2019). Users are regarded as target nodes, and instruments are used as context nodes in the downstream task. For pretraining in Amazon, context nodes are items in the categories of arts, crafts, sewing, grocery, gourmet food, office products, electronics, sports, outdoors, toys, and games. For Amazon, we predict the link between users and items. The main statistics of the three datasets are summarized in Table 1. For downstream link prediction tasks in all the datasets, we split of edges for training and the remaining for testing.
5.1.2. Baselines
We regard users as target nodes and items as context nodes in all the datasets. Thus recommendation methods, including LightGCN (He et al., 2020), SGL (Wu et al., 2021), HCCF (Xia et al., 2022) and DHCF (Ji et al., 2020), are applied as strong baselines to prediction interactions between target and context nodes, besides baseline models designed for general graph tasks, such as DirectAU (Wang et al., 2022b) and GraphFormers (Yang et al., 2021). As a pretraining framework, we also compare IHP with the following pretraining baselines:
-
•
AttriMask (Hu et al., 2020b). This method applies GNN to obtained node embeddings and then adds a linear model to predict masked attributes during pretraining. We use node categories as the masked attributes, so it is not suitable for Goodreads-P where all pretraining nodes are comics.
-
•
GCC (Qiu et al., 2020). This self-supervised pretraining framework leverages contrastive learning with random walks to capture structure information in graphs.
-
•
GraphMAE (Hou et al., 2022). This method applies a masked graph autoencoder for generative self-supervised graph pretraining.
For the pretraining baselines, we use the same finetuning stage as IHP, which is shown in Figure 2(a), with no instructions and instruction prompting intensity .
5.1.3. Evaluation metric
We evaluate the pretraining framework by ranking the test context nodes with all non-interacted target nodes during finetuning. Recall and NDCG are adopted as evaluation metrics.
5.1.4. Implementations
For all the datasets, the pretraining learning rate is set to . The regularization parameter is set to 1e-7. The node embedding size is set to 64. The learning rate to finetune context nodes is set to 0.1 for the two Goodreads datasets, and 0.01 for Amazon. For the Goodreads-P/Goodreads-H/Amazon dataset, we set the number of PHC layers as 4/1/3, the prompting intensity in the target hypergraph as 1e-3/1e-4/1e-1, the prompting intensity in the context hypergraph as 1/1/1e-4, and the adaptation intensity as 1e-2/1e-3/10. We implement early stopping based on loss for pretraining and Recall@10 for finetuning. All the experiments are conducted on an 8GB RTX 2080. As Table 3 shows, the framework can be pretrained and finetuned within one minute for all the datasets, benefiting from the compact size of learnable parameters and the high efficiency. Our implementation is available at https://anonymous.4open.science/r/IHP-ECC8.
| Dataset | Goodreads-P | Goodreads-H | Amazon |
|---|---|---|---|
| Pretraining time (s) | 7.80 | 5.60 | 23.79 |
| Finetuning time (s) | 10.61 | 28.78 | 24.11 |
5.2. Performance on Link Prediction
We show the overall comparison of link prediction performance in Table 2. The best results are in boldface. We observe that the proposed IHP framework achieves the best results and outperforms all the baselines in the three datasets. We hypothesize these large and stable gains result from prior knowledge learned from pretraining under the explicit guidance of instructions. In addition, baseline pretraining frameworks achieve better performance than models without pretraining in Goodreads-P and Amazon. However, they are surpassed by other baselines in Goodreads-H. Since the pretrained edges in Goodreads-H are densest, and pretrained node types in it are fewer than in Amazon, the risk of overfitting for baseline pretraining frameworks is high in such a dataset. In contrast, instructions provide explicit information about certain tasks, which explains IHP’s better generalization and adaptation for the downstream task.
| Dataset | Goodreads-H | Amazon | ||
|---|---|---|---|---|
| Metric | Acc. | F1 | Acc. | F1 |
| DirectAU | 0.64494 | 0.64135 | 0.77066 | 0.77006 |
| HGNN | 0.64924 | 0.64566 | \ul0.77315 | \ul0.77302 |
| GraphFormers | 0.64412 | 0.64042 | 0.76871 | 0.77148 |
| AttriMask | \ul0.64951 | \ul0.64626 | 0.77298 | 0.77284 |
| GCC | 0.64949 | 0.64620 | 0.77284 | 0.77271 |
| GraphMAE | 0.64935 | 0.64610 | 0.77315 | 0.77301 |
| IHP | 0.64962 | 0.64641 | 0.77341 | 0.77328 |
5.3. Node Classification and Performance
We also evaluate IHP on node classification as the downstream task, optimized by cross-entropy loss (Good, 1952). Besides the previous baselines designed for general graph learning, HGNN (Feng et al., 2019) leveraging hypergraph convolution for classification is also used as a baseline. For Goodreads-H, books in the categories of children and young adults are pretraining context nodes, and history, biography, mystery, thriller and crime books are used in downstream classification. For Amazon, items in the categories of arts, crafts, sewing, grocery, gourmet food and office products are used for pretraining context nodes, and items in the categories of electronics, sports, outdoors, toys, games and instruments are used in downstream classification. We split of nodes for training and the remaining for testing. Accuracy and F1 scores are adopted as evaluation metrics. To prevent data leakage, we removed node category information from task descriptions in the instructions. The parameters remain the same as the settings for the link prediction.
The comparison is shown in Table 4. The performance verifies the efficacy of IHP in node classification tasks. The pretraining framework baselines have better performance than other baselines in most cases, which indicates that the node features can be accurately captured with the prior knowledge learned during pretraining. HGNN surpasses all other non-pretrained baselines, showing the benefit of modeling high-order relations by hypergraph learning. In addition, with inconsistency in pretraining and finetuning structures, pretrained baselines slightly degrade the downstream performance of hypergraph learning in Amazon, compared with HGNN. However, IHP with frozen prompt transformation maintains the consistency between pretraining and finetuning stages, and leverages instructions to offer information on downstream node features, which is a more comprehensive pretraining framework for node classification.
5.4. Ablation Study
| Dataset | Goodreads-P | Goodreads-H | Amazon | |||
|---|---|---|---|---|---|---|
| Metric | R@10 | N@10 | R@10 | N@10 | R@10 | N@10 |
| w/o PLM | 0.2717 | 0.1974 | 0.0944 | 0.0824 | 0.0545 | 0.0406 |
| Instructor (Su et al., 2023) | 0.2763 | 0.2225 | 0.1019 | 0.0905 | 0.0787 | 0.0662 |
| GTR (Ni et al., 2022) | 0.2764 | \ul0.2226 | 0.1020 | 0.0900 | 0.0793 | 0.0665 |
| S-BERT (Reimers and Gurevych, 2019) | \ul0.2765 | 0.2218 | \ul0.1024 | 0.0903 | 0.0831 | 0.0698 |
| E5 (Wang et al., 2022a) | 0.2764 | 0.2227 | 0.1023 | \ul0.0909 | 0.0808 | 0.0675 |
| MiniLM (Wang et al., 2020) | 0.2782 | 0.2189 | 0.1032 | 0.0915 | \ul0.0814 | \ul0.0692 |
5.4.1. PLMs as text encoders.
To quantify the contribution of PLMs as the text encoder in our framework, we compare the link prediction performance of IHP with different PLMs and without PLM in Table 5. For the variant of IHP without PLM, we randomly initialize the text embedding as the input of the prompt layer. It is apparent that employing PLM to encode instructions leads to significant enhancement in all the datasets. The results also imply that the benefits of different PLMs depend on the data distribution of the certain dataset. In IHP, we use MiniLM as the sentence encoder because of its stable performance in all the datasets.
5.4.2. Task information in Instructions.
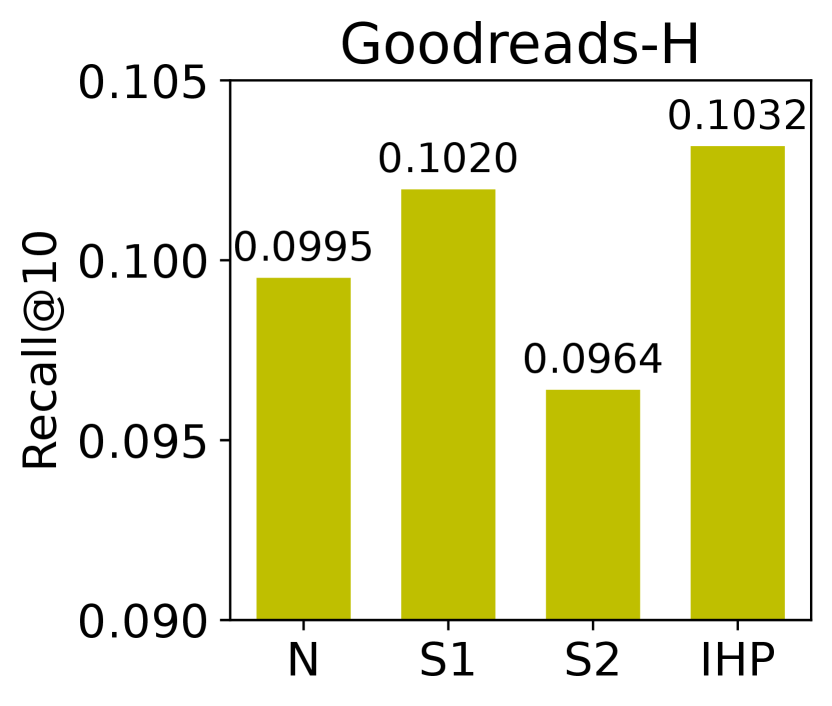
Besides node descriptions, the instructions in IHP also contain task descriptions (e.g., ”promote electronics to the reader”). In Figure 3, We demonstrate the performance of IHP with different ways of leveraging task information as a part of the instruction. In addition to concatenating node descriptions and task information for text encoding, we investigate three other variants of IHP: (N) Without text-based task information, only node descriptions are encoded as text embeddings and then concatenated to a learnable task vector for each task before prompt transformation; (S1) node descriptions and task information are encoded by the PLM separately, and then concatenated for prompt transformation; (S2) same as S1, but the encoded task embeddings skip both prompt transformation and hypergraph convolution. Instead, they are concatenated to corresponding node embeddings after PHC layers for the final prediction.
We observe that IHP performs the best on three datasets. This justifies the superiority of GTGS, which simultaneously encodes node and task information inside instructions. The poor performance of N verifies the limitation of learnable vectors compared to text-based task descriptions in instruction construction. S1 allows task information to participate in information propagation through PHC layers, which results in better performance than S2 in Goodreads datasets. When tasks become diverse in Amazon, S2 allocating task information to corresponding nodes can more accurately capture dependencies among nodes. However, separately encoding node descriptions and task information ignores the semantic connection between them, so both S1 and S2 are worse than IHP.


5.4.3. Instruction-based finetuning settings.
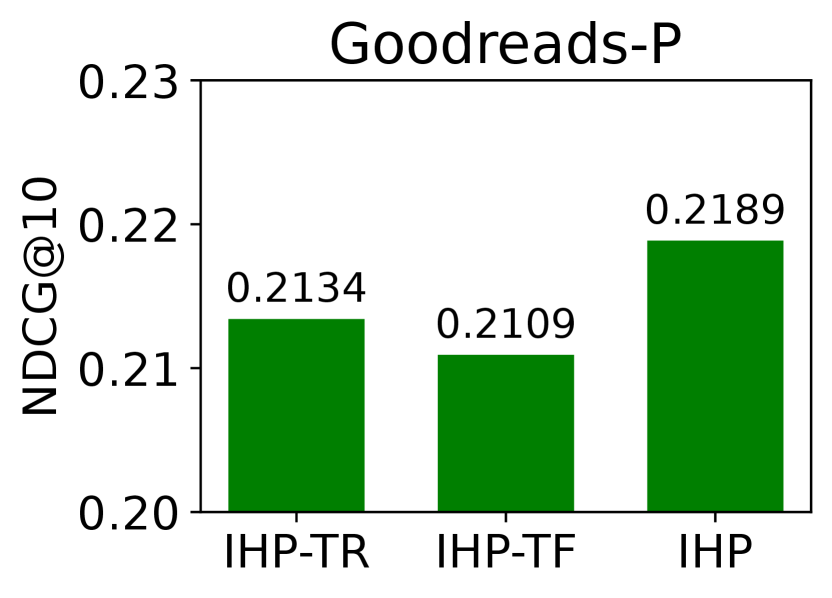
The prior knowledge is preserved in target node embeddings and parameters of prompt layer in the pretraining stage, and transferred to the downstream tasks. Hence, we conducted an ablation study to investigate the influence of different finetuning settings on downstream performance. For instruction-based finetuning in IHP, we freeze the prompt layer and update the target node embeddings with context node embeddings during downstream tasks. We compare IHP with the other four variants of finetuning settings: (i) IHP-TR with randomly initialized in finetuning; (ii) IHP-TF with pretrained frozen in finetuning; (iii) IHP-PR with randomly initialized in finetuning; (iv) IHP-PU with pretrained updated by the objective in finetuning.
The comparison between the performance of IHP and its variants in Figures 4 and 6 confirms the advantage of our instruction-based finetuning paradigm. Freezing target node embeddings reduces the flexibility and limits the adaptability to downstream data for the pretraining framework. This issue becomes more pronounced with the growing discrepancy between pretrained and downstream data. As shown in Figure 4, IHP-TF with frozen target node embeddings can hardly adapt to the downstream instrument data from the pretrained item data from diverse categories in Amazon. Additionally, updating the prompt layer scarcely improves the downstream performance, compared with using randomly initialized parameters in Figure 6. On the contrary, IHP with a frozen prompt layer maintains the consistency of the model’s response to instructions during pretraining and finetuning, and thus archives a better performance.










5.5. Inductive Learning Analysis
To validate the effectiveness of IHP in dynamically evolving graph structures, we add inductive target nodes which account for , , and of the original target nodes into Amazon, Goodreads-P, and Goodreads-H datasets. The embeddings of inductive nodes are never trained in either pretraining or finetuning stages. Instead, the inductive nodes are connected to other downstream training nodes by hyperedges defined in Section 4.2 and fed into IHP only for inference. Then, we evaluate the link prediction performance on those inductive nodes. In addition to the pretraining baselines (Hu et al., 2020b; Qiu et al., 2020; Hou et al., 2022), we also compare IHP with GraphSage (Hamilton et al., 2017) which is a general inductive graph learning method.
The results are demonstrated in Table 6. One can observe that IHP exhibits the best performance on inductive nodes in all the datasets, especially in larger Goodreads-H and Amazon datasets. With prior knowledge from abundant pretrained data in these two datasets, pretraining baselines always perform better than scratch-training GraphSage. Nonetheless, they are worse than IHP, which better captures dependencies between inductive and trained nodes by directly prompting text-based instruction to hyperedges.
| Dataset | Goodreads-P | Goodreads-H | Amazon | |||
|---|---|---|---|---|---|---|
| Metric | R@10 | N@10 | R@10 | N@10 | R@10 | N@10 |
| GraphSage | 0.2415 | \ul0.1988 | 0.0305 | 0.0210 | 0.0330 | 0.0166 |
| AttriMask | - | - | 0.0605 | 0.0489 | 0.0887 | 0.0505 |
| GCC | 0.2601 | 0.1960 | 0.0589 | 0.0483 | \ul0.0929 | \ul0.0520 |
| GraphMAE | \ul0.2620 | 0.1981 | \ul0.0606 | \ul0.0503 | 0.0869 | 0.0494 |
| IHP | 0.2622 | 0.2002 | 0.0998 | 0.0783 | 0.0939 | 0.0672 |
5.6. Adaptation Intensity Analysis
To maintain the balance between retaining prior knowledge and adapting for various downstream tasks, we deploy the adaptation intensity coefficient to differentiate the learning rates of target and context node embeddings during finetuning. We demonstrate the impact of this coefficient on three datasets in Figure 7. It becomes obvious that the performance is always suboptimal when the learning rates of target and context node embeddings remain the same, i.e., . For the two Goodreads datasets, a small prevents the framework from forgetting the prior knowledge during finetuning. For Amazon, a large is required to endow the model with the higher adaptivity to the downstream data.
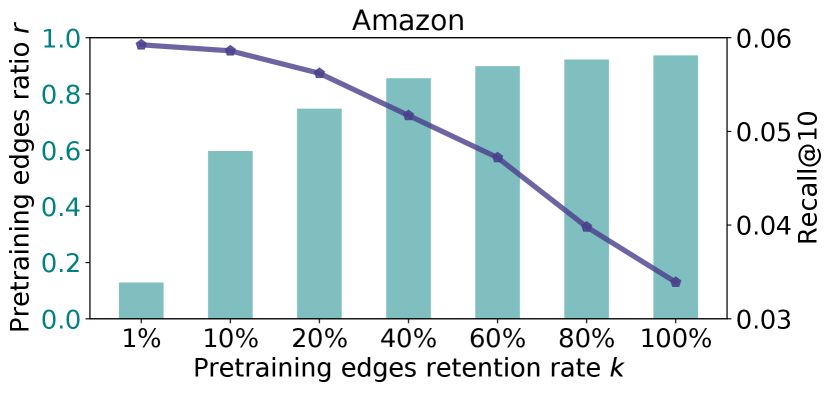
We believe the difference of in Goodreads and Amazon results from the discrepancy between the pretraining and downstream data in each dataset. For verification, we evaluate the model performance with the same learning rates of target and context nodes after merging the pretraining and downstream data. To be specific, we randomly select a subset of edges from the set of all the pretraining edges, add them to the downstream data, and then finetune the model with on the downstream tasks. In other words, the edges become for the downstream tasks. The proportion of the selected edges in all the pretrained edges is defined as pretraining edges retention rate . The ratio of these selected edges to all the downstream edges is denoted as pretraining edges ratio . Pretraining context nodes connected by are also added to the downstream task. In this way, the model is finetuned directly with the original pretraining data.
The results are demonstrated in Figure 5. In the two Goodreads datasets, We observe that the downstream performance is generally improved with the pretraining data added to the downstream task. In Amazon, on the contrary, the performance is degraded after adding the pretraining data when . The reason is that all the pretraining and downstream context nodes are books in Goodreads, so the discrepancy between the pretraining and downstream data in Goodreads is minor compared to the discrepancy in Amazon, where pretraining and downstream context nodes are items in more diverse categories. That explains why a small is necessary to prevent the framework from forgetting the prior knowledge in Goodreads, while a large can help the pretrain model faster adapt to the significantly different downstream data in Amazon.
6. conclusion
In this paper, we propose a novel graph pretraining framework IHP, which applies text-based instructions to overcome the discrepancy between pretraining and downstream tasks. In IHP, we construct hyperedges to capture high-order relations among nodes under the guidance of instructions, and a PHC layer is introduced to integrate instructions into context-aware information propagation in hypergraph learning. We conduct extensive experiments and detailed analyses on three real-world datasets to verify the effectiveness of IHP. In the future, further research is needed to evaluate the scalability and generalization of IHP on a broader range of datasets. With potential additional information in specific scenarios, hyperedges can be further customized (e.g., one hyperedge connecting all nodes with the same attribute) or used to connect arbitrary nodes as the objectives of an instruction. Given such flexibility of hypergraph construction, future studies could explore how to extend the IHP framework into multi-task pretraining, where different hypergraphs could be designed for diverse pretraining tasks.
7. acknowledgements
This work is supported in part by NSF under grant III-2106758.
References
- (1)
- Bai et al. (2021) Song Bai, Feihu Zhang, and Philip H. S. Torr. 2021. Hypergraph convolution and hypergraph attention. Pattern Recognit. 110 (2021), 107637. https://doi.org/10.1016/j.patcog.2020.107637
- Bodnar et al. (2022) Cristian Bodnar, Francesco Di Giovanni, Benjamin Paul Chamberlain, Pietro Lió, and Michael M. Bronstein. 2022. Neural Sheaf Diffusion: A Topological Perspective on Heterophily and Oversmoothing in GNNs. In NeurIPS. http://papers.nips.cc/paper_files/paper/2022/hash/75c45fca2aa416ada062b26cc4fb7641-Abstract-Conference.html
- Brown et al. (2020) Tom B. Brown, Benjamin Mann, Nick Ryder, Melanie Subbiah, Jared Kaplan, Prafulla Dhariwal, Arvind Neelakantan, Pranav Shyam, Girish Sastry, Amanda Askell, Sandhini Agarwal, Ariel Herbert-Voss, Gretchen Krueger, Tom Henighan, Rewon Child, Aditya Ramesh, Daniel M. Ziegler, Jeffrey Wu, Clemens Winter, Christopher Hesse, Mark Chen, Eric Sigler, Mateusz Litwin, Scott Gray, Benjamin Chess, Jack Clark, Christopher Berner, Sam McCandlish, Alec Radford, Ilya Sutskever, and Dario Amodei. 2020. Language Models are Few-Shot Learners. In Advances in Neural Information Processing Systems 33: Annual Conference on Neural Information Processing Systems 2020, NeurIPS 2020, December 6-12, 2020, virtual, Hugo Larochelle, Marc’Aurelio Ranzato, Raia Hadsell, Maria-Florina Balcan, and Hsuan-Tien Lin (Eds.). https://proceedings.neurips.cc/paper/2020/hash/1457c0d6bfcb4967418bfb8ac142f64a-Abstract.html
- Feige et al. (2015) Uriel Feige, Michal Feldman, Nicole Immorlica, Rani Izsak, Brendan Lucier, and Vasilis Syrgkanis. 2015. A Unifying Hierarchy of Valuations with Complements and Substitutes. In Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence, January 25-30, 2015, Austin, Texas, USA, Blai Bonet and Sven Koenig (Eds.). AAAI Press, 872–878. https://doi.org/10.1609/AAAI.V29I1.9314
- Feng et al. (2019) Yifan Feng, Haoxuan You, Zizhao Zhang, Rongrong Ji, and Yue Gao. 2019. Hypergraph Neural Networks. In The Thirty-Third AAAI Conference on Artificial Intelligence, AAAI 2019, The Thirty-First Innovative Applications of Artificial Intelligence Conference, IAAI 2019, The Ninth AAAI Symposium on Educational Advances in Artificial Intelligence, EAAI 2019, Honolulu, Hawaii, USA, January 27 - February 1, 2019. AAAI Press, 3558–3565. https://doi.org/10.1609/aaai.v33i01.33013558
- Good (1952) I. J. Good. 1952. Rational Decisions. Journal of the Royal Statistical Society. Series B (Methodological) 14, 1 (1952), 107–114. http://www.jstor.org/stable/2984087
- Hamilton et al. (2017) William L. Hamilton, Rex Ying, and Jure Leskovec. 2017. Inductive Representation Learning on Large Graphs (NIPS’17). Curran Associates Inc., Red Hook, NY, USA, 1025–1035.
- He et al. (2020) Xiangnan He, Kuan Deng, Xiang Wang, Yan Li, YongDong Zhang, and Meng Wang. 2020. LightGCN: Simplifying and Powering Graph Convolution Network for Recommendation. Association for Computing Machinery, New York, NY, USA, 639–648.
- Hou et al. (2022) Zhenyu Hou, Xiao Liu, Yukuo Cen, Yuxiao Dong, Hongxia Yang, Chunjie Wang, and Jie Tang. 2022. GraphMAE: Self-Supervised Masked Graph Autoencoders. In KDD ’22: The 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, August 14 - 18, 2022, Aidong Zhang and Huzefa Rangwala (Eds.). ACM, 594–604. https://doi.org/10.1145/3534678.3539321
- Hu et al. (2020b) Weihua Hu, Bowen Liu, Joseph Gomes, Marinka Zitnik, Percy Liang, Vijay S. Pande, and Jure Leskovec. 2020b. Strategies for Pre-training Graph Neural Networks. In 8th International Conference on Learning Representations, ICLR 2020, Addis Ababa, Ethiopia, April 26-30, 2020. OpenReview.net. https://openreview.net/forum?id=HJlWWJSFDH
- Hu et al. (2020a) Ziniu Hu, Yuxiao Dong, Kuansan Wang, Kai-Wei Chang, and Yizhou Sun. 2020a. GPT-GNN: Generative Pre-Training of Graph Neural Networks. In KDD ’20: The 26th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Virtual Event, CA, USA, August 23-27, 2020, Rajesh Gupta, Yan Liu, Jiliang Tang, and B. Aditya Prakash (Eds.). ACM, 1857–1867. https://doi.org/10.1145/3394486.3403237
- Ji et al. (2020) Shuyi Ji, Yifan Feng, Rongrong Ji, Xibin Zhao, Wanwan Tang, and Yue Gao. 2020. Dual Channel Hypergraph Collaborative Filtering. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (Virtual Event, CA, USA) (KDD ’20). Association for Computing Machinery, New York, NY, USA, 2020–2029. https://doi.org/10.1145/3394486.3403253
- Jia et al. (2021) Renqi Jia, Xiaofei Zhou, Linhua Dong, and Shirui Pan. 2021. Hypergraph Convolutional Network for Group Recommendation. In IEEE International Conference on Data Mining, ICDM 2021, Auckland, New Zealand, December 7-10, 2021, James Bailey, Pauli Miettinen, Yun Sing Koh, Dacheng Tao, and Xindong Wu (Eds.). IEEE, 260–269. https://doi.org/10.1109/ICDM51629.2021.00036
- Jiang et al. (2021) Xunqiang Jiang, Tianrui Jia, Yuan Fang, Chuan Shi, Zhe Lin, and Hui Wang. 2021. Pre-training on Large-Scale Heterogeneous Graph. In KDD ’21: The 27th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Virtual Event, Singapore, August 14-18, 2021, Feida Zhu, Beng Chin Ooi, and Chunyan Miao (Eds.). ACM, 756–766. https://doi.org/10.1145/3447548.3467396
- Jin et al. (2023a) Bowen Jin, Yu Zhang, Yu Meng, and Jiawei Han. 2023a. Edgeformers: Graph-Empowered Transformers for Representation Learning on Textual-Edge Networks. In The Eleventh International Conference on Learning Representations, ICLR 2023, Kigali, Rwanda, May 1-5, 2023. OpenReview.net. https://openreview.net/pdf?id=2YQrqe4RNv
- Jin et al. (2023b) Bowen Jin, Yu Zhang, Qi Zhu, and Jiawei Han. 2023b. Heterformer: Transformer-Based Deep Node Representation Learning on Heterogeneous Text-Rich Networks. In Proceedings of the 29th ACM SIGKDD Conference on Knowledge Discovery and Data Mining (¡conf-loc¿, ¡city¿Long Beach¡/city¿, ¡state¿CA¡/state¿, ¡country¿USA¡/country¿, ¡/conf-loc¿) (KDD ’23). Association for Computing Machinery, New York, NY, USA, 1020–1031. https://doi.org/10.1145/3580305.3599376
- Jin et al. (2021) Di Jin, Xiangchen Song, Zhizhi Yu, Ziyang Liu, Heling Zhang, Zhaomeng Cheng, and Jiawei Han. 2021. BiTe-GCN: A New GCN Architecture via Bidirectional Convolution of Topology and Features on Text-Rich Networks (WSDM ’21). Association for Computing Machinery, New York, NY, USA, 157–165. https://doi.org/10.1145/3437963.3441774
- Keriven (2022) Nicolas Keriven. 2022. Not too little, not too much: a theoretical analysis of graph (over)smoothing. In NeurIPS. http://papers.nips.cc/paper_files/paper/2022/hash/0f956ca6f667c62e0f71511773c86a59-Abstract-Conference.html
- Kingma and Ba (2015) Diederik P. Kingma and Jimmy Ba. 2015. Adam: A Method for Stochastic Optimization. In 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, May 7-9, 2015, Conference Track Proceedings.
- Kipf and Welling (2017) Thomas N. Kipf and Max Welling. 2017. Semi-Supervised Classification with Graph Convolutional Networks. In 5th International Conference on Learning Representations, ICLR 2017, Toulon, France, April 24-26, 2017, Conference Track Proceedings.
- Li et al. (2021) Chaozhuo Li, Bochen Pang, Yuming Liu, Hao Sun, Zheng Liu, Xing Xie, Tianqi Yang, Yanling Cui, Liangjie Zhang, and Qi Zhang. 2021. AdsGNN: Behavior-Graph Augmented Relevance Modeling in Sponsored Search. In Proceedings of the 44th International ACM SIGIR Conference on Research and Development in Information Retrieval (Virtual Event, Canada) (SIGIR ’21). Association for Computing Machinery, New York, NY, USA, 223–232. https://doi.org/10.1145/3404835.3462926
- Liu et al. (2023b) Pengfei Liu, Weizhe Yuan, Jinlan Fu, Zhengbao Jiang, Hiroaki Hayashi, and Graham Neubig. 2023b. Pre-Train, Prompt, and Predict: A Systematic Survey of Prompting Methods in Natural Language Processing. ACM Comput. Surv. 55, 9, Article 195 (jan 2023), 35 pages. https://doi.org/10.1145/3560815
- Liu et al. (2023a) Zemin Liu, Xingtong Yu, Yuan Fang, and Xinming Zhang. 2023a. GraphPrompt: Unifying Pre-Training and Downstream Tasks for Graph Neural Networks. In Proceedings of the ACM Web Conference 2023 (Austin, TX, USA) (WWW ’23). Association for Computing Machinery, New York, NY, USA, 417–428. https://doi.org/10.1145/3543507.3583386
- Lu et al. (2021) Yuanfu Lu, Xunqiang Jiang, Yuan Fang, and Chuan Shi. 2021. Learning to Pre-train Graph Neural Networks. In Thirty-Fifth AAAI Conference on Artificial Intelligence, AAAI 2021, Thirty-Third Conference on Innovative Applications of Artificial Intelligence, IAAI 2021, The Eleventh Symposium on Educational Advances in Artificial Intelligence, EAAI 2021, Virtual Event, February 2-9, 2021. AAAI Press, 4276–4284. https://ojs.aaai.org/index.php/AAAI/article/view/16552
- Lung et al. (2018) Rodica Ioana Lung, Noémi Gaskó, and Mihai Alexandru Suciu. 2018. A hypergraph model for representing scientific output. Scientometrics 117, 3 (2018), 1361–1379. https://doi.org/10.1007/S11192-018-2908-2
- Ni et al. (2019) Jianmo Ni, Jiacheng Li, and Julian McAuley. 2019. Justifying Recommendations using Distantly-Labeled Reviews and Fine-Grained Aspects. In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP), Kentaro Inui, Jing Jiang, Vincent Ng, and Xiaojun Wan (Eds.). Association for Computational Linguistics, Hong Kong, China, 188–197. https://doi.org/10.18653/v1/D19-1018
- Ni et al. (2022) Jianmo Ni, Chen Qu, Jing Lu, Zhuyun Dai, Gustavo Hernandez Abrego, Ji Ma, Vincent Zhao, Yi Luan, Keith Hall, Ming-Wei Chang, and Yinfei Yang. 2022. Large Dual Encoders Are Generalizable Retrievers. In Proceedings of the 2022 Conference on Empirical Methods in Natural Language Processing, Yoav Goldberg, Zornitsa Kozareva, and Yue Zhang (Eds.). Association for Computational Linguistics, Abu Dhabi, United Arab Emirates, 9844–9855. https://doi.org/10.18653/v1/2022.emnlp-main.669
- Qiu et al. (2020) Jiezhong Qiu, Qibin Chen, Yuxiao Dong, Jing Zhang, Hongxia Yang, Ming Ding, Kuansan Wang, and Jie Tang. 2020. GCC: Graph Contrastive Coding for Graph Neural Network Pre-Training. In KDD ’20: The 26th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Virtual Event, CA, USA, August 23-27, 2020, Rajesh Gupta, Yan Liu, Jiliang Tang, and B. Aditya Prakash (Eds.). ACM, 1150–1160. https://doi.org/10.1145/3394486.3403168
- Reimers and Gurevych (2019) Nils Reimers and Iryna Gurevych. 2019. Sentence-BERT: Sentence Embeddings using Siamese BERT-Networks. In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing, EMNLP-IJCNLP 2019, Hong Kong, China, November 3-7, 2019, Kentaro Inui, Jing Jiang, Vincent Ng, and Xiaojun Wan (Eds.). Association for Computational Linguistics, 3980–3990. https://doi.org/10.18653/v1/D19-1410
- Rendle et al. (2009) Steffen Rendle, Christoph Freudenthaler, Zeno Gantner, and Lars Schmidt-Thieme. 2009. BPR: Bayesian Personalized Ranking from Implicit Feedback. In Proceedings of the Twenty-Fifth Conference on Uncertainty in Artificial Intelligence (Montreal, Quebec, Canada) (UAI ’09). AUAI Press, Arlington, Virginia, USA, 452–461.
- Saifuddin et al. (2023) Khaled Mohammed Saifuddin, Corey May, Farhan Tanvir, Muhammad Ifte Khairul Islam, and Esra Akbas. 2023. Seq-HyGAN: Sequence Classification via Hypergraph Attention Network. In Proceedings of the 32nd ACM International Conference on Information and Knowledge Management, CIKM 2023, Birmingham, United Kingdom, October 21-25, 2023, Ingo Frommholz, Frank Hopfgartner, Mark Lee, Michael Oakes, Mounia Lalmas, Min Zhang, and Rodrygo L. T. Santos (Eds.). ACM, 2167–2177. https://doi.org/10.1145/3583780.3615057
- Su et al. (2023) Hongjin Su, Weijia Shi, Jungo Kasai, Yizhong Wang, Yushi Hu, Mari Ostendorf, Wen-tau Yih, Noah A. Smith, Luke Zettlemoyer, and Tao Yu. 2023. One Embedder, Any Task: Instruction-Finetuned Text Embeddings. In Findings of the Association for Computational Linguistics: ACL 2023, Anna Rogers, Jordan Boyd-Graber, and Naoaki Okazaki (Eds.). Association for Computational Linguistics, Toronto, Canada, 1102–1121. https://doi.org/10.18653/v1/2023.findings-acl.71
- Sun et al. (2022) Mingchen Sun, Kaixiong Zhou, Xin He, Ying Wang, and Xin Wang. 2022. GPPT: Graph Pre-training and Prompt Tuning to Generalize Graph Neural Networks. In KDD ’22: The 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, August 14 - 18, 2022, Aidong Zhang and Huzefa Rangwala (Eds.). ACM, 1717–1727. https://doi.org/10.1145/3534678.3539249
- Sun et al. (2023) Xiangguo Sun, Hong Cheng, Jia Li, Bo Liu, and Jihong Guan. 2023. All in One: Multi-Task Prompting for Graph Neural Networks. In Proceedings of the 29th ACM SIGKDD Conference on Knowledge Discovery and Data Mining (¡conf-loc¿, ¡city¿Long Beach¡/city¿, ¡state¿CA¡/state¿, ¡country¿USA¡/country¿, ¡/conf-loc¿) (KDD ’23). Association for Computing Machinery, New York, NY, USA, 2120–2131. https://doi.org/10.1145/3580305.3599256
- Tang et al. (2023) Jiabin Tang, Yuhao Yang, Wei Wei, Lei Shi, Lixin Su, Suqi Cheng, Dawei Yin, and Chao Huang. 2023. GraphGPT: Graph Instruction Tuning for Large Language Models. CoRR abs/2310.13023 (2023). https://doi.org/10.48550/ARXIV.2310.13023 arXiv:2310.13023
- Wan et al. (2019) Mengting Wan, Rishabh Misra, Ndapa Nakashole, and Julian J. McAuley. 2019. Fine-Grained Spoiler Detection from Large-Scale Review Corpora. In Proceedings of the 57th Conference of the Association for Computational Linguistics, ACL 2019, Florence, Italy, July 28- August 2, 2019, Volume 1: Long Papers, Anna Korhonen, David R. Traum, and Lluís Màrquez (Eds.). Association for Computational Linguistics, 2605–2610. https://doi.org/10.18653/V1/P19-1248
- Wang et al. (2022b) Chenyang Wang, Yuanqing Yu, Weizhi Ma, Min Zhang, Chong Chen, Yiqun Liu, and Shaoping Ma. 2022b. Towards Representation Alignment and Uniformity in Collaborative Filtering. In KDD ’22: The 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, August 14 - 18, 2022, Aidong Zhang and Huzefa Rangwala (Eds.). ACM, 1816–1825. https://doi.org/10.1145/3534678.3539253
- Wang et al. (2022a) Liang Wang, Nan Yang, Xiaolong Huang, Binxing Jiao, Linjun Yang, Daxin Jiang, Rangan Majumder, and Furu Wei. 2022a. Text Embeddings by Weakly-Supervised Contrastive Pre-training. CoRR abs/2212.03533 (2022). https://doi.org/10.48550/ARXIV.2212.03533 arXiv:2212.03533
- Wang et al. (2021) Liyuan Wang, Mingtian Zhang, Zhongfan Jia, Qian Li, Chenglong Bao, Kaisheng Ma, Jun Zhu, and Yi Zhong. 2021. AFEC: Active Forgetting of Negative Transfer in Continual Learning. In Advances in Neural Information Processing Systems 34: Annual Conference on Neural Information Processing Systems 2021, NeurIPS 2021, December 6-14, 2021, virtual, Marc’Aurelio Ranzato, Alina Beygelzimer, Yann N. Dauphin, Percy Liang, and Jennifer Wortman Vaughan (Eds.). 22379–22391. https://proceedings.neurips.cc/paper/2021/hash/bc6dc48b743dc5d013b1abaebd2faed2-Abstract.html
- Wang et al. (2020) Wenhui Wang, Furu Wei, Li Dong, Hangbo Bao, Nan Yang, and Ming Zhou. 2020. MINILM: Deep Self-Attention Distillation for Task-Agnostic Compression of Pre-Trained Transformers. In Proceedings of the 34th International Conference on Neural Information Processing Systems (Vancouver, BC, Canada) (NIPS’20). Curran Associates Inc., Red Hook, NY, USA, Article 485, 13 pages.
- Wu et al. (2021) Jiancan Wu, Xiang Wang, Fuli Feng, Xiangnan He, Liang Chen, Jianxun Lian, and Xing Xie. 2021. Self-Supervised Graph Learning for Recommendation. In Proceedings of the 44th International ACM SIGIR Conference on Research and Development in Information Retrieval (Virtual Event, Canada) (SIGIR ’21). Association for Computing Machinery, New York, NY, USA, 726–735. https://doi.org/10.1145/3404835.3462862
- Xia et al. (2022) Lianghao Xia, Chao Huang, Yong Xu, Jiashu Zhao, Dawei Yin, and Jimmy X. Huang. 2022. Hypergraph Contrastive Collaborative Filtering. In SIGIR ’22: The 45th International ACM SIGIR Conference on Research and Development in Information Retrieval, Madrid, Spain, July 11 - 15, 2022, Enrique Amigó, Pablo Castells, Julio Gonzalo, Ben Carterette, J. Shane Culpepper, and Gabriella Kazai (Eds.). ACM, 70–79. https://doi.org/10.1145/3477495.3532058
- Yang et al. (2021) Junhan Yang, Zheng Liu, Shitao Xiao, Chaozhuo Li, Defu Lian, Sanjay Agrawal, Amit Singh, Guangzhong Sun, and Xing Xie. 2021. GraphFormers: GNN-nested Transformers for Representation Learning on Textual Graph. In Advances in Neural Information Processing Systems, M. Ranzato, A. Beygelzimer, Y. Dauphin, P.S. Liang, and J. Wortman Vaughan (Eds.), Vol. 34. Curran Associates, Inc., 28798–28810. https://proceedings.neurips.cc/paper_files/paper/2021/file/f18a6d1cde4b205199de8729a6637b42-Paper.pdf
- Yu et al. (2021) Junliang Yu, Hongzhi Yin, Jundong Li, Qinyong Wang, Nguyen Quoc Viet Hung, and Xiangliang Zhang. 2021. Self-Supervised Multi-Channel Hypergraph Convolutional Network for Social Recommendation. In WWW ’21: The Web Conference 2021, Virtual Event / Ljubljana, Slovenia, April 19-23, 2021, Jure Leskovec, Marko Grobelnik, Marc Najork, Jie Tang, and Leila Zia (Eds.). ACM / IW3C2, 413–424. https://doi.org/10.1145/3442381.3449844
- Zhang et al. (2019) Chuxu Zhang, Ananthram Swami, and Nitesh V. Chawla. 2019. SHNE: Representation Learning for Semantic-Associated Heterogeneous Networks. In Proceedings of the Twelfth ACM International Conference on Web Search and Data Mining (Melbourne VIC, Australia) (WSDM ’19). Association for Computing Machinery, New York, NY, USA, 690–698. https://doi.org/10.1145/3289600.3291001
- Zhou et al. (2006) Dengyong Zhou, Jiayuan Huang, and Bernhard Schölkopf. 2006. Learning with Hypergraphs: Clustering, Classification, and Embedding. In Advances in Neural Information Processing Systems 19, Proceedings of the Twentieth Annual Conference on Neural Information Processing Systems, Vancouver, British Columbia, Canada, December 4-7, 2006, Bernhard Schölkopf, John C. Platt, and Thomas Hofmann (Eds.). MIT Press, 1601–1608. https://proceedings.neurips.cc/paper/2006/hash/dff8e9c2ac33381546d96deea9922999-Abstract.html
- Zhou and Cao (2021) Fan Zhou and Chengtai Cao. 2021. Overcoming Catastrophic Forgetting in Graph Neural Networks with Experience Replay. In Thirty-Fifth AAAI Conference on Artificial Intelligence, AAAI 2021, Thirty-Third Conference on Innovative Applications of Artificial Intelligence, IAAI 2021, The Eleventh Symposium on Educational Advances in Artificial Intelligence, EAAI 2021, Virtual Event, February 2-9, 2021. AAAI Press, 4714–4722. https://doi.org/10.1609/AAAI.V35I5.16602
- Zhu et al. (2021) Jason Zhu, Yanling Cui, Yuming Liu, Hao Sun, Xue Li, Markus Pelger, Tianqi Yang, Liangjie Zhang, Ruofei Zhang, and Huasha Zhao. 2021. TextGNN: Improving Text Encoder via Graph Neural Network in Sponsored Search (WWW ’21). Association for Computing Machinery, New York, NY, USA, 2848–2857. https://doi.org/10.1145/3442381.3449842